人教高二数学选修4 教案--第13课时 几个著名的不等式之——排序不等式
高中数学人教B版选修4-5教学案第二章 2.2 排序不等式

.排序不等式[读教材·填要点].顺序和、乱序和、反序和的概念设≤≤≤…≤,≤≤≤…≤是两组实数,,,,…,为,,…,的任何一个排列,称++…+),称顺序和为这两个实数组的顺序积之和(简称+-+…+),称反序和为这两个实数组的反序积之和(简称 ++…+).乱序和为这两个实数组的乱序积之和(简称.排序原理…+-+,的任一排列,则有…,是,,…数,,,为两组实≤≤…≤,≤≤…≤设.+…++≤+…++≤+等号成立⇔==…=或==…=.顺序和.≤乱序和≤反序和排序原理可简记作:[小问题·大思维].排序不等式的本质含义是什么?提示:排序不等式的本质含义是:两实数序列同方向单调(同时增或同时减)时所得两两乘积之和最大,反方向单调(一增一减)时所得两两乘积之和最小,注意等号成立条件是其中一序列为常数序列..已知两组数≤≤≤≤,≤≤≤≤,其中=,=,=,=,=,=,=,=,=,=,将(=)重新排列记为,,,,,则++…+的最大值和最小值分别为何值?提示:由顺序和最大知 最大值为:++++=,由反序和最小知最小值为:++++=.[例]已知,,为正数,≥≥,求证:()≥≥;()++≥++.[思路点拨]本题考查排序不等式的直接应用,解答本题需要分析式子结构,然后通过对比、联想公式,构造数组,利用公式求解.[精解详析]()∵≥>,于是≤,又>,∴>.从而≥.同理,∵≥>,于是≤,∵>,∴>,于是得≥.从而≥≥.()由()≥≥,于是由顺序和≥乱序和得,++≥++=++≥++=++=++.利用排序不等式证明不等式的关键是构造出不等式中所需要的带大小顺序的两个数组,由于本题已知≥≥,所以可直接利用已知构造两个数组..设,,为正数,求证:++≥++.证明:不妨设≥≥>,则≥≥,≥≥>,∴由顺序和≥乱序和,得++≥++=++.①又∵≥≥,≥≥,∴由乱序和≥反序和得:++≥++=++,②由①②两式得:++≥++.[例]设>,求证:+++…+≥(+).[思路点拨]本题考查排序不等式的应用.解答本题需要注意:题目中只给出了>,但对。
人教版高中选修4-5第三讲柯西不等式与排序不等式教学设计

人教版高中选修4-5第三讲柯西不等式与排序不等式教学设计一、教学目标1.理解柯西不等式和排序不等式的概念和基本性质。
2.能够应用柯西不等式和排序不等式解决实际问题。
3.培养学生的数学思维能力、解决问题的能力和团队协作精神。
二、教学内容1.柯西不等式的定义和证明。
2.柯西不等式及其应用。
3.排序不等式的定义和证明。
4.排序不等式及其应用。
三、教学重点和难点1.理解柯西不等式和排序不等式的定义和基本性质。
2.掌握柯西不等式的证明方法,理解其应用。
3.熟练掌握排序不等式的证明方法,能够应用排序不等式解决实际问题。
四、教学方法和手段1.教师引导学生自主发现和探究柯西不等式和排序不等式。
2.采用运用举例的方法,引导学生理解和记忆柯西不等式和排序不等式,提高学生举一反三的能力。
3.推崇探究式学习方法,鼓励学生主动探究,组织学生研究、合作探讨,提升学生的团队合作能力。
五、教学流程1.柯西不等式的引入通过真实生活中的例子,引出两个变量之间的关系,小组探究两正数之积的最大值、两负数之积的最大值、正数与负数之积的最小值。
教授柯西不等式的定义和证明。
2.柯西不等式的应用通过计算题目,引出使用柯西不等式求出积分值最大值的方法,题目的复杂程度逐渐加深,教授柯西不等式在解题中的应用。
3.排序不等式引入介绍排序不等式的定义和证明过程,并从生活中的例子引出排序不等式的应用场景。
4.排序不等式的应用通过计算题目,引导学生掌握人教版高中选修4-5第三讲柯西不等式与排序不等式的解题方法,解决实际问题。
六、教学评价1.通过出题考核,检测学生掌握柯西不等式和排序不等式的基础知识和应用能力。
2.通过实际应用问题,检验学生对柯西不等式和排序不等式的理解和应用能力。
七、小组探究设计在小组合作过程中,让学生组织实验、调查等自主探究柯西不等式和排序不等式。
小组探究产生的报告可作为课后作业,让学生进行总结和讨论。
最后,本课程旨在为学生提供基本数学知识和运用能力,建立实际生活场景与知识的联系。
高二数学(人教版)选修4-5教案:第13课时 几个著名的不等式之——排序不等式
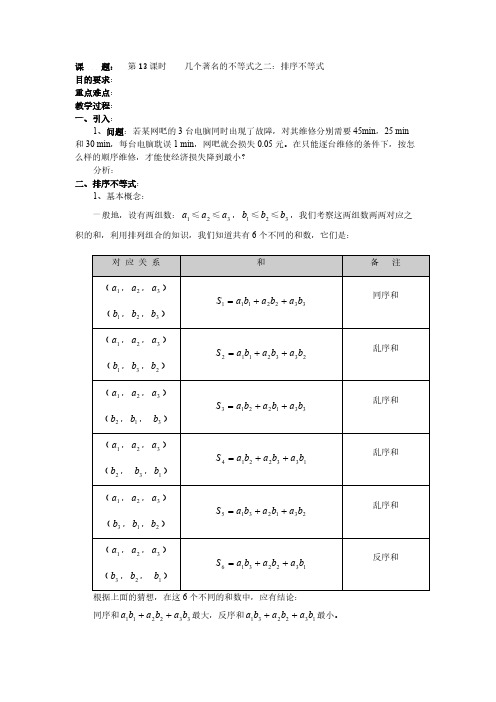
1、基本概念:
一般地,设有两组数: a1 ≤ a2 ≤ a3 , b1 ≤ b2 ≤ b3 ,我们考察这两组数两两对应之
积的和,利用排列组合的知识,我们知道共有 6 个不同的和数,它们是:
对应关系
和
备注
( a1 , a2 , a3 ) ( b1 , b2 , b3 )
S1 a1b1 a2b2 a3b3
5、若 a1,a2,…,an
为两两不等的正整数,求证: n ak k2
k 1
பைடு நூலகம்
n1
.
k 1 k
6、若
x1,x2,…,xn≥0,x1+x2+…+xn≤
1 2
,则
(1
x1 )(1
x2
)L
(1 xn )
1
.
2
反序时最小,即:
a1b1 a2b2 L anbn a1c1 a2c2 L ancn a1bn a2bn1 L anb1 , 等号当且仅当 a1 a2 L an 或 b1 b2 L bn 时成立。
分析:用逐步调整法
四、小结:
五、练习:
六、作业:
1、求证: a 2 b2 c 2 d 2 ab bc cd da 。
一般地,设有两组实数: a1 , a2 , a3 ,…, an 与 b1 , b2 , b3 ,…, bn ,且它们满
足:
a1 ≤ a2 ≤ a3 ≤…≤ an , b1 ≤ b2 ≤ b3 ≤…≤ bn ,
若 c1 , c2 , c3 ,…, cn 是 b1 , b2 , b3 ,…, bn 的任意一个排列,则和数 a1c1 a2c2 L ancn 在 a1 , a2 , a3 ,…, an 与 b1 , b2 , b3 ,…, bn 同序时最大,
高中数学 第三讲 柯西不等式与排序不等式 3.3 排序不等式教案 新人教A版选修4-5-新人教A版高

3.3排序不等式一、教学目标1.了解排序不等式的数学思想和背景.2.理解排序不等式的结构与基本原理,会用排序不等式解决简单的不等式问题.二、课时安排1课时三、教学重点1.了解排序不等式的数学思想和背景.2.理解排序不等式的结构与基本原理,会用排序不等式解决简单的不等式问题.四、教学难点1.了解排序不等式的数学思想和背景.2.理解排序不等式的结构与基本原理,会用排序不等式解决简单的不等式问题.五、教学过程(一)导入新课某班学生要开联欢会,需要买价格不同的礼品4件,5件和2件.现在选择商店中单价分别为3元,2元和1元的礼品,则至少要花________元,最多要花________元.【解析】取两组实数(2,4,5)和(1,2,3),则顺序和为2×1+4×2+5×3=25,反序和为2×3+4×2+5×1=19.所以最少花费为19元,最多花费为25元.【答案】19 25(二)讲授新课教材整理1 顺序和、乱序和、反序和的概念设a1≤a2≤a3≤…≤a n,b1≤b2≤b3≤…≤b n为两组实数,c1,c2,…,是b1,b2,…,b n 的任一排列,则称a i与b i(i=1,2,…,n)的相同顺序相乘所得积的和为顺序和,和为乱序和,相反顺序相乘所得积的和称为反序和.教材整理2 排序不等式设a1≤a2≤…≤a n,b1≤b2≤…≤b n为两组实数,c1,c2,…,是b1,b2,…,b n的任一排列,则≤≤,当且仅当a1=a2=…=a n或b1=b2=…=b n时,反序和等于顺序和,此不等式简记为≤≤顺序和.(三)重难点精讲题型一、用排序不等式证明不等式(字母大小已定)例1已知a ,b ,c 为正数,a ≥b ≥c ,求证:(1)1bc ≥1ca ≥1ab; (2)a 2b 2c 2+b 2c 2a 2+c 2a 2b 2≥1a 2+1b 2+1c 2. 【精彩点拨】 由于题目条件中已明确a ≥b ≥c ,故可以直接构造两个数组.【自主解答】 (1)∵a ≥b >0,于是1a ≤1b. 又c >0,∴1c >0,从而1bc ≥1ca, 同理,∵b ≥c >0,于是1b ≤1c ,∴a >0,∴1a >0,于是得1ca ≥1ab, 从而1bc ≥1ca ≥1ab. (2)由(1)知1bc ≥1ca ≥1ab>0且a ≥b ≥c >0, ∴1b 2c 2≥1c 2a 2≥1a 2b 2,a 2≥b 2≥c 2. 由排序不等式,顺序和≥乱序和得a 2b 2c 2+b 2c 2a 2+c 2a 2b 2≥b 2b 2c 2+c 2c 2a 2+a 2a 2b 2=1c 2+1a 2+1b 2=1a 2+1b 2+1c 2, 故a 2b 2c 2+b 2c 2a 2+c 2a 2b 2≥1a 2+1b 2+1c 2. 规律总结:利用排序不等式证明不等式的技巧在于仔细观察、分析所要证明的式子的结构,从而正确地构造出不等式中所需要的带有大小顺序的两个数组.[再练一题]1.本例题中条件不变,求证:a 5b 3c 3+b 5c 3a 3+c 5a 3b 3≥c 2a 3+a 2b 3+b 2c 3. 【证明】 ∵a ≥b ≥c ≥0,∴a 5≥b 5≥c 5,1c ≥1b ≥1a >0.∴1bc ≥1ac ≥1ba, ∴1b 3c 3≥1a 3c 3≥1b 3a 3,由顺序和≥乱序和得a 5b 3c 3+b 5a 3c 3+c 5b 3a 3≥b 5b 3c 3+c 5a 3c 3+a 5b 3a 3=b 2c 3+c 2a 3+a 2b 3, ∴a 5b 3c 3+b 5a 3c 3+c 5b 3a 3≥c 2a 3+a 2b 3+b 2c 3. 题型二、字母大小顺序不定的不等式证明例2设a ,b ,c 为正数,求证:a 2+b 22c +b 2+c 22a +c 2+a 22b ≤a 3bc +b 3ca +c 3ab. 【精彩点拨】 (1)题目涉及到与排序有关的不等式;(2)题目中没有给出a ,b ,c 的大小顺序.解答本题时不妨先设定a ≤b ≤c ,再利用排序不等式加以证明.【自主解答】 不妨设0<a ≤b ≤c ,则a 3≤b 3≤c 3,0<1bc ≤1ca ≤1ab ,由排序原理:乱序和≤顺序和,得a 3·1ca +b 3·1ab +c 3·1bc ≤a 3·1bc +b 3·1ca +c 3·1ab, a 3·1ab +b 3·1bc +c 3·1ca ≤a 3·1bc +b 3·1ca +c 3·1ab. 将上面两式相加得a 2+b 2c +b 2+c 2a +c 2+a 2b ≤2⎝ ⎛⎭⎪⎫a 3bc +b 3ca +c 3ab , 将不等式两边除以2,得a 2+b 22c +b 2+c 22a +c 2+a 22b ≤a 3bc +b 3ca +c 3ab. 规律总结:在排序不等式的条件中需要限定各数值的大小关系,对于没有给出大小关系的情况:(1)要根据各字母在不等式中地位的对称性,限定一种大小关系.(2)若给出的字母不具有对称性,一定不能直接限定字母的大小顺序,而要根据具体环境分类讨论.2.设a 1,a 2,…,a n 为正数,求证:a 21a 2+a 22a 3+…+a 2n -1a n +a 2n a 1≥a 1+a 2+…+a n . 【证明】 不妨设0<a 1≤a 2≤…≤a n ,则a 21≤a 22≤…≤a 2n ,1a 1≥1a 2≥…≥1a n . 由排序不等式知,乱序和不小于反序和,所以a 21a 2+a 22a 3+…+a 2n -1a n +a 2n a 1≥a 21·1a 1+a 22·1a 2+…+a 2n ·1a n,即 a 21a 2+a 22a 3+…+a 2n -1a n +a 2n a 1≥a 1+a 2+…+a n . 题型三、利用排序不等式求最值例3 设A ,B ,C 表示△ABC 的三个内角,a ,b ,c 表示其对边,求aA +bB +cC a +b +c的最小值(A ,B ,C 用弧度制表示).【精彩点拨】 不妨设a ≥b ≥c >0,设法构造数组,利用排序不等式求解.【自主解答】 不妨设a ≥b ≥c ,则A ≥B ≥C .由排序不等式,得 aA +bB +cC =aA +bB +cC ,aA +bB +cC ≥bA +cB +aC ,aA +bB +cC ≥cA +aB +bC ,将以上三式相加,得3(aA +bB +cC )≥(a +b +c )·(A +B +C )=π(a +b +c ),当且仅当A =B =C =π3时,等号成立. ∴aA +bB +cC a +b +c ≥π3, 即aA +bB +cC a +b +c 的最小值为π3. 规律总结:1.分析待求函数的结构特征,构造两个有序数组.2.运用排序原理求最值时,一定要验证等号是否成立,若等号不成立,则取不到最值.3.已知x ,y ,z 是正数,且x +y +z =1,求t =x 2y +y 2z +z 2x的最小值. 【解】 不妨设x ≥y ≥z >0,则x 2≥y 2≥z 2,1z ≥1y ≥1x. 由排序不等式,乱序和≥反序和. x 2y +y 2z +z 2x≥x 2·1x +y 2·1y +z 2·1z=x +y +z .又x +y +z =1,x 2y +y 2z +z 2x≥1, 当且仅当x =y =z =13时,等号成立. 故t =x 2y +y 2z +z 2x的最小值为1. 题型四、利用排序不等式求解简单的实际问题例4 若某网吧的3台电脑同时出现了故障,对其维修分别需要45 min,25 min 和30 min ,每台电脑耽误1 min ,网吧就会损失0.05元.在只能逐台维修的条件下,按怎样的顺序维修,才能使经济损失降到最小?【精彩点拨】 这是一个实际问题,需要转化为数学问题.要使经济损失降到最小,即三台电脑维修的时间与等候的总时间之和最小,又知道若维修第一台用时间t 1 min 时,三台电脑等候维修的总时间为3t 1 min ,依此类推,等候的总时间为3t 1+2t 2+t 3 min ,求其最小值即可.【自主解答】 设t 1,t 2,t 3为25,30,45的任一排列,由排序原理知3t 1+2t 2+t 3≥3×25+2×30+45=180(min),所以按照维修时间由小到大的顺序维修,可使经济损失降到最小.规律总结:1.首先理解题意,实际问题数学化,建立恰当模型.2.三台电脑的维修时间3t 1+2t 2+t 3就是问题的数学模型,从而转化为求最小值(运用排序原理).[再练一题]4.有5个人各拿一只水桶到水龙头接水,如果水龙头注满这5个人的水桶需要时间分别是4 min,8 min,6 min,10 min,5 min ,那么如何安排这5个人接水的顺序,才能使他们等待的总时间最少?【解】 根据排序不等式的反序和最小,可得最少时间为4×5+5×4+6×3+8×2+10×1=84(min).即按注满时间为4 min,5 min,6 min,8 min,10 min 依次等水,等待的总时间最少.(四)归纳小结排序不等式—⎪⎪⎪—反序和、乱序和、顺序和—排序原理—排序原理的应用(五)随堂检测1.已知x ≥y ,M =x 4+y 4,N =x 3y +y 3x ,则M 与N 的大小关系是( ) A .M >N B .M ≥N C .M <N D.M ≤N 【解析】 由排序不等式,知M ≥N . 【答案】 B 2.设a ,b ,c 为正数,P =a 3+b 3+c 3,Q =a 2b +b 2c +c 2a ,则P 与Q 的大小关系是( )A .P >QB .P ≥QC .P <Q D.P ≤Q【答案】 B3.已知两组数1,2,3和4,5,6,若c 1,c 2,c 3是4,5,6的一个排列,则c 1+2c 2+3c 3的最大值是________,最小值是________.【解析】 由排序不等式,顺序和最大,反序和最小,∴最大值为1×4+2×5+3×6=32,最小值为1×6+2×5+3×4=28.【答案】 32 28六、板书设计七、作业布置八、教学反思。
高二数学选修4-5 几个著名的不等式之一:柯西不等式

高二数学选修4-5 几个著名的不等式之一:柯西不等式目的要求: 重点难点: 教学过程: 一、引入:除了前面已经介绍的贝努利不等式外,本节还将讨论柯西不等式、排序不等式、平均不等式等著名不等式。
这些不等式不仅形式优美、应用广泛,而且也是进一步学习数学的重要工具。
1、什么是柯西不等式:定理1:(柯西不等式的代数形式)设d c b a ,,,均为实数,则22222)())((bd ac d c b a +≥++,其中等号当且仅当bc ad =时成立。
证明:几何意义:设α,β为平面上以原点O 为起点的两个非零向量,它们的终点分别为A (b a ,),B (d c ,),那么它们的数量积为bd ac +=•βα, 而22||b a +=α,22||d c +=β,所以柯西不等式的几何意义就是:||||||βαβα•≥⋅,其中等号当且仅当两个向量方向相同或相反(即两个向量共线)时成立。
2、定理2:(柯西不等式的向量形式)设α,β为平面上的两个向量,则||||||βαβα•≥⋅,其中等号当且仅当两个向量方向相同或相反(即两个向量共线)时成立。
3、定理3:(三角形不等式)设332211,,,,,y x y x y x 为任意实数,则: 分析:思考:三角形不等式中等号成立的条件是什么?4、定理4:(柯西不等式的推广形式):设n 为大于1的自然数,ii b a ,(=i 1,2,…,n )为任意实数,则:211212)(∑∑∑===≥ni i i ni in i i b a ba ,其中等号当且仅当nn a b a b a b === 2211时成立(当0=i a 时,约定0=i b ,=i 1,2,…,n )。
证明:构造二次函数:2222211)()()()(n n b x a b x a b x a x f -++-+-=即构造了一个二次函数:∑∑∑===+-=ni i n i i i ni ib x b a x ax f 121212)(2)()(由于对任意实数x ,0)(≥x f 恒成立,则其0≤∆, 即:0))((4)(4121221≤-=∆∑∑∑===ni i n i i ni i i b a b a ,即:))(()(121221∑∑∑===≤ni i ni i n i i i b a b a ,等号当且仅当02211=-==-=-n n b x a b x a b x a ,即等号当且仅当nn a b a b a b === 2211时成立(当0=i a 时,约定0=i b ,=i 1,2,…,n )。
人教版高中数学选修4-5《§3.3排序不等式》

§3.3排序不等式
经典不等式
基本不等式(均值不等式)
ab (1)a, b R , ab 当且仅当a b时“ ”成立 2 abc (2)a, b, c R , abc 当且仅当"a b c "时 2 ? ”成立 a1 a2 ... an (3)a1 , a2 ,....an R , n a1.a2 ...an 当且仅 n 当"a1 a2 ...an "时“ ”成立
如果数大一点呢? 探究 2.已知两组数 1 , 2, 3 和 45,25,30,若 c1 , c2 , c3 是 45 ,25,30 的一个排列,则 1c1 2c2 3c3 的最 大值是_____,最小值是_____.
对 应 关 系 ( 1,2,3) ( 25,30,45) ( 1,2,3) ( 25,45,30) ( 1,2,3) ( 30,25,45) ( 1,2,3) ( 30,45,25) ( 1,2,3) ( 45,25,30) ( 1,2,3) ( 45,30,25)
§3.3排序不等式
学习目标
知识目标 1、掌握排序不等式的基本内容
2、会初步运用排序不等式解决简单问题
3、了解“逐步调整比较法”证明不等式的基本思路 能力目标 培养由特殊事物发现一般规律进而证明一般规律的能力
探究与猜想
探究 1:已知两组数 1,2,3 和 4,5,6, c1 , c2 , c3 是 4,5,6 的一个排列,则 1c1 2c2 3c3 的 28 32 最小值是_____. 最大值是 _____,
人教版高中选修4-5第三讲柯西不等式与排序不等式课程设计

人教版高中选修4-5第三讲柯西不等式与排序不等式课程设计
一、课程目标
1.1 掌握柯西不等式的概念及其意义;
1.2 学会在实际问题中应用柯西不等式;
1.3 掌握排序不等式的概念及应用;
1.4 学会在实际问题中应用排序不等式。
二、教学内容
2.1 柯西不等式的概念与应用;
2.2 排序不等式的概念与应用;
2.3 利用柯西不等式、排序不等式解决实际问题。
三、教学重点与难点
3.1 教学重点:柯西不等式、排序不等式的概念及应用。
3.2 教学难点:如何在实际问题中应用柯西不等式、排序不等式。
四、教学过程设计
教学环节教学内容教学目标与要
求
教师活动与学生活动
1。
2017-2018年人教A版选修4-5排序不等式教案

2017-2018年人教A 版选修4-5 排序不等式 教案本节主要内容有排序不等式、琴生不等式、幂平均不等式、切比雪夫不等式及应用.排序不等式(又称排序定理):给定两组实数a 1,a 2,……,a n ;b 1,b 2,……,b n .假设a 1≤a 2≤……≤a n ;b 1≤b 2≤……≤b n .那么a 1b n +a 2b n -1+……+a n b 1(反序和)≤a 11i b +a 22ib +……+a n n i b (乱序和)≤a 1b 1+a 2b 2+……+a n b n (同序和),其中i 1,i 2,……,i n 是1,2,……,n 的一个排列.该不等式所表达的意义是和式∑=nj i j jba 1在同序和反序时分别取得最大值和最小值.切比雪夫不等式:设有两个有序数组a 1≤a 2≤……≤a n ;b 1≤b 2≤……≤b n .则1n(a 1b n+a 2b n -1+……+a n b 1)≤a 1+a 2+……+a n n ·b 1+b 2+……+b n n ≤1n(a 1b 1+a 2b 2+……+a nb n ),其中等号仅当a 1=a 2=……=a n 或b 1=b 2=……=b n 时取得.琴生不等式又称凸函数不等式,它建立在凸函数的基础上.定义 设连续函数f (x )的定义域是[a ,b ] (开区间(a ,b )或(-∞,+∞)上均可),假设对于区间[a ,b ]内的任意两点x 1,x 2有f (x 1+x 22 )≤12[f (x 1)+f (x 2)],则称f (x )为[a ,b ]上的下凸函数.如图(1)定理一.若f (x )是下凸函数,则对其定义域中的任意几个点x 1,x 2,……,x n ,恒有f (x 1+x 2+……+x n n )≤1n[f (x 1)+f (x 2)+……+f (x n )].定义 设连续函数f (x )的定义域是[a ,b ](开区间(a ,b )或(-∞,+∞)上均可),假设对于区间[a ,b ]内的任意两点x 1,x 2有f (x 1+x 22 )≥12[f (x 1)+f (x 2)],则称f (x )为[a ,b ]上的下凸函数.如图(2)定理二:若)(x f 是上凸函数,则对其定义域中的任意n 个点n x x x ,...,,21恒有)](...)()([1)...(2121n n x f x f x f n n x x x f +++≥+++,容易验证x x x f 21log ,tan )(=分x 1 x 2 M (1) x 1x 2M (2)别是),0(),2,0(+∞π上的下凸函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课 题: 第13课时 几个著名的不等式之二:排序不等式 目的要求: 重点难点: 教学过程: 一、引入:
1、问题:若某网吧的3台电脑同时出现了故障,对其维修分别需要45min ,25 min 和30 min ,每台电脑耽误1 min ,网吧就会损失0.05元。
在只能逐台维修的条件下,按怎么样的顺序维修,才能使经济损失降到最小?
分析: 二、排序不等式:
1、基本概念:
一般地,设有两组数:1a ≤2a ≤3a ,1b ≤2b ≤3b ,我们考察这两组数两两对应之积的和,利用排列组合的知识,我们知道共有6个不同的和数,它们是:
b 同序和33221
1b a b a b a ++最大,反序和132231b a b a b a ++最小。
2、对引例的验证:。
