一次函数的应用第一课时
《一次函数的应用》一次函数PPT教学课件(第1课时)

(2)已知某“快递小哥”的日收入不少于110元,则他至少要派送多少件?
答案
7.【解析】 (1)设y与x之间的函数关系式为y=kx+b,
将点(0,70),(30,100)代入,得
= 70,
= 1,
解得
30 + = 100,
的表达式为
.
答案
4.y=x+2 【解析】 设该一次函数的表达式为y=kx+b,易知点B的坐标为(-1,1),由一次函数的图象经过点A(0,2),
且与正比例函数y=-x的图象交于点B(-1,1),可得
2 = ,
= 2,
解得
所以该一次函数的表达式为 y=x+2.
1 = − + ,
= 1,
知识点 2
2
1
综上,直线l对应的函数表达式为y=-2x或y=- x.
2
3
3
2
2
y=0,则x=- ,所以点P的坐标为(- ,0).故选C.
3.[2018陕西西安铁一中月考]已知一次函数y=kx+b,当0≤x≤2时,对应的函数值y的取值范围是-2≤y≤4,则kb的值为
(
)
A.12
B.-6
C.6或12
D.-6或-12
答案
3.D 【解析】 分两种情况:(1)当k>0时,y随x的增大而增大,所以当x=0时,y=-2,当x=2时,y=4,分别代入一次函数
答案
5.【解析】 (1)设直线l对应的函数表达式为y=kx+b,
因为直线l与直线y=-x平行,
所以k=-1,所以y=-x+b,
鲁教版七年级上册6.5 一次函数的应用(第一课时)

随堂练习 课本163页为了提高某种农作物的产量,农场通常采
用喷施药物的方法控制其高度,已知该农作物的平均高度
y(米)与每公顷所喷施药物的质
量 x(千克)之间的关系如图所示,
经验表明,该种农作物高度在
1.25 米左右时它的产量最高,此
时每公顷应喷施药物多少千克? 解:仔细观察图形可知直线过(0,1.5),(10,0.5)两点
图2
干旱造成的灾情
由于持续高温和连日无雨,某水库的蓄水量随着时间
的增加而减少.干旱持续时间 t( 天)与蓄水量V(万立方
米 ) 的关系如图所示,
V/万米3
想一想
(1).水库干旱前的蓄水量是多少? (2).干旱持续10天,蓄水量为多少?
连续干旱23天呢?
(3).蓄水量小于400 万立方米时,将发生
10-8=2
(3)将y=1代入上式 解得 x=450
(1).一箱汽油可供摩托车行驶多少 千米? (2). 摩托车每行驶100千米消耗多 少升? (3). 油箱中的剩余油量小于1升时 将自动报警.行驶多少千米后,摩托 车将自动报警?
总结:如何解答实际情景函数图象的信息?
1:理解横纵坐标分别表示的的实际意义
t/天
例1 某种摩托车的油箱最多可储油10升,加满油 后,油箱中的剩余油量y(升)与摩托车行驶路程 x(千米)之间的关系如图所示(:1).一箱汽油可供摩托车行驶多
少千米?
(2). 摩托车每行驶100千米消耗 多少升? (3). 油箱中的剩余油量小于1升 时将自动报警.行驶多少千米后, 摩托车将自动报警?
当y=1时,x=450,因此行驶了450千米后,摩托车将 自动报警.
(450,1)
还有其他方法做吗?
北师大版八年级数学上册一次函数的应用教学课件(第一课时24张)

解:(1)设使用会员卡租书金额y1(元)与租书时间x(天)之间的关系式为y1=kx+b. 从图象可知它过(0,20),可得b=20,将(10,50),代入关系式得k=3.∴y1= 3x+20.设使用租书卡租书金额y2(元)与租书时间x(天)之间的关系式为y2=mx. 它经过(10,50),代入得10m=50,m=5.∴y2=5x (2)会员卡方式每天收费(50-20)÷10=3(元),租书卡方式每天收费5元
二 确定一次函数的表达式
例2:已知一次函数的图象经过(0,5)、(2,-5)两点,求一次函 数的表达式.
解:设一次函数的表达式为y=kx+b,根据题意得, ∴-5=2k+b,5=b, 解得b=5,k=-5. ∴一次函数的表达式为y=-5x+5.
练一练
已知直线l与直线y=-2x平行,且与y轴交于点(0,2),求直线l 的表达式.
(1)设出式子中的未知系数;
将已知数据代入 (2)
;
(3) 求出未知系数的值 ;
(4) 写出一次函数表达式 .
1.正比例函数 y=kx 的图象如右图所示,则这个函数的表达式是(B ) A.y=x B.y=-x C.y=-2x
D.y=-12x
2.如图,一次函数的图象过点A,且与正比例函数y=-x的图象交于点B, 则该一次函数的表达式为( ) B
解:由题易得一次函数为 y=x+2,当 y=0 时,x+2=0, x=-2,∴C(-2,0),∴S△AOC=12×2×4=4
11.某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用 租书卡,使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如下 图所示:
(1)分别写出用租书卡和会员卡租书金额y(元)与租书时间x(天)之间的关系式 ;
一次函数的应用(1).ppt[上学期]--浙教版(201910)
![一次函数的应用(1).ppt[上学期]--浙教版(201910)](https://img.taocdn.com/s3/m/00ab5229fe4733687f21aa1e.png)
57 t(h)
例4:某市出租车计费方法如图所示,请根据图象回答下
面的问题:
5元
3km
(1)出租车的起步价是多少元?在多少路程内只收起步价?
(2)用恰当的方式表示费用y与 路程s之间的关系。
y费用(元)
(3)起步价里程走完之后, 9
每行驶1km需多少车费?
(4)某外地客人坐出租车游
5
览本市,车费为31元,试求 出他乘车的里程。
例2:生物学家测得7条成熟的雄性鲸的全长y和吻尖到 喷水孔的长度x的数据如下表(单位:米)
吻尖到喷水
孔的长度 1.78 1.91 2.06 2.32 2.59 2.82 2.95
x(m)
全长y(m) 10.00 10.25 10.72 11.52 12.50 13.16 13.90
问能否用一次函数刻画两个变量的关系?如果能,请求 出这个一次函数的解析式。
7.5一次函数的应用(1)
在日常生活和生产劳动中,有不少问题 的数量关系可以用一次函数来刻画。在运用 一次函数解决实际问题时:
首先,判断问题中的两个变量之间是 不是一次函数关系;
如确定是一次函数关系时,可求出解析式;
再运用一次函数的图象和性质进一步 求得我们需要的结果。
例1:经实验检测,不同气温下声音传播的速度如下表所示
例3 :沙尘暴发生后,经过开阔荒漠时加速,经过乡镇、 遇到防护林则减速,最终停止。某气象研究所观察一场 沙尘暴从发生到结束的全过程,记录了风速y(km/h) 随着时间t(h)变化的图象(如图)。
(1)求沙尘暴的最大风速;
(2)用恰当的方法表示
y(km/h)
沙尘暴风速与时间之间 32
的关系。 8
0 4 10 25
初二数学(北京版)一次函数的应用(第一课时)1教案
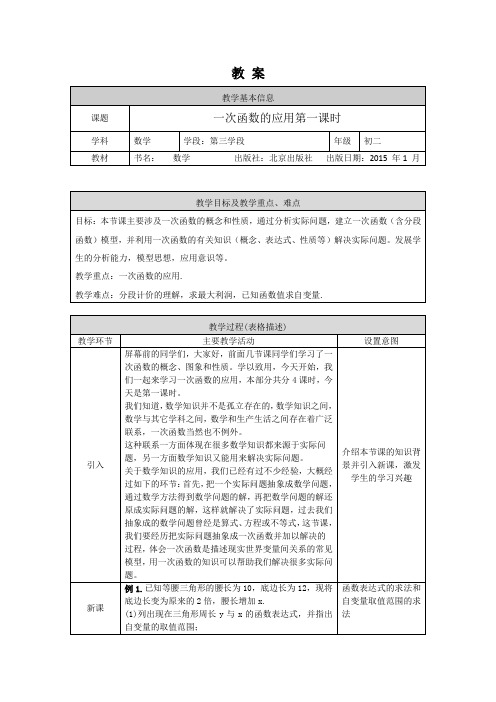
教案(2)求当x为何值时,周长y变为原来的3倍.解:(1)y=12×2+(10+x)×2.化简得y=2x+44. 自变量的取值范围是x>2(2)依题意得,y=32×3=96,把y=96代入y=2x+44得2x+44=96.解得x=26.答:当x=26时,周长变为原来的3倍。
小结:1.首先要理清实际问题的数量关系,根据数量关系求函数表达式。
2.在实际问题中,字母所表示的变量有实际背景,要使实际问题有意义,这些变量往往有限制条件,我们要找到这些限制条件,并通过这些限制条件求自变量的取值范围;3.通过例1可以看出,函数和方程有着密切联系,函数问题往往可以转化为方程问题进行求解。
事实上,当已知一次函数的自变量或因变量时,函数表达式就是一个例2.某生产资料门市部出售化肥,每袋售价80元.为了促进销售,规定了优惠办法:买3袋按售价计算,从第4袋开始,每袋优惠5%.(1)写出购买这种化肥的总金额M(元)与购买袋数n 的函数表达式,并指出它的自变量的取值范围;(2)为了快速得到购买这种化肥的总金额,利用这个函数的表达式制作一个购买1~10袋化肥的总金额对照表.解(1):当0≤n≤3时,函数的表达式为 M=80n.自变量n的取值范围是0≤n≤3且n是整数当n≥4时,函数的表达式为M=76n+12.自变量n的取值范围是n≥4且n是整数(2)小结:1.分段(计价)问题要分段处理;2.要写出每段中自变量的取值范围;3.对于给定自变量的值要判断在哪一段,在哪一段,就用这一段对应的函数表达式解决.思考:如果给定的是函数值呢?练习 1.北京居民用水价按家庭年用水量计算,标准如下:第一阶梯上限180立方米,水费价格为5元/立方米;第二阶梯为180以上至260立方米,水费价格为7元/立方米;分段计价问题的分析方法和分段函数的应用阶梯水价问题的理解和分段函数的应用。
《一次函数的应用》一次函数PPT优质课件(第1课时)

《一次函数的应用》一次函数PPT优质课件(第1课时)北师大版八年级数学上册《一次函数的应用》一次函数PPT优质课件(第1课时),共23页。
素养目标1.理解待定系数法的意义.2.学会运用待定系数法和数形结合思想求一次函数解析式.探究新知待定系数法求一次函数的解析式某物体沿一个斜坡下滑,它的速度 v (米/秒)与其下滑时间t (秒)的关系如右图所示:(1)请写出 v 与 t 的关系式;(2)下滑3秒时物体的速度是多少?解:(1)设v=kt,因为(2,5)在图象上,所以5=2k,k=2.5,即v=2.5t.(2) v=7.5 米/秒像这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法,叫做待定系数法.求一次函数解析式的步骤:(1)设:设一次函数的一般形式y=kx+b(k≠0)(2)列:把图象上的点(x1y1),(x2y2)代入一次函数的解析式,组成几个_________方程;(3)解:解几个一次方程得k,b;(4)还原:把k,b的值代入一次函数的解析式.已知两点利用待定系数法求一次函数的解析式例1 一次函数图像经过点(2,0)和点(0,6),写出函数解析式.解:设这个一次函数的解析式为y=kx+b.把点(2,0)与(0,6)分别代入y=kx+b,得:这个一次函数的解析式为y=-3x+6.已知一点利用待定系数法求一次函数的解析式例2 若一次函数的图象经过点 A(2,0)且与直线y=-x+3平行,求其解析式.解:设这个一次函数的解析式为y=kx+b.因为一次函数图象与直线y= -x+3平行,所以k= -1.又因为直线过点(2,0),所以0=-1某2+b, 解得b=2,所以解析式为y=-x+2.课堂小结用待定系数法求一次函数的解析式1. 设所求的一次函数解析式为y=kx+b(k≠0);2. 根据已知条件列出关于k,b的方程;3. 解方程,求出k,b;4. 把求出的k,b代回解析式即可.... ... ...关键词:一次函数的应用PPT课件免费下载,一次函数PPT下载,.PPTX 格式;。
一次函数的应用第一课时.1 一次函数的应用(第1课时) 教学设计

第四章一次函数4. 一次函数的应用(第1课时)大方县第五中学张刚一、学生起点分析本节课之前,学生已初步掌握了函数的概念、一次函数的图象及性质,并了解了函数的三种表达方式:图象法、列表法、解析式法。
在此基础上引导学生根据图象等信息列出一次函数表达式的方法,并进一步感受数形结合的思想方法.二、教学目标分析①了解两个条件可确定一次函数;能根据所给信息(图象、表格、实际问题等)利用待定系数法确定一次函数的表达式;并能利用所学知识解决简单的实际问题.②经历对正比例函数及一次函数表达式的探求过程,掌握用待定系数法求一次函数的表达式,进一步发展数形结合的思想方法;③经历从不同信息中获取一次函数表达式的过程,体会到解决问题的多样性,拓展学生的思维.三、教学重难点教学重点:确定一次函数的表达式教学难点:应用一次函数四、教学准备PPT、多媒体等等五、教学方法合作探究六、教学过程设计本节课设计了六个教学环节:本节课设计了六个教学环节:第一环节:复习引入;第二环节:初步探究;第三环节:深入探究;第四环节:反馈练习与知识拓展;第五环节:课时小结;第六环节:作业布置.第一环节复习引入内容:提问:(1)什么是一次函数?(2)一次函数的图象是什么?(3)一次函数具有什么性质?目的:学生回顾一次函数相关知识,温故而知新.第二环节初步探究内容1:展示实际情境提供两个问题情境,供老师选用.实际情境一:某物体沿一个斜坡下滑,它的速度v(米/秒)与其下滑时间t(秒 )的关系如图所示.(1)写出v与t之间的关系式;(2)下滑3秒时物体的速度是多少?分析:要求v与t之间的关系式,首先应观察图象,确定函数的类型,然后根据函数的类型设它对应的解析式,再把已知点的坐标代入解析式求出待定系数即可.内容2:想一想:确定正比例函数的表达式需要几个条件?确定一次函数的表达式呢?目的:在实践的基础上学生加以归纳总结。
这个问题涉及到数学对象的一个本质概念——基本量.由于一次函数有两个基本量k、b,所以需要两个条件来确定.第三环节深入探究内容1:例1如图所示,已知直线AB和x轴交于点B,和y轴交于点A①写出AB两点的坐标②求直线AB的表达式在弹性限度内,弹簧的长度y (厘米)是所挂物体的质量x (千克)的一次函数,一根弹簧不挂物体时长14.5cm ;当所挂物体的质量为3kg 时,弹簧长16cm 。
一次函数的应用课件

热学
在热学中,描述温度随时间变化 的规律时,一次函数经常被使用 。例如,当物体被加热或冷却时 ,其温度变化率往往是一次函数
。
电学
在电学中,电流、电压和电阻之 间的关系也可以用一次函数来表 示。通过这些关系,可以计算出
电流、电压和电阻的值。
日常生活中的应用
购物
在购物时,一次函数可以用来计算购物后的总花费。例如, 如果一件商品的价格随着购买数量的增加而增加,那么这个 价格和数量之间的关系就可以用一次函数来表示。
二次函数在金融、经济、工程等领域 应用较多,如投资、贷款、工程设计 等。
05 一次函数与不等式的关系
通过图像解不等式
01
函数图像与x轴的关系
当函数值大于0时,函数图像位于x轴上方;当函数值小于0时,函数图
像位于x轴下方。
02
函数图像与y轴的关系
当自变量为0时,函数值即为y轴截距,正数表示函数值大于0,负数表
在物理学中,一次函数可 以用来描述物体的运动规 律,例如速度、加速度和 时间之间的关系。
自然科学中的应用
化学反应速率
化学反应的速率可以用一次函数表示 ,描述反应物浓度和反应速率之间的 关系。
细胞生长
在生物学中,一次函数可以用来描述 细胞生长过程中细胞数量和时间之间 的关系。
1.谢谢聆 听
单调性判断
根据斜率正负和函数图像升降规律判断单调性,当函数图 像向上倾斜时,函数单调递增;当函数图像向下倾斜时, 函数单调递减。
单调性与函数最值关系
单调性决定了函数在区间上的最值,单调递增函数在区间 上取得最小值,单调递减函数在区间上取得最大值。
03 一次函数的应用
解析几何中的应用
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:设y=kx+b(k≠0)由题意,得
14.5=b, 16=3k+b.
课题课时第一课时
教学补充
·导学目标:
教学目标:进一步体会数形结合的思想,发展数形结合解决问题的能力。
教学重难点:利用一次函数图像分析、解决简单实际问题。
·导学过程:
1、自主学习:
1.什么是一次函数?
若两个变量x,y间的关系式可以表示成y=kx+b(k,b为常数,k≠0)的形式,则称y是x的一次函数.
∵l与直线y=-2x平行,
∴k= -2
又直线过点(0,2).
∴2=-2×0+b.
∴b=2
∴原直线为y=-2x+2.
·导学小结:
本节课主要运用一次函数解决一些简单实际问题,从学生练习情况来看,大部分学生学得很好。
2.一次函数的图象是什么?
1条直线
那怎样去确定一次函数的表达式呢?
二、合作探究:
某物体沿一个斜坡下滑,它的速度v(m/s)与其下滑时间t(s)的关系如右图所示:图略
解:设v=kt;
∵(2,5)在函数图象上
∴5=2k
∴k=2.5
∴v=2.5t
当t=3时,v=2.5×3=7.5(m/s)
确定正比例函数的表达式需要几个条件?
解得:b=14.5,k=0.5.
所以,在弹性限度内,y=0.5x+14.5.
当x=4时,y=0.5×4+14.5=16.5(cm).
即物体的质量为4kg时,弹簧长度为16.5cm.
3、学生展示:
随堂练习P89
4、巩固训练:
已知直线l与直线y=-2x平行,且与y轴交于点(0,2),求直线l的解析式.解:设直线l为y=kx+b,
