大学物理与实验(I)2时间空间与运动学
大学物理第二章第二部分

变力问题的处理方法(1)力随时间变化:F =f (t )在直角坐标系下,以x方向为例,由牛顿第二定律:()x dv m f t dt=且:t =t 0时,v x =v 0 ;x =x 0则:1()x dv f t dt m =直接积分得:1()()x x v dv f t dt mv t c===+∫∫其中c由初条件确定。
由速度求积分可得到运动学方程:2()x x v dt x t c ==+∫其中c 2由初条件确定。
例:飞机着陆时受到的阻力为F=-ct(c为常数)且t=0时,v=v 0。
求:飞机着陆时的速度。
解:根据牛顿第二定律:-ct =m dv / dt212c v dv tdt mc t c m==−=−+∫∫当t =0时,v =v 0,代入得:v 0=c 1202c v v t m=−(2)力随速度变化:F=f(v)直角坐标系中,x 方向f (v )=m dv ⁄dt 经过移项可得:()dv dt m f v =等式两边同时积分得:01()()m t t dt dv m dv f v f v −===∫∫∫具体给出f(v)的函数试就可进行积分运算例:质量为m的物体以速度v 0投入粘性流体中,受到阻力f=-cv (c为常数)而减速,若物体不受其它力,求:物体的运动速度。
解:根据牛顿第二定律:dv cv m dt−=移项变换:-c/m dt =dv/v 1ln c dv dt m vc t v c m−=−=+∫∫积分得由初条件定c 1:当t =0时,v =v 0∴0=lnv 0+c 1∴c 1=-lnv 00ln c t mc v t m v v v e −−==(3)力随位移变化:F =f (x)直角坐标系中,x方向:()dv dx dv dv f x m m mv dt dt dx dx===经过移项可得:f (x )dx =mv dv等式两边同时积分得:2201()()2f x dx mvdv m v v ==−∫∫例:光滑的桌面上一质量为M,长为L的匀质链条,有极小一段被推出桌子边缘。
(完整)《大学物理》概念
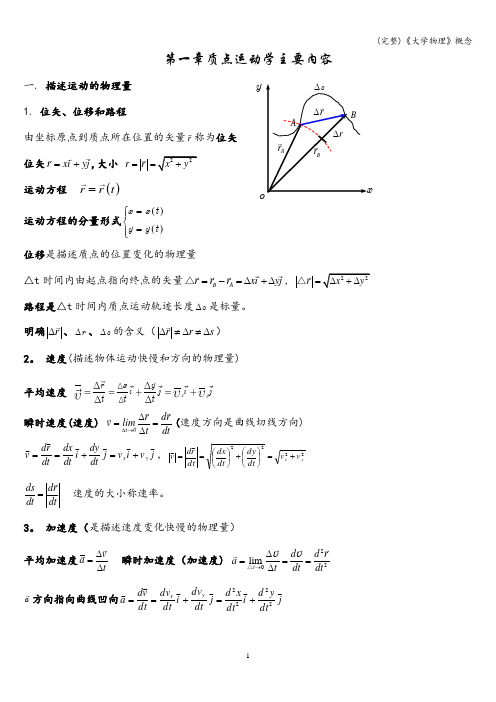
Br ∆A rB ryr ∆第一章质点运动学主要内容一. 描述运动的物理量 1. 位矢、位移和路程由坐标原点到质点所在位置的矢量r 称为位矢 位矢r xi yj =+,大小 2r r x y ==+运动方程 ()r r t =运动方程的分量形式()()x x t y y t =⎧⎪⎨=⎪⎩位移是描述质点的位置变化的物理量△t 时间内由起点指向终点的矢量B A r r r xi yj =-=∆+∆△,2r x =∆+△路程是△t 时间内质点运动轨迹长度s ∆是标量。
明确r ∆、r ∆、s ∆的含义(∆≠∆≠∆r r s ) 2。
速度(描述物体运动快慢和方向的物理量) 平均速度x yr x y i j ij ttt瞬时速度(速度) t 0r dr v limt dt∆→∆==∆(速度方向是曲线切线方向)j v i v j dt dy i dt dx dt r d v y x +=+==,2222yx v v dt dy dt dx dt r d v +=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛== ds drdt dt=速度的大小称速率。
3。
加速度(是描述速度变化快慢的物理量)平均加速度v a t ∆=∆ 瞬时加速度(加速度) 220limt d d ra t dt dtυυ→∆===∆△ a 方向指向曲线凹向j dty d i dt x d j dt dv i dt dv dt v d a y x2222+=+==2222222222⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+=dt y d dt x d dt dv dt dv a a a y x y x二。
抛体运动运动方程矢量式为 2012r v t gt =+分量式为 020cos ()1sin ()2αα==-⎧⎪⎨⎪⎩水平分运动为匀速直线运动竖直分运动为匀变速直线运动x v t y v t gt 三.圆周运动(包括一般曲线运动) 1.线量:线位移s 、线速度ds v dt= 切向加速度t dva dt=(速率随时间变化率) 法向加速度2n v a R=(速度方向随时间变化率).2。
大学物理第1章质点运动学

则有
ax 2 R cost;
a y 2 R sint
加速度的大小
2 2 2 2 2 2 a ax a2 ( R cos t ) ( R sin t ) R y
根据矢量的点积运算,分别计算
v r [(R sint )i (R cost ) j ] [(R cost )i ( R sint ) j ] 0 2 2 v a [(R sint )i (R cost ) j ] [( R cost )i ( R sint ) j ] 0
大学物理
第一章 质点运动学
1.1 运动学的一些基本概念 1.1.1、参考系(reference frame)和坐标系(coordinate) 参考系:为了描述物体的运动而选取的参考标准物体。 (运动描述的相对性) 坐标系:直角坐标系、自然坐标系、极坐标系、球坐标系等. 说明 在运动学中,参考系的选择是任意的;在动力学中则不然 1.1.2、时间和空间的计量 1、时间及其计量 时间表征物理事件的顺序性和物质运动的持续性。时间测量的 标准单位是秒。1967年定义秒为铯—133原子基态的两个超精细 能级之间跃迁辐射周期的9192631770倍。量度时间范围从宇宙 年龄1018s(约200亿年)到微观粒子的最短寿命 10-24s.极限的时 间间隔为普朗克时间10-43s,小于此时间,现有的时间概念就不适 用了。
运动学中的两类问题
1、已知质点的运动学方程求质点的速度、加速度等问
题常称为运动学第一类问题.
r r (t )
微分
v, a
2、由加速度和初始条件求速度方程和运动方程的问题称 为运动学的第二类问题.
a , v0 , r0
大学物理

绪论物理学是研究物质的基本结构、物质间相互作用的基本规律的科学,目的在于揭示物质运动的基本规律及物质各层次的内部结构。
物理学是自然科学的一门非常重要的学科,可以用博、大、精、深四个字来概括。
博:物理学涉及的范围广博,大至整个宇宙,小到基本粒子,而且“基本粒子”就是最基本的吗?它有没有新的层次?这也是物理学家在努力探求的工作。
物理学与天文学是既互相合作又相互促进的兄弟学科。
物理是工科院校一门重要的基础课,其研究的领域涉及力学、热学、光学、电学以及20世纪以来发展起来的量子物理。
从宏观到微观,从低速到高速,从物质的固态、液态、气态到等离子态、超导态,时间跨度达140亿年以上,空间跨度达1044m,温度跨度达1010K,不可称为不博。
大:可以说上至天文,下至地理,物理学无处不在。
物理学研究物质间的相互作用,称为力。
自然界中四种基本的作用力都在物理学的研究范围中。
以强相互作用的相对强度为1,四种基本作用的相对强度和范围如下所示:力的种类相对强度作用范围/m力的种类相对强度作用范围/m强相互作用110-15弱相互作用10-12< 10-17电磁相互作用10-2长引力相互作用10-40长爱因斯坦(1879—1955)生前追求统一场论,试图建立一个包括引力场(引力作用)和电磁场(电磁作用)的统一场理论。
建立四个基本作用之间的统一的理论是物理学家们追求的目标。
爱因斯坦为之奋斗了30年,但未能成功,最终带着热切的期望和必定成功的信念离开人世。
这之后,1961年美国物理学家格拉肖首先提出弱相互作用和电磁作用统一的基本模型,1967年美国物理学家温伯格和巴基斯坦物理学家萨拉姆独立地对此模型进行了发展和完善,之后该理论得到实验证实。
物理学向统一场论迈出了坚实的一步。
精:物理学家研究的问题既涉及定性的描述(如力是物体间的相互作用,感应电动势是因回路包围面积的磁通量变化而引起的),还必须有精准的定量的计算。
这就涉及建立物理模型和充分利用数学工具进行运算两方面的问题。
大学物理学与物理实验课程修改意见

大学物理学与物理实验课程开设修改意见一、开设大学物理学与物理实验的政策依据教育部高等学校教学指导委员会[2005]1号文件,大学物理课程是本科院校非物理专业一门重要的基础课,它在培养学生辩证唯物主义世界观和学习能力、观察能力、实验动手能力、思维能力、创新能力等方面起着十分重要的作用。
2011年6月11日~13日,教指委物理基础课程分委员会在浙江省杭州市召开了“2011年大学物理和大学物理实验课程教学基本要求研讨、培训会议”,针对教学面临的困难进行了广泛的讨论,号召物理老师要积极面向非本专业学生开设大学物理学与物理实验课程,提升大学生的科技素养,增强社会责任感,为大学生的全面发展奠定基础。
二、开设大学物理课程的意义第一、大学物理不同于高中物理大学物理和中学物理有很大的区别,高中基本上是讲三百年前的物理知识,大学是讲近三百年的现代物理知识。
大学物理学采用的是分析实际问题,建立物理模型,运用理论或公式,解决问题这样一个学习途径。
学习重点放在分析实际问题,建立物理模型这个层次,提高学生的解决实际问题的能力。
如运动学问题中从数学几何关系出发,导出运动的速度关系,同时加入角速度等概念,例如分析旗杆的投影伸长的速度问题,学生就感兴趣,解决了他们多年来只背公式解题的问题。
而有些学生反映大学物理学和高中物理没有区别,那是他只听了名词相同就想当然地认为内容一样,也有我们的老师没有突出教学重点所形成的原因。
第二、大学物理学与专业课程关系密切理工科有这样一个排序:哲学、物理、化学、生物、医学,下一级的要学上一级的基础课程,也就是物理、化学、生物、医学专业都要学大学物理的基础课,工科要学习大学物理,农科也要学大学物理。
我们提议文科也要学大学物理(人文物理),见教学大纲。
物理学在生物学发展中的贡献众多,虽然分子生物学已经构成了生命科学的前沿领域,但生物物理学显然也是大有可为的,农科领域也有土壤物理学,林业领域有生态物理学,还有光生物物理学。
大学物理工科教材习题(附答案)

时间 空间与运动学1 下列哪一种说法是正确的( )(A )运动物体加速度越大,速度越快 (B )作直线运动的物体,加速度越来越小,速度也越来越小(C )切向加速度为正值时,质点运动加快 (D )法向加速度越大,质点运动的法向速度变化越快2 一质点在平面上运动,已知质点的位置矢量的表示式为j i r 22bt at +=(其中a 、b 为常量),则该质点作( ) (A )匀速直线运动 (B )变速直线运动 (C )抛物线运动 (D )一般曲线运动3 一个气球以1s m 5-⋅速度由地面上升,经过30s 后从气球上自行脱离一个重物,该物体从脱落到落回地面的所需时间为( )(A )6s (B )s 30 (C )5. 5s (D )8s4 如图所示湖中有一小船,有人用绳绕过岸上一定高度处的定滑轮拉湖上的船向岸边运动,设该人以匀速率0v 收绳,绳长不变,湖水静止,则小船的运动是( )(A )匀加速运动 (B )匀减速运动 (C )变加速运动(D )变减速运动5 已知质点的运动方程j i r 33)s m 4()3(t m -⋅+=,则质点在2s 末时的速度和加速度为( )(A )j a j i v )s m 48( , )s m 48()s m 3(211---⋅=⋅+⋅=(B )j a j v )s m 48( , )s m 48(21--⋅=⋅=(C )j a j i v )s m 32( , )s m 32()s m 3(211---⋅=⋅+⋅=(D )j a j v )s m 32( , )s m 32(21--⋅=⋅=6 一质点作竖直上抛运动,下列的t v -图中哪一幅基本上反映了该质点的速度变化情况( )7 有四个质点A 、B 、C 、D 沿Ox 轴作互不相关的直线运动,在0=t 时,各质点都在00=x 处,下列各图分别表示四个质点的t v -图,试从图上判别,当s 2=t 时,离坐标原点最远处的质点( )8 一质点在0=t 时刻从原点出发,以速度0v 沿Ox 轴运动,其加速度与速度的关系为2kv a -=,k 为正常数,这质点的速度与所经历的路程的关系是( )(A )kx e v v -=0 (B ))21(200v x v v -=(C )201x v v -= (D )条件不足,无地确定9 气球正在上升,气球下系有一重物,当气球上升到离地面100m 高处,系绳突然断裂,重物下落,这重物下落到地面的运动与另一个物体从100m 高处自由落到地面的运动相比,下列哪一个结论是正确的( )(A )下落的时间相同 (B )下落的路程相同(C )下落的位移相同 (D )落地时的速度相同10 质点以速度231)s m 1(s m 4t v --⋅+⋅=作直线运动,沿直线作Ox 轴,已知s 3=t 时质点位于m 9=x 处,则该质点的运动方程为( ) (A )t x )s m 2(1-⋅= (B )221)s m 21()s m 4(t t x --⋅+⋅= (C )m t t x 12)s m 31()s m 4(331-⋅+⋅=-- (D )m t t x 12)s m 31()s m 4(331+⋅+⋅=--11 已知质点作直线运动,其加速度t a )s m 3(sm 232--⋅-⋅=,当0=t 时,质点位于00=x 处,且10s m 5-⋅=v ,则质点的运动方程为( ) (A )33221)s m 21()s m 1()s m 5(t t t x ---⋅-⋅+⋅= (B )3322)s m 21()s m 1(t t x --⋅-⋅=(C )3322)s m 31()s m 21(t t x --⋅-⋅= (D )3322)s m 1()s m 1(t t x --⋅-⋅=12 一个质点在Oxy 平面运动,其速度为j i v t )s m 8()s m 2(21--⋅-⋅=,已知质点0=t 时,它通过(3,7)位置处,那么该质点任意时刻的位矢是( )(A )j i r 221)s m 4()s m 2(t t --⋅-⋅= (B )j 7i r m])s m 4[(]3)s m 2[(221+⋅-+⋅=--t m t(C )j -(8m) (D )条件不足,不能确定13 质点作平面曲线运动,运动方程的标量函数为)( , )(t y y t x x ==,位置矢量大小22 y x +=r ,则下面哪些结论是正确的?( )(A )质点的运动速度是t x d d (B )质点的运动速率是t d d r v = (C ) d d t r v = (D ) d d t r 可以大于或小于 v14 质点沿轨道AB 作曲线运动,速率逐渐减小,在图中哪一个图正确表示了质点C 的加速度?( )15 以初速度0v 将一物体斜向上抛出,抛射角为o 45>θ,不计空气阻力,在g v t )cos (sin 0θθ-=时刻该物体的( )(A )法向加速度为g (B )法向加速度为g 32- (C )切向加速度为g 23- (D )切向加速度为g 32-16 一质点从静止出发绕半径为R 的圆周作匀变速圆周运动,角加速度为α,当质点走完一圈回到出发点时,所经历的时间是( )(A )R 221α (B )απ4(C )απ2 (D )不能确定17 一飞轮绕轴作变速转动,飞轮上有两点21 P P 和,它们到转轴的距离分别为d d 2 和,则在任意时刻,21 P P 和两点的加速度大小之比)/21a a 为( )(A )21 (B )41(C )要由该时刻的角速度决定 (D )要由该时刻的角加速度决定18 沿直线运动的物体,其速度与时间成反比,则其加速度与速度的关系是( )(A )与速度成正比 (B )与速度平方成正比 (C )与速度成反比 D )与速度平方成反比19 抛物体运动中,下列各量中不随时间变化的是( )(A )v (B )v (C )t v d d (D )t d d v20 某人以1h km 4-⋅速率向东前进时,感觉到风从正北方吹来,如果将速率增加一倍,则感觉风从东北吹来,实际风速和风向为( )(A )1h km 4-⋅从正北方吹来 (B )1h km 4-⋅从西北方吹来 (C )1h km 24-⋅从东北方向吹来 (D )1h km 24-⋅从西北方向吹来 C a c b d a a c c a b c c d b a b d d牛顿运动定律1 下列说法中哪一个是正确的?( )(A )合力一定大于分力 (B )物体速率不变,所受合外力为零(C )速率很大的物体,运动状态不易改变(D )质量越大的物体,运动状态越不易改变2 物体自高度相同的A 点沿不同长度的光滑斜面自由下滑,如右图所示,斜面倾角多大时,物体滑到斜面底部的速率最大()(A )30o (B)45o (C)60o (D )各倾角斜面的速率相等。
大学物理质点运动时间空间

dr
dt
dx2 dt
ddyt2
练习1 一质点沿x轴作直线运动,其位置坐标与时间的 关系为 x=10+8t-4t2,求:
(1)质点在第一秒、第二秒内的平均速度。
(2)质点在t=0、1、2秒时的速度。 解:( 1 ) t时x 刻 1 0 8 t 4 t2
t t 时 ( x x 刻 ) 1 8 ( t 0 t ) 4 ( t t ) 2
t 时间内, 质点的平均速度 z
x
v r t
r(tΔt)r(t)平均速度 v
Δt
与 r同方向.
➢瞬时速度
当 t 0 时平均速度的极限叫做瞬时速度,简
称速度,即在某时刻或某位置处质点位矢对时间的变
化v 率. lim rdr t 0t dt
y
B s
r(tt)
当 t0时, drds
v
ds dt
et
O
•描述物质运动具有相对性 参考系: 为确定物理位置和描述物体运动而选为依 据的一个或一组彼此相对静止的物体.
选取的参考系不同,对物体运动情况的描述不同,这就是运 动描述的相对性.
(1) 参考系的引入是由于运动相对性的需要。 (2)参考系的选择是任意的,对不同的参考系质点运动
形式不同。 (3)通常我们选地面或固定于地面的物体为参考系。
t内位 x 移 8 t 8 t为 t 4 (t)2
x vt1 t2 t8 8 t1 4 (t2 t1)
v018044(ms)方 向 x轴 与正 向 相
v128844(ms)方向 x轴 与正向相
(2)vt
dx88t dt
代入 t = 0 , 1 , 2 得:
v0 8ms v10 v2 8ms
大学物理第一章

r v
r g
近日点
r g r v
r v
注意: 直线运动中“位移、速度、加速度”的矢量性。 注意: 直线运动中“位移、速度、加速度”的矢量性。
当质点作直线运动时 当质点作直线运动时 直线 矢量的方向性体现在指向上,用正、负号表示 矢量的方向性体现在指向上,
x = x(t )
dx v= dt
注意
r v r a
r v r a
r a
r v
速率增大,加速度与速度的夹角小于90° 速率增大,加速度与速度的夹角小于 °。 速率减小,加速度与速度的夹角大于90° 速率减小,加速度与速度的夹角大于 °。
r g
r v r v r g
r g r v
r v
r 远日点 g r v
r v r g r v r r g g
第一篇
力 学
力学
——研究机械运动的规律 研究机械运动的规律 研究机械运动
物体位置随时间的变化
(mechanics)
力学
研究随时间的推移,物体空间位置的变动。 运动学 —研究随时间的推移,物体空间位置的变动。
动力学 —研究物体间相互作用与运动的关系。 研究物体间相互作用与运动的关系。 研究物体间相互作用与运动的关系
∆S
是矢量
S
r r( t )
r ∆r
r r ( t + ∆t )
o
路程 ∆S 平均速率= = >0 时间 ∆t 是标量
( 2 ) 瞬时速度
质点在t时刻的瞬时速度等于t至t + ∆t时间内 的平均速度当∆t → 0时的极限。
r r r ∆r dr v = lim = ∆t → 0 ∆t dt
即:质点的瞬时速度等于位置矢量对时间的 变化率或一阶导数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)平动 )
(2)本身线度 << 其活动范围 )
地球
太阳
地球绕太阳公转
三,时间 空间 时间是物体运动过程的持续性和顺序性的反映 时间是物体运动过程的持续性和顺序性的反映 持续性 空间是物体运动过程的广延性或物体形状, 空间是物体运动过程的广延性或物体形状,相 广延性 对位置的反映 对位置的反映
o t
o t
vz = v0z + ∫ az (t )dt
o
v =vxi + vy j + vz k
例1:一质点在(X,Y)平面内运动, 一质点在( , )平面内运动, 一质点在 运动方程为: 运动方程为:
r (t ) = 2ti + (2 t ) j
2
(SI )
求: (1)质点的轨迹; )质点的轨迹; (2)在最初 内质点的位移和平均 )在最初2S内 速度; 速度; (3)在第2S时质点的速度和加速度. )在第 时质点的速度和加速度.
t dx ∴∫ = ∫ dt 0 1+ 2x 0 x
1 ln(1+ 2x) = t 2
1 2t ∴x = (e 1) 2
d x 2t a = 2 = 2e dt
2
平面内运动, [例4]一质点在xOy平面内运动,运动方 4]一质点在 y=19(1)写出质点任意 程为x=2t,y=19-2t2.(1)写出质点任意 时刻的位置矢量, 时刻的位置矢量,速度矢量和加速度矢 (2)写出轨迹方程 写出轨迹方程; 量;(2)写出轨迹方程; 2 解 : 1) (
d x(t) 1 2 ∵ v(t) = = 2+t + t dt 2 x( t ) t 1 2 ∴∫ d x(t ) = ∫ (2 + t + t )dt x0 0 2
质点的运动方程: 质点的运动方程:
1 2 1 3 x(t ) = 1 + 2t + t + t 2 6
[例3]质点沿x轴作直线运动,速度 3]质点沿 轴作直线运动, 质点沿x v=1+2x,初始时刻质点位于原点, v=1+2x,初始时刻质点位于原点,求质点 的位置和加速度 解:∵v = dx dt =1+ 2x
r = 2ti + (19 2t ) j v = dr dt = 2i 4tj a = dv dt = 4 j
2
(2)消去t: 消去t
∴y =19 2(x 2) =19 x 2
2
[例5]质点沿x轴正向作直线运动,加速 5]质点沿 轴正向作直线运动, 质点沿x a=-mx(m为正常数 为正常数) t=0时 度a=-mx(m为正常数).t=0时, x=0, v 在什么位置质点开始停止运动? =v0,在什么位置质点开始停止运动? 问什么位置质点停止运动?需令速度等零, 解: 问什么位置质点停止运动?需令速度等零,
v0 ∴x = m
七, 运动学的一类特殊的微分问题
求当 为匀速时, v0为匀速时, ? v =?
v0
h
a
s
v
l = s +h
2 2
2
求导: 两边对 t 求导:
dl ds 2l = 2s dt dt
ds = v dt
2 2
dl = v0 而 dt
l s +h ∴ v = v0= v0 s s
八.抛体运动 二维运动,分解成两个一维运动 X: v0 x = v0 cos θ ,
时间, 第二章 时间,空间与质点运动学
的物体的运动规律. 研究可简化为质点的物体的运动规律.
参考系, §2–1 参考系,坐标系和质点 §2-2位矢,速度和加速度 位矢, §2-3圆周运动,自然坐标(内禀坐标) 圆周运动,自然坐标(内禀坐标) §2-4运动的相对性,Galileo坐标变换 运动的相对性,Galileo坐标变换
(3)a=a( x)
dv dv dx dv = 由 a( x) = =v dt dx dt dx
得 积分: 积分: 得
2
vdv = a( x)dx
vdv = ∫ a( x)dx
x x0
2 0 x x0
∫
v
v0
v = v + 2∫ a( x)dx
(4)v=v( t)
dx 由 v= dt
两边取定积分
o
地心系
Y
的数学抽象. 坐标系: 参考系的数学抽象 坐标系: 参考系的数学抽象. 常用: 常用: 直角坐标系 自然坐标系 球坐标系 柱坐标系 极坐标系
二,质点: 质点: 具有物体的全部质量, 不考虑其 具有物体的全部质量,而不考虑其大小 物体的全部质量 形状的理想物体 的理想物体. 和形状的理想物体. 物体可简化为质点的情况: 物体可简化为质点的情况:
§2–1 参考系和坐标系
一, 参考系
质点
研究物体的运动时所选的参考物体. 研究物体的运动时所选的参考物体. 同一物体,对不同参考系, 同一物体,对不同参考系,运动不同 ----运 运 动描述的相对性. 动描述的相对性.
可根据研究问题的方便,选不同参考系 可根据研究问题的方便,选不同参考系
Z
地面系 日心系 X
方向: 方向: dv 沿
在直角坐标系中
dvy dv dvx dvz a= = i+ j+ k dt dt dt dt
d x d y d z = 2 i+ 2 j+ 2 k dt dt dt
2 2 2
= ax i + ay j + az k
六, 运动学的两类问题 1,已知 r , = r (t),求 r v和 a
故需求速度
dv dv dx dv ∵a = = =v dt dx dt dx dv ∴v = mx dx v x vdv = ∫ mxdx 积分 ∫
v0 0
得
2
1 2 2 1 2 (v v0 ) = mx 2 2
∴v v = mx
2 0
2
v = v0 mx
2
2
质点停止运动时
v =0
v0 ( x= 舍去) 舍去) m
解:(1)运动方程的分量形式: :( )运动方程的分量形式:
x = 2t 2 y = 2 t
两式联立消去 t ,得轨迹方程: 得轨迹方程:
x y = 2 4
2
(2)在最初 内质点的位移: )在最初2S内质点的位移:
r = r (2) r (0) = 4i 4 j
= (x2 x0 )i + ( y2 y0 ) j
x = 2t 2 y = 2 t
x y = 2 4
2
路程:质点经历的实际路径长度. 路程:质点经历的实际路径长度.
二,位移矢量(位移) r 位移矢量(位移) 一段时间内位矢( 增量. 一段时间内位矢(置)的增量.
PP = r = r2 r 1 2 1
分量式: r分量式:
z
r = r2 r1
x
o
t
( )dt
∫
v
vo
dv = ∫ a(t )dt
t o
0
= ∫ a(t )dt或v = v0 + ∫ a(t )dt
t o o
(2)a=a(v)
dv 得 由 a(v) = dt
t
dv dt = a(v)
v
dv 两边取定积分: 两边取定积分: dt = ∫0 ∫v0 a(v) v dv 得 t =∫ 运动方程) (运动方程) v0 a(v)
P (x,y,z)
i
k 0
y
rz
j
x
Y
在直角系中分量表达式: r在直角系中分量表达式:
r = xi + yj + zk
大小: 大小:
r = r= x + y + z
2 2
2
方向余弦: 方向余弦:
x cosα = r
y cos β = r
z cosγ = r
运动方程: 位置随 变化的函数式, 运动方程:----位置随 t 变化的函数式,
a = t +1 1 x0 = 1m , v0 = 2m s
求:质点的运动方程. 质点的运动方程.
dv 解: = = t +1 a dt
分离变量, 分离变量, dv = (t + 1)dt 两边积分, 两边积分,
∫
v(t )
v0
dv = ∫ (t +1)dt
0
t
得
1 2 v(t ) = 2 + t + t 2
--矢量 v --矢量
r 大小: 大小: v = t
方向: 方向: r的方向
2,瞬时速度(速度): ,瞬时速度(速度)
r lim 的极限值, t → 0时, v 的极限值, v = t→0 t
dr v= dt
dr 大小: 大小: = v = v dt v矢量
----速率 速率
方向:dr方向, 轨道切向. 方向: 方向, 轨道切向. ----轨道切向
r = r (t)= x(t)i + y(t) j + z(t)k
分量式: 分量式:
空间运动
平面运动
x = 2t 2 y = 2 t
x = x(t ) y = y(t )
x = x (t ) y = y (t ) z = z (t )
轨迹(道 :运动质点在空间经过路径的形状. 轨迹 道):运动质点在空间经过路径的形状 运动方程分量式中消去t,可得轨迹方程. 运动方程分量式中消去 ,可得轨迹方程.
ds v= dt
∵ dr = ds
五,加速度 ----速度随时间的变化率 速度随时间的变化率
v1
