第13讲反比例函数

合集下载

中考数学复习第13课时《反比例函数》说课稿

中考数学复习第13课时《反比例函数》说课稿一. 教材分析《中考数学复习第13课时》这一课时，是在学生已经掌握了比例函数的基础上进行教学的。

本课时主要让学生了解反比例函数的定义、性质及其图象，能够熟练运用反比例函数解决实际问题。

教材通过丰富的实例，引导学生探究反比例函数的图象和性质，培养学生的观察能力、思维能力和创新能力。

二. 学情分析初中生在学习反比例函数时，已经具备了一定的函数基础，对比例函数的概念和图象有一定的了解。

但学生在学习过程中，可能会对反比例函数的定义和性质产生混淆，特别是在解决实际问题时，不知道如何运用反比例函数。

因此，在教学过程中，我要注重引导学生理解反比例函数的定义，掌握其性质，并能运用到实际问题中。

三. 说教学目标1.知识与技能目标：让学生掌握反比例函数的定义、性质及其图象，能够熟练运用反比例函数解决实际问题。

2.过程与方法目标：通过观察、实验、探究等方法，让学生了解反比例函数的图象和性质，培养学生的观察能力、思维能力和创新能力。

3.情感态度与价值观目标：激发学生学习反比例函数的兴趣，培养学生的团队合作意识，使学生感受到数学在生活中的应用价值。

四. 说教学重难点1.教学重点：反比例函数的定义、性质及其图象。

2.教学难点：反比例函数在实际问题中的应用。

五. 说教学方法与手段1.教学方法：采用问题驱动法、案例教学法、小组合作学习法等，引导学生主动探究、积极参与。

2.教学手段：利用多媒体课件、反比例函数图象软件等，直观展示反比例函数的图象和性质，提高学生的学习兴趣。

六. 说教学过程1.导入：通过复习比例函数的知识，引出反比例函数的概念，激发学生的学习兴趣。

2.新课导入：讲解反比例函数的定义，让学生通过实例理解反比例函数的概念。

3.性质探究：引导学生观察反比例函数的图象，总结反比例函数的性质。

4.应用拓展：通过实际问题，让学生运用反比例函数解决问题，巩固所学知识。

5.练习环节：布置一些有关反比例函数的练习题，让学生独立完成，检测学习效果。

第十三讲反比例函数详解

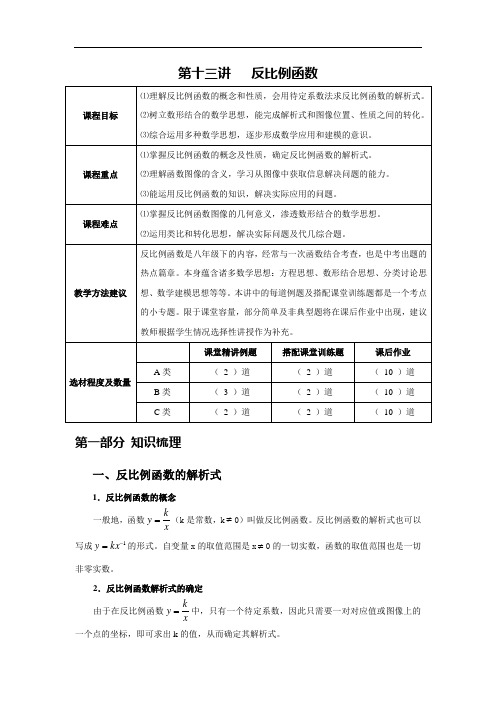
第十三讲反比例函数第一部分知识梳理一、反比例函数的解析式1．反比例函数的概念一般地，函数xky =（k 是常数，k ≠0）叫做反比例函数。

反比例函数的解析式也可以写成1-=kx y 的形式。

自变量x 的取值范围是x ≠0的一切实数，函数的取值范围也是一切非零实数。

2．反比例函数解析式的确定由于在反比例函数xky =中，只有一个待定系数，因此只需要一对对应值或图像上的一个点的坐标，即可求出k 的值，从而确定其解析式。

二、反比例函数的图像及性质1．反比例函数的图象反比例函数的图象是双曲线，有两个分支，这两个分支分别位于第一、三象限，或第二、四象限，它们关于原点对称。

由于反比例函数中自变量x≠0，函数y≠0，所以，它的图象与x轴、y轴都没有交点，即双曲线的两个分支无限接近坐标轴，但永远达不到坐标轴。

2．反比例函数的性质3．反比例函数中反比例系数的几何意义(如图)面积为k 。

连接该点和原点，所得三三角形（如图）的面积m 的值D ．21-〖选题意图〗对于反比例函数)0(≠=k xky 。

由于11-=x x ，所以反比例函数也可以写成1-=x y （k 是常数，k ≠0）的形式，有时也以xy=k （k 是常数，k ≠0）的形式出现。

（1）k ＞0，反比例函数图象在一、三象限；（2）k ＜0，反比例函数图象在第二、四象限内．本题需要理解好反比例函数定义中的系数和指数，同时需要掌握反比例函数的性质，这样才能防止漏解或多解。

〖解题思路〗根据反比例函数的定义m 2﹣5=﹣1，又图象在第二、四象限，所以m+1＜0，两式联立方程组求解即可．〖参考答案〗解：∵函数()521-+=m xm y 是反比例函数，且图象在第二、四象限内，∴⎩⎨⎧+-=-01152＜m m ，解得m =±2且m ＜﹣1，∴m =﹣2．故选B ．【课堂训练题】1．已知y=y 1+y 2，y 1与x 成正比例，y 2与x ﹣2成反比例，且当x =1时，y =﹣1；当x=3时，y=5．求y 与x 的函数关系式．〖难度分级〗A 类〖参考答案〗解：设y 1=k 1x （k 1≠0），y 2=错误！未找到引用源。

中考数学专题复习讲座第十三讲反比例函数

中考数学专题复习第十三讲反比例函数【基础知识回顾】一、反比例函数的概念：一般地：互数y （k是常数，k≠0）叫做反比例函数【名师提醒：1、在反比例函数关系式中：k≠0、x≠0、y≠02、反比例函数的另一种表达式为y= （k是常数，k≠0）3、反比例函数解析式可写成xy= k（k≠0）它表明反比例函数中自变量x 与其对应函数值y之积，总等于】二、反比例函数的同象和性质：1、反比例函数y=kx（k≠0）的同象是它有两个分支，关于对称2、反比例函数y=kx（k≠0）当k>0时它的同象位于象限，在每一个象限内y随x的增大而当k<0时，它的同象位于象限，在每一个象限内，y随x的增大而【名师提醒：1、在反比例函数y=kx中，因为x≠0，y≠0所以双曲线与坐标轴无限接近，但永不与x轴y轴2、在反比例函数y随x的变化情况中一定注明在每一个象限内】3、反比例函数中比例系数k的几何意义：反曲线y=kx（k≠0）上任意一点向两坐标轴作垂线→两线与坐标轴围成的形面积，即如图： AOBP=S△AOP=【名师提醒：k的几何意义往常与前边提示中所谈到的xy=k联系起来理解和应用】三、反比例函数解析式的确定因为反比例函数y=kx（k≠0）中只有一个被定系数所以求反比例函数关系式只需知道一组对应的x、y值或一个点的坐标即可，步骤同一次函数解析式的求法一、反比例函数的应用二、解反比例函数的实际问题时，先确定函数解析式，再利用同象找出解决问题的方案，这里要特别注意自变量的【重点考点例析】考点一：反比例函数的同象和性质例1 （2012•张家界）当a≠0时，函数y=ax+1与函数ayx在同一坐标系中的图象可能是（）A． B．C． D．思路分析：分a＞0和a＜0两种情况讨论，分析出两函数图象所在象限，再在四个选项中找到正确图象．解：当a＞0时，y=ax+1过一、二、三象限，y=ayx=过一、三象限；当a＜0时，y=ax+1过一、二、四象限，y=ayx=过二、四象限；故选C．点评：本题考查了一次函数与二次函数的图象和性质，解题的关键是明确在同一a值的前提下图象能共存．例2 （2012•佳木斯）在平面直角坐标系中，反比例函数22a ayx-+ =图象的两个分支分别在（）A．第一、三象限 B．第二、四象限C．第一、二象限 D．第三、四象限思路分析：把a2-a+2配方并根据非负数的性质判断出是恒大于0的代数式，再根据反比例函数的性质解答．解：a2-a+2，=a2-a+14-14+2，=（a-12）2+7 4 ，∵（a-12）2≥0，∴（a-12）2+7 4 ＞0，∴反比例函数图象的两个分支分别位于第一、三象限．故选A．点评：本题考查了反比例函数图象的性质，先判断出a2-a+2的正负情况是解题的关键，对于反比例函数kyx=（k≠0）：（1）k＞0，反比例函数图象在一、三象限；（2）k＜0，反比例函数图象在第二、四象限内．例3 （2012•台州）点（-1，y1），（2，y2），（3，y3）均在函数6yx=的图象上，则y1，y2，y3的大小关系是（）A．y3＜y2＜y1 B．y2＜y3＜y1 C．y1＜y2＜y3 D．y1＜y3＜y2思路分析：先根据反比例函数的解析式判断出此函数图象所在的象限，再根据各点的坐标判断出各点所在的象限，根据函数图象在各象限内点的坐标特点解答．解：∵函数6yx=中k=6＞0，∴此函数的图象在一、三象限，且在每一象限内y随x的增大而减小，∵-1＜0，∴点（-1，y1）在第三象限，∴y1＜0，∵0＜2＜3，∴（2，y2），（3，y3）在第一象限，∴y2＞y3＞0，∴y2＞y3＞y1．故选D．点评：本题考查的是反比例函数图象上点的坐标特点，根据题意判断出函数图象所在象限是解答此题的关键．对应训练1．（2012•毕节地区）一次函数y=x+m（m≠0）与反比例函数myx=的图象在同一平面直角坐标系中是（）A． B． C． D．1．C2．（2012•内江）函数1y xx=的图象在（）A．第一象限 B．第一、三象限 C．第二象限 D．第二、四象限2．A2x中x≥0，1x中x≠0，故x＞0，此时y＞0，则函数在第一象限．故选A．3．（2012•佛山）若A（x1，y1）和B（x2，y2）在反比例函数2yx=的图象上，且0＜x1＜x2，则y1与y2的大小关系是y1 y2．3．＞考点二：反比例函数解析式的确定例4 （2012•哈尔滨）如果反比例函数1kyx-=的图象经过点（-1，-2），则k的值是（）A．2 B．-2 C．-3 D．3思路分析：根据反比例函数图象上点的坐标特征，将（-1，-2）代入已知反比例函数的解析式，列出关于系数k的方程，通过解方程即可求得k的值．解答：解：根据题意，得-2=11k--，即2=k-1，解得k=3．故选D．点评：此题考查的是用待定系数法求反比例函数的解析式，是中学阶段的重点．解答此题时，借用了“反比例函数图象上点的坐标特征”这一知识点．对应训练4．（2012•广元）已知关于x的方程（x+1）2+（x-b）2=2有唯一的实数解，且反比例函数1b yx+ =的图象在每个象限内y随x的增大而增大，那么反比例函数的关系式为（）A．3yx=- B．1yx= C．2yx= D．2yx=-4．D4．分析：关于x的方程（x+1）2+（x-b）2=2有唯一的实数解，则判别式等于0，据此即可求得b的值，然后根据反比例函数1byx+=的图象在每个象限内y随x的增大而增大，则比例系数1+b＜0，则b的值可以确定，从而确定函数的解析式．解：关于x的方程（x+1）2+（x-b）2=2化成一般形式是：2x2+（2-2b）x+（b2-1）=0，△=（2-2b）2-8（b2-1）=-4（b+3）（b-1）=0，解得：b=-3或1．∵反比例函数1byx+=的图象在每个象限内y随x的增大而增大，∴1+b＜0 ∴b＜-1，∴b=-3．则反比例函数的解析式是：y=13yx-=，即2yx=-．故选D．考点三：反比例函数k的几何意义例5 （2012•铁岭）如图，点A在双曲线4yx=上，点B在双曲线kyx=（k≠0）上，AB∥x轴，分别过点A、B向x轴作垂线，垂足分别为D、C，若矩形ABCD的面积是8，则k的值为（）A．12 B．10 C．8 D．6思路分析：先根据反比例函数的图象在第一象限判断出k的符号，再延长线段BA，交y轴于点E，由于AB∥x轴，所以AE⊥y轴，故四边形AEOD是矩形，由于点A在双曲线4yx=上，所以S矩形AEOD=4，同理可得S矩形OCBE=k，由S矩形ABCD=S矩形OCBE-S矩形AEOD即可得出k的值．解：∵双曲线kyx=（k≠0）上在第一象限，∴k＞0，延长线段BA，交y轴于点E，∵AB∥x轴，∴AE⊥y轴，∴四边形AEOD是矩形，∵点A在双曲线4yx=上，∴S矩形AEOD=4，同理S矩形OCBE=k，∵S矩形ABCD=S矩形OCBE-S矩形AEOD=k-4=8，∴k=12．故选A．点评：本题考查的是反比例函数系数k的几何意义，即反比例函数kyx=图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．对应训练5．（2012•株洲）如图，直线x=t（t＞0）与反比例函数21,y yx x-==的图象分别交于B、C两点，A为y轴上的任意一点，则△ABC的面积为（）A．3 B．3 2 tC．32D．不能确定5．C5．解：把x=t分别代入21,y yx x-==，得21,y yt t==-，所以B（t，2t）、C（t，1t-），所以BC=2t-（1t-）=3t．∵A为y轴上的任意一点，∴点A到直线BC的距离为t，∴△ABC的面积=133 22tt⨯⨯=．故选C．考点四：反比例函数与一次函数的综合运用例6 （2012•岳阳）如图，一次函数y1=x+1的图象与反比例函数22yx=的图象交于A、B 两点，过点作AC⊥x轴于点C，过点B作BD⊥x轴于点D，连接AO、BO，下列说法正确的是（）A．点A和点B关于原点对称B．当x＜1时，y1＞y2C．S△AOC=S△BODD．当x＞0时，y1、y2都随x的增大而增大思路分析：求出两函数式组成的方程组的解，即可得出A、B的坐标，即可判断A；根据图象的特点即可判断B；根据A、B的坐标和三角形的面积公式求出另三角形的面积，即可判断C；根据图形的特点即可判断D．解：A、12y xyx=+⎧⎪⎨=⎪⎩①②，∵把①代入②得：x+1=2x，解得：x1=-2，x2=1，代入①得：y1=-1，y2=2，∴B（-2，-1），A（1，2），∴A、B不关于原点对称，故本选项错误；B、当-2＜x＜0或x＞1时，y1＞y2，故本选项错误；C、∵S△AOC=12×1×2=1，S△BOD=12×|-2|×|-1|=1，∴S△BOD=S△AOC，故本选项正确；D、当x＞0时，y1随x的增大而增大，y2随x的增大而减小，故本选项错误；故选C．点评：本题考查了一次函数与反比例函数的交点问题的应用，主要考查学生观察图象的能力，能把图象的特点和语言有机结合起来是解此题的关键，题目比较典型，是一道具有一定代表性的题目．对应训练6．（2012•达州）一次函数y1=kx+b（k≠0）与反比例函数y2=mx(m≠0)，在同一直角坐标系中的图象如图所示，若y1＞y2，则x的取值范围是（）A．-2＜x＜0或x＞1 B．x＜-2或0＜x＜1 C．x＞1 D．-2＜x＜16．A6．解：由函数图象可知一次函数y1=kx+b与反比例函数y2=mx(m≠0)的交点坐标为（1，4），（-2，-2），由函数图象可知，当-2＜x＜0或x＞1时，y1在y2的上方，∴当y1＞y2时x的取值范围是-2＜x＜0或x＞1．故选A．【聚焦山东中考】1．（2012•青岛）点A（x1，y1），B（x2，y2），C（x3，y3）都是反比例函数3yx-=的图象上，若x1＜x2＜0＜x3，则y1，y2，y3的大小关系是（）A．y3＜y1＜y2 B．y1＜y2＜y3 C．y3＜y2＜y1 D．y2＜y1＜y31．A1．解：∵反比例函数y=-3 x 中，k=-3＜0，∴此函数图象在二四象限，且在每一象限内y随x的增大而增大，∵x1＜x2＜0＜x3，∴y3＜0，y3＜0＜y1＜y2，∴y3＜y1＜y2．故选A．2．（2012•菏泽）反比例函数2yx=的两个点（x1，y1）、（x2，y2），且x1＞x2，则下式关系成立的是（）A．y1＞y2 B．y1＜y2 C．y1=y2 D．不能确定2．D3．（2012•滨州）下列函数：①y=2x-1；②y=5x-；③y=x2+8x-2；④y=22x；⑤y=12x；⑥y=ax中，y是x的反比例函数的有（填序号）。

【大师特稿】中考数学一轮复习第13讲：反比例函数教案

第13讲:反比例函数一、复习目标1、理解反比例函数的意义，能根据已知条件确定反比例函数的解析式，能画出反比例函数的图象2、能够将反比例函数有关的实际应用题转化为函数问题二、课时安排1课时三、复习重难点1、反比例函数图象与性质2、反比例函数图象、性质的应用四、教学过程（一）知识梳理反比例函数的图象与性质·PN＝|y|·|x|＝（二）题型、技巧归纳考点1：反比例函数的概念技巧归纳：判断点是否在反比例函数图象上的方法有两种：一是口算选项中点的横坐标与纵坐标乘积是否都等于比例系数，二是将选项中点的坐标诸个代入反比例函数关系式，看能否使等式成立．考点2：反比例函数的图象与性质技巧归纳：1、比较反比例函数值的大小，在同一个象限内根据反比例函数的性质比较，在不同象限内，不能按其性质比较，函数值的大小只能根据特征确定．2、过反比例函数y ＝kx的图象上的某点向两坐标轴作垂线，两垂线与坐标轴围成的矩形的面积就等于|k |，故而常过图象上某点向坐标轴作一条或两条垂线，引出三角形或矩形的面积来解决问题．考点3反比例函数的应用技巧归纳：先根据双曲线上点C 的坐标求出m 的值，从而确定点C 的坐标，再将点C 的坐标代入一次函数关系式中确定n 的值，在求出两个函数关系式后结合条件可求出三角形的面积．过反比例函数y ＝k x的图象上的某点向两坐标轴作垂线，两垂线与坐标轴围成的矩形的面积就等于|k |，故而常过图象上某点向坐标轴作一条或两条垂线，引出三角形或矩形的面积来解决问题．（三）典例精讲例1 某反比例函数的图象经过(－1,6)，则下列各点中，此函数图象也经过的点是( ) A ．(－3,2) B ．(3,2) C ．(2,3) D ．(6,1)[解析] 设反比例函数的关系式为y ＝kx，把点(－1，6)代入可求出k ＝－6，所以反比例函数的关系式为y ＝－6x，故此函数也经过点(－3，2)，答案选A.例2在反比例函数y ＝k x (k <0)的图象上有两点()－1，y 1，⎝ ⎛⎭⎪⎫－14，y 2，则y 1－y 2的值是( ) A ．负数 B ．非正数C ．正数D ．不能确定 [解析] 反比例函数y ＝kx ：当k ＜0时，该函数图象位于第二、四象限，且在每一象限内，y 随x 的增大而增大．又∵点(－1，y 1)和⎝ ⎛⎭⎪⎫－14，y 2均位于第二象限，－1＜－14， ∴y 1＜y 2，∴y 1－y 2＜0，即y 1－y 2的值是负数，故选A.例3 如图点A ，B 在反比例函数y ＝ (k>0，x>0)的图象上，过点A ，B 作x 轴的垂线，垂足分别为M ，N ，延长线段AB 交x 轴于点C ，若OM ＝MN ＝NC ，△AOC 的面积为6，则k 的值为________．[解析] ∵S △AOC ＝6，OM ＝MN ＝NC ＝13OC ，∴S △OAC ＝12×OC×AM，S △AOM ＝12×OM×AM＝13 S △OAC ＝2＝12|k|.又∵反比例函数的图象在第一象限，k ＞0，则k ＝4.例4 如图13－2，在平面直角坐标系xOy 中，直线y ＝2x ＋n 与x 轴、y 轴分别交于点A 、B ，与双曲线y ＝4y x=在第一象限内交于点C (1，m )． (1)求m 和n 的值；(2)过x 轴上的点D (3,0)作平行于y 轴的直线l ，分别与直线AB 和双曲线y ＝交于点P 、Q ，求△APQ 的面积．解：(1) ∵点C(1，m)在双曲线y ＝4x上，∴m ＝4，将点C(1，4)代入y ＝2x ＋n 中，得n ＝2；(2)在y ＝2x ＋2中，令y ＝0，得x ＝－1，即A(－1，0)．将x ＝3代入y ＝2x ＋2和y ＝4x，得点P(3，8)，Q ⎝ ⎛⎭⎪⎫3，43，∴PQ ＝8－43＝203.又∵AD ＝3－(－1)＝4，∴△APQ 的面积＝12×4×203＝403. （四）归纳小结本部分内容要求熟练掌握反比例函数的求法，能画出反比例函数的图象，能够将反比例函数有关的实际应用题转化为函数问题（五）随堂检测1、已知点A(－2，y 1)、B(1，y 2)和C(2，y 3)都在反比例函数ky x= (k<0)的图象上，那么y 1、y 2和y 3的大小关系如何？2、已知反比例函数7y x=-图象上三个点的坐标分别是A(－2，y 1)、B(－1，y 2)、C(2，y 3)，能正确反映y 1、y 2、y 3的大小关系的是( )A ．y 1>y 2>y 3B ．y 1>y 3>y 2C ．y 2>y 1>y 3D ．y 2>y 3>y 13、已知反比例函数y=（k 为常数，k≠0）的图象经过点A （2，3）．（Ⅰ）求这个函数的解析式；（Ⅱ）判断点B （﹣1，6），C （3，2）是否在这个函数的图象上，并说明理由；（Ⅲ）当﹣3＜x ＜﹣1时，求y 的取值范围．4、如图，在平面直角坐标系xOy 中，正比例函数y=kx 的图象与反比例函数y=的图象有一个交点A （m ，2）．（1）求m 的值；（2）求正比例函数y=kx 的解析式；（3）试判断点B（2，3）是否在正比例函数图象上，并说明理由．五、板书设计反比例函数六、作业布置反比例函数课时作业七、教学反思借助多媒体形式，使同学们能直观感受本模块内容，以促进学生对所学知识的充分理解与掌握。

中考总复习数学13-第一部分第13讲反比例函数及其应用

返回思维导图
第13讲反比例函数及其应用— 考点梳理
返回栏目导航
续表
在每个象限内,y随x的增大
增减性
而⑤ 减小
对称性
是轴对称图形,对称轴为直线y=⑦
⑧ 原点O
在每个象限内,y随x的增大
而⑥增大
±x
; 是中心对称图形,对称中心是
图象由分别位于两个象限的双曲线组成,图象无限接近坐标轴,但不与
图象特征
坐标轴相交.
第13讲反比例函数及其应用— 考点梳理
返回思维导图
返回栏目导航
考点 4 反比例函数的应用
1.判断同一坐标系中反比例函数图象和一次函数图象的方法
(假设法)假设反比例函数正确,即可确定 k的取值范围,再根据 k 的取值范围
确定一次函数图象,无矛盾,则正确.
2.已知两个函数图象,求交点坐标
(1)求一次函数图象与反比例函数图象的交点,将两个函数解析式联立方程组
位置关系,依据图象在上方的函数值总比图象在下方的函数值大 ,在各区域
内找对应的x的取值范围.
4.求图形面积
(1)当图形有一边在坐标轴上时,通常将坐标
轴上的边作为底边,再利用点的坐标求出底边上的高,最后用面积公式求解.
(2)当图形三边都不在坐标轴上时,一般用“割补法”.
第13讲反比例函数及其应用— 考点梳理
返回思维导图
2.与反比例函数中k的几何意义有关的面积计算
S△AOP=⑩
S△APP‘=

|k|

2|k|

S△OBP= |k|
S△ABC=
|k|
S矩形OAPB=|k|
S▱ABCD=
|k|
返回栏目导航

中考复习：反比例函数

第13讲┃ 归类示例
k [解析] 设反比例函数的关系式为 y＝，把点(－ x 1，6)代入可求出 k＝－6，所以反比例函数的关系式－6 为 y＝，故此函数也经过点(－3，2)，答案选 A. x
第13讲┃ 归类示例
判断点是否在反比例函数图象上的方法有两种：一是口算选项中点的横坐标与纵坐标乘积是否都等于比例系数，二是将选项中点的坐标诸个代入反比例函数关系式，看能否使等式成立．
反比例函数
第13讲┃ 考点聚焦
考点聚焦
考点1 反比例函数的概念
k y＝形如________(k≠0，k 为常数) x 的函数叫做反比例函数，其中 x 是________，y 是 x 的函数，k 是自变量 ________ 比例系数
定义
关系式防错提醒
k y＝或 y＝kx－1 或 xy＝k(k≠0) x
(1)k≠0；(2)自变量 x≠0；(3) 函数值 y≠0
第13讲┃ 考点聚焦
考点2
反比例函数的图象与性质
(1) 反比例函数的图象呈现形式反比例函数y＝ (k≠0)的图象是 ________ 双曲线
k x
原点它既是关于________对称的中心对称图形，也是轴对称图形，其对称轴为第一、三象对称性限或第二、四象限坐标轴夹角的平分线，即直线y＝x或直线y＝－x
第13讲┃ 归类示例
归类示例
► 类型之一反比例函数的概念命题角度： 1. 反比例函数的概念； 2. 求反比例函数的解析式． [2013·扬州 ]某反比例函数的图象经过(－1,6)，
例1
则下列各点中，此函数图象也经过的点是( A ) A．(－3,2) B．(3,2) C．(2,3) D．(6,1)
第13讲┃ 归类示例 ► 类型之三反比例函数的应用

第13课时反比例函数(共26张PPT)

A. 0<y<1 B. 1<y<2 C. 2<y<6 D. y>6
(4) (2014湘潭)如图，A、B两点在双曲线y=
4 x
上,
分别经过A、B两点向轴作垂线段,已知S阴影=1，则S1+S2=( D ) A. 3 B.4 C.5 D. 6
变式训练（2016· 龙东）已知反比例函数 y= ，当 1＜x＜3 时，
{
{
例 7 （2016· 湖州）湖州市菱湖镇某养鱼专业户准备挖一个面积为
2000 平方米的长方形鱼塘．（1）求鱼塘的长 y（米）关于宽 x（米）的函数表达式；（2）由于受场地的限制，鱼塘的宽最多只能挖 20 米，当鱼塘的宽是 20 米，鱼塘的长为多少米？
解：（1）由长方形面积为 2000 平方米，得到 xy=2000，即 y= ； =100（米），（2）当 x=20（米）时，y=
中，一次函数 y=ax+b（a≠0）的图形与反比例函数 y= （k≠0）的图象交于第二、四象限内的 A、B 两点，与 y 轴交于 C 点，过点 A 作 AH⊥y 轴，垂足为 H，OH=3，tan∠ AOH= ，点 B 的坐标为（m，﹣2）．（1）求△ AHO 的周长；（2）求该反比例函数和一次函数的表达式．
k ，一次函数 y ＝ x ＋ b ，得 k ＝ 1 × 4 ， 1 ＋ b ＝ 4 ，解得 k ＝ 4 ， b ＝ x 4 3，∴反比例函数的表达式是y＝x，一次函数表达式是y＝x＋3. (2)设直线y＝x＋3与x轴交于点C，当x＝－4时，y＝－1， ∴B(－4，－1)．当y＝0时，x＋3＝0，x＝－3，∴C(－3，0)， 1 1 15 S△AOB＝S△AOC＋S△BOC＝ ×3×4＋ ×3×1＝ . 2 2 2 (3)∵B(－4，－1)，A(1，4)，∴根据图象可知：当x＞1或－4＜x＜0时，一次函数值大于反比例函数值．

(中考复习)第13讲反比例函数及其图象

C．y1＝y2
基础知识 · 自主学习
题组分类 · 深度剖析
课堂回顾 · 巩固提升
浙派名师中考
5． (2012· 达州)一次函数 y1＝kx＋b(k≠0)与反 m 比例函数 y2＝ (m≠0)，在同一直角坐标 x 系中的图象如图 13－3 所示，若 y1>y2，则 x 的取值范围是 ( A )
A．－2<x<0或x>1
基础知识 · 自主学习题组分类 · 深度剖析
课堂回顾 · 巩固提升
浙派名师中考
2 3． (2012· 菏泽)反比例函数 y＝图象上的两个点为 (x1， y1)， (x2， x y2)，且 x1<x2，则下式关系成立的是 ( D ) A．y1>y2 B．y1<y2
D．不能确定 1－2k 4． (2013· 哈尔滨 )反比例函数 y＝的图象经过点 (－ 2，3)，则 x k 的值为 ( C ) 7 7 A． 6 B．－ 6 C. D．－ 2 2
轴对称图形． ______________ 4．应用：
如图 13－1 所示，点 A 和点 C 是反比 k 例函数 y＝ (k≠0)的图象上任意两点， x 画 AB⊥x 轴于 B，CD⊥y 轴于 D，则 |k| 有 S△AOB＝S△COD＝ . 2
图13－1
课堂回顾 · 巩固提升
基础知识 · 自主学习
图13－4
基础知识 · 自主学习
题组分类 · 深度剖析
课堂回顾 · 巩固提升
浙派名师中考
题组一
反比例函数解析式的确定
已知图象上一点求解析式
【例 1】2 ( 0 1 3 · 巴中 )如图 1 3 －5 所示，在平面直角坐标系 x O y 中，一次函数 y＝ k x ＋ b(k≠ 0 ) 的图象与反比例 k 函数 y＝的图象交于一、三象限内 x 的 A、B 两点，直线 AB 与 x 轴交于点 C，点 B 的坐标为 (－ 6，n)，线段 OA＝ 5，E 为 x 轴正半轴上一点，且 4 a t n ∠A O E ＝ . 3

13讲：反比例函数

反比例函数【课前热身】1（2010浙江宁波）已知反比例函数1y x=，下列结论不正确．．．的是（） (A)图象经过点(1,1) (B)图象在第一、三象限(C)当1x >时，01y << (D)当0x <时，y 随着x 的增大而增大 2（2010山东潍坊）若正比例函数y ＝2kx 与反比例函数y ＝kx（k ≠0）的图象交于点 A （m ，1），则k 的值是（）．AB．2或－2 C．2D3（2010 浙江台州市）反比例函数xy 6=图象上有三个点)(11y x ，，)(22y x ，，)(33y x ，，其中3210x x x <<<，则1y ，2y ，3y 的大小关系是( )A ．321y y y <<B ．312y y y <<C ．213y y y <<D ．123y y y << 4. （2010 四川成都）如图，已知反比例函数k y x=与一次函数y x b =+的图象在第一象限相交于点(1,4)A k -+．（1）试确定这两个函数的表达式；（2）求出这两个函数图象的另一个交点B 的坐标，并根据图象写出使反比例函数的值大于一次函数的值的x 的取值范围．2x <-或01x <<【考纲解读】1.结合具体情境理解反比例函数的概念，能根据已知条件确定反比例函数的解析式2.会画反比例函数的图像，能根据图像理解其性质3.会用反比例函数解决某些实际问题【考点剖析】1．反比例函数的定义：一般地，如果两个变量x 、y 之间的关系可以表示成k y x=或1y kx -=（k 为常数，k ≠0）的形式，那么称y 是x 的反比例函数．注意：一般情况下，x 的取值范围是0x ≠的一切实数；y 的取值范围也是一切非零实数. 2. 反比例函数的图象和性质3.用待定系数法确定反比例函数ky x=的解析式基本思路：根据题意，建立方程，求出k 的值4.利用反比例函数确定k 的取值情况：一看象限，二看y 随x 的变化情况 5．k 的几何含义：反比例函数y ＝kx(k ≠0)中比例系数k 的几何意义，即过双曲线y ＝kx(k ≠0)上任意一点P 作x 轴、y 轴垂线，设垂足分别为A 、B ，则所得矩形OAPB 的面积为 . 即过双曲线上任意一点，向两坐标轴作垂线，两条垂线与坐标轴所围成的矩形的面积为常数.同时要注意它的演变情况 1. 反比例函数的实际应用(1) 反比例函数的图像反映变化规律明显，常利用它的图象找出解决问题的方案 (2) 列出函数关系式后，注意自变量的取值范围 (3) 注意函数思想、方程思想和不等式思想方法的应用【典型例题】※【针对性练习】例1 近视眼镜的度数y （度）与镜片焦距x （米）成反比例，已知400度近视眼镜镜片的焦距为0.25米，则眼镜度数y 与镜片焦距x 之间的函数关系式为．练1.1 在反比例函数3k y x-=图象的每一支曲线上，y 都随x 的增大而减小，则k 的取值范围是（）A ．k ＞3 B ．k ＞0 C ．k ＜3 D ． k ＜0练1.2 已知反比例函数的图象经过点（m ，2）和（－2，3），则m 的值为练1.3 某反比例函数的图象经过点(23)-，，则此函数图象也经过点（）A ．(23)-，B ．(33)--，C ．(23)，D ．(46)-，例2若正方形AOBC 的边OA 、OB 在坐标轴上，顶点C 在第一象限且在反比例函数y ＝x1的图像上，则点C 的坐标是 .练2.1某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P ( kPa ) 是气体体积V ( m 3) 的反比例函数，其图象如图1所示．当气球内的气压大于 120 kPa 时，气球将爆炸．为了安全起见，气球的体积应（） A ．不小于54m3B ．小于54m 3C ．不小于45m 3D ．小于45m 3练2.2 若点A 在反比例函数(0)ky k x=≠的图象上，AM x ⊥轴于点M ， AMO △的面积为3，则k = ．例3（2010山东济宁）如图，正比例函数12y x =的图象与反比例函数ky x =(0)k ≠在第一象限的图象交于A 点，过A 点作x 轴的垂线，垂足为M ，已知OAM ∆的面积为1. （1）求反比例函数的解析式；（2）如果B 为反比例函数在第一象限图象上的点（点B 与点A 不重合），且B 点的横坐标为1，在x 轴上求一点P ，使PA PB +最小.练3.1（2010重庆潼南）如图, 已知在平面直角坐标系xOy 中，一次函数b kx y +=(k ≠0)的图象与反比例函数x m y =(m ≠0)的图象相交于A 、B 两点，且点B 的纵坐标为21-，过点A 作AC ⊥x 轴于点C ， AC =1,OC =2.求：（1）求反比例函数的解析式；（2）求一次函数的解析式.MxA练3.2（2010甘肃兰州）如图，P 1是反比例函数)0(＞k x ky =在第一象限图像上的一点，点A 1 的坐标为(2，0)．（1）当点P 1的横坐标逐渐增大时，△P 1O A 1的面积将如何变化？（2）若△P 1O A 1与△P 2 A 1 A 2均为等边三角形，求此反比例函数的解析式及A 2点的坐标．练3.3（2010 河北）如图13，在直角坐标系中，矩形OABC 的顶点O 与坐标原点重合，顶点A ，C 分别在坐标轴上，顶点B 的坐标为（4，2）．过点D （0，3）和E （6，0）的直线分别与AB ，BC 交于点M ，N ．（1）求直线DE 的解析式和点M 的坐标；（2）若反比例函数xmy =（x ＞0）的图象经过点M ，求该反比例函数的解析式，并通过计算判断点N 是否在该函数的图象上；（3）若反比例函数xmy =（x ＞0）的图象与△MNB 有公共点，请直接．．写出m 的取值范围．图【复习小结】近几年中考题主要考查反比例函数的图像及性质，且多以选择、填空的形式出现【课后作业】反比例函数中考真题集锦 1（2010山东日照）已知反比例函数y =x2，则下列点中在这个反比例函数图象的上的是（）（A ）（－2，1）（B ）（1，-2）（C ）（-2，-2）（D ）（1，2） 2（2010四川凉山）已知函数25(1)m y m x-=+是反比例函数，且图像在第二、四象限内，则m 的值是（）A ．2B ．2-C ．2±D ．12-3（2010福建福州）已知反比例函数的图象y ＝kx 过点P (1，3)，则该反比例函数图象位于( )A ．第一、二象限 B ．第一、三象限 C ．第二、四象限 D ．第三、四象限4（2010湖北鄂州）正比例函数y=x 与反比例函数ky x=（k ≠0）的图像在第一象限交于点A,且则k 的值为( )A.2B.1C.D.25（2010山东青岛）函数y ax a =-与ay x=（a ≠0）在同一直角坐标系中的图象可能是（）6（2010 山东滨州）如图,P 为反比例函数y=kx的图象上一点,PA ⊥x 轴于点A, △PAO 的面积为6.下面各点中也在这个反比例函数图象上的点是( )A.(2,3)B. (-2,6)C. (2,6)D. (-2,3)7．（2010安徽芜湖）二次函数y ＝ax 2＋bx ＋c 的图象如图所示，反比例函数y ＝ ax 与正比例函数y ＝（b＋c ）x 在同一坐标系中的大致图象可能是（）A ．B ．C ．D ．8（2010四川内江）如图，反比例函数y ＝kx(x ＞0)的图象经过矩形OABC 对角线的交点M ，分别与AB 、BC相交于点D 、E ．若四边形ODBE 的面积为6，则k 的值为 A ．1B ．2C ．3D ．49（2010江苏无锡）如图，已知梯形ABCO 的底边AO 在x 轴上，BC ∥AO ，AB ⊥AO ，过点C 的双曲线ky x=交OB 于D ，且OD ：DB=1:2，若△OBC 的面积等于3，则k 的值（）A ．等于2B ．等于34C ．等于245D ．无法确定10（2010 湖北孝感）双曲线xy x y 21==与在第一象限内的图象如图所示，作一条平行于y 轴的直线分别交双曲线于A 、B 两点，连接OA 、OB ，则△AOB 的面积为（）A ．1B ．2C ．3D ．411（2010江苏盐城）如图，A 、B 是双曲线 y = kx (k >0) 上的点， A 、B 两点的横坐标分别是a 、2a ，线段AB 的延长线交x 轴于点C ，若S △AOC =6．则k= ．第13题图12（2010 山东济南）若1122()()A x y B x y ，，，是双曲线3y x=上的两点，且120x x >>，则12_______y y {填“>”、“=”、“<”}．13（2010湖北武汉）如图，直线y＝3x b -+与y 轴交于点A ，与双曲线y ＝kx在第一象限交于点B ，C 两点，且AB ⋅AC ＝4，则k ＝． 14（2010陕西西安）已知),(),,(2211y x B y x A 都在反比例函数xy 6=的图象上。

反比例函数课件

反比例函数与实际问题的应用
1 经济学
反比例函数可以用于描述商品的需求和价格的关系。
2 物理学
反比例函数可以用于描述物体的速度和时间的关系。
3 工程学
4 生物学
反比例函数可以用于描述电阻与电流的关系。
反比例函数可以用于描述生物种群的增长和资源的关系。
简单的反比例函数例题
例题1
已知某种物体的质量与体积成反比，当质量为8时，体积为6。求该物体的质量为12时，体积为多少？
当反比例函数的解析式为分式时，解题的方法与简单例题类似，只是需要通过代入法或正比例的求解方法进行计算。
练习题目与答案解析
1
题目1
已知一根长10米的绳子均匀地系在8个钉子上，如图所示。绳子从钉子1到钉子8 的长度比为3:1 :2 :1 :2 :1 :4 :3 。求每段绳子的长度。
2Hale Waihona Puke 题目2已知电阻与电流成反比，当电流为4A时，电阻为10欧姆。求电流为8A时，电阻为多少欧姆？
反比例函数ppt课件
欢迎来到反比例函数ppt课件！通过本课件，你将学到反比例函数的定义、图像、性质以及实际应用。我会带你从简单例题到解析式为分式的例题，并提供练习题目与答案解析。让我们开始吧！
反比例函数的定义
反比例函数是指一个函数，其自变量和因变量之间成反比关系。当自变量增大时，因变量就会减小；当自变量减小时，因变量就会增大。
3
题目3
某种物体的密度与体积成反比，当体积为20时，密度为5。求该物体的体积为8 时，密度为多少？
例题2
小明骑自行车到学校的时间与他的速度成反比，当速度是10km/h时，他需要30分钟到达学校。问他以15km/h的速度骑车到学校需要多长时间？

2023年河北省中考数学复习全方位第13讲反比例函数及其应用课件

4
.
返回子目录
7. (2020·河北,19)如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每

个台阶凸出的角的顶点记作Tm(m为1~8的整数).函数y= (x<0)的图象为曲线L.
(1)若L过点T1,则k= -16
;
(2)若L过点T4,则它必定还过另一点Tm,则m= 5
;
(3)若曲线L使得T 1 ~T 8 这些点分布在它的两侧,每侧各4个点,则k的整数值有
(2)通过计算,说明一次函数y=kx+3-3k
(k≠0)的图象一定过点C;
(3)对于一次函数y=kx+3-3k(k≠0),当y
随x的增大而增大时,确定点P横坐标的取值范围(不必写出过程).
返回子目录
解:(1)∵点B,C的横坐标相等,∴BC⊥x轴.
∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.

∵当x=4时,y= =1,∴点N在反比例函数y= 的图象上.
(3)4≤m≤8.
考点梳理
考点 1
反比例函数的概念
考点 2
反比例函数的图象及性质
考点 3
反比例函数解析式的确定
返回子目录
2
考点1
考点梳理
反比例函数的概念
1. 定义:一般地,形如①

y=

(k是常数,k≠0)的函数,叫反比例函数,其中x
是自变量,y是函数.自变量x的取值范围是x≠0.

2. 三种表达式(k为常数,k≠0):y= ;y=kx-1;xy=k.
返回子目录
考点2
反比例函数的图象及性质
1. 反比例函数图象与性质

第13讲反比例函数

(2013.河南)20.(9分)如图,矩形 OABC的顶点A、C分别在x轴和y
轴上,点B 的坐标为(2,3) .双曲线 y=k/x(x＞0)的图
像经过BC的中点D，且与AB交于点E ,连接DE 。
(1)求k的值及点E的坐标；
(2)若点F是OC边上一点，且△FBC
∽ △DEB ，求直线FB的解析式.
考点梳理
于点A(1，a),则k＝
.
(2014•河南)20.(9分)如图，在直角梯形OABC中，BC∥AO，
∠AOC=90°，点A，B的坐标分别为(5，0)，(2，6)，点D为AB上
一点，且BD=2AD，双曲线y= k/x
（k＞0）经过点D，交BC于点E．
（1）求双曲线的解析式；
（2）求四边形ODBE的面积．
复习大讲义
2、讨论交流“考点梳理”
要求：（1分钟）解决自己的疑惑、加深对概念的理解和记忆。
考点梳理
典例精析
当堂训练
复习大讲义
3、课堂展示：（2分钟）
(1)本节课复习了哪些知识点？ (2)你认为哪些是易错点？ (3)你认为哪些是重点、易考点？
考点梳理
典例精析
当堂训练
复习大讲义
(2015河南)11.(3分)如图，直线 y=kx与双曲线 y=2/x(x＞0)交
典例精析
当堂训练
复习大讲义
4、典例精析：《讲义》例1—例4
要求：（4分钟） (1)先自己解答以下各例题； (2)再快速浏览解析，对比思路； (3)画出自己不会做、看不懂的。
考点梳理
典例精析
当堂训练
复习大讲义
5、讨论交流：
要求：（2分钟） (1)通过交流尽力解决自己的困难； (2)通过交流还有解决不了的问题，也要弄清是哪方面的问题； (3)总结出你认为的高频考点。

人教版数学九年级上册第13讲反比例函数-课件

－2
2
【思路点拨】根据反比例函数的性质可以得到△AOB的面积等于|k|的一半，由此可以得到它们的关系；由点 A的坐标以及AB∥x轴，可得出点B的坐标，从而得出AD、AB的长度，利用矩形的面积公式即可得出结论．
【思路点拨】根据点A坐标，以及AB＝3BD求出D坐标，代入反比例函数解析式求出k的值；直线y＝3x与反比例函数解析式联立方程组即可求出点C坐标；作C关于y轴的对称点C′，连接C′D交y轴于M，则d＝MC＋ MD最小，得到C′点坐标，求得直线C′D的解析式，直线与y轴的交点即为所求．
都二
能分
运浇
用灌
好，
“八
二分八等Βιβλιοθήκη 定待律；”二
，分
我管
们教
一，
起八
，分
静放
待手
花；
开二
。分
成
➢ Pure of heart， life is full of sweet and joy!
绩，
八
分
方
法
。
愿
全
天
下
所
有
父
母
我们，还在路上……
第13讲反比例函数
D
－2 1
【思路点拨】反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．
A
A
解析：∵k1＜0＜k2，b＝－1＜0，∴直线过第二、三、四象限；双曲线位于第一、三象限．故选A. 【思路点拨】反比例函数的图象是中心对称图形，则它与经过原点的直线的两个交点一定关于原点对称；根据反比例函数的图象性质及正比例函数的图象性质可作出判断．

第13讲反比例函数

上一页
下一页
考点知识精讲
首页
(2)k＜0⇔图象(双曲线)的两个分支分别在第二、四象限，如图 ②所示．图象自左向右是上升的⇔当x＜0或x＞0时，y随x的增大而增大
(或y随x的减小而减小)．
宇轩图书
上一页
下一页
考点知识精讲
首页
考点三反比例函数解析式的确定由于反比例函数的关系式中只有一个未知数，因此只需已知一组对应值就可以．待定系数法求解析式的步骤： (1)设出含有待定系数的函数解析式； (2)把已知条件代入解析式，得到关于待定系数的方程； (3)解方程求出待定系数．
比例函数 y＝x2的图象，则关于 x 的方程 kx＋b＝2x的解为(
)
宇轩图书
上一页
下一页
考点训练
首页
A．x1＝1，x2＝2 B．x1＝－2，x2＝－1 C．x1＝1，x2＝－2 D．x1＝2，x2＝1
【解析】y＝kx＋b 与 y＝2x图象的交点横坐标即为 kx＋b
宇轩图书
上一页
下一页
举一反三
首页
1．若反比例函数 y＝kx的图象经过点(－3,2)，则 k 的值为(
)
A．－6
B．6
C．－5
D．5
答案：A
2．已知反比例函数 y＝1x，下列结论不．正．确．的是(
)
A．图象经过点(1,1) B．图象在第一、三象限 C．当 x>1 时，0<y<1 D．当 x<0 时，y 随着 x 的增大而增大
∴AB＝a2－(－4a)＝a6.∴S△ABC＝12AB·OP＝12×6a×a＝3.
宇轩图书
上一页
下一页
中考典例精析
首页
(2011·成都) 如图所示，已知反比例函数 y＝

第13讲 反比例函数

中考数学复习第13课时《反比例函数》说课稿

第十三讲反比例函数详解

中考数学专题复习讲座第十三讲反比例函数

【大师特稿】中考数学一轮复习第13讲：反比例函数教案

中考总复习数学13-第一部分 第13讲 反比例函数及其应用

中考复习：反比例函数

第13课时 反比例函数(共26张PPT)

(中考复习)第13讲 反比例函数及其图象

13讲：反比例函数

反比例函数课件

2023年河北省中考数学复习全方位第13讲 反比例函数及其应用 课件

第13讲反比例函数

人教版数学九年级上册第13讲 反比例函数-课件

第13讲反比例函数

第13讲反比例函数

中考总复习数学13-第一部分第13讲反比例函数及其应用

第13课时反比例函数(共26张PPT)

(中考复习)第13讲反比例函数及其图象

2023年河北省中考数学复习全方位第13讲反比例函数及其应用课件

人教版数学九年级上册第13讲反比例函数-课件