高考数学(理科)异构异模复习对点练:2-7-2函数图象的应用
【学霸优课】2017数学(理)一轮对点训练:2-7-2 函数图象的应用 Word版含解析

1.函数f (x )=ax +b(x +c )2的图象如图所示,则下列结论成立的是( )A .a >0,b >0,c <0B .a <0,b >0,c >0C .a <0,b >0,c <0D .a <0,b <0,c <0 答案 C解析 ∵f (x )=ax +b(x +c )2的图象与x ,y 轴分别交于N ,M ,且点M的纵坐标与点N 的横坐标均为正,∴x =-b a >0,y =bc 2>0,故a <0,b >0,又函数图象间断点的横坐标为正,∴-c >0,故c <0,故选C.2.已知函数f (x )=x 2+e x-12(x <0)与g (x )=x 2+ln (x +a )的图象上存在关于y 轴对称的点,则a 的取值范围是( )A.⎝ ⎛⎭⎪⎫-∞,1eB .(-∞,e) C.⎝ ⎛⎭⎪⎫-1e ,e D.⎝⎛⎭⎪⎫-e ,1e 答案 B解析 由已知得函数f (x )的图象关于y 轴对称的函数为h (x )=x 2+e -x -12(x >0).令h (x )=g (x ),得ln (x +a )=e -x-12,作函数M (x )=e -x-12的图象,显然当a ≤0时,函数y =ln (x +a )的图象与M (x )的图象一定有交点.当a >0时,若函数y =ln (x +a )的图象与M (x )的图象有交点,则ln a <12,则0<a < e.综上a < e.故选B.3.如图,函数f (x )的图象为折线ACB ,则不等式f (x )≥log 2(x +1)的解集是( )A .{x |-1<x ≤0}B .{x |-1≤x ≤1}C .{x |-1<x ≤1}D .{x |-1<x ≤2}答案 C解析在平面直角坐标系中作出函数y=log2(x+1)的图象如图所示.所以f(x)≥log2(x+1)的解集是{x|-1<x≤1},所以选C.4.已知函数y=f(x)的大致图象,如图所示,则函数y=f(x)的解析式应为()A.f(x)=e x ln xB.f(x)=e-x ln (|x|)C.f(x)=e x ln (|x|)D.f(x)=e|x|ln (|x|)答案 C解析由定义域是{x|x∈R,且x≠0},排除A;由函数图象知函数不是偶函数,排除D;当x→+∞时,f(x)=ln |x|e x→0,排除B,故选C.5.设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则不等式f(x)-f(-x)x<0的解集为()A.(-1,0)∪(1,+∞) B.(-∞,-1)∪(0,1)C.(-∞,-1)∪(1,+∞) D.(-1,0)∪(0,1)答案 D解析 f (x )为奇函数,所以不等式f (x )-f (-x )x <0化为f (x )x <0, 即xf (x )<0,f (x )的大致图象如图所示.所以xf (x )<0的解集为(-1,0)∪(0,1).6.对实数a 和b ,定义运算“□”:a □b =⎩⎪⎨⎪⎧a ,a -b ≤1,b ,a -b >1.设函数f (x )=(x 2-2)□(x -1),x ∈R .若函数y =f (x )-c 的图象与x 轴恰有两个公共点,则实数c 的取值范围是( )A .(-1,1]∪(2,+∞)B .(-2,-1]∪(1,2]C .(-∞,-2)∪(1,2]D .[-2,-1] 答案 B解析 令(x 2-2)-(x -1)≤1, 得-1≤x ≤2,∴f (x )=⎩⎪⎨⎪⎧x 2-2,-1≤x ≤2,x -1,x <-1或x >2.若y =f (x )-c 与x 轴恰有两个公共点,画函数f (x )的图象知实数c 的取值范围是(-2,-1]∪(1,2].7.已知函数f (x )=⎩⎪⎨⎪⎧sinπx ,0≤x ≤1,log 2014x ,x >1,若a ,b ,c 互不相等,且f (a )=f (b )=f (c ),则a +b +c 的取值范围是( )A .(1,2014)B .(1,2015)C .(2,2015)D .[2,2015]答案 C解析 函数f (x )=⎩⎪⎨⎪⎧sinπx ,0≤x ≤1,log 2014x ,x >1的图象如下图所示,不妨令a <b <c ,由正弦曲线的对称性可知a +b =1,而1<c <2014.所以2<a +b +c <2015,故选C.。
高考数学(文科)异构异模复习考案撬分法习题 第二章 函数的概念及其基本性质2-3-2 Word版含答案

1.定义在R 上的函数f (x )满足f (-x )=-f (x ),f (x -2)=f (x +2),且x ∈(-1,0)时,f (x )=2x +15,则f (log 220)=( ) A .-1 B.45C .1D .-45 答案 A解析 由f (x -2)=f (x +2),得f (x +4)=f (x ),∴f (x )的周期T =4,结合f (-x )=-f (x ),有f (log 220)=f (1+log 210)=f (log 210-3)=-f (3-log 210),∵3-log 210∈(-1,0),∴f (log 220)=-23-log 210-15=-45-15=-1.故选A. 2.函数f (x )=lg |sin x |是( )A .最小正周期为π的奇函数B .最小正周期为2π的奇函数C .最小正周期为π的偶函数D .最小正周期为2π的偶函数答案 C解析 易知函数的定义域为{x |x ≠k π,k ∈Z },关于原点对称,又f (-x )=lg |sin(-x )|=lg |-sin x |=lg |sin x |=f (x ),所以f (x )是偶函数,又函数y =|sin x |的最小正周期为π,所以函数f (x )=lg |sin x |是最小正周期为π的偶函数.故选C.3.已知函数f (x )是(-∞,+∞)上的奇函数,且f (x )的图象关于x =1对称,当x ∈时,f (x )=2x -1,则f (2013)+f (2014)的值为( )点击观看解答视频A .-2B .-1C .0D .1答案 D解析 ∵函数f (x )为奇函数,则f (-x )=-f (x ),又函数的图象关于x =1对称,则f (2+x )=f (-x )=-f (x ),∴f (4+x )=f =-f (x +2)=f (x ).∴f (x )的周期为4.又函数的图象关于x =1对称,∴f (0)=f (2),∴f (2013)+f (2014)=f (1)+f (2)=f (1)+f (0)=21-1+20-1=1.故选D.4.已知定义在R 上的奇函数f (x )满足f (x +1)=-f (x ),且在[0,1)上单调递增,记a =f ⎝ ⎛⎭⎪⎫12,b =f (2),c =f (3),则a ,b ,c 的大小关系为( ) A .a >b =cB .b >a =cC .b >c >aD .a >c >b答案 A解析 由题意得,f (x +2)=-f (x +1)=f (x ),即函数f (x )是以2为周期的奇函数,所以f (2)=f (0)=0.因为f (x +1)=-f (x ),所以f (3)=-f (2)=0.又f (x )在[0,1)上是增函数,于是有f ⎝ ⎛⎭⎪⎫12>f (0)=f (2)=f (3),即a >b =c .故选A. 5.已知函数f (x )=⎩⎪⎨⎪⎧ ⎝ ⎛⎭⎪⎫12x ,x ≥4,f x +,x <4,则f (2+log 23)的值为( )A.124B.112C.16D.13答案 A解析 ∵2+log 23<4,∴f (2+log 23)=f (3+log 23).∵3+log 23>4,∴f (2+log 23)=f (3+log 23)=⎝ ⎛⎭⎪⎫123+log 23=18×⎝ ⎛⎭⎪⎫12log 23=18×13=124.故选A. 6.若y =f (x )既是周期函数,又是奇函数,则其导函数y =f ′(x )( )A .既是周期函数,又是奇函数B .既是周期函数,又是偶函数C .不是周期函数,但是奇函数D .不是周期函数,但是偶函数答案 B解析 因为y =f (x )是周期函数,设其周期为T ,则有f (x +T )=f (x ),两边同时求导,得f ′(x +T )(x +T )′=f ′(x ),即f ′(x +T )=f ′(x ),所以导函数为周期函数.因为y =f (x )是奇函数,所以f (-x )=-f (x ),两边同时求导,得f ′(-x )(-x )′=-f ′(x ),即-f′(-x)=-f′(x),所以f′(-x)=f′(x),即导函数为偶函数,选B.。
2019-2020年高考数学异构异模复习第二章函数的概念及其基本性质2.7.1函数图象的识辨撬题文

2019-2020年高考数学异构异模复习第二章函数的概念及其基本性质2.7.1函数图象的识辨撬题文1.如图,长方形ABCD 的边AB =2,BC =1,O 是AB 的中点.点P 沿着边BC ,CD 与DA 运动,记∠BOP =x .将动点P 到A ,B 两点距离之和表示为x 的函数f (x ),则y =f (x )的图象大致为( )答案 B解析 由于f (0)=2,f ⎝ ⎛⎭⎪⎫π4=1+5,f ⎝ ⎛⎭⎪⎫π2=22<f ⎝ ⎛⎭⎪⎫π4,故排除选项C 、D ;当点P 在BC 上时,f (x )=BP +AP =tan x +4+tan 2x ⎝ ⎛⎭⎪⎫0≤x ≤π4,不难发现f (x )的图象是非线性的,排除选项A ,故选B.2.汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程.下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是( )A .消耗1升汽油,乙车最多可行驶5千米B .以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多C .甲车以80千米/小时的速度行驶1小时,消耗10升汽油D .某城市机动车最高限速80千米/小时.相同条件下, 在该市用丙车比用乙车更省油 答案 D解析 对于A 选项,从图中可以看出当乙车的行驶速度大于40 km/h 时的燃油效率大于5 km/L ,故乙车消耗1升汽油的行驶路程可大于5千米,所以A 错误.对于B 选项,由图可知甲车消耗汽油最少.对于C 选项,甲车以80 km/h 的速度行驶时的燃油效率为10 km/L ,故行驶1小时的路程为80千米,消耗8 L 汽油,所以C 错误,对于D 选项,当最高限速为80 km/h 且速度相同时丙车的燃油效率大于乙车的燃油效率,故用丙车比用乙车更省油,所以D 正确.3.函数f (x )=⎩⎪⎨⎪⎧ 3x x ≤1,log 13 x x >1,则y =f (1-x )的图象是( )答案 C解析 画出y =f (x )的图象,再作其关于y 轴对称的图象,得到y =f (-x )的图象,再将所得图象向右平移1个单位,得到y =f [-(x -1)]=f (-x +1)的图象,故选C.4.函数y =x |x |的图象大致是( )答案 A解析 y =x |x |=⎩⎪⎨⎪⎧ x 2 x ≥0,-x 2 x <0,借助二次函数的图象易知应选A.5.函数y =x ln |x ||x |的图象可能是( )答案 B解析 显然函数y =x ln |x ||x |为定义域上的奇函数,可排除选项A 、C ,而当x >0时,y =x ln x x =ln x ,排除选项D ,所以答案选B.6.函数f (x )=ln ⎝ ⎛⎭⎪⎫x -1x 的图象是( )答案 B解析 自变量x 满足x -1x =x 2-1x>0,当x >0时可得x >1,当x <0时可得-1<x <0,即函数f (x )的定义域是(-1,0)∪(1,+∞),据此排除选项A 、D.函数y =x -1x单调递增.故函数f (x )=ln ⎝ ⎛⎭⎪⎫x -1x 在(-1,0),(1,+∞)上单调递增.故选B.7.已知函数f (x )的图象如图所示,则f (x )的解析式可以是( )A .f (x )=ln |x |xB .f (x )=e x xC .f (x )=1x 2-1D .f (x )=x -1x答案 A解析 由函数图象可知,函数f (x )为奇函数,应排除B 、C ;若函数图象对应解析式为f (x )=x -1x ,则x →+∞时,f (x )→+∞,排除D.故选A.。
高考数学(文科)异构异模复习考案撬分法习题 第二章 函数的概念及其基本性质课时撬分练2-1 Word版含答案

………………………………………………………………………………………………时间:45分钟基础组1.已知集合A =,集合B =,则下列对应关系中,不能看作从A 到B 的映射的是( ) A .f :x →y =18xB .f :x →y =14xC .f :x →y =12xD .f :x →y =x答案 D解析 按照对应关系f :x →y =x ,对A 中某些元素(如x =8),B 中不存在元素与之对应.2. 函数f (x )=x +1-2x的定义域是( )点击观看解答视频A .(-3,0)B .(-3,0]C .(-∞,-3)∪(0,+∞)D .(-∞,-3)∪(-3,0)答案 A 解析 ∵f (x )=x +1-2x,∴要使函数f (x )有意义,需使⎩⎪⎨⎪⎧x +3>0,1-2x>0,即-3<x <0.3.设函数f (x )=⎩⎨⎧x ,x ≥0,-x ,x <0,若f (a )+f (-1)=2,则a =( )A .-3B .±3C .-1D .±1答案 D解析 当a ≥0时,f (a )=a ,由已知得a +1=2,得a =1;当a <0时,f (a )=-a ,由已知得-a +1=2,得a =-1,综上a =±1.4.已知函数f (n )=⎩⎪⎨⎪⎧n -3,n ≥10,f f n +,n <10.其中n ∈N *,则f (6)的值为( ) A .6 B .7 C .8 D .9答案 B解析 由函数解析式,可知f (6)=f (f (11))=f (8)=f (f (13))=f (10)=10-3=7. 5.已知函数g (x )=1-2x ,f =1-x 2x 2(x ≠0),则f ⎝ ⎛⎭⎪⎫12等于( ) A .1 B .3 C .15 D .30答案 C解析 令1-2x =12,得x =14,∴f ⎝ ⎛⎭⎪⎫12=1-116116=15,故选C.6.函数f (x )=11-x-x的最大值是( )A.45B.54C.34D.43 答案 D解析 1-x (1-x )=⎝ ⎛⎭⎪⎫x -122+34≥34,所以0<11-x -x ≤43.7.已知函数f (x )的定义域为(0,2],则函数f (x +1)的定义域为( ) A . C .[5,3) D .(0,5)答案 B解析 根据题意,得0<x +1≤2,即0<x +1≤4,解得-1<x ≤3,故选B.8.设函数f (x )=⎩⎪⎨⎪⎧x ,x ≥0,⎝ ⎛⎭⎪⎫12x,x <0,则f (f (-4))=________.答案 4解析 因为x =-4<0,所以f (-4)=⎝ ⎛⎭⎪⎫12-4=16,因为x =16>0,所以f (16)=16=4.9.函数f (x )=x +1-2x 的值域为________. 答案 (-∞,1]解析 函数的定义域为⎝ ⎛⎦⎥⎤-∞,12,令t =1-2x (t ≥0),则x =1-t 22.∴y =1-t 22+t =-12(t -1)2+1(t ≥0),故t =1(即x =0)时,y 有最大值1,故值域为(-∞,1].10.已知f (x )是二次函数,若f (0)=0,且f (x +1)=f (x )+x +1.求函数f (x )的解析式.解 设f (x )=ax 2+bx +c (a ≠0),又f (0)=0, ∴c =0,即f (x )=ax 2+bx . 又∵f (x +1)=f (x )+x +1.∴a (x +1)2+b (x +1)=ax 2+bx +x +1. ∴(2a +b )x +a +b =(b +1)x +1,∴⎩⎪⎨⎪⎧2a +b =b +1a +b =1,解得⎩⎪⎨⎪⎧a =12b =12.∴f (x )=12x 2+12x.11.甲同学家到乙同学家的途中有一公园,甲从家到公园的距离与乙从家到公园的距离都是2 km ,甲10时出发前往乙家.如图所示,表示甲从家出发到达乙家为止经过的路程y (km)与时间x (分)的关系.试写出y =f (x )的函数解析式.解 当x ∈,设y =k 1x +b 1,由已知得⎩⎪⎨⎪⎧b 1=0,30k 1+b 1=2,∴k 1=115,b 1=0,y =115x ;当x ∈(30,40)时,y =2; 当x ∈时,设y =k 2x +b 2,由⎩⎪⎨⎪⎧40k 2+b 2=2,60k 2+b 2=4,∴k 2=110,b 2=-2,y =110x -2,∴f (x )=⎩⎪⎨⎪⎧115x ,x ∈[0,30],2,x ∈,,110x -2,x ∈[40,60].12.已知函数f (x )=x 2-4ax +2a +6,x ∈R . (1)若函数的值域为函数y =log 12x 2-的定义域是( )A .B .(-3,-1)∪(1,2)C .D .(-2,-1)∪(1,2)答案 A解析 由题意得⎩⎪⎨⎪⎧log 12x 2-,x 2-1>0.即⎩⎪⎨⎪⎧x 2-1≤1,x 2-1>0,也就是1<x 2≤2,所以x∈.14.设函数f (x )=⎩⎨⎧ex -1, x <1,x 13 , x ≥1,则使得f (x )≤2成立的x 的取值范围是________.答案 (-∞,8]解析 f (x )≤2⇒⎩⎪⎨⎪⎧x <1,e x -1≤2或⎩⎨⎧x ≥1,x 13 ≤2⇒⎩⎪⎨⎪⎧x <1,x ≤ln 2+1或⎩⎪⎨⎪⎧x ≥1,x ≤8⇒x <1或1≤x ≤8⇒x ≤8,故填(-∞,8].15.若函数f (x )满足f (x )+2f (1-x )=x ,则f (x )的解析式为________. 答案 f (x )=23-x解析 ∵f (x )+2f (1-x )=x ,① ∴f (1-x )+2f (x )=1-x .②①-2×②,得f (x )=-x +23.16. 已知函数f (x )=⎩⎪⎨⎪⎧cx +1 x <c ,2-xc 2+c ≤x满足f (c 2)=98.(1)求常数c 的值; (2)解不等式f (x )>28+1.点击观看解答视频解 (1)∵0<c <1,∴0<c 2<c , 由f (c 2)=98得c 3+1=98,解得c =12.(2)由(1)得f (x )=⎩⎪⎨⎪⎧12x +1 ⎝⎛⎭⎪⎫0<x <12,2-4x+1 ⎝ ⎛⎭⎪⎫12≤x <1.由f (x )>28+1,得 当0<x <12时,则有12x +1>28+1,解得24<x <12;当12≤x <1时,则有2-4x+1>28+1,解得12≤x <58. 所以f (x )>28+1的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪24<x <58.。
2019-2020年高考数学异构异模复习第三章导数及其应用3.2.1函数的单调性与导数撬题理

2019-2020年高考数学异构异模复习第三章导数及其应用3.2.1函数的单调性与导数撬题理1.设函数f (x )=e x(2x -1)-ax +a ,其中a <1,若存在唯一的整数x 0使得f (x 0)<0,则a 的取值范围是( )A.⎣⎢⎡⎭⎪⎫-32e ,1 B.⎣⎢⎡⎭⎪⎫-32e ,34 C.⎣⎢⎡⎭⎪⎫32e ,34D.⎣⎢⎡⎭⎪⎫32e ,1答案 D解析 由题意可知存在唯一的整数x 0,使得e x 0(2x 0-1)<ax 0-a ,设g (x )=e x(2x -1),h (x )=ax -a ,由g ′(x )=e x (2x +1)可知g (x )在⎝⎛⎭⎪⎫-∞,-12上单调递减,在⎝⎛⎭⎪⎫-12,+∞上单调递增,作出g (x )与h (x )的大致图象如图所示,故⎩⎪⎨⎪⎧h0>g 0h-1≤g -1,即⎩⎪⎨⎪⎧a <1-2a ≤-3e ,所以32e≤a <1,故选D.2.设函数f ′(x )是奇函数f (x )(x ∈R )的导函数,f (-1)=0,当x >0时,xf ′(x )-f (x )<0,则使得f (x )>0成立的x 的取值范围是( )A .(-∞,-1)∪(0,1)B .(-1,0)∪(1,+∞)C .(-∞,-1)∪(-1,0)D .(0,1)∪(1,+∞) 答案 A 解析 令F (x )=f xx,因为f (x )为奇函数,所以F (x )为偶函数,由于F ′(x )=xf ′x -f x x 2,当x >0时,xf ′(x )-f (x )<0,所以F (x )=f xx在(0,+∞)上单调递减,根据对称性,F (x )=f xx在(-∞,0)上单调递增,又f (-1)=0,f (1)=0,数形结合可知,使得f (x )>0成立的x 的取值范围是(-∞,-1)∪(0,1).故选A.3.若定义在R 上的函数f (x )满足f (0)=-1,其导函数f ′(x )满足f ′(x )>k >1,则下列结论中一定错误的是( )A .f ⎝ ⎛⎭⎪⎫1k<1kB .f ⎝ ⎛⎭⎪⎫1k >1k -1C .f ⎝⎛⎭⎪⎫1k -1<1k -1D .f ⎝⎛⎭⎪⎫1k -1>k k -1答案 C解析 构造函数g (x )=f (x )-kx +1,则g ′(x )=f ′(x )-k >0,∴g (x )在R 上为增函数. ∵k >1,∴1k -1>0,则g ⎝ ⎛⎭⎪⎫1k -1>g (0). 而g (0)=f (0)+1=0, ∴g ⎝⎛⎭⎪⎫1k -1=f ⎝ ⎛⎭⎪⎫1k -1-k k -1+1>0, 即f ⎝⎛⎭⎪⎫1k -1>k k -1-1=1k -1,所以选项C 错误,故选C.4.已知函数f (x )=ax 3-3x 2+1,若f (x )存在唯一的零点x 0,且x 0>0,则a 的取值范围是( )A .(2,+∞)B .(1,+∞)C .(-∞,-2)D .(-∞,-1)答案 C解析 (1)当a =0时,显然f (x )有两个零点,不符合题意.(2)当a ≠0时,f ′(x )=3ax 2-6x ,令f ′(x )=0,解得x 1=0,x 2=2a.当a >0时,2a>0,所以函数f (x )=ax 3-3x 2+1在(-∞,0)与⎝ ⎛⎭⎪⎫2a ,+∞上为增函数,在⎝ ⎛⎭⎪⎫0,2a 上为减函数,因为f (x )存在唯一零点x 0,且x 0>0,则f (0)<0,即1<0,不成立. 当a <0时,2a<0,所以函数f (x )=ax 3-3x 2+1在⎝ ⎛⎭⎪⎫-∞,2a 和(0,+∞)上为减函数,在⎝ ⎛⎭⎪⎫2a ,0上为增函数,因为f (x )存在唯一零点x 0,且x 0>0,则f ⎝ ⎛⎭⎪⎫2a >0,即a ·8a 3-3·4a 2+1>0,解得a >2或a <-2,又因为a <0,故a 的取值范围为(-∞,-2).选C.5.已知函数f (x )=-2(x +a )ln x +x 2-2ax -2a 2+a ,其中a >0. (1)设g (x )是f (x )的导函数,讨论g (x )的单调性;(2)证明:存在a ∈(0,1),使得f (x )≥0在区间(1,+∞)内恒成立,且f (x )=0在区间(1,+∞)内有唯一解.解 (1)由已知,函数f (x )的定义域为(0,+∞),g (x )=f ′(x )=2(x -a )-2ln x -2⎝⎛⎭⎪⎫1+a x,所以g ′(x )=2-2x+2a x2=2⎝ ⎛⎭⎪⎫x -122+2⎝ ⎛⎭⎪⎫a -14x2当0<a <14时,g (x )在区间⎝ ⎛⎭⎪⎫0,1-1-4a 2,⎝ ⎛⎭⎪⎫1+1-4a 2,+∞上单调递增,在区间⎝⎛⎭⎪⎫1-1-4a 2,1+1-4a 2上单调递减; 当a ≥14时,g (x )在区间(0,+∞)上单调递增.(2)证明:由f ′(x )=2(x -a )-2ln x -2⎝⎛⎭⎪⎫1+a x=0,解得a =x -1-ln x1+x-1. 令φ(x )=-2⎝⎛⎭⎪⎫x +x -1-ln x 1+x -1ln x +x 2-2⎝ ⎛⎭⎪⎫x -1-ln x 1+x -1x -2⎝ ⎛⎭⎪⎫x -1-ln x 1+x -12+x -1-ln x1+x-1. 则φ(1)=1>0,φ(e)=-ee -21+e -1-2⎝ ⎛⎭⎪⎫e -21+e -12<0. 故存在x 0∈(1,e),使得φ(x 0)=0. 令a 0=x 0-1-ln x 01+x -1,u (x )=x -1-ln x (x ≥1). 由u ′(x )=1-1x≥0知,函数u (x )在区间(1,+∞)上单调递增. 所以0=u 11+1<u x 01+x -10=a 0<u e 1+e -1=e -21+e-1<1.即a 0∈(0,1).当a =a 0时,有f ′(x 0)=0,f (x 0)=φ(x 0)=0. 由(1)知,f ′(x )在区间(1,+∞)上单调递增, 故当x ∈(1,x 0)时,f ′(x )<0, 从而f (x )>f (x 0)=0;当x ∈(x 0,+∞)时,f ′(x )>0, 从而f (x )>f (x 0)=0.所以,当x ∈(1,+∞)时,f (x )≥0.综上所述,存在a ∈(0,1),使得f (x )≥0在区间(1,+∞)内恒成立,且f (x )=0在区间(1,+∞)内有唯一解.6.设函数f (x )=3x 2+axex(a ∈R ). (1)若f (x )在x =0处取得极值,确定a 的值,并求此时曲线y =f (x )在点(1,f (1))处的切线方程;(2)若f (x )在[3,+∞)上为减函数,求a 的取值范围. 解 (1)对f (x )求导得f ′(x )=6x +ae x-3x 2+ax exex 2=-3x 2+6-a x +aex, 因为f (x )在x =0处取得极值,所以f ′(0)=0,即a =0.当a =0时,f (x )=3x 2e x ,f ′(x )=-3x 2+6x e x,故f (1)=3e ,f ′(1)=3e , 从而f (x )在点(1,f (1))处的切线方程为y -3e =3e (x -1),化简得3x -e y =0.(2)由(1)知f ′(x )=-3x 2+6-a x +aex, 令g (x )=-3x 2+(6-a )x +a , 由g (x )=0解得x 1=6-a -a 2+366,x 2=6-a +a 2+366.当x <x 1时,g (x )<0,即f ′(x )<0,故f (x )为减函数; 当x 1<x <x 2时,g (x )>0,即f ′(x )>0,故f (x )为增函数; 当x >x 2时,g (x )<0,即f ′(x )<0,故f (x )为减函数. 由f (x )在[3,+∞)上为减函数, 知x 2=6-a +a 2+366≤3,解得a ≥-92,故a 的取值范围为⎣⎢⎡⎭⎪⎫-92,+∞.7.已知函数f (x )=e x -e -x-2x . (1)讨论f (x )的单调性;(2)设g (x )=f (2x )-4bf (x ),当x >0时,g (x )>0,求b 的最大值; (3)已知1.4142<2<1.4143,估计ln 2的近似值(精确到0.001).解 (1)f ′(x )=e x +e -x-2≥0,等号仅当x =0时成立,所以f (x )在(-∞,+∞)单调递增.(2)g (x )=f (2x )-4bf (x )=e 2x-e-2x-4b (e x -e -x)+(8b -4)x ,g ′(x )=2[e 2x +e -2x -2b (e x +e -x )+(4b -2)]=2(e x +e -x -2)(e x +e -x -2b +2).①当b ≤2时,g ′(x )≥0,等号仅当x =0时成立,所以g (x )在(-∞,+∞)单调递增. 而g (0)=0,所以对任意x >0,g (x )>0; ②当b >2时,若x 满足2<e x+e -x<2b -2,即0<x <ln (b -1+b 2-2b )时,g ′(x )<0.而g (0)=0,因此当0<x <ln (b -1+b 2-2b )时,g (x )<0.综上,b 的最大值为2. (3)由(2)知,g (ln 2)=32-22b +2(2b -1)ln 2.当b =2时,g (ln 2)=32-42+6ln 2>0,ln 2>82-312>0.6928;当b =324+1时,ln (b -1+b 2-2b )=ln 2,g (ln 2)=-32-22+(32+2)ln 2<0,ln 2<18+228<0.6934. 所以ln 2的近似值为0.693.。
2019-2020年高考数学异构异模复习第二章函数的概念及其基本性质2.6对数与对数函数课件理

(2)已知
a
2 3
=49(a>0),则
log2
3
a=__3______.
解析 (1)∵2a=5b=10,∴a=log210,b=log510,∴1a=lg 2,1b=lg 5,∴1a+1b=lg 2+lg 5=1.
(2)因为
a
2 3
=49(a>0),所以
a=94
3 2
=323,
故
log2
3
a=log2
3
323=3.
撬法·命题法 解题法
[考法综述] 考查对数运算,换底公式及对数函数的图象和性质,对数函数与幂指数函数相结合.综 合考查利用单调性比较大小、解不等式等是高考热点.主要以选择题、填空题形式出现.
命题法 对数的运算及对数函数的图象和性质的应用
典例 (1)函数 f(x)=2ln x 的图象与函数 g(x)=x2-4x+5 的图象的交点个数为( )
性
质
当 x>1 时, y>0 当 0<x<1 时, y<0
当 x>1 时,y<0 当 0<x<1 时, y>0
在(0,+∞)上是 增 函 在(0,+∞)上是 减 函
数
数
注意点 对数的运算性质及公式成立的条件
对数的运算性质以及有关公式都是在式子中所有的对数符号有意义的前提下才成立的,不能出现
log212=log2[(-3)×(-4)]=log2(-3)+log2(-4)等错误.
A.3
B.2
C.1
D.0
(2)已知函数 f(x)=|lg x|,若 a≠b,且 f(a)=f(b),则 a+b 的取值范围是( )
A.(1,+∞)
高考数学异构异模复习第三章导数及其应用3.1.2积分的

1.思维辨析
(1)设函数 y=f(x)在区间[a,b]上连续,则bf(x)dx=bf(t)dt.( √ )
a
a
(2)定积分一定是曲边梯形的面积.( × )
(3)若bf(x)dx<0,那么由 y=f(x),x=a,x=b 以及 x 轴所围成的图形一定在 x 轴下方.( × ) a
2.定积分1(2x+ex)dx 的值为( ) 0
A.e+2
B.e+1
C.e
D.e-1
1
解析 01(2x+ex)dx=(x2+ex)0 =1+e1-1=e,故选 C.
3.(1)已知 f(x)为偶函数且6f(x)dx=8,则 0
6 f(x)dx 等于( )
-6
A.y=1125x3-35x
B.y=1225x3-45x
C.y=1325x3-x
第三章 导数及其应用
第1讲 导数与积分
考点二 积分的运算及应用
撬点·基础点 重难点
1 定积分的几何意义
f(x) f(x)≥0
bf(x)dx 的几何意义
a
表示由直线 x=a,x=b,y=0 及曲线 y=f(x) 所围成的曲边梯形的面积
f(x)<0
表示由直线 x=a,x=b,y=0 及曲线 y=f(x) 所围成的曲边梯形的面积的 相反数
(5)ab1xdx=ln
xb
a
;
b
(6)abexdx=exa .
注意点 利用定积分求解曲边图形的面积应把握的两点
(1)准确确定被积函数,根据曲边图形的结构特征,结合定积分的运算性质,用上方曲线对应的函数解
析式减去下方曲线对应的函数解析式.
(2)准确确定定积分的上、下限,一般为曲边图形左、右两边对应点的横坐标.
18高考数学异构异模复习第二章函数的概念及其基本性质2.8函数与方程撬题理
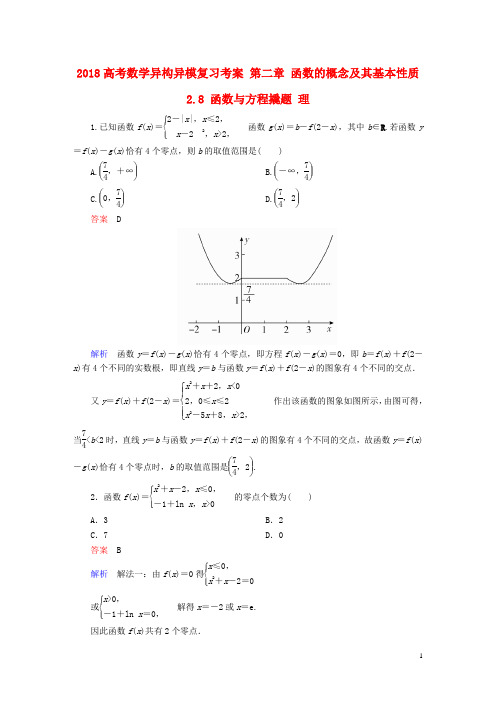
2018高考数学异构异模复习考案 第二章 函数的概念及其基本性质2.8 函数与方程撬题 理1.已知函数f (x )=⎩⎪⎨⎪⎧2-|x |,x ≤2,x -2,x >2,函数g (x )=b -f (2-x ),其中b ∈R .若函数y=f (x )-g (x )恰有4个零点,则b 的取值范围是( )A.⎝ ⎛⎭⎪⎫74,+∞B.⎝⎛⎭⎪⎫-∞,74 C.⎝ ⎛⎭⎪⎫0,74 D.⎝ ⎛⎭⎪⎫74,2答案 D解析 函数y =f (x )-g (x )恰有4个零点,即方程f (x )-g (x )=0,即b =f (x )+f (2-x )有4个不同的实数根,即直线y =b 与函数y =f (x )+f (2-x )的图象有4个不同的交点.又y =f (x )+f (2-x )=⎩⎪⎨⎪⎧x 2+x +2,x <02,0≤x ≤2x 2-5x +8,x >2,作出该函数的图象如图所示,由图可得,当74<b <2时,直线y =b 与函数y =f (x )+f (2-x )的图象有4个不同的交点,故函数y =f (x )-g (x )恰有4个零点时,b 的取值范围是⎝ ⎛⎭⎪⎫74,2. 2.函数f (x )=⎩⎪⎨⎪⎧x 2+x -2,x ≤0,-1+ln x ,x >0的零点个数为( )A .3B .2C .7D .0答案 B解析 解法一:由f (x )=0得⎩⎪⎨⎪⎧x ≤0,x 2+x -2=0或⎩⎪⎨⎪⎧x >0,-1+ln x =0,解得x =-2或x =e.因此函数f (x )共有2个零点.解法二:函数f (x )的图象如图所示,由图象知函数f (x )共有2个零点.3.设f (x )=e x+x -4,则函数f (x )的零点位于区间( ) A .(-1,0) B .(0,1) C .(1,2) D .(2,3)答案 C解析 ∵f (x )=e x+x -4,∴f ′(x )=e x+1>0,∴函数f (x )在R 上单调递增.对于A 项,f (-1)=e -1+(-1)-4=-5+e -1<0,f (0)=-3<0,f (-1)f (0)>0,A 不正确;同理可验证B 、D 不正确.对于C 项,∵f (1)=e +1-4=e -3<0,f (2)=e 2+2-4=e 2-2>0,f (1)f (2)<0.故f (x )的零点位于区间(1,2).4.设函数f (x )=⎩⎪⎨⎪⎧2x-a ,x <1,x -a x -2a ,x ≥1.(1)若a =1,则f (x )的最小值为________;(2)若f (x )恰有2个零点,则实数a 的取值范围是________.答案 (1)-1 (2)⎣⎢⎡⎭⎪⎫12,1∪[2,+∞) 解析 (1)若a =1,则f (x )=⎩⎪⎨⎪⎧2x-1,x <1x -x -,x ≥1,作出函数f (x )的图象如图所示.由图可得f (x )的最小值为-1.(2)当a ≥1时,要使f (x )恰有2个零点,需满足21-a ≤0,即a ≥2,所以a ≥2,当a <1时,要使f (x )恰有2个零点,需满足⎩⎪⎨⎪⎧a <1≤2a21-a >0,解得12≤a <1.综上,实数a 的取值范围为⎣⎢⎡⎭⎪⎫12,1∪[2,+∞). 5.函数f (x )=4cos 2x 2cos ⎝ ⎛⎭⎪⎫π2-x -2sin x -|ln (x +1)|的零点个数为________.答案 2解析 因为f (x )=4cos 2x 2cos ⎝ ⎛⎭⎪⎫π2-x -2sin x -|ln (x +1)|=2(1+cos x )·sin x -2sin x -|ln (x +1)|=sin2x -|ln (x +1)|,所以函数f (x )的零点个数为函数y =sin2x 与y =|ln (x +1)|图象的交点的个数.函数y =sin2x 与y =|ln (x +1)|的图象如图所示,由图知,两函数图象有2个交点,所以函数f (x )有2个零点.6.设x 3+ax +b =0,其中a ,b 均为实数.下列条件中,使得该三次方程仅有一个实根的是________.(写出所有正确条件的编号)①a =-3,b =-3;②a =-3,b =2;③a =-3,b >2;④a =0,b =2;⑤a =1,b =2. 答案 ①③④⑤解析 令f (x )=x 3+ax +b ,则f ′(x )=3x 2+a .对于①,由a =b =-3,得f (x )=x 3-3x -3,f ′(x )=3(x +1)(x -1),f (x )极大值=f (-1)=-1<0,f (x )极小值=f (1)=-5<0,函数f (x )的图象与x 轴只有一个交点,故x 3+ax +b =0仅有一个实根;对于②,由a =-3,b =2,得f (x )=x 3-3x +2,f ′(x )=3(x +1)(x -1),f (x )极大值=f (-1)=4>0,f (x )极小值=f (1)=0,函数f (x )的图象与x 轴有两个交点,故x 3+ax +b =0有两个实根;对于③,由a =-3,b >2,得f (x )=x 3-3x +b ,f ′(x )=3(x +1)(x -1),f (x )极大值=f (-1)=2+b >0,f (x )极小值=f (1)=b -2>0,函数f (x )的图象与x 轴只有一个交点,故x 3+ax +b =0仅有一个实根;对于④,由a =0,b =2,得f (x )=x 3+2,f ′(x )=3x 2≥0,f (x )在R 上单调递增,函数f (x )的图象与x 轴只有一个交点,故x 3+ax +b =0仅有一个实根;对于⑤,由a =1,b =2,得f (x )=x 3+x +2,f ′(x )=3x 2+1>0,f (x )在R 上单调递增,函数f (x )的图象与x 轴只有一个交点,故x 3+ax +b =0仅有一个实根.7.已知函数f (x )=⎩⎪⎨⎪⎧x 3,x ≤a ,x 2,x >a .若存在实数b ,使函数g (x )=f (x )-b 有两个零点,则a 的取值范围是________.答案 (-∞,0)∪(1,+∞)解析 令φ(x )=x 3(x ≤a ),h (x )=x 2(x >a ),函数g (x )=f (x )-b 有两个零点,即函数y =f (x )的图象与直线y =b 有两个交点,结合图象可得a <0或φ(a )>h (a ),即a <0或a 3>a 2,解得a <0或a >1,故a ∈(-∞,0)∪(1,+∞).8.已知函数f (x )=e x -ax 2-bx -1,其中a ,b ∈R ,e =2.71828…为自然对数的底数. (1)设g (x )是函数f (x )的导函数,求函数g (x )在区间[0,1]上的最小值; (2)若f (1)=0,函数f (x )在区间(0,1)内有零点,求a 的取值范围. 解 (1)由f (x )=e x-ax 2-bx -1,有g (x )=f ′(x )=e x-2ax -b . 所以g ′(x )=e x-2a .因此,当x ∈[0,1]时,g ′(x )∈[1-2a ,e -2a ].当a ≤12时,g ′(x )≥0,所以g (x )在[0,1]上单调递增,因此g (x )在[0,1]上的最小值是g (0)=1-b ;当a ≥e2时,g ′(x )≤0,所以g (x )在[0,1]上单调递减,因此g (x )在[0,1]上的最小值是g (1)=e -2a -b ;当12<a <e2时,令g ′(x )=0,得x =ln (2a )∈(0,1). 所以函数g (x )在区间[0,ln (2a )]上单调递减,在区间(ln (2a ),1]上单调递增. 于是,g (x )在[0,1]上的最小值是g (ln (2a ))=2a -2a ln (2a )-b . 综上所述,当a ≤12时,g (x )在[0,1]上的最小值是g (0)=1-b ;当12<a <e2时,g (x )在[0,1]上的最小值是g (ln (2a ))=2a -2a ln (2a )-b ; 当a ≥e2时,g (x )在[0,1]上的最小值是g (1)=e -2a -b .(2)设x 0为f (x )在区间(0,1)内的一个零点,则由f (0)=f (x 0)=0可知,f (x )在区间(0,x 0)上不可能单调递增,也不可能单调递减.则g (x )不可能恒为正,也不可能恒为负. 故g (x )在区间(0,x 0)内存在零点x 1. 同理g (x )在区间(x 0,1)内存在零点x 2. 所以g (x )在区间(0,1)内至少有两个零点.由(1)知,当a ≤12时,g (x )在[0,1]上单调递增,故g (x )在(0,1)内至多有一个零点.当a ≥e2时,g (x )在[0,1]上单调递减,故g (x )在(0,1)内至多有一个零点.所以12<a <e 2.此时g (x )在区间[0,ln (2a )]上单调递减,在区间(ln (2a ),1]上单调递增. 因此x 1∈(0,ln (2a )],x 2∈(ln (2a ),1),必有g (0)=1-b >0,g (1)=e -2a -b >0. 由f (1)=0有a +b =e -1<2,有g (0)=1-b =a -e +2>0,g (1)=e -2a -b =1-a >0.解得e -2<a <1.当e -2<a <1时,g (x )在区间[0,1]内有最小值g (ln (2a )). 若g (ln (2a ))≥0,则g (x )≥0(x ∈[0,1]),从而f (x )在区间[0,1]上单调递增,这与f (0)=f (1)=0矛盾,所以g (ln (2a ))<0.又g(0)=a-e+2>0,g(1)=1-a>0,故此时g(x)在(0,ln (2a))和(ln (2a),1)内各只有一个零点x1和x2.由此可知f(x)在[0,x1]上单调递增,在(x1,x2)上单调递减,在[x2,1]上单调递增.所以f(x1)>f(0)=0,f(x2)<f(1)=0,故f(x)在(x1,x2)内有零点.综上可知,a的取值范围是(e-2,1).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.函数f (x )=
ax +b
x +c 2
的图象如图所示,则下列结论成立的是( )
A .a >0,b >0,c <0
B .a <0,b >0,c >0
C .a <0,b >0,c <0
D .a <0,b <0,c <0 答案 C 解析 ∵f (x )=
ax +b
x +c 2
的图象与x ,y 轴分别交于N ,M ,且点M 的纵坐标与点N 的
横坐标均为正,∴x =-b a >0,y =b
c 2>0,故a <0,b >0,又函数图象间断点的横坐标为正,∴
-c >0,故c <0,故选C.
2.已知函数f (x )=x 2+e x -1
2(x <0)与g (x )=x 2+ln (x +a )的图象上存在关于y 轴对称的点,
则a 的取值范围是( )
A.⎝⎛⎭⎫-∞,1e B .(-∞,e) C.⎝
⎛⎭
⎫-
1
e ,e D.⎝
⎛⎭
⎫
-e ,
1e 答案 B
解析 由已知得函数f (x )的图象关于y 轴对称的函数为h (x )=x 2+e -
x -12
(x >0).
令h (x )=g (x ),得ln (x +a )=e -x -12,作函数M (x )=e -
x -12的图象,显然当a ≤0时,函
数y =ln (x +a )的图象与M (x )的图象一定有交点.
当a >0时,若函数y =ln (x +a )的图象与M (x )的图象有交点,则ln a <1
2,则0<a < e.综
上a < e.故选B.
3.如图,函数f (x )的图象为折线ACB ,则不等式f (x )≥log 2(x +1)的解集是( )
A .{x |-1<x ≤0}
B .{x |-1≤x ≤1}
C .{x |-1<x ≤1}
D .{x |-1<x ≤2}
答案 C
解析 在平面直角坐标系中作出函数y =log 2(x +1)的图象如图所示.所以f (x )≥log 2(x +1)的解集是{x |-1<x ≤1},所以选C.
4.已知函数y =f (x )的大致图象,如图所示,则函数y =f (x )的解析式应为( ) A .f (x )=e x ln x B .f (x )=e -
x ln (|x |)
C .f (x )=e x ln (|x |)
D .f (x )=e |x |ln (|x |) 答案 C
解析 由定义域是{x |x ∈R ,且x ≠0},排除A ;由函数图象知函数不是偶函数,排除D ;当x →+∞时,f (x )=ln |x |
e
x →0,排除B ,故选C.
5.设奇函数f (x )在(0,+∞)上为增函数,且f (1)=0,则不等式f x -f -x
x <0的解
集为( )
A .(-1,0)∪(1,+∞)
B .(-∞,-1)∪(0,1)
C .(-∞,-1)∪(1,+∞)
D .(-1,0)∪(0,1)
答案 D
解析 f (x )为奇函数,所以不等式f x -f -x x <0化为f x
x <0,
即xf (x )<0,f (x )的大致图象如图所示.所以xf (x )<0的解集为(-1,0)∪(0,1).
6.对实数a 和b ,定义运算“□”:a □b =⎩
⎪⎨⎪⎧
a ,a -
b ≤1,
b ,a -b >1.设函数f (x )=(x 2-2)□(x -1),x
∈R.若函数y =f (x )-c 的图象与x 轴恰有两个公共点,则实数c 的取值范围是( )
A .(-1,1]∪(2,+∞)
B .(-2,-1]∪(1,2]
C .(-∞,-2)∪(1,2]
D .[-2,-1] 答案 B
解析 令(x 2-2)-(x -1)≤1, 得-1≤x ≤2,
∴f (x )=⎩
⎪⎨⎪⎧
x 2-2,-1≤x ≤2,
x -1,x <-1或x >2.
若y =f (x )-c 与x 轴恰有两个公共点,画函数f (x )的图象知实数c 的取值范围是(-2,-1]∪(1,2].
7.已知函数f (x )=⎩⎪⎨⎪
⎧
sinπx ,0≤x ≤1,log 2014
x ,x >1,若a ,b ,c 互不相等,且f (a )=f (b )=f (c ),则a +b
+c 的取值范围是( )
A .(1,2014)
B .(1,2015)
C .(2,2015)
D .[2,2015]
答案 C
解析 函数f (x )=⎩⎪⎨⎪
⎧
sinπx ,0≤x ≤1,log 2014
x ,x >1的图象如下图所示,不妨令a <b <c ,
由正弦曲线的对称性可知a +b =1,而1<c <2014.所以2<a +b +c <2015,故选C.。
