第四讲 刚体平面运动
理论力学PPT课件第4章 刚体的平面运动

2024年3月15日
1. 轮C作平面运动,
C1为其速度瞬心,C。
2. BD作平面运动,
C2为其速度瞬心,BD。
3. AB作平面运动,
C3为其速度瞬心,AB。
43
平面图形在任一瞬时的运动可以 视为绕速度瞬心的瞬时转动,速度瞬 心又称为平面图形的瞬时转动中心。 若点C 为速度瞬心,则任意一点A的速
度大小为 vA AC ω 方向A C,指
16
车轮的运动分解
车轮的平面运动可以看成 是车轮随同车厢的平移和 相对车厢的转动的合成.
车轮相对定系(Oxy)的平面运动(绝对运动)
车厢(动系 A x y ) 相对定系的平移(牵连运动) 车轮相对车厢(动系 A x y )的转动(相对运动)
2024年3月15日
17
2024年3月15日
18
转动部分的角度、角速度、角加速度与基点的选择无关。
aB cos 300 aBnA
式中
aBnA
AB
2 AB
15 3 ( 2 )2 20 3 2cm/s2
3
3
aB aBnA / cos 300
40 2cm/s2
3
aB 8 2cm/s2
R9
2024年3月15日
64
例2. 已知 : OA = r AB = l、ω
求: vc、ac 解: 各联接点速度如图.
将 vB vA vBA 在AB连线上投影
vBA AB
有 [vB ]AB [vA ]AB
基点法投影式.
或 vB cos vA cos
2024年3月15日
53
结 论:S上任意两点的速度在这两点
连线上投影相等. 意 义:刚体上两点距离不变. 注 意:仅在两点连线上成立.
理论力学经典课件-第四章 刚体的平面运动

刚体运动的基本方程
我们可以利用牛顿运动定律和刚体平衡的条件,推导出描述刚体运动的基本 方程。
刚体的旋转运动
刚体的旋转运动大小和方向都与作用力矩有关。通过研究刚体的转动定律,我们可以了解刚体的旋转运 动规律。
刚体的转动惯量
刚体的转动惯量是衡量刚体对旋转运动的惯性大小的物理量。它与刚体的质 量分布和轴线的位置有关。
理论力学经典课件-第四 章 刚体的平面运动
在这一章中,我们将对刚体的平面运动进行详细的介绍。内容包括刚体的定 义和特性、平面运动概述、自由度、基本方程以及旋转运动。让我们一起探 索刚体运动的奥秘!
刚体的定义和特性
刚体是指在运动或静止过程中形状不变的物体。它具有固定的质量和几何形状,不受外力的影响而发生 形变。刚体的特性使得我们能够研究它们的平面运动。
பைடு நூலகம்
刚体的平动与转动的动力学方 程
刚体同时进行平动和转动时,动力学方程描述了刚体受力和受力矩的关系, 以及刚体的运动状态。
刚体的平面运动概述
1
平动
刚体在平面内做直线运动,所有点的速度矢量相等。
2
转动
刚体绕固定轴进行旋转运动,相对于轴线各点的运动速度不同。
3
平动与转动的组合
刚体可以同时进行平动和转动,例如滚动。
刚体的自由度
平动自由度
在平面上,刚体有3个平动自由度,可以在x 轴、y轴和绕z轴的转动自由度。
转动自由度
刚体有3个转动自由度,分别对应绕x轴、y 轴和z轴的转动。
4刚体的平面运动

A2
M
刚体的平面运动可以简化为平面图形在其自身平面S内的运动。
3 刚体平面运动的分解
平面图形S在其平面上的位置完 全可由图形内任意线段O'M的位置来 确定,而要确定此线段的位置,只需 确 定 线 段 上 任 一 点 O' 的 位 置 和 线 段 O'M与固定坐标轴Ox间的夹角 即可。 点O'的坐标和 角都是时间的函数, 即 y S M
以A为基点,分析点B的速度。
vB v A vBA
vBA wII BA wO (r1 r2 ) vA
vBA与vA垂直且相等,点B的速度
2 2 vB vA vBA 2vA 2wO (r1 r2 )
vC vA vB vBA vA B vA D vCA C A II wII
例7 直杆AB与圆柱O相切于D点, 杆的A端以 vA 60cm s匀速向前滑动, B r ,圆柱与地面、圆 10 cm 圆柱半径 柱与直杆之间均无滑动,如图,求 w 时圆柱的角速度。 60 O 解一:圆柱作平面运动,其 C1点,设其角速度为 w 。 瞬心在
w AB
D
C2
vD
3 刚体平面运动的分解
刚体上每一点都在与固定 平面M平行的平面内运动。 若作一平面N与平面M平行, 并以此去截割刚体得一平 面图形S。 可知该平面图 形S始终在平面N内运动。 因而垂直于图形S的任一条 直线A1A2必然作平动。 A1A2 的运动可用其与图形 S的交点 A的运动来替代。
A1 N A S
vCA
N
S
C
vA
A
vC vA w AC
如果取AC= vA /w ,则
vC vA w AC 0
08第四章 刚体的平面运动

3、平面运动的运动方程 、
y
P
O′
ϕ
S
yO′
O
xO′
x
xO′ = f1 (t ) yO′ = f 2 (t )
平面运动的运动方程
ϕ = f 3 (t )
4、平面运动可视为平动和转动的合成运动 、
y
P
O′
ϕ
S
yO′
O
xO′
x
当平面图形S 平面内运动时, 保持不变, 当平面图形 在Oxy平面内运动时,若 ϕ 保持不变,则 平面内运动时 刚体作平面平动; 保持不变, 点不动, 刚体作平面平动;若xO′和yO′保持不变,即O′点不动,则刚体 点不动 点作定轴转动。 绕O′点作定轴转动。当刚体作平面运动时 O′, yO′和ϕ 都随时 点作定轴转动 当刚体作平面运动时x 间而变化, 间而变化,可见平面图形在其平面内的运动是由平动和转动 组合而成的。 组合而成的。
取点A为 基点 为
v aB = v eB + v rB
vB = vA + vBA
B
vB = v A + vBA
vA
A
点 A: 基点
平面图形上任意一点的速度等于 基点的速度和相对于基点转动的速度 的矢量和。 的矢量和。
基点法是求平面运动图形上点的速度的基本方法。 基点法是求平面运动图形上点的速度的基本方法。 此式表明了平面图形上任意两点的速度之间的关系。 此式表明了平面图形上任意两点的速度之间的关系。
2、确定速度瞬心位置的常用方法 1) 已知条件: 已知条件: 平面图形的角速度以及其上某点A的速度 的速度。 平面图形的角速度以及其上某点 的速度。
vA A
将过A点沿 将过 点沿vA 方向的半直线顺角速度转 点沿 向转90° 其上可得: 向转 °,其上可得
刚体平面运动分解为平动和转动

对于平面图形 S 对静坐标系Oxy 做平面运动的一般情况,可在平面
图形上任选一点 A,并以 A点为原点作坐标系 Axy 。平面图形 S 运动时,坐标系随之运动,并保持其原点与 S 上的 A 点重合,并且
坐标轴 Ax ,Ay 的方位不变。为明确起见,令 Ax 和 Ay 轴始终分别
与Ox 和 Oy 轴平行,如图7-6所示。因此,Axy 是一平动坐标系,A
点称为基点。这样,平面图形 S 的运动就可以分解成为:
(1)跟随平动坐标系的平动,简称为随基 点的平动; (2)相对平动坐标系绕基点的转动,简称 为绕基点的转动。
图7-6
在平面图形上选 A点为基点,线段 AC 的转角为A ,如取另一 点 B 为基点,线段 BC的转角B ,如图7-7所示。这两个转角只
理论力学
刚体平面运动分解为平动和转动
从平面运动方程式(7-1)可看出,平面图形 S 的运动有两种特殊情况:
(1)若 常数,即平面图形在运动过程中,线段 B 的方位保持 不变。显然,这是平面图形在平面内做运动,平面图形上任一点的 运动与 A 点的运动相同,而 A 点的运动由运动方程式(7-1a)和式 (7-1b)二式给出。 (2)若 xA 和 yA同为常数,说明 A 点不动,平面图形将绕过 A 点且 垂直于平面图形的固定轴转动,其转动规律由运动方程式(7-1c) 给出。
选 B点为基点,则 AB 先随 B 点平动到 A2B1 ,再绕 B1 点转动 到 A1B1 ,转角为1 ,显然有 A1B2 ∥ A2B1 ,从而 1 ,并且
转向相同。
图7-8
平面图形分解的平动部分与基点选择有关,转动部分 与基点选择无关。
理论力学
在一般情况下,刚体的平面运动可以看成是平动和转动这两种 刚体的基本运动合成的结果。也就是说,平面运动可分解成平 动和转动。例如,轮子在地面上滚动,如图7-5所示,轮子从位 置Ⅰ 到位置Ⅱ 的平面运动可以看成是:① 轮子随轮心 O平动到 假想的中间位置Ⅰ;② 再由该中间位置绕 O轴转动到位置Ⅱ 。 当然轮子的平面运动并不是先平动而后转动,它的运动是一个 连续过程,应当看成为同时进行着平动和转动。
刚体平面运动动力学

av)c
作用在刚体上的力矩使刚体旋转,绕质心轴的角加速度为 z'
P.236 图 r
r
将力F沿作用线大小方向不变地滑移到 ,F不' 影响两种效果
7.27
作用在刚体上的力是滑移矢量
刚体力的三要素:大小、方向、作用线
4 刚体平面运动
二、作用于刚体上的力
2.力偶和力偶矩
力偶:大小相等方向相反彼此平行的一对力
平面运动动能定理
A外ຫໍສະໝຸດ Ek(1 2
mvc2
1 2
Ic2 )
P.240 例题 3
刚体平面运动的基本动力学方程:
v Fi
mavc
M I Z'
z' z'
力偶作用效果:
力偶不改变质心的运动状态 只改变刚体的转动状态
4 刚体平面运动
二、作用于刚体上的力
2.力偶和力r偶矩
r
F' O1
C
O2
F
Od' MZ O"
F O"C F O'C F ( O"C O'C )
4 刚体平面运动
v Fi
mavc
MZ' Iz' z' 0
二维平动:刚体作平面运动又只作平动
P.239 例题 2
4 刚体平面运动
三、刚体平面运动的动能
平面运动 = 平动 + 定轴转动 平面运动动能 = 随质心平动动能 + 绕质心轴转动的动能
Ek
1 2
mvc2
1 2
I c 2
4 刚体平面运动
刚体的平面运动
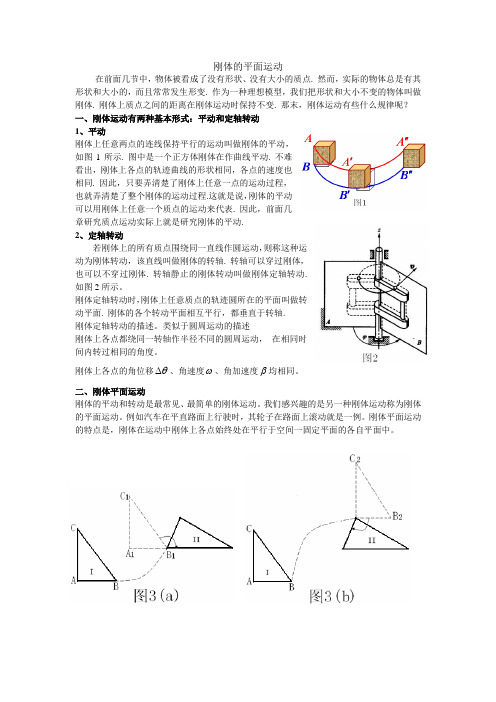
刚体的平面运动在前面几节中,物体被看成了没有形状、没有大小的质点. 然而,实际的物体总是有其形状和大小的,而且常常发生形变. 作为一种理想模型,我们把形状和大小不变的物体叫做刚体. 刚体上质点之间的距离在刚体运动时保持不变. 那末,刚体运动有些什么规律呢?一、刚体运动有两种基本形式:平动和定轴转动1、平动刚体上任意两点的连线保持平行的运动叫做刚体的平动,如图1所示. 图中是一个正方体刚体在作曲线平动. 不难看出,刚体上各点的轨迹曲线的形状相同,各点的速度也相同. 因此,只要弄清楚了刚体上任意一点的运动过程,也就弄清楚了整个刚体的运动过程.这就是说,刚体的平动可以用刚体上任意一个质点的运动来代表. 因此,前面几章研究质点运动实际上就是研究刚体的平动.2、定轴转动若刚体上的所有质点围绕同一直线作圆运动,则称这种运动为刚体转动,该直线叫做刚体的转轴. 转轴可以穿过刚体,也可以不穿过刚体. 转轴静止的刚体转动叫做刚体定轴转动.如图2所示。
刚体定轴转动时,刚体上任意质点的轨迹圆所在的平面叫做转动平面. 刚体的各个转动平面相互平行,都垂直于转轴.刚体定轴转动的描述。
类似于圆周运动的描述刚体上各点都绕同一转轴作半径不同的圆周运动,在相同时间内转过相同的角度。
刚体上各点的角位移θ∆、角速度ω、角加速度β均相同。
二、刚体平面运动刚体的平动和转动是最常见、最简单的刚体运动。
我们感兴趣的是另一种刚体运动称为刚体的平面运动。
例如汽车在平直路面上行驶时,其轮子在路面上滚动就是一例。
刚体平面运动的特点是,刚体在运动中刚体上各点始终处在平行于空间一固定平面的各自平面中。
1、刚体平面运动概述和运动分解(1)如图3所示,刚体运动中由位形Ⅰ到位形Ⅱ,总可以认为以刚体上任意选定的参考点(称为基点)为代表的刚体的平动,加上刚体绕此参考点的一个转动的叠加完成。
(2)由图3(a )、(b )看出,基点选取不同,刚体平动运动将不同,但绕基点的转动却是相同的。
《刚体的平面运动 》课件

鲁棒性分析
分析控制系统对参数变化和外部干扰的鲁棒 性表现。
05
刚体的平面运动的展望
刚体的平面运动的发展趋势
理论研究的深入
随着数学和物理学理论的不断发展,人们对刚体的平面运动的理 解将更加深入,这有助于推动相关领域的研究和应用。
航空航天领域
在航空航天领域,刚体的平面运动对于飞行器的姿态调整和机动性有着 至关重要的作用,未来随着空间探索的深入,其应用前景将更加广阔。
03
医疗器械
刚体的平面运动在医疗器械领域也有着广泛的应用,例如在手术机器人
中用于精确控制手术器械的动作,提高手术的精度和安全性。
刚体的平面运动的挑战与机遇
挑战
刚体的平面运动的研究和应用面临着 一些挑战,如精确控制、稳定性、复 杂环境下的适应性等问题,需要不断 探索和创新来解决。
自动化生产线
刚体的平面运动在自动化生产线中起到关键作用, 如传送带、机器人手臂等。
机械设备的维护和检修
刚体的平面运动在机械设备的维护和检修中也有应 用,如对机械设备进行定位和调整。
航空航天中的应用
飞机起降系统
刚体的平面运动在飞机起降系统中起 到关键作用,如飞机滑行、转向等。
航天器对接
航空航天器的制造和测试
刚体的平面运动的重要性
实际应用
刚体的平面运动在实际生活中广泛存 在,如机械设备的运作、车辆的行驶 等。
理论意义
刚体的平面运动是刚体运动的基础, 对于理解更复杂的刚体运动形式具有 重要意义。
刚体的平面运动的基本原理
平移原理
刚体在平面内沿直线进行平移时,其上任意一点都沿着该直线进行等距离的移 动。
旋转原理
详细描述
在实际的物理问题中,刚体往往不会只进行平动或转动,而是同时进行这两种运动。这种复杂的平面运动形式通 常包括椭圆运动、抛物线运动等。这种复杂的运动形式通常需要综合考虑平动和转动的共同作用,以确定刚体的 最终运动轨迹。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
推论 刚体上不共线的三点的速度完全确定
刚体上任意点的速度。
v2 P2
P1
P
v1
vp
思考题:
P3
v3
1)刚体上两个点的速度可否确定刚体
上任意一点的速度?为什么?
2)刚体上两个点的速度可以确定刚体 上哪些点的速度?
2刚Biblioteka 平面运动的速度瞬心瞬时速度中心:平面运动刚体上瞬时速度为零的点
(1) 已知两点的速度方 向,且互不平行
平面运动刚体的角速度、角加速度
基点法:借助刚体上任意一点的运动和随该点运动的平动坐 标系研究刚体运动的方法。
基点是任意选定的刚体上的一个点, 一般选运动情况已知 或部分已知的点。
刚体相对基点平动系作定轴转 动,角速度、角加速度分别为:
ω = ϕ&k ε = ϕ&&k
y
yp
ω
B
rAB ϕ
xp
A
命题:刚体相对两个相互平动的 参考系的角速度相同。
4、应用速度合成定理
A x'
O ω0
ϕ0
vB= vA+ vr vB = vA/cosϕ0 = rω0/cosϕ0
vr = ωAB × rAB vr = ω ABl
连杆的瞬时角速度 ωAB = vr / l = vAtanϕ0 / l = rω0tanϕ0 / l
ωAB 顺时针方向!
1
例2: 曲柄-滑块机构,OA=r,AB=l,曲柄以等角速度ω0绕
速度合成定理:平面图形上任意
点的速度,等于基点的速度及该点相 对基点平动系的速度之矢量和。
B点的速度
vB
vr
ω
B
vA
y
yp v rAB A
A xp
vB = vA + vr = vA + ω × rAB
rOA
O
x
基点速度 vA
相对速度 vr = ω × rAB
有时记作 vBA
4
平面运动刚体的加速度合成定理
ω AB
vr = ωABlAB
O 60o
ωAB = vr / lAB = ω0 / 3
vA
vB
B
vr
解: 2、加速度分析:
y'
ωAB = ω0 / 3
B点的加速度aB 和 AB杆的角
A x'
加速度 ε AB。
90o
aB 沿着水平方向
ω0
aA
A点的加速度 aA ,方向指 O 60o 向O,大小
ω AB
ωA
=
vA r
=
R+r r
ω
vM =CMωA = 2(R+r)ω
vM ⊥CM
解法二:基点法 取A为基点 vC =vA +vr
vA =(R+r)ω vr =rω' vC =0
rω'=(R+r)ω ω'=(R+r)ω /r
对M点: vM = vA + vr vr = rω ' = (R + r)ω
vM = 2(R + r)ω ω ' =ωA
= vO R
εO
=
aO R
A点加速度分析:
aA = aO + art + arn
art = RεO = aO
arn
=
−aBsin30o=− aA + art
投影法!
art = aA − aBsin30o=εABl
ε AB = 8 3ω02 / 27(逆时针) 解毕!
刚体的运动性质:速度投影定理 定义1:运动中始终不变形的物体称为刚体。 定义2:其上任意两点间的距离始终不变的物体称为刚体。
rAB • rAB = C(常数)
§2-4 定点运动刚体的角加速度与加速度分析
§2-5 刚体一般运动及基点法 描述刚体运动使用的坐标系、 基点法及其运动合成定理
§2-6 刚体的平面运动:
基点法运动合成定理、投影法 速度投影定理(适用于刚体的一般运动)、速度瞬心法
2-6 刚体的平面运动
刚体的平面运动: 刚体上任意点的运动轨迹都在一固定平面之 内,且这些固定平面相互平行。
二点的速度vA和vB的方向都
可以确定。作二者的垂直线,
vD D
相交于C∗,此即速度瞬心。
vB B
90o
图中的几何关系:
90o O1
OA= 2l, AB = BC∗ = 3l 2 AC∗ = 3 2l 2, DC∗ = 3 5l 4
vA = OAω 0 = 2lω 0 vB = BC∗ωAB = lω0
运动;相对于平动系O x´y´、 绕O点的转动-相对运动。
确定圆轮的转动角速度
s = Rϕ , s& = Rϕ& = RωO ,
进而求得圆轮滚动时的角加速度
vO = RωO ,
ωO
=
vO R
εO
= ω&O
=
v&O R
=
aO R
5
例题1
yε´
ω
OO
O
x´
O vO aO
arn aA
art
A
aO
解:
ωO
C
求:轮缘上A、B、C、D四 点的速度。
B
O
D
vO
A
例题4
C
B
O
D
vO
A
ω
C∗
解:圆轮与地面接触点A,由于 没有相对滑动,因而在这一瞬时, A点的速度vA=0。A点即为速度瞬
心C∗。假设这一瞬时的角速度为 ζ。
由vO =R ω得到 ω = vO R
vB = ω × rC*B
vA = 0 , vB = 2v0 vC = 2v0 , vD = 2v0
刚体平面运动模型与运动方程 基点法:速度、加速度分析、瞬心法
矢量计算的投影法、
速度投影定理(适用于刚体一般运动)
本周作业
习题 2-1、2-3、2-12、 2-13、 2-16
引理:动点绝对(加)速度等于其相对平动系(加)速度与平动系
的(加)速度之和: vB = vA + vr , aB = aA + ar 。
U 瞬时速度中心及其应用 例题5
A
ω0 45o
O
B D 90o
90o O1
已知:四连杆机构中
O1B = l, AB = 3l 2, AD = DB
OA以ω 0绕O轴转动。
求:1、B和D点的速度; 2、AB杆的角速度。
例题5
vA A
ω0 45o
O
ω AB
解:机构作平面运动,OA C∗ 和O1B都作定轴转动,A、B
定瞬心轨迹为以 O 为圆心的 1/4圆周: xC2 + yC2 = l 2
y
B C
l
ϕ
η
ξ
u
O
Ax
建立固联坐标系 Aξη,瞬心 C 的坐标为:
ξC = l cosϕ sinϕ ηC = l cos2 ϕ
ξC2 + (ηC − l / 2)2 = l2 / 4
动瞬心轨迹为以杆中点为圆心的1/2圆周。
刚体的平面运动要点
刚体运动的性质1
A α
rAB
vB
β
vA
B
速度投影定理 刚体上任意两点的 速度在其连线上的投影相等。
vA cosα = vB cos β vA • rAB = vB • rAB
速度投影定理证明
rAB • rAB = C(常数)
d dt
(rAB
•
rAB
)
=
0
= 2rAB • r&AB
= 2rAB • (r&B − r&A )
平面图形-在刚体上作平行于 固定平面的平面,这样的平面 与刚体轮廓的交线所构成的图 形。
平面图形上的任意直线-这一 直线的运动可以代表平面图形 的运动,也就是刚体的平面运 动。
A: 称为 基点
自由度 N=3
刚体平面运动的方程 (基点法)
⎧ ⎪ ⎨
xA yA
= =
f1(t) f2 (t )
⎪⎩ϕ = f3(t)
第 2 章 刚体运动及复合运动
"Plato is my friend, Aristotle is my friend, but my best friend is truth" ——Isaac Newton
§2-1 刚体的平动和定点转动 §2-2 动系单位基矢量的时间导数定理 §2-3 定点运动刚体的角速度与速度分析
k
rOA x
O
B点相对 轨迹:圆
基点法运动合成定理:刚体上一点的运动速度/加速度等于基点的速
度/加速度再加上该点相对基点平动坐标系的速度/加速度。
vB
= =
vA vA
+ +
ωvr
×
rAB
aB
= =
aA aA
+ +
ωar×
(ω
×
rAB )
+ε
×
rAB
平面运动 ω = ϕ&k ε = ϕ&&k 平面运动 = aA − ω2 rAB +ε ×rAB
A
rAB
vB
rA vA
B
Z
rB
Y
O
X
rAB = rB − rA
vA • rAB = vB • rAB
证毕
例题 曲柄-连杆-滑块机构
已知 曲柄滑块机构中OA的半
径R、角速率ω 。 求 图示瞬时(位置)的
