几何证明与计算(解析版)
2020年中考数学压轴题-专题28几何证明综合复习(判定四边形形状)(解析版)

专题28 几何证明综合复习(判定四边形形状)教学重难点1.培养学生通过探索和证明,发展推理意识和能力2.通过证明举例的学习和实践,懂得演绎推理的一般规则,并掌握规范表达的格式;了解证明之前进行分析的基本思路;3.体会用“分析综合法”探求解题思路;4.学习添置辅助线的基本方法,会添置常见的辅助线;5.会用文字语言、图形语言、符号语言三种数学语言进行证明说理。
【说明】:本部分为知识点方法总结性梳理,目的在于让学生能从题目条件和所证明结论,去寻找证明思路,用时大概 5-8 分钟左右。
【知识点、方法总结】:中考几何题证明思路总结几何证明题重点考察的是学生的逻辑思维能力,能通过严密的" 因为"、"所以 " 逻辑将条件一步步转化为所要证明的结论。
这类题目出法相当灵活,不像代数计算类题目容易总结出固定题型的固定解法,而更看重的是对重要模型的总结、常见思路的总结。
所以本文对中考中最常出现的若干结论做了一个较为全面的思路总结。
一、证明两线段相等1.两全等三角形中对应边相等。
2.同一三角形中等角对等边。
3.等腰三角形顶角的平分线或底边的高平分底边。
4.平行四边形的对边或对角线被交点分成的两段相等。
5.直角三角形斜边的中点到三顶点距离相等。
6.线段垂直平分线上任意一点到线段两段距离相等。
7.角平分线上任一点到角的两边距离相等。
8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。
9.同圆(或等圆)中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。
10.两前项(或两后项)相等的比例式中的两后项(或两前项)相等。
、证明两角相等1.两全等三角形的对应角相等。
2.同一三角形中等边对等角。
3.等腰三角形中,底边上的中线(或高)平分顶角。
4.两条平行线的同位角、内错角或平行四边形的对角相等。
5.同角(或等角)的余角(或补角)相等。
6.同圆(或圆)中,等弦(或弧)所对的圆心角相等;7.相似三角形的对应角相等;8.等于同一角的两个角相等。
中考几何证明与计算(5)

专题----<<几何>>证明与计算(5)30.已知:如图,ABC△中,45ABC∠=°,CD AB⊥于D,BE平分ABC∠,且B E A C⊥于E,与CD相交于点F H,是BC边的中点,连结DH与BE相交于点G.(1)求证:BF AC=;(2)求证:12CE BF=;(3)CE与BG的大小关系如何?试证明你的结论.31.如图,ACB△和ECD△都是等腰直角三角形,A C D,,三点在同一直线上,连结BD,AE,并延长AE交BD于F.(1)求证:ACE BCD△≌△.(2)直线AE与BD互相垂直吗?请证明你的结论.32,已知;如图,在△ABC中,AB =AC,∠ABC=90°.F为AB延长线上一点,点E在BC上,BE = CF,连接AE、EF和CF.(1)求证:AE=CF;(2)若∠CAE=30°,求∠EFC的度数.33,已知:如图所示,在 Rt△ABC中,AB=AC,∠A=90°,点D为BA上任一点,DF⊥AB于F,DE⊥AC于E,M为BC的中点.试判断△MEF是什么形状的三角形,并证明你的结论.34,如图所示, 已知∠ABC=90º,AC=BC,CE交AB于F,BE⊥CF于E,AD⊥CF于D。
DAEFCHGBFECA(图1)(图2)(1)求证:△CEB≌△ADC(2)若AD=9,DE=6,求BE及EF的长35如图,已知ABC△是等边三角形,点D、F分别在线段BC、AB上,∠60EFB=°,DC EF=.(1) 求证:四边形EFCD是平行四边形;(2) 若BF EF=,求证AE AD=.36如图(1),在△ABC和△EDC中,AC=CE=CB=CD,∠ACB=∠ECD=90,AB与CE交于F,ED与AB、BC分别交于M、H.(1)求证:CF=CH;(2)如图(2),△ABC不动,将△EDC绕点C旋转到∠BCE=45时,试判断四边形ACDM是什么四边形?并证明你的结论.37,已知两个全等的直角三角形纸片ABC、DEF,如图(1)放置,点B、D重合,点F在BC上,AB与EF交于点G.∠C=∠EFB=90°,∠E=∠ABC=30°,AB=DE=4.(1)求证:EGB∆是等腰三角形;(2)若纸片DEF不动,问ABC∆绕点F逆时针旋转最小____度时,四边形ACDE成为以ED为底的梯形(如图(2)).求此梯形的高.38.已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点,(1)如图,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?证明你的结论.39,在Rt ABC△中,902BAC AB AC∠===,,点D在BC所在的直线上运动,作45ADE∠= (A D E,,按逆时针方向).(1)如图1,若点D在线段BC上运动,DE交AC于E.①求证:ABD DCE△∽△;②当ADE△是等腰三角形时,求AE的长.(2)①如图2,若点D在BC的延长线上运动,DE的反向延长线与AC的延长线相交于点E',是否存在点D,使ADE'△是等腰三角形?若存在,写出所有点D的位置;若不存在,请简要说明理由;②如图3,若点D在BC的反向延长线上运动,是否存在点D,使ADE△是等腰三角形?若存在,写出所有点D的位置;若不存在,请简要说明理由.45AB D CE图1。
中考数学临考题号押广东卷21题(几何证明与计算)(解析版)
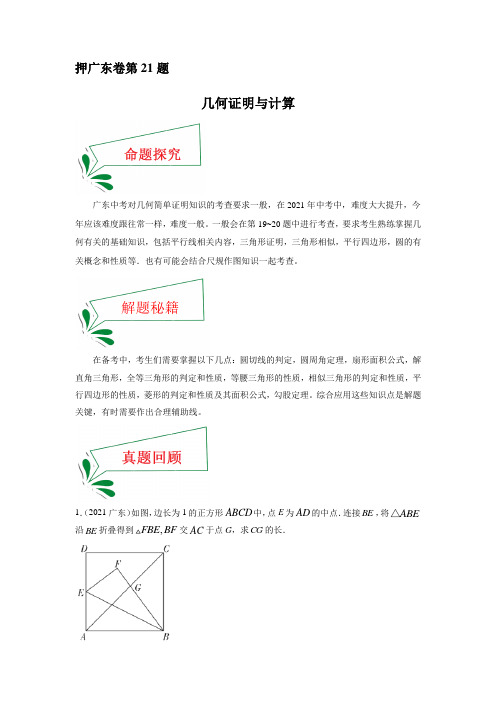
【小问2详解】
根据(1)的结论,平行四边形AFCE是菱形,
∴EF、AC相互垂直平分,且AE=EC=CF=FA,
∴EF=2OE,AC=2OA,
∵BC=8,AB=4,
∴BE=BC-EC=8-EC=8-AE, ,
∴OA= ,
在Rt△ABE中,利用勾股定理,有 ,
即: ,解得:AE=5,
(1)求证:四边形 是菱形.
(2)当AB 4,BC 8时,求线段EF的长.
【分析】(1)利用EF是AC的垂直平分线,可得∠EAC=∠ECA,∠CAF=∠FCA,在矩形中有 ,即有∠ECA=∠CAF,∠ECF=∠CFD,即可证得∠CFD=∠EAF,则有 ,再结合 ,AE=EC,可证四边形AFCE是菱形;
∴∠ACF=∠EDC.
∴ED=EC.
【小问2详解】
解:如(1)中图所示,过点C作CG⊥OB于点G,设线段OE与 交于点H.
∵ 的直径 ,OC,OB是 的半径,
∴ .
∵∠A和∠BOC分别是 所对的圆周角和圆心角,∠A=30°,
∴∠BOC=2∠A=60°.
∴ ,S扇OBC .
∴ .
∴点C右侧的阴影面积S右=S扇OBC- .
(2)连接 ,根据同弧所对的圆周角相等,可得 ,进而根据正切值以及已知条件可得 的长,勾股定理即可求得 ,进而即可求得圆的半径.
【详解】
(1)连接 ,如图,
是 的切线,
,
,
,
,
,
,
.
(2)连接
是 的直径,
,
,
,
,
,
,
,
,
.
即 的半径为 .
6.(2021·山东青岛·中考真题)如图,在 中, 为 边的中点,连接 并延长,交 的延长线于点 ,延长 至点 ,使 ,分别连接 , , .
2022年上海市15区中考数学一模考点分类汇编09 几何证明(解答题23题)(讲解版)

2022年上海市15区中考数学一模考点分类汇编专题09 几何证明一.解答题(共15小题)1.(普陀区)已知:如图,在△ABC中,点D、E分别在边AC、BC上,BD=DC,BD•BC=BE•AC.(1)求证:∠ABE=∠DEB;(2)延长BA、ED交于点F,求证:.【分析】(1)由BD•BC=BE•AC得出=,BD=DC得出∠DBC=∠C,从而得出结论;(2)根据(1)的结论和已知证明△FAD∽△FDB即可.【解答】证明:(1)∵BD=DC,∴∠DBC=∠C,∵BD•BC=BE•AC,∴=,∴△ABC∽△DEB,∴∠ABC=∠DEB,即∠ABE=∠DEB;(2)如图所示:∵△ABC∽△DEB,∴∠CAB=∠BDE,∴∠FAD=∠FDB,∵∠F=∠F,∴△FAD∽△FDB,∴=,∵∠ABE=∠DEB,∴FB=FE,又∵BD=DC,∴=.【点评】本题考查相似三角形的判定和性质,关键是找到相似的三角形.2.(崇明区)已知:如图,在Rt△ACB中,∠ACB=90°,CD⊥AB,垂足为点D,E为边AC上一点,联结BE交CD于点F,并满足BC2=CD•BE.求证:(1)△BCE∽△ACB;(2)过点C作CM⊥BE,交BE于点G,交AB于点M,求证:BE•CM=AB•CF.【分析】(1)通过证明△BCD∽△EBC,可得∠CEB=∠CBD,可得结论;(2)通过证明△BCE∽△ACB,△ACB∽△CDB,△CDM∽△BDF,可得,,,可得结论.【解答】证明:(1)∵BC2=CD•BE,∴,设=k,则BC=k•CD,BE=k•BC,∴CE==×BC,BD==×CD,∴=,又∵∠ACB=∠CDB=90°,∴△BCD∽△EBC,∴∠CEB=∠CBD,又∵∠ACB=∠BCE=90°,∴△BCE∽△ACB;(2)如图,∵△BCE∽△ACB,∴,∵∠CEB=∠CBA,∴∠A=∠CBE,∵∠A+∠ABC=90°=∠DCB+∠CBD,∴∠A=∠DCB,∴∠DCB=∠EBC,∴CF=BF,∵∠A=∠DCB,∠CDB=∠ACB=90°,∴△ACB∽△CDB,∴,∵CM⊥BE,∴∠ABE+∠CMD=90°=∠CMD+∠MCD,∴∠MCD=∠ABE,又∵∠CDB=∠CDM=90°,∴△CDM∽△BDF,∴,∴,∴BE•CM=AB•CF.【点评】本题考查了相似三角形的判定和性质,直角三角形的性质,灵活运用相似三角形的性质是解题的关键.3.(嘉定区)如图,已知正方形ABCD和正方形BEFG,点E在边BC上,点G在边AB的延长线上,联结AE,并延长AE交CG于点K.(1)求证:△ABE∽△CKE;(2)如果CG与EF交于点H,求证:BE2=FH•AB.【分析】(1)由“SAS”可证△ABE≌△CBG,可得∠BAE=∠ECK,可得结论;(2)通过证明△ABE∽△GFH,可得,可得结论.【解答】证明:(1)∵四边形ABCD是正方形,∴AB=CB,∠ABC=90°,∵四边形BEFG是正方形,∴FG=BG=BE,∠CBG=90°,∴∠ABE=∠CBG=90°,在△ABE和△CBG中,,∴△ABE≌△CBG(SAS),∴∠BAE=∠ECK,又∵∠AEB=∠CEK,∴△ABE∽△CKE;(2)由题意,得∠CEF=∠F=∠ABE=90°,∴FG∥BC,∴∠ECK=∠FGH,∵∠BAE=∠ECK,∴∠BAE=∠FGH,∴△ABE∽△GFH,∴,∵FG=BE,∴,∴BE2=FH•AB.【点评】本题考查了相似三角形的判定和性质,正方形的性质,全等三角形的判定和性质,灵活运用这些性质解决问题是解题的关键.4.(宝山区)如图,已知△ABC和△DCE都是等边三角形,点B、C、E在同一直线上,联结BD交AC边于点F.(1)如果∠ABD=∠CAD,求证:BF2=DF•DB;(2)如果AF=2FC,S四边形ABCD=18,求S△DCE的值.【分析】(1)证明△ABF≌△CAD(ASA),由全等三角形的性质可得出BF=AD,证明△ADF∽△BDA,由相似三角形的性质得出,则可得出结论;(2)证明△DCF∽△BAF,由相似三角形的性质得出=,设S△DCF=x,则S△ADF=S△BCF=2x,S△ABF=4x,由四边形ABCD的面积可得出x+2x+2x+4x=18,求出x=2,求出三角形ABC的面积,证明△ABC∽△DCE,由相似三角形的性质得出=,则可得出结论.【解答】(1)证明:∵△ABC和△DCE都是等边三角形,∴AB=AC,∠BAC=∠DCE=∠ACB=60°,又∵∠ABD=∠CAD,∴△ABF≌△CAD(ASA),∴BF=AD,∵∠ADF=∠BDA,∠ABD=∠CAD,∴△ADF∽△BDA,∴,∴AD2=DF•BD,∴BF2=DF•BD;(2)解:∵∠ACB=∠DCE=60°,∴∠ACD=60°,∴∠ACD=∠BAC,∴AB∥CD,∴△DCF∽△BAF,∴=,∴,,,设S△DCF=x,则S△ADF=S△BCF=2x,S△ABF=4x,∵S四边形ABCD=18,∴x+2x+2x+4x=18,解得x=2,∴S△ABF=8,S△BCF=4,∴S△ABC=S△ABF+S△BCF=8+4=12,∵△ABC和△DCE都是等边三角形,∴△ABC∽△DCE,∴=,∴S△DCE==×12=3.【点评】本题考查了等边三角形的性质,相似三角形的判定与性质,全等三角形的判定与性质,证明△DCF∽△BAF是解题的关键.5.(杨浦区)已知,如图,在四边形ABCD中,∠ABC=∠BCD,点E在边BC上,AE∥CD,DE ∥AB,过点C作CF∥AD,交线段AE于点F,联结BF.(1)求证:△ABF≌△EAD;(2)如果射线BF经过点D,求证:BE2=EC•BC.【分析】(1)先证AB=AE,DE=DC,再证四边形ADCF是平行四边形,得出AF=CD,进而得出AF=DE,再由平行线性质得∠AED=∠BAF,进而证得结论;(2)通过证明△BEF∽△BCD,△DEF∽△BAF,可得,即可得结论.【解答】证明:(1)∵AE∥CD,∴∠AEB=∠BCD,∵∠ABC=∠BCD,∴∠ABC=∠AEB,∴AB=AE,∵DE∥AB,∴∠DEC=∠ABC,∠AED=∠BAF,∵∠ABC=∠BCD,∴∠DEC=∠BCD,∴DE=DC,∵CF∥AD,AE∥CD,∴四边形ADCF是平行四边形,∴AF=CD,∴AF=DE,在△ABF和△EAD中,,∴△ABF≌△EAD(SAS);(2)如图,连接FD,∵射线BF经过点D,∴点B,点F,点D三点共线,∵AE∥DC,∴△BEF∽△BCD,∴,,∵DE∥AB,∴△DEF∽△BAF,∴,∴,∵CD=AF,∴,∴BE2=EC•BC.【点评】本题考查了相似三角形的判定和性质,全等三角形的判定和性质,平行四边形的判定和性质,利用相似三角形的性质得到线段的关系是解题的关键.6.(松江区)已知:如图,梯形ABCD中,DC∥AB,AC=AB,过点D作BC的平行线交AC于点E.(1)如果∠DEC=∠BEC,求证:CE2=ED•CB;(2)如果AD2=AE•AC,求证:AD=BC.【分析】(1)通过证明△DEC∽△CEB,可得,可得结论;(2)通过证明△BCE∽△ACB,可得,由相似三角形的性质可得,可得,通过证明△ADE∽△ACD,可得=,可得结论.【解答】证明:(1)∵AC=AB,∴∠ACB=∠ABC,∵DC∥AB,∴∠DCE=∠CAB,∵DE∥BC,∴∠DEC=∠BCE,∵∠DEC=∠BEC,∴∠DEC=∠BCE=∠BEC=∠ABC,∴∠BAC=∠CBE=∠DCE,BE=BC,∴△DEC∽△CEB,∴,∴CE2=DE•BE=DE•CB;(2)∵∠BAC=∠CBE,∠ACB=∠BCE,∴△BCE∽△ACB,∴,∵△DEC∽△CEB,∴,∠CDE=∠BCE=∠CED=∠BEC,∴,CD=CE,∵AD2=AE•AC,∴,又∵∠DAE=∠DAC,∴△ADE∽△ACD,∴=,∴,∴AD=BC.【点评】本题考查了相似三角形的判定和性质,熟练运用相似三角形的判定是解题的关键.7.(浦东新区)如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,∠B=∠ADE=30°,AC 与DE相交于点F,联结CE,点D在边BC上.(1)求证:△ABD∽△ACE;(2)若=,求的值.【分析】(1)根据相似三角形的判定定理得到△BAC∽△DAE,根据相似三角形的性质得到,求得∠BAD=∠CAE,根据相似三角形的判定定理得到结论;(2)根据相似三角形的性质和直角三角形的性质即可得到结论.【解答】(1)证明:∵∠ADE=∠DAE,∠B=∠ADE,∴△BAC∽△DAE,∴,∵∠BAC=∠DAE,∴∠BAD=∠CAE,∴△BAD∽△CAE;(2)解:∵△ABD∽△ACE,∴,∵∠DAE=90°,∠ADE=30°,∴=,∴=•==3,∵△ADF∽△ECF,∴==3.【点评】本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质定理是解题的关键.8.(徐汇区)如图,已知△ADE的顶点E在△ABC的边BC上,DE与AB相交于点F,∠FEA=∠B,∠DAF=∠EAC.(1)求证:AE2=AF•AB;(2)求证:=.【分析】(1)利用两个角相等证明△BAE∽△EAF,得,即可证明结论;(2)首先证明△DAE∽△CAB,得,∠D=∠C,再证明△DAF∽△CAE,得,等量代换即可.【解答】证明:(1)∵∠FEA=∠B,∠BAE=∠EAF,∴△BAE∽△EAF,∴,∴AE2=AF•AB,(2)∵∠DAF=∠CAE,∠FAE=∠FAE,∴∠DAE=∠CAF,∵∠FEA=∠B,∴△DAE∽△CAB,∴,∠D=∠C,∵∠DAF=∠EAC,∴△DAF∽△CAE,∴,∴,∴.【点评】本题主要考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题的关键.9.(金山区)已知:如图,梯形ABCD中,AD∥BC,AB=DC=6,E是对角线BD上一点,DE=4,∠BCE=∠ABD.(1)求证:△ABD∽△ECB;(2)如果AD:BC=3:5,求AD的长.【分析】(1)先由AD∥BC得到∠ADB=∠EBC,然后由∠ABD=∠ECB得证△ABD∽△ECB;(2)先由AB=DC得到∠ABC=∠BCD,再由∠∠ABD=∠BCE得到∠DBC=∠DCE,从而得到△DBC∽△DCE,然后利用相似三角形的性质求得BD的长,进而得到BE的长,再由△ABD∽△ECB得到AD的长.【解答】解:(1)∵AD∥BC,∴∠ADB=∠EBC,又∵∠BCE=∠ABD,∴△ABD∽△ECB.(2)∵梯形ABCD中,AD∥BC,AB=DC=6,∴∠ABC=∠BCD,又∵∠BCE=∠ABD,∴∠DBC=∠DCE∵∠BDC=∠CDE,∴△BDC∽△CDE,∴,∵DC=6,DE=4,∴BD=9,∴BE=5,∵△ABD∽△ECB,∴,由AD:BC=3:5,设AD=3x,BC=5x,∴,解得:x=或x=﹣(舍),∴AD=.【点评】本题考查了梯形的性质、相似三角形的判定与性质、平行线的性质,解题的关键是熟练应用等量代换得证∠DBC=∠DCE.10.(静安区)如图,边长为1的正方形ABCD中,对角线AC、BD相交于点O,点Q、R分别在边AD、DC上,BR交线段OC于点P,QP⊥BP,QP交BD于点E.(1)求证:△APQ∽△DBR;(2)当∠QED等于60°时,求的值.【分析】(1)利用正方形的性质可得∠QAP=∠BDR=45°,AC⊥BD,根据已知QP⊥BP,利用同角的余角相等可得∠APQ=∠DBR,即可解答;(2)由(1)可得△APQ∽△DBR,从而可得=,根据已知可得∠BEP=60°,设OE 为a,然后在Rt△OEP中,表示出OP=a,EP=2a,从而在Rt△BEP中求出BE=4a,进而求出OB,然后进行计算即可解答.【解答】(1)证明:∵四边形ABCD是正方形,∴AC⊥BD,OA=OC=AC,OB=OD=BD,AC=BD,∠QAP=∠BDR=45°,∴∠BOC=∠DOC=90°,OA=OB,∴∠OBP+∠OPB=90°,∵QP⊥BP,∴∠QPB=90°,∴∠OPB+∠QPA=90°,∴∠APQ=∠DBR,∴△APQ∽△DBR;(2)解:由(1)可得△APQ∽△DBR,∴=,∵∠QED=60°,∴∠BEP=∠QED=60°,∴∠OPE=90°﹣∠BEP=30°,∴PE=2OE,OP=OE,设OE为a,则EP=2a,OP=a,在Rt△BEP中,BE===4a,∴OB=BE﹣OE=4a﹣a=3a,∴BD=2OB=6a,∵OA=3a,OP=a,∴AP=OA+OP=3a+a,∴==,∴=.【点评】本题考查了正方形的性质,相似三角形的判定与性质,全等三角形的判定与性质,根据题目的已知条件并结合图形分析是解题的关键.11.(虹口区)如图,在梯形ABCD中,∠ABC=90°,AD∥BC,BC=2AD,对角线AC与BD交于点E.点F是线段EC上一点,且∠BDF=∠BAC.(1)求证:EB2=EF•EC;(2)如果BC=6,sin∠BAC=,求FC的长.【分析】(1)先由AD∥BC得到△EAD∽△ECB,从而得到,然后由∠BDF=∠BAC、∠AEB=∠DEF得证△EAB∽△EDF,进而得到,最后得到结果;(2)先利用条件得到AC、AB的长,然后利用BC=2AD得到AD、BD的长,再结合相似三角形的性质得到EB、EC的长,进而得到EF的长和FC的长.【解答】(1)证明:∵AD∥BC,∴△EAD∽△ECB,∴,即,∵∠BDF=∠BAC,∠AEB=∠DEF,∴△EAB∽△EDF,∴,∴,∴EB2=EF•EC.(2)解:∵BC=6,sin∠BAC==,BC=2AD∴AC=9,AD=3,∵∠ABC=90°,AD∥BC,∴∠BAD=90°,∴AB===3,∴BD===3,∵△EAD∽△ECB,∴,∴EC=AC=×9=6,EB=BD=×3=2,∵EB2=EF•EC,即(2)2=6EF,∴EF=4,∴FC=EC﹣EF=6﹣4=2.【点评】本题考查了直角梯形的性质、相似三角形的判定与性质、勾股定理,解题的关键是熟知“8”字模型相似三角形的判定与性质.12.(奉贤区)根据相似形的定义可以知道,如果一个四边形的四个角与另一个四边形的四个角对应相等,且它们各有的四边对应成比例,那么这两个四边形叫做相似四边形.对应相等的角的顶点叫做这两个相似四边形的对应顶点,以对应顶点为端点的边是这两个相似四边形的对应边,对应边的比叫做这两个相似多边形的相似比.(我们研究的四边形都是指凸四边形)(1)某学习小组在探究相似四边形的判定时,得到如下两个命题,请判断它们是真命题还是假命题(直接在横线上填写“真”或“假”)①梯形的中位线将原梯形分成的两个小的梯形相似;假命题;②有一个内角对应相等的两个菱形相似;真命题.(2)已知:如图1,△ABC是以BC为斜边的等腰直角三角形,以BC为直角边作等腰直角三角形BCD,再以BD为直角边作等腰直角三角形BDE求证:四边形ABDC与四边形CBED相似.(3)已知:如图2,在△ABC中,点D、E分别在边AB、AC上,BE、CD相交于点F,点G在AF的延长线上,联结BG、CG.如果四边形ADFE与四边形ABGC相似,且点A、D、F、E分别对应A、B、G、C.求证:AF•BF=AG•EF.【分析】(1)根据相似多边形的定义,分别从对应边和对应角两个方面判断即可;(2)由等腰直角三角形的性质可知,两个四边形符合相似四边形的定义;(3)根据相似四边形对应角相等得,∠ADF=∠ABG,∠AEF=∠ACG,则CD∥BG,BE∥CG,从而证明四边形BGCF是平行四边形,有BF=CG,再证明△EAF∽△CAG,则,等量代换即可证明结论.【解答】(1)解:①梯形的中位线将原梯形分成的两个小的梯形满足四个角对应线段,但边不是对应成比例,所以原命题是假命题;②有一个内角对应相等的两个菱形满足四个角线段,对应边成比例,所以是真命题,故答案为:假,真;(2)证明:由题意知,∠A=∠CBE=90°,∠ACD=∠CDE=135°,∠ABD=∠BCD=90°.∠CDB=∠E=45°,∴四边形ABDC与四边形CBED的四个角对应相等,设AB=AC=x,则CD=x,BD=DE=2x,BE=2x,∴,∴四边形ABDC与四边形CBED的四边对应成比例,∴四边形ABDC与四边形CBED相似;(3)证明:∵四边形ADFE与四边形ABGC相似,且点A、D、F、E分别对应A、B、G、C.∴∠ADF=∠ABG,∠AEF=∠ACG,∴CD∥BG,BE∥CG,∴四边形BGCF是平行四边形,∴BF=CG,∵∠AEF=∠ACG,∠EAF=∠CAG,∴△EAF∽△CAG,∴,∴,∴AF•BF=AG•EF.【点评】本题是相似形综合题,主要考查了相似四边形的定义,等腰直角三角形的性质,平行四边形的判定与性质,相似三角形的判定与性质等知识,读懂定义,紧扣定义中从边和角两个方面进行考虑是解题的关键.13.(青浦区)已知:如图,在四边形ABCD中,AC、BD相交于点E,∠ABD=∠CBD,DC2=DE•DB.(1)求证:△AEB∽△DEC;(2)求证:BC•AD=CE•BD.【分析】(1)根据已知条件先证明△DCE∽△DBC,可得∠DCE=∠DBC,进而可以证明结论;(2)结合(1)的结论证明△AED∽△BEC,可得∠ADE=∠BCE,再证明△BDA∽△BCE,进而可得结论.【解答】证明:(1)∵DC2=DE⋅DB,∴,∵∠CDE=∠BDC,∴△DCE∽△DBC,∴∠DCE=∠DBC,∵∠ABD=∠DBC,∴∠DCE=∠ABD,∵∠AEB=∠DEC,∴△AEB∽△DEC;(2)∵△AEB∽△DEC,∴,∵∠AED=∠BEC,∴△AED∽△BEC,∴∠ADE=∠BCE,∵∠ABD=∠DBC,∴△BDA∽△BCE,∴,∴BC•AD=CE•BD.【点评】本题考查了相似三角形的判定与性质,解决本题的关键是得到△BDA∽△BCE.14.(徐汇区)如图,已知Rt△ABC中,∠ACB=90°,射线CD交AB于点D,点E是CD上一点,且∠AEC=∠ABC,联结BE.(1)求证:△ACD∽△EBD;(2)如果CD平分∠ACB,求证:AB2=2ED•EC.【分析】(1)根据已知条件先证明△ADE∽△CDB,可得,因为∠ADC=∠EDB,即可得证;(2)结合(1)证明△EAB是等腰直角三角形,进而可得结论.【解答】证明:(1)∵∠AEC=∠ABC,∠ADE=∠BDC,∴△ADE∽△CDB,∴,又∵∠ADC=∠EDB,∴△ACD∽△EBD;(2)∵△ADE∽△CDB,∴∠DCB=∠EAB,∵△ACD∽△EBD,∴∠ACD=∠EBD,∵∠ACB=90°,∴∠EAB+∠EBD=∠DCB+∠ACD=90°,∴∠AEB=90°,∵CD平分∠ACB,∴∠ACD=∠BCD=45°,∴∠EBD=∠EAB=45°,∴EA=EB,∴△EAB是等腰直角三角形,∴∠EAD=∠ACE,∠AED=∠CEA,∵△AED∽△CEA,∴=,∴AE2=ED•EC,∵AE2+EB2=AB2,∴2AE2=AB2,∴AE2=AB2,∴AB2=ED•EC,∴AB2=2ED•EC.【点评】本题考查了相似三角形的判定与性质,等腰直角三角形的判定与性质,勾股定理,解决本题的关键是得到△EAB是等腰直角三角形.15.(黄浦区)已知:如图,在四边形ABCD中,AB∥CD,过点D作DF∥CB,分别交AC、AB点E、F,且满足AB•AF=DF•BC.(1)求证:∠AEF=∠DAF;(2)求证:=.【分析】(1)根据DF∥CB,可得∠B=∠AFD,根据AB•AF=DF•BC.证明△ABC∽△DAF,进而可以解决问题;(2)由△DCE∽△FAE,可得=,所以=,再由△AFE∽△DFA,可得AF2=EF•DF,由△AEF∽△ACB,得=,进而可得结论.【解答】(1)证明:∵AB∥CD,DF∥CB,∴四边形FBCD是平行四边形,∴DC=FB,DF=CB,∵AB•AF=DF•BC.∴=,∵DF∥CB,∴∠B=∠AFD,∴△ABC∽△DAF,∴∠ACB=∠DAF,∵DF∥CB,∴∠AEF=∠ACB,∴∠AEF=∠DAF;(2)证明:∵AB∥CD,∴△DCE∽△FAE,∴=,∴=,∴=,∵∠AEF=∠DAF,∠AFE=∠DFA,∴△AFE∽△DFA,∴=,∴AF2=EF•DF,∴====,∵DF∥CB,∴△AEF∽△ACB,∴=,∴=.【点评】本题考查了相似三角形的判定与性质,解决本题的关键是掌握相似三角形的判定与性质,得到△AEF∽△ACB.。
2019届中考数学复习《几何证明与计算》专题训练含答案
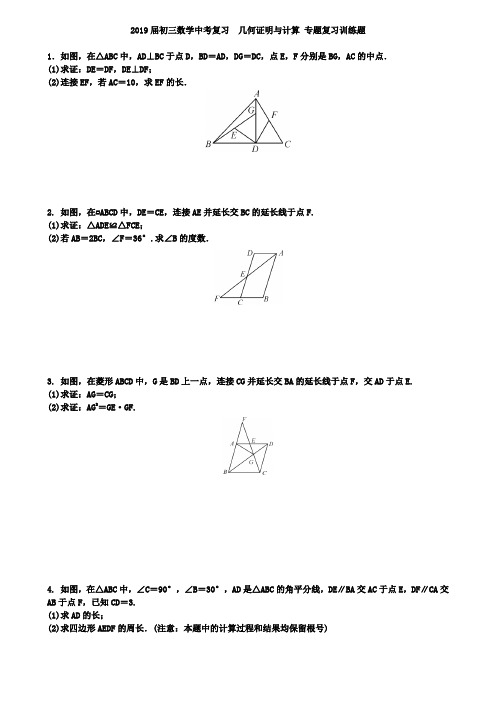
2019届初三数学中考复习几何证明与计算专题复习训练题1.如图,在△ABC中,AD⊥BC于点D,BD=AD,DG=DC,点E,F分别是BG,AC的中点.(1)求证:DE=DF,DE⊥DF;(2)连接EF,若AC=10,求EF的长.2. 如图,在▱ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.(1)求证:△ADE≌△FCE;(2)若AB=2BC,∠F=36°.求∠B的度数.3. 如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.(1)求证:AG=CG;(2)求证:AG2=GE·GF.4. 如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE∥BA交AC于点E,DF∥CA交AB于点F,已知CD=3.(1)求AD的长;(2)求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号)5. 如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.(1)求证:△BCE≌△DCF;(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.6. 如图,点E是正方形ABCD的边BC延长线上一点,连接DE,过顶点B作BF⊥DE,垂足为F,BF分别交AC于点H,交CD于点G.(1)求证:BG=DE;(2)若点G为CD的中点,求HGGF的值.7. 如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连接AG.(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.8. 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.(1)求证:△ACD∽△BFD;(2)当tan∠ABD=1,AC=3时,求BF的长.9. 如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.(1)求证:AG=CG;(2)求证:AG2=GE·GF.10. 如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF,延长DB交EF于点N.(1)求证:AD=AF;(2)求证:BD=EF;(3)试判断四边形ABNE的形状,并说明理由.11. 在△ABC中,∠ABM=45°,AM⊥BM,垂足为M,点C是BM延长线上一点,连接AC.(1)如图①,若AB=32,BC=5,求AC的长;(2)如图②,点D是线段AM上一点,MD=MC,点E是△ABC外一点,EC=AC,连接ED并延长交BC于点F,且点F是线段BC的中点,求证:∠BDF=∠CEF.12. 如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.(1)求证:△ABM∽△EFA;(2)若AB=12,BM=5,求DE的长.参考答案:1. 解:(1)证明:∵AD⊥BC,∴∠ADB=∠ADC=90°.在△BDG和△ADC中,⎩⎪⎨⎪⎧BD =AD ,∠BDG =∠ADC DG =DC ,,∴△BDG ≌△ADC. ∴BG =AC ,∠BGD =∠C.∵∠ADB=∠ADC=90°, E ,F 分别是BG ,AC 的中点,∴DE =12BG =EG ,DF =12AC =AF.∴DE=DF ,∠EDG =∠EGD,∠FDA =∠FAD.∴∠EDG+∠FDA=90°,∴DE ⊥DF.(2)∵AC=10,∴DE =DF =5,由勾股定理,得EF =DE 2+DF 2=5 2. 2. 解:(1)证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD =BC.∴∠D=∠ECF.在△ADE 和△FCE 中,⎩⎪⎨⎪⎧∠D=∠ECF,DE =CE ,∠AED =∠FEC,∴△ADE ≌△FCE(ASA).(2)∵△ADE≌△FCE,∴AD=FC.∵AD=BC ,AB =2BC ,∴AB=FB.∴∠BAF=∠F=36°.∴∠B=180°-2×36°=108°. 3. 证明:(1)∵四边形ABCD 是菱形,∴AB ∥CD ,AD =CD ,∠ADB =∠CDB.又GD 为公共边,∴△ADG ≌△CDG(SAS),∴AG =CG. (2)∵△ADG≌△CDG,∴∠EAG =∠DCG.∵AB∥CD,∴∠DCG =∠F.∴∠EAG=∠F.∵∠AGE=∠AGE,∴△AGE ∽△FGA.∴AG FG =EG AG.∴AG 2=GE·GF. 4. 解:(1)∵∠C=90°,∠B =30°,∴∠CAB =60°.∵AD 平分∠CAB ,∴∠CAD =12∠CAB=30°.在Rt △ACD 中,∵∠ACD =90°,∠CAD =30°,∴AD =2CD =6. (2)∵DE∥BA 交AC 于点E ,DF ∥CA 交AB 于点F , ∴四边形AEDF 是平行四边形,∠EAD =∠ADF=∠DAF. ∴AF=DF.∴四边形AEDF 是菱形.∴AE=DE =DF =AF. 在Rt △CED 中,∵DE ∥AB ,∴∠CDE =∠B=30°. ∴DE =CDcos30°=2 3.∴四边形AEDF 的周长为8 3.5. 解:(1)证明:∵四边形ABCD 是菱形,∴∠B =∠D,AB =BC =DC =AD.∵点E ,O ,F 分别为AB ,AC ,AD 的中点,∴AE =BE =DF =AF ,OF =12DC ,OE =12BC ,OE ∥BC.在△BCE 和△DCF 中,⎩⎪⎨⎪⎧BE =DF ,∠B =∠D,BC =DC ,∴△BCE ≌△DCF(SAS). (2)当AB⊥BC 时,四边形AEOF 是正方形, 理由如下:由(1)得AE =OE =OF =AF ,∴四边形AEOF 是菱形.∵AB⊥BC,OE∥BC,∴OE⊥AB.∴∠AEO=90°.∴四边形AEOF 是正方形.6. 解:(1)证明:∵BF⊥DE,∴∠GFD =90°.∵∠BCG =90°,∠BGC =∠DGF,∴∠CBG =∠CDE. 在△BCG 与△DCE 中.⎩⎪⎨⎪⎧∠CBG=∠CDE,BC =CD ,∠BCG =∠DCE,∴△BCG ≌△DCE(ASA),∴BG =DE.(2)设CG =x ,∵G 为CD 的中点,∴GD =CG =x , 由(1)可知△BCG≌△DCE(ASA),∴CG =CE =x.由勾股定理可知DE =BG =5x ,∵sin ∠CDE =CE DE =GFGD ,∴GF=55x.∵AB∥CG,∴△ABH ∽△CGH.∴AB CG =BH GH =21. ∴BH=253x ,GH =53x.∴HG GF =53.7. 解:(1)结论:AG 2=GE 2+GF 2.理由:连接CG.∵四边形ABCD 是正方形,∴点A ,C 关于对角线BD 对称. ∵点G 在BD 上,∴GA=GC.∵GE⊥DC 于点E ,GF⊥BC 于点F , ∴∠GEC=∠ECF=∠CFG=90°.∴四边形EGFC 是矩形.∴CF=GE.在Rt △GFC 中,∵CG 2=GF 2+CF 2,∴AG 2=GF 2+GE 2.(2)过点B 作BN⊥AG 于点N ,在BN 上取一点M ,使得AM =BM.设AN =x.∵∠AGF=105°,∠FBG =∠FGB=∠ABG=45°, ∴∠AGB =60°,∠GBN =30°,∠ABM =∠MAB=15°.∴∠AMN =30°.∴AM =BM =2x ,MN =3x.在Rt △ABN 中,∵AB 2=AN 2+BN 2,∴1=x 2+(2x +3x)2,解得x =6-24,∴BN =6+24.∴BG=BN cos30°=32+66. 8. 解:(1)∵AD⊥BC,BE ⊥AC ,∴∠BDF =∠ADC=∠BEC=90°,∴∠C +∠DBF=90°,∠C +∠DAC=90°,∴∠DBF =∠DAC,∴△ACD ∽△BFD(2)∵tan ∠ABD =1,∠ADB =90°,∴AD BD =1,∵△ACD ∽△BFD ,∴AC BF =ADBD=1,∴BF =AC =39. 解:(1)∵四边形ABCD 是菱形,∴AB ∥CD ,AD =CD ,∠ADB =∠CDB,可证△ADG≌△CDG(SAS),∴AG =CG(2)∵△ADG≌△CDG,∴∠EAG =∠DCG,∵AB ∥CD ,∴∠DCG =∠F,∴∠EAG =∠F,∵∠AGE =∠AGE,∴△AGE ∽△FGA ,∴AG FG =EG AG,∴AG 2=GE·GF10. 解:(1)∵AB=AC ,∠BAC =90°,∴∠ABC =∠ACB =45°,∴∠ABF =135°,∵∠BCD =90°,∴∠ACD =∠ACB+∠BCD=135°,∴∠ABF =∠ACD,∵CB =CD ,CB =BF ,∴BF =CD ,可证△ABF≌△ACD(SAS),∴AD =AF(2)由(1)知AF =AD ,△ABF ≌△ACD ,∴∠FAB =∠DAC,∵∠BAC =90°,∴∠EAB =∠BAC=90°,∴∠EAF =∠BAD,可证△AEF≌△ABD(SAS),∴BD =EF(3)四边形ABNE 是正方形.理由如下:∵CD=CB ,∠BCD =90°,∴∠CBD =45°,又∵∠ABC=45°,∴∠ABD =∠ABC+∠CBD=90°,由(2)知∠EAB=90°,△AEF ≌△ABD ,∴∠AEF =∠ABD=90°,∴四边形ABNE 是矩形,又∵AE=AB ,∴四边形ABNE 是正方形 11. 解:(1)∵∠ABM=45°,AM ⊥BM ,∴AM =BM =ABcos45°=32×22=3. 则CM =BC -BM =5-3=2,∴AC =AM 2+CM 2=22+32=13.(2)证明:延长EF 到点G ,使得FG =EF ,连接BG.∵DM =MC ,∠BMD =∠AMC ,BM =AM ,∴△BMD≌△AMC(SAS).∴AC =BD.又CE =AC ,∴BD =CE.∵BF =FC ,∠BFG =∠EFC ,FG =FE ,∴△BFG≌△CFE.∴BG=CE ,∠G=∠E.∴BD=CE =BG ,∴∠BDG=∠G=∠E. 12. 解:(1)证明:∵四边形ABCD 是正方形, ∴AB=AD ,∠B=90°,AD∥BC.∴∠AMB=∠EA F.又∵EF⊥AM,∴∠AFE=90°.∴∠B=∠AFE.∴△ABM∽△EFA. (2)∵∠B=90°,AB =AD =12,BM =5,∴AM =122+52=13.∵F 是AM 的中点,∴AF =12AM =6.5.∵△ABM∽△EFA,∴BM AF =AM AE ,即56.5=13AE.∴AE =16.9,∴DE =AE -AD =4.9.2019-2020学年数学中考模拟试卷一、选择题1.下列各组的两项是同类项的为()A.3m2n2与-m2n3B.12xy与2yxC.53与a3D.3x2y2与4x2z22.如图,小明站在自家阳台上A处观测到对面大楼底部C的俯角为α,A处到地面B处的距离AB=35m,则两栋楼之间的距离BC(单位:m)为()A.35tanαB.35sinαC.35sinαD.35tanα3.12019的倒数是()A.12019B.﹣12019C.2019D.﹣20194.如图,传送带和地面所成斜坡AB的坡度为1:2,物体从地面沿着该斜坡前进了10米,那么物体离地面的高度为()A.5 米米5.不等式组21331563xxx+≥-⎧⎪-⎨--⎪⎩>的解集在数轴上表示正确的是()A.B .C .D.6.有这样一道题:如图,在正方形ABCD中,有一个小正方形EFGH,其中E,F,G分别在AB,BC,FD上,连接DH,如果12BC=,3BF=.则tan HDG∠的值为()A.12B.14C.25D.137.如图,Rt △ABC 中,∠C =90°,AB =10,BC =8,将△ABC 折叠,使B 点与AC 的中点D 重合,折痕为EF ,则线段BF 的长是( )A .53B .2C .166D .73168.如图,在4×4的正方形网格中,每个小正方形的边长都为1,△AOB 的三个顶点都在格点上,现将△AOB 绕点O 逆时针旋转90°后得到对应的△COD ,则点A 经过的路径弧AC 的长为( )A .3π2B .πC .2πD .3π9.在下列二次函数中,其图象对称轴为x=2的是 A .y=2x 2﹣4 B .y=2(x-2)2 C .y=2x 2+2D .y=2(x+2)210.如图,反比例函数y 1=1x与二次函数y 1=ax 2+bx+c 图象相交于A 、B 、C 三个点,则函数y =ax 2+bx ﹣1x+c 的图象与x 轴交点的个数是( )A .0B .1C .2D .311.伴随着经济全球化的发展,中外文化交流日趋频繁,中国以其悠久的历史文化和热情吸引了越来越多的外国游客的光临,据国家统计局统计,2007年至2017年中国累计接待外国游客入境3.1亿人次.小元制作了2007年至2017年外国人入境情况统计图,如图所示.数据来源:国家统计局,2016年含边民入境人数.根据以上信息,下列推断合理的是( ) A.2007年45岁以上外国人入境游客约为2611万人次 B.外国游客入境人数逐年上升C.每年的外国游客入境人数中,25﹣44岁游客人数占全年游客入境人数的13D.外国游客入境人数较前一年増涨幅度最大的是2017年12.二次函数y=ax 2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)2a+b=0;(2)9a+c >3b ;(3)5a+7b+2c >0;(4)若点A(-3,y 1)、点B(12-,y 2)、点C(72,y 3)在该函数图象上,则y 1<y 2<y 3;(5)若方程a(x+1)(x-5)=c 的两根为x 1和x 2,且x 1<x 2,则x 1<-1<5<x 2,其中正确的结论有( )A .1个B .2个C .3个D .4个二、填空题13.如图,在ABC △中,,点D 在BC 上,且BD BA =,ABC ∠的平分线BE 交AD 于点E ,点F 是AC 的中点,连结EF .若四边形DCFE 和△BDE 的面积都为3,则△ABC 的面积为____.14.计算:|﹣5|.15.解方程:3x 2﹣6x+1=2.16.使代数式21x -有意义的x 的取值范围是_____. 17.计算:= . 18.计算1023-+=_____.三、解答题19.计算:()201sin 3022-︒⎛⎫-- ⎪⎝⎭. 20.我国古代的优秀数学著作《九章算术》有一道“竹九节”问题,大意是说:现有﹣一根上细下粗共九节的竹子,自上而下从第2节开始,每一节与前一节的容积之差都相等,且最上面三节的容积共9升,最下面三节的容积共45升,求第五节的容积,及每一节与前一节的容积之差.请解答上述问题.21.有3张不透明的卡片,除正面写有不同的数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作二次函数表达式y =a (x ﹣2)2+c 中的a ,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作表达式中的c .(1)求抽出a 使抛物线开口向上的概率;(2)求抛物线y =a (x ﹣2)2+c 的顶点在第四象限的概率.(用树状图或列表法求解)22.我市今年中考体育测试,男生必考项目是1000米跑,男生还须从以下六个项目中任选两个项目进行考核:①坐位体前屈、②立定跳远、③掷实心球、④跳绳、⑤50m 、⑥引体向上.(1)男生在确定体育选项中所有可能选择的结果有 种;(2)已知某班男生只在①坐位体前屈、②立定跳远、④跳绳中任选两项,请你用列表法或画树状图法,求出两名男生在体育测试中所选项目完全相同的概率.23.某校为了了解学生的安全意识,在全校范围内随机抽取部分学生进行问卷调查.根据调查结果,把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如下两幅尚不完整的统计图.根据以上信息,解答下列问题:(1)这次调查一共抽取了名学生,将条形统计图补充完整;(2)扇形统计图中,“较强”层次所占圆心角的大小为°;(3)若该校有1800名学生,现要对安全意识为“淡薄”、“一般”的学生强化安全教育,根据调查结果,请你估计全校需要强化安全教育的学生人数.24.某特产店出售大米,一天可销售20袋,每袋可盈利40元,为了扩大销售,增加盈利,尽快减少库存,决定采取降价措施,据统计发现,若每袋降价2元,平均每天可多售4袋.(1)设每袋大米降价为x(x为偶数)元时,利润为y元,写出y与x的函数关系式.(2)若每天盈利1200元,则每袋应降价多少元?(3)每袋大米降价多少元时,商店可获最大利润?最大利润是多少?25.如图,在△ABD中,AB=AD,AB是⊙O的直径,DA、DB分别交⊙O于点E、C,连接EC,OE,OC.(1)当∠BAD是锐角时,求证:△OBC≌△OEC;(2)填空:①若AB=2,则△AOE的最大面积为;②当DA与⊙O相切时,若AB AC的长为.【参考答案】***一、选择题二、填空题14.215.x 1 ,x 2. 16.x≥0且x≠217..18.5三、解答题19.0【解析】【分析】根据三角函数、0指数幂,负指数幂的定义进行计算.【详解】解:原式=1+3﹣4=0.【点睛】考核知识点:三角函数、0指数幂,负指数幂.理解定义是关键.20.第五节的容积9升,每一节与前一节的容积之差2升.【解析】【分析】从题目中可知,第2节开始相邻两节的容积差相等设为y ,第5节的容积直接设为x ,然后根据第5节和容积差建立等量关系:第1节容积+第2节容积+第3节容积=9,第7节容积+第8节容积+第9节容积=45构建二元一次方程组求解.【详解】解:设第五节的容积为x 升,每一节与前一节的空积之差为y 升,依题意得: (4)(3)(2)9(2)(3)(4)45x y x y x y x y x y x y -+-+-=⎧⎨+++++=⎩, 解得:92x y =⎧⎨=⎩, 答:第五节的容积9升,每一节与前一节的容积之差2升.【点睛】本题考查了二元一次方程组在古典数学中的应用,突出了我国古人在数学方面的成就.难点是用第5节容积和相邻容积来表示竹子各节的容积.21.(1)抽出a 使抛物线开口向上的概率为13;(2)抛物线y =a (x ﹣2)2+c 的顶点在第四象限的概率为23. 【解析】(1)三张牌中正数只有一个3,求出a为正数的概率即可;(2)根据题意列表得出所有等可能的情况数,找出符合题意的情况数,即可求出所求概率.【详解】(1)∵共有3张牌,只有1张是正数,∴抽出a使抛物线开口向上的概率为13;(2)画树状图如下:由树状图知,抛物线的顶点坐标为(2,﹣2),(2,3),(2,﹣1),(2,3),(2,﹣2),(2,﹣1)共6种可能结果,其中,顶点在第四象限的有4种结果,所以抛物线y=a(x﹣2)2+c的顶点在第四象限的概率为42 63 .【点睛】此题考查了二次函数的图像与性质,平面直角坐标系点的坐标特征,列表法与树状图法求概率,概率=所求情况数与总情况数之比.当a>0时,抛物线开口向上,当a<0时,抛物线开口向下. 第四象限内点的坐标特征为(+,-).22.(1)30;(2)16.【解析】【分析】(1)画树状图可得所有等可能结果;(2)画树状图得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式计算可得.【详解】解:(1)根据题意画图如下:一共有30种不同的情况,故答案为:30;(2)画树状图如下:由树状图知,共有18种等可能结果,其中两名男生在体育测试中所选项目完全相同的有3种结果,所以两名男生在体育测试中所选项目完全相同的概率为31 186=.【点睛】此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.23.(1)200;(2)108;(3)450.【解析】【分析】(1)由安全意识为“很强”的学生数除以占的百分比得到抽取学生总数,再用总人数分别减去安全意识“淡薄”、“一般”、“很强”的人数,得出安全意识为“较强”的学生数,补全条形统计图即可;(2)用360°乘以安全意识为“较强”的学生占的百分比即可;(3)由安全意识为“淡薄”、“一般”的学生占的百分比的和,乘以1800即可得到结果.【详解】(1)调查的总人数是:90÷45%=200(人).安全意识为“很强”的学生数是:200﹣20﹣30﹣90=60(人).条形图补充如下:故答案为:200;(2)“较强”层次所占圆心角的大小为:360°×60200=108°.故答案为108;(3)根据题意得:1800×2030200+=450(人),则估计全校需要强化安全教育的学生人数为450人【点睛】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.也考查了利用样本估计总体.24.(1)y=-2x2+60x+800(2)x=20(3)x=14或16时获利最大为1248元【解析】【分析】(1)根据题意设出每天降价x元以后,准确表示出每天大米的销售量,列出利润y关于降价x的函数关系式;(2)根据题意列出关于x 的一元二次方程,通过解方程即可解决问题;(3)运用函数的性质即可解决.【详解】(1)当每袋大米降价为x (x 为偶数)元时,利润为y 元,则每天可出售20+4×2x =20+2x ; 由题意得:y=(40-x )(20+2x )=-2x 2+80x-20x+800=-2x 2+60x+800;(2)当y=1200时,-2(x-15)2+1250=1200,整理得:(x-15)2=25,解得x=10或20但为了尽快减少库存,所以只取x=20,答:若每天盈利1200元,为了尽快减少库存,则应降价20元;(3)∵y=-2(x-15)2+1250=1200,解得x=15,∵每袋降价2元,则当x=14或16时获利最大为1248元.【点睛】题考查了二次函数及一元二次方程在现实生活中的应用问题;解题的关键是准确列出二次函数解析式,灵活运用函数的性质解题.25.(1)见解析;(2)①S △AOE 最大=12;②AC =1. 【解析】【分析】(1)利用垂直平分线,判断出∠BAC =∠DAC ,得出EC =BC ,用SSS 判断出结论;(2)①先判断出三角形AOE 面积最大,只有点E 到直径AB 的距离最大,即是圆的半径即可;②根据切线的性质和等腰直角三角形的性质解答即可.【详解】(1)连接AC ,如图1,∵AB 是⊙O 的直径,∴AC ⊥BD ,∵AD =AB ,∴∠BAC =∠DAC ,∴BC EC=,∴BC=EC,在△OBC和△OEC中BC EC OB E OC COO=⎧⎪=⎨⎪=⎩,∴△OBC≌△OEC(SSS),(2)①∵AB是⊙O的直径,且AB=2,∴OA=1,设△AOE的边OA上的高为h,∴S△AOE=12OA×h=12×1×h=12h,∴要使S△AOE最大,只有h最大,∵点E在⊙O上,∴h最大是半径,即h最大=1∴S△AOE最大=12,故答案为12;②如图2:当DA与⊙O相切时,∴∠DAB=90°,∵AD=AB,∴∠ABD=45°,∵AB是直径,∴∠ADB=90°,∴AC=BC=1 22AB==,故答案为:1【点睛】此题是圆的综合题,主要考查了圆的性质,全等三角形的判定和性质,解本题的关键是确定面积最大时,点E到AB的距离最大是半径.2019-2020学年数学中考模拟试卷一、选择题1.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )A .3cm ,4cm ,8cmB .8cm ,7cm ,15cmC .13cm ,12cm ,20cmD .5cm ,5cm ,11cm2.如图,▱ABCD 中,点A 在反比例函数y=(0)k k x≠的图像上,点D 在y 轴上,点B 、点C 在x 轴上.若▱ABCD 的面积为10,则k 的值是( )A .5B .5-C .10D .10-3.如图,在Rt △ABC 中,∠ACB =90°,∠A =60°,AC =2,D 是AB 边上一个动点(不与点A 、B 重合),E 是BC 边上一点,且∠CDE =30°.设AD =x ,BE =y ,则下列图象中,能表示y 与x 的函数关系的图象大致是( )A .B .C .D .4.若一组数据为:2,3,1,3,3.则下列说法错误的是( )A.这组数据的众数是3B.事件“在这组数据中随机抽取1个数,抽到的数是0.“是不可能事件C.这组数据的中位数是3D.这组数据的平均数是35.如图,ABC ∆中,90ACB ∠=︒,4AC =,6BC =,CD 平分ACB ∠交AB 于点D ,点E 是AC 的中点,点P 是CD 上的一动点,则PA PE +的最小值是( )A.B .6 C.D6.关于x ,y 的方程组32451x y m x y m +=+⎧⎨-=-⎩的解满足237x y +>,则m 的取值范围是( ) A .14m <- B .0m < C .13m > D .7m >7.如图,AB 是O e 的直径,点D 是半径OA 的中点,过点D 作CD ⊥AB ,交O e 于点C ,点E 为弧BC 的中点,连结ED 并延长ED 交O e 于点F ,连结AF 、BF ,则( )A .sin ∠AFE=12B .cos ∠BFE=12C .tan ∠D .tan ∠8.某市的住宅电话号码是由7位数字组成的,某人到电信公司申请安装一部住宅电话,那么该公司配送这部电话的号码末尾数字为6的概率是( )A .16B .17C .19D .1109.如图,△ABC 中,DE ∥BC ,DE 分别交AB ,AC 于D ,E ,S △ADE =2S △DCE ,则ADEABC S S =( )A .14B .12C .23D .49 10.下列运算正确的是( )A .(y+1)(y ﹣1)=y 2﹣1B .x 3+x 5=x 8C .a 10÷a 2=a 5D .(﹣a 2b )3=a 6b 311.测试五位学生的“一分钟跳绳”成绩,得到五个各不相同的数据,在统计时出现了一处错误:将最高成绩写得更高了,则计算结果不受影响的是( ) A .中位数B .平均数C .方差D .极差12.下列由年份组成的各项图形中,是中心对称图形的是( )A .B .C .D .二、填空题13.在平面直角坐标系中,点A (﹣4,3)关于原点对称的点A′的坐标是_____. 14.若一个多边形的内角和等于外角和,那么这个多边形的边数是_____. 15.若2a-b=5,则多项式6a-3b 的值是______.16.某学校组织600名学生分别到野生动物园和植物园开展社会实践活动,到野生动物园的人数比到植物园人数的2倍少30人,若设到植物园的人数为x 人,依题意,可列方程为________________. 17.如图,一条船从灯塔C 的南偏东42°的A 处出发,向正北航行8海里到达B 处,此时灯塔C 在船的北偏西84°方向,则船距离灯塔C _____海里.18.在矩形ABCD 中,AD =12,E 是AB 边上的点,AE =5,点P 在AD 边上,将△AEP 沿FP 折叠,使得点A 落在点A′的位置,如图,当A′与点D 的距离最短时,△A′PD 的面积为_____.三、解答题 19.计算:(1221(1)()3-⨯--- (2)a (a ﹣8)﹣(a ﹣2)220.如图,AB 是⊙O 的直径,D ,E 为⊙O 上位于AB 异侧的两点,连结BD 并延长至点C ,使得CD =BD ,连结AC 交⊙O 于点F ,连接BE ,DE ,DF .(1)若∠E=35°,求∠BDF的度数.(2)若DF=4,cos∠CFD=23,E是AB的中点,求DE的长.21.某校为了调查初三男生和女生周日学习用时情况,随机抽取了初三男生和女生各50人,对他们的周日学习时间进行了统计,分别得到了初三男生的学习时间的频率分布表和女生学习时间的频率分布直方图(学习时间x,单位:小时,0≤x≤6).男生周日学习时间频率表(1)请你判断该校初三年级周日学习用时较长的是男生还是女生,并说明理由;(2)从这100名学生中周日学习用时在5≤x≤6内的学生中抽取2人,求恰巧抽到一男一女的概率.22.“2019宁波国际山地马拉松赛”于2019年3月31日在江北区举行,小林参加了环绕湖8km的迷你马拉松项目(如图1),上午8:00起跑,赛道上距离起点5km处会设置饮水补给站,在比赛中,小林匀速前行,他距离终点的路程s(km)与跑步的时间t(h)的函数图象的一部分如图2所示(1)求小林从起点跑向饮水补给站的过程中与t的函数表达式(2)求小林跑步的速度,以及图2中a的值(3)当跑到饮水补给站时,小林觉得自己跑得太悠闲了,他想挑战自己在上午8:55之前跑到终点,那么接下来一段路程他的速度至少应为多少?23.水果基地为了选出适应市场需求的小西红柿秧苗,在条件基本相同的情况下,把两个品种的小西红柿秧苗各300株分别种植在甲、乙两个大棚,对市场最为关注的产量和产量的稳定性进行了抽样调查,过程如下:收集数据从甲、乙两个大棚中分别随机收集了相同生产周期内25株秧苗生长出的小西红柿的个数:甲:26,32,40,51,44,74,44,63,73,74,81,54,62,41,33,54,43,34,51,63,64,73,64,54,33乙:27,35,46,55,48,36,47,68,82,48,57,66,75,27,36,57,57,66,58,61,71,38,47,46,71整理数据按如下分组整理样本数据:(说明:45个以下为产量不合格,45个及以上为产量合格,其中45≤x<65个为产量良好,65≤x<85个为产量优秀)分析数据两组样本数据的平均数、众数和方差如下表所示:得出结论(1)补全上述表格;(2)可以推断出大棚的小西红柿秩苗品种更适应市场需求,理由为(至少从两个不同的角度说明推断的合理性);(3)估计乙大棚的300株小西红柿秧苗中产量优秀的有多少株?24|12sin 60︒-25.合肥合家福超市为了吸引顾客,设计了一种促销活动:在三等分的转盘上依次标有“合”,“家”,“福”字样,购物每满200元可以转动转盘1次,转盘停下后,指针所指区域是“福”时,便可得到30元购物券(指针落在分界线上不计次数,可重新转动一次),一个顾客刚好消费400元,并参加促销活动,转了2次转盘.(1)求出该顾客可能获得购物券的最高金额和最低金额;(2)请用画树状图法或列表法求出该顾客获购物券金额不低于30元的概率.【参考答案】*** 一、选择题二、填空题 13.(4,﹣3). 14.4 15.1516.(230)600x x +-= 17. 18.403三、解答题19.(1)0;(2)﹣4a ﹣4. 【解析】 【分析】根据实数运算法则和整式运算法则分别计算即可,要注意负指数幂的意义. 【详解】解:(1221(1)()3-⨯--- =4+5×1﹣9 =4+5﹣9 =0;(2)a (a ﹣8)﹣(a ﹣2)2 =a 2﹣8a ﹣a 2+4a ﹣4=﹣4a﹣4.【点睛】本题考查实数运算和整式运算,负指数幂的意义,熟练掌握运算顺序和运算法则是解题关键.20.(1)∠BDF=110°;(2)DE=.【解析】【分析】(1)连接EF,BF,由AB是⊙O的直径,得到∠AFB=∠BFC=90°,推出DF BD=,得到∠DEF=∠BED=35°,根据圆内接四边形的性质即可得到结论;(2)连接AD,OE,过B作BG⊥DE于G,解直角三角形得到AB=6,由E是AB的中点,AB是⊙O的直径,得到∠AOE=90°,根据勾股定理即可得到结论.【详解】(1)如图1,连接EF,BF,∵AB是⊙O的直径,∴∠AFB=∠BFC=90°,∵CD=BD,∴DF=BD=CD,∴DF BD=,∴∠DEF=∠BED=35°,∴∠BEF=70°,∴∠BDF=180°﹣∠BEF=110°;(2)如图2,连接AD,OE,过B作BG⊥DE于G,∵∠CFD=∠ABD,∴cos∠ABD=cos∠CFD=23,在Rt△ABD中,BD=DF=4,∴AB=6,∵E是AB的中点,AB是⊙O的直径,∴∠AOE=90°,∵BO=OE=3,∴BE=,∴∠BDE=∠ADE=45°,∴DG=BG BD=,∴GE,∴DE=DG+GE=.【点睛】本题考查了圆周角定理,解直角三角形,正确的作出辅助线是解题的关键.21.(1)该校初三年级周日学习用时较长的是男生;(2)3 5【解析】【分析】(1)分别求出男生和女生周日学习用时的平均数,由此判断即可;(2)从被抽到的100名学生中周日学习用时在[5,6]内的学生中男生由2人,女生由4人,列树状图求得抽到1男1女的概率即可.【详解】解:(1)由频数分布直方图得女生学习时间的平均数为:150(10×1.5+10×2.5+14×3.5+8×4.5+2×5.5)=2.75;由男生周日学习时间频率表得男生学习时间的平均数为:0.5×0.34+1.5×0.36+2.5×0.38+3.5×0.22+4.5×0.14+5.5×0.06=3.39,∵2.75<3.39,∴该校初三年级周日学习用时较长的是男生;(2)这100名学生中周日学习用时在5≤x≤6内的学生中,男生有3人,女生有2人, 列树状图如图所示,由树状图可知,共有20种情况; 刚好抽到一男一女的有12种等可能结果, 所以刚好抽到一男一女的概率为123205=.【点睛】此题考查了概率公式与列表法或树状图法求概率.列表法或树状图法可以不重不漏的列举出所有可能发生的情况,列举法适合于两步完成的事件,树状图法适合于两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比. 22.(1)3685s t =-+;(2)速度为:365km/h ,a =2536;(3)接下来一段路程他的速度至少为13.5km/h . 【解析】 【分析】(1)根据图象可知,点(0,8)和点(512,5)在函数图象上,利用待定系数法求解析式即可; (2)由题意,可知点(a ,3)在(1)中的图象上,将其代入求解即可; (3)设接下来一段路程他的速度为xkm/h ,利用 【详解】解:(1)设小林从起点跑向饮水补给站的过程中s 与t 的函数关系式为:s =kt+b , (0,8)和(512,5)在函数s =kt+b 的图象上, ∴85512b k b =⎧⎪⎨+=⎪⎩,解得:36k 5b 8⎧=-⎪⎨⎪=⎩,∴s 与t 的函数关系式为:3685s t =-+; (2)速度为:5363125÷=(km/h ), 点(a ,3)在3685s t =-+上, ∴36835a -+=,解得:2536a =; (3)设接下来一段路程他的速度为xkm/h , 根据题意,得:55256036⎛⎫-⎪⎝⎭x≥3,解得:x≥13.5答:接下来一段路程他的速度至少为13.5km/h.【点睛】本题主要考查一次函数的应用,解决第(3)题的关键是明确,要在8点55之前到达,需满足在接下来的路程中,速度×时间≥路程.23.(1)5,5,6,54;(2)乙,乙的方差较小,众数比较大;(3)84株【解析】【分析】(1)利用划计法统计即可.(2)从平均数,众数,方差三个方面分析即可.(3)利用样本估计总体的思想解决问题即可.【详解】(1)甲:35≤x<45时,小西红柿的株数为5,55≤x<65时,小西红柿的株数为5.甲的众数为54,乙:45≤<55时,小西红柿的株数为6.故答案为:5,5,6,54.(2)选:乙.理由:乙的方差较小,众数比较大.故答案为:乙,乙的方差较小,众数比较大.(3)300725⨯=84(株)答:估计乙大棚的300株小西红柿秧苗中产量优秀的有84株.【点睛】本题考查了方差,众数,平均数,样本估计总体等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.24.5【解析】【分析】根据二次根式的乘法法则、绝对值的意义和特殊角的三角函数值计算.【详解】12-61=+=5.【点睛】本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.25.(1)最高金额为60元、最低金额为0元;(2)5 9【解析】【分析】(1)两次都抽到“福”时可得最高金额,两次都没有抽到“福”时可得最低金额;(2)画出树状图,利用概率公式计算即可;【详解】解:(1)根据题意,该顾客可能获得购物券的最高金额为60元、最低金额为0元;(2)画树状图如下:由树状图知,共有9种等可能结果,其中该顾客获购物券金额不低于30元的有5种结果,所以该顾客获购物券金额不低于30元的概率为59.【点睛】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.。
中考几何证明与计算(1)
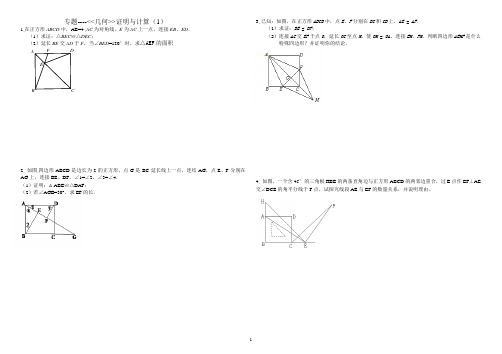
专题----<<几何>>证明与计算(1)1,在正方形ABCD中,AB=4 ,AC为对角线,E为AC上一点,连接EB、ED.(1)求证:△BEC≌△DEC;F,当∠BED=120°时,求△AEF的面积2, 如图,四边形ABCD是边长为2的正方形,点G是BC延长线上一点,连结AG,点E、F分别在AG上,连接BE、DF,∠1=∠2,∠3=∠4.(1)证明:△ABE≌△DAF;(2)若∠AGB=30°,求EF的长.3,已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE = AF.(1)求证:BE = DF;(2)连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.4, 如图,一个含45°的三角板HBE的两条直角边与正方形ABCD的两邻边重合,过E点作EF⊥AE交∠DCE的角平分线于F点,试探究线段AE与EF的数量关系,并说明理由。
125. 在正方形ABCD 中,点E 、F 分别在BC 、CD 上,且∠BAE=30º,∠DAF=15 º.(1)求证: EF=BE+DF ; (2)若AB=3,求△AEF 的面积。
6,如图,已知在正方形ABCD 中,AB=2,P 是边BC 上的任意一点,E 是边BC 延长线上一点,E 是边BC 延长线上一点,连接AP ,过点P 作PF 垂直于AP ,与角DCE 的平分线CF 相交于点F ,连接AF ,于边CD 相交于点G ,连接PG 。
(1)求证:AP=FP(2)当BP 取何值时,PG//CFE7,如图,在ABC ∆中,点D 为射线BC 上一动点,连接AD ,以AD 为一边且在AD 的右侧作正方形ADEF .如果,90,AB AC BAC =∠=//点D 在线段BC 上运动.且45BCA ∠= 时,①请你判断线段CF BD 、之间的位置..关系,并说明理由(要求写出证明过程).②若,3,24==CF AC 求正方形ADEF 的边长(要求写出计算过程).8,如图,已知正方形ABCD 的边长是2,E 是AB 的中点,延长BC 到点F 使CF =AE . (1)若把ADE △绕点D 旋转一定的角度时,能否与CDF △重合?请说明理由. (2)现把DCF △向左平移,使DC 与AB 重合,得ABH △,AH 交ED 于点G .求证:AH ED ⊥,并求AG 的长FE D C B AF H E B C。
高三数学解析几何试题答案及解析

高三数学解析几何试题答案及解析1.(本小题满分10分)选修4-1:几何证明选讲如图,是圆的直径,是半径的中点,是延长线上一点,且,直线与圆相交于点、(不与、重合),与圆相切于点,连结,,.(Ⅰ)求证:;(Ⅱ)若,求.【答案】(Ⅰ)详见解析(Ⅱ)【解析】(Ⅰ)证明目标可看做线段成比例,即证明思路确定为证明三角形相似:利用切割线定理得:,又由与相似,得;所以(Ⅱ)由(1)知,,与相似,则,所以试题解析:(1)连接,,,为等边三角形,则,可证与相似,得;又,则(2)由(1)知,,与相似,则因为,所以【考点】三角形相似,切割线定理2.(本小题满分10分)选修4—4:坐标系与参数方程在直角坐标系中,直线的参数方程为为参数),以该直角坐标系的原点为极点,轴的正半轴为极轴的极坐标系下,圆的方程为.(Ⅰ)求直线的普通方程和圆的圆心的极坐标;(Ⅱ)设直线和圆的交点为、,求弦的长.【答案】(Ⅰ)的普通方程为,圆心;(Ⅱ).【解析】(Ⅰ)消去参数即可将的参数方程化为普通方程,在直角坐标系下求出圆心的坐标,化为极坐标即可;(Ⅱ)求出圆心到直线的距离,由勾股定理求弦长即可.试题解析:(Ⅰ)由的参数方程消去参数得普通方程为 2分圆的直角坐标方程, 4分所以圆心的直角坐标为,因此圆心的一个极坐标为. 6分(答案不唯一,只要符合要求就给分)(Ⅱ)由(Ⅰ)知圆心到直线的距离, 8分所以. 10分【考点】1.参数方程与普通方程的互化;2.极坐标与直角坐标的互化.:的焦点,且抛物线3.(本题满分12分)如图,O为坐标原点,点F为抛物线C1C1上点P处的切线与圆C2:相切于点Q.(Ⅰ)当直线PQ的方程为时,求抛物线C1的方程;(Ⅱ)当正数变化时,记S1,S2分别为△FPQ,△FOQ的面积,求的最小值.【答案】(Ⅰ);(Ⅱ).【解析】第一问要求抛物线的方程,任务就是求的值,根据导数的几何意义,设出切点坐标,从而求得,再根据切点在切线上,得,从而求得,进而得到抛物线的方程,第二问根据三角形的面积公式,利用题中的条件,将两个三角形的面积转化为关于和切点横坐标的关系式,从而有,利用基本不等式求得最值.试题解析:(Ⅰ)设点,由得,,求导,……2分因为直线PQ的斜率为1,所以且,解得,所以抛物线C1的方程为.(Ⅱ)因为点P处的切线方程为:,即,根据切线又与圆相切,得,即,化简得,由,得,由方程组,解得,所以,点到切线PQ的距离是,所以,,所以,当且仅当时取“=”号,即,此时,,所以的最小值为.【考点】导数的几何意义,三角形的面积,基本不等式.4.(本小题满分12分)已知椭圆的左、右焦点分别为F1(-3,0),F2(3,0),直线y=kx与椭圆交于A、B两点.(Ⅰ)若三角形AF1F2的周长为,求椭圆的标准方程;(Ⅱ)若,且以AB为直径的圆过椭圆的右焦点,求椭圆离心率e的取值范围.【答案】(Ⅰ);(Ⅱ).【解析】(Ⅰ)直接由题意和椭圆的概念可列出方程组,进而可求出椭圆的标准方程即可;(Ⅱ)首先设出点,然后联立直线与椭圆的方程并整理可得一元二次方程,进而由韦达定理可得,再结合可列出等式并化简即可得到等式,最后结合已知,即可求出参数的取值范围,进而得出椭圆离心率e的取值范围即可.试题解析:(Ⅰ)由题意得,得.结合,解得,.所以,椭圆的方程为.(Ⅱ)由得.设.所以,易知,,因为,,所以.即,将其整理为.因为,所以,即,所以离心率.【考点】1、椭圆的标准方程;2、直线与椭圆的相交综合问题;5.(本小题满分12分)椭圆()的上顶点为,是上的一点,以为直径的圆经过椭圆的右焦点.(1)求椭圆的方程;(2)动直线与椭圆有且只有一个公共点,问:在轴上是否存在两个定点,它们到直线的距离之积等于?如果存在,求出这两个定点的坐标;如果不存在,说明理由.【答案】(1);(2)存在两个定点,.【解析】(1)由题设可得①,又点P在椭圆C上,可得②,又③,由①③联立解得c,b2,即可得解.(2)设动直线l的方程为y=kx+m,代入椭圆方程消去y,整理得(﹡),由△=0,得,假设存在,满足题设,则由对任意的实数k恒成立.由即可求出这两个定点的坐标.试题解析:(1),,由题设可知,得①又点在椭圆上,,②③①③联立解得,,故所求椭圆的方程为(2)当直线的斜率存在时,设其方程为,代入椭圆方程,消去,整理得()方程()有且只有一个实根,又,所以,得假设存在,满足题设,则由对任意的实数恒成立,所以,解得,或当直线的斜率不存在时,经检验符合题意.总上,存在两个定点,,使它们到直线的距离之积等于.……12分【考点】1、直线与圆锥曲线的关系;2、椭圆的标准方程.【方法点晴】本题主要考查了椭圆的标准方程的解法,考查了直线与圆锥曲线的关系,综合性较强,属于中档题.处理直线与圆锥曲线的关系问题时,注意韦达定理的应用,同时还得特别注意直线斜率不存在时的情况的验证.6.直线被圆截得的弦长为()A.1B.2C.4D.【答案】C【解析】圆心,圆心到直线的距离,半径,所以最后弦长为.故选C.【考点】点到直线的距离.7.(本小题12分)己知、、是椭圆:()上的三点,其中点的坐标为,过椭圆的中心,且,。
第56讲 解析法证几何题

第56讲 解析法证 几何题解析法是利用代数方法解决几何问题的一种常用方法.其一般的顺序是:建立坐标系,设出各点坐标及各线的方程,然后根据求解或求证要求进行代数推算.它的优点是具有一般性与程序性,几何所有的平面几何问题都可以用解析法获解,但对于有些题目演算太繁.此外,如果建立坐标系或设点坐标时处理不当,也可能增加计算量.建系设点坐标的一般原则是使各点坐标出现尽量多的0,但也不可死搬教条,对于一些“地位平等”的点、线,建系设点坐标时,要保持其原有的“对称性”.A 类例题例1.如图,以直角三角形ABC 的斜边AB 及直角边BC 为边向三角形两侧作正方形ABDE 、CBFG .求证:DC ⊥F A .分析 只要证k CD ·k AF =-1,故只要求点D 的坐标.证明 以C 为原点,CB 为x 轴正方向建立直角坐标系.设A (0,a),B(b,0),D(x,y).则直线AB的方程为ax+by-ab=0.故直线BD的方程为bx-ay-(b·b-a·0)=0,即bx-ay-b2=0.ED方程设为ax+by+C=0.由AB、ED距离等于|AB|,得|C+ab|a2+b2=a2+b2,解得C=±(a2+b2)-ab.如图,应舍去负号.所以直线ED方程为ax+by+a2+b2-ab=0.解得x=b-a,y=-b.(只要作DH⊥x轴,由△DBH≌△BAC就可得到这个结果).即D(b-a,-b).因为k AF=b-ab,k CD=-bb-a,而k AF·k CD=-1.所以DC⊥F A.例2.自ΔABC的顶点A引BC的垂线,垂足为D,在AD上任取一点H,直线BH交AC于E,CH交AB于F.试证:AD平分ED与DF所成的角.证明建立直角坐标系,设A(0,a),B(b,0),C(c,0),H(0,h),于是BH:xb+yh=1AC:xc+ya=1过BH、AC的交点E的直线系为:λ(xb+yh-1)+μ(xc+ya-1)=0.以(0,0)代入,得λ+μ=0.分别取λ=1,μ=-1,有x(1b-1c)+y(1h-1a)=0.所以,上述直线过原点,这是直线DE.同理,直线DF为x(1c-1b)+y(1h-1a)=0.显然直线DE与直线DF的斜率互为相反数,故AD平分ED与DF所成的角.说明写出直线系方程要求其中满足某性质的直线,就利用此性质确定待定系数,这实际上并不失为一种通法.例3.证明:任意四边形四条边的平方和等于两条对角线的平方和再加上对角线中点连线的平方的4倍.证明在直角坐标系中,设四边形四个顶点的坐标为A1(x1,y1),A2(x2,y2),A3(x3,y3),A4(x4,y4).由中点公式知对角中点的坐标为B(x1+x32,y1+y32),C(x2+x42,y2+y42).则4(x1+x32-x2+x42)2+(x1-x3)2+(x2-x4)2x=(x1+x3-x2-x4)2+(x1-x3)2+(x2-x4)2=2(x21+x22+x23+x24-x1x2-x2x3-x3x4-x4x1) =(x1-x2)2+(x2-x3)2+(x3-x4)2+(x4-x1)2,同理有4(y1+y32-y2+y42)2+(y1-y3)2+(y2-y4)2=(y1-y2)2+(y2-y3)2+(y3-y4)2+(y4-y1)2,两式相加得:|A1A2|2+|A2A3|2+|A3A4|2+|A4A1|2=4|BC|2+|A1A3|2+|A2A4|2.说明本题纯几何证法并不容易,而采用解析法,只需要简单的计算便达到目的.另外本例中巧妙地抓住了各点的“对称性”,设了最为一般的形式,简化了计算.情景再现1.如图,⊙O的弦CD平行于直径AB,过C、D的圆的切线交于点P,直线AC、BC分别交直线OP于Q、R.求证:|PQ|=|PR|.2.自圆M外一点E作圆的切线,切点为F,又作一条割线EAB,交圆M于A、B,连结EF的中点O与B,交圆M于D,ED交圆M于C.x求证:AC ∥EF .3.CH 是ΔABC 中边AB 上的高,H 为垂足,点K 、P 分别是H 关于边AC 和BC 的对称点.证明:线段KP 与AC ,BC (或它们的延长线)的交点是ΔABC 高线的垂足.B 类例题例4.P 、Q 在ΔABC 的AB 边上,R 在AC 边上,并且P ,Q ,R 将ΔABC 的周长分为三等分.求证:S ΔPQR S ΔABC >29.证明 如图,以A 为原点,直线AB 为x 轴,建立直角坐标系. 设AB =c ,BC =a ,CA =b ,Q (q ,0),P (p ,0). 则q -p =13(a +b +c ),AR =PQ -AP =q -2p , 从而y R y C =ARAC =q -2p b.由于2S ΔPQR =y R (q -p ),2S ΔABC =x B y C , 所以S ΔPQRS ΔABC =y R (q -p )y C x B =(q -p )(q -2p )bC .注意到p =q -13(a +b +c )<c -13(a +b +c ), 所以q -2p >23(a +b +c )-c >23(a +b +c )-12(a +b +c )=16(a +b +c ),S ΔPQR S ΔABC >29·(a +b +c )24bc >29·(b +c )24bc >29.说明 本题中29是不可改进的,取b =c ,Q 与B 重合,则当a 趋向于0时,p 趋向于13q ,面积比趋向于29. 例5.设H 是锐角三角形ABC 的垂心,由A 向以BC 为直径的圆作切线AP 、AQ ,切点分别为P 、Q .证明:P 、H 、Q 三点共线.(1996年中国数学奥林匹克) 证明 如图以BC 为x 轴BC 中点O 为原点建立直角坐标系. 设B (-1,0),C (1,0),A (x 0,y 0), 则PQ 方程为x 0x +y 0y =1.点H 的坐标为H (x 0,y ),满足yx 0+1·y 0x 0-1=-1, 即 y =1-x 20y 0,显然H 满足PQ 方程,即H 在PQ 上. 从而P 、H 、Q 三点共线.例6.设A 、B 、C 、D 是一条直线上依次排列的四个不同的点,分别以AC 、BD 为直径的两圆相交于X 和Y ,直线XY 交BC于xyZ .若P 为直线XY 上异于Z 的一点,直线CP 与以AC 为直径的圆相交于C 和M ,直线BP 与以BD 为直径的圆相交于B 和N .试证:AM 、DN 、XY 三线共点.分析 只要证明AM 与XY 的交点也是DN 与XY 的交点即可,为此只要建立坐标系,计算AM 与XY 的交点坐标.证明 如图,以XY 为弦的任意圆O ,只需证明当P 确定时,S 也确定.以Z 为原点,XY 为y 轴建立平面直角坐标系,设X (0,m ),P (0,y 0),∠PCA =α,其中m 、y 0为定值.于是有x C =y 0cotα. 但是-x A ·x C =y X2,则x A =-m 2y 0tanα.因此,直线AM 的方程为:y =cotα(x +m 2y 0tanα).令x =0,得y S =m 2y 0,即点S 的坐标为(0,m 2y 0).同理,可得DN 与XY 的交点坐标为(0,m 2y 0).所以AM 、DN 、XY 三线共点.x情景再现4.在RtΔABC中,AD是斜边上的高,M,N分别是ΔABD与ΔACD的内心,连接MN并延长分别交AB、AC于K、L两点.求证:SΔABC≥2SΔAKL.5.已知△ABC中,∠A=α,且1|AB|+1|AC|=m.求证:BC边过定点.6.设△ABC的重心为G,AG、BG、CG的延长线交△ABC的外接圆于P、Q、R.求证:AGGP+BGGQ+CGGR=3.C类例题例7.以ΔABC的边BC为直径作半圆,与AB、AC分别交于D 和E.过D、E作BC的垂线,垂足分别为F、G.线段DG、EF交于点M.求证:AM⊥BC.(1996年国家队选拔题)分析建立以BC为x轴的坐标系,则只要证明点A、M的横坐标相等即可.证明以BC所在的直线为x轴,半圆圆心O为原点建立直角坐标系.设圆的半径为1,则B(-1,0),C(1,0).令∠EBC=α,∠DCB=β,则直线BD的方程为y=cotβ·(x+1).同样,直线CE的方程为y=-cotα·(x-1),联立这两个方程,解得A点的横坐标x A=cotα-cotβcotα+cotβ=sin(α-β)sin(α+β).因为∠EOC=2∠EBC=2α,∠DOB=2β,故E(cos2α,sin2α),D(-cos2β,sin2β),G(cos2α,0),F(-cos2β,0).于是直线DG的方程为y=sin2β-(cos2α+cos2β)·(x-cos2α),直线EF的方程为y=sin2α-(cos2α+cos2β)·(x+cos2β).联立这两个方程,解得M点的横坐标x M=sin2α·cos2β-cos2α·sin2βsin2α+sin2β=sin2(α-β)sin(α+β)cos(α-β)=sin(α-β)sin(α+β)=x A.故AM⊥BC.例8.如图,一条直线l与圆心为O的圆不相交,E是l上一点,OE⊥l,M是l上任意异于E的点,从M作圆O的两条切线分别切圆于A和B,C是MA上的点,使得EC⊥MA,D是MB上的点,使得ED ⊥MB ,直线CD 交OE 于F .求证:点F 的位置不依赖于M 的位置(1994年IMO 预选题) 分析 若以l 为x 轴,OE 为y 轴建立坐标系,则只要证明F 点的纵坐标与点M 的坐标无关即可.证明 建立如图所示的平面直角坐标系,设圆O 的半径为r ,OE =a ,∠OME =α,∠OMA =θ,显然有sinθsinα=ra. y C =MC ·sin(α-θ)=ME ·sin(α-θ)cos(α-θ) =a cotα·sin(α-θ)cos(α-θ),x C =-y C ·tan(α-θ)=-a cotαsin 2(α-θ). 同理,y D =a cotα·sin(α+θ)cos(α+θ),x D =-a cotαsin 2(α+θ).所以,k CD =sin2(α+θ)-sin2(α-θ)2[sin 2(α-θ)-sin 2(α+θ)]=-cot2α.则直线CD 的方程为y -a cotα·sin(α+θ)cos(α+θ)=-cot2α[x +a cotαsin 2(α+θ)]. 令x =0,得y F =a cotα·sin(α+θ)[cos(α+θ)-cot2αsin(α+θ)] =a cotα·sin (α+θ)sin(α-θ)sin2αxl=a ·-cos2α+cos2θ4sin 2θ=a 2(1-sin 2θsin 2α) =a 2-r 22a.由于a 2-r 22a是定值,这就表明F 的位置不依赖于点M 的位置.情景再现7.在筝形ABCD 中,AB =AD ,BC =CD ,经AC 、BD 交点O 作二直线分别交AD 、BC 、AB 、CD 于点E 、F 、G 、H ,GF 、EH 分别交BD 于点I 、J .求证:IO =OJ .(1990年冬令营选拔赛题)8.水平直线m 通过圆O 的中心,直线l ⊥m ,l 与m 相交于M ,点M 在圆心的右侧,直线l 上不同的三点A 、B 、C 在圆外,且位于直线m 上方,A 点离M 点最远,C 点离M 点最近,AP 、BQ 、,CR 为圆O 的三条切线,P 、Q,、R 为切点.试证:(1)l 与圆O 相切时,AB ⨯CR +BC ⨯AP =AC ⨯BQ ;(2)l 与圆O 相交时,AB ⨯CR +BC ⨯AP <AC ⨯BQ ; (3)l 与圆O 相离时,AB ⨯CR +BC ⨯AP >AC ⨯BQ .(1993年全国高中数学联合竞赛)习题561.已知AM 是 ABC 的一条中线,任一条直线交AB 于P ,交AC 于Q ,交AM 于N .求证:AB AP ,AM AN ,ACAQ成等差数列.2.在四边形ABCD 中,AB 与CD 的垂直平分线相交于P ,BC 和AD 的垂直平分线相交于Q ,M 、N 分别为对角线AC 、BD 中点.求证:PQ ⊥MN .3.证明,如一个凸八边形的各个角都相等,而所有各邻边边长之比都是有理数,则这个八边形的每组对边一定相等.(1973年奥地利数学竞赛题)4.设△ABC 是锐角三角形,在△ABC 外分别作等腰直角三角形BCD 、ABE 、CAF ,在此三个三角形中,∠BDC 、∠BAE 、∠CF A 是直角.又在四边形BCFE 外作等腰直角三角形EFG ,∠EFG 是直角.求证:⑴GA =2AD ;⑵∠GAD =135°;(上海市1994年高中数学竞赛) 5.如图△ABC 和△ADE 是两个不全等的等腰直角三角形,现固定△ABC ,而将△ADE 绕A 点在平面上旋转.试证:不论△ADE 旋转到什么位置,线段EC 上必存在点M ,使△BMD 为等腰直角三角形.(1987年全国高中数学联赛)D ECBA6.设A1A2A3A4为⊙O的内接四边形,H1、H2、H3、H4依次为ΔA2A3A4、ΔA3A4A1、ΔA4A1A2、ΔA1A2A3的垂心.求证:H1、H2、H3、H4四点在同一个圆上,并定出该圆的圆心位置.(1992年全国高中数学联赛)7.证明:ΔABC的重心G,外心O,垂心H三点共线,且OG:GH=1:2.8.已知MN是圆O的一条弦,R是MN的中点,过R作两弦AB 和CD,过A、B、C、D四点的二次曲线交MN于P、Q.求证:R是PQ的中点.本节“情景再现”解答:1.以圆心O为原点,BA为y轴建立坐标系,设点C的坐标为(x0,y0),且⊙O的半径等于1.可得R点横坐标x R=x01-y0,Q点横坐标x Q=x01+y0,P点横坐标x P=1x0.所以x R+x q=x01-y0+x01+y0=x01-y20=2x0=2x P.即点P为QR的中点,所以|PQ|=|PR|.2.以O 为原点,EF 为x 轴,建立直角坐标系.设E (-x 0,0),F (x 0,0).圆M 的半径设为r ,则圆M 的方程为x 2+y 2-2xx 0-2yr +x 02=0 (1).过E 的两直线AB 、CD 的方程可设为h 1y =x +x 0,h 2y =x +x 0,合为(x -h 1y +x 0)(x -h 2y +x 0)=0 (2).直线BD 、AC 的方程又可设为y =kx ,ax +by +c =0.合为(y -kx )(ax +by +c )=0 (3).(1)与(2)所成的曲线系过交点A 、B 、C 、D ,又曲线(3)过点A 、B 、C 、D ,故为该曲线系中的一条.比较(1)与(2)所成的曲线系与(3)中常数项即可知(3)能由(1)、(2)相减得到,此时项中无x 2项.所以(3)中a =0,即AC ∥EF .3.建立如图所示的平面直角坐标系,设A 、B 、C 三点的坐标依次为A (a ,0),B (b ,0),C (0,c ).则P 点和K 点的坐标分别为:P (2bc 2b 2+c 2,2b 2c b 2+c 2),K (2ac 2a 2+c 2,2a 2ca 2+c 2).于是KP 所在的直线方程是c (a +b )x +(ab -c 2)y-2abc =0 ①,另一方面,BC 所在直线的方程是cx +by -bc =0 ②,BC 边上的高所在的直线方程是bx -cy -ab =0 ③,由于②×a +③×c =①,于是KP 经过BC 边上高线的垂足,同理,KP 与经过AC 边上高线的垂足.4.分别以AC 、AB 所在直线为x 轴和y 轴建立直角坐标系,并设|AC |=a ,|AB |=b ,|OD |=xc ,则c =aba 2+b2.设ΔACD 、ΔABD 的内切圆半径分别为r 1,r 2,则N ,M 的坐标分别为N (c -r 1,r 1),M (r 2,c -r 2).于是直线MN 的斜率为k MN =c -r 2-r 1r 2-c +r 1=-1.这说明ΔAKL 为等腰直角三角形,直线MN 的方程为y -r 1=-(x -c +r 1),其横、纵截距均为c ,所以2S ΔAKL=c 2=a 2b 2a 2+b 2≤a 2b 22ab=ab2=S ΔABC .5.以A 为原点,AB 为x 轴正方向建立直角坐标系.设|AB |=p ,|AC |=q .则1p +1q =m ,q =pmp -1,点B (p ,0),C (q cos α,q sin α).直线BC 的方程为yq sin α=x -p q cos α-p.整理得p (my -sin α)+[x sin α-(1+cos α)y ]=0,即无论p 为何值时,直线BC 经过两条定直线my -sin =0与x sin α-(1+cos α)y =0的交点.(两条直线斜率不等,故必有交点),即直线BC 过定点.6.以外接⊙O 的圆心O 为原点,平行于BC 的直线为x 轴建立坐标系.设A (x 1,y 1),B (x 2,y 2),则C (-x G (x 13,y 1+2y 23).设外接圆半径为r .则=x 22+y 22=r 2.由相交弦定理,知AG GP =|AG |2r 2-|OG |2,同理BG GQ =|BG |2r 2-|OG |2,CG GR =|CG |r 2-|OG |2;|AG |2+|BG |2+|CG |2=(x 1-x 13)2+(x 2-x 13)2+(x 2+x 13)2+(y 1-y 1+2y 23)2+2(y 2-y 1+2y 23)2=23[x 12+(y 1-y 2)2]+2x 22=43(r 2+x 22-y 1y 2),r 2-|OG |2=r 2-[x 209+(y 1+2y 2)29]=49(2r 2-y 22-y 1y 2).注意到x 22+y 22=r 2,就得AG GP +BG GQ +CGGR=|AG |2+|BG |2+|CG |2r 2-|OG |2=3.7.如图,以O 为原点,OD 为x 轴正方向建立直角坐标系,设A (0,a ),D (d ,0),C (0,c ),则B (-d ,0).直线AB 方程为:x -d+ya -1=0;设GH 方程:ky -x =0. (因为求I 点坐标时要取y =0,故把系数k 置 于y 前).于是GF 方程为x -d +ya -1+λ(ky-x )=0 ①,BC 方程为x -d +yc -1=0,设EF 方程为hy -x =0.于是GF 方程又可表 示为x -d+yc -1+μ(hy -x )=0 ②. ①与②是同一个方程,比较系数得λ=μ,1a +λk =1c+μh .则λ=1h -k (1a -1c ).在①中,令y =0得I 点的横坐标x I =d1+d λ;同理,点J 的横坐标为x J =-d 1-d λ',其中λ'=1k -h (1a-1c ),于是x I=-x j .即IO =OJ .从而得证.8.证略.本节“习题56”解答:1.以BC所在直线为x轴,高AD所在直线为y轴建立直角坐标系.设A(0,a),B(m-b,0),C(m+b,0),直线PQ方程:y=kx+q.设ABAP=λ,则AP+PBAP=λ,BPP A=λ-1.所以P点坐标为x=m-bλ,y=(λ-1)aλ,故(λ-1)a=k(m-b)+qλ,则λ=k(m-b)+aa-q ,即ABAP=k(m-b)+aa-q,同理,AMAN=km+aa-q,ACAQ=k(m+b)+a a-q .则ABAP+ACAQ=2AMAN.这说明ABAP,AMAN,ACAQ成等差数列.2.提示:设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),利用式子的对称性即可证得结论.3.此八边形的每个内角都等于135︒.不妨设每边的长都是有理数.依次设其八边长为有理数a,b,c,d,e,f,g,h.把这个八边形放入坐标系中,使长为a的边的一个顶点为原点,这边在x轴上,于是a+b cos45︒+d cos135︒-e+f cos225︒+h cos315︒=0,整理得a+e+22(b-d-f+h)=0;b cos45︒+c+d cos(-45︒)+f cos135︒-g+h cos225︒=0,整理得c+g+E22(b+d-f-h)=0.所以a=e,b-d-f+h=0;c=g,b+d-f-h=0.则b-f=0,g-h=0.从而凸八边形的每组对边相等.4.以A为原点建立直角坐标系,设B、C对应的复数为z B,z C.则点E对应复数z E=-iz B,点D对应复数z D=12(1+i)(z B-z C)+z C=12[(1+i)z B+(1-i)z C],点F对应复数z F=12(1+i)z C.向量→FE=z E-z F=-iz B-12(1+i)z C.z G=z F-i→FE=12(1+i)z C-i[-iz B-12(1+i)z C]=-z B+12(1+i)2z C=-z B+iz C.则z G=(-1+i)z D=2(cos135︒+i sin135︒)z D.则GA=2AD;∠GAD=135°.5.以A为原点,AC为x轴正方向建立复平面.设C表示复数c,点E表示复数e(c、e∈R).则点B表示复数b=12c+12ci,点D表示复数d=12e-12ei.把△ADE绕点A旋转角θ得到△AD'E',则点E'表示复数e'=e(cosθ+i sinθ).点D'表示复数d'=d(cosθ+i sinθ)表示E'C中点M的复数m=12(c+e').则表示向量→MB的复数:z1=b-12(c+e')=12c+12ci-12c-12e(cosθ+i sinθ)=-12e cosθ+12(c-e sinθ)i.表示向量→MD '的复数:z 2=d '-m =(12e -12ei )(cos θ+i sin θ)-12c -12e (cos θ+i sin θ)=12(e sin θ-c )-12ie cos θ.显然:z 2=z 1i .于是|MB |=|MD '|,且∠BMD '=90°.即△BMD '为等腰直角三角形.故证.6.以O 为坐标原点,⊙O 的半径为长度单位建立直角坐标系,设OA 1、OA 2、OA 3、OA 4与OX 正方向所成的角分别为α、β、γ、δ,则点A 1、A 2、A 3、A 4的坐标依次是(cos α,sin α)、(cos β,sin β)、(cos γ,sin γ)、(cos δ,sin δ).显然,⊿A 2A 3A 4、⊿A 3A 4A 1、⊿A 4A 1A 2、⊿A 1A 2A 3的外心都是点O ,而它们的重心依次是(13(cos β+cos γ+cos δ),13(sin β+sin γ+sin δ))、(13(cos γ+cos δ+cos α),13(sin α+sin δ+sin γ))、(13(cos δ+cos α+cos β),13(sin δ+sin α+sin β))、(13(cos α+cos β+cos γ),13(sin α+sin β+sin γ)).从而,⊿A 2A 3A 4、⊿A 3A 4A 1、⊿A 4A 1A 2、⊿A 1A 2A 3的垂心依次是H 1(cos β+cos γ+cos δ,sin β+sin γ+sin δ)、H 2(cos γ+cos δ+cos α,sin α+sin δ+sin γ)、H 3(cos δ+cos α+cos β,sin δ+sin α+sin β)、H 4(cos α+cos β+cos γ,sin α+sin β+sin γ).而H 1、H 2、H 3、H 4点与点O 1(cos α+cos β+cos γ+cos δ,sin α+sin β+sin γ+sin δ)的距离都等于1,即H 1、H 2、H 3、H 4四点在以O 1为圆心,1为半径的圆上.证毕.7.以ΔABC 的外心O 为坐标原点,不妨设ΔABC 的外接圆半径为1,设A (cosα,sinα),B (cosβ,sinβ),C (cosγ,sinγ),则重心G 的坐标为G (cosα+cosβ+cosγ3,sinα+sinβ+sinγ3).设H '(cosα+cosβ+cosγ,sinα+sinβ+sinγ).则k AH '=sinβ+sinγcosβ+cosγ=tan β-γ2,k BC =sinβ-sinγcosβ-cosγ=-cot β-γ2.则可得k AH '·k BC =-1,则AH '⊥BC .同理,BH '⊥CA ,CH '⊥AB .因此,H '(cosα+cosβ+cosγ,sinα+sinβ+sinγ)为ΔABC 的垂心H .观察O 、G 、H 的坐标可知,G 、O 、H 三点共线,且OG :GH =1:2.8.以R 为原点,MN 为x 轴,建立如图所示的平面直角坐标系.设圆心O 的坐标为(0,a ),圆半径为r ,则圆的方程为x 2+(y -a )2=r 2 ①,设AB 、CD 的方程分别为y =k 1x 和y =k 2x .将它们合成为(y -k 1x )(y-k 2x )=0 ②,于是过①与②的四个交点A 、B 、C 、D 的曲线系方程为(y -k 1x )(y -k 2x )+λ[x 2+(y -a )2-r 2]=0 ③,令③中y =0,得(λ+k 1k 2)x 2+λ(a 2-r 2)=0 ④.④的两个根是二次曲线与MN 交点P 、Q 的横坐标,因为x P +x Q =0,即R 是PQ 的中点.从而得证.说明:本例实质上是平面几何中蝴蝶定理得推广.平面几何中许多x命题都可以通过解析法获证.第21 页共21 页。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何证明与计算考向1以圆为背景的特殊四边形的动态探究题1.(2019年河南省中原名校中考第三次大联考数学试卷)如图,AB为⊙O的直径,射线AG为⊙O的切线,点A为切点,点C为射线AG上任意一点,连接OC交⊙O于点E,过点B作BD∥OC交⊙O于点D,连接CD,DE,O D.(1)求证:△OAC≌△ODC;(2)①当∠OCA的度数为时,四边形BOED为菱形;②当∠OCA的度数为时,四边形OACD为正方形.【答案】(1)证明见解析;(2)①∠OCA=30°,②∠OCA=45°.【解析】(1)依据SAS可证明△OAC≌△ODC;(2)①依据菱形的四条边都相等,可得△OBD是等边三角形,则∠AOC=∠OBD=60°,求出∠OCA=30°;②由正方形的性质得出∠ACD=90°,则∠ACO=45°.【详解】(1)证明:∵OB=OD,∴∠B=∠ODB,∵BD∥OC,∴∠AOC=∠B,∠DOC=∠ODB,∴∠AOC=∠COD,∵OA=OD,OC=OC,∴△OAC≌△ODC(SAS);(2)①∵四边形BOED是菱形,∴OB=D B.又∵OD=OB,∴OD=OB=D B.∴△OBD为等边三角形,∴∠OBD=60°.∵CO∥DB,∴∠AOC=60°,∵射线AG为⊙O的切线,∴OA⊥AC,∴∠OAC=90°,∴∠OCA=∠OAC﹣∠AOC=90°﹣60°=30°,②∵四边形OADC是正方形,∴∠ACD=90°,∵∠ACO=∠DCO,∴∠OCA=45°,故答案30°,45°.【点睛】本题主要考查的是切线的性质、全等三角形的判定和性质、菱形的性质、等边三角形的性质和判定,正方形的性质,熟练掌握相关知识是解题的关键.2. (2019年许昌二模)如图,AB 是半圆O 的直径,C 是半圆上一个动点(不与点A ,B 重合),D 是弦AC 上一点,过点D 作DE ⊥AB ,垂足为E ,过点C 作半圆O 的切线,交ED 的延长线于点F .(1)求证:FC =F D .(2)①当∠CAB 的度数为 时,四边形OEFC 是矩形;②若D 是弦AC 的中点,⊙O 的半径为5,AC =8,则FC 的长为 .【答案】(1)证明见解析;(2)∠CAB =45°310 FC 【解析】(1)证明∠FDC =∠FCD ,即可求解;(2)①当∠CAB =45°时,∠COB =90°,即可求解;②D 是弦AC 的中点,则OD ⊥AC ,AD =DC ,cosα==,FD ===,即可求解.解:(1)∵FC 是圆的切线,∴∠FCD +∠ACO =90°,∵FE ⊥BA ,∴∠ADC +∠CAO =90°,而∠CAO =∠ACO ,∠ADE =∠FDC ,∴∠FDC =∠FCD ,∴FC=FD;(2)①当∠CAB=45°时,∠COB=90°,则四边形OEFC是矩形,故答案是45;②连接OD,∵D是弦AC的中点,∴OD⊥AC,AD=DC,则∠ADE=∠AOD=∠FDC=α,则AD=CD=AC=4,OA=5,DO=4,cosα==,则△FDC中,FD====F C.【点评】本题为圆的综合运用题,涉及到解直角三角形、矩形的基本性质,其中(2),垂径定理的运用,是解题的关键.3.(2019年河南省南阳市镇平县中考数学三模试)如图,已知在Rt△ABC中,∠ABC=90°,点O是AB边上一点,以O为圆心OB为半径的⊙O与边AB相交于点E,与AC边相切于D 点,连接OC交⊙O于点F.(1)连接DE,求证:OC∥DE;(2)若⊙O的半径为3.①连接DF,若四边形OEDF为菱形,弧BD的长为________.(结果保留π)②若AE=2,则AD的长为________.【答案】(1)见解析;(2)①2π;②4.【解析】(1)利用HL可证明Rt△OCD≌Rt△OCB,可得∠COD=∠COB,利用三角形外角性质可得∠DOB=∠ODE+∠OED,即可证明∠DOC=∠ODE,即可得OC//DE;(2)①根据菱形的性质可求出∠BOD,利用弧长公式即可得答案;②由DE∥OC,推出==,设AD=2k,CD=3k,由Rt△OCD≌Rt△OCB,可得BC=CD=3k,在Rt△ABC中,利用勾股定理构建方程即可解决问题.【详解】(1)证明:连接O D.∵AC是切线,∴OD⊥AC,∠ODC=∠OBC=90°,∵OC=OC,OD=OB,∴Rt△OCD≌Rt△OCB(HL),∴∠COD=∠COB,∵OD=OE,∴∠ODE=∠OED,∵∠DOB=∠ODE+∠OED,∴∠DOC=∠ODE,∴DE∥O C.(2)①∵四边形DEOF是菱形,∴DF=OD=OF,∴△ODF是等边三角形,∴∠DOF=60°,∴∠BOD=2∠DOC=120°,∴的长==2π.故答案为2π.②∵DE∥OC,∴==,设AD=2k,CD=3k,∵Rt△OCD≌Rt△OCB,∴BC=CD=3k,在Rt△ABC中,则有25k2=9k2+82,∴k=2或﹣2(舍弃),∴AD=4.故答案为4.4.(河南省信阳市2019-2020学年九年级上学期期末数学试题)如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点.(1)直接写出ED和EC的数量关系:_________;(2)DE是⊙O的切线吗?若是,给出证明;若不是,说明理由;(3)填空:当BC=_______时,四边形AOED是平行四边形,同时以点O、D、E、C为顶点的四边形是_______.【答案】(1). ED=EC(2).DE是⊙O的切线;证明见解析(3).2 正方形【解析】(1)连结CD,如图,由圆周角定理得到∠ADC=90°,然后根据直角三角形斜边上的中线直线得到DE=CE=BE;(2)连结OD,如图,利用切线性质得∠2+∠4=90°,再利用等腰三角形的性质得∠1=∠2,∠3=∠4,所以∠1+∠3=∠2+∠4=90°,于是根据切线的判定定理可判断DE是⊙O的切线;(3)要判断四边形AOED是平行四边形,则DE=OA=1,所以BC=2,当BC=2时,△ACB为等腰直角三角形,则∠B=45°,又可判断△BCD为等腰直角三角形,于是得到DE⊥BC,DE=12BC=1,所以四边形AOED是平行四边形;然后利用OD=OC=CE=DE=1,∠OCE=90°,可判断四边形OCED为正方形.【详解】(1)连结CD,如图,∵AC是⊙O的直径,∴∠ADC=90°,∵E是BC的中点,∴DE=CE=BE;(2)DE是⊙O的切线.理由如下:连结OD,如图,∵BC为切线,∴OC⊥BC,∴∠OCB=90°,即∠2+∠4=90°,∵OC=OD,ED=EC,∴∠1=∠2,∠3=∠4,∴∠1+∠3=∠2+∠4=90°,即∠ODB=90°,∴OD⊥DE,∴DE是⊙O的切线;(3)当BC=2时,∵CA=CB=2,∴△ACB 为等腰直角三角形,∴∠B =45°,∴△BCD 为等腰直角三角形,∴DE ⊥BC ,DE =12BC =1, ∵OA =DE =1,AO ∥DE ,∴四边形AOED 是平行四边形;∵OD =OC =CE =DE =1,∠OCE =90°,∴四边形OCED 为正方形.故答案为ED=EC ;2,正方形.【点睛】此题考查了切线的判定与性质,直角三角形斜边上的中线性质,以及平行四边形的判定与性质,熟练掌握切线的判定与性质是解本题的关键.5.(河南省外国语中学2019届九年级中招适应性测试卷数学试题)如图,AB 是O e 的直径,4AB =,点P 是AB 上方圆上的一个动点,连接AP ,作PAB ∠的平分线AC ,交O e 于点C ,过点C 作CD AP ⊥交AP 的延长线于点D .(1)求证:CD 是O e 的切线;(2)当AP =________时,四边形APCO 是平行四边形.【答案】(1)证明见解析;(2)2.【解析】(1)连接OC,根据等腰三角形的性质得到∠CAO=∠ACO,由角平分线的定义得到∠DAC=∠OAC,等量代换得到∠DAC=∠ACO,根据平行线的判定定理得到AD∥OC,由平行线的性质即可得到结论;(2)根据“一组对边平行且相等的四边形是平行四边形”可以得到结论;【详解】(1)连接OC.∠,∵AC平分PAB∠=∠.∴PAC BAC=,∵OA OC∠=∠,∴BAC OCA∠=∠,∴PAC OCAP,∴AD OC⊥,∵CD AD⊥,∴OC CDe的切线.∴CD是O(2)∵AP∥OC,∴当AP=OC时,四边形APCO是平行四边形.∵OC =2,∴AP =2.【点睛】本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.6.(2020年1月河南省郑州市一模数学试题)如图,△ABC 内接于⊙O ,且AB =AC ,延长BC 至点D ,使CD =CA ,连接AD 交⊙O 与点E ,连接BE ,CE .(1)求证:△ABE ≌△CDE ;(2)填空:①当∠ABC 的度数为______时,四边形AOCE 是菱形;②若AE AB =,则DE 的长为______.【答案】(1)见解析;(2)①60°;②3【解析】(1)由AB =AC ,CD =CA 得出AB =CD ,再根据圆内接四边形的性质和圆周角的性质可知BAE ECD ∠=∠,∠CED =∠AEB 从而可证△ABE ≌△CDE(2)①根据菱形的性质可知,AOE OCE V V为等边三角形,进而可推出60ABC ∠=︒ ②由△ABE ≌△CDE 可得ABE BDA ∠=∠进而可可ADB ABE ∽△△,再利用相似三角形的性质可知AB AE AD AB=,从而DE AD AE =-可求. 【详解】(1)证明:∵AB =AC ,CD =CA∴∠ABC =∠ACB ,AB =CD.∵四边形ABCE 是圆内接四边形180,180,ABC AEC BAE BCE ∴∠+∠=︒∠+∠=︒180,180,CED AEC ECD BCE ∠+∠=︒∠+∠=︒Q,ABC CED BAE ECD ∴∠=∠∠=∠ACB CED ∴∠=∠ACB AEB ∴∠=∠∴∠CED =∠AE B.在ABE △和CDE △中BAE ECD AEB CED AB CD∠=∠⎧⎪∠=∠⎨⎪=⎩ ∴△ABE ≌△CDE(2)①当60ABC ∠=︒时,四边形AOCE 是菱形理由如下:连接AO,CO,OE ,如下图∵四边形AOCE 是菱形∴OC CE AE OA ===又OA OE OC ==QOA AE OE EC ∴===∴,AOE OCE V V为等边三角形 120AOC ∴∠=︒60ABC ∴∠=︒②由△ABE ≌△CDE可得ABE BDA ∠=∠,ABE BDA BAE DAB ∠=∠∠=∠Q∴ADB ABE ∽△△AB AE AD AB∴=即22AB AD AE ===DE AD AE ∴=-== 【点睛】本题主要考查圆内接四边形的性质,全等三角形的判定与性质,菱形的性质,圆周角定理及推论,能够对所学知识灵活应用是解题的关键.考向2 以圆为背景的证明与计算1.(河南省漯河市临颍县2019-2020学年九年级上学期期末数学试题)如图,已知⊙O 的直径AB =10,弦AC =6,∠BAC 的平分线交⊙O 于点D ,过点D 作DE ⊥AC 交AC 的延长线于点E .(1)求证:DE是⊙O的切线.(2)求DE的长.【答案】(1)详见解析;(2)4.【解析】试题分析:(1)连结OD,由AD平分∠BAC,OA=OD,可证得∠ODA=∠DAE,由平行线的性质可得OD∥AE,再由DE⊥AC即可得OE⊥DE,即DE是⊙O的切线;(2)过点O作OF⊥AC于点F,由垂径定理可得AF=CF=3,再由勾股定理求得OF=4,再判定四边形OFED 是矩形,即可得DE=OF=4.试题解析:(1)连结OD,∵AD平分∠BAC,∴∠DAE=∠DAB,∵OA=OD,∴∠ODA=∠DAO,∴∠ODA=∠DAE,∴OD∥AE,∵DE ⊥AC∴OE ⊥DE∴DE 是⊙O 的切线;(2)过点O 作OF ⊥AC 于点F ,∴AF =CF =3,∴OF =,∵∠OFE =∠DEF =∠ODE =90°,∴四边形OFED 是矩形,∴DE =OF =4.考点:切线的判定;垂径定理;勾股定理;矩形的判定及性质.2.(河南省南阳市淅川县2019-2020学年九年级上学期期末数学试题)如图,AB 是O e 的直径,点C 在O e 上,AD 平分CAB ∠,BD 是O e 的切线,AD 与BC 相交于点E ,与O e 相交于点F ,连接EF .(1)求证:BD BE =;(2)若4DE =,BD =AE 的长.【答案】(1)见解析;(2)6=AE【解析】(1)利用圆周角定理得到∠ACB =90°,再根据切线的性质得∠ABD =90°,则∠BAD +∠D =90°,然后利用等量代换证明∠BED =∠D ,从而判断BD =BE ;(2)利用圆周角定理得到∠AFB =90°,则根据等腰三角形的性质DF =EF =2,再证明BDF ADB △∽△,列比例式求出AD 的长,然后计算AD -DE 即可.【详解】(1)证明:∵AB 是O e 的直径,∴90ACB ∠=︒,∴90CAE CEA ∠+∠=︒.∵BED CEA ∠=∠,∴90CAE BED ∠+∠=︒.∵BD 是O e 的切线,∴90ABD ∠=︒,∴90BAD BDA ∠+∠=︒.又∵AO 平分CAB ∠,∴CAE BAD ∠=∠,∴BED BDA ∠=∠,∴BD BE =;(2)解:∵AB 是O e 的直径,∴90AFB ∠=︒,又∵BE BD =, ∴122D F E F E D ===. 在Rt BDF △中,根据勾股定理得,4BF =.∵D D ∠=∠,90BFD ABD ∠=∠=︒,∴BDF ADB △∽△, ∴BD DF AD BD=,即525AD =, 解得10AD =,∴6AE AD DE =-=.【点睛】本题考查了圆周角定理、等腰三角形的判定与性质和相似三角形的判定与性质、切线的性质.熟练掌握切线的性质和相似三角形的判定与性质是解答本题的关键.3.(河南省濮阳市县区2019-2020学年九年级上学期期末数学试题)如图,在ABC ∆中,AB AC =,以AB 为直径作O e 交BC 于点D .过点D 作EF AC ⊥,垂足为E ,且交AB 的延长线于点F .(1)求证:EF 是O e 的切线;(2)若10AB =,60A ∠=o ,求BD 长.【答案】(1)见解析;(2)BD 长为5.【解析】(1)连接OD ,AD ,根据等腰三角形三线合一得BD =CD ,根据三角形的中位线可得OD ∥AC ,所以得OD ⊥EF ,从而得结论;(2)根据等腰三角形三线合一的性质证得∠BAD =12∠BAC =30°,由30°的直角三角形的性质即可求得B D.【详解】(1)证明:连接OD,AD,∵AB是⊙O的直径,∴∠ADB=90°,∴AD⊥BC,∵AB=AC,∴BD=CD,∵OA=OB,∴OD是△BAC的中位线,∴OD∥AC,∵EF⊥AC,∴OD⊥EF,∴EF是⊙O的切线;(2)解:∵AB=AC,AD⊥BC,∴∠BAD=12∠BAC=30°,∴BD=12AB=12×10=5,即BD长为5.【点睛】本题主要考查的是圆的综合应用,解答本题主要应用了圆周角定理、等腰三角形的性质,圆的切线的判定,30°的直角三角形的性质,掌握本题的辅助线的作法是解题的关键.4.(河南省新乡市辉县市2019-2020学年九年级上学期期末数学试题)如图,AB是⊙O的弦,过点O作OC⊥OA,OC交于AB于P,且CP=C B.(1)求证:BC是⊙O的切线;(2)已知∠BAO=25°,点Q是弧AmB上的一点.①求∠AQB的度数;②若OA=18,求弧AmB的长.【答案】(1)见解析;(2)①∠AQB=65°,②l弧AmB=23π.【解析】(1)连接OB,根据等腰三角形的性质得到∠OAB=∠OBA,∠CPB=∠CBP,再根据∠P AO+∠APO=90°,继而得出∠OBC=90°,问题得证;(2)①根据等腰三角形的性质可得∠ABO=25°,再根据三角形内角和定理可求得∠AOB的度数,继而根据圆周角定理即可求得答案;②根据弧长公式进行计算即可得.【详解】(1)连接OB,∵CP=CB,∴∠CPB=∠CBP,∵OA⊥OC,∴∠AOC=90°,∵OA=OB,∴∠OAB=∠OBA,∵∠P AO+∠APO=90°,∴∠ABO+∠CBP=90°,∴∠OBC=90°,∴BC是⊙O的切线;(2)①∵∠BAO=25° ,OA=OB,∴∠OBA=∠BAO=25°,∴∠AOB=180°-∠BAO-∠OBA=130°,∴∠AQB=12∠AOB=65°;②∵∠AOB=130°,OB=18,∴l弧AmB=36013018018π-⨯()=23π.【点睛】本题考查了圆周角定理,切线的判定等知识,正确添加辅助线,熟练掌握和灵活运用相关知识是解题的关键.5.(河南省许昌市襄城县2019-2020学年九年级上学期期末数学试题)如图,AB 是⊙O 的直径,弦CD AB ⊥,垂足为H ,连接AC .过»BD上一点E 作//EG AC 交CD 的延长线于点G ,连接AE 交CD 于点F ,且EG FG =.(1)求证:EG 是⊙O 的切线;(2)延长AB 交GE 的延长线于点M ,若2AH =,CH =OM 的长.【答案】(1)见解析(2)OM = 【解析】(1)连接OE ,由GE GF =,推GEF AFH ∠=∠,证OEA OAF ∠=∠,得90GEO ︒∠=,根据切线判定定理可得;(2)连接OC ,设⊙O 的半径为r ,则OC r =,2OH r =-,在Rt OCH ∆中,求得3r =,在Rt ACH ∆中,求得AC ==,由//AC GE ,证Rt △OEM ∽Rt △CHA ,得OM OEAC CH==OM . 【详解】(1)证明:连接OE ,如图,∵GE GF =,∴GEF GFE ∠=∠,而GFE AFH ∠=∠,∴GEF AFH ∠=∠,∵AB CD ⊥,∴90OAF AFH ︒∠+∠=,∴90GEA OAF ︒∠+∠=,∵OA OE =,∴OEA OAF ∠=∠,∴90GEA OEA ︒∠+∠=,即90GEO ︒∠=,∴OE GE ⊥,∴EG 是⊙O 的切线;(2)解:连接OC ,如图,设⊙O 的半径为r ,则OC r =,2OH r =-,在Rt OCH ∆中,222(2)r t -+=,解得3r =,在Rt ACH ∆中,AC ==∵//AC GE ,∴M CAH ∠=∠,∴Rt △OEM ∽Rt △CHA ,∴OM OEAC CH==∴OM =.【点睛】考核知识点:切线判定,相似三角形判定和性质.理解切线判定和相似三角形判定是关键.6.(新乡市名校联考2019-2020学年九年级上学期期末数学试题)如图,已知点P 是O e 外一点,直线PA 与O e 相切于点B ,直线PO 分别交O e 于点C 、D ,PAO PDB ∠=∠,OA 交BD 于点E .(1)求证://OA BC ;(2)当O e 的半径为10,8BC =时,求AE 的长.【答案】(1)证明见解析;(2)21.【解析】(1)连接OB ,由切线的性质可得OB ⊥P A ,然后根据直径所对的圆周角为直角得到∠CBD =90°,再根据等角的余角相等推出∠BCD =∠BOA ,由等量代换得到∠CBO =∠BOA ,即可证平行;(2)先由勾股定理求出BD ,然后由垂径定理得到DE ,求出OE ,再利用△ABE ∽△DOE 的对应边成比例,即可求出AE .【详解】(1)如图,连接OB ,e相切于点B,∵直线P A与O∴OB⊥P A,∴∠P AO+∠BOA=90°e的直径∵CD是O∴∠CBD=90°,∠PDB+∠BCD=90°又∵∠P AO=∠PDB∴∠BOA=∠BCD∵OB=OC∴∠BCD=∠CBO∴∠CBO=∠BOA∴OA∥BCBC=,(2)∵半径为10,8∴BD由(1)可知∠CBD=90°,OA∥BC ∴OE⊥BD∴E 是BD 的中点,DE =12BD=∴∵BAE D ∠=∠,AEB DEO ∠=∠∴△ABE ∽△DOE , ∴AE BE DE OE=4=∴=AE . 【点睛】本题考查圆综合问题,熟练掌握切线的性质与相似三角形的判定与性质是解题的关键.7.(郑州市一中2019年中考三模数学试卷)如图所示,⊙O 是等腰三角形ABC 的外接圆,AB =AC,延长BC 至点D,使CD =AC,连接AD 交⊙O 于点E,连接BE 、CE,BE 交AC 于点F .(1)求证:CE =AE(2)若AE =6,DE =9,求EF 的长.【答案】(1)见解析;(2)4.【解析】 (1)根据内接四边形的性质和圆周角定理,由AAS 得到△ABE ≌△CDE ,即可得到答案; 的(2)证明△AEF∽△DEC,推出AE EFDE EC=即可求得EF的长.【详解】解:(1)证明:∵四边形ABCE为圆O的内接四边形,∴∠ABC=∠CED,∠DCE=∠BAE,又AB=AC,∴∠ABC=∠ACB,∴∠CED=∠ACB,又∠AEB和∠ACB都为»AB所对的圆周角,∴∠AEB=∠ACB,∴∠CED=∠AEB,∵AB=AC,CD=AC,∴AB=CD,在△ABE和△CDE中,BAE DCEAEB CEDAB CD∠∠⎧⎪∠∠⎨⎪⎩===∴△ABE≌△CDE(AAS)(2)∵△ABE≌△CDE,∴AE=EC=6,ED=BE=9,即AE ECDE EB=,且∠AEB=∠CED,∴△AEF∽△DEC,∴AE EFDE EC=.∴EF=AE ECDE•=4.【点睛】本题考查圆周角定理、垂径定理和相似三角形的判定与性质,解题的关键是掌握圆周角定理、垂径定理和相似三角形的判定与性质.。
