§7.3 离散时间系统的数学模型
7-4离散系统的数学模型全篇

2. 线性常系数差分方程及其解法
c(k
)
a1c(k b1r(k
11))ba22rc((kk22))bamnrc((kk
n) m);
n
m
c(k) aic(k i) bjr(k j);
i 1
j 1
后向差分方程:时间概念清楚,便于编制程序。
c(kn) a1c(kn 1) a2c(kn 2) anc(k) b1r(kn 1) b2r(kn 2) bmr(kn m);
n
m
c(k n) aic(k n i) bjr(k n j);
i 1
j 1
前向差分方程:便于讨论系统阶次、使用Z变换 法计算初始条件不为零的解。
上述几个差分方程在书写上都很烦琐,为书 写简便可采用时间移动算子。
0.1 0.4 16k 0.3 81k
c(nT
)
0.1 0.8 16k 0.1 1.6 16k
0.9 81k 2.7 81k
0.1 3.2 16k 8.1 81k
k 0, 1, 2, 3, 4, ;
n 4k
n 4k 1 ; n 4k 2
n 4k 3
3. 脉冲传递函数(定义、意义) 使用 脉冲传递函数,便于分析和校正线性离
c(k) 0.5c(k 1) 0.5c(k 2) r(k); r(k) 1(k); c(k) 0, k 0;
试用递推法计算输出序列c(k),k= 0,1,2,…。
解例7采-16用-1递续推关系 c(k) = 1+0.5c(k-1)– 0.5c(k-2);
c(0) 1; c(1) 1 0.5 1.5;
c(2) 1 0.51.5 0.5 1.25; c(3) 1 0.51.25 0.51.5 0.875;
离散系统的数学模型

2326.4 离散系统的数学模型为研究离散系统的性能,需要建立离散系统的数学模型。
线性离散系统的数学模型有差分方程、脉冲传递函数和离散状态空间表达式三种。
本节主要介绍差分方程及其解法,脉冲传递函数的定义,以及求开环脉冲传递函数和闭环脉冲传递函数的方法。
有关离散状态空表达式及其求解,将在第8章介绍。
6.4.1 线性常系数差分方程及其解法对于线性定常离散系统,k 时刻的输出)(k c ,不但与k 时刻的输入)(k r 有关,而且与k 时刻以前的输入 ),2(),1(--k r k r 有关,同时还与k 时刻以前的输出 ),2(),1(--k c k c 有关。
这种关系一般可以用n 阶后向差分方程来描述,即∑∑==-+--=mj jni i j k r bi k c a k c 01)()()( (6-34)式中,i a ,i =1,2,…,n 和j b ,j =0,1,…,m 为常系数,n m ≤。
式(6-34)称为n 阶线性常系数差分方程。
线性定常离散系统也可以用n 阶前向差分方程来描述,即∑∑==-++-+-=+mj jni i j m k r bi n k c a n k c 01)()()( (6-35)工程上求解常系数差分方程通常采用迭代法和z 变换法。
1. 迭代法若已知差分方程式(6-34)或式(6-35),并且给定输出序列的初值,则可以利用递推关系,在计算机上通过迭代一步一步地算出输出序列。
例6-10 已知二阶差分方程)2(6)1(5)()(---+=k c k c k r k c输入序列1)(=k r ,初始条件为1)1(,0)0(==c c ,试用迭代法求输出序列)(k c , ,5,4,3,2,1,0=k 。
解 根据初始条件及递推关系,得0)0(=c 1)1(=c6)0(6)1(5)2()2(=-+=c c r c 25)1(6)2(5)3()3(=-+=c c r c 90)2(6)3(5)4()4(=-+=c c r c301)3(6)4(5)5()5(=-+=c c r c2. z 变换法233设差分方程如式(6-34)所示,对差分方程两端取z 变换,并利用z 变换的实数位移定理,得到以z 为变量的代数方程,然后对代数方程的解)(z C 取z 反变换,可求得输出序列)(k c 。
离散时间系统的数学模型

2.线性差分方程 a0(n)y(n)+ a1(n)y(n-1)+ …... aN(n)y(n-N)
= b0(n)x(n)+ b1(n)x(n-1)+ …... bM(n)x(n-M) 其中ai(n) 、bj(n)、 x(k) ,i=0,1,……N; j=0,1,……M; k=n-M,……n。
返回
二、差分方程
在连续时间系统中,系统内部的数学运算关系可归结 为微分(积分)、乘系数、相加的关系,即:微分方程。
在离散时间系统中,基本运算关系是延时(移位)、 乘系数、相加的关系,即:差分方程。 这是由于系统的组成以及所处理的信号的性质不同, 因此描述系统的数学手段也不同。
(一)数学模型的基本单元 (二)差分 (三)差分方程 (四)差分方程的建立 (五)差分方程的特点
i
2
2
d i un
n
n
i
n
in+1 u n u
n
1 iu i n n + 1 u n 2 i
i
1 2 i u i n n + 1 2 n + 1 u n 6 i
n + 1 1 a i a u i u n 1 a i n
xi xn
n
a 1
返回
(三)差分方程
1.一般差分方程
ky(n))=0 表达式F(n,y(n), y(n), …… 或 Q(n,y(n), y(n-1), ……, y(n-k))=0 称为未知序列y(n)的差分方程,F、Q是已知函数。
k
(k阶差分)
3.典型序列的差分(后向) n = n -(n-1)=1 u(n) = u(n) -u(n-1)=d (n) n2= n2 -(n-1)2= 2n - 1 n2u(n) = n2u(n) - (n-1)2u(n-1)= (2n-1)u(n-1) 2 n 1 sin n sin n sin n 1 2 sin cos 4.差分的逆运算———求和 典型序列的求和
离散时间信号与离散时间系统
§7-1 概述一、 离散时间信号与离散时间系统离散时间信号:只在某些离散的时间点上有值的信号。
离散时间系统:处理离散时间信号的系统。
混合时间系统:既处理离散时间信号,又处理连续时间信号的系统。
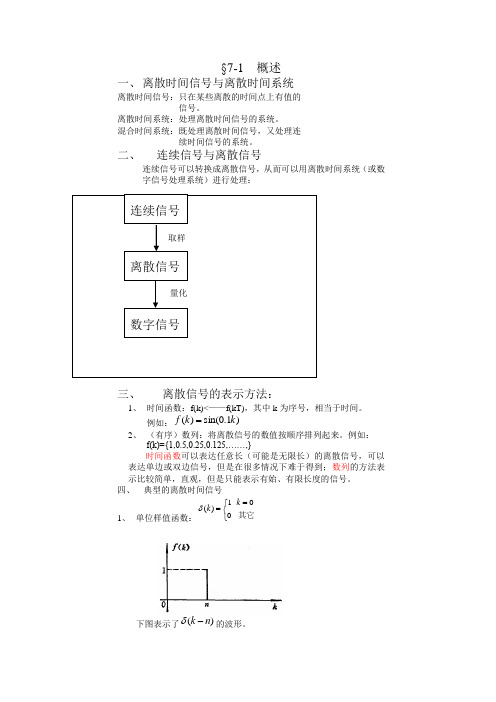
二、 连续信号与离散信号连续信号可以转换成离散信号,从而可以用离散时间系统(或数字信号处理系统)进行处理:三、 离散信号的表示方法:1、 时间函数:f(k)<——f(kT),其中k 为序号,相当于时间。
例如:)1.0sin()(k k f =2、 (有序)数列:将离散信号的数值按顺序排列起来。
例如:f(k)={1,0.5,0.25,0.125,……,}时间函数可以表达任意长(可能是无限长)的离散信号,可以表达单边或双边信号,但是在很多情况下难于得到;数列的方法表示比较简单,直观,但是只能表示有始、有限长度的信号。
四、 典型的离散时间信号1、 单位样值函数:⎩⎨⎧==其它001)(k k δ下图表示了)(n k -δ的波形。
连续信号离散信号 数字信号 取样量化这个函数与连续时间信号中的冲激函数)(t δ相似,也有着与其相似的性质。
例如:)()0()()(k f k k f δδ=, )()()()(000k k k f k k k f -=-δδ。
2、 单位阶跃函数:⎩⎨⎧≥=其它001)(k k ε这个函数与连续时间信号中的阶跃函数)(t ε相似。
用它可以产生(或表示)单边信号(这里称为单边序列)。
3、 单边指数序列:)(k a k ε比较:单边连续指数信号:)()()(t e t e t a at εε=,其底一定大于零,不会出现负数。
4、 单边正弦序列:)()cos(0k k A εφω+(a) 0.9a = (d) 0.9a =-(b) 1a = (e) 1a =-(c) 1.1a = (f) 1.1a =-双边正弦序列:)cos(0φω+k A五、 离散信号的运算1、 加法:)()()(21k f k f k f +=<—相同的k 对应的数相加。
自动控制原理第7章 离散控制系统

b(t )
H (s)
图7.5 数字控制系统的简化框图
2019/2/19
7
数字控制系统较之一般的连续控制系统具有如下一 些优点: 能够保证足够的计算精度; 在数字控制系统中可以采用高精度检测元件和执 行元件,从而提高整个系统的精度; 数字信号或脉冲信号的抗干扰性能好,可以提高 系统的抗干扰能力; 可以采用分时控制方式,提高设备的利用率,并 且可以采用不同的控制规律进行控制; 可以实现一些模拟控制器难以实现的控制律,特 别对复杂的控制过程,如自适应控制、最优控制、 智能控制等,只有数字计算机才能完成。
2019/2/19
9
7.2.1 采样过程及其数学描述
将连续信号通过采样开关(或采样器)变换成离 散信号的过程称为采样过程。相邻两次采样的时间 间隔称为采样周期T。 采样频率:f s 1/ T 采样角频率: s 2 /T 采样可分为:
等速采样:采样开关以相同的采样周期T动作,又 称为周期采样 多速采样:系统中有n个采样开关分别按不同周期 动作 随机采样:采样开关动作是随机的 本章仅限于讨论等速同步采样过程。
j t xj ( ) xt () e d t
1 X( s ) Xs ( j k s) T k
*
2019/2/19
(7-7)
15
X ( j )
max
2max
(a)
o
max
图7.7 连续信号及离散信号的频谱
式中ω s=2π/T为采样频率,X(s)为x(t)的拉氏变 换。若X*(s)的极点全都位于s左平面,可令s=jω , 求得x*(t)的傅氏变换为
离散控制系统最常见形式是数字控制系统。图 7.4是数字控制系统的结构图。图中用于控制的计算 机D工作在离散状态,被控对象G(s)工作在模拟状态。
《自动控制原理》离散系统的数学模型

K (t) L1[G(s)]
(7-55)
再将 K (t) 按采样周期离散化,得加权序列 K (nT ) ;最后将 K (nT ) 进
行 z 变换,按式(7-53)求出 G(z) 。这一过程比较复杂。其实,如果把 z 变
换表 7—2 中的时间函数 e(t) 看成 K (t) ,那么表中的 E(s) 就是 G(s) (见式 (7-55),而 E(z) 则相当于 G(z) 。因此,根据 z 变换表 7—2,可以直接从 G(s) 得到 G(z) ,而不必逐步推导。
本章所研究的离散系统为线性定常离散系统。 注意 zx:离散系统有本质连续和本质离散两种情况
本质连续的离散系统:如液位 炉温采样控制系统中的被控对象 本质离散的离散系统:如计算机。系统直接进行离散计算 问题:如何建立离散系统的数学模型? c(n) F[r(n)] F 的具体形式? 分析:本质连续的离散系统的方框图, 能否 G(s)?G(z)=?
众所周知,利用传递函数研究线性连续系统的特性,有公认的方便 之处。对于线性连续系统,传递函数定义为在零初始条件下,输出量的 拉氏变换与输入量的拉氏变换之比。对于线性离散系统,定义类似。
设开环离散系统如图 7-22 所示,如果系统的初始条件为零,输入信号
为 r(t) ,采样后 r*(t) 的 z 变换函数为 R(z) ,系统连续部分的输出为 c(t) ,
微分方程的经典解法类似,差分方程的经典解法[EX]*也要求出齐次方程 的通解和非齐次方程的一个特解,非常不便。这里仅介绍工程上常用的 后两种解法。
(1)迭代法 又称递推法 若已知差分方程(7-49)或(7-50),并且给定输入序列和输出序列的初 值,则可以利用递推关系可以一步一步地算出输出序列。 例 7-14 已知差分方程
第七章 离散系统的数学模型

第四节 离散系统的数学模型
例
系统结构如上图所示,求G(z).
-1)G (z) 1 1 G ( z ) = (1 -z G1(s)= S(S+1) G2(s)=2S2(S+1) T = 1S (z-1) z[(z-e-1)-(-Ts z-1)( z-e-1) + (z-1)2] (1-e ) 2 1 = 解: -1) z · G(s)= ( z-1) S (z-e (S+1) S e-1z+(1-2e-1) 0.386 z +0.264 1 1 1 1 = = 1 ] 2-1.368 ] + = Z [ G2(z)(= Z[ z-e z-1)( ) z z+ 0.386 S+1 S S2 S2(S+1)
四、开环系统的脉冲传递函数
采样系统的脉冲传递函数的求取与 连续系统求传递函数类似。但脉冲传递 函数与采样开关的位置有关。当采样系 统中有环节串联时,根据它们之间有无 采样开关,其等效的脉冲传递函数是不 相同的。
第四节 离散系统的数学模型
1.串联环节间无采样开关
G1(s)和G2(s)的两个环节相串联如图:
n阶离散定常系统脉冲传递函数为: b0 b1 z 1 bm1 z ( m1) bm z m C( z) G( z ) R( z) 1+a1 z 1 a2 z 2 an1 z ( n1) an z n
第四节 离散系统的数学模型
例:已知差分方程 c(k ) r (k ) 5c(k 1) 6c(k 2) 输入序列r(k)=1,初始条件c(0)=0,c(1)=1,试用迭代法求 输出序列c(k),k=0, 1, 2, · · · , 10。 解:根据初始条件及递推关系,得 c ( 0) 0
§7.3 离散时间系统的数学模型

3)若bj(n)=0, j=0,1,……M,则方程是齐次差分方程。
与微分方程的分类相对应,差分方程也可划分为 线性的与非线性的、常系数的与参变系数的等。
一般情况下,线性、时不变离散时间系统需要由 常系数线性差分方程描述。这也本课程所要讨论的。 返回
(四)差分方程的建立
差分方程是处理离散变量函数关系的一种数学 工具,其应用遍及许多科学领域,方程的建立与 变量的选取因具体问题而异,方法多种多样。 下面给出几种常用方法。
i 0 i j 0 j
N
M
或(令a0=1):y(n)+a1 y(n-1)+ a2 y(n-2)+……+ aN y(n-N) = b0 x(n)+b1 x(n-1)+ ……+ bM x(n-M)
2n 1 sin n sin n sinn 1 2 sin cos 2 2
4.差分的逆运算———求和 典型序列的求和
i n
d i un
n
i n
ui n + 1un
n
1 iui nn + 1un 2 i
返回
(一)数学模型的基本单元
延时器
y n
1 E
y n 1
y n
z
1
y n 1
或T、D 标量乘法器
x1 n
x n
a
axn
xn
a
axn
加法器:
x1 n + x 2 n
x1 n
x1 n + x 2 n
x 2 n
x2 n
yn + 1 xn + ayn
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
然后,利用边界电压条件v(0)=E, v(N)=0可求得v(n)。
2)增序形式
对任一结点 n+1,如图所示:
v(n)
R
v(n+1)
R
v(n+2)
R
运用KCL不难写出
v n v n + 1 v n + 1 v n + 1 v n + 2 + R R R
经整理后得出: v(n+2) - 3v(n+1) +v(n)=0
D3x(n) = x(n+3) -3x(n+2)+ 3x(n+1)- x(n)
(三阶差分) (k阶差分)
D xn 1 C km xn + k m
k m m 0
k
2.序列x(n)的后向差分 x(n) = x(n) - x(n-1)
(一阶差分)
(二阶差分)
2x(n)
前差形式为: dyt yt + T yt dt T
对上述微分方程,若选用后差形式,则:
y t y t T ay t + x t T
若在t=nT 各点取得样值,则:
yt ynT yn
n代表序号
xt xnT xn y n y n 1 ay n + x n T 1 T y n y n 1 + x n 1 aT 1 aT 当前 前一个 输入 输出 输出
然后,利用边界电压条件v(0)=E, v(N)=0可求得v(n)。 我们可以看出:无论是减序形式,还是增序形式,
二者本质是相同的,不论采用何种形式列写差分方程
均可以,二者之间相互转换也很简单。
例7-3-4 假定每对兔子每月可以生育一对小兔,新生的
小兔子要隔一个月才具有生育能力,若第一个 月只有一对新生小兔,求第n个月兔子对的数目是多少。 解:设第n个月兔子对的数目是y(n), 第n个月兔子对的数目=第n-1个月的兔子对 +第n个月新生的兔子对 根据题意,第n个月新生的兔子对, 应等于第n-2个月兔子对的数目。 所以, y(n)= y(n-1)+ y(n-2)
返回
(一)线性系统
具有均匀(齐次)性、叠加性的系统称为线性系统。 若:
x1 ( n ) y1 ( n )
离散时间系统
x2 ( n )
离散时间系统
离散时间系统
y2 ( n )
则有:
c1 x1 ( n ) + c2 x2 ( n )
c1 y1 ( n ) + c2 y2 ( n )
(c1、c2为任意常数) 返回
因果系统的充要条件: h(n) 0, n<0
h(n)为单位脉冲响应。
返回
(四)稳定系统
有界输入、产生有界输出的系统称为稳定系统。 稳定系统的充要条件: hn
n
即:单位脉冲响应绝对可和。
lim 注意: h( n ) 0,只是系统稳定的必要条件,
n
而非充分条件。
返回
i
1 i 2 ui nn + 12n + 1un 6 i
xi xn
n
1 a n+1 a i ui un 1a i
n
a 1
返回
(三)差分方程
1.一般差分方程
表达式F(n,y(n), y(n), …… ky(n))=0 或 Q(n,y(n), y(n-1), ……, y(n-k))=0 称为未知序列y(n)的差分方程,F、Q是已知函数。
注意:微分方程近似写作差分方程的条件是样值间隔T 要足够小, T越小,近似程度越好。实际上,利用计算 机来求解微分方程时,就是根据这一原理完成的。 返回
3.由实际问题直接得到差分方程
例7-3-2 y(n)表示一个国家在第n年的人口数 a(常数):出生率
b(常数): 死亡率
设x(n)是国外移民的净增数 解: 则该国在第n+1年的人口总数为: y(n+1)=y(n)+ay(n)-by(n)+x(n) =(a-b+1)y(n)+x(n) 例7-3-3 如图所示电阻梯形网络,其各支路电阻都为R,每 个结点对地的电压为v(n),n=0,1,2,……N。 已知两边界结点对地的电压为v(0)=E, v(N)=0 。 试写出第n个结点电压v(n)的差分方程。
已知 y(0)=0, y(1)=1, y(2)=1 可以推知: y(3)=2, y(4)=3, y(5)=5,……。
例7-3-5 一个乒乓球从H米高度自由下落至地面,每次
弹跳起的最高值是前一次最高值的2/3。若以y(n)表示 第n次跳起的最高值,试列写描述此过程的差分方程。
解: y(n)表示第n次跳起的最高值,每次弹跳起的最 高值是前一次最高值的2/3。由题意可得: 2 2 y n y n 1 y n y n 1 即: 3 3
0
例7-3-6 如果在第n个月初向银行存款x(n)元,月息为a,
解: 第n月初的本利和共由:本月存入、上月结余、 上月利息三部分组成。由此可得:
yn xn + yn 1 + ayn 1
每月利息不取出,试用差分方程写出第n月初的本利和y(n) 。
即: yn 1 + a yn 1 xn
中心差分dx(n)定义为: dx(n) = x(n+h/2) - x(n- h/2)
式中h( h>0)为步长,一般取步长h=1。 1.序列x(n)的前向差分 Dx(n) = x(n+1) - x(n) (一阶差分) D2x(n) = Dx(n+1) -Dx(n) = x(n+2) -x(n+1)-[x(n+1) -x(n)] = x(n+2) -2x(n+1)+x(n) (二阶差分)
i 0 i j 0 j
N
M
或(令a0=1):y(n)+a1 y(n-1)+ a2 y(n-2)+……+ aN y(n-N) = b0 x(n)+b1 x(n-1)+ ……+ bM x(n-M)
§7.3离散时间系统的数学模型——
差分方程
一、线性、时不变离散系统
二、差分方程 三、离散时间系统的模拟
返回
一、线性、时不变离散系统
系统功能的本质:是将输入序列转变成输出序列
的运算(映射)。即:y(n)=T[x(n)]
运算关系
x(n) (一)线性系统
T[ . ]
y(n)
(二)时不变系统 (三)因果系统 (四)稳定系统
二、差分方程
在连续时间系统中,系统内部的数学运算关系可归结 为微分(积分)、乘系数、相加的关系,即:微分方程。
在离散时间系统中,基本运算关系是延时(移位)、 乘系数、相加的关系,即:差分方程。 这是由于系统的组成以及所处理的信号的性质不同, 因此描述系统的数学手段也不同。
(一)数学模型的基本单元 (二)差分 (三)差分方程 (四)差分方程的建立 (五)差分方程的特点
n
整个序列右移N位
1
1 O 1 2 3
n
返回
(三)因果系统
系统的输出y(n)只取决于此时刻、以及此时刻以前 的输入,即 : x(n)、 x(n-1)、 x(n-2)……。则称为 因果系统。
{若y(n)取决于x(n+1)、 x(n+2)……,即:系统的 输出取决于未来的输入,这在时间上就违背了因果关 系,因而是非因果系统。}
a0(n)y(n)+ a1(n)y(n-1)+ …... aN(n)y(n-N) = b0(n)x(n)+ b1(n)x(n-1)+ …... bM(n)x(n-M) 1)若 a0 0 , a N 0 ,方程是N阶差分方程。 2)若ai(n),bj(n)是常数(与n无关),则方程或被描述 的系统是时不变的。
x1 n x 2 n
乘法器:
x1 n
x 2 n
若x2(n)=a,则为标量乘法器 返回
(二)差分
对于一个离散信号x(n) ,差分运算有三种形式: 前向差分Dx(n)定义为: Dx(n) = x(n+h) - x(n)
后向差分x(n)定义为: x(n) = x(n) - x(n- h)
yn + 1 xn + ayn
一阶前向差分方程
1 或 y( n) y n + 1 x n a
返回
2.由微分方程导出差分方程
dy t ay t + x t dt
y(t):输出
x(t):输入
若取时间间隔为:T
dyt yt yt T 则后差形式为: dt T
返回
(五)差分方程的特点
1、输出序列的第n个值不仅决定于同一瞬间的输入样值, 而且还与前面输出值有关,每个输出值必须依次保留。
2、差分方程的阶数:差分方程中变量的最高和最 低序号差数为阶数。 如果一个系统的第n个输出决定于刚过去的几个输 出值及输入值,那么描述它的差分方程就是几阶的。
减序通式:
a yn i b xn j
最前项变量减最后项变量 n- (n-k)= k 称为差分 方程的阶数。
2.线性差分方程 a0(n)y(n)+ a1(n)y(n-1)+ …... aN(n)y(n-N)
= b0(n)x(n)+ b1(n)x(n-1)+ …... bM(n)x(n-M) 其中ai(n) 、bj(n)、 x(k) ,i=0,1,……N; j=0,1,……M; k=n-M,……n。
