录简单均质几何体的重心和转动惯量
最全的转动惯量的计算

最全的转动惯量的计算转动惯量是物体对绕轴旋转的惯性特性的度量。
它是一个重要的物理量,在机械工程、物理学和工程技术等领域有广泛的应用。
转动惯量的计算有许多方法和技巧,下面将介绍一些常见的计算方法。
1.刚体转动惯量的定义:刚体转动惯量(或者称为惯性矩)是物体在绕任意轴旋转时,由物体的质量分布确定的。
它可以表示为I,即:I = ∫ r² dm其中,r是距离轴线的距离,dm是质量微元。
2.转动惯量的计算方法:(1)几何法计算:几何法是根据物体的几何形状和分布来计算转动惯量。
常见的几何形状包括球体、圆柱体、长方体等。
根据不同形状,使用不同的公式进行计算。
(2)积分法计算:积分法是通过对物体的质量分布进行积分来计算转动惯量。
这种方法适用于任意形状的物体,需要进行积分计算。
根据不同的质量分布,可以使用不同的坐标系和积分区域。
3.常见物体的转动惯量计算:(1)球体的转动惯量:对于球体,其转动惯量公式为:I=2/5*m*r²其中,m是球体的质量,r是球体的半径。
(2)圆柱体的转动惯量:对于圆柱体,其转动惯量公式为:I=1/2*m*r²其中,m是圆柱体的质量,r是圆柱体的半径。
(3)长方体的转动惯量:对于长方体,其转动惯量公式为:I=1/12*m*(a²+b²)其中,m是长方体的质量,a和b是长方体的宽度和高度。
如果长方体绕距离中心轴旋转,转动惯量计算公式会有所不同。
(4)其它常见物体的转动惯量:对于其它常见的物体,如圆环、圆盘、棒体等,都有相应的转动惯量计算公式。
这些公式可以在物理学的相关教材和参考资料中找到。
4.复杂物体的转动惯量计算:对于复杂物体,其转动惯量的计算相对较为复杂,通常需要使用积分法或数值计算的方法来求解。
这种方法适用于任意形状的物体,可以将物体分成无数微小的质量元,并对每个微小质量元的转动惯量进行积分求和。
总结起来,转动惯量的计算方法有几何法和积分法两种,常见的物体有相应的转动惯量公式。
转动惯量计算折算公式

转动惯量计算折算公式
转动惯量(即转动惯性矩)是描述物体对转动运动的惯性的物理量,
它可以用公式I=mr^2来计算,其中I是转动惯量,m是物体的质量,r是
物体的转动半径。
然而,在实际问题中,物体的形状往往是复杂的,不可能直接通过上
述公式来计算转动惯量。
为了解决这个问题,我们可以通过一些折算公式
来将复杂物体的转动惯量转换为一些简单形状的转动惯量之和。
以下是一些常见的折算公式:
1.对于长方体:
-绕通过质心垂直于一条边的转动轴转动:I=(1/12)*m*(a^2+b^2),
其中m是质量,a和b是长方体的两个边长。
-绕通过质心垂直于两条平行边的转动轴转动:I=(1/3)*m*(a^2+b^2),其中m是质量,a和b是长方体的两个边长。
2.对于球体:
-绕通过质心的任意轴转动:I=(2/5)*m*r^2,其中m是质量,r是球
体的半径。
3.对于圆环:
-绕通过圆环中心的垂直于其平面的转动轴转动:I=m*r^2,其中m是
质量,r是圆环的半径。
4.对于圆盘:
-绕通过圆盘中心的垂直于其平面的转动轴转动:I=(1/2)*m*r^2,其中m是质量,r是圆盘的半径。
5.对于薄杆(在转动轴与薄杆所在直线垂直的情况下):
-绕通过薄杆中心的转动轴转动:I=(1/12)*m*L^2,其中m是质量,L 是薄杆的长度。
这些折算公式可以帮助我们将复杂物体的转动惯量转换为一些简单形状的转动惯量之和,从而简化计算过程。
在实际应用中,我们可以根据物体的形状选择合适的折算公式来计算转动惯量,从而更好地描述物体的转动运动。
附录II 简单均质几何体的质心、转动惯量和惯性矩
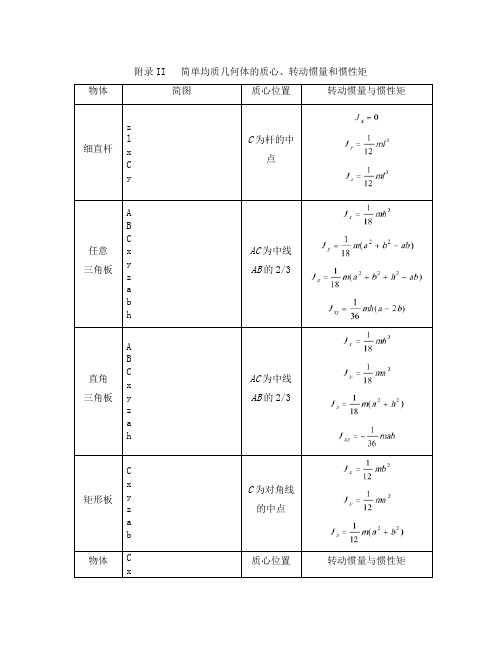
附录II 简单均质几何体的质心、转动惯量和惯性矩物体简图质心位置转动惯量与惯性矩细直杆zlxCyC为杆的中点任意三角板ABCxyzabhAC为中线AB的2/3直角三角板ABCxyzahAC为中线AB的2/3矩形板CxyzabC为对角线的中点物体 Cx质心位置转动惯量与惯性矩圆板C为圆心半圆板C x y z r yC O四分之一圆板yC r C x y z O xC椭圆板bCxyzaC为椭圆中心物体简图质心位置转动惯量与惯性矩圆柱体zrCyxhC为上、下底圆的圆心连线的中点中空圆柱体RzrCyxhC为上、下底圆的圆心连线的中点细圆环() azyxrCC为圆环中心线的圆心物体简图质心位置转动惯量与惯性矩粗圆环(R > r) rzyxRCC为圆环中心线的圆心圆锥体zC y r球形体CyzxrC为球心椭球体yCbzxacC为椭球心物体简图质心位置转动惯量与惯性矩半圆柱体z r C y x h xC h/2半圆锥体z r C y x h zC xC半球形壳zCCyzxr物体简图质心位置转动惯量与惯性矩四分之一椭圆板bCxyxCayC扇形板OCxyxCr(的单位为弧度)(的单位为弧度)任意三角板细直杆直角三角板矩形板arOxCchChhCcrh/2 xCrzCyC。
附录II-简单均质几何体的质心、转动惯量和惯性矩

附录II-简单均质几何体的质心、转动惯量和惯性矩附录II 简单均质几何体的质心、转动惯量和惯性矩物体简图质心位置转动惯量与惯性矩细直杆C为杆的中点=xJ2121mlJy=2121mlJz=任意三角板AC为中线AB的2/32181mhJ x=)(18122abbamJ y-+=)(181222abhbamJ z-++=)2(361bamhJxy-=直角三角板AC为中线AB的2/32181mhJ x=2181maJ y=)(18122hamJ z+=mahJ xy361-=矩形板C为对角线的中点2121mbJ x=2121maJ y=)(12122bamJ z+=zlxCyABCxyzabhABCxyzahC xyzab圆板C 为圆心241mr J x =241mr J y =221mr J z =半圆板π34ry C =)649(361222-=ππmr J x 241mr J y =)329(181222-=ππmr J z 四分之一圆板π34rx C = π34r y C = )649(361222-=ππmr J x )649(361222-=ππmr J y )649(181222-=ππmr J z )329(181222-=ππmr J xy 椭圆板C 为椭圆中心241mb J x =241ma J y =)(4122b a m J z +=C xy zrC xy zry C O y C rC xy zO x C bC xy za长方体C 为对角线交点)(12122c b m J x +=)(12122a c m J y +=)(12122b a m J z +=圆柱体C 为上、下底圆的圆心连线的中点)3(12122h r m J x +=)3(12122h r m J y +=221mr J z =中空圆柱体C 为上、下底圆的圆心连线的中点)33(121222h r R m J x ++=)33(121222h r R m J y ++=)(2122r R m J z +=细圆环 (a r >>)C 为圆环中心线的圆心221mr J x = 221mr J y =2mr J z =z rC yxh bCyzxac R z r C yxh az yxrC粗圆环(R > r) C为圆环中心线的圆心)45(2122rRmJx+=)45(2122rRmJy+=)43(22rRmJz+=圆锥体hzC41=)4(80322hrmJx+=)4(80322hrmJy+=2103mrJz=球形体C为球心252mrJx=252mrJy=252mrJz=椭球体C为椭球心)(5122cbmJx+=)(5122acmJy+=)(5122bamJz+=rzyx RCzCyrzxChCyzxryCbzxac半圆柱体π34r x C =)3(12122h r m J x +=2222121)649(361mh mr J y +-=ππ)329(181222-=ππmr J z 半圆锥体πrx C =4h z C =)4(80322h r m J x +=222803)1803(mh mr J y +-=π22)1803(mr J y π-=mrh J xz π201-=半球体r z C 83=232083mr J x =232083mr J y =252mr J z =半球形壳r z C 21=2125mr J x =2125mr J y =232mr J z =z rC yxh x C h /2 z rCy xhz Cx CC yz xr z C z C C yzxr四分之一椭圆板π34axC=π34byC=222)36649(mbJxππ-=222)36649(maJyππ-=)()36649(2222bamJz+-=ππmabJxy)18649(22ππ-=扇形板2sin34ααrxC=(α的单位为弧度)2)sin(41mrJxααα-=22)cos1(984sinmrJy⎥⎦⎤⎢⎣⎡--+=ααααα22)cos1(9821mrJz⎥⎦⎤⎢⎣⎡--=αα(α的单位为弧度)b CxyxCayCO C xyxCr2α2αzlxC y 细直杆ABC x y z ab任意三角板A B Cxy za h直角三角板C xyza b矩形板圆板Cxyzr半圆板Cxy zry CO 四分之一圆板C rCxyz O x C 椭圆板bCxyza圆柱体z rCyxh 长方体bCy zxac 中空圆柱体Rz rCyxh 细圆环az y xrC粗圆环rz yxRC 圆锥体z C yrzxCh球形体Cyzxr椭球体yCbzxa c半圆柱体z r Cyxhx C h /2 半圆锥体zrC y xhz C x C 半球体C yz xrz C 半球形壳z C C yz xr四分之一椭圆板b Cxyx Cay C扇形板OC xyx C r2α 2α。
转动惯量公式表
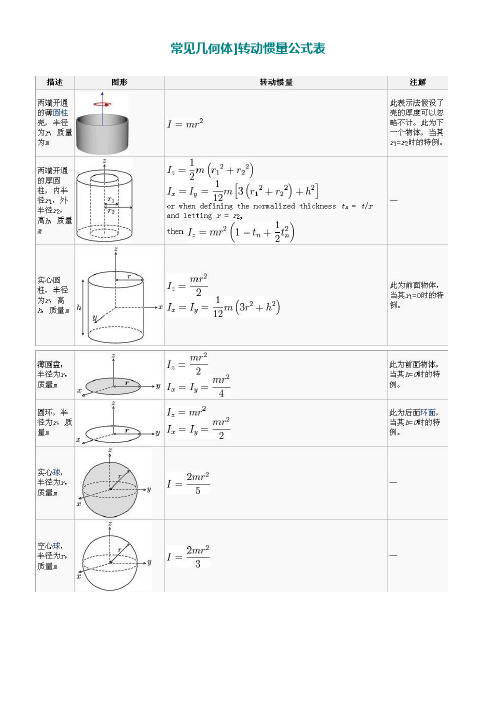
常见几何体]转动惯量公式表关于细杆当回转轴过杆的中点并垂直于杆时;J=m(L^2)/12 其中m是杆的质量,L是杆的长度。
当回转轴过杆的端点并垂直于杆时:J=m(L^2)/3 其中m是杆的质量,L是杆的长度。
关于圆柱体当回转轴是圆柱体轴线时;J=m(r^2)/2其中m是圆柱体的质量,r是圆柱体的半径。
关于细圆环当回转轴通过中心与环面垂直时,J=mR^2;当回转轴通过边缘与环面垂直时,J=2mR^2;R为其半径关于薄圆盘当回转轴通过中心与盘面垂直时,J=﹙1/2﹚mR^2;当回转轴通过边缘与盘面垂直时,J=﹙3/2﹚mR^2;R为其半径关于空心圆柱当回转轴为对称轴时,J=﹙1/2﹚m[(R1)^2+(R2)^2];R1和R2别离为其内外半径。
关于球壳当回转轴为中心轴时,J=﹙2/3﹚mR^2;当回转轴为球壳的切线时,J=﹙5/3﹚mR^2;R为球壳半径。
关于实心球体当回转轴为球体的中心轴时,J=﹙2/5﹚mR^2;当回转轴为球体的切线时,J=﹙7/5﹚mR^2;R为球体半径关于立方体当回为其中心轴时,J=﹙1/6﹚mL^2;当回转轴为其棱边时,J=﹙2/3﹚mL^2;当回转轴为其体对角线时,J=(3/16)mL^2;L为立方体边长。
只明白转动惯量的计算方式而不能利用是没成心义的。
下面给出一些(绕定轴转动时)的刚体动力学公式。
角加速度与合外力矩的关系:角加速度与合外力矩式中M为合外,β为。
能够看出那个式子与牛顿第二定律是对应的。
角动量:角动量刚体的定轴转动动能:转动动能注意这只是刚体绕定轴的转动动能,其总动能应该再加上质心动能。
只用E=(1/2)mv^2不行分析转动刚体的问题,是因为其中不包括刚体的任何转动信息,里面的速度v只代表刚体的质心运动情形。
由这一公式,能够从能量的角度分析刚体动力学的问题。
惯量(Moment of Inertia)是绕轴转动时惯性(回转物体维持其或静止的特性)的,用字母I或J表示。
转动惯量公式表

转动惯量公式表 Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】常见几何体]转动惯量公式表对于细杆当回转轴过杆的中点并垂直于杆时;J=m(L^2)/12其中m是杆的质量,L是杆的长度。
当回转轴过杆的端点并垂直于杆时:J=m(L^2)/3其中m是杆的质量,L是杆的长度。
对于圆柱体当回转轴是圆柱体轴线时;J=m(r^2)/2其中m是圆柱体的质量,r是圆柱体的半径。
对于细圆环当回转轴通过中心与环面垂直时,J=mR^2;当回转轴通过边缘与环面垂直时,J=2mR^2;R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时,J=﹙1/2﹚mR^2;当回转轴通过边缘与盘面垂直时,J=﹙3/2﹚mR^2;R为其半径对于空心圆柱当回转轴为对称轴时,J=﹙1/2﹚m[(R1)^2+(R2)^2];R1和R2分别为其内外半径。
对于球壳当回转轴为中心轴时,J=﹙2/3﹚mR^2;当回转轴为球壳的切线时,J=﹙5/3﹚mR^2;R为球壳半径。
对于实心球体当回转轴为球体的中心轴时,J=﹙2/5﹚mR^2;当回转轴为球体的切线时,J=﹙7/5﹚mR^2;R为球体半径对于立方体当回为其中心轴时,J=﹙1/6﹚mL^2;当回转轴为其棱边时,J=﹙2/3﹚mL^2;当回转轴为其体对角线时,J=(3/16)mL^2;L为立方体边长。
只知道转动惯量的计算方式而不能使用是没有意义的。
下面给出一些(绕定轴转动时)的刚体动力学公式。
角加速度与合外力矩的关系:角加速度与合外力矩式中M为合外,β为。
可以看出这个式子与牛顿第二定律是对应的。
角动量:角动量刚体的定轴转动动能:转动动能注意这只是刚体绕定轴的转动动能,其总动能应该再加上质心动能。
只用E=(1/2)mv^2不好分析转动刚体的问题,是因为其中不包含刚体的任何转动信息,里面的速度v只代表刚体的质心运动情况。
由这一公式,可以从能量的角度分析刚体动力学的问题。
工程力学之转动惯量

取Y轴与Y*重合
M
M
把 xi* xi , yi* yi d 代入
Jz* r *2dm (x *2 y *2 )dm
M
M
x2 y d 2 dm x2 y2 2 yd d 2 dm
M
M
x2 y2 dm d 2dm + d ydm
M
M
M
r 2dm Jz
13-4 刚体的转动惯量
一般公式 简单形状均质物体的转动惯量
转动惯量的平行移轴定理
转动惯量的一般公式 z
1、刚体对转轴z的转动惯量
Jz mr 2( 1)
2、质量连续分布刚体
对转轴z的转动惯量
Mi
Jz r 2dm( 2 ) r i
mi
M
3、转动惯量 与刚体的运动状态无关
•为一恒正标量 •计算
M
因为Z轴过质心C
0 yc Md
d 2 M Jz* Jz d 2 M
转动惯量的平行轴定理
刚体对于任何轴的转动惯量, 等于刚体对通过其质心并与该轴平 行的轴的转动惯量加上刚体质量与 这两轴间距离平方的乘积。
J z* J z d 2 M
M
M
dm ab ds ab ady
Jy
r 2dm
M
b 0
x2
M ab
bdx
1 3
Ma3
Jx
r 2dm
M
b 0
y2
M ab
ady
1 3
Mb2
M
M
dm ds bdx
ab ab
均质细圆环的转动惯量
均质细圆环,半径为 R,质量为M,求其对Z轴的惯性矩。
解∶
y
dm
重心的知识点总结

重心的知识点总结重心是物体受重力作用时所处的平衡位置,也是物体的质心。
在物理学和工程学中,重心是一个重要的概念,它在力学、静力学、动力学以及结构设计和分析中起着关键作用。
了解重心的概念和相关知识对于理解物体的平衡、稳定性和运动特性非常重要。
本文将围绕重心的概念、计算方法、应用和相关理论进行综合总结。
一、重心的概念重心是一个物体在受重力作用时的平衡位置,也称为质心。
它是物体整体质量的平均位置,也可以理解为物体在受重力作用时的“集中位置”。
对于一个均匀材料构成的物体,其重心通常位于物体的几何中心或对称轴上,但对于复杂形状、不均匀密度分布的物体,其重心位置需要通过计算得出。
重心的概念对于力学、静力学、动力学的理论分析和工程设计具有重要的意义。
二、重心的计算方法重心的计算方法取决于物体的形状和密度分布。
对于规则形状的物体,可以通过几何方法直接计算出重心位置;对于不规则形状和复杂密度分布的物体,通常需要通过积分或数值计算的方法求解重心位置。
以下是常见物体重心计算方法的概述:1. 离散质点组的重心计算:对于由离散的质点组成的物体,其重心位置可以通过每个质点的质量及坐标的加权平均来计算。
2. 连续体的重心计算:对于连续分布的物体,其重心位置可以通过积分计算来求解。
通常需要将物体划分成微元,然后对每个微元的质量及坐标进行积分求和,最终得到整个物体的重心位置。
3. 特殊形状重心的计算:对于特殊形状的物体,比如圆环、弧形等,可以利用几何性质和积分计算来求解重心位置。
以上是重心计算的基本方法,根据具体情况可以结合不同的数学工具和技术来求解重心位置。
三、重心的应用重心的概念在工程领域有着广泛的应用,它对于物体的平衡、稳定性和运动特性具有重要影响。
以下是重心在工程应用中的几个典型案例:1. 结构设计:在建筑、机械、航天等领域的结构设计中,重心的位置是一个重要考虑因素。
合理设计和布置物体的结构和材料,可以使重心位置处于合适的位置,从而确保物体的平衡和稳定性。
