附录II 简单均质几何体的质心、转动惯量和惯性矩
转动惯量理论力学

z
刚体对轴OL的转动惯量
式中
J mrL2
rL2 (OA)2 (OB)2
其中OB是矢 r =OA 在轴OL上的投影。 由矢量投影定理得
OB x cos y cos z cos
因 ( OA )2 x2 y2 z2 ,故
L α B rL A
O
β
y
J x mrx2 m( y2 z2 )
J y mry2 m(z2 x2) J z mrz2 m(x2 y2)
rz
A
O
z
x
rz
y
x
y
图2
转动惯量
§1 转动惯量的概念
4.极转动惯量
对于平面薄板,使平板表面重合于坐标平面Oxy(如图3),
如果薄板内各点的坐标 z 可以忽略,则式简写成
O
z
rz
y
x
x y
图1
在国际单位制中,转动惯量的常用单位是kg·m2 。
转动惯量
§1 转动惯量的概念
2.回转半径
刚体对于某轴z的转动惯量与其质量m之比值的平方根为一 个当量长度,称为刚体对于该轴的回转半径。因此,有关系式
z
Jz , m
J z mz2
可见,如果假想地把刚体的全部质量集中于一点,而不改变 这刚体对于该轴的转动惯量,则这个点到该轴的距离应等于回转 半径。
解:取任一半径为ζ,宽为dζ的圆环,其质量是
dm
m πr2
2πd
2m r2
d
对轴z的转动惯量元素是
dJ z
(dm)
2
2m r2
3d
于是,求得圆盘对轴z转动惯量
y
r
常见刚体的转动惯量
习题答案
第一章
F (h − 3r ), M y = 3 F (r + h ), M z = − Fr . 1-3 4 4 2 2 bc ab ca a ab M ξ = −513.36 N ⋅ m . 1-4 M x = M − F ,My = M + F ,Mz = M, k1 k1 k1 2k 2 2k 2 abc 2 2 2 2 2 2 F. 其中: k1 = (ab ) + (bc ) + (ca ) , k2 = a + b / 4 + c . 1-5 M τ = rAB b 2 + c 2
ρz =
3 r 10 3 (4r 2 + l 2 ) 80
ρx = ρy
=
圆环
3 J z = m( R 2 + r 2 ) 4
ρ z = R2 + r2
3 4
Jz =
椭圆形 薄 板
m 2 (a + b2 ) 4 m J y = a2 4 m J y = b2 4
1 2 a + b2 2 a ρx = 2 b ρy = 2
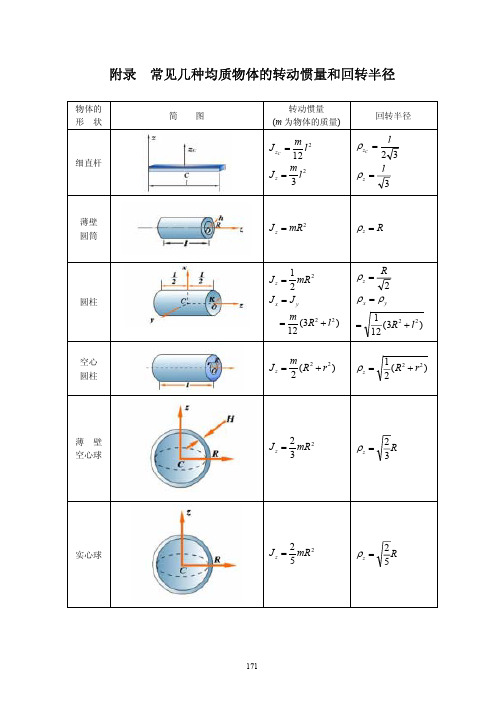
附录常见几种均质物体的转动惯量和回转半径物体的转动惯量简图回转半径形状m为物体的质量m2ljlzzcc1223细直杆m2ljzlz33薄壁2jmrr圆筒zz12rjmrzz22jj圆柱xyxym221223rl3rl1212空心m22122jzrrzrr圆柱22薄壁222jzmrzr空心球33222实心球jzmrzr55171323jzmrzr1010jj圆锥体xyxy322322m4rl4rl8080232232圆环jzmrrzrr44m22122jzabzab42椭圆形m2ajyax薄板42m2bjyby42m22122jzabzab1212m22122长方体jyacxac1212m22122jy12bcy12bcm22jz12ab122zab矩形m212ja薄板y120289axm20289bjbyy12172参考书目1朱照宣周起钊殷金生编
惯性矩总结(含常用惯性矩公式)

惯性矩是一个物理量,通常被用作描述一个物体抵抗扭动,扭转的能力。
惯性矩的国际单位为(m^4)。
工程构件典型截面几何性质的计算2.1面积矩1.面积矩的定义图2-2.1任意截面的几何图形如图2-31所示为一任意截面的几何图形(以下简称图形)。
定义:积分和分别定义为该图形对z轴和y轴的面积矩或静矩,用符号S z和S y,来表示,如式(2—2.1)(2—2.1)面积矩的数值可正、可负,也可为零。
面积矩的量纲是长度的三次方,其常用单位为m3或mm3。
2.面积矩与形心平面图形的形心坐标公式如式(2—2.2)(2—2.2)或改写成,如式(2—2.3)(2—2.3)面积矩的几何意义:图形的形心相对于指定的坐标轴之间距离的远近程度。
图形形心相对于某一坐标距离愈远,对该轴的面积矩绝对值愈大。
图形对通过其形心的轴的面积矩等于零;反之,图形对某一轴的面积矩等于零,该轴一定通过图形形心。
3.组合截面面积矩和形心的计算组合截面对某一轴的面积矩等于其各简单图形对该轴面积矩的代数和。
如式(2—2.4)(2—2.4)式中,A和y i、z i分别代表各简单图形的面积和形心坐标。
组合平面图形的形心位置由式(2—2.5)确定。
(2—2.5)2.2极惯性矩、惯性矩和惯性积1.极惯性矩任意平面图形如图2-31所示,其面积为A。
定义:积分称为图形对O点的极惯性矩,用符号I P,表示,如式(2—2.6)(2—2.6)极惯性矩是相对于指定的点而言的,即同一图形对不同的点的极惯性矩一般是不同的。
极惯性矩恒为正,其量纲是长度的4次方,常用单位为m4或mm4。
(1)圆截面对其圆心的极惯性矩,如式(2—7)(2—2.7)(2)对于外径为D、内径为d的空心圆截面对圆心的极惯性矩,如式(2—2.8)(2—2.8)式中,d/D为空心圆截面内、外径的比值。
2.惯性矩在如图6-1所示中,定义积分,如式(2—2.9)(2—2.9)称为图形对z轴和y轴的惯性矩。
惯性矩是对一定的轴而言的,同一图形对不同的轴的惯性矩一般不同。
转动惯量详细资料大全

转动惯量详细资料大全转动惯量(Moment of Inertia)是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度,用字母I或J表示。
在经典力学中,转动惯量(又称质量惯性矩,简称惯距)通常以I或J表示,SI 单位为kg·m2。
对于一个质点,I = mr2,其中 m 是其质量,r 是质点和转轴的垂直距离。
转动惯量在旋转动力学中的角色相当于线性动力学中的质量,可形式地理解为一个物体对于旋转运动的惯性,用于建立角动量、角速度、力矩和角加速度等数个量之间的关系。
基本介绍•中文名:转动惯量•外文名:Moment of Inertia•表达式:I=mr2•套用学科:物理学•适用领域范围:刚体动力学•适用领域范围:土木工程基本含义,质量转动惯量,面积转动惯量,相关定理,平行轴定理,垂直轴定理,动力学公式,张量定义,实验测定,实验原理,实验内容,计算公式,对于细杆,对于圆柱体,对于细圆环,对于薄圆盘,对于空心圆柱,对于球壳,对于实心球体,对于立方体,对于长方体,基本含义质量转动惯量其量值取决于物体的形状、质量分布及转轴的位置。
刚体的转动惯量有着重要的物理意义,在科学实验、工程技术、航天、电力、机械、仪表等工业领域也是一个重要参量。
电磁系仪表的指示系统,因线圈的转动惯量不同,可分别用于测量微小电流(检流计)或电量(冲击电流计)。
在发动机叶片、飞轮、陀螺以及人造卫星的外形设计上,精确地测定转动惯量,都是十分必要的。
转动惯量只决定于刚体的形状、质量分布和转轴的位置,而同刚体绕轴的转动状态(如角速度的大小)无关。
形状规则的匀质刚体,其转动惯量可直接用公式计算得到。
而对于不规则刚体或非均质刚体的转动惯量,一般通过实验的 ... 来进行测定,因而实验 ... 就显得十分重要。
转动惯量套用于刚体各种运动的动力学计算中。
转动惯量的表达式为若刚体的质量是连续分布的,则转动惯量的计算公式可写成(式中表示刚体的某个质元的质量,r表示该质元到转轴的垂直距离,ρ表示该处的密度,求和号(或积分号)遍及整个刚体。
附录(惯性矩、静矩)

O
记住图形对形心轴的惯性矩, 记住图形对形心轴的惯性矩,便可求出对所有 平行于此形心轴的各轴的惯性矩。 平行于此形心轴的各轴的惯性矩。 为形心坐标,注意其正负号。 惯性积公式中 a, b 为形心坐标,注意其正负号。
附录 平面图形的几何性质
几何性质——只与横截面的几何形状和尺 只与横截面的几何形状和尺 几何性质 寸 有关的某些几何量, 有关的某些几何量,对杆件的应力和变形 起 着重要作用,如横截面面积A, 着重要作用,如横截面面积 ,圆轴横截面 F Fl N 拉压杆 对圆心的极惯性矩I σ= 对圆心的极惯性矩 P等。∆l = N A EA 圆轴扭转
材料力学
中南大学土木建筑学院
8
组合图形的静矩和形心有如下公式
S y = ∑ Ai zCi ; S z = ∑ Ai yCi
i =1 i =1
n
n
yC =
∑Ay
i =1 i
n
Ci
A
; zC =
∑Az
i =1
n
i Ci
A
材料力学
中南大学土木建筑学院
9
组合图形的静矩和形心
z Ⅰ
C1(yC1, zC1) C (yC ,zC)
I y + Iz I y − Iz 主惯性轴 Iy = + cos 2α − I yz sin 2α 的意义 1 2 2
对α求导
d Iy1 dα
即
材料力学
=−2
Iy − Iz 2
sin2 −2Iyz cos2 =−2Iy1z1 = 0 α α
主惯性轴就是使得图形的 惯性矩取极值时的坐标轴
附录II-简单均质几何体的质心、转动惯量和惯性矩

附录II-简单均质几何体的质心、转动惯量和惯性矩附录II 简单均质几何体的质心、转动惯量和惯性矩物体简图质心位置转动惯量与惯性矩细直杆C为杆的中点=xJ2121mlJy=2121mlJz=任意三角板AC为中线AB的2/32181mhJ x=)(18122abbamJ y-+=)(181222abhbamJ z-++=)2(361bamhJxy-=直角三角板AC为中线AB的2/32181mhJ x=2181maJ y=)(18122hamJ z+=mahJ xy361-=矩形板C为对角线的中点2121mbJ x=2121maJ y=)(12122bamJ z+=zlxCyABCxyzabhABCxyzahC xyzab圆板C 为圆心241mr J x =241mr J y =221mr J z =半圆板π34ry C =)649(361222-=ππmr J x 241mr J y =)329(181222-=ππmr J z 四分之一圆板π34rx C = π34r y C = )649(361222-=ππmr J x )649(361222-=ππmr J y )649(181222-=ππmr J z )329(181222-=ππmr J xy 椭圆板C 为椭圆中心241mb J x =241ma J y =)(4122b a m J z +=C xy zrC xy zry C O y C rC xy zO x C bC xy za长方体C 为对角线交点)(12122c b m J x +=)(12122a c m J y +=)(12122b a m J z +=圆柱体C 为上、下底圆的圆心连线的中点)3(12122h r m J x +=)3(12122h r m J y +=221mr J z =中空圆柱体C 为上、下底圆的圆心连线的中点)33(121222h r R m J x ++=)33(121222h r R m J y ++=)(2122r R m J z +=细圆环 (a r >>)C 为圆环中心线的圆心221mr J x = 221mr J y =2mr J z =z rC yxh bCyzxac R z r C yxh az yxrC粗圆环(R > r) C为圆环中心线的圆心)45(2122rRmJx+=)45(2122rRmJy+=)43(22rRmJz+=圆锥体hzC41=)4(80322hrmJx+=)4(80322hrmJy+=2103mrJz=球形体C为球心252mrJx=252mrJy=252mrJz=椭球体C为椭球心)(5122cbmJx+=)(5122acmJy+=)(5122bamJz+=rzyx RCzCyrzxChCyzxryCbzxac半圆柱体π34r x C =)3(12122h r m J x +=2222121)649(361mh mr J y +-=ππ)329(181222-=ππmr J z 半圆锥体πrx C =4h z C =)4(80322h r m J x +=222803)1803(mh mr J y +-=π22)1803(mr J y π-=mrh J xz π201-=半球体r z C 83=232083mr J x =232083mr J y =252mr J z =半球形壳r z C 21=2125mr J x =2125mr J y =232mr J z =z rC yxh x C h /2 z rCy xhz Cx CC yz xr z C z C C yzxr四分之一椭圆板π34axC=π34byC=222)36649(mbJxππ-=222)36649(maJyππ-=)()36649(2222bamJz+-=ππmabJxy)18649(22ππ-=扇形板2sin34ααrxC=(α的单位为弧度)2)sin(41mrJxααα-=22)cos1(984sinmrJy⎥⎦⎤⎢⎣⎡--+=ααααα22)cos1(9821mrJz⎥⎦⎤⎢⎣⎡--=αα(α的单位为弧度)b CxyxCayCO C xyxCr2α2αzlxC y 细直杆ABC x y z ab任意三角板A B Cxy za h直角三角板C xyza b矩形板圆板Cxyzr半圆板Cxy zry CO 四分之一圆板C rCxyz O x C 椭圆板bCxyza圆柱体z rCyxh 长方体bCy zxac 中空圆柱体Rz rCyxh 细圆环az y xrC粗圆环rz yxRC 圆锥体z C yrzxCh球形体Cyzxr椭球体yCbzxa c半圆柱体z r Cyxhx C h /2 半圆锥体zrC y xhz C x C 半球体C yz xrz C 半球形壳z C C yz xr四分之一椭圆板b Cxyx Cay C扇形板OC xyx C r2α 2α。
理论力学 哈尔滨工业大学 第12章

对 z 轴的动量矩 Mz (m ) 等于 [m ]xy 对点O的矩。 v v 对点 的矩。 的矩
Mz (m ) v 是代数量,从 是代数量,
z 轴正向看,逆时针为正,顺 轴正向看,逆时针为正,
时针为负。 时针为负。
[MO(m )]z = Mz (m ) v v
单位: 单位:kg·m2/s 2.质点系的动量矩 . 对点的动量矩
O
d [Jω+m ] = M −m sinθ ⋅ R vR g dt
(e MO ) =a , 得 dt R
M −m 2 sinθ R gR a= 2 J +m R
水轮机转轮, 例12-2 水轮机转轮,进口水速度 求水流对转轮的转动力矩。 求水流对转轮的转动力矩。
v ×m = 0 v
因此
d MO(m ) = MO(F) v dt
称为质点的动量矩定理: 称为质点的动量矩定理:质点对某定点的动量矩对 质点的动量矩定理 时间的一阶导数,等于作用力对同一点的矩。 时间的一阶导数,等于作用力对同一点的矩。 投影式: 投影式: d Mx (m ) = Mx (F) v dt d My (m ) = My (F) v dt
解:J1α1 = M1 − F′R J2α2 = F R2 −M2 t t 1
α1 R = i12 = 2 ,得 因 F′ = F , t t α2 R 1
M2 M− 1 i12 α1 = J J1 + 22 i12
R 2 , M , M2 1 R 1
,求: 1 。 α
§12-4 刚体对轴的转动惯量
kgm简单形状物体的转动惯量计算1均质细直杆对一端的转动惯量1均质细直杆对一端的转动惯量2均质薄圆环对中心轴的转动惯量2均质薄圆环对中心轴的转动惯量3均质圆板对中心轴的转动惯量3均质圆板对中心轴的转动惯量3
13.2转动惯量(重庆大学土木理论力学课件)解析

许多常见简单的均质物体的转动惯量 可在工程手册中查到,书中列出了几种 常见的简单形状的均质物体的转动惯量。
二、平行轴定理
1、问题的提出 例如均质圆盘,对于 通过质心轴C的转动 惯量JC已知,但圆盘并不是绕C点转动,而是 绕O点转动。
2. 平行移轴定理 刚体对于某轴的转动惯量,等于刚体对于过质心、并 与该轴平行的轴的转动惯量,加上刚体质量与轴距平 方的乘积,即 2
出现大小相等、符号相反项,故 J xz mi xi zi 0。
同理, J xy 0
。所以z轴必是主轴之一。
dA
y1
图13-10
应当注意,主轴是对某一点而言的,对于不同的点,主轴 的方位一般是不同的。但是,不论在哪一点,总能找到三 个相互垂直的主轴。 通过刚体质心的主轴称为中心惯性主轴。 通常,求惯性主轴的计算较繁。 但是,如果刚体具有对称面或对称轴,则决定主轴的 问题大为简化。设刚体具有一对称面,则垂直于对称 面的轴即为该轴与对称面交点的主轴之一。 因为,如以对称面为xy面,z轴垂直于对称面,根 据对称面的定义,在(xi、yi、zi)处有一质点,则在(xi、 yi、—zi)处必有一相同质点与之对应。
起来就是整个物体的转动惯量。 若物体有空心
部分, 要把此部分的转动惯量视为负值来处理。
例 均质圆盘与均质杆组成的复摆如图 ,已
知:圆盘质量为m1,半径r,杆质量m2,长L,试 求复摆对悬挂轴O的转动惯量。 解: J o J o杆 J o盘
l J o杆 J c1 m 2 2 1 1 1 2 2 m 2l m 2l m 2l 2 12 4 3
称刚体对x、y轴的惯性积 称刚体对x、z轴的惯性积 称刚体对y、z轴的惯性积
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
附录II 简单均质几何体的质心、转动惯量和惯性矩
物体简图质心位置转动惯量与惯性矩
细直杆z
l
x
C
y
C为杆的中
点
任意三角板A
B
C
x
y
z
a
b
h
AC为中线
AB的2/3
直角三角板A
B
C
x
y
z
a
h
AC为中线
AB的2/3
矩形板C
x
y
z
a
b
C为对角线
的中点
物体 C
x
质心位置转动惯量与惯性矩
圆板C为圆心
半圆板C x y z r yC O
四分之一圆板yC r C x y z O xC
椭圆板b
C
x
y
z
a
C为椭圆中
心
物体简图质心位置转动惯量与惯性矩
圆柱体z
r
C
y
x
h
C为上、下
底圆的圆
心连线的
中点
中空圆柱
体R
z
r
C
y
x
h
C为上、下
底圆的圆
心连线的
中点
细圆环() a
z
y
x
r
C
C为圆环中
心线的圆
心
物体简图质心位置转动惯量与惯性矩
粗圆环(R > r) r
z
y
x
R
C
C为圆环中心
线的圆心
圆锥体zC y r
球形体C
y
z
x
r
C为球心
椭球体y
C
b
z
x
a
c
C为椭球心
物体简图质心位置转动惯量与惯性矩
半圆柱体z r C y x h xC h/2
半圆锥体z r C y x h zC xC
半球
形壳
zC
C
y
z
x
r
物体简图质心位置转动惯量与惯性矩
四分
之一
椭圆
板
b
C
x
y
xC
a
yC
扇形
板
O
C
x
y
xC
r
(的单位为
弧度)
(的
单位为弧度)
任意三角板
细直杆
直角三角板
矩形板a
r
O
xC
c
h
C
h
h
C
c
r
h/2 xC
r
zC
yC。
