人教版中考数学二轮复习专题练习上常用辅助线-构造等边三角形
中考数学几何辅助线大全及常考题型解析
中考数学几何辅助线大全及常考题型解析中考数学几何辅助线作法及常考题型解析第一部分常见辅助线做法等腰三角形:1.作底边上的高，构成两个全等的直角三角形2.作一腰上的高； 3.过底边的一个端点作底边的垂线，与另一腰的延长线相交，构成直角三角形。
梯形1.垂直于平行边2.垂直于下底，延长上底作一腰的平行线3.平行于两条斜边4.作两条垂直于下底的垂线5.延长两条斜边做成一个三角形菱形1.连接两对角2.做高平行四边形1.垂直于平行边2.作对角线——把一个平行四边形分成两个三角形3.做高——形内形外都要注意矩形1.对角线2.作垂线很简单。
无论什么题目，第一位应该考虑到题目要求，比如AB=AC+BD....这类的就是想办法作出另一条AB等长的线段，再证全等说明AC+BD=另一条AB,就好了。
还有一些关于平方的考虑勾股，A字形等。
三角形图中有角平分线，可向两边作垂线（垂线段相等）。
也可将图对折看，对称以后关系现。
角平分线平行线，等腰三角形来添。
角平分线加垂线，三线合一试试看。
线段垂直平分线，常向两端把线连。
要证线段倍与半，延长缩短可试验。
三角形中两中点，连接则成中位线。
三角形中有中线，延长中线等中线。
解几何题时如何画辅助线①见中点引中位线，见中线延长一倍在几何题中，如果给出中点或中线，可以考虑过中点作中位线或把中线延长一倍来解决相关问题。
②在比例线段证明中，常作平行线。
③对于梯形问题，常用的添加辅助线的方法有1、过上底的两端点向下底作垂线2、过上底的一个端点作一腰的平行线3、过上底的一个端点作一对角线的平行线4、过一腰的中点作另一腰的平行线5、过上底一端点和一腰中点的直线与下底的延长线相交6、作梯形的中位线7、延长两腰使之相交四边形平行四边形出现，对称中心等分点。
梯形里面作高线，平移一腰试试看。
平行移动对角线，补成三角形常见。
证相似，比线段，添线平行成习惯。
等积式子比例换，寻找线段很关键。
直接证明有困难，等量代换少麻烦。
备战中考数学二轮专题归纳提升真题几何模型—三角形中的旋转模型(解析版)
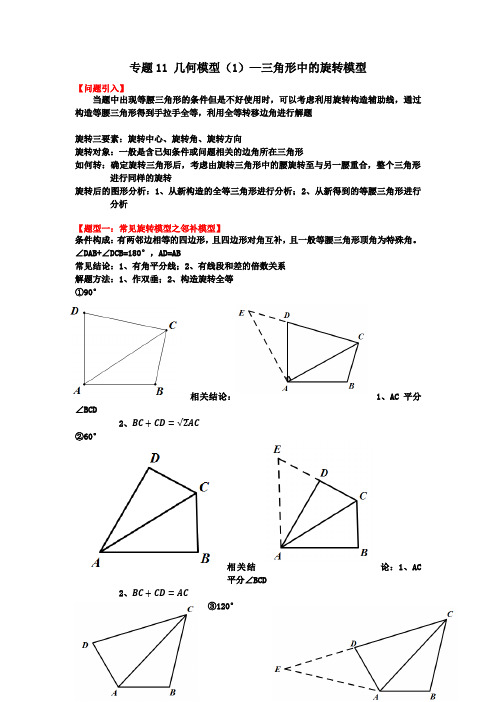
专题11 几何模型（1）—三角形中的旋转模型【问题引入】当题中出现等腰三角形的条件但是不好使用时，可以考虑利用旋转构造辅助线，通过构造等腰三角形得到手拉手全等，利用全等转移边角进行解题旋转三要素：旋转中心、旋转角、旋转方向旋转对象：一般是含已知条件或问题相关的边角所在三角形如何转：确定旋转三角形后，考虑由旋转三角形中的腰旋转至与另一腰重合，整个三角形进行同样的旋转旋转后的图形分析：1、从新构造的全等三角形进行分析；2、从新得到的等腰三角形进行分析【题型一：常见旋转模型之邻补模型】条件构成：有两邻边相等的四边形，且四边形对角互补，且一般等腰三角形顶角为特殊角。
∠DAB+∠DCB=180°，AD=AB常见结论：1、有角平分线；2、有线段和差的倍数关系解题方法：1、作双垂；2、构造旋转全等①90°相关结论：1、AC平分∠BCD2、BC+CD=√2AC②60°相关结论：1、AC平分∠BCD2、BC+CD=AC③120°相关结论：1、AC平分∠BCD2、BC+CD=√3AC补充说明：对角互补、邻边相等、角平分线三个条件知到其中两个就可求另外第三个，辅助线的构造与三角形全等相同，但是全等判定会有差异，需要根据具体情况判断【例】如图，在Rt△ABC和Rt△BCD中，∠BAC＝∠BDC＝90°，BC＝8，AB＝AC，∠CBD＝30°，BD＝4√3，M，N分别在BD，CD上，∠MAN＝45°，则△DMN的周长为_____．【答案】4√3+4．【解析】将△ACN绕点A逆时针旋转，得到△ABE，如图：由旋转得：∠NAE＝90°，AN＝AE，∠ABE＝∠ACD，∠EAB＝∠CAN，∵∠BAC＝∠D＝90°，∴∠ABD+∠ACD＝360°﹣90°﹣90°＝180°，∴∠ABD+∠ABE＝180°，∴E，B，M三点共线，∵∠MAN＝45°，∠BAC＝90°，∴∠EAM＝∠EAB+∠BAM＝∠CAN+∠BAM＝∠BAC﹣∠MAN＝90°﹣45°＝45°，∴∠EAM＝∠MAN，在△AEM和△ANM中，{AE=AN∠EAM=∠NAMAM=AM，∴△AEM≌△ANM（SAS），∴MN＝ME，∴MN＝CN+BM，∵在Rt△BCD中，∠BDC＝90°，∠CBD＝30°，BD＝4√3，CD＝BD×tan∠CBD＝4，∴△DMN的周长为DM+DN+MN＝DM+DN+BM+CN＝BD+DC＝4√3+4，故答案为：4√3+4．【练1】如图，在平面直角坐标系xOy中，A,B两点分别在x轴，y轴的正半轴上，且OA=OB，点C在第一象限，OC=3，连接BC，AC，若∠BCA=90°，则BC+AC的值为_________．【答案】3√2【解析】解：将△OBC绕O点旋转90°，∵OB=OA∴点B落在A处，点C落在D处且有OD=OC=3，∠COD=90°，∠OAD=∠OBC，在四边形OACB中∵∠BOA=∠BCA=90°，∴∠OBC+∠OAC=180°，∴∠OAD+∠OAC=180°∴C、A、D三点在同一条直线上，∴△OCD为等要直角三角形，根据勾股定理CD2=OC2+OD2即CD2=32+32=18解得CD=3√2即BC+AC=3√2.【练2】如图，P是等边三角形ABC内一点，将线段BP绕点B逆时针旋转60°得到线段BQ，连接AQ．若PA=4，PB=5，PC=3，则四边形APBQ的面积为_______．【答案】5√34+6【解析】解：如图，连接PQ，由旋转的性质可得，BP=BQ，又∵∠PBQ=60°，∴△BPQ是等边三角形，∴PQ=BP，在等边三角形ABC中，∠CBA=60°，AB=BC，∴∠ABQ=60°-∠ABP∠CBP=60°-∠ABP∴∠ABQ=∠CBP在△ABQ与△CBP中{BQ=BP∠ABQ=∠CBPAB=CB∴△ABQ≌△CBP(SAS)，∴AQ=PC，又∵PA=4，PB=5，PC=3，∴PQ=BP=5，PC=AQ=3，在△APQ中，AQ2=9,AP2=16,PQ2=25，25=16+9，∴由勾股定理的逆定理可知△APQ是直角三角形，∴S 四边形APBQ =S △BPQ +S △APQ =√34×52+12×3×4=5√34+6， 故答案为：5√34+6【练3】如图，在△ABC 中，∠ACB =120°，BC >AC ，点E 在BC 上，点D 在AB 上，CE =CA ，连接DE ，180ACB ADE ∠+∠=︒，CH ⊥AB ，垂足为H ．证明：DE AD +=．【答案】见解析【解析】证明：如图，延长BA 到点F ，使AF=DE ，连接CF 、CD ，∵∠ACB+∠ADE=180°∴∠CAD+∠CED=360°－180°=180°∵∠CAD+∠CAF=180°∴∠CAF=∠CED∵AC=EC ，AF=ED∴△AFC ≌△EDC∴CF=CD ，∠ACF=∠ECD∴∠FCD=∠ACF+∠ACD=∠ECD+∠ACD=∠ACB=120°∵CF=CD ，CH ⊥DF∴FH=DH=12DF =12(DE+AD)，∠HCD=12∠FCD=60°∴tan ∠HCD=DH CH =√3∴DH=√3CH∴DE+AD=2DH=2√3CH【题型二：旋转与三角形全等的构造】【例】问题背景：如图①设P 是等边△ABC 内一点，PA ＝6，PB ＝8，PC ＝10，求∠APB 的度数．小君研究这个问题的思路是：将△ACP 绕点A 逆时针旋转60°得到△ABP '，易证：△APP'是等边三角形，△PBP'是直角三角形，所以∠APB＝∠APP'+∠BPP'＝150°．简单应用：（1）如图2，在等腰直角△ABC中，∠ACB＝90°．P为△ABC内一点，且PA ＝5，PB＝3，PC＝2√2，则∠BPC＝°（2）如图3，在等边△ABC中，P为△ABC内一点，且PA＝5，PB＝12，∠APB＝150°，则PC＝．拓展廷伸：①如图4，∠ABC＝∠ADC＝90°，AB＝BC．求证：√2BD＝AD+DC．②若图4中的等腰直角△ABC与Rt△ADC在同侧如图5，若AD＝2，DC＝4，请直接写出BD的长．【答案】（1）135°（2）PC=13；拓展延伸①：证明见解析②：BD=√2【解析】解：简单应用：（1）如图2，∵△ABC是等腰直角三角形，∴∠ACB＝90°，AC＝BC，将△ACP绕点C逆时针旋转90°得到△CBP'，连接PP'，∴BP'＝AP＝5，∠PCP'＝90°，CP'＝CP＝2√2，∴∠CPP'＝∠CP'P＝45°，根据勾股定理得，PP'=√2CP＝4，∵BP'＝5，BP＝3，∴PP'2+BP2＝BP'，∴△BPP'是以BP'为斜边的直角三角形，∴∠BPP'＝90°，∴∠BPC＝∠BPP'+∠CPP'＝135°，（2）如图3，∵△ABC是等边三角形，∴∠BAC＝60°，AC＝AB，将△ACP绕点A逆时针旋转60°得到△ABP'，连接PP'，∴BP'＝CP，AP'＝AP＝5，∠PAP'＝60°，∴△APP'是等边三角形，∴PP'＝AP＝5，∠APP'＝60°，∵∠APB＝150°，∴∠BPP'＝∠APB﹣∠APP'＝90根据勾股定理得，BP'=√BP2+PP′2=13，∴CP＝13，拓展廷伸：①如图4，在△ABC中，∠ABC＝90°，AB＝BC，将△ABD绕点B顺时针旋转90°得到△BCD'，∴BD'＝BD，CD'＝AD，∠BCD'＝∠BAD，∵∠ABC＝∠ADC＝90°，∴∠BAD+∠BCD＝180°，∴∠BCD+∠BCD'＝180°，∴点D'在DC的延长线上，∴DD'＝CD+CD'＝CD+AD，在Rt△DBD'中，DD'=√2BD，∴√2BD＝CD+AD；②如图5，在△ABC中，∠ABC＝90°，AB＝BC，将△CBD绕点B顺时针旋转90°得到△ABD'，∴BD'＝BD，CD＝AD'，∠DBD'＝90°，∠BCD＝∠BAD'，AB与CD的交点记作G，∵∠ADC＝∠ABC＝90°，∴∠DAB+∠AGD＝∠BCD+∠BGC＝180°，∵∠AGD＝∠BGC，∴∠BAD＝∠BCD，∴∠BAD＝∠BAD'，∴点D'在AD的延长线上，∴DD'＝AD'﹣AD＝CD﹣AD＝2，在Rt△BDD'中，BD=√22DD'=√2．【练1】如图，在等边△ABC中，点D为△ABC内的一点，∠ADB＝120°，∠ADC＝90°，将△ABD绕点A逆时针旋转60°得△ACE，连接DE．（1）求证：AD＝DE；（2）求∠DCE的度数；（3）若BD＝1，求AD，CD的长．【答案】（1）见解析（2）90°（3）√3【解析】（1）证明：∵将△ABD绕点A逆时针旋转60°得△ACE∴△ABD≌△ACE，∠BAC＝∠DAE，∴AD＝AE，BD＝CE，∠AEC＝∠ADB＝120°，∵△ABC为等边三角形∴∠BAC＝60°∴∠DAE＝60°∴△ADE为等边三角形，∴AD＝DE，（2）∠ADC＝90°，∠AEC＝120°，∠DAE＝60°∴∠DCE＝360°﹣∠ADC﹣∠AEC﹣∠DAE＝90°，（3）∵△ADE为等边三角形∴∠ADE＝60°∴∠CDE＝∠ADC﹣∠ADE＝30°又∵∠DCE＝90°∴DE＝2CE＝2BD＝2，∴AD＝DE＝2在Rt△DCE中，DC=√DE2−CE2=√22−12=√3．【练2】如图，四边形ABCD中，∠ABC＝∠ADC＝45°，将△BCD绕点C顺时针旋转一定角度后，点B的对应点恰好与点A重合，得到△ACE．（1）请求出旋转角的度数；（2）请判断AE与BD的位置关系，并说明理由；（3）若AD＝2，CD＝3，试求出四边形ABCD的对角线BD的长．【答案】（1）90°（2）证明见解析（3）BD=√22【解析】解：（1）∵将△BCD绕点C顺时针旋转得到△ACE ∴△BCD'≌△ACE∴AC＝BC，又∵∠ABC＝45°，∴∠ABC＝∠BAC＝45°∴∠ACB＝90°故旋转角的度数为90°（2）AE⊥BD．理由如下：在Rt△BCM中，∠BCM＝90°∴∠MBC+∠BMC＝90°∵△BCD'≌△ACE∴∠DBC＝∠EAC即∠MBC＝∠NAM又∵∠BMC＝∠AMN∴∠AMN+∠CAE＝90°∴∠AND＝90°∴AE⊥BD（3）如图，连接DE，由旋转图形的性质可知CD＝CE，BD＝AE，旋转角∠DCE＝90°∴∠EDC＝∠CED＝45°∵CD＝3，∴CE＝3在Rt△DCE中，∠DCE＝90°∴DE=√CD2+CE2=√9+9=3√2∵∠ADC＝45°∴∠ADE＝∠ADC+∠EDC＝90°在Rt△ADE中，∠ADE＝90°∴EA=√AD2+DE2=√18+4=√22∴BD=√22【练3】如图1，已知：已知：等边△ABC，点D是边BC上一点（点D不与点B、点C重合），求证：BD+DC＞AD．下面的证法供你参考：把△ACD绕点A顺时针旋转60°得到△ABE，连接ED，则有△ACD≌△ABE，DC＝EB，∵AD ＝AE，∠DAE＝60°，∴△ADE是等边三角形，∴AD＝DE．在△DBE中，BD+EB＞DE，即：BD+DC＞AD实践探索：（1）请你仿照上面的思路，探索解决下面的问题：如图3，点D是等腰直角三角形△ABC边上的点（点D不与B、C重合）．求证：BD+DC＞√2AD．（2）如果点D运动到等腰直角三角形△ABC外或内时，BD、DC和AD之间又存在怎样的数量关系？直接写出结论．创新应用：（3）已知：如图4，等腰△ABC中，AB＝AC，且∠BAC＝α（α为钝角），D是等腰△ABC外一点，且∠BDC+∠BAC＝180°，BD、DC与AD之间存在怎样的数量关系？写出你的猜想，并证明．【答案】（1）证明见解析（2）BD+DC≥√2AD；（3）猜想：BD+DC＜2AD；证明见解析【解析】解：（1）证明：把△ACD绕点A顺时针旋转90°得到△ABE，连接ED则有△ACD≌△ABE，DC＝EB∵AD＝AE，∠DAE＝90°∴△ADE是等腰直角三角形∴DE=√2AD在△DBE中，BD+EB＞DE，即：BD+DC＞√2AD；（2）把△ABD旋转，使AB与AC AC旋转，得到△ACD′，则BD＝CD′，在△CDD′中，CD+CD′＞DD′，即BD+CD＞DD′，∵△ADD′是钝角三角形，则DD′＞√2AD当D运动到B的位置时，DD′＝BC=√2AD．∴BD+DC≥√2AD；（3）猜想1：BD+DC＜2AD证明：把△ACD绕点A顺时针旋转α，得到△ABE则有△ACD≌△ABE，DC＝EB，∠ACD＝∠ABE∵∠BAC+∠BDC＝180°∴∠ABD+∠ACD＝180°∴∠ABD+∠ABE＝180°即：E、B、D三点共线．∴在△ADE中，AE+AD＞ED，即BD+DC＜2AD．【题型三：旋转与相似三角形的构造】【例】如图，在矩形ABCD中，E是AD边的中点，BE⊥AC于点F，连接DF，给出下列四个结论：①△AEF∽△CAB；②CF＝2AF；③DF＝DC；④S△ABF：S四边形CDEF＝2：5，其中正确的结论有（）A．1个B．2个C．3个D．4个【答案】D【解析】解：如图，过D作DM∥BE交AC于N，∵四边形ABCD是矩形，∴AD∥BC，∠ABC＝90°，AD＝BC，∵BE⊥AC于点F，∴∠EAC＝∠ACB，∠ABC＝∠AFE＝90°，∴△AEF∽△CAB，故①正确；∴△AEF ∽△CBF ，∴AE BC ＝AF CF ，∵AE ＝12AD ＝12BC ，∴AF CF ＝12，∴CF ＝2AF ，故②正确，∵DE ∥BM ，BE ∥DM ，∴四边形BMDE 是平行四边形，∴BM ＝DE ＝12BC ，∴BM ＝CM ，∴CN ＝NF ，∵BE ⊥AC 于点F ，DM ∥BE ，∴DN ⊥CF ，∴DF ＝DC ，故③正确；∵△AEF ∽△CBF ，∴EF BF ＝AE BC ＝12，∴S △AEF ＝12S △ABF ，S △ABF ＝16S 矩形ABCD ，∴S △AEF ＝112S 矩形ABCD ，又∵S 四边形CDEF ＝S △ACD ﹣S △AEF ＝12S 矩形ABCD ﹣112S 矩形ABCD ＝512S 矩形ABCD ，∴S △ABF ：S 四边形CDEF ＝2：5，故④正确；【练1】如图，正方形ABCD 的边长为8，线段CE 绕着点C 逆时针方向旋转，且CE =3，连接BE ，以BE 为边作正方形BEFG ，M 为AB FM 的长最小时，tan ∠ECB =______．【答案】13【解析】解：连接BD ，BF ，FD ，如图，∵BD BC =BF BE =√2，∴BD BF =BC BE ，∵∠FBD+∠DBE=45°，∠EBC+∠DBE=45°，∴∠FBD=∠EBC，∴△EBC∽△FBD，∴∠FDB=∠ECB，DFCE =BDBC=√2，∴DF=√2CE=3√2，由题意知：FM、DF、DM三条线段满足FM+DF≥MD，其中DM、DF的值一定，∴当M，F，D三点一线时，FM最小，过点M作MN⊥BD，垂足为G，∵∠MBN=45°，BM=12AB=4，∴MN=BN=2√2，∵MD=√AM2+AD2=√42+82=4√5，∴DG=√MD2−MG2=√(4√5)2−(2√2)2=6√2，∴tan∠ECB=tan∠FDG=MGDG =√26√2=13，故答案为：13．【练2】如图，在△ABC中，AB＝5，D为边AB上－动点，以CD为一边作正方形CDEF，当点D从点B运动到点A时，点E运动的路径长为_________．【答案】5√2【解析】解：如图，作GB⊥BC于B，取GB=BC，当点D与点B重合时，则点E与点G重合，∴∠CBG=90°，∴CG=√2BC，∠GCB=45°，∵四边形CDEF是正方形，∴CE=√2DC，∠ECD=45°，∴∠BCD+∠DCG =∠GCE+∠DCG =45°，∴∠BCD =∠GCE，且CGBC =CEDC=√2，∴△CGE∽△CBD，∴GEBD =CEDC=√2，即GE=√2BD，∵BD=5，∴点E运动的路径长为GE=√2BD=5√2．【练3】在△ABC和△ADE中，BA=BC，DA=DE，且∠ABC=∠ADE=α，点E在△ABC的内部，连接EC，EB，EA和BD，并且∠ACE+∠ABE=90°．（观察猜想）（1）如图①，当α=60°时，线段BD与CE的数量关系为__________，线段EA，EB，EC的数量关系为__________．（探究证明）（2）如图②，当α=90°时，（1）中的结论是否依然成立？若成立，请给出证明，若不成立，请说明理由；（拓展应用）（3）在（2）的条件下，当点E在线段CD上时，若BC=2√5，请直接写出△BDE的面积．【答案】（1）BD=CE，EB2+EC2=EA2；（2）不成立，理由见解析；（3）2【解析】（1）如图①中，∵BA=BC，DA=DE．且∠ABC=∠ADE=60°，∴△ABC，△ADE都是等边三角形，∴AD=AE，AB=AC，∠DAE=∠BAC=60°，∴∠DAB=∠EAC，∴△DAB≌△EAC（SAS），∴BD=EC，∠ABD=∠ACE，∵∠ACE+∠ABE=90°，∴∠ABD+∠ABE=90°，∴∠DBE=90°，∴DE2=BD2+BE2，∵EA=DE，BD=EC，∴EA2=BE2+EC2．故答案为：BD=EC，EA2=EB2+EC2．（2）结论：EA2=EC2+2BE2．理由：如图②中，∵BA =BC ，DA =DE ．且∠ABC =∠ADE =90°， ∴△ABC ，△ADE 都是等腰直角三角形， ∴∠DAE =∠BAC =45°，∴∠DAB =∠EAC ， ∵AD AE =√22，AB AC =√22， ∴AD AE =ABAC ，∴△DAB ∽△EAC ，∴DB EC =AB AC =√22，∠ACE =∠ABD ， ∵∠ACE +∠ABE =90°，∴∠ABD +∠ABE =90°，∴∠DBE =90°，∴DE 2=BD 2+BE 2，∵EA =√2DE ，BD =√22EC ， ∴12EA 2=12EC 2+BE 2，∴EA 2=EC 2+2BE 2．（3）如图③中，∵∠AED =45°，D ，E ，C 共线， ∴∠AEC =135°，∵△ADB ∽△AEC ，∴∠ADB =∠AEC =135°，∵∠ADE =∠DBE =90°，∴∠BDE =∠BED =45°，∴BD =BE ，∴DE =√2BD ，∵EC =√2BD ，∴AD =DE =EC ，设AD =DE =EC =x ，在Rt△ABC中，∵AB=BC=2√5，∴AC=2√10，在Rt△ADC中，∵AD2+DC2=AC2，∴x2+4x2=40，∴x=2√2（负根已经舍弃），∴AD=DE=2√2，∴BD=BE=2，×2×2=2．∴S△BDE=12。
中考数学第四章 三角形 重难 微专项3 全等三角形中常用的辅助线技巧
= ,
在△ACD和△AED中,ቐ ∠1 = ∠2,
= ,
∴△ACD≌△AED,
∴∠AED=∠C=90°,CD=ED.
重难·微专项3 全等三角形中常用的辅助线技巧
例题
又AC=BC,∴∠B=45°,∴∠EDB=∠B=45°,
∴DE=BE,∴CD=BE.
∴∠DBE=60°,
1
∴BD= BE,
2
∴TF=2BD,即BF-AB=2BD.
重难·微专项3 全等三角形中常用的辅助线技巧
突破点2 旋转
运用旋转的全等变换,可以把分散的条件集中到一个三角形中.
模型1
绕定点旋转60°,构造全等三角形
如图,△ABC为等边三角形,点P在△ABC内,将△ABP绕点A逆时针旋转
明剩下的线段等于另一条短线段.
补短法:延长短线段,使其延长部分等于另一条短线段,然后证明延长
后的线段等于长线段(或延长短线段,使延长后的线段等于长线段,然
后证明延长部分等于另一条短线段).
重难·微专项3 全等三角形中常用的辅助线技巧
例题
例1
如图,在Rt△ABC中,∠C=90°,BC=AC,AD平分∠BAC交BC于点D.
60°,得到△ACP',则△ABP≌△ACP',且△APP'为等边三角形.
重难·微专项3 全等三角形中常用的辅助线技巧
例题
例2
如图,在四边形ABCD中,AB=BC,∠ABC=60°,∠ADC=30°,则线段
AD,CD和BD之间的数量关系为 AD2+CD2=BD2 .
重难·微专项3 全等三角形中常用的辅助线技巧
∵BA=BT,∠ABT=60°,
中考数学专题复习全等三角形之辅助线补全图形法
中考数学专题复习全等三角形（辅助线补全图形法）学校:___________姓名：___________班级：___________考号：___________评卷人得分一、解答题1．如图，ABC中，AC＝BC，∠ACB＝90°，AD平分∠BAC交BC于点D，过点B作BE∠AD，交AD延长线于点E，F为AB的中点，连接CF，交AD于点G，连接BG．（1）线段BE与线段AD有何数量关系？并说明理由；（2）判断BEG的形状，并说明理由．2．如图1，在平面直角坐标系中，直线AB分别交x轴、y轴于(,0) ,(0,)A aB b两点，且,a b满足2()|4|0a b a t，且0,t t>是常数，直线BD平分OBA∠，交x轴于点D．（1）若AB的中点为M，连接OM交BD于点N，求证：ON OD=；（2）如图2，过点A作AE BD⊥，垂足为E，猜想AE与BD间的数量关系，并证明你的猜想．3．如图，在△ABC中，点D为边BC的中点，点E在△ABC内，AE平分∠BAC，CE∠AE点F在AB上，且BF=DE（1）求证：四边形BDEF是平行四边形（2）线段AB，BF，AC之间具有怎样的数量关系？证明你所得到的结论4．已知，如图ABC∆中，AB AC=，90A∠=︒，ACB∠的平分线CD交AB于点E，90BDC∠=︒，求证：2CE BD=.5．在∠ABC 中，AB=AC ，将线段AC 绕着点C 逆时针旋转得到线段CD ，旋转角为α，且0180α<<，连接AD 、BD ． （1）如图1，当∠BAC=100°，60α=时，∠CBD 的大小为_________； （2）如图2，当∠BAC=100°，20α=时，求∠CBD 的大小；（3）已知∠BAC 的大小为m （60120m <<），若∠CBD 的大小与（2）中的结果相同，请直接写出α的大小．6．（1）阅读理解：问题：如图1，在四边形ABCD 中，对角线BD 平分ABC ∠，180A C ∠+∠=︒．求证：DA DC =． 思考：“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题．方法1：在BC 上截取BM BA =，连接DM ，得到全等三角形，进而解决问题； 方法2：延长BA 到点N ，使得BN BC =，连接DN ，得到全等三角形，进而解决问题．结合图1，在方法1和方法2中任选一种．．．．，添加辅助线并完成证明． （2）问题解决：如图2，在（1）的条件下，连接AC ，当60DAC ∠=︒时，探究线段AB ，BC ，BD 之间的数量关系，并说明理由；（3）问题拓展：如图3，在四边形ABCD 中，180A C ∠+∠=︒，DA DC =，过点D 作DE BC ⊥，垂足为点E ，请直接写出线段AB 、CE 、BC 之间的数量关系．参考答案：1．（1）BE ＝12AD ，见解析；（2）BEG 是等腰直角三角形，见解析【解析】【分析】（1）延长BE 、AC 交于点H ，先证明△BAE ∠∠HAE ，得BE ＝HE ＝12BH ，再证明△BCH ∠∠ACD ，得BH ＝AD ，则BE ＝12AD ；（2）先证明CF 垂直平分AB ，则AG ＝BG ，再证明∠CAB ＝∠CBA ＝45°，则∠GAB ＝∠GBA ＝22.5°，于是∠EGB ＝∠GAB +∠GBA ＝45°，可证明△BEG 是等腰直角三角形．【详解】证：（1）BE ＝12AD ，理由如下：如图，延长BE 、AC 交于点H ，∠BE ∠AD ，∠∠AEB ＝∠AEH ＝90°，∠AD 平分∠BAC ，∠∠BAE ＝∠HAE ，在△BAE 和△HAE 中，AEB AEH AE AEBAE HAE ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∠∠BAE ∠∠HAE （ASA ），∠BE ＝HE ＝12BH ，∠∠ACB ＝90°，∠∠BCH ＝180°﹣∠ACB ＝90°＝∠ACD ，∠∠CBH ＝90°﹣∠H ＝∠CAD ，在△BCH 和△ACD 中，BCH ACD BC ACCBH CAD ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∠∠BCH ∠∠ACD （ASA ），∠BH ＝AD ，∠BE ＝12AD ． （2）△BEG 是等腰直角三角形，理由如下：∠AC ＝BC ，AF ＝BF ，∠CF ∠AB ，∠AG ＝BG ，∠∠GAB ＝∠GBA ，∠AC ＝BC ，∠ACB ＝90°，∠∠CAB ＝∠CBA ＝45°，∠∠GAB ＝12∠CAB ＝22.5°，∠∠GAB ＝∠GBA ＝22.5°， ∠∠EGB ＝∠GAB +∠GBA ＝45°，∠∠BEG ＝90°，∠∠EBG ＝∠EGB ＝45°，∠EG ＝EB ，∠∠BEG 是等腰直角三角形．【点睛】本题考查等腰直角三角形的判定与性质，全等三角形的判定与性质等，理解等腰直角三角形的基本性质，并且掌握全等三角形中常见辅助线的作法是解题关键．2．（1）见解析；（2）2BD AE =,证明见解析．【解析】【分析】（1）由已知条件可得AO BO =，进而得OBA OAB ∠=∠，由直线BD 平分OBA ∠及直角三角形斜边上中线的性质得BOM OAB ∠=∠，再由三角形的外角定理，分别求得,ODN OND ∠∠，根据角度的等量代换，即可得ODN OND ∠=∠，最后由等角对等边的性质即可得证；（2）如图，延长AE 交y 轴于点C ，先证明BCE BAE △≌△，得AE EC =，再证明DOB COA ∠≌△，即可得2BD AC AE ==．【详解】（1）2()|4|0a b a t ，4a b t ∴==，AO BO ∴=，∴OBA OAB ∠=∠，直线BD 平分OBA ∠，ABD OBD ∴∠=∠，M 为AB 的中点，∴12OM AB BM AM ===， BOM OBA ∴∠=∠，OBA OAB ∠=∠，BOM OAB ∴∠=∠，OND OBD BOM ∠=∠+∠，ODN OAB ABD ∠=∠+∠，OND ODN ∴∠=∠，ON OD ∴=． （2）2BD AE =，证明：如图，延长AE 交y 轴于点C ，直线BD 平分OBA ∠，AE BD ⊥，ABD OBD ∴∠=∠，AEB CEB ∠=∠，又BE BE =，∴BCE BAE △≌△（ASA ），∴AE CE =1=2AC ， AO BC ⊥，∴DOB COA ∠=∠，即90OAC OCA OCA CBE ∠+∠=∠+∠=︒， OAC OBD ∴∠=∠，又OB OA =，∴DOB COA ∠≌△（ASA ），2BD AC AE ∴==，即2BD AE =．【点睛】本题考查了平面直角坐标系的定义，非负数之和为零，三角形角平分线的定义，三角形中线的性质，三角形外角定理，三角形全等的性质与判定，等角对等边，熟练掌握以上知识，添加辅助线是解题的关键．3．（1）见解析；（2）1()2BF AB AC =-，理由见解析 【解析】【分析】（1）延长CE交AB于点G，证明AEG∆≅AEC∆，得E为中点，通过中位线证明DE// AB，结合BF=DE，证明BDEF是平行四边形（2）通过BDEF为平行四边形，证得BF=DE=12BG，再根据AEG∆≅AEC∆，得AC=AG，用AB-AG=BG，可证1()2BF AB AC=-【详解】（1）证明：延长CE交AB于点G∠AE⊥CE∠90AEG AEC︒∠=∠=在AEG∆和AEC∆GAE CAEAE AEAEG AEC∠=∠⎧⎪=⎨⎪∠=∠⎩∠AEG∆≅AEC∆∠GE=EC∠BD=CD∠DE为CGB∆的中位线∠DE//AB∠DE=BF∠四边形BDEF是平行四边形（2）1()2BF AB AC=-理由如下：∠四边形BDEF是平行四边形∠BF=DE∠D，E分别是BC，GC的中点∠BF=DE=12BG∠AEG∆≅AEC∆∠AG=ACBF=12（AB-AG）=12（AB-AC）．【点睛】本题主要考查了平行四边形的证明，中位线的性质，全等三角形的证明等综合性内容，作好适当的辅助线，是解题的关键．4．见解析.【解析】【分析】延长BD交CA的延长线于F，先证得∠ACE∠∠ABF，得出CE=BF；再证∠CBD∠∠CFD，得出BD=DF；由此得出结论即可．【详解】证明：如图，延长BD交CA的延长线于F，90BAC︒∠=90,90BAF BAC ACE AEC︒︒∴∠=∠=∠+∠=90BDC︒∠=90BDC FDC︒∴∠=∠=90ABF BED︒∴∠+∠=AEC BED∠=∠ACE ABF∴∠=∠AB AC=()ACE ABF ASA∴∆∆≌CE BF ∴=CD 平分ACB ∠ACD BCD ∴∠=∠CD CD =()CBD CFD ASA ∴∆∆≌12BD FD BF ∴== 12BD CE ∴= 2CE BD ∴=【点睛】此题考查三角形全等的判定与性质，角平分线的性质，根据已知条件，作出辅助线是解决问题的关键．5．（1）30°；（2）30°；（3）α为60︒或120m ︒-或240m ︒-．【解析】【分析】（1）由100BAC ∠=︒，AB AC =，可以确定40ABC ACB ∠=∠=︒，旋转角为α，60α=︒时ACD ∆是等边三角形，且AC AD AB CD ===，知道BAD ∠的度数，进而求得CBD ∠的大小；（2）由100BAC ∠=︒，AB AC =，可以确定40ABC ACB ∠=∠=︒，连接DF 、BF ．AF FC AC ==，60FAC AFC ∠=∠=︒，20ACD ∠=︒，由20DCB ∠=︒案．依次证明DCB FCB ∆≅∆，DAB DAF ∆≅∆．利用角度相等可以得到答案．（3）结合（1）（2）的解题过程可以发现规律，ACD ∆是等边三角形时，CD 在ABC ∆内部时，CD 在ABC ∆外部时，求得答案．【详解】解：（1）解（1）∠AB AC =，100BAC ∠=︒，∠40ABC ∠=︒，∠AC CD =，60ACD α=∠=︒，∠ACD △为等边三角形，∠40BAD BAC DAC ∠=∠-∠=︒．又∠AD AC AB ==，∠ABD △为等腰三角形，∠180702BAD ABD ︒-∠∠==︒， ∠30CBD ABD ABC ∠=∠-∠=︒．（2）方法1：如图作等边AFC △，连接DF 、BF ．AF FC AC ∴==，60FAC AFC ∠=∠=︒．100BAC ∠=︒，AB AC =，40ABC BCA ∴∠=∠=︒．20ACD ∠=︒，20DCB ∴∠=︒．20DCB FCB ∴∠=∠=︒．∠AC CD =，AC FC =，DC FC ∴=．∠ BC BC =，∠∴由∠∠∠，得DCB FCB ≅，DB BF ∴=，DBC FBC ∠=∠．100BAC ∠=︒，60FAC ∠=︒，40BAF ∴∠=︒．20ACD ∠=︒，AC CD =，80CAD ∴∠=︒．20DAF ∴∠=︒．20BAD FAD ∴∠=∠=︒．∠AB AC =，AC AF =，AB AF ∴=．∠AD AD =，∠∴由∠∠∠，得DAB DAF ≅．FD BD ∴=．FD BD FB ∴==．60DBF ∴∠=︒．30CBD ∴∠=︒．方法2 如下图所示，构造等边三角形ADE ，连接CE ．∠在等腰三角形ACD 中，20ACD ∠=︒，∠80CAD CDA ∠=∠=︒，∠100BAC ∠=︒，∠20BAD ∠=︒．可证ACE DCE ≌．结合角度，可得20CAE CDE ∠=∠=︒，10ACE DCE ∠=∠=︒．在ADB △和ACE 中，20AB AC BAD CAE AD AE =⎧⎪∠=∠=︒⎨⎪=⎩，∠△≌△ADB AEC ，∠10ABD ACE ∠=∠=︒．∠40ABC ∠=︒，∠30CBD ABC ABD ∠=∠-∠=︒．方法3 如下图所示，平移CD 至AE ，连接ED ，EB ，则四边形ACDE 是平行四边形．∠AC DC =，∠四边形ACDE 是菱形，∠20AED ACD ∠=∠=︒，180EAC ACD ∠+∠=︒．∠160EAC ∠=︒，∠60EAB ∠=︒，∠ABE △是等边三角形，EBD △是等腰三角形，∠40BED ∠=︒，70EBD ∠=︒，∠10ABD ∠=︒．∠30CBD ABC ABD ∠=∠-∠=︒．（3）由（1）知道，若100BAC ∠=︒，60α=︒时，则30CBD ∠=︒；∠由（1）可知，设60α∠=︒时可得60BAD m ∠=-︒，902m ABC ACB ∠=∠=︒-， 19012022m ABD BAD ∠=︒-∠=︒-， 30CBD ABD ABC ∠=∠-∠=︒．∠由（2）可知，翻折BDC ∆到△1BD C ，则此时130CBD ∠=︒，60302m BCD ACB ∠=︒-∠=-︒， 190(30)12022m m ACB BCD ACB BCD m α∠=∠-∠=∠-∠=︒---︒=︒-， ∠以C 为圆心CD 为半径画圆弧交BD 的延长线于点2D ，连接2CD ，2303022m m CDD CBD BCD ∠=∠+∠=︒+-︒=， 221802180DCD CDD m ∠=︒-∠=︒-260240DCD m α∠=︒+∠=︒-．综上所述，α为60︒或120m ︒-或240m ︒-时，30CBD ∠=︒．【点睛】本题是一道几何结论探究题，解答这类题目的关键是要善于从探究特殊结论中归纳出一般性解题方法，并灵活运用这种方法解答一般性的问题，真正达到举一反三的目的． 6．（1）证明见解析；（2）AB BC BD +=；理由见解析；（3）2BC AB CE -=．【解析】【分析】（1）方法1：在BC 上截取BM BA =，连接DM ，得到全等三角形，进而解决问题；方法2：延长BA 到点N ，使得BN BC =，连接DN ，得到全等三角形，进而解决问题； （2）延长CB 到点P ，使BP BA =，连接AP ，证明ΔΔPAC BAD ≌，可得PC BD =，即PC BP BC AB BC =+=+（3）连接BD ，过点D 作DF AC ⊥于F ，证明ΔΔDFA DEC ≌，Rt ΔRt ΔBDF BDE ≌，进而根据2BC BE CE BA AF CE BA CE =+=++=+即可得出结论．【详解】解：（1）方法1：在BC 上截BM BA =，连接DM ，如图．BD 平分ABC ∠，ABD CBD ∴∠=∠．在ΔABD 和ΔMBD 中，BD BD ABD MBD BA BM =⎧⎪∠=∠⎨⎪=⎩，ΔΔABD MBD ∴≌，A BMD ∴∠=∠，AD MD =．180BMD CMD ︒∠+∠=，180C A ︒∠+∠=．C CMD ∴∠=∠．DM DC ∴=，DA DC ∴=．方法2：延长BA 到点N ，使得BN BC =，连接DN ，如图．BD平分ABC∠，NBD CBD∴∠=∠．在ΔNBD和ΔCBD中，BD BDNBD CBDBN BC=⎧⎪∠=∠⎨⎪=⎩，ΔΔNBD CBD∴≌．BND C∴∠=∠，ND CD=．180NAD BAD︒∠+∠=，180C BAD︒∠+∠=．BND NAD∴∠=∠，DN DA∴=，DA DC∴=．（2）AB、BC、BD之间的数量关系为：AB BC BD+=．（或者：BD CB AB-=，BD AB CB-=）．延长CB到点P，使BP BA=，连接AP，如图2所示．由（1）可知AD CD =，60DAC ︒∠=．ΔADC ∴为等边三角形．AC AD ∴=，60ADC ︒∠=．180BCD BAD ︒∠+∠=，36018060120ABC ︒︒︒︒∴∠=--=．18060PBA ABC ︒︒∴∠=-∠=．BP BA =，ΔABP ∴为等边三角形．60PAB ︒∴∠=，AB AP =．60DAC ︒∠=，PAB BAC DAC BAC ∴∠+∠=∠+∠，即PAC BAD ∠=∠．在ΔPAC 和ΔBAD 中，PA BA PAC BAD AC AD =⎧⎪∠=∠⎨⎪=⎩，ΔΔPAC BAD ∴≌． PC BD ∴=， PC BP BC AB BC =+=+，AB BC BD ∴+=．（3）AB ，CE ，BC 之间的数量关系为：2BC AB CE -=．（或者：2BC CE AB -=，2AB CE BC +=）解：连接BD ，过点D 作DF AC⊥于F ，如图3所示．180BAD C ︒∠+∠=，180BAD FAD ︒∠+∠=．FAD C ∴∠=∠．在ΔDFA 和ΔDEC 中，DFA DEC FAD C DA DC ∠=∠⎧⎪∠=∠⎨⎪=⎩，ΔΔDFA DEC ∴≌，DF DE ∴=，AF CE =．在Rt ΔBDF 和Rt ΔBDE 中，BD BD DF DE =⎧⎨=⎩， Rt ΔRt ΔBDF BDE ∴≌．BF BE ∴=，2BC BE CE BA AF CE BA CE ∴=+=++=+，2BC BA CE ∴-=．【点睛】本题考查了三角形全等的性质与判定，正确的添加辅助线是解题的关键．。
中考数学-全等三角形问题中常见的8种辅助线的作法
全等三角形问题中常见的辅助线的作法(有答案)总论：全等三角形问题最主要的是构造全等三角形，构造二条边之间的相等，构造二个角之间的相等【三角形辅助线做法】图中有角平分线，可向两边作垂线。
也可将图对折看，对称以后关系现。
角平分线平行线，等腰三角形来添。
角平分线加垂线，三线合一试试看。
线段垂直平分线，常向两端把线连。
要证线段倍与半，延长缩短可试验。
三角形中两中点，连接则成中位线。
三角形中有中线，延长中线等中线。
1.等腰三角形“三线合一”法：遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题2.倍长中线：倍长中线，使延长线段与原中线长相等，构造全等三角形3.角平分线在三种添辅助线4.垂直平分线联结线段两端5.用“截长法”或“补短法”：遇到有二条线段长之和等于第三条线段的长，6.图形补全法：有一个角为60度或120度的把该角添线后构成等边三角形7.角度数为30、60度的作垂线法：遇到三角形中的一个角为30度或60度，可以从角一边上一点向角的另一边作垂线，目的是构成30-60-90的特殊直角三角形，然后计算边的长度与角的度数，这样可以得到在数值上相等的二条边或二个角。
从而为证明全等三角形创造边、角之间的相等条件。
8.计算数值法：遇到等腰直角三角形，正方形时，或30-60-90的特殊直角三角形，或40-60-80的特殊直角三角形,常计算边的长度与角的度数，这样可以得到在数值上相等的二条边或二个角，从而为证明全等三角形创造边、角之间的相等条件。
常见辅助线的作法有以下几种：最主要的是构造全等三角形，构造二条边之间的相等，二个角之间的相等。
1)遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变D C BAED F CB A换中的“对折”法构造全等三角形．2)遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形，利用的思维模式是全等变换中的“旋转”法构造全等三角形．3)遇到角平分线在三种添辅助线的方法，（1）可以自角平分线上的某一点向角的两边作垂线，利用的思维模式是三角形全等变换中的“对折”，所考知识点常常是角平分线的性质定理或逆定理．（2）可以在角平分线上的一点作该角平分线的垂线与角的两边相交，形成一对全等三角形。
2020--2021学年九年级数学中考二轮复习 专题 三角形辅助线作法攻略
《三角形辅助线作法攻略》➢考点考向1. 与角平分线有关的辅助线2. 与线段长度相关的辅助线3. 与等腰、等边三角形相关的辅助线4. 与中点相关的辅助线5. 构造一线三垂直（等角）6. 等面积法✧考点一：与角平分线有关的辅助线（1）可向两边作垂线。
（2）可构造等腰三角形（3）在角的两边截取相等的线段，构造全等三角形【例1】已知：∠AOB＝90°，OM是∠AOB的平分线，将三角板的直角顶点P在射线OM 上滑动，两直角边分别与OA、OB交于C、D，PC和PD有怎样的数量关系，请说明理由．【例2】如图，在△ABC中，AB＝AC，∠BAC＝90°，BD平分∠ABC交AC于D，过C作CE ⊥BD交BD延长线于E．求证：CE＝BD．【例3】如图，AC平分∠BAD，CD＝CB，AB＞AD，求证：∠B+∠D＝180°．考点二：与线段长度有关的辅助线（1）截长：证明某两条线段的和或差等于第三条线段时，经常在较长的线段上截取一段，使得它和其中的一条相等，再利用全等证明余下的等于另一条线段即可（2）补短：证明某两条线段的和或差等于第三条线段时，也可以在较短的线段上延长一段，使得延长的部分等于另外一条较短的线段，再利用全等证明延长后的线段等于那一条长线段即可（3）倍长中线：题目中如果出现了三角形的中线，方法是将中线延长一倍，再将端点连结，便可得到全等三角形。
【例4】如图，在△ABC中，AD平分∠BAC，∠C＝2∠B，求证：AB＝AC+CD．✧考点三：与等腰、等边三角形相关的辅助线（1）考虑三线合一（2）旋转一定的度数，构造全都三角形，等腰一般旋转顶角的度数，等边旋转60 °【例5】如图，在△ABC中，AC＝BC，∠C＝90°，D是AB的中点，DE⊥DF，点E，F分别在AC，BC上，求证：DE＝DF.✧考点四：与中点有关的辅助线遇到中点，考虑中位线或等腰等边中的三线合一。
【例6】如图1，在四边形ABCD中，AB＝CD，E，F分别是AD，BC的中点，连接FE并延长，分别与BA，CD的延长线交于点M，N．求证：∠BME＝∠CNE；（提示：取BD的中点H，连接FH，HE作辅助线）（2）如图2，在△ABC中，F是BC边的中点，D是AC边上一点，E是AD的中点，直线FE 交BA的延长线于点G，若AB＝DC＝2，∠FEC＝45°，求FE的长度．考点五：构造一线三垂直（等角）【例7】（1）观察猜想：如图①点B、A、C在同一条直线上，DB⊥BC，EC⊥BC且∠DAE ＝90°，AD＝AE，则BC、BD、CE之间的数量关系为；（2）问题解决：如图②，在Rt△ABC中，∠ABC＝90°，CB＝4，AB＝2，以AC为直角边向外作等腰Rt△DAC，连结BD，求BD的长；（3）拓展延伸：如图③，在四边形ABCD中，∠ABC＝∠ADC＝90°，CB＝4，AB＝2，DC＝DA，请直接写出BD的长．考点六：等面积法（1）利用连线将一个大的三角形的面积切割为几个小三角形的面积和；（2）连线后得到等底等高的三角形面积相等。
初中数学中考复习几何辅助线规律总结(共102条)
初中数学几何辅助线规律线、角、相交线、平行线【规律】1如果平面上有n(n≥2)个点，其中任何三点都不在同一直线上，那么每两点画一条直线，一共可以画出n(n－1)条。
【规律】2平面上的n条直线最多可把平面分成〔n(n+1)+1〕个部分。
【规律】3如果一条直线上有n个点，那么在这个图形中共有线段的条数为n(n－1)条。
【规律】4线段（或延长线）上任一点分线段为两段，这两条线段的中点的距离等于线段长的一半。
【规律】5有公共端点的n条射线所构成的交点的个数一共有n(n－1)个。
【规律】6如果平面内有n条直线都经过同一点，则可构成小于平角的角共有2n（n－1）个。
【规律】7如果平面内有n条直线都经过同一点，则可构成n（n－1）对对顶角。
【规律】8平面上若有n（n≥3）个点，任意三个点不在同一直线上，过任意三点作三角形一共可作出n(n－1)(n－2）个。
【规律】9互为邻补角的两个角平分线所成的角的度数为90°。
【规律】10平面上有n条直线相交，最多交点的个数为n(n－1)个。
【规律】11互为补角中较小角的余角等于这两个互为补角的角的差的一半。
【规律】12当两直线平行时，同位角的角平分线互相平行，内错角的角平分线互相平行，同旁内角的角平分线互相垂直。
【规律】13已知AB∥DE,如图⑴～⑹,规律如下：【规律】14成“8”字形的两个三角形的一对内角平分线相交所成的角等于另两个内角和的一半。
三角形部分【规律】15在利用三角形三边关系证明线段不等关系时，如果直接证不出来，可连结两点或延长某边构造三角形，使结论中出现的线段在一个或几个三角形中，再利用三边关系定理及不等式性质证题。
注意：利用三角形三边关系定理及推论证题时，常通过引辅助线，把求证的量（或与求证有关的量）移到同一个或几个三角形中去然后再证题。
【规律】16三角形的一个内角平分线与一个外角平分线相交所成的锐角，等于第三个内角的一半。
【规律】17三角形的两个内角平分线相交所成的钝角等于90o加上第三个内角的一半。
中考数学总复习《构造三角形中位线模型解题》专项提升练习题(附答案)
中考数学总复习《构造三角形中位线模型解题》专项提升练习题(附答案)学校:___________班级：___________姓名：___________考号：___________一、三角形中位线的概念和性质1.连接三角形两边中点的线段叫做三角形的中位线2.三角形中位线定理：三角形的中位线平行于第三遍，且等于第三边的一半3.隐含中点的条件：等腰三角形三线合一（顶角的角平分线底边的中垂线），平行四边形对角线的交点。
例1.如图,点D、E分别为△ABC的边AB、AC的中点,点F在DE的延长线上,CF∥BA,若BC=8,则EF=( ) A.4 B.8 C.5 D.3例2.如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠EPF=136°,则∠EFP的度数是( ) A.68° B.34° C.22° D.44°二、连接两点构造三角形的中位线例3.如图,在四边形ABCD中,∠A=90°,AB=12,AD=5.点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF的最大值是.4例4.如图1,已知点E ,F ,G ,H 分别是四边形ABCD 的边AB ,BC ,CD ,DA 的中点,根据以下思路可以证明四边形EFGH 是平行四边形:如图2,将图1中的点C 移动至与点E 重合的位置,F ,G ,H 仍是BC ,CD ,DA 的中点,求证:四边形CFGH 是平行四边形.三．已知角平分线+垂直构造中位线例5．如图，AD 为ABC 中BAC ∠的外角平分线，BD AD ⊥于D ，E 为BC 中点5DE =，3AC =则AB 长为（ ）A ．8.5B ．8C ．7.5D ．7例6.如图,在△ABC 中,∠ABC =90°,在边AC 上截取AD =AB ,连接BD ,过点A 作AE ⊥BD 于点E ,F 是边BC 的中点,连接EF.若AB =5,BC =12,求EF 的长度.例7.如图,在△ABC中,已知AB＝6,AC＝10,AD平分∠BAC,BD⊥AD于点D,点E为BC的中点,求DE的长.四．倍长法构造三角形的中位线例8.如图,在△ABC中,∠ABC＝90°,BA＝BC,△BEF为等腰直角三角形,∠BEF＝90°,M为AF的中点.求证ME＝12CF.例9.如图,在△ABC中,∠ABC＝90°,AB＝BC,BD⊥AC于点D,CE平分∠ACB,交AB于点E,交BD于点F.求证:(1)△BEF是等腰三角形；(2)BD＝12(BC＋BF)．五．已知一边中点,取另一边中点构造三角形的中位线例10.如图,四边形ABCD中,点E,F分别是边AB,CD的中点,且AD=6,BC=10,则线段EF的长可能为( )A.7B.8.5C.9D.10六．已知两边中点,取第三边中点构造三角形的中位线例11.如图，菱形ABCD 的对角线AC BD ，相交于点O ．E ，F 分别是AD OC ，的中点，若1207BAD EF ∠=︒=，ABCD 的周长为（ ）A ．8B ．16C ．3D ．3例12.如图，已知四边形ABCD 中AC BD ⊥，AC=6，8BD =点E 、F 分别是边AD 、BC 的中点，连接EF ，则EF 的长是 __．强化训练题一．选择题1．如图 在△ABC 中 AB ＝4 BC ＝5 AC ＝8．点D E F 分别是相应边上的中点 则四边形DFEB 的周长等于（ ）A ．8B ．9C ．12D ．132．如图 △ABC 中 AB ＝AC ＝12 BC ＝10 AD 平分∠BAC 交BC 于点D 点E 为AC 的中点 连接DE 则△CDE 的周长为（ ）A ．11B ．17C ．18D ．163．如图 在ABC 中 45B ∠=︒ 60C ∠=︒ AD BC ⊥于点D 6BD = 若E F 分别为AB BC 的中点 则EF 的长为（ ）A 2B 6C 6D 34．如图 ABCD 的对角线AC BD 交于点O AE 平分BAD ∠交BC 于点E且60ADC ∠=︒ 12AB BC = 连接OE ．下列结论中不成立的是( )A ．30CAD ∠=︒B ．ABCD S AB AC =⋅ C ．OB AB =D ．14OE BC =5．如图 四边形ABCD 中 ∠B ＝90° AB ＝8 BC ＝6 点M 是对角线AC 的中点 点N 是AD 边的中点 连结BM MN 若BM ＝3MN 则线段CD 的长是（ ）A ．53B ．3C ．103D ．56．已知三角形三边长分别为7cm 8cm 9cm 作三条中位线组成一个新的三角形 同样方法作下去 一共做了五个新的三角形 则这五个新三角形的周长之和为（ ）A ．46.5cmB ．22.5cmC ．23.25cmD ．以上都不对7．如图 在ABC 中 AE 平分BAC ∠ BE AE ⊥于点E 点F 是BC 的中点 若10AB = 6AC = 则EF 的长为（ ）A ．2B ．3C ．4D ．58.如图 在四边形ABCD 中 点E F 分别为AD DC 的中点 连接EB BF EF △EBF 的面积为 S 1 ．点G 为四边形ABCD 外一点 连接AG BG EG FG 使得AG ＝BC ∠GAB ＝∠ABC △EGF 的面积为 S 2 则 S 1 与 S 2 满足的关系是（ ）A ．S 1 = S 2B ．2 S 1 =3 S 2C ．3 S 1 =4 S 2D ．3 S 1 =2 S 29．如图 平行四边形ABCD 中 O 为对角线交点 DP 平分ADC ∠ CP 平分BCD ∠ 7AB = 10AD = 则OP 的长为（ ）A ．1.5B ．2C ．2.5D ．310.如图 ▱ABCD 的顶点A D 分别在直角∠MON 的两边OM ON 上运 动（不与点O 重合） ▱ABCD 的对角线AC BD 相交于点P 连接OP 若OP=5 则▱ABCD 的周长最小值是（ ）A ．20B ．25C ．10D ．15二 填空题11.如图 在平行四边形ABCD 中 E 是CD 的中点 F 是AE 的中点 CF 交BE 于点G 若BE ＝8 则GE ＝ ．12．如图 DE 为△ABC 的中位线 点F 在DE 上 且∠AFC 为直角 若AC ＝6cm BC ＝8cm 则DF 的长为 ．13.如图已知三角形纸片ABC第1次折叠使点B落在BC边上的点B'处折痕AD交BC于点D；第2次折叠使点A落在点D处折痕MN交AB'于点P．若12BC=则MP与MN的和是_________．14．如图在▱ABCD中AC是对角线∠ACD=90°点E是BC的中点AF平分∠BAC CF⊥AF于点F连接EF.已知AB=5BC=13则EF的长为.15．如图在Rt△ABC中∠ACB＝90°AC＝BC＝6 点D是AC边上的一点且AD＝2 以AD为直角边作等腰直角三角形ADE连接BE并取BE的中点F连接CF则CF的长为．16．如图 EF是△ABC的中位线 O是EF上一点且满足OE=2OF.则△ABC的面积与△AOC的面积之比为．17．如图□ABCD的顶点C在等边△BEF的边BF上点E在AB的延长线上 G为DE的中点连接CG．若AD=5 AB=CF=3 则CG的长为．三．解答题18.如图△ABC的中线BE CF相交于G且AB＝12 AC＝16 BC＝20 求GC的长．19．如图在平行四边形ABCD中对角线AC BD、相交于点O点E是边BC中点连接OE并延长至点F使EF OE、．连接BF CF(1)求证：四边形OBFC是平行四边形；(2)求证：OF CD∥．20．如图四边形ABCD为平行四边形 E为AD上的一点连接EB并延长使BF=BE 连接EC并延长使CG=CE连接FG H为FG的中点连接DH（1）求证：四边形AFHD为平行四边形；（2）若CB=CE∠EBC=75°∠DCE=10°求∠DAB的度数.21.如图,点B为AC上一点,分别以AB,BC为边在AC同侧作等边三角形ABD和等边三角形BCE,点P,M,N分别为AC,AD,CE的中点.(1)求证:PM＝PN;(2)求∠MPN的度数.22.如图,在△ABC中,AB＝AC,AD⊥BC于点D,点P是AD的中点,延长BP交AC于点N,求证:AN＝13AC.23．（1）如图1 在四边形ABCD中AB＝CD E F分别是AD BC的中点连接FE 并延长分别与BA CD的延长线交于点M N．求证：∠BME＝∠CNE；（提示：取BD的中点H连接FH HE作辅助线）（2）如图2 在△ABC中F是BC边的中点D是AC边上一点E是AD的中点直线FE交BA的延长线于点G若AB＝DC＝2 ∠FEC＝45°求FE的长度．24．【发现与证明】如图在四边形ABCD中 E F G H是各边中点对角线AC BD相交于点O I J是AC BD的中点连接EF EH HG GF EI GI EJ FJ IJ GJ IH.结论1：四边形EFGH是平行四边形；结论2：四边形EJGI是平行四边形；结论3：S四边形EFGH =12S四边形ABCD；……（1）请选择其中一个结论加以证明（只需证明一个结论）.（2）【探究与应用】（★温馨提示：以下问题可以直接使用上述结论）①如图1 在四边形ABCD中 F H分别为边AB DC的中点连结HF.已知AD=6 BC=4线段HF的取值范围是 .②如图2 在四边形ABCD中点E F G H分别是AB BC CD DA的中点连接EG FH交于点O EG=8cm FH=6cm ∠EOF=60°求S四边形ABCD.答案部分：例1.A ∵点D E 分别为△ABC 的边AB AC 的中点 ∴DE 是△ABC 的中位线 ∴DE ∥BC ,DE =12BC =4.∴DF ∥BC ∵DF ∥BC ,CF ∥BA∴四边形BCFD 是平行四边形 ∴DF =BC =8,∴EF =DF -DE =4.例2.C ∵P 是BD 的中点,E 是AB 的中点 ∴PE =12AD ,同理,PF =12BC ∵AD =BC ,∴PE =PF∴∠EFP =12×(180°-∠EPF )=22°. 故选C.例3.答案 6.5解：如图,连接DN DB∵点E F 分别为DM MN 的中点 ∴EF 是△MDN 的中位线 ∴EF =12DN当N与点B重合时,DN最大,此时EF的值最大∵∠A=90°,AB=12,AD=5∴DB=√AD2+AB2=13,∴EF的最大值为6.5 故答案为6.5.例4.证明如图,连接BD∵C,H分别是AB,DA的中点∴CH是△ABD的中位线BD∴CH∥BD,CH=12BD同理,FG∥BD,FG=12∴CH∥FG,CH=FG∴四边形CFGH是平行四边形.例5．D解：延长BD CA交于点F∠的外角平分线∵AD为ABC中BAC∴FAD BAD∠=∠∵BD AD⊥∴90∠=∠=︒ADF ADB在ABD△和AFD△中FAD BAD AD ADADF ADB ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ABD AFD △≌△ ∴AB AF = BD DF = 又E 为BC 中点 5DE = ∴210CF DE == 又3AC =∴7AF CF AC AB =-==． 故选：D ．例6.解： 在△ABC 中,∠ABC =90°,AB =5,BC =12 则AC =√AB 2+BC 2=√52+122=13 ∵AD =AB =5∴DC =AC -AD =13-5=8 ∵AD =AB ,AE ⊥BD ,∴BE =ED ∵BF =FC ,∴EF =12DC =4.解:如图,延长BD 交AC 于点F ,∵AD 平分∠BAC ,∴∠BAD ＝∠CAD .∵BD ⊥AD ∴∠ADB ＝∠ADF又∵AD ＝AD ,∴△ADB ≌△ADF (ASA ).∴AF ＝AB ＝6,BD ＝FD .∵AC ＝10,∴CF ＝AC －AF ＝10－6＝4.∵E 为BC 的中点,∴DE 是△BCF 的中位线.∴DE ＝12CF ＝12×4＝2.例8.证明:如图,延长FE 至N ,使EN ＝EF ,连接BN ,AN ,则ME ＝12AN . ∵EF ＝EN ,∠BEF ＝90°,∴BE 垂直平分FN . ∴BF ＝BN .∴∠BNF ＝∠BFN . ∵△BEF 为等腰直角三角形,∠BEF ＝90°,∴∠BFN ＝45°.∴∠BNF ＝45°. ∴∠FBN ＝90°,即∠FBA ＋∠ABN ＝90°.又∠FBA ＋∠CBF ＝90° ∴∠CBF ＝∠ABN .在△BCF 和△BAN 中,∵BF ＝BN ,∠CBF ＝∠ABN ,BC ＝BA∴△BCF ≌△BAN (SAS ).∴CF ＝AN .∴ME ＝12AN ＝12CF .例9.(1)证明:在△ABC 中,∵AB ＝BC ,∠ABC ＝90°,∴∠ACB ＝45°. ∵CE 平分∠ACB ,∴∠ECB ＝∠ACE ＝22.5°.∴∠BEF ＝∠CFD ＝∠BFE ＝67.5°.∴BE ＝BF ,即△BEF 是等腰三角形． (2)解:如图,延长AB 至点M ,使得BM ＝AB ,连结CM .易知D 是AC 的中点∴BD ∥MC ,BD ＝12MC .∴∠BFE ＝∠MCE .由(1)得∠BEF ＝∠BFE ,BE ＝BF ,∴∠BEF ＝∠MCE .∴ME ＝MC .∵BM ＝AB ＝BC ,∴BD ＝12MC ＝12ME ＝12(MB ＋BE )＝12(BC ＋BF )．例10.A 如图,连接BD ,取BD 的中点H ,连接HF ,HE∵点E ,H 分别是AB ,BD 的中点,∴EH 是△ABD 的中位线,∴EH =12AD =3 同理可得FH =12BC =5,∴EF ≤FH +EH =8,故选A .例11．B 解：取CD 的中点G 连接EG FG点E 为AD 的中点 点F 为OC 的中点12EG AC ∴=EG AC ∥ 12FG OD = //FG OD四边形ABCD 是菱形 120BAD ∠=︒AC BD ∴⊥ 60ADC ∠=︒ 1302ODC ADC ∠=∠=︒EG GF ∴⊥ AD DC AC ==设CD x = 则12EG x = 3FG 7EF =22213()()(7)2x ∴+= 解得4x =4CD ∴=∴菱形ABCD的周长为：44416CD=⨯=故选：B．例12解：如图取AB的中点G连接EG FG∵E F分别是边AD CB的中点∴EG BD∥且118422EG BD==⨯=FG AC且116322FG AC==⨯=∵AC BD⊥∴EG FG⊥∴2222435EF EG FG=++=．故答案为：5．强化训练题一．选择题1．如图在△ABC中AB＝4 BC＝5 AC＝8．点D E F分别是相应边上的中点则四边形DFEB的周长等于（）A．8 B．9 C．12 D．13解：∵点D F分别是AB AC的中点∴DF＝BC＝2.5同理EF＝AB＝2∴四边形DFEB的周长＝EF+FD+DB+BE＝9故选：B ．2．解：∵AB ＝AC AD 平分∠BAC ∴BD ＝DC ＝BC ＝5 ∵点E 为AC 的中点∴CE ＝AC ＝6 DE ＝AB ＝6 ∴△CDE 的周长＝CD +CE +DE ＝17 故选：B ． 3．A 解：45B ∠=︒ AD BC ⊥ABD ∴是等腰直角三角形 6AD BD ∴=60C ∠=︒30DAC ∴∠=︒12DC AC ∴=2233AD AC DC DC AC ∴-=36AC =22AC ∴=E F 分别为AB BC 的中点1122222EF AC ∴==⨯=故选：A ． 4．C解：四边形ABCD 是平行四边形60ABC ADC ∴∠=∠=︒ 120BAD ∠=︒AE 平分BAD ∠60BAE EAD ∴∠=∠=︒ABE ∴是等边三角形AE AB BE ∴==AB =12BC AE ∴=12BC90BAC ∴∠=︒30CAD ∴∠=︒ 故A 正确； AC AB ⊥∴ABCDSAB AC =⋅ 故B 正确AB =12BC OB =12BDBD BC >AB OB ∴≠ 故C 错误； CE BE = CO OA = OE ∴=12ABOE ∴=14BC 故D 正确． 故选：C ． 5．【答案】C6．已知三角形三边长分别为7cm 8cm 9cm 作三条中位线组成一个新的三角形 同样方法作下去 一共做了五个新的三角形 则这五个新三角形的周长之和为（ ） A ．46.5cmB ．22.5cmC ．23.25cmD ．以上都不对解：由△ABC 三边长分别为7cm 8cm 9cm 三条中位线组成一个新的三角形 可知新三角形与原三角形相似 相似比是1：2 即：后一个三角形的周长都是前一个三角形周长的∵原三角形的周长＝7+8+9＝24 ∴这个新三角形的周长＝×24＝12 ∴这个五个新三角形的周长之和＝24+×24+×24+×24+×24＝23.25故选：C ．7．A解：延长AC BE 交于点M∵AE 平分BAC ∠ BE AE ⊥∴90AEB AEM ∠=∠=︒ CAE BAE ∠=∠∵AE AE =∴ABE AME ≌∴10AB AM == BE EM =∵6AC =∴4CM AM AC =-=∵点F 是BC 的中点 BE EM =∴EF 为BCM 中位线 ∴122EF CM ==．故选：A ．8.【答案】A解：连接 AC∵∠GAB =∠ABC∴AG ∥BC .又 AG = BC可知四边形 AGBC 是平行四边形∴AC ∥BG点 E F 分别为 AD DC 的中点∴EF 是△ ADC 的中位线∴EF ∥AC∴ EF ∥BG .∴点 B 与点 G 到 EF 的距离相等△EBF 与△ EGF 是同底等高的关系∴ S △ EBF = S △ EGF 即S1=S2故选： A9．A解：如图 延长DP 交BC 于点F四边形ABCD 是平行四边形AD BC ∴∥ OD OB = 7AB CD == 10BC AD ==180ADC BCD ∴∠+∠=︒ ADF CFD ∠=∠ DP 平分ADC ∠ CP 平分BCD ∠ADF CDF ∠=∠∴ FCP DCP ∠=∠90CDP DCP ∴∠+∠=︒ CDF CFD ∠=∠7DC CF ∴== DP PF =OP ∴是DBF 的中位线()()111107 1.5222OP BF BC CF ∴==-=-= 故选：A ．10.解：如图 取 AD 的中点 H ,连接 PH , OH∵四边形 ABCD 是平行四边形 ∴AP = PC又∵点 H 是 AD 中点 LAOD =90°∴PH =- AB , OH =- AD∴OH + PH ≥ OP∴AB + AD ≥2OP∴四边形 ABCD 的周长最小值为20故选： A .二．填空题11.解：取 BE 的中点 M 连接 FM , CM∵F 为AE 的中点 M 为 BE 的中点∴MF =AB , FM // AB∵四边形 ABCD 是平行四边形∴DC = AB , DC // AB∵E 为 CD 的中点∴CE =DC∴ CE = FM , CE // FM .∴四边形 EFMC 是平行四边形∴EG = GM∵BM = EM = BE =x8=4∴ EG =x4=2故答案为：212.如图 DE 为△ABC 的中位线 点F 在DE 上 且∠AFC 为直角 若AC ＝6cmBC ＝8cm则DF 的长为 1cm ．解：∵DE 为△ABC 的中位线∴DE ＝BC ＝4（cm ）∵∠AFC 为直角 E 为AC 的中点∴FE ＝AC ＝3（cm ）∴DF ＝DE ﹣FE ＝1（cm ）故答案为：1cm ．13．6解：如图2 由折叠得：AM MD = MN AD ⊥ AD BC ⊥ 连接GD∴GN BC∥GN是AD的垂直平分线∴AG DG=∴GAD GDA∠=∠∵90GBD GAD GDB GDA∠+∠=︒=∠+∠∴GBD GDB∠=∠∴GB GD=∴AG BG=同理可得：AN CN=∴GN是ABC的中位线而12BC=∴162GN BC==∵PM GM=∴6 MP MN GM MN GN+=+==．故答案为：6．14.【答案】7215.解：延长AE BC交于点H∵△ADE是等腰直角三角形∴∠HAC＝45°AE＝AD＝2∴CH＝AC＝BC AH＝AC＝6∴EH＝AH﹣AE＝4∵BC＝CH BF＝FE∴FC＝EH＝2故答案为：2．16．【答案】3 （或3：1）】解： EF 是△ ABC 的中位线.. EF / BC , EF = BCOE =20F: OE =BC =BC设点 A 到 BC 的距离为 h则 S △ ABC = BC · h , S △ aoc =OE · h =BC · h =BC · h:△ ABC 的面积与△ AOC 的面积之比＝3:1.故选： D .17．【答案】52解答】解：∵四边形 ABCD 是平行四边形∴AD = BC , CD = AB , DC / AB∵AD =5, AB = CF =3.∴CD =3, BC =5∴BF = BC + CF =8∵△ BEF 是等边三角形 G 为 DE 的中点∴BF = BE =8, DG = EG延长 CG 交 BE 于点 H∵DC / AB∴∠CDG=∠HEG在△ DCG 和△ EHG 中∠CDG=∠HEGDG = EG∠DGC =∠ EGH∴△ DCGR △ EHG ( ASA ).∴DC = EH , CG = HG∵ CD =3, BE =8∴HE =3, BH =5∵ LCBH =60°, BC = BH =5∴△CBH 是等边三角形∴CH = BC =5∴CG = CH =52故答案为：52三．解答题18．如图△ABC的中线BE CF相交于G且AB＝12 AC＝16 BC＝20 求GC的长．解：∵AB＝12 AC＝16 BC＝20∴AB2+AC2＝BC2∴△ABC是直角三角形∴∠A＝90°∵F是AB中点∴AF＝6∴CF＝＝＝2∵中线BE CF相交于G∴G是△ABC重心∴CG：GF＝2：1∴CG＝．19．(1)证明见解析(2)证明见解析（1）证明：∵点E是边BC中点∴BE CE=又∵EF OE=∴四边形OBFC是平行四边形；（2）证明：∵四边形ABCD是平行四边形对角线AC BD、相交于点O ∴点O是BD的中点又∵点E是边BC中点∴OE是BCD△的中位线∴OE CD即OF CD∥．20．【答案】（1）证明：∵BF=BE CG=CE∴BC为△FEG的中位线FG∴BC//FG BC=12又∵H是FG的中点∴FH=1FG2∴BC=FH .又∵四边形ABCD是平行四边形∴AD//BC AD=BC∴AD//FH AD=FH∴四边形AFHD是平行四边形；（2）解：∵四边形ABCD是平行四边形∴∠DAB=∠DCB∵CE=CB∴∠BEC=∠EBC=75°∴∠BCE=180°−75°−75°=30°∴∠DCB=∠DCE+∠BCE=10°+30°=40°∴∠DAB=40° .21.解:(1)如图,连接CD,AE.由三角形中位线定理可得PM∥12CD,PN∥12AE.∵△ABD和△BCE是等边三角形,∴AB＝DB,BE＝BC,∠ABD＝∠CBE＝60°∴∠ABE＝∠DBC.∴△ABE≌△DBC,∴AE＝DC.∴PM＝PN.(2)如图,设PM交AE于F,PN交CD于G,AE交CD于H,AE交BD于Q.由(1)知△ABE≌△DBC,∴∠BAE ＝∠BDC.又∵∠DQH＝∠BQA,∴∠AHD＝∠ABD＝60°,∴∠FHG＝120°.22.证明:如图,取NC的中点H,连接DH过点H作HE∥AD,交BN的延长线于E.∵AB＝AC,AD⊥BC,∴D为BC的中点.∵H为NC的中点,∴DH∥BN.又∵PD∥EH,∴四边形PDHE是平行四边形.∴HE＝PD.∵P为AD的中点,∴AP＝PD. ∴AP＝EH.又∵HE∥AD,∴∠PAN＝∠EHN,∠APN＝∠HEN.∴△APN≌△HEN(ASA).∴AN＝NH. ∴AN＝NH＝HC. ∴AN＝13AC.23．（1）证明：连接BD取DB的中点H连接EH FH ∵E H分别是AD BD的中点∴EH∥AB EH＝AB∴∠BME＝∠HEF∵F H分别是BC BD的中点∴FH∥CD FH＝CD∴∠CNE＝∠HFE∵AB＝CD∴HE＝FH∴∠HEF＝∠HFE∴∠BME＝∠CNE；（2）连接BD取DB的中点H连接EH FH∵E F分别是AD BC的中点∴EH＝AB FH＝CD FH∥AC∴∠HFE＝∠FEC＝45°∵AB＝CD＝2∴HF＝HE＝1∴∠HEF＝∠HFE＝45°∴∠EHF＝180°﹣∠HFE﹣HEF＝90°∴．24．【答案】（1）解：结论1：四边形EFGH是平行四边形；证明：∵在四边形ABCD中 E F G H是各边中点∴EF为∆ABD的中位线∴EF∥BD EF=12BD同理可得GH∥BD GH=12BD∴GH∥EF GH=EF∴四边形EFGH是平行四边形；结论2：四边形EJGI是平行四边形；证明：∵E J G I分别为DA DB BC AC中点∴EJ为∆ABD的中位线∴EJ∥AB EJ=12AB同理可得IG∥AB IG=12AB∴EJ∥IG EJ=IG∴四边形EJGI是平行四边形；结论3：S四边形EFGH=12S四边形ABCD；证明：由结论1证明可得 EF=12BD GH=12BD∴∆AEF的高为∆ADB高的一半∆CHG的高为∆BCD高的一半∴S�AEF=14S�ADB S�CHG=14S�CDB同理：S�DEH=14S�DAC S�BFG=14S�BCA∴S四边形EFGH=S四边形ABCD−S�AEF−S�CHG−S�DEH−S�BFG=12S四边形ABCD；（2）解：①连接AC 取AC的中点E 连接FE HE∵点E F为AC AB的中点∴EF=12BC=2同理：EH=12AD=3第 31 页 共 31 页 ∴EH-EF<FH<EF+EH即1<EH<5故答案为：1<FH<5；②如图所示 连接EFGH 由结论1可得四边形EFGH 为平行四边形如图所示 过点E 作EM ∥FH 交GH 延长线于点M 过点G 作GN ⊥EM∵EF ∥GM EM ∥FH∴四边形FHME 为平行四边形∴FH=EM=6 ∠EOF=∠GEM=60° FE=HM∴∠EGN=30°∴EN=12EG =4∴GN =√EG 2−EN 2=4√3∴S �EGM =12EM ×GN =12√3由图可得S 四边形EFGH =S �EGM =12√3由结论3可得：S 四边形ABCD =2S 四边形EFGH =24√3.。
人教版数学中考复习《三角形相关问题》专项练习含答案
三角形相关问题一、综合题1.（•北京）如图，在四边形ABCD中，BD为一条对角线，AD∥BC，AD=2BC，∠ABD=90°，E为AD的中点，连接BE．（1）求证：四边形BCDE为菱形；（2）连接AC，若AC平分∠BAD，BC=1，求AC的长．2.（•北京）在平面直角坐标系xOy中的点P和图形M，给出如下的定义：若在图形M上存在一点Q，使得P、Q两点间的距离小于或等于1，则称P为图形M的关联点．（1）当⊙O的半径为2时，①在点P1（，0），P2（，），P3（，0）中，⊙O的关联点是________．②点P在直线y=﹣x上，若P为⊙O的关联点，求点P的横坐标的取值范围．（2）⊙C的圆心在x轴上，半径为2，直线y=﹣x+1与x轴、y轴交于点A、B．若线段AB上的所有点都是⊙C的关联点，直接写出圆心C的横坐标的取值范围．3.（•河南）如图1，在Rt△ABC中，∠A=90°，AB=AC，点D，E分别在边AB，AC上，AD=AE，连接DC，点M，P，N分别为DE，DC，BC的中点．（1）观察猜想图1中，线段PM与PN的数量关系是________，位置关系是________；（2）探究证明把△ADE绕点A逆时针方向旋转到图2的位置，连接MN，BD，CE，判断△PMN的形状，并说明理由；（3）拓展延伸把△ADE绕点A在平面内自由旋转，若AD=4，AB=10，请直接写出△PMN面积的最大值．4.（•荆州）如图，在矩形ABCD中，连接对角线AC、BD，将△ABC沿BC方向平移，使点B移到点C，得到△DCE．（1）求证：△ACD≌△EDC；（2）请探究△BDE的形状，并说明理由．5.（•十堰）已知O为直线MN上一点，OP⊥MN，在等腰Rt△ABO中，∠BAO=90°，AC∥OP交OM于C，D为OB的中点，DE⊥DC交MN于E．（1）如图1，若点B在OP上，则①AC________OE（填“＜”，“=”或“＞”）；②线段CA、CO、CD满足的等量关系式是________；（2）将图1中的等腰Rt△ABO绕O点顺时针旋转α（0°＜α＜45°），如图2，那么（1）中的结论②是否成立？请说明理由；（3）将图1中的等腰Rt△ABO绕O点顺时针旋转α（45°＜α＜90°），请你在图3中画出图形，并直接写出线段CA、CO、CD满足的等量关系式________．6.（•玉林）如图，在等腰直角三角形ABC中，∠ACB=90°，AC=BC=4，D是AB的中点，E，F分别是AC，BC上的点（点E不与端点A，C重合），且AE=CF，连接EF并取EF的中点O，连接DO并延长至点G，使GO=OD，连接DE，DF，GE，GF．（1）求证：四边形EDFG是正方形；（2）当点E在什么位置时，四边形EDFG的面积最小？并求四边形EDFG面积的最小值．7.（•黄石）在现实生活中，我们会看到许多“标准”的矩形，如我们的课本封面、A4的打印纸等，其实这些矩形的长与宽之比都为：1，我们不妨就把这样的矩形称为“标准矩形”，在“标准矩形”ABCD中，P 为DC边上一定点，且CP=BC，如图所示．（1）如图①，求证：BA=BP；（2）如图②，点Q在DC上，且DQ=CP，若G为BC边上一动点，当△AGQ的周长最小时，求的值；（3）如图③，已知AD=1，在（2）的条件下，连接AG并延长交DC的延长线于点F，连接BF，T为BF 的中点，M、N分别为线段PF与AB上的动点，且始终保持PM=BN，请证明：△MNT的面积S为定值，并求出这个定值．8.（•荆门）已知：如图，在Rt△ACB中，∠ACB=90°，点D是AB的中点，点E是CD的中点，过点C作CF∥AB交AE的延长线于点F．（1）求证：△ADE≌△FCE；（2）若∠DCF=120°，DE=2，求BC的长．9.（•海南）如图，四边形ABCD是边长为1的正方形，点E在AD边上运动，且不与点A和点D重合，连结CE，过点C作CF⊥CE交AB的延长线于点F，EF交BC于点G．（1）求证：△CDE≌△CBF；（2）当DE= 时，求CG的长；（3）连结AG，在点E运动过程中，四边形CEAG能否为平行四边形？若能，求出此时DE的长；若不能，说明理由．10.（•大连）如图1，四边形ABCD的对角线AC，BD相交于点O，OB=OD，OC=OA+AB，AD=m，BC=n，∠ABD+∠ADB=∠ACB．（1）填空：∠BAD与∠ACB的数量关系为________；（2）求的值；（3）将△ACD沿CD翻折，得到△A′CD（如图2），连接BA′，与CD相交于点P．若CD= ，求PC 的长．11.（•呼和浩特）如图，等腰三角形ABC中，BD，CE分别是两腰上的中线．（1）求证：BD=CE；（2）设BD与CE相交于点O，点M，N分别为线段BO和CO的中点，当△ABC的重心到顶点A的距离与底边长相等时，判断四边形DEMN的形状，无需说明理由．12.（•张家界）如图，在平行四边形ABCD中，边AB的垂直平分线交AD于点E，交CB的延长线于点F，连接AF，BE．（1）求证：△AGE≌△BGF；（2）试判断四边形AFBE的形状，并说明理由．13.（•北京）在等腰直角△ABC中，∠ACB=90°，P是线段BC上一动点（与点B、C不重合），连接AP，延长BC至点Q，使得CQ=CP，过点Q作QH⊥AP于点H，交AB于点M．（1）若∠PAC=α，求∠AMQ的大小（用含α的式子表示）．（2）用等式表示线段MB与PQ之间的数量关系，并证明．14.（•百色）已知反比例函数y= （k≠0）的图象经过点B（3，2），点B与点C关于原点O对称，BA⊥x 轴于点A，CD⊥x轴于点D．（1）求这个反比函数的解析式；（2）求△ACD的面积．15.（•百色）矩形ABCD中，E、F分别是AD、BC的中点，CE、AF分别交BD于G、H两点．求证：（1）四边形AFCE是平行四边形；（2）证明：EG=FH．16.（•河池）解答题（1）如图1，在正方形ABCD中，点E，F分别在BC，CD上，AE⊥BF于点M，求证：AE=BF；（2）如图2，将（1）中的正方形ABCD改为矩形ABCD，AB=2，BC=3，AE⊥BF于点M，探究AE与BF 的数量关系，并证明你的结论．17.（•东营）如图，在等腰三角形ABC中，∠BAC=120°，AB=AC=2，点D是BC边上的一个动点（不与B、C重合），在AC上取一点E，使∠ADE=30°．（1）求证：△ABD∽△DCE；（2）设BD=x，AE=y，求y关于x的函数关系式并写出自变量x的取值范围；（3）当△ADE是等腰三角形时，求AE的长．18.（•青岛）已知：如图，在菱形ABCD中，点E，O，F分别为AB，AC，AD的中点，连接CE，CF，OE，OF．（1）求证：△BCE≌△DCF；（2）当AB与BC满足什么关系时，四边形AEOF是正方形？请说明理由．19.（•威海）如图，四边形ABCD为一个矩形纸片，AB=3，BC=2，动点P自D点出发沿DC方向运动至C 点后停止，△ADP以直线AP为轴翻折，点D落在点D1的位置，设DP=x，△AD1P与原纸片重叠部分的面积为y．（1）当x为何值时，直线AD1过点C？（2）当x为何值时，直线AD1过BC的中点E？（3）求出y与x的函数表达式．20.（•达州）如图，在△ABC中，点O是边AC上一个动点，过点O作直线EF∥BC分别交∠ACB、外角∠ACD 的平分线于点E、F．（1）若CE=8，CF=6，求OC的长；（2）连接AE、AF．问：当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由．21.（•达州）小明在求同一坐标轴上两点间的距离时发现，对于平面直角坐标系内任意两点P1（x1，y1），P2（x2，y2），可通过构造直角三角形利用图1得到结论：P1P2= 他还利用图2证明了线段P1P2的中点P（x，y）P的坐标公式：x= ，y= ．（1）请你帮小明写出中点坐标公式的证明过程；（2）①已知点M（2，﹣1），N（﹣3，5），则线段MN长度为________；②直接写出以点A（2，2），B（﹣2，0），C（3，﹣1），D为顶点的平行四边形顶点D的坐标：________；（3）如图3，点P（2，n）在函数y= x（x≥0）的图象OL与x轴正半轴夹角的平分线上，请在OL、x轴上分别找出点E、F，使△PEF的周长最小，简要叙述作图方法，并求出周长的最小值．22.（•常德）如图，直角△ABC中，∠BAC=90°，D在BC上，连接AD，作BF⊥AD分别交AD于E，AC于F．（1）如图1，若BD=BA，求证：△ABE≌△DBE；（2）如图2，若BD=4DC，取AB的中点G，连接CG交AD于M，求证：①GM=2MC；②AG2=AF•AC．23.（•扬州）我们规定：三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差．如图1，在△ABC中，AO是BC边上的中线，AB与AC的“极化值”就等于AO2﹣BO2的值，可记为AB△AC=AO2﹣BO2．（1）在图1中，若∠BAC=90°，AB=8，AC=6，AO是BC边上的中线，则AB△AC=________，OC△OA=________；（2）如图2，在△ABC中，AB=AC=4，∠BAC=120°，求AB△AC、BA△BC的值；（3）如图3，在△ABC中，AB=AC，AO是BC边上的中线，点N在AO上，且ON= AO．已知AB△AC=14，BN△BA=10，求△ABC的面积．24.（•赤峰）△OPA和△OQB分别是以OP、OQ为直角边的等腰直角三角形，点C、D、E分别是OA、OB、AB的中点．（1）当∠AOB=90°时如图1，连接PE、QE，直接写出EP与EQ的大小关系；（2）将△OQB绕点O逆时针方向旋转，当∠AOB是锐角时如图2，（1）中的结论是否成立？若成立，请给出证明；若不成立，请加以说明．（3）仍将△OQB绕点O旋转，当∠AOB为钝角时，延长PC、QD交于点G，使△ABG为等边三角形如图3，求∠AOB的度数．答案解析部分一、综合题1.【答案】（1）证明：∵AD=2BC，E为AD的中点，∴DE=BC，∵AD∥BC，∴四边形BCDE是平行四边形，∵∠ABD=90°，AE=DE，∴BE=DE，∴四边形BCDE是菱形（2）解：连接AC．∵AD∥BC，AC平分∠BAD，∴∠BAC=∠DAC=∠BCA，∴AB=BC=1，∵AD=2BC=2，∴sin∠ADB= ，∴∠ADB=30°，∴∠DAC=30°，∠ADC=60°，在Rt△ACD中，∵AD=2，∴CD=1，AC= ．【解析】【分析】（1）由DE=BC，DE∥BC，推出四边形BCDE是平行四边形，再证明BE=DE即可解决问题；（2）在Rt△只要证明∠ADC=60°，AD=2即可解决问题；2.【答案】（1）解：①P2，P3②根据定义分析，可得当最小y=﹣x上的点P到原点的距离在1到3之间时符合题意，∴设P（x，﹣x），当OP=1时，由距离公式得，OP= =1，∴x= ，当OP=3时，OP= =3，解得：x=± ；∴点P的横坐标的取值范围为：﹣≤≤﹣，或≤x≤（2）解：∵直线y=﹣x+1与x轴、y轴交于点A、B，∴A（1，0），B（0，1），如图1，当圆过点A时，此时，CA=3，∴C（﹣2，0），如图2，当直线AB与小圆相切时，切点为D，∴CD=1，∵直线AB的解析式为y=﹣x+1，∴直线AB与x轴的夹角=45°，∴AC= ，∴C（1﹣，0），∴圆心C的横坐标的取值范围为：﹣2≤x C≤1﹣；如图3，当圆过点A，则AC=1，∴C（2，0），如图4，当圆过点B，连接BC，此时，BC=3，∴OC= =2 ，∴C（2 ，0）．∴圆心C的横坐标的取值范围为：2≤x C≤2 ；综上所述；圆心C的横坐标的取值范围为：﹣2≤x C≤1﹣或2≤x C≤2【解析】【解答】（1）①∵点P1（，0），P2（，），P3（，0），∴OP1= ，OP2=1，OP3= ，∴P1与⊙O的最小距离为，P2与⊙O的最小距离为1，OP3与⊙O的最小距离为，∴⊙O，⊙O的关联点是P2，P3；故答案为：P2，P3；【分析】（1）①根据点P1（，0），P2（，），P3（，0），求得P1= ，P2=1，OP3= ，于是得到结论；②根据定义分析，可得当最小y=﹣x上的点P到原点的距离在1到3之间时符合题意，设P（x，﹣x），根据两点间的距离公式得到即可得到结论；（2根据已知条件得到A（1，0），B（0，1），如图1，当圆过点A时，得到C（﹣2，0），如图2，当直线AB与小圆相切时，切点为D，得到C（1﹣，0），于是得到结论；如图3，当圆过点A，则AC=1，得到C（2，0），如图4，当圆过点B，连接BC，根据勾股定理得到C（2 ，0），于是得到结论．3.【答案】（1）PM=PN；PM⊥PN（2）解：由旋转知，∠BAD=∠CAE，∵AB=AC，AD=AE，∴△ABD≌△ACE（SAS），∴∠ABD=∠ACE，BD=CE，同（1）的方法，利用三角形的中位线得，PN= BD，PM= CE，∴PM=PN，∴△PMN是等腰三角形，同（1）的方法得，PM∥CE，∴∠DPM=∠DCE，同（1）的方法得，PN∥BD，∴∠PNC=∠DBC，∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC，∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC，∵∠BAC=90°，∴∠ACB+∠ABC=90°，∴∠MPN=90°，∴△PMN是等腰直角三角形（3）解：如图2，同（2）的方法得，△PMN是等腰直角三角形，∴MN最大时，△PMN的面积最大，∴DE∥BC且DE在顶点A上面，∴MN最大=AM+AN，连接AM，AN，在△ADE中，AD=AE=4，∠DAE=90°，∴AM=2 ，在Rt△ABC中，AB=AC=10，AN=5 ，∴MN最大=2 +5 =7 ，∴S△PMN最大= PM2= × MN2= ×（7 ）2= ．【解析】【解答】解：（1）∵点P，N是BC，CD的中点，∴PN∥BD，PN= BD，∵点P，M是CD，DE的中点，∴PM∥CE，PM= CE，∵AB=AC，AD=AE，∴BD=CE，∴PM=PN，∵PN∥BD，∴∠DPN=∠ADC，∵PM∥CE，∴∠DPM=∠DCA，∵∠BAC=90°，∴∠ADC+∠ACD=90°，∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°，∴PM⊥PN，故答案为：PM=PN，PM⊥PN，【分析】（1）利用三角形的中位线得出PM= CE，PN= BD，进而判断出BD=CE，即可得出结论，另为利用三角形的中位线得出平行线即可得出结论；（2）先判断出△ABD≌△ACE，得出BD=CE，同（1）的方法得出PM= BD，PN= BD，即可得出PM=PN，同（1）的方法即可得出结论；（3）先判断出MN最大时，△PMN的面积最大，进而求出AN，AM，即可得出MN最大=AM+AN，最后用面积公式即可得出结论．4.【答案】（1）证明：∵四边形ABCD是矩形，∴AB=DC，AC=BD，AD=BC，∠ADC=∠ABC=90°，由平移的性质得：DE=AC，CE=BC，∠DCE=∠ABC=90°，DC=AB，∴AD=EC，在△ACD和△EDC中，，∴△ACD≌△EDC（SAS）（2）解：△BDE是等腰三角形；理由如下：∵AC=BD，DE=AC，∴BD=DE，∴△BDE是等腰三角形【解析】【分析】（1）由矩形的性质得出AB=DC，AC=BD，AD=BC，∠ADC=∠ABC=90°，由平移的性质得：DE=AC，CE=BC，∠DCE=∠ABC=90°，DC=AB，得出AD=EC，由SAS即可得出结论；（2）由AC=BD，DE=AC，得出BD=DE即可．5.【答案】（1）=；AC2+CO2=CD2（2）如图2，（1）中的结论②不成立，理由是：连接AD，延长CD交OP于F，连接EF，∵AB=AO，D为OB的中点，∴AD⊥OB，∴∠ADO=90°，∵∠CDE=90°，∴∠ADO=∠CDE，∴∠ADO﹣∠CDO=∠CDE﹣∠CDO，即∠ADC=∠EDO，∵∠ADO=∠ACO=90°，∴∠ADO+∠ACO=180°，∴A、D、O、C四点共圆，∴∠ACD=∠AOB，同理得：∠EFO=∠EDO，∴∠EFO=∠AOC，∵△ABO是等腰直角三角形，∴∠AOB=45°，∴∠DCO=45°，∴△COF和△CDE是等腰直角三角形，∴OC=OF，∵∠ACO=∠EOF=90°，∴△ACO≌△EOF，∴OE=AC，AO=EF，∴AC2+OC2=FO2+OE2=EF2，Rt△DEF中，EF＞DE=DC，∴AC2+OC2＞DC2，所以（1）中的结论②不成立（3）OC﹣AC= CD【解析】【解答】解：（1）①AC=OE，理由：如图1，∵在等腰Rt△ABO中，∠BAO=90°，∴∠ABO=∠AOB=45°，∵OP⊥MN，∴∠COP=90°，∴∠AOC=45°，∵AC∥OP，∴∠CAO=∠AOB=45°，∠ACO=∠POE=90°，∴AC=OC，连接AD，∵BD=OD，∴AD=OD，AD⊥OB，∴AD∥OC，∴四边形ADOC是正方形，∴∠DCO=45°，∴AC=OD，∴∠DEO=45°，∴CD=DE，∴OC=OE，∴AC=OE；②在Rt△CDO中，∵CD2=OC2+OD2，∴CD2=AC2+OC2；故答案为：AC2+CO2=CD2；（3.）如图3，结论：OC﹣CA= CD，理由是：连接AD，则AD=OD，同理：∠ADC=∠EDO，∵∠CAB+∠CAO=∠CAO+∠AOC=90°，∴∠CAB=∠AOC，∵∠DAB=∠AOD=45°，∴∠DAB﹣∠CAB=∠AOD﹣∠AOC，即∠DAC=∠DOE，∴△ACD≌△OED，∴AC=OE，CD=DE，∴△CDE是等腰直角三角形，∴CE2=2CD2，∴（OC﹣OE）2=（OC﹣AC）2=2CD2，∴OC﹣AC= CD，故答案为：OC﹣AC= CD．【分析】（1）①如图1，证明AC=OC和OC=OE可得结论；②根据勾股定理可得：AC2+CO2=CD2；（2）如图2，（1）中的结论②不成立，作辅助线，构建全等三角形，证明A、D、O、C四点共圆，得∠ACD=∠AOB，同理得：∠EFO=∠EDO，再证明△ACO≌△EOF，得OE=AC，AO=EF，根据勾股定理得：AC2+OC2=FO2+OE2=EF2，由直角三角形中最长边为斜边可得结论；（3）如图3，连接AD，则AD=OD证明△ACD≌△OED，根据△CDE是等腰直角三角形，得CE2=2CD2，等量代换可得结论（OC﹣OE）2=（OC ﹣AC）2=2CD2，开方后是：OC﹣AC= CD．6.【答案】（1）证明：连接CD，如图1所示．∵△ABC为等腰直角三角形，∠ACB=90°，D是AB的中点，∴∠A=∠DCF=45°，AD=CD．在△ADE和△CDF中，，∴△ADE≌△CDF（SAS），∴DE=DF，∠ADE=∠CDF．∵∠ADE+∠EDC=90°，∴∠EDC+∠CDF=∠EDF=90°，∴△EDF为等腰直角三角形．∵O为EF的中点，GO=OD，∴GD⊥EF，且GD=2OD=EF，∴四边形EDFG是正方形（2）解：过点D作DE′⊥AC于E′，如图2所示．∵△ABC为等腰直角三角形，∠ACB=90°，AC=BC=4，∴DE′= BC=2，AB=4 ，点E′为AC的中点，∴2≤DE＜2 （点E与点E′重合时取等号）．∴4≤S四边形EDFG=DE2＜8．∴当点E为线段AC的中点时，四边形EDFG的面积最小，该最小值为4．【解析】【分析】（1）连接CD，根据等腰直角三角形的性质可得出∠A=∠DCF=45°、AD=CD，结合AE=CF 可证出△ADE≌△CDF（SAS），根据全等三角形的性质可得出DE=DF、ADE=∠CDF，通过角的计算可得出∠EDF=90°，再根据O为EF的中点、GO=OD，即可得出GD⊥EF，且GD=2OD=EF，由此即可证出四边形EDFG是正方形；（2）过点D作DE′⊥AC于E′，根据等腰直角三角形的性质可得出DE′的长度，从而得出2≤DE ＜2 ，再根据正方形的面积公式即可得出四边形EDFG的面积的最小值．7.【答案】（1）证明：如图①中，设AD=BC=a，则AB=CD= a．∵四边形ABCD是矩形，∴∠C=90°，∵PC=AD=BC=a，∴PB= = a，∴BA=BP（2）解：如图②中，作Q关于BC的对称点Q′，连接AQ′交BC于G，此时△AQG的周长最小．设AD=BC=QD=a，则AB=CD= a，∴CQ=CQ′= a﹣a，∵CQ′//AB，∴= = =（3）证明：如图③中，作TH//AB交NM于H，交BC于K．由（2）可知，AD=BC=1，AB=CD= ，DP=CF= ﹣1，∵S△MNT= •TH•CK+ •TH•BK= HT•（KC+KB）= HT•BC= HT，∵TH//AB//FM，TF=TB，∴HM=HN，∴HT= （FM+BN），∵BN=PM，∴HT= （FM+PM）= PF= •（1+ ﹣1）= ，∴S△MNT= HT= =定值【解析】【分析】（1）如图①中，设AD=BC=a，则AB=CD= a．通过计算得出AB=BP= a，由此即可证明；（2）如图②中，作Q关于BC的对称点Q′，连接AQ′交BC于G，此时△AQG的周长最小．设AD=BC=QD=a，则AB=CD= a，可得CQ=CQ′= a﹣a，由CQ′//AB，推出= = = ；（3）如图③中，作TH//AB交NM于H，交BC于K．由S△MNT= •TH•CK+ •TH•BK= HT•（KC+KB）= HT•BC= HT，利用梯形的中位线定理求出HT即可解决问题；8.【答案】（1）证明：∵点E是CD的中点，∴DE=CE．∵AB∥CF，∴∠BAF=∠AFC．在△ADE与△FCE中，∵，∴△ADE≌△FCE（AAS）（2）解：由（1）得，CD=2DE，∵DE=2，∴CD=4．∵点D为AB的中点，∠ACB=90°，∴AB=2CD=8，AD=CD= AB．∵AB∥CF，∴∠BDC=180°﹣∠DCF=180°﹣120°=60°，∴∠DAC=∠ACD= ∠BDC= ×60°=30°，∴BC= AB= ×8=4【解析】【分析】（1）先根据点E是CD的中点得出DE=CE，再由AB∥CF可知∠BAF=∠AFC，根据AAS 定理可得出△ADE≌△FCE；（2）根据直角三角形的性质可得出AD=CD= AB，再由AB∥CF可知∠BDC=180°﹣∠DCF=180°﹣120°=60°，由三角形外角的性质可得出∠DAC=∠ACD= ∠BDC=30°，进而可得出结论．9.【答案】（1）证明：如图，在正方形ABCD中，DC=BC，∠D=∠ABC=∠DCB=90°，∴∠CBF=180°﹣∠ABC=90°，∠1+∠2=∠DCB=90°，∵CF⊥CE，∴∠ECF=90°，∴∠3+∠2=∠ECF=90°，∴∠1=∠3，在△CDE和△CBF中，，∴△CDE≌△CBF（2）解：在正方形ABCD中，AD∥BC，∴△GBF∽△EAF，∴，由（1）知，△CDE≌△CBF，∴BF=DE= ，∵正方形的边长为1，∴AF=AB+BF= ，AE=AD﹣DE= ，∴，∴BG= ，∴CG=BC﹣BG=（3）解：不能，理由：若四边形CEAG是平行四边形，则必须满足AE∥CG，AE=CG，∴AD﹣AE=BC﹣CG，∴DE=BG，由（1）知，△CDE≌△ECF，∴DE=BF，CE=CF，∴△GBF和△ECF是等腰直角三角形，∴∠GFB=45°，∠CFE=45°，∴∠CFA=∠GFB+∠CFE=90°，此时点F与点B重合，点D与点E重合，与题目条件不符，∴点E在运动过程中，四边形CEAG不能是平行四边形．【解析】【分析】（1）先判断出∠CBF=90°，进而判断出∠1=∠3，即可得出结论；（2）先求出AF，AE，再判断出△GBF∽△EAF，可求出BG，即可得出结论；（3）假设是平行四边形，先判断出DE=BG，进而判断出△GBF和△ECF是等腰直角三角形，即可得出∠GFB=∠CFE=45°，即可得出结论．10.【答案】（1）∠BAD+∠ACB=180°（2）解：如图1中，作DE∥AB交AC于E．∴∠DEA=∠BAE，∠OBA=∠ODE，∵OB=OD，∴△OAB≌△OED，∴AB=DE，OA=OE，设AB=DE=CE=CE=x，OA=OE=y，∵∠EDA+∠DAB=180°，∠BAD+∠ACB=180°，∴∠EDA=∠ACB，∵∠DEA=∠CAB，∴△EAD∽△ABC，∴= = = ，∴= ，∴4y2+2xy﹣x2=0，∴（）2+ ﹣1=0，∴= （负根已经舍弃），∴= ．（3）解：如图2中，作DE∥AB交AC于E．由（1）可知，DE=CE，∠DCA=∠DCA′，∴∠EDC=∠ECD=∠DCA′，∴DE∥CA′∥AB，∴∠ABC+∠A′CB=180°，∵△EAD∽△ACB，∴∠DAE=∠ABC=∠DA′C，∴∠DA′C+∠A′CB=180°，∴A′D∥BC，∴△PA′D∽△PBC，∴= = ，∴= ，即=∵CD= ，∴PC=1．【解析】【解答】解：（1.）如图1中，在△ABD中，∵∠BAD+∠ABD+∠ADB=180°，又∵∠ABD+∠ADB=∠ACB，∴∠BAD+∠ACB=180°，故答案为∠BAD+∠ACB=180°．【分析】（1）在△ABD中，根据三角形的内角和定理即可得出结论：∠BAD+∠ACB=180°；（2）如图1中，作DE∥AB交AC于E．由△OAB≌△OED，可得AB=DE，OA=OE，设AB=DE=CE=CE=x，OA=OE=y，由△EAD∽△ABC，推出= = = ，可得= ，可得4y2+2xy﹣x2=0，即（）2+﹣1=0，求出的值即可解决问题；（3）如图2中，作DE∥AB交AC于E．想办法证明△PA′D∽△PBC，可得= = ，可得= ，即= ，由此即可解决问题；11.【答案】（1）解：由题意得，AB=AC，∵BD，CE分别是两腰上的中线，∴AD= AC，AE= AB，∴AD=AE，在△ABD和△ACE中，∴△ABD≌△ACE（ASA）．∴BD=CE；（2）四边形DEMN是正方形，证明：∵E、D分别是AB、AC的中点，∴AE= AB，AD= AC，ED是△ABC的中位线，∴ED∥BC，ED= BC，∵点M、N分别为线段BO和CO中点，∴OM=BM，ON=CN，MN是△OBC的中位线，∴MN∥BC，MN= BC，∴ED∥MN，ED=MN，∴四边形EDNM是平行四边形，由（1）知BD=CE，又∵OE=ON，OD=OM，OM=BM，ON=CN，∴DM=EN，∴四边形EDNM是矩形，在△BDC与△CEB中，，∴△BDC≌△CEB，∴∠BCE=∠CBD，∴OB=OC，∵△ABC的重心到顶点A的距离与底边长相等，∴O到BC的距离= BC，∴BD⊥CE，∴四边形DEMN是正方形．【解析】【分析】（1）根据已知条件得到AD=AE，根据全等三角形的性质即可得到结论；（2）根据三角形中位线的性质得到ED∥BC，ED= BC，MN∥BC，MN= BC，等量代换得到ED∥MN，ED=MN，推出四边形EDNM是平行四边形，（1）知BD=CE，求得DM=EN，得到四边形EDNM是矩形，根据全等三角形的性质得到OB=OC，由三角形的重心的性质得到O到BC的距离= BC，根据直角三角形的判定得到BD⊥CE，于是得到结论．12.【答案】（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠AEG=∠BFG，∵EF垂直平分AB，∴AG=BG，在△AGEH和△BGF中，，∴△AGE≌△BGF（AAS）（2）解：四边形AFBE是菱形，理由如下：∵△AGE≌△BGF，∴AE=BF，∵AD∥BC，∴四边形AFBE是平行四边形，又∵EF⊥AB，∴四边形AFBE是菱形【解析】【分析】（1）由平行四边形的性质得出AD∥BC，得出∠AEG=∠BFG，由AAS证明△AGE≌△BGF 即可；（2）由全等三角形的性质得出AE=BF，由AD∥BC，证出四边形AFBE是平行四边形，再根据EF⊥AB，即可得出结论．13.【答案】（1）解：∠AMQ=45°+α；理由如下：∵∠PAC=α，△ACB是等腰直角三角形，∴∠BAC=∠B=45°，∠PAB=45°﹣α，∵QH⊥AP，∴∠AHM=90°，∴∠AMQ=180°﹣∠AHM﹣∠PAB=45°+α（2）解：PQ= MB；理由如下：连接AQ，作ME⊥QB，如图所示：∵AC⊥QP，CQ=CP，∴∠QAC=∠PAC=α，∴∠QAM=45°+α=∠AMQ，∴AP=AQ=QM，在△APC和△QME中，，∴△APC≌△QME（AAS），∴PC=ME，∴△AEB是等腰直角三角形，∴PQ= MB，∴PQ= MB．【解析】【分析】（1）由等腰直角三角形的性质得出∠BAC=∠B=45°，∠PAB=45°﹣α，由直角三角形的性质即可得出结论；（2）连接AQ，作ME⊥QB，由AAS证明△APC≌△QME，得出PC=ME，△AEB是等腰直角三角形，由等腰直角三角形的性质即可得出结论．14.【答案】（1）解：将B点坐标代入函数解析式，得=2，解得k=6，∴反比例函数的解析式为y= ；（2）解：由B（3，2），点B与点C关于原点O对称，得C（﹣3，﹣2）．由BA⊥x轴于点A，CD⊥x轴于点D，得A（3，0），D（﹣3，0）．∴S△ACD= AD•CD= × [3﹣（﹣3）]×|﹣2|=6．【解析】【分析】（1）根据待定系数法，可得函数解析式；（2）根据三角形的面积公式，可得答案．15.【答案】（1）证明：∵四边形ABCD是矩形，∴AD//BC，AD=BC，∵E、F分别是AD、BC的中点，∴AE= AD，CF= BC，∴AE CF，∴四边形AFCE是平行四边形；（2）证明：∵四边形AFCE是平行四边形，∴CE//AF，∴∠DGE=∠AHD=∠BHF，∵AB//CD，∴∠EDG=∠FBH，在△DEG和△BFH中，∴△DEG≌△BFH（AAS），∴EG=FH．【解析】【分析】（1）根据一组对边平行且相等的四边形是平行四边形证明即可；（2）可证明EG和FH所在的△DEG、△BFH全等即可．16.【答案】（1）证明：∵四边形ABCD是正方形，∴∠ABC=∠C，AB=BC．∵AE⊥BF，∴∠AMB=∠BAM+∠ABM=90°，∵∠ABM+∠CBF=90°，∴∠BAM=∠CBF．在△ABE和△BCF中，，∴△ABE≌△BCF（ASA），∴AE=BF；（2）解：AB= BC，理由：∵四边形ABCD是矩形，∴∠ABC=∠C，∵AE⊥BF，∴∠AMB=∠BAM+∠ABM=90°，∵∠ABM+∠CBF=90°，∴∠BAM=∠CBF，∴△ABE∽△BCF，∴= ，∴AE= BF．【解析】【分析】（1）根据正方形的性质，可得∠ABC与∠C的关系，AB与BC的关系，根据两直线垂直，可得∠AMB的度数，根据直角三角形锐角的关系，可得∠ABM与∠BAM的关系，根据同角的余角相等，可得∠BAM与∠CBF的关系，根据ASA，可得△ABE≌△BCF，根据全等三角形的性质，可得答案；（2）根据矩形的性质得到∠ABC=∠C，由余角的性质得到∠BAM=∠CBF，根据相似三角形的性质即可得到结论．17.【答案】（1）证明：∵△ABC是等腰三角形，且∠BAC=120°，∴∠ABD=∠ACB=30°，∴∠ABD=∠ADE=30°，∵∠ADC=∠ADE+∠EDC=∠ABD+∠DAB，∴∠EDC=∠DAB，∴△ABD∽△DCE；（2）解：如图1，∵AB=AC=2，∠BAC=120°，过A作AF⊥BC于F，∴∠AFB=90°，∵AB=2，∠ABF=30°，∴AF= AB=1，∴BF= ，∴BC=2BF=2 ，∵BD=x，AE=y则DC=2 ﹣x，EC=2﹣y，∵△ABD∽△DCE，∴，∴，化简得：y= x+2（0＜x＜2 ）；（3）解：当AD=DE时，如图2，由（1）可知：此时△ABD∽△DCE，则AB=CD，即2=2 ﹣x，x=2 ﹣2，代入y= x+2，解得：y=4﹣2 ，即AE=4﹣2 ，当AE=ED时，如图3，∠EAD=∠EDA=30°，∠AED=120°，∴∠DEC=60°，∠EDC=90°，则ED= EC，即y= （2﹣y），解得：y= ，即AE= ，当AD=AE时，∠AED=∠EDA=30°，∠EAD=120°，此时点D与点B重合，不符合题意，此情况不存在，∴当△ADE是等腰三角形时，AE=4﹣2 或．【解析】【分析】（1）根据两角相等证明：△ABD∽△DCE；（2）如图1，作高AF，根据直角三角形30°的性质求AF的长，根据勾股定理求BF的长，则可得BC的长，根据（1）中的相似列比例式可得函数关系式，并确定取值；（3）分三种情况进行讨论：①当AD=DE时，如图2，由（1）可知：此时△ABD∽△DCE，则AB=CD，即2=2 ﹣x；②当AE=ED时，如图3，则ED= EC，即y= （2﹣y）；③当AD=AE时，∠AED=∠EDA=30°，∠EAD=120°，此时点D与点B重合，不符合题意，此情况不存在．18.【答案】（1）证明：∵四边形ABCD是菱形，∴∠B=∠D，AB=BC=DC=AD，∵点E，O，F分别为AB，AC，AD的中点，∴AE=BE=DF=AF，OF= DC，OE= BC，OE∥BC，在△BCE和△DCF中，，∴△BCE≌△DCF（SAS）；（2）解：当AB⊥BC时，四边形AEOF是正方形，理由如下：由（1）得：AE=OE=OF=AF，∴四边形AEOF是菱形，∵AB⊥BC，OE∥BC，∴OE⊥AB，∴∠AEO=90°，∴四边形AEOF是正方形．【解析】【分析】（1）由菱形的性质得出∠B=∠D，AB=BC=DC=AD，由已知和三角形中位线定理证出AE=BE=DF=AF，OF= DC，OE= BC，OE∥BC，由SAS证明△BCE≌△DCF即可；（2）由（1）得：AE=OE=OF=AF，证出四边形AEOF是菱形，再证出∠AEO=90°，四边形AEOF是正方形．19.【答案】（1）解：如图1，∵由题意得：△ADP≌△AD1P，∴AD=AD1=2，PD=PD1=x，∠D=∠AD1P=90°，∵直线AD1过C，∴PD1⊥AC，在Rt△ABC中，AC= = ，CD1= ﹣2，在Rt△PCD1中，PC2=PD12+CD12，即（3﹣x）2=x2+（﹣2）2，解得：x= ，∴当x= 时，直线AD1过点C（2）解：如图2，连接PE，∵E为BC的中点，∴BE=CE=1，在Rt△ABE中，AE= = ，∵AD1=AD=2，PD=PD1=x，∴D1E= ﹣2，PC=3﹣x，在Rt△PD1E和Rt△PCE中，x2+（﹣2）2=（3﹣x）2+12，解得：x= ，∴当x= 时，直线AD1过BC的中点E；（3）解：如图3，当0＜x≤2时，y=x，如图4，当2＜x≤3时，点D1在矩形ABCD的外部，PD1交AB于F，∵AB∥CD，∴∠1=∠2，∵∠1=∠3（根据折叠），∴∠2=∠3，∴AF=PF，作PG⊥AB于G，设PF=AF=a，由题意得：AG=DP=x，FG=x﹣a，在Rt△PFG中，由勾股定理得：（x﹣a）2+22=a2，解得：a= ，所以y= = ，综合上述，当0＜x≤2时，y=x；当2＜x≤3时，y=【解析】【分析】（1）根据折叠得出AD=AD1=2，PD=PD1=x，∠D=∠AD1P=90°，在Rt△ABC中，根据勾股定理求出AC，在Rt△PCD1中，根据勾股定理得出方程，求出即可；（2）连接PE，求出BE=CE=1，在Rt△ABE中，根据勾股定理求出AE，求出AD1=AD=2，PD=PD1=x，D1E= ﹣2，PC=3﹣x，在Rt△PD1E 和Rt△PCE中，根据勾股定理得出方程，求出即可；（3）分为两种情况：当0＜x≤2时，y=x；当2＜x≤3时，点D1在矩形ABCD的外部，PD1交AB于F，求出AF=PF，作PG⊥AB于G，设PF=AF=a，在Rt△PFG中，由勾股定理得出方程（x﹣a）2+22=a2，求出a即可．20.【答案】（1）解：∵EF交∠ACB的平分线于点E，交∠ACB的外角平分线于点F，∴∠OCE=∠BCE，∠OCF=∠DCF，∵MN∥BC，∴∠OEC=∠BCE，∠OFC=∠DCF，∴∠OEC=∠OCE，∠OFC=∠OCF，∴OE=OC，OF=OC，∴OE=OF；∵∠OCE+∠BCE+∠OCF+∠DCF=180°，∴∠ECF=90°，在Rt△CEF中，由勾股定理得：EF= =10，∴OC=OE= EF=5（2）解：当点O在边AC上运动到AC中点时，四边形AECF是矩形．理由如下：当O为AC的中点时，AO=CO，∵EO=FO，∴四边形AECF是平行四边形，∵∠ECF=90°，∴平行四边形AECF是矩形．【解析】【分析】（1）根据平行线的性质以及角平分线的性质得出∠OEC=∠OCE，∠OFC=∠OCF，证出OE=OC=OF，∠ECF=90°，由勾股定理求出EF，即可得出答案；（2）根据平行四边形的判定以及矩形的判定得出即可．21.【答案】（1）证明：∵P1（x1，y1），P2（x2，y2），∴Q1Q2=OQ2﹣OQ1=x2﹣x1，∴Q1Q= ，∴OQ=OQ1+Q1Q=x1+ = ，∵PQ为梯形P1Q1Q2P2的中位线，∴PQ= = ，即线段P1P2的中点P（x，y）P的坐标公式为x= ，y=（2）；（﹣3，3）或（7，1）或（﹣1，﹣3）（3）解：如图，设P关于直线OL的对称点为M，关于x轴的对称点为N，连接PM交直线OL于点R，连接PN交x轴于点S，连接MN交直线OL于点E，交x轴于点F，由对称性可知EP=EM，FP=FN，∴PE+PF+EF=ME+EF+NF=MN，∴此时△PEF的周长即为MN的长，为最小，设R（x，x），由题意可知OR=OS=2，PR=PS=n，∴=2，解得x=﹣（舍去）或x= ，∴R（，），∴=n，解得n=1，∴P（2，1），∴N（2，﹣1），设M（x，y），则= ，= ，解得x= ，y= ，∴M（，），∴MN= = ，即△PEF的周长的最小值为【解析】【解答】（2）①∵M（2，﹣1），N（﹣3，5），∴MN= = ，故答案为：；②∵A（2，2），B（﹣2，0），C（3，﹣1），∴当AB为平行四边形的对角线时，其对称中心坐标为（0，1），设D（x，y），则x+3=0，y+（﹣1）=2，解得x=﹣3，y=3，∴此时D点坐标为（﹣3，3），当AC为对角线时，同理可求得D点坐标为（7，1），当BC为对角线时，同理可求得D点坐标为（﹣1，﹣3），综上可知D点坐标为（﹣3，3）或（7，1）或（﹣1，﹣3），故答案为：（﹣3，3）或（7，1）或（﹣1，﹣3）；【分析】（1）用P1、P2的坐标分别表示出OQ和PQ的长即可证得结论；（2）①直接利用两点间距离公式可求得MN的长；②分AB、AC、BC为对角线，可求得其中心的坐标，再利用中点坐标公式可求得D点坐标；（3）设P关于直线OL的对称点为M，关于x轴的对称点为N，连接PM交直线OL于点R，连接PN交x轴于点S，则可知OR=OS=2，利用两点间距离公式可求得R的坐标，再由PR=PS=n，可求得n的值，可求得P点坐标，利用中点坐标公式可求得M点坐标，由对称性可求得N点坐标，连接MN交直线OL于点E，交x轴于点S，此时EP=EM，FP=FN，此时满足△PEF的周长最小，利用两点间距离公式可求得其周长的最小值．22.【答案】（1）证明：在Rt△ABE和Rt△DBE中，，∴△ABE≌△DBE（2）证明：①过G作GH∥AD交BC于H，∵AG=BG，∴BH=DH，∵BD=4DC，设DC=1，BD=4，∴BH=DH=2，∵GH∥AD，∴= = ，∴GM=2MC；②过C作CN⊥AC交AD的延长线于N，则CN∥AG，∴△AGM∽△NCM，∴= ，由①知GM=2MC，∴2NC=AG，∵∠BAC=∠AEB=90°，∴∠ABF=∠CAN=90°﹣∠BAE，∴△ACN∽△BAF，∴= ，∵AB=2AG，∴= ，∴2CN•AG=AF•AC，∴AG2=AF•AC．【解析】【分析】（1）根据全等三角形的判定定理即可得到结论；（2）①过G作GH∥AD交BC于H，由AG=BG，得到BH=DH，根据已知条件设DC=1，BD=4，得到BH=DH=2，根据平行线分线段成比例定理得到= = ，求得GM=2MC；②过C作CN⊥AD交AD的延长线于N，则CN∥AG，根据相似三角形的性质得到= ，由①知GM=2MC，得到2NC=AG，根据相似三角形的性质得到= ，等量代换得到= ，于是得到结论．23.【答案】（1）0；7（2）解：①如图2，取BC的中点O，连接AO，∵AB=AC，∴AO⊥BC，在△ABC中，AB=AC，∠BAC=120°，∴∠ABC=30°，在Rt△AOB中，AB=4，∠ABC=30°，∴AO=2，OB=2 ，∴AB△AC=AO2﹣BO2=4﹣12=﹣8，②取AC的中点D，连接BD，∴AD=CD= AC=2，过点B作BE⊥AC交CA的延长线于E，在Rt△ABE中，∠BAE=180°﹣∠BAC=60°，∴∠ABE=30°，∵AB=4，∴AE=2，BE=2 ，∴DE=AD+AE=4，在Rt△BED中，根据勾股定理得，BD= = =2 ，∴BA△BC=BD2﹣CD2=24；（3）解：如图3，设ON=x，OB=OC=y，∴BC=2y，OA=3x，∵AB△AC=14，∴OA2﹣OB2=14，∴9x2﹣y2=14①，取AN的中点D，连接BD，∴AD=DB= AN= × OA=ON=x，∴OD=ON+DN=2x，在Rt△BOD中，BD2=OB2+OD2=y2+4x2，∵BN△BA=10，∴BD2﹣DN2=10，∴y2+4x2﹣x2=10，∴3x2+y2=10②联立①②得，或（舍），∴BC=4，OA=3 ，∴S△ABC= BC×AO=6 ．【解析】【解答】解：①∵∠BAC=90°，AB=8，AC=6，∴BC=10，∵点O是BC的中点，∴OA=OB=OC= BC=5，∴AB△AC=AO2﹣BO2=25﹣25=0，②如图1，取AC的中点D，连接OD，∴CD= AC=3，∵OA=OC=5，∴OD⊥AC，在Rt△COD中，OD= =4，∴OC△OA=OD2﹣CD2=16﹣9=7，故答案为0，7；【分析】（1）①先根据勾股定理求出BC=10，再利用直角三角形的性质得出OA=OB=OC=5，最后利用新定义即可得出结论；②再用等腰三角形的性质求出CD=3，再利用勾股定理求出OD，最后用新定义即可得出结论；（2）①先利用含30°的直角三角形的性质求出AO=2，OB=2 ，再用新定义即可得出结论；②先构造直角三角形求出BE，AE，再用勾股定理求出BD，最后用新定义即可得出结论；（3）先构造直角三角形，表述出OA，BD2，最后用新定义建立方程组求解即可得出结论．24.【答案】（1）解：如图1，延长PE，QB交于点F，∵△APO和△BQO是等腰直角三角形，∴∠APO=∠BQO=90°，∠AOP=∠BOQ=45°，∵∠AOB=90°，∴∠AOP+∠AOB+∠BOQ=180°，∴点P，O，Q在同一条直线上，∵∠APO=∠BQO=90°，∵点E是AB中点，∴AE=BE，∵∠AEP=∠BEF，∴△APE≌△BFE，∴PE=EF，∴点E是Rt△PQF的斜边PF的中点，∴EP=EQ；（2）解：成立，证明：∵点C，E分别是OA，AB的中点，∴CE∥OB，CE= OB，∴∠DOC=∠ECA，∵点D是Rt△OQB斜边中点，∴DQ= OB，∴CE=DQ，同理：PC=DE，∠DOC=∠BDE，∴∠ECA=∠BDE，∵∠PCE=∠EDQ，∴△EPC≌△QED，∴EP=EQ；（3）解：如图2，连接GO，∵点D，C分别是OB，OA的中点，△APO与△QBO都是等腰直角三角形，∴CQ，GP分别是OB，OA的垂直平分线，∴GB=GO=GA，∴∠GBO=∠GOB，∠GOA=∠GAO，设∠GOB=x，∠GOA=y，∴x+x+y+y+60°=360°【解析】【分析】（1）先判断出点P，O，Q在同一条直线上，再判断出△APE≌△BFE，最后用直角三角形的斜边的中线等于斜边的一半即可得出结论；（2）先判断出CE=DQ，PC=DE，进而判断出△EPC≌△QED 即可得出结论；（3）先判断出CQ，GP分别是OB，OA的垂直平分线，进而得出∠GBO=∠GOB，∠GOA=∠GAO，即可得出结论．。
2024年中考数学复习几何专项练习：动点运动路径之瓜豆原理(含答案解析)
2024年中考数学复习几何专项练习：动点运动路径之瓜豆原理（含答案解析）一、填空题1．如图，等边三角形ABC 中，AB =4，高线AHD 是线段AH 上一动点，以BD 为边向下作等边三角形BDE ，当点D 从点A 运动到点H 的过程中，点E 所经过的路径为线段CM ，则线段CM 的长为，当点D 运动到点H ，此时线段BE 的长为．【答案】2【分析】由“SAS ”可得△ABD ≌△CBE ，推出AD =EC ，可得结论，再由勾股定理求解2,BH =当,D H 重合时，2,BE BH ==从而可得答案.【详解】解：如图，连接EC ．∵△ABC ，△BDE 都是等边三角形，∴BA =BC ，BD =BE ，∠ABC =∠DBE =60°，∴∠ABD =∠CBE ，在△ABD 和△CBE 中，BA BC ABD CBE BD BE =⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△CBE （SAS ），∴AD =EC ，∵点D 从点A 运动到点H ，∴点E的运动路径的长为CM AH ==，当,D H 重合，而BDE △（即BHE ）为等边三角形，,BE BH \=4,,AB AH AH BC ==^Q2,BH ==2,BE ∴=故答案为：．【点睛】本题考查等边三角形的性质，全等三角形的判定和性质，动点的轨迹等知识，解题的关键是正确寻找全等三角形解决问题．2．如图，正方形ABCD 的边长为4，E 为BC 上一点，且1BE =，F 为AB 边上的一个动点，连接EF ，以EF 为边向右侧作等边EFG∆，连接CG ，则CG 的最小值为．【答案】52【分析】由题意分析可知，点F 为主动点，G 为从动点，所以以点E 为旋转中心构造全等关系，得到点G 的运动轨迹，之后通过垂线段最短构造直角三角形获得CG 最小值．【详解】由题意可知，点F 是主动点，点G 是从动点，点F 在线段上运动，点G 也一定在直线轨迹上运动将EFB ∆绕点E 旋转60︒，使EF 与EG 重合，得到EFB EHG ∆≅∆，从而可知EBH ∆为等边三角形，点G 在垂直于HE 的直线HN 上，作CM HN ⊥，则CM 即为CG 的最小值，作EP CM ⊥，可知四边形HEPM 为矩形，则1351222CM MP CP HE EC =+=+=+=.故答案为52．【点睛】本题考查了线段极值问题，分清主动点和从动点，通过旋转构造全等，从而判断出点G 的运动轨迹，是本题的关键．3．如图，等边ABC 中，8AB =，O 是BC 上一点，且14BO BC =，点M 为AB 边上一动点，连接OM ，将线段OM 绕点O 按逆时针方向旋转60︒至ON ，连接BN CN 、，则BCN △周长的最小值为．【答案】8+8【分析】过点N 作ND BC ⊥于点D ，过点O 作OH BM ⊥于点H ，则90OHM ODN ∠=∠=︒，证明HOM DNO ≌，可得DN OH =，从而得到点N 的运动轨迹是直线，且该直线与直线BC 平行，在BC 的左侧，与BCC 关于该直线的对称点E ，连接BE 交该直线于N ，即当点B ，N ，E 三点共线时，BCN △的周长最小，连接CE 交该直线于G ，则22CE CG DN ===CE BC ⊥，求出BE ，即可求解．【详解】解：如图，过点N 作ND BC ⊥于点D ，过点O 作OH BM ⊥于点H ，则90OHM ODN ∠=∠=︒，∵ABC 为等边三角形，∴60ABC ∠=︒，8BC AB ==，∴120BMO BOM ∠+∠=︒，根据题意得：60MON ∠=︒，OM ON =，∴120NOD BOM ∠+∠=︒，∴NOD BMO ∠=∠，∴HOM DNO ≌，∴DN OH =，∵14BO BC =，∴2BO =，∵60ABC ∠=︒，∴30BOH ∠=︒，∴112BH OB ==，∴DN OH ==∴点N 的运动轨迹是直线，且该直线与直线BC 平行，在BC 的左侧，与BC作点C 关于该直线的对称点E ，连接BE 交该直线于N ，即当点B ，N ，E 三点共线时，BCN △的周长最小，连接CE 交该直线于G ，则22CE CG DN ===，CE BC ⊥，∴BE =∴△ACN 的周长的最小值为8+故答案为：8+．【点睛】本题考查旋转变换，全等三角形的判定和性质，轴对称，勾股定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考填空题中的压轴题．4．如图，正方形ABCD 的边长为P 是CD 边上的一动点，连接AP ，将AP 绕点A 顺时针方旋转60︒后得到AQ ，连接CQ ，则点P 在整个运动过程中，线段CQ 所扫过的图形面积为．【答案】3-【分析】根据题意画出点P 在CD 上移动的过程，线段CQ 所扫过的面积就是COQ 的面积，根据正方形的性质，等边三角形的性质以及全等三角形的判定和性质，得出线段CQ 所扫过的图形面积()12ACQ AOQ S S S =- ，再根据等边三角形，等腰直角三角形面积的计算方法进行计算即可．【详解】解：如图，当点P 在点D 时，相应的点Q 落在点O ，当点P 移动到点C 时，相应的点Q 在点Q ，CQ 扫过的面积就是COQ 的面积，由题意可知，AOD △、ACQ 都是等边三角形，AO DO AD ∴===AQ CQ AC ====，四边形ABCD 是正方形，AOD △是等边三角形，906030ODC ∴∠=︒-︒=︒，45ACD ∠=︒，OD CD = ，18030752DOC DCO ︒-︒∴∠=∠==︒，754530ACO ∴∠=︒-︒=︒，45607530QCO QCD DCO ∠=∠-∠=︒+︒-︒=︒，ACO QCO ∴∠=∠，AC QC = ，CO CO =，AOC ∴ ≌()SAS QOC ，AO QO ∴=，604515CQO CAO ∠=∠=︒-︒=︒，()3601801530290AOQ ∴∠=︒-︒-︒-︒⨯=︒，即AOQ △是等腰直角三角形，∴线段CQ 所扫过的图形面积()12ACQ AOQ S S S =- 111222⎛=⨯⨯⨯ ⎝3=，故答案为：3．【点睛】本题考查正方形、等边三角形，等腰直角三角形以及全等三角形的判定和性质，掌握正方形、等边三角形，等腰直角三角形以及全等三角形的判定和性质是正确解答的前提．5．如图，点D 是等边ABC 边AB 上的一动点(不与端点重合)，点D 绕点C 引顺时针方向旋转60 得点E ，所得的CDE 边DE 与BC 交于点F ，则CF DE的最小值为．【分析】由旋转的性质得CDE 为等边三角形，由CEF CAD ∽△△得到CF CE CD AC =，即CF CD DE AC =，从而得到当CD 最小时，比值最小，再由“垂线段最短”得到当CD AB ⊥时，CD 值最小，作出对应图形，利用“ACD 是含30︒角的直角三角形”求出CD AC，从而得解．【详解】解：由旋转的性质得：CD CE =，60DCE ∠=︒，CDE ∴ 为等边三角形，DE CD CE ∴==，60A DEC ∠=∠=︒60ACD DCB ∠+∠=︒60DCB ECF ∠+∠=︒ACD ECF∴∠=∠∵60A DEC ∠=∠= ，ACD ECF∠=∠CEF CAD∴ ∽CF CE CD AC ∴=，即CF CD DE AC=AC 为定值，∴当CD 最小时，比值最小．根据“垂线段最短”可知：当CD AB ⊥时，CD 值最小，过点C 作CD AB ⊥于D ，并补全图形如下：ABC 是等边三角形，CD AB ⊥，60ACB ∠=︒∴1302ACD ACB ∠=∠=︒设AC 2a =，则12AD AC a ==∴CD ==，∴此时CF CD DE AC ==即CF DE 的最小值为2．故答案为：2．【点睛】此题考查图形的旋转变化与性质，等边三角形的判定和性质，相似三角形的判定与性质，含30︒角的直角三角形的性质，垂线段最短，理解“垂线段最短”和利用相似三角形的性质将CF DE转化为CD AC 是解题的关键．6．如图，在ACB △中，60ACB ∠=︒，75BAC ∠=︒，12AC =，点D 是边BC 上的一动点，连接AD ，将线段AD 绕点A 按逆时针方向旋转75︒得到线段AE ，连接CE ，则线段CE 长度的最小值是．【答案】/-【分析】过点A 作AF BC ⊥于点F ，在AB 上取点N ，使12AN AC ==，连接DN ，过点N 作点NM BD ⊥于点M ，证明()SAS NAD DAE ≌，求出CE DN =，得出当DN 最小时，CE 最小，根据垂线段最短，得出当点D 与点M 重合时，DN 最小，则CE 最小，求出最小结果即可．【详解】解：过点A 作AF BC ⊥于点F ，在AB 上取点N ，使12AN AC ==，连接DN ，过点N 作点NM BD ⊥于点M ，如图所示：根据旋转可知，AD AE =，75DAE ∠=︒，∵75BAC DAE ==︒∠∠，∴BAC DAC DAE DAC ∠-∠=∠-∠，即NAD CAE =∠∠，∵AN AC =，AD AE =，∴()SAS NAD CAE ≌，∴CE DN =，∴当DN 最小时，CE 最小，∵垂线段最短，∴当点D 与点M 重合时，DN 最小，则CE 最小，∵90AFC ∠=︒，60BCA ∠=︒，∴906030CAF ∠=︒-︒=︒，∴162CF AC ==，∴AF ==，∵45BAF BAC CAF =-=︒∠∠∠，90AFB ∠=︒，∴904545B ∠=︒-︒=︒，∴B BAF ∠=∠，∴BF AF ==∴AB ==∴12BN AB AN =-=-，∵90BMN ∠=︒，45B ∠=︒，∴904545BNM =︒-︒=︒∠，∴B BNM =∠∠，∴BM NM =，∵222BN NM BM =+，∴()22212NM =-，解得：NM =-，∴CE 的最小值为-．故答案为：【点睛】本题主要考查了全等三角形的判定和性质，勾股定理，等腰三角形的判断和性质，直角三角形的性质，垂线段最短，解题的关键是作出辅助线，构造全等三角形，证明CE DN =．7．如图，点A 的坐标为3⎫⎪⎪⎝⎭，点B 是x 轴正半轴上的一点，将线段AB 绕点A 按逆时针方向旋转60︒得到线段AC ．若点C 的坐标为(,4)k ，则k 的值为．【分析】连接BC ，过A 点作AF x ⊥轴于F ，C 作CD x ⊥轴于点D ，CE AF ⊥于点E ，则四边形DCEF 是矩形，根据将线段AB 绕点A 按逆时针方向旋转60︒得到线段AC ，可得ABC 是等边三角形，AB AC BC ==，由点A 的坐标为，(,4)C k ，有AC ==，而BD ==FB ==OF BF BD OD k ++==，可得k =，解方程可得答案．【详解】解：连接BC ，过A 点作AF x ⊥轴于F ，C 作CD x ⊥轴于点D ，CE AF ⊥于点E ，则四边形DCEF 是矩形，如图：∵将线段AB 绕点A 按逆时针方向旋转60︒得到线段AC ，∴AB AC =，60BAC ∠=︒，∴ABC 是等边三角形，∴AB AC BC ==，∵点A 的坐标为，(,4)C k ，，∴3CE k FD =-=，4CD =，3AF =，∴1AE EF AF CD AF =-=-=，∴AC BC AB ====，在Rt BCD 中，BD =，在Rt AFB 中，FB =∵OF BF BD OD k ++==，∴3k =，设k x =x =，化简变形得：42346490x x -=-，解得21x =-（舍去）或2493x =，∴3x =或3x =-（不符合题意，舍去），∴k ，∴k =，．【点睛】本题考查直角坐标系中的旋转变换，解题的关键是熟练应用勾股定理，用含k 的代数式表示相关线段的长度．8．如图，在边长为6的等边ABC 中，直线AD BC ⊥，E 是AD 上的一个动点连接EC ，将线段EC 绕点C 逆时针方向旋转60︒得到FC ，连接DF ，则点E 运动过程中，DF 的最小值是．【答案】32【分析】取线段AC 的中点G ，连接EG ，根据等边三角形的性质可得出CD CG =以及FCD ECG Ð=Ð，由旋转的性质可得出EC FC =，由此即可利用全等三角形的判定定理SAS 证出FCD ≌ECG ，进而即可得出DF GE =，再根据点G 为AC 的中点，即可得出EG 的最小值，此题得解．【详解】解：取线段AC 的中点G ，连接EG ，如图所示．ABC 为等边三角形，6AC BC ==，且AD 为ABC 的对称轴，132CD CG AB ∴===，60ACD ∠=︒，60ECF =︒∠ ，FCD ECG \Ð=Ð．FCD ∴ ≌()ECG SAS ，DF GE ∴=．当EG BC ∥时，EG 最小，点G 为AC 的中点，∴此时1133222EG DF CD ===⨯=．故答案为：32．【点睛】本题考查了等边三角形的性质以及全等三角形的判定与性质，解题的关键是通过全等三角形的性质找出DF GE =．9．如图，在ABC ∆中，90ACB ︒∠=，点D 在BC 边上，5BC =，2CD =，点E 是边AC 所在直线上的一动点，连接DE ，将DE 绕点D 顺时针方向旋转60︒得到DF ，连接BF ，则BF 的最小值为．【答案】72【分析】当E 与点C 重合时，点F 与等边三角形CDG 的点G 重合，当点F 开始运动时，△ECD ≌△FGD ，故点F 在线段GF 上运动，根据垂线段最短原理，当BF ⊥GF 时，BF 有最小值，根据直角三角形的性质计算即可．【详解】当E与点C重合时，点F与等边三角形CDG的点G重合，∵DE绕点D顺时针方向旋转60 得到DF，∴△DEF是等边三角形，∴∠GDC=∠FDE=60°，ED=FD，∴∠GDC-∠GDE=∠FDE-∠GDE，∴∠EDC=∠FDG，∵△DEF是等边三角形，∴CD=GD，∴△ECD≌△FGD，∴EC=GF，∠ECD=∠FGD=90°，∴点F在线段GF上运动，根据垂线段最短原理，当BF⊥GF时，BF有最小值，如图，当旋转到BF∥DG 时,BF⊥GF，垂足为F，过点D作DH⊥BF，垂足为H，∵∠FGD=90°，∴四边形FGDH是矩形，∴∠GDH=90°，GD=FH=2，∵∠GDC=60°，∴∠BDH=30°，∵BD=BC-CD=5-2=3，∴BH=1232 BD=，∴BF=FH+BH=2+32=72，故答案为：7 2．【点睛】本题考查了等边三角形的判定和性质，矩形的判定和性质，垂线段最短，直角三角形的性质，熟练掌握等边三角形的判定，灵活运用直角的判定和直角三角形的性质是解题的关键．10．如图，正方形ABCD的边长为4，E为BC上一点，且1BE=，F为AB边上的一个动点，连接EF，将EF 烧点E顺时什旋转60°得到EG，连接CG，则CG的最小值为．【答案】5 2【分析】由题意分析可知，点F为主动点，G为从动点，所以以点E为旋转中心构造全等关系，得到点G 的运动轨迹，之后通过垂线段最短构造直角三角形获得CG最小值．【详解】解：由题意可知，点F是主动点，点G是从动点，点F在线段上运动，点G也一定在直线轨迹上运动，将△EFB绕点E旋转60°，使EF与EG重合，得到△EBH为等边三角形，△EBF≌△EHG，∴∠EHG=∠ABC=90°，HE=BE=1，∠BEH=60°，∴点G在垂直于HE的直线HN上．作CM⊥HN，则CM即为CG的最小值，作EP⊥CM，可知四边形HEPM为矩形，∴∠CEP=180°-60°-90°=30°，∴CP=12CE=12×(4-1)=32，则CM=MP+CP=35122 HE PC+=+=，即CG的最小值为5 2．故答案为5 2．【点睛】本题考查了旋转的性质，线段最值问题，全等三角形的性质，正方形的性质，矩形的判定与性质，含30°角的直角三角形的性质，以及垂线段最短等知识，分清主动点和从动点，通过旋转构造全等，从而判断出点G的运动轨迹，是本题的关键，之后运用垂线段最短，构造图形计算，是极值问题中比较典型的类型．11．如图，△ABC是边长为4的等边三角形，点D是AB上异于A，B的一动点，将△ACD绕点C逆时针旋转60°得△BCE，则旋转过程中△BDE周长的最小值【答案】．【分析】由旋转的性质得到BE=AD，于是得到C△DBE=BE+DB+DE=AB+DE=4+DE，根据等边三角形的性质得到DE=CD ，由垂线段最短得到当CD ⊥AB 时，△BDE 的周长最小，于是得到结论．【详解】∵将△ACD 绕点C 逆时针方向旋转60°得到△BCE ，∴∠DCE=60°，DC=EC ，∴△CDE 是等边三角形，由旋转的性质得，BE=AD ，∴C △DBE =BE+DB+DE=AB+DE=4+DE ，∵△CDE 是等边三角形，∴DE=CD ，∴C △DBE =CD+4，由垂线段最短可知，当CD ⊥AB 时，△BDE 的周长最小，此时，∴△BDE 的最小周长，故答案为．【点睛】本题考查了旋转的性质，等边三角形的判定和性质，三角形周长的计算，熟练掌握旋转的性质是解题的关键．12．如图，在ABC 中，8AC BC ==，60BCA ∠= ，直线AD BC ⊥，E 是AD 上的一个动点，连接EC ，将线段EC 绕点C 按逆时针方向旋转60 得到FC ，连接DF ，则点E 运动过程中，DF 的最小值是．【答案】2【分析】根据题意取线段AC 的中点G ，连接EG ，根据等边三角形的性质以及角的计算即可得出CD=CG 以及∠FCD=∠ECG ，由旋转的性质可得出EC=FC ，由此即可利用全等三角形的判定定理SAS 证出△FCD ≌△ECG ，进而即可得出DF=GE ，再根据点G 为AC 的中点，即可得出EG 的最小值．【详解】取线段AC 的中点G ，连接EG，如图所示．8AC BC == ，60BCA ∠= ，ABC ∴为等边三角形，且AD 为ABC 的对称轴，142CD CG AB ∴===，60ACD ∠= ，60ECF ∠= ，FCD ECG ∴∠=∠．在FCD 和ECG 中，FC EC FCD ECG DC GC =⎧⎪∠=∠⎨⎪=⎩，FCD ∴ ≌()ECG SAS ，DF GE ∴=．当//EG BC 时，EG 最小，点G 为AC 的中点，∴此时11224EG DF CD BC ====．故答案为2．【点睛】本题考查了等边三角形的性质以及全等三角形的判定与性质，解题的关键是通过全等三角形的性质找出.DF GE =本题属于中档题，难度不大，解决该题型题目时，根据全等三角形的性质找出相等的边是关键．13．如图，等边△AOB 的边长为4，点P 从点O 出发，沿OA 以每秒1个单位的速度向点A 匀速运动，当点P 到达点A 时停止运动，设点P 运动的时间是t 秒．将线段BP 的中点绕点P 按顺时针方向旋转60°得点C ，点C 随点P 的运动而运动，连接CP 、CA ．在点P 从O 向A 运动的过程中，当△PCA 为直角三角形时t 的值为.【答案】2或83【详解】如图（1）过点P 作PD ⊥OB 于点D ，过C 作CE ⊥OA 于E ，∴∠PDO=∠PEC=90°，∵∠O=60°，∴∠OPD=30°，∴OD=12t ，∴BD=4-12t ，，∵线段BP 的中点绕点P 按顺时针方向旋转60°得点C ，∴∠BPC=60°，BP=2PC ，∵∠OPD=30°，∴∠BPD+∠CPE=90°，∴∠DBP=∠CPE ，∴△PCE ∽△BPD ，∴CE PE PC PD BD PB==，11242PE t ==-，∴，PE=2-14t ，OE=2+34t ，如图（2）当∠PCA=90度时，作CF ⊥PA ，∴△PCF ∽△ACF ，∴△PCF ∽△ACF ，∴PF CF CF AF =，∴CF 2=PF•AF ，∵PF=2-14t ，AF=4-OF=2-34t ，，）2=（2-14t ）（=2-34t ），∴t=2，这时P 是OA 的中点；如图（3）当∠CAP=90°时，此时OA=OE ，∴2+34t=4，∴t=83，故答案为2或83.【点睛】本题考查了相似三角形的判定与性质，勾股定理的运用，等边三角形的性质，直角三角形的性质，旋转的性质等，正确地添加辅助线，求出OE 的长是解题的关键.二、解答题14．在平面直角坐标系中，A （a ，0）、B （b ，0），且a ，b 满足26930a a b -+++=，C 、D 两点分别是y 轴正半轴、x 轴负半轴上的两个动点；（1）如图1，若C （0，4），求△ABC 的面积；（2）如图1，若C （0，4），BC =5，BD=AE ，且∠CBA=∠CDE ，求D 点的坐标；（3）如图2，若∠CBA =60°，以CD 为边，在CD 的右侧作等边△CDE ，连接OE ，当OE 最短时，求A ，E 两点之间的距离．【答案】（1）△ABC 的面积为12；（2）D 点的坐标为（-2，0）；（3）A ，E 两点之间的距离为32【分析】（1）利用完全平方式和绝对值的性质求出a ，b ，然后确定A 、B 两点坐标，从而利用三角形面积公式求解即可；（2）根据题意判断出CBD DAE △≌△，从而得到CB AD =，然后利用勾股定理求出CB ，及可求出结论；（3）首先根据“双等边”模型推出DCB ECA ≌，得到120DBC EAC ∠=∠=︒，进一步推出AE BC ∥，从而确定随着D 点的运动，点E 在过点A 且平行于BC 的直线PQ 上运动，再根据点到直线的最短距离为垂线段的长度，确定OE 最短时，各点的位置关系，最后根据含30°角的直角三角形的性质求解即可．【详解】解：（1）∵26930a a b -+++=，∴()2330a b -++=，由非负性可知，3030a b -=⎧⎨+=⎩，解得：33a b =⎧⎨=-⎩，∴()3,0A ，()3,0B -，()336AB =--=，∵()0,4C ，∴4OC =，∴11641222ABC S AB OC ==⨯⨯= ；（2）由（1）知()3,0A ，()3,0B -，∴OA OB =，∵OC AB ⊥，∴90AOC BOC ∠=∠=︒，在AOC 和BOC 中，OA OB AOC BOC OC OC =⎧⎪∠=∠⎨⎪=⎩∴()AOC BOC SAS △≌△，∴CBO CAO ∠=∠，∵CDA CDE ADE BCD CBA ∠=∠+∠=∠+∠，CBA CDE ∠=∠，∴ADE BCD ∠=∠，在BCD △和ADE V 中，BCD ADE CBD DAE BD AE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()BCD ADE AAS ≌，∴CB AD =，∵()3,0B -，()0,4C ，∴3OB =，4OC =，∴5BC ==，∴5AD BC ==，∵()3,0A ，∴()2,0D -；（3）由（2）可知CB =CA ，∵∠CBA =60°，∴△ABC 为等边三角形，∠BCA =60°，∠DBC =120°，∵△CDE 为等边三角形，∴CD =CE ，∠DCE =60°，∵∠DCE =∠DCB +∠BCE ，∠BCA =∠BCE +∠ECA ，∴∠DCB =∠ECA ，在△DCB 和△ECA 中，CD CE DCB ECA CB CA =⎧⎪∠=∠⎨⎪=⎩∴()DCB ECA SAS ≌，∴120DBC EAC ∠=∠=︒，∵12060180EAC ACB ∠+∠=︒+︒=︒，∴AE BC ∥，即：随着D 点的运动，点E 在过点A 且平行于BC 的直线PQ 上运动，∵要使得OE 最短，∴如图所示，当OE ⊥PQ 时，满足OE 最短，此时∠OEA =90°，∵120DBC EAC ∠=∠=︒，60CAB ∠=︒，∴60OAE EAC CAB ∠=∠-∠=︒，30AOE ∠=︒，∵()3,0A ，∴3OA =，∴1322AE OA ==，∴当OE 最短时，A ，E 两点之间的距离为32．【点睛】本题考查坐标与图形，全等三角形的判定与性质，等腰三角形和等边三角形的判定与性质等，理解平面直角坐标系中点坐标的特征，掌握等腰或等边三角形的性质，熟练使用全等三角形的判定与性质是解题关键．15．在▱ABCD中，∠ABC＝60°，AB＝4，BC＝6．点E'在BC边上且BE'＝4，将B E'绕点B逆时针旋转a°得到BE（0°＜a＜180°）．(1)如图1，当∠EBA＝90°时，求S△BCE；(2)如图2，在旋转过程中，连接CE，取CE中点F，作射线BF交直线AD于点G．①求线段BF的取值范围；②当∠EBF＝120°时，求证：BC﹣DG＝2BF；(3)如图3．当∠EBA＝90°时，点S为线段BE上一动点，过点E作EM⊥射线AS于点M，N为AM中点，直接写出BN的最大值与最小值．=6；【答案】(1)S△BCE(2)①1＜BF＜5；②证明见解答；(3)BNBN的最大值为【分析】（1）如图1，过点E 作EF ⊥BC 交CB 的延长线于点F ，根据题意求得∠EBF =180°-∠EBA -∠ABC =180°-90°-60°=30°，再根据特殊直角三角形的性质进而求得BC 上的高EF =2，代入面积公式算出结果；（2）①如图，在线段FG 上截取FK =BF ，连接EK 、CK ，可证得四边形BCKE 是平行四边形，得出：BE =CK =BE '=4，BC =6，再运用三角形三边关系即可求得答案；②可证△EKB ≌△BGA （AAS ），得出BK =AG ，由AG =AD -DG ，即可推出结论；（3）连接AE ，取AE 的中点P ，PA 的中点Q ，连接BP 、NP 、NQ 、BQ ，可证△ABE 是等腰直角三角形，得出：AE AB P 是AE 的中点，可得：BP ⊥AE ，且BP =AP =EP ，利用勾股定理得BQ，当B 、Q 、N 三点共线时，BN 的最小值=BQ -NQ，当点S 与点E 重合时，EM =0，PN =0，此时，BN 的最大值=BP 【详解】（1）解：如图1，过点E 作EH ⊥BC 交CB 的延长线于点H ，∴∠EHC =90°，∵∠ABC =60°，∠EBA =90°，∴∠EBH =180°-∠EBA -∠ABC =180°-90°-60°=30°，∵点E '在BC 边上且BE '=4，将B E '绕点B 逆时针旋转α°得到BE ，∴BE =B E '=4，∴EH =12BE =12×4=2，又∵BC =6，∴S △BCE =12BC •EH =12×6×2=6；（2）解：①如图，在线段FG 上截取FK =BF ，连接EK 、CK ，∵EF=FC，BF=FK，∴四边形BCKE是平行四边形，∴BE=CK=BE'=4，BC=6，在△BCK中，BC-CK＜BK＜BC+CK，∴6-4＜BK＜6+4，即2＜2BF＜10，∴1＜BF＜5；②证明：∵四边形ABCD是平行四边形，且∠ABC=60°，AB=4，∴∠A=180°-∠ABC=180°-60°=120°，AD∥BC，AD=BC，BE=AB，∵∠EBF=120°，即∠EBK=120°，∴∠EBK=∠A，∵EK∥BC，∴EK∥AD，∴∠EKB=∠BGA，在△EKB和△BGA中，EKB BGAEBK ABE AB∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△EKB≌△BGA（AAS），∴BK=AG，由①知：BK=2BF，又∵AG=AD-DG，∴2BF =BC -DG ；（3）解：连接AE ，取AE 的中点P ，PA 的中点Q ，连接BP 、NP 、NQ 、BQ ，∵∠ABE =90°，AB =BE =4，∴△ABE 是等腰直角三角形，∴AE ，∵点P 是AE 的中点，∴BP ⊥AE ，且BP =AP =EP ，∵N 是AM 的中点，P 是AE 的中点，∴PN 是△AEM 的中位线，∴PN ∥EM ，∴∠ANP =∠AME =90°，∵点Q 是AP 的中点，∴QN =PQ =12AP在Rt △BPQ 中，BQ =当B 、Q 、N 三点共线时，BN 的最小值=BQ -NQ 当点S 与点E 重合时，EM =0，PN =0，此时，BN 的最大值=BP 【点睛】本题是几何变换综合题，主要考查了旋转的性质，平行四边形的性质，等腰直角三角形的性质，全等三角形的判定与性质，三角形中位线定理及勾股定理等知识，解题的关键是灵活运用所学知识解决问题．16．如图，线段AB ＝10cm ，C 是线段AB 上的一个动点（不与A 、B 重合），在AB 上方分别以AC 、BC 为边作正△ACD 和正△BCE ，连接AE ，交CD 于M ，连接BD ，交CE 于N ，AE 、BD 交于H ，连接CH .(1)求sin ∠AHC ；(2)连接DE ，设AD ＝x ，DE ＝y ，求y 与x 之间的函数关系式；(3)把正△BCE 绕C 顺时针旋转一个小于60°的角，在旋转过程中H 到△DCE 的三个顶点距离和最小，即HC +HD +HE 的值最小，HC +HD +HE 的值总等于线段BD 的长.若AC ＝，旋转过程中某一时刻2AH ＝3DH ，此刻△ADH 内有一点P ，求PA +PD +PH 的最小值.【答案】(1)2；(2)y0＜x ＜10）；【分析】（1）过点C 作CT ⊥AE 于点T ，CR ⊥BD 于点R ，先证△ACE ≌△DCB 得∠CAM ＝∠HDM ，由直角三角函数可得sin sin ＝CT CA CAM CD HDM CR ∠=∠= ，从而得CH 平分∠AHB ，进而求得∠AHC ＝∠BHC ＝60°即可求解；（2）如图2中，如图，过点D 作DP ⊥CE 于点P ，先由三角函数求得CP ＝12CD ＝12x ，DP ＝2x ，又由AB ＝10cm ，得CE ＝CB ＝（10﹣x ）cm ，进而得PE ＝|10﹣x ﹣12x |＝|10﹣32x |，最后由勾股定理即可求得y 与x 之间的函数关系式；（3）如图3中，以AD 为边向外作等边△ADW ，连接WH ，由题意WH 是PA +PD +PH ．过点D 作DS ⊥AH 于H ，过点W 作WG ⊥AD 于点G ，过点H 作HK ⊥AD 于K ，过点W 作WQ ⊥HK 于点Q ．假设AH ＝3k ，DH ＝2k ，由勾股定理得AH ＝6，DH ＝4，DSHKDKWQ ＝KGGW ＝KWHQWH 的长即PA +PD +PH 的最小值．【详解】（1）解：过点C 作CT ⊥AE 于点T ，CR ⊥BD 于点R．∵△ADC ，△ECB 都是等边三角形，∴CA ＝CD ，CE ＝CB ，∠ACD ＝∠ECB ＝60°，∴∠ACE ＝∠DCB ，在△ACE 和△DCB 中，CA CD ACE DCB CE CB =⎧⎪∠=∠⎨⎪=⎩，∴△ACE ≌△DCB （SAS ），∴∠CAM ＝∠HDM ，∵CT ⊥AE ，CR ⊥BD ，∴sin sin ＝CT CA CAM CD HDM CR ∠=∠= ，∴CH 平分∠AHB ，∵∠AMC ＝∠DMH ，∴∠AHM ＝∠ACM ＝60°，∴∠AHC ＝∠BHC ＝60°，∴sin ∠AHC ＝2；（2）解：如图2中，如图，过点D 作DP ⊥CE 于点P ．∵AC ＝CD ＝x （cm ），∠DCE ＝60°，∴CP ＝12CD ＝12x ，DP ，∵AB ＝10cm ，∴BC ＝AB ﹣AC ＝（10﹣x ）cm ，∴CE ＝CB ＝（10﹣x ）cm ，∴PE ＝|10﹣x ﹣12x |＝|10﹣32x |，∴y ＝DE （0＜x ＜10）；（3）解：如图3中，以AD 为边向外作等边△ADW ，连接WH ，由题意WH 是PA +PD +PH ．过点D 作DS ⊥AH 于H ，过点W 作WG ⊥AD 于点G ，过点H 作HK ⊥AD 于K ，过点W 作WQ ⊥HK 于点Q ．∵2AH ＝3DH ，∴可以假设AH ＝3k ，DH ＝2k ，∵∠DHS ＝60°，DS ⊥AH ，∴SH ＝12DH ＝k ，DS ，AM ＝2k ，∵AD 2＝AS 2+DS 2，∴（）2＝（2k ）2+）2，∴k ＝2（负根已经舍弃），∴AH ＝6，DH ＝4，DS∵12•AH •DS ＝12•AD •HK ，∴HK ＝7，DK 7，∵AG ＝DG WQKG 是矩形，∴WQ ＝KG GW ＝KW∴HQ ＝KH +KQ ＝7，∴WH ＝∴PA +PD +PH 的最小值为【点睛】本题考查了等边三角形的性质，全等三角形的判定和性质，解直角三角形等知识，添加常用辅助线，构造直角三角形解决问题是解本题的关键．17．在学习了图形的旋转知识后，某数学兴趣小组对教材中有关图形旋转的问题进行了进一步探究．（1）问题梳理，问题呈现：如图1，点D 在等边ABC 的边BC 上，过点C 画AB 的平行线l ，在l 上取CE BD =，连接AE ，则在图1中会产生一对旋转图形．请结合问题中的条件，证明：ABD ACE ≌△△；（2）初步尝试：如图2，在ABC 中，AB AC =，点D 在BC 边上，且BD DC <，将ABD △沿某条直线翻折，使得AB 与AC 重合，点D 与BC 边上点F 重合，再将ACF △沿AC 所在直线翻折，得到ACE △，则在图2中会产生一对旋转图形．若30BAC ∠=︒，6AD =，连接DE ，求ADE V 的面积；（3）深入探究：如图3，在ABC 中，60ACB ∠=︒，75BAC ∠=︒，6AC =，点D 是边BC 上的任意一点，连接AD ，将线段AD 绕点A 按逆时针方向旋转75°，得到线段AE ，连接CE ，求线段CE 长度的最小值．【答案】（1）见解析；（2）9；（3）【分析】（1）根据△ABC 是等边三角形，可得AB ＝AC ，∠BAC ＝∠B ＝60°，进而利用SAS 可证明△ABD ≌△ACE ．（2）如图2，过点E 作EH ⊥AD 于H ，由翻折可得△ACE ≌△ABD ≌△ACF ，可得AE ＝AD ＝6，EH ＝3，再运用S △ADE ＝12×AD ×EH ，即可求得答案．（3）如图3中，在AB 上截取AN ＝AC ，连接DN ，作NH ⊥BC 于H ，作AM ⊥BC 于M ．利用SAS 证明△EAC ≌△DAN ，推出当DN 的值最小时，EC 的值最小，求出HN 的值即可解决问题．【详解】（1）如图1，∵△ABC 是等边三角形，∴AB ＝AC ，∠BAC ＝∠B ＝60°，∵CE ∥AB ，∴∠ACE ＝∠BAC ＝60°，∴∠B ＝∠ACE ，在△ABD 和△ACE 中，AB AC B ACE BD CE =⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△ACE （SAS ）；（2）如图2，过点E 作EH ⊥AD 于H，∵由翻折可得：△ACF ≌△ABD ，△ACE ≌△ACF ，∴△ACE ≌△ABD ≌△ACF ，∴AE ＝AD ＝6，∠CAE ＝∠BAD ，∴∠DAE ＝∠BAC ＝30°，∵EH ⊥AD ，∴EH ＝12AE ＝3，∴S △ADE ＝12×AD ×EH ＝12×6×3＝9；（3）如图3中，在AB 上截取AN ＝AC ，连接DN ，作NH ⊥BC 于H ，作AM ⊥BC 于M．∵∠CAB ＝∠DAE ，∴∠EAC ＝∠DAN ，∵AE ＝AD ，AC ＝AN ，∴△EAC ≌△DAN （SAS ），∴CE ＝DN ，∴当DN 的值最小时，EC 的值最小，在Rt △ACM 中，∵∠ACM ＝60°，AC ＝6，∴30CAM ∠=︒,∴132CM AC ==,∴AM∵∠MAB ＝∠BAC −∠CAM ＝75°−30°＝45°，∴AMB 为等腰直角三角形，∴AB=，∴NB ＝AB −AN ＝−6，在Rt △NHB 中，∵∠B ＝45°，∴NBH △为等腰直角三角形，∴NH根据垂线段最短可知，当点D 与H 重合时，DN 的值最小，∴CE 的最小值为．【点睛】本题属于几何变换综合题，考查了全等三角形的判定和性质，等腰三角形的性质，垂线段最短等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会利用垂线段最短解决最值问题，属于中考压轴题．18．（一）发现探究在△ABC中AB＝AC，点P在平面内，连接AP并将线段AP绕点A顺时针方向旋转与∠BAC相等的角度，得到线段AQ，连接BQ；【发现】如图1如果点P是BC边上任意一点，则线段BQ和线段PC的数量关系是；【探究】如图2，如果点P为平面内任意一点．前面发现的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由．请仅以图2所示的位置关系加以证明（或说明）；（二）拓展应用【应用】如图3，在△DEF中，DE＝6，∠EDF＝60°，∠DEF＝90°，P是线段EF上的任意一点连接DP，将线段DP绕点D顺时针方向旋转60°，得到线段DQ，连接EQ请求出线段EQ长度的最小值．【答案】【发现】BQ＝PC；【探究】BQ＝PC仍然成立，证明见解析；【应用】线段EQ长度的最小值为3．【分析】[发现]先判断出∠BAQ＝∠CAP，进而用SAS判断出△BAQ≌△CAP，即可得出结论；[探究]结论BQ＝PC仍然成立，理由同【发现】的方法；[应用]在DF上取一点H，使DH＝DE，连接PH，过点H作HM⊥EF于M，构造出△DEQ≌△DHP，得出EQ＝HP，当HP⊥EF（点P和点M重合）时，EQ最小，求HM即可．【详解】[发现]由旋转知，AQ＝AP，∵∠PAQ＝∠BAC，∴∠PAQ﹣∠BAP＝∠BAC﹣∠BAP，∴∠BAQ＝∠CAP，∵AB＝AC，∴△BAQ≌△CAP（SAS），∴BQ＝CP，故答案为：BQ＝PC；【探究】结论：BQ＝PC仍然成立，理由：由旋转知，AQ＝AP，∵∠PAQ＝∠BAC，∴∠PAQ﹣∠BAP＝∠BAC﹣∠BAP，∴∠BAQ＝∠CAP，∵AB＝AC，∴△BAQ≌△CAP（SAS），∴BQ＝CP，【应用】如图3，在DF上取一点H，使DH＝DE，连接PH，过点H作HM⊥EF于M，由旋转知，DQ＝DP，∠PDQ＝60°，∵∠EDF＝60°，∴∠PDQ＝∠EDF，∴∠EDQ＝∠HDP，∴△DEQ≌△DHP（SAS），∴EQ＝HP，求EQ最小，就是求HP最小，当HP⊥EF（点P和点M重合）时，HP最小，最小值为HM，∵∠EDF＝60°，∠DEF＝90°，∴∠F＝30°，∵DE＝6，∴DF＝2DE＝12，∵DH＝DE=6，∴FH＝6，∵∠F＝30°，∴HM=3．线段EQ长度的最小值为3．．【点睛】此题是几何变换综合题，主要考查了旋转的性质，全等三角形的判定和性质，含30°角的直角三角形的性质，恰当的作辅助线，把所求线段转化为与动点P有关的线段，根据垂线段最短确定线段位置是解本题的关键．。
中考数学复习：三角形中常用的辅助线作法举例
三角形11种常用的辅助线一、在利用三角形三边关系证明线段不等关系时，若直接证不出来，可连接两点或延长某边构成三角形，使结论中出现的线段在一个或几个三角形中，再运用三角形三边的不等关系证明，如例1：已知如图1-1：D 、E 为△ABC 内两点,求证:AB ＋AC ＞BD ＋DE ＋CE.证明：（法一）将DE 两边延长分别交AB 、AC 于M 、N ， 在△AMN 中，AM ＋AN ＞ MD ＋DE ＋NE;（1） 在△BDM 中，MB ＋MD ＞BD ； （2） 在△CEN 中，CN ＋NE ＞CE ； （3） 由（1）＋（2）＋（3）得：AM ＋AN ＋MB ＋MD ＋CN ＋NE ＞MD ＋DE ＋NE ＋BD ＋CE ∴AB ＋AC ＞BD ＋DE ＋EC（法二：）如图1-2， 延长BD 交 AC 于F ，延长CE 交BF 于G ， 在△ABF 和△GFC 和△GDE 中有：AB ＋AF ＞ BD ＋DG ＋GF （三角形两边之和大于第三边）（1） GF ＋FC ＞GE ＋CE （同上）....................................（2） DG ＋GE ＞DE （同上） (3)11-图21-图由（1）＋（2）＋（3）得：AB ＋AF ＋GF ＋FC ＋DG ＋GE ＞BD ＋DG ＋GF ＋GE ＋CE ＋DE ∴AB ＋AC ＞BD ＋DE ＋EC 。
二、在利用三角形的外角大于任何和它不相邻的内角时如直接证不出来时，可连接两点或延长某边，构造三角形，使求证的大角在某个三角形的外角的位置上，小角处于这个三角形的内角位置上，再利用外角定理：例如：如图2-1：已知D 为△ABC 内的任一点，求证：∠BDC ＞∠BAC 。
分析：因为∠BDC 与∠BAC 不在同一个三角形中，没有直接的联系，可适当添加辅助线构造新的三角形，使∠BDC 处于在外角的位置，∠BAC 处于在内角的位置；证法一：延长BD 交AC 于点E ，这时∠BDC 是△EDC 的外角， ∴∠BDC ＞∠DEC ，同理∠DEC ＞∠BAC ，∴∠BDC ＞∠BAC证法二：连接AD ，并延长交BC 于F ∵∠BDF 是△ABD 的外角 ∴∠BDF ＞∠BAD ，同理，∠CDF ＞∠CAD∴∠BDF ＋∠CDF ＞∠BAD ＋∠CAD 即：∠BDC ＞∠BAC 。
2021届中考数学专题复习训练——二次函数 专题9二次函数综合之等腰直角三角形和等边三角形的判定
等边三角形的判定【经典例题1】如图所示，已知抛物线的顶点为坐标原点O ，矩形ABCD 的顶点A ，D 在抛物线上，且AD 平行x 轴，交y 轴于点F ，AB 的中点E 在x 轴上，B 点的坐标为（2，1），点P （a ，b ）在抛物线上运动．（点P 异于点O ）(1)求此抛物线的解析式．(2)过点P 作CB 所在直线的垂线，垂足为点R ，①求证：PF=PR ；②是否存在点P ，使得△PFR 为等边三角形？若存在，求出点P 的坐标；若不存在，请说明理由；③延长PF 交抛物线于另一点Q ，过Q 作BC 所在直线的垂线，垂足为S ，试判断 △RSF 的形状．【解析】(1)∵抛物线的顶点为坐标原点，∴A 、D 关于抛物线的对称轴对称；∵E 是AB 的中点，∴O 是矩形ABCD 对角线的交点，又B(2，1)∴A(2，−1)、D(−2，−1)；由于抛物线的顶点为(0，0)，可设其解析式为：y=ax 2，则有：4a =−1，a =−41 ∴抛物线的解析式为：y=−41x 2.(2)①证明：由抛物线的解析式知：P(a ，−41a 2)，而R(a ，1)、F(0，−1)， 则：PF=222)141()0(+-+-a a ，PR=1−(−41a 2)=41a 2+1. ∴PF=PR.②由①得：RF=42+a ；若△PFR 为等边三角形，则RF=PF=PR ，得：42+a =41a 2+1，即：161a 4−21a 2−3=0，得： a 2=−4(舍去)，a 2=12；∴a =±23，−41a 2=−3； ∴存在符合条件的P 点，坐标为(23，−3)、(−23，−3).③同①可证得：QF=QS ；在等腰△SQF 中，∠1=21(180°−∠SQF)； 同理，在等腰△RPF 中，∠2=21(180°−∠RPF)； ∵QS ⊥BC 、PR ⊥BC ，∴QS ∥PR ，∠SQP+∠RPF=180°∴∠1+∠2=21(360°−∠SQF−∠RPF)=90° ∴∠SFR=180°−∠1−∠2=90°，即△SFR 是直角三角形。
新人教版2021年中考数学二轮复习专题练习上常用辅助线_构造等边三角形
6.构造等边三角形1.公园里有一块形如四边形ABCD 的草地，测得10BC CD ==米，120B C ∠=∠=︒，45A ∠=︒．请你求出这块草地的面积？答案：见解析 解析：延长DC AB 、交于E ，连结DB ，∵120ABC BCD ∠=∠=︒，∴60EBC ECB ∠=∠=︒， ∴EBC ∆是等边三角形，∵DC CB =，∴30CDB DBC ∠=∠=︒， ∴90DBA ∠=︒，103BD =， ∵45A ∠=︒，∴103AB =，∴()211031502ABDS ∆==，11110103253222BCD BDE S S ∆∆==⨯⨯⨯=，∴这块草地的面积为()150253+平方米．DCBAEABCD2.如图：已知10AB =,点C D 、在线段AB 上且2AC DB ==；P 是线段CD 上的动点,分别以AP PB 、为边在线段AB 的同侧作等边AEP 和等边PFB ,连结EF ,设EF 的中点为G ；当点P 从点C 运动到点D 时,则点G 移动路径的长是____．答案：3解析：分别延长AE BF 、交于点H ，易证四边形EPFH 为平行四边形，得出G 为PP 中点，则P 的运行轨迹为三角形PPP 的中位线PP ．再求出PP 的长，运用中位线的性质求出PP 的长度即可．解：如图，分别延长PP、PP 交于点P ．∵∠P ＝∠PPP ＝60°，∴PP ∥PP ，∵∠P ＝∠PPP ＝60°，∴PP ∥PP ，∴四边形PPPP 为平行四边形，∴PP 与PP 互相平分．∵P 为PP 的中点，∴P 正好为PP 中点，即在P 的运动过程中，P 始终为PP 的中点，所以P 的运行轨迹为三角形PPP 的中位线PP ．∵PP ＝10－2－2＝6，∴PP＝3，即P 的移动路径长为33.四边形ABCD ，有BC CD =，120B C ∠=∠=︒，45A ∠=︒．请你求D ∠=____︒.AB C DP EFG答案：75 解析：延长DC AB 、交于E ，连结DB ，∵120ABC BCD ∠=∠=︒，∴60EBC ECB ∠=∠=︒， ∴EBC ∆是等边三角形，∵DC CB =，∴30CDB DBC ∠=∠=︒， ∴90DBA ∠=︒，∵45A ∠=︒，∴904545ADB ∠=︒-︒=︒， ∴453075ADC ADB BDC ∠=∠+∠=︒+︒=︒4.如图，四边形ABCD 中，AC BD ， 是对角线，ABC 是等边三角形．3035ADC AD BD ∠=︒==，， ，则CD 的长为____.DCBAEABCD答案：4解析：首先以CD 为边作等边CDE ，连接AE ，利用全等三角形的判定得出BCD ACE ≌ ，进而求出DE 的长即可．解：如图，以CD 为边作等边CDE ，连接AEBCD BCA ACD DCE ACD ACE ∠=∠+∠=∠+∠=∠ ，∴ 在BCD 和ACE 中， AC BC ACE BCD CD CE =⎧⎪∠=∠⎨⎪=⎩BCD ACE SAS ∴≌（）， BD AE ∴= ．又30ADC ∠=︒ ，90ADE ∴∠=︒ ．在Rt ADE 中，53AE AD ==， ， 于是224DE AE AD =-= ，4CD DE ∴==．5.如图所示，在ABC 中，AB AC D E =，、是ABC 内两点，AD 平分60BAC EBC E ∠∠=∠=︒．，若62BE DE ==，，则BC 的长度是__.答案：8解析：作出辅助线后根据等腰三角形的性质得出62BE DE ==，，进而得出BEM 为等边三角形，EFD 为等边三角形，从而得出BN 的长，进而求出答案． 解：延长ED 交BC 于M ，延长AD 交BC 于N ，作DF BC 于F ，AB AC AD =，平分BAC ∠ ， AN BC BN CN ∴⊥=， ， 60EBC E ∠=∠=︒ ，BEM ∴为等边三角形， EFD ∴为等边三角形，62BE DE ==， ，4DM ∴= ，BEM 为等边三角形，60EMB ∴∠=︒ ， AN BC ⊥ ， 90DNM ∴∠=︒ ， 30NDM ∴∠=︒ ，2NM ∴= ， 4BN ∴= ， 28BC BN ∴== ，6.如图，六边形ABCDEF 中，每一个内角都是1201230828AB BC CD DE ︒====，，，，．求这个六边形的周长为_____.答案：116解析：凸六边形ABCDEF ，并不是一规则的六边形，但六个角都是120︒ ，所以通过适当的向外作延长线，可得到等边三角形，进而求解．解：如图，分别作直线AF ED BC 、、 的延长线和反向延长线使它们交于点G H P 、、 ．六边形ABCDEF 的六个角都是120°，∴ 六边形ABCDEF 的每一个外角的度数都是60°． PGH BGA DHC EFP ∴、、、 都是等边三角形． 128GC BC DH CH ∴====， ．1230850GH ∴=++=，5028814FE PE PH ED DH ==--=--=，50141224AF PG PF AG =--=--=．∴ 六边形的周长为：24123082814116+++++= ．7.如图，已知120ABC ∠=︒ ，BD 平分60ABC DAC ∠∠=︒， ，若23AB BC ==， ，则BD 的长是_____.答案：5解析：在CB 的延长线上取点E ，使BE AB =，连接AE ，则可证得ABE 为等边三角形，再结合条件可证明ABD AEC ≌ ，可得BD CE = ，再利用线段的和差可求得CE ，则可求得BD .解：在CB 的延长线上取点E ，使BE AB =，连接AE ，120ABC ∠=︒ ，18060ABE ABC ∴∠=∠=︒﹣ ，BE AB = ，ABE ∴ 为等边三角形，60AE AB BAE E ∴=∠=∠=︒， ， 60DAC ∠=︒ ，DAC BAE ∴∠= ，BAD BAC DAC EAC BAC BAE ∠=∠+∠∠=∠+∠， ， BAD EAC ∴∠=∠ ，BD 平分ABC ∠ ，，ABD E ∴∠=∠ ，在ABD 和AEC 中，BAD EAC AB AEABD E ∠=∠⎧⎪=⎨⎪∠=∠⎩， ABD AEC ASA ∴≌（）， BD CE ∴= ，325CE BE BC AB BC =+=+=+= ，5BD ∴= ，8.如图，在ABC 中，AB AC D E =，、 是ABC 内两点，AD 平分60BAC EBC E ∠∠=∠=︒， ，若602BE cm DE cm ==， ，则BC = ____cm ．答案：62解析：作出辅助线后根据等腰三角形的性质得出62BE DE ==， ，进而得出BEM 为等边三角形，EFD 为等边三角形，从而得出BN 的长，进而求出答案．解：延长ED交BC于M，延长AD交BC于N，作DF BC，=，AD平分BAC∠，AB AC，，∴⊥=AN BC BN CN∠=∠=︒，EBC E60∴为等边三角形，BEM∴为等边三角形，EFD，，==BE DE602DM∴=，58BEM为等边三角形，∴∠=︒，60EMB⊥，AN BC∴∠=︒，DNM90∴∠=︒，NDM30∴=，NM29∴=，BN31∴==，BC BN262故答案为62．9.如图，过边长为1的等边ABC 的边AB 上一点P ，作PE AC ⊥ 于E Q ， 为BC 延长线上一点，当PA CQ = 时，连PQ 交AC 边于D ，则DE 的长为____.（注：若答案不是整数，请化为小数）答案：0.5 解析：过P 作PFBC 交AC 于F ，得出等边三角形APF ，推出AP PF QC == ，根据等腰三角形性质求出EF AE = ，证PFD QCD ≌ ，推出FD CD = ，推出12DE AC =即可．解：过P 作PFBC 交AC 于F ．PF BC ，ABC 是等边三角形， PFD QCD APF ∴∠=∠， 是等边三角形，AP PF AF ∴== ，PE AC ⊥ ，AE EF ∴= ，AP PF AP CQ ==， ，PF CQ ∴= ．在PFD 和QCD 中，PFD QCD PDF QDC PF CQ ∠=∠⎧⎪∠=∠⎨⎪=⎩，PFD QCD AAS ∴≌（） ，FD CD ∴= ，AE EF = ，EF FD AE CD ∴+=+ ，12AE CD DE AC ∴+==， 1AC = ， 10.52DE ∴== ．10.如图，ABC 中，AB AC AD =， 平分BAC D E ∠，、 是ABC 内两点，且60ECB E ∠=∠=︒ ，若82CE DE ==， ，则BC =_____.答案：10解析：延长ED交BC于M，延长AD交BC于N，根据等腰三角形的性质得出，，进而得出CEM为等边三角形，从而得出BN的长，进而求出答案．==CE DE82解：延长ED交BC于M，延长AD交BC于N，∠，=，平分BACAB AC AD∴⊥=，，AN BC BN CNECB E∠=∠=︒，60∴为等边三角形，CEM，，==82CE DE∴=，6DMCEM为等边三角形，60∴∠=︒，EMC⊥，AN BC∴∠=︒，90DNM∴∠=︒，NDM30∴=，NM3﹣，∴==CN835∴=，5BN∴==．BC BN210故答案为：10．11.如图，凸四边形ABCD 满足条件：60120AB AD BAD BCD =∠=︒∠=︒，， 那么AC ____BC CD +．（填“大于”或“小于”或“等于”）答案：等于解析：延长DC 到点E ，使得BC CE = ，连接BE 和BD ，根据已知条件和所作辅助线可得ABD 与BCE 均为等边三角形，证明ABC 和DBE 全等即可证明；解：延长DC 到点E ，使得BC CE = ，连接BE 和BD .∵120BCD ∠=︒∴18012060BCE ∠=︒-︒=︒又BC CE = ，60AB AD BAD =∠=︒，ABD ∴ 与BCE 均为等边三角形60BD AB BE BC ABD EBC ∴==∠=∠=︒，，ABD DBC EBC DBC ∴∠+∠=∠+∠ ,即ABC DBE ∠=∠在ABC 和DBE 中AB BD ABC DBE BC BE =∠=∠=⎧⎪⎨⎪⎩，∴ABC DBE ≌∴BD DE =∵DE CD EC CD BC =+=+AC BC CD ∴=+ ．故答案为：相等12.已知：如图，等边ABC 中，1AB P =， 是AB 边上一动点，作PE BC ⊥ ，垂足为E ；作EF AC ⊥ ，垂足为F ；作FQ AB ⊥ ，垂足为Q ．（1）设BP x AQ y ==， ，求y 与x 之间的函数关系式；（2）当点P 和点Q 重合时，求线段EF 的长；（3）当点P 和点Q 不重合，但线段PE FQ 、 延长线相交时，求它们与线段EF 围成的三角形周长的取值范围．答案：见解析解析：（1）由已知等边ABC 中，可得每个角都是60︒ ，由作PE BC ⊥ ，垂足为E ；作EF AC ⊥ ，垂足为F ；作FQ AB ⊥ ，垂足为Q ，得三个直角三角形且都有30︒的角，据此用x 可表示出BE CE CF ，， ，相继表示出AF AQ ， ，求出y 与x 之间的函数关系式．（2）由已知可列出方程组结合已知求出EF 的长．（3）当线段PE FQ 、 相交时，根据已知得到它们与线段EF 围成的三角形三个角都是60︒ 解：（1）ABC 是等边三角形，1AB = ．601A B C BC CA AB ∴∠=∠=∠=︒===， ．又90BEP CFE FQA BP x ∠=∠=∠=︒=， ．11122BE x CE x ∴==-， ，1111111242424CF x AF x x =-=--=+，（）． 11112224AQ AF x ∴==+（） ， 1184y x ∴=+ ．（2）由方程组11184x y y x +=⎧⎪⎨=+⎪⎩得23x = ． ∴ 当点P 和点Q 重合时，23x =，11333243EF CF x ∴==-=（） ．（3）设线段EP FQ 、 的延长线相交于点M ，EF AC ⊥ ，390QFE ∴∠+∠=︒ ，FQ AB ⊥ ，390A ∴∠+∠=︒ ，60A QFE ∴∠=∠=︒ ，190C ∠+∠=︒ ，1290∠+∠=︒ ，260C ∴∠=∠=︒ ，MEF ∴ 是等边三角形，且当点P 和点Q 重合时，EF 最短为33. 且当点P 和点B 重合时，EF 最长为32 3332m ∴<≤ ．13.如图，在四边形ABCD 中，60120AB AD BAD BCD =∠=︒∠=︒，， ，连接AC BD ， 交于点E ．（1）若2BC CD == ，M 为线段AC 上一点，且12AM CM =：： ，连接BM ，求点C 到BM 的距离．（2）证明：BC CD AC += ．答案：见解析解析：（1）由条件可以证明ABC ADC ≌，可以得出30BAC DAC ∠=∠=︒ ，6090ACB ACD AEB ∠=∠=︒∠=︒， ，求出90ABC ∠=︒ ，由勾股定理可以求出423AC AB ==， ，由12AM CM =：： 可以求得AM CM 、 的值，在Rt BEC 中由勾股定理可以求出CE BE 、 的值，从而求出BM 的值，过点C 作CF MB ⊥ 于F ，利用三角形的面积相等建立等量关系就可以求出结论．（2）要证BC DC AC += ，延长BC 到E ，使CE CD = ，则求AC BE = 即可．由60AB AD ABD =∠=︒， ，得ABD 是等边三角形，进而得60ADB AD BD ∠=︒=，，又有120BCD ∠=︒ ，则DCE 是等边三角形，所以得ACD BDE ≌ ，则AC BE BC CD ==+ ．解：（1）60AB AD BAD =∠=︒， ，ABD ∴ 是等边三角形，60ABD ADB ∴∠=∠=︒ ．BC CD = ，ABC ADC ∴≌ ，3060BAC DAC ACB ACD ∴∠=∠=︒∠=∠=︒， ．9090AEB BEC ABC ∴∠=∠=︒∠=︒， ， 112CE BC ∴==，324BE AC BC ===， ． 12AM CM =：： ，43AM ∴=，83CM = ， 53EM ∴= ，在Rt BEM 中由勾股定理得 225213(3)()33BM =+= 过点C 作CF BM ⊥ 于点F ．22BM CF CM BE ⋅⋅∴= ． 213833322CF ⨯∴= ， 43913CF ∴= ． 即点C 到BM的距离43913． （2）证明：延长BC 到点F ，使CF CB = ，连接DF ， ，60AB AD ABD =∠=︒，ABD ∴ 是等边三角形，60ADB AD BD ∴∠=︒=， ，BC CD ∴= ，CF CD ∴= ．120BCD ∠=︒ ，18060DCF BCD ∴∠=︒∠=︒﹣ ，DCF ∴ 是等边三角形，60CDF ADB DC DF ∴∠=∠=︒=， ，ADC BDF ∴∠=∠ ，又AD BD = ，ACD BDF ∴≌ ，AC BF BC CF ∴==+ ，即AC BC CD =+ ．14.已知：如图，在等边三角形ABC 中，点D 是AC 边上的一个动点（D 与A C ， 不重合），延长AB 到E ，使BE CD = ，连接DE 交BC 于点F ．（1）求证：DF EF = ；（2）若ABC 的边长为10 ，设CD x BF y ==， ，求y 与x 的函数关系式，写出自变量x 的取值范围．答案：见解析解析：（1）过D 作DM AB 交BC 于M ，则CDM 为等边三角形，得CD DM = ，而BE CD = ，得到DM BE = ，易证得FDM FEB ≌ ，根据全等三角形的性质即可得到结论；（2）由（1）得FDM FEB ≌ ，得到MF BF y == ，易得CM CD x == ，而10BC = ，即有10x y y ++= ，即可得到y 与x 间的函数关系式．解：（1）证明：过D 作DM AB 交BC 于M ，CDM A CMD ABC ∴∠=∠∠=∠， ，又∵在等边三角形ABC 中，60A ABC C ∠=∠=∠=︒ ，CDM CMD C ∴∠=∠=∠ ，CDM ∴ 是等边三角形，CD DM ∴= ，又CD BE = ，BE DM ∴= ，DM AE ，MDF E ∴∠=∠ ，在DMF 和EBF 中，MDF E ∠=∠ ，DFM EFB ∠=∠ ，DM BE = ，DMF EBF AAS ∴≌（）， DF EF ∴= ；（2）由（1）得DMF EBF ≌ ，BF MF y ∴== ，由（1）得CDM 是等边三角形，CM CD x ∴== ，又10CM MF FB BC ++== ，210y x ∴+= ， 即152010x y x =-（＜＜）．15.如图，在四边形ABCD 中，260254AB AD A BC CD ==∠=︒==，，， ．（1）求ADC ∠ 的度数．（2）求四边形ABCD 的面积．答案：见解析解析：（1）连接BD ，根据260AB AD A ==∠=︒， ，得出ABD 是等边三角形，求得2BD = ，然后根据勾股定理的逆定理判断三角形BDC 是直角三角形，从而求得150ADC ∠=︒ ；（2）根据四边形的面积等于三角形ABD 和三角形BCD 的和即可求得；解：（1）连接BD ，260AB AD A ==∠=︒， ，ABD ∴ 是等边三角形，260BD ADB ∴=∠=︒，，254BC CD ==， ， 则22222224202520BD CD BC +=+===，（） ， 222BD CD BC ∴+= ，90BDC ∴∠=︒ ，150ADC ∴∠=︒ ；（2）131131••222443222222ABD BDC S S S AD AD BD DC =+=+=⨯⨯⨯+⨯⨯=+．16.已知：如图，四边形ABCD 中，6030ADC ABC AD CD ∠=︒∠=︒=，， ．（1）连接AC ACD ， 的形状是？（2）求证：222BD AB BC =+ ．答案：见解析解析：（1）根据全等三角形的判定定理“有一内角为60︒ 的等腰三角形是等边三角形”推知ACD 是等边三角形．（2）如图，以BC 为边向形外作等边BCE ，连接AE ．构造全等三角形（BCD ECA ≌ ），然后根据全等三角形的性质、勾股定理证得结论．解：（1）如图，连接AC ．60ADC AD CD ∠=︒=， ，ACD ∴ 是等边三角形；故答案是：等边三角形；（2）如图，以BC 为边向形外作等边BCE ，连接AE ．由（1）知，ACD 是等边三角形，则60DC AC EC BC ACD BCE ==∠=∠=︒，， ，在BCD 与ECA ，∵DC AC DCB ACE BC EC =⎧⎪∠=∠⎨⎪=⎩，BCD ECA SAS ∴≌（）， AE BD ∴= ，90ABE ∠=︒ ，∴ 在Rt ABE 中，有222AB BE AE += ，即222AB BC BD += ．17.如图，在ABC 中，AB AC D =， 是三角形外一点，且60ABD BD DC AB ∠=︒+=， ．求证：ACD ∠= ____°．答案：60解析：首先延长BD 至E ，使CD DE = ，连接AE AD ， ，由BD DC AB += ，易得ABE 是等边三角形，继而证得ACD ADE ≌ ，则可证得：60ACD E ∠=∠=︒ ． 证明：延长BD 至E ，使CD DE = ，连接AE AD ，，BD CD AB BE BD DE +==+， ，BE AB ∴= ，60ABD ∠=︒ ，ABE ∴ 是等边三角形，60AE AB AC E ∴==∠=︒， ，在ACD 和ADE 中，AC AE CD DE AD AD =⎧⎪=⎨⎪=⎩，ACD ADE SSS ∴≌（），60ACD E ∴∠=∠=︒ ．18.如图，凸六边形ABCDEF 的六个角都是120︒ ，边长28116AB cm BC cm CD cm DE cm ====，，， ，求出这个六边形的周长为____cm .答案：46解析：凸六边形ABCDEF ，并不是一规则的六边形，但六个角都是120︒ ，所以通过适当的向外作延长线，可得到等边三角形，进而求解．解：如图，分别作直线AB CD EF 、、 的延长线使它们交于点G H P 、、 ．因为六边形ABCDEF 的六个角都是120︒，所以六边形ABCDEF 的每一个外角的度数都是60︒ ．所以三角形APF 、三角形BGC 、三角形DHE 、三角形GHP 都是等边三角形． 所以86GC BC cm DH DE cm ====， ．所以811625GH cm =++= ，252815FA PA PG AB BG cm ==--=--= ，251564EF PH PF EH cm =--=--= ．所以六边形的周长为2811641546cm +++++= ．19.如图，在六边形ABCDEF 中，A B C D E F ∠=∠=∠=∠=∠=∠ ．（1）试说明MAF 为等边三角形；（2）请探索AB BC EF DE ，，， 之间的关系（等量关系或位置关系）并说明理由．答案：见解析解析：（1）根据多边形的内角和定理求出120A B C D E F ∠=∠=∠=∠=∠=∠=︒ ，求出60MAF MFA ∠=∠=︒ ，得出等边三角形MAF ，推出MA MF = ，同理求出NBC MNG EDG 、、 是等边三角形，推出BN BC DE EG ==， ，求出AN FG = ，即可求出答案．解：（1）作直线AB 、直线EF 、直线CD AB ， 和EF 交于M AB ， 和CD 交于N EF ， 和CD 交于G ，A B C D E F ∠=∠=∠=∠=∠=∠ ，62180A B C D E F ∠+∠+∠+∠+∠+∠=-⨯︒（） ，120A B C D E F ∴∠=∠=∠=∠=∠=∠=︒ ，18012060MAF MFA ∴∠=∠=︒-︒=︒ ，MF MA ∴= ，MAF ∴为等边三角形．（2）AB BC EF DE +=+ ，理由是：120ABC BCD ∠=∠=︒ ，18012060NBC NCB ∴∠=∠=︒︒=︒﹣ ，NB NC ∴= ，BNC ∴ 是等边三角形，60BC BN N ∴=∠=︒， ，同理60DE EG G =∠=︒， ，60G N ∴∠=∠=︒ ，MN MG ∴= ， MAF 为等边三角形，MA MF ∴= ，MN MA MG MF ∴=﹣﹣ ，AN FG ∴= ，AB BC AB BN AN +=+= ，FG EF EG EF DE =+=+ ，AB BC EF DE ∴+=+ ．20.如图所示，一个六边形的六个内角都是120︒ ，其中连续四边的长依次是1995、、、 ．求这个六边形的周长为____.答案：42解析：首先延长并反向延长AB CD EF ，， ，两两相交于点G H I 、、 ，可得GHI GBC ， 是等边三角形，同理：HAF DEI ， 是等边三角形，即可求得AF 与EF 的长，继而求得答案.解：如图，延长并反向延长AB CD EF ，， ，两两相交于点G H I 、、，六边形ABCDEF 的每个内角都是120︒，6060G H I GCB GBC ∴∠=∠=∠=︒∠=∠=︒， ，GHI GBC ∴， 是等边三角形，同理：HAF DEI ， 是等边三角形，95BG GC BC DE DI EI ∴======， ，99523GI GC CD DI ∴=++=++= ，23GH GI HI ∴=== ，13AH GH BG AB ∴=--= ，13AF AH FH ∴=== ，5EF HI EI FH ∴=--= ，∴ 六边形ABCDEF 的周长113559942AB AF EF DE CD BC =+++++=+++++= ．。
2024辽宁中考数学二轮专题训练 微专题 构造全等的四大方法 (含答案)
2024辽宁中考数学二轮专题训练微专题构造全等的四大方法方法一倍长中线法方法解读(1)倍长中线在△ABC中，AD是BC边的中线．辅助线作法：延长AD至点E，使AD＝DE，连接BE.结论：△ACD≌①________．(2)倍长类中线在△ABC中，点D是边BC的中点，点E是边AB上一点，连接DE.辅助线作法：延长ED至点F，使DF＝DE，连接CF.结论：△BDE≌②________．1.如图．AB＝AE，AB⊥AE，AD＝AC，AD⊥AC，点M为BC的中点，连接AM.求证：DE＝2AM.第1题图方法解读当题目中出现线段的倍差关系时，一般考虑用截长补短法．如图，在△ABC中，∠1＝∠2，∠C＝2∠B.(1)截长法辅助线作法：在AB上截取AF＝AC，连接DF.结论：(1)△AFD≌③______；(2)线段AB，AC，CD的数量关系为④______________．(2)补短法辅助线作法：延长AC至点E，使CE＝CD，连接DE.结论：(1)△AED≌⑤______；(2)线段AB，AC，CD的数量关系为⑥______________．2.如图，在△ABC中，∠A＝60°，BD，CE分别平分∠ABC和∠ACB，BD、CE交于点O.猜想线段BE，CD，BC的数量关系，并证明．第2题图方法解读如图，在△ABC中，点D是AB上一点，点E是AC延长线上一点，连接DE交BC于点F，且DF＝EF.【方法一】辅助线作法：过点D作DH∥AC，交BC于点H.结论：△CEF≌⑦________．【方法二】辅助线作法：过点E作EI平行于BD交BC的延长线于点I.结论：△BDF≌⑧____________．3.如图，在△ABC中，AD平分∠BAC，E为BC的中点，过点E作EF∥AD交AB于点G，交CA的延长线于点F.请写出线段BG与CF的数量关系，并证明．第3题图方法四旋转法方法解读有共顶点，等线段时考虑用旋转构造全等．(1)等腰三角形在△ABC中，AB＝BC，共顶点B，点D为△ACB内一点．辅助线作法：将△ABD旋转至AB与BC重合，旋转角为∠ABC，连接DD′，C D.结论：△ABD≌⑨________；△DBD′为○10________；∠ABC＝⑪________．(2)正方形在正方形ABCD中，CB＝CD，共顶点C，点E为正方形ABCD内一点．辅助线作法：将△BCE旋转至BC与DC重合，旋转角为∠BCD，连接BD，EF.结论：△BCE≌⑫________；△CEF为⑬__________；∠BCD＝⑭________．4.(1)如图①，点E，F分别在正方形ABCD的边BC，CD上，连接AE、AF，且∠EAF＝45°，连接EF，猜想线段EF，BE，DF应满足的等量关系，并说明理由；(2)如图②，在△ABC中，∠BAC＝90°，AB＝AC，点D，E均在边BC上，点D在点E的左侧，连接AD、AE，且∠DAE＝45°，猜想线段BD，DE，EC应满足的等量关系，并说明理由；第4题图参考答案【方法解读】①△EBD；②△CDF；③△ACD；④AB＝AC＋CD；⑤△ABD；⑥AB＝AC＋CD；⑦△HDF；⑧△IEF；⑨△CBD＇；⑩等腰三角形；⑪∠DBD′；⑫△DCF；⑬等腰直角三角形；⑭∠ECF.1.证明：如解图，延长AM至点N，使MN＝AM，连接BN，∵点M为BC的中点，∴CM＝BM，在△AMC和△NMB中，＝NM，AMC＝∠NMB＝BM∴△AMC≌△NMB，∴AC＝NB，∠C＝∠NBM，∵AB⊥AE，AD⊥AC，∴∠EAB＝∠DAC＝90°，∴∠EAD＋∠BAC＝180°，∴∠ABN＝∠ABC＋∠NBM＝∠ABC＋∠C＝180°－∠BAC＝∠EAD，∵AD＝AC，∴BN＝AD，在△EAD和△ABN中，＝BA，EAD＝∠ABN＝BN∴△EAD≌△ABN，∴DE＝AN＝2AM.第1题解图2.解：BE＋CD＝BC，证明：如解图，在BC上取点F，使得CF＝CD，连接OF，∵∠BOC＝180°－(∠OBC＋∠OCB)＝180°－12(∠ABC＋∠ACB)＝180°－12×(180°－60°)＝120°，∴∠BOE＝∠COD＝180°－∠BOC＝60°，∵CE平分∠ACB，∴∠DCO＝∠FCO，在△COD和△COF中，＝CFDCO＝∠FCO＝CO，∴△COD≌△COF，∴CD＝CF，∠COF＝∠COD，又∵∠BOC＝120°，∴∠BOF＝60°＝∠BOE，∵BD平分∠ABC，∴∠EBO＝∠FBO，∴在△BOE和△BOF中，EBO＝∠FBO＝BOBOE＝∠BOF，∴△BOE≌△BOF，∴BE＝BF，∵BF＋FC＝BC，∴BE＋CD＝BC.第2题解图【一题多解】解：BE＋CD＝BC，证明：如解图，在BC上取点F，使得BF＝BE，连接OF，∵∠BOC＝180°－(∠OBC＋∠OCB)＝180°－12(∠ABC＋∠ACB)＝180°－12×(180°－60°)＝120°，∴∠BOE＝∠COD＝180°－∠BOC＝60°，∵BD平分∠ABC，∴∠EBO＝∠FBO，∴在△BOE和△BOF中，＝BFEBO＝∠FBO＝BO，∴△BOE≌△BOF，∴BE＝BF，∠BOF＝∠BOE＝60°.又∵∠BOC＝120°，∴∠COF＝60°＝∠COD，∵CE平分∠ACB，∴∠DCO＝∠FCO，在△COD和△COF中，DCO＝∠FCO＝COCOD＝∠COF，∴△COD≌△COF，∴CD＝CF，∵BF＋FC＝BC，∴BE＋CD＝BC.3.解：BG＝CF；证明如下：如解图①，过点C作CM∥AB交FE的延长线于点M.∵BG∥CM，∴∠B＝∠MCE，∵E是BC中点，∴BE＝EC，在△BEG和△CEM中，B＝∠MCE，＝ECBEG＝∠MEC∴△BEG≌△CEM，∴BG＝CM，∵AD∥EF，∴∠BAD＝∠FGA，∠DAC＝∠F，∵AD平分∠BAC，∴∠BAD＝∠DAC，∴∠F＝∠FGA，∵AB∥CM，∴∠FGA＝∠M，∴∠F＝∠M，∴CF＝CM，∴BG＝CF.第3题解图①【一题多解】解：BG＝CF；证明如下：如解图②，过点B作BM∥CF交FE的延长线于点M.∵BM∥CF，∴∠C＝∠MBC，∠M＝∠F，∵E是BC中点，∴BE＝EC，MBE＝∠C，＝CEBEM＝∠CEF∴△BEM≌△CEF(ASA)，∴BM＝CF，∵AD∥EF，∴∠DAC＝∠F，∠BGF＝∠BAD，∵AD平分∠BAC∴∠BAD＝∠DAC，∴∠BGM＝∠DAC，∴∠BGM＝∠M，∴BM＝BG，∴BG＝CF.第3题解图②4.解：(1)BE＋DF＝EF；理由如下：∵四边形ABCD是正方形，∴AB＝AD，∠BAD＝∠D＝∠ABC＝90°，∵如解图①，将△ADF绕点A顺时针旋转90°至△ABG，∴AG＝AF,BG＝DF，∠GAB＝∠FAD，∠ABG＝∠D＝90°，∴∠ABG＋∠ABC＝90°＋90°＝180°，∴点G、B、E三点共线，∵∠EAF＝45°，∴∠BAE＋∠FAD＝45°，∴∠BAE＋∠GAB＝45°，即∠GAE＝45°，＝AF，GAE＝∠FAE＝AE∴△AEG≌△AEF，∴GE＝EF，∵GE＝BE＋BG＝BE＋DF，∴BE＋DF＝EF；第4题解图①(2)BD2＋EC2＝DE2，理由如下：∵∠BAC＝90°，AB＝AC，∴∠ABC＝∠ACB＝45°，如解图②，将△ABD绕点A逆时针旋转90°至△ACG，连接EG,∴AG＝AD,CG＝BD，∠GAC＝∠DAB，∠ACG＝∠ABC＝45°，∴∠ACG＋∠ACB＝45°＋45°＝90°，∴在Rt△ECG中GE2＝CG2＋CE2，∵∠DAE＝45°，∴∠DAB＋∠EAC＝45°，∴∠GAC＋∠EAC＝45°，即∠GAE＝45°，在△GAE和△DAE中，＝AD，GAE＝∠DAE＝AE∴△GAE≌△DAE，∴GE＝DE，∵GE2＝CG2＋CE2＝BD2＋CE2，∴BD2＋EC2＝DE2.第4题解图②。
中考数学二轮复习专题练习(上)常用辅助线—构造等边三角形新人教版
6.构造等边三角形1.公园里有一块形如四边形ABCD 的草地，测得10BC CD ==米，120B C ∠=∠=︒，45A ∠=︒．请你求出这块草地的面积？答案：见解析 解析：延长DC AB 、交于E ，连结DB ，∵120ABC BCD ∠=∠=︒，∴60EBC ECB ∠=∠=︒， ∴EBC ∆是等边三角形，∵DC CB =，∴30CDB DBC ∠=∠=︒， ∴90DBA ∠=︒，BD =， ∵45A ∠=︒，∴AB =∴(211502ABDS ∆==，11110222BCD BDE S S ∆∆==⨯⨯⨯=∴这块草地的面积为(150+平方米．DCBAEABCD2.如图：已知10AB =,点C D 、在线段AB 上且2AC DB ==；P 是线段CD 上的动点,分别以AP PB 、为边在线段AB 的同侧作等边AEP V 和等边PFB V ,连结EF ,设EF 的中点为G ；当点P 从点C 运动到点D 时,则点G 移动路径的长是____．答案：3解：如图，分别延长PP、PP 交于点P ．∵∠P ＝∠PPP ＝60°，∴PP ∥PP ，∵∠P ＝∠PPP ＝60°，∴PP ∥PP ，∴四边形PPPP 为平行四边形，∴PP 与PP互相平分．∵P 为PP 的中点，∴P 正好为PP 中线PP ．∵PP ＝10－2－2＝6，∴PP＝3，即P 的移动路径长为33.四边形ABCD ，有BC CD =，120B C ∠=∠=︒，45A ∠=︒．请你求D ∠=____︒.答案：75 解析：延长DC AB 、交于E ，连结DB ，∵120ABC BCD ∠=∠=︒，∴60EBC ECB ∠=∠=︒， ∴EBC ∆是等边三角形，∵DC CB =，∴30CDB DBC ∠=∠=︒， ∴90DBA ∠=︒，∵45A ∠=︒，∴904545ADB ∠=︒-︒=︒， ∴453075ADC ADB BDC ∠=∠+∠=︒+︒=︒4.如图，四边形ABCD 中，AC BD ， 是对角线，ABC V 是等边三角形．3035ADC AD BD ∠=︒==，， ，则CD 的长为____.DCBAEABCD答案：4解析：首先以CD 为边作等边CDE V ，连接AE，利用全等三角形的判定得出BCD ACE V V ≌ ，进而求出DE 的长即可．解：如图，以CD 为边作等边CDE V ，连接AEBCD BCA ACD DCE ACD ACE ∠=∠+∠=∠+∠=∠Q ，∴ 在BCD V 和ACE V 中，AC BC ACE BCD CD CE =⎧⎪∠=∠⎨⎪=⎩BCD ACE SAS ∴V V ≌（）， BD AE ∴= ．又30ADC ∠=︒Q ，90ADE ∴∠=︒ ．在Rt ADE V 中，53AE AD ==， ，于是4DE == ，4CD DE ∴==．5.如图所示，在ABC V 中，AB AC D E =，、是ABC V 内两点，AD 平分60BAC EBC E ∠∠=∠=︒．，若62BE DE ==，，则BC 的长度是__.答案：8解析：作出辅助线后根据等腰三角形的性质得出62BE DE ==，，进而得出BEM V 为等边三角形，EFD V 为等边三角形，从而得出BN 的长，进而求出答案． 解：延长ED 交BC 于M ，延长AD 交BC 于N ，作DF BC P 于F ，AB AC AD =Q ，平分BAC ∠ ， AN BC BN CN ∴⊥=， ， 60EBC E ∠=∠=︒Q ，BEM ∴V 为等边三角形， EFD ∴V 为等边三角形，62BE DE ==Q ， ，4DM ∴= ，BEM QV 为等边三角形，60EMB ∴∠=︒ ， AN BC ⊥Q ， 90DNM ∴∠=︒ ，30NDM ∴∠=︒ ，2NM ∴= ， 4BN ∴= ， 28BC BN ∴== ，6.如图，六边形ABCDEF 中，每一个内角都是1201230828AB BC CD DE ︒====，，，，．求这个六边形的周长为_____.答案：116解析：凸六边形ABCDEF ，并不是一规则的六边形，但六个角都是120︒ ，所以通过适当的向外作延长线，可得到等边三角形，进而求解．解：如图，分别作直线AF ED BC 、、 的延长线和反向延长线使它们交于点G H P 、、 ．Q 六边形ABCDEF 的六个角都是120°，∴ 六边形ABCDEF 的每一个外角的度数都是60°．PGH BGA DHC EFP ∴V V V V 、、、 都是等边三角形． 128GC BC DH CH ∴====， ．1230850GH ∴=++=，5028814FE PE PH ED DH ==--=--=，50141224AF PG PF AG =--=--=．∴ 六边形的周长为：24123082814116+++++= ．7.如图，已知120ABC ∠=︒ ，BD 平分60ABC DAC ∠∠=︒， ，若23AB BC ==， ，则BD 的长是_____.答案：5解析：在CB 的延长线上取点E ，使BE AB =，连接AE ，则可证得ABE V 为等边三角形，再结合条件可证明ABD AEC V V ≌ ，可得BD CE = ，再利用线段的和差可求得CE ，则可求得BD .解：在CB 的延长线上取点E ，使BE AB =，连接AE ，120ABC ∠=︒Q ，18060ABE ABC ∴∠=∠=︒﹣ ，BE AB =Q ，ABE ∴V 为等边三角形，60AE AB BAE E ∴=∠=∠=︒， ， 60DAC ∠=︒Q ，DAC BAE ∴∠= ，BAD BAC DAC EAC BAC BAE ∠=∠+∠∠=∠+∠Q ， ， BAD EAC ∴∠=∠ ，BD Q 平分ABC ∠ ，，ABD E ∴∠=∠ ，在ABD V 和AEC V 中，BAD EAC AB AEABD E ∠=∠⎧⎪=⎨⎪∠=∠⎩， ABD AEC ASA ∴V V ≌（）， BD CE ∴= ，325CE BE BC AB BC =+=+=+=Q ，5BD ∴= ，8.如图，在ABC V 中，AB AC D E =，、 是ABC V 内两点，AD 平分60BAC EBC E ∠∠=∠=︒， ，若602BE cm DE cm ==， ，则BC = ____cm ．答案：62解析：作出辅助线后根据等腰三角形的性质得出62BE DE ==， ，进而得出BEM V 为等边三角形，EFD V 为等边三角形，从而得出BN 的长，进而求出答案．P，解：延长ED交BC于M，延长AD交BC于N，作DF BC∠，Q，AD平分BACAB AC=，，∴⊥=AN BC BN CNQ，∠=∠=︒EBC E60∴V为等边三角形，BEM∴V为等边三角形，EFDQ，，==BE DE602DM∴=，58QV为等边三角形，BEM∴∠=︒，60EMBQ，AN BC⊥∴∠=︒，DNM90∴∠=︒，30NDM∴=，NM29∴=，BN31∴==，BC BN262故答案为62．9.如图，过边长为1的等边ABC V 的边AB 上一点P ，作PE AC ⊥ 于E Q ， 为BC 延长线上一点，当PA CQ = 时，连PQ 交AC 边于D ，则DE 的长为____.（注：若答案不是整数，请化为小数）答案：0.5 解析：过P 作PFBC P 交AC 于F ，得出等边三角形APF ，推出AP PF QC == ，根据等腰三角形性质求出EF AE = ，证PFD QCD V V≌ ，推出FD CD = ，推出12DE AC =即可．解：过P 作PFBC P 交AC 于F ．PF BC Q P ，ABC V 是等边三角形， PFD QCD APF ∴∠=∠V ， 是等边三角形，AP PF AF ∴== ，PE AC ⊥Q ，AE EF ∴= ，AP PF AP CQ ==Q ， ，PF CQ ∴= ．Q 在PFD V 和QCD V中， PFD QCD PDF QDC PF CQ ∠=∠⎧⎪∠=∠⎨⎪=⎩，PFD QCD AAS ∴V V ≌（） ，FD CD ∴= ，AE EF =Q ，EF FD AE CD ∴+=+ ，12AE CD DE AC ∴+==， 1AC =Q ， 10.52DE ∴== ．10.如图，ABC V 中，AB AC AD =， 平分BAC D E ∠，、 是ABC V 内两点，且60ECB E ∠=∠=︒ ，若82CE DE ==， ，则BC =_____.答案：10解析：延长ED交BC于M，延长AD交BC于N，根据等腰三角形的性质得出V为等边三角形，从而得出BN的长，进而求出答案．，，进而得出CEMCE DE82==解：延长ED交BC于M，延长AD交BC于N，∠，Q，平分BAC=AB AC AD，，AN BC BN CN∴⊥=Q，∠=∠=︒ECB E60∴V为等边三角形，CEMQ，，82==CE DEDM∴=，6QV为等边三角形，CEM∴∠=︒，60EMCQ，AN BC⊥∴∠=︒，DNM90NDM∴∠=︒，30∴=，NM3∴==﹣，CN835BN∴=，5∴==．BC BN210故答案为：10．11.如图，凸四边形ABCD 满足条件：60120AB AD BAD BCD =∠=︒∠=︒，， 那么AC ____BC CD +．（填“大于”或“小于”或“等于”）答案：等于解析：延长DC 到点E ，使得BC CE = ，连接BE 和BD ，根据已知条件和所作辅助线可得ABD V 与BCE V 均为等边三角形，证明ABC V 和DBE V 全等即可证明；解：延长DC 到点E ，使得BC CE = ，连接BE 和BD .∵120BCD ∠=︒∴18012060BCE ∠=︒-︒=︒又BC CE =Q ，60AB AD BAD =∠=︒，ABD ∴V 与BCE V 均为等边三角形60BD AB BE BC ABD EBC ∴==∠=∠=︒，，ABD DBC EBC DBC ∴∠+∠=∠+∠ ,即ABC DBE ∠=∠在ABC V 和DBE V 中AB BD ABC DBE BC BE =∠=∠=⎧⎪⎨⎪⎩，∴ABC DBE V V ≌∴BD DE =∵DE CD EC CD BC =+=+AC BC CD ∴=+ ．故答案为：相等12.已知：如图，等边ABC V 中，1AB P =， 是AB 边上一动点，作PE BC ⊥ ，垂足为E ；作EF AC ⊥ ，垂足为F ；作FQ AB ⊥ ，垂足为Q ．（1）设BP x AQ y ==， ，求y 与x 之间的函数关系式；（2）当点P 和点Q 重合时，求线段EF 的长；（3）当点P 和点Q 不重合，但线段PE FQ 、 延长线相交时，求它们与线段EF 围成的三角形周长的取值范围．答案：见解析解析：（1）由已知等边ABC V 中，可得每个角都是60︒ ，由作PE BC ⊥ ，垂足为E ；作EF AC ⊥ ，垂足为F ；作FQ AB ⊥ ，垂足为Q ，得三个直角三角形且都有30︒的角，据此用x 可表示出BE CE CF ，， ，相继表示出AF AQ ， ，求出y 与x 之间的函数关系式．（2）由已知可列出方程组结合已知求出EF 的长．（3）当线段PE FQ 、 相交时，根据已知得到它们与线段EF 围成的三角形三个角都是60︒ 解：（1）ABC QV 是等边三角形，1AB = ．601A B C BC CA AB ∴∠=∠=∠=︒===， ．又90BEP CFE FQA BP x ∠=∠=∠=︒=Q ， ．11122BE x CE x ∴==-， ，1111111242424CF x AF x x =-=--=+，（）． 11112224AQ AF x ∴==+（） ， 1184y x ∴=+ ．（2）由方程组11184x y y x +=⎧⎪⎨=+⎪⎩得23x = ． ∴ 当点P 和点Q 重合时，23x =，11243EF x ∴==-=） ．（3）设线段EP FQ 、 的延长线相交于点M ，EF AC ⊥Q ，390QFE ∴∠+∠=︒ ，FQ AB ⊥Q ，390A ∴∠+∠=︒ ，60A QFE ∴∠=∠=︒ ，190C ∠+∠=︒Q ，1290∠+∠=︒ ，260C ∴∠=∠=︒ ，MEF ∴V 是等边三角形，且当点P 和点Q 重合时，EF 最短为3.且当点P 和点B 重合时，EF 最长为22m <≤．13.如图，在四边形ABCD 中，60120AB AD BAD BCD =∠=︒∠=︒，， ，连接AC BD ， 交于点E ．（1）若2BC CD == ，M 为线段AC 上一点，且12AM CM =：： ，连接BM ，求点C 到BM 的距离．（2）证明：BC CD AC += ．答案：见解析解析：（1）由条件可以证明ABC ADC V V ≌，可以得出30BAC DAC ∠=∠=︒ ，6090ACB ACD AEB ∠=∠=︒∠=︒， ，求出90ABC ∠=︒ ，由勾股定理可以求出4AC AB ==，，由12AM CM =：： 可以求得AM CM 、 的值，在Rt BEC V 中由勾股定理可以求出CE BE 、 的值，从而求出BM 的值，过点C 作CF MB ⊥ 于F ，利用三角形的面积相等建立等量关系就可以求出结论．（2）要证BC DC AC += ，延长BC 到E ，使CE CD = ，则求AC BE = 即可．由60AB AD ABD =∠=︒， ，得ABD V 是等边三角形，进而得60ADB AD BD ∠=︒=，，又有120BCD ∠=︒ ，则DCE V 是等边三角形，所以得ACD BDE V V ≌ ，则AC BE BC CD ==+ ．解：（1）60AB AD BAD =∠=︒Q ， ，ABD ∴V 是等边三角形，60ABD ADB ∴∠=∠=︒ ．BC CD =Q ，ABC ADC ∴V V ≌ ，3060BAC DAC ACB ACD ∴∠=∠=︒∠=∠=︒， ．9090AEB BEC ABC ∴∠=∠=︒∠=︒， ， 112CE BC ∴==，324BE AC BC ===， ． 12AM CM =Q ：： ，43AM ∴=，83CM = ， 53EM ∴= ，在Rt BEM V 中由勾股定理得BM == 过点C 作CF BM ⊥ 于点F ．22BM CFCM BE⋅⋅∴= ．83322∴= ，CF ∴= ．即点C 到BM的距离43913．（2）证明：延长BC 到点F ，使CF CB = ，连接DF ，，60AB AD ABD =∠=︒Q ，ABD ∴V 是等边三角形，60ADB AD BD ∴∠=︒=， ，BC CD ∴= ，CF CD ∴= ．120BCD ∠=︒Q ，18060DCF BCD ∴∠=︒∠=︒﹣ ，DCF ∴V 是等边三角形，60CDF ADB DC DF ∴∠=∠=︒=， ，ADC BDF ∴∠=∠ ，又AD BD =Q ，ACD BDF ∴V V ≌ ，AC BF BC CF ∴==+ ，即AC BC CD =+ ．14.已知：如图，在等边三角形ABC 中，点D 是AC 边上的一个动点（D 与A C ， 不重合），延长AB 到E ，使BE CD = ，连接DE 交BC 于点F ．（1）求证：DF EF = ；（2）若ABC V 的边长为10 ，设CD x BF y ==， ，求y 与x 的函数关系式，写出自变量x 的取值范围．答案：见解析解析：（1）过D 作DM AB P 交BC 于M ，则CDM V 为等边三角形，得CD DM = ，而BE CD = ，得到DM BE = ，易证得FDM FEB V V ≌ ，根据全等三角形的性质即可得到结论；（2）由（1）得FDM FEB V V ≌ ，得到MF BF y == ，易得CM CD x == ，而10BC = ，即有10x y y ++= ，即可得到y 与x 间的函数关系式．解：（1）证明：过D 作DM AB P 交BC 于M ，CDM A CMD ABC ∴∠=∠∠=∠， ，又∵在等边三角形ABC 中，60A ABC C ∠=∠=∠=︒ ，CDM CMD C ∴∠=∠=∠ ，CDM ∴V 是等边三角形，CD DM ∴= ，又CD BE =Q ，BE DM ∴= ，DM AE Q P ，MDF E ∴∠=∠ ，在DMF V 和EBF V 中，MDF E ∠=∠ ，DFM EFB ∠=∠ ，DM BE = ，DMF EBF AAS ∴V V ≌（）， DF EF ∴= ；（2）由（1）得DMF EBF V V ≌ ，BF MF y ∴== ，由（1）得CDM V 是等边三角形，CM CD x ∴== ，又10CM MF FB BC ++==Q ，210y x ∴+= ， 即152010x y x =-（＜＜）．15.如图，在四边形ABCD 中，2604AB AD A BC CD ==∠=︒==，， ．（1）求ADC ∠ 的度数．（2）求四边形ABCD 的面积．答案：见解析解析：（1）连接BD ，根据260AB AD A ==∠=︒， ，得出ABD V 是等边三角形，求得2BD = ，然后根据勾股定理的逆定理判断三角形BDC 是直角三角形，从而求得150ADC ∠=︒ ；（2）根据四边形的面积等于三角形ABD 和三角形BCD 的和即可求得；解：（1）连接BD ，260AB AD A ==∠=︒Q ， ，ABD ∴V 是等边三角形，260BD ADB ∴=∠=︒，，4BC CD == ，则222222242020BD CD BC +=+===，（ ， 222BD CD BC ∴+= ，90BDC ∴∠=︒ ，150ADC ∴∠=︒ ；（2）1111•222442222ABD BDC S S S AD AD BD DC =+=+=⨯+⨯⨯=+V V 16.已知：如图，四边形ABCD 中，6030ADC ABC AD CD ∠=︒∠=︒=，， ．（1）连接AC ACD V ， 的形状是？（2）求证：222BD AB BC =+ ．答案：见解析解析：（1）根据全等三角形的判定定理“有一内角为60︒ 的等腰三角形是等边三角形”推知ACD V 是等边三角形．（2）如图，以BC 为边向形外作等边BCE V ，连接AE ．构造全等三角形（BCD ECA V V ≌ ），然后根据全等三角形的性质、勾股定理证得结论． 解：（1）如图，连接AC ．60ADC AD CD ∠=︒=Q ， ，ACD ∴V 是等边三角形；故答案是：等边三角形；（2）如图，以BC 为边向形外作等边BCE V ，连接AE ．由（1）知，ACD V 是等边三角形，则60DC AC EC BC ACD BCE ==∠=∠=︒，， ，在BCD V 与ECA V ，∵DC AC DCB ACE BC EC =⎧⎪∠=∠⎨⎪=⎩，BCD ECA SAS ∴V V ≌（）， AE BD ∴= ，90ABE ∠=︒Q ，∴ 在Rt ABE V 中，有222AB BE AE += ，即222AB BC BD += ．17.如图，在ABC V 中，AB AC D =， 是三角形外一点，且60ABD BD DC AB ∠=︒+=， ．求证：ACD ∠= ____°．答案：60解析：首先延长BD 至E ，使CD DE = ，连接AE AD ， ，由BD DC AB += ，易得ABE V 是等边三角形，继而证得ACD ADE V V ≌ ，则可证得：60ACD E ∠=∠=︒ ． 证明：延长BD 至E ，使CD DE = ，连接AE AD ，，BD CD AB BE BD DE +==+Q ， ，BE AB ∴= ，60ABD ∠=︒Q ，ABE ∴V 是等边三角形，60AE AB AC E ∴==∠=︒， ，在ACD V 和ADE V 中，AC AE CD DE AD AD =⎧⎪=⎨⎪=⎩，ACD ADE SSS ∴V V ≌（），60ACD E ∴∠=∠=︒ ．18.如图，凸六边形ABCDEF 的六个角都是120︒ ，边长28116AB cm BC cm CD cm DE cm ====，，， ，求出这个六边形的周长为____cm .答案：46解析：凸六边形ABCDEF ，并不是一规则的六边形，但六个角都是120︒ ，所以通过适当的向外作延长线，可得到等边三角形，进而求解．解：如图，分别作直线AB CD EF 、、 的延长线使它们交于点G H P 、、 ．因为六边形ABCDEF 的六个角都是120︒，所以六边形ABCDEF 的每一个外角的度数都是60︒ ．所以三角形APF 、三角形BGC 、三角形DHE 、三角形GHP 都是等边三角形． 所以86GC BC cm DH DE cm ====， ．所以811625GH cm =++= ，252815FA PA PG AB BG cm ==--=--= ，251564EF PH PF EH cm =--=--= ．所以六边形的周长为2811641546cm +++++= ．19.如图，在六边形ABCDEF 中，A B C D E F ∠=∠=∠=∠=∠=∠ ．（1）试说明MAF V 为等边三角形；（2）请探索AB BC EF DE ，，， 之间的关系（等量关系或位置关系）并说明理由．答案：见解析解析：（1）根据多边形的内角和定理求出120A B C D E F ∠=∠=∠=∠=∠=∠=︒ ，求出60MAF MFA ∠=∠=︒ ，得出等边三角形MAF ，推出MA MF = ，同理求出NBC MNG EDG V V V 、、 是等边三角形，推出BN BC DE EG ==， ，求出AN FG = ，即可求出答案．解：（1）作直线AB 、直线EF 、直线CD AB ， 和EF 交于M AB ， 和CD 交于N EF ， 和CD 交于G ，A B C D E F ∠=∠=∠=∠=∠=∠Q ，62180A B C D E F ∠+∠+∠+∠+∠+∠=-⨯︒（） ，120A B C D E F ∴∠=∠=∠=∠=∠=∠=︒ ，18012060MAF MFA ∴∠=∠=︒-︒=︒ ，MF MA ∴= ，MAF ∴V 为等边三角形．（2）AB BC EF DE +=+ ，理由是：120ABC BCD ∠=∠=︒Q ，18012060NBC NCB ∴∠=∠=︒︒=︒﹣ ，NB NC ∴= ，BNC ∴V 是等边三角形，60BC BN N ∴=∠=︒， ，同理60DE EG G =∠=︒， ，60G N ∴∠=∠=︒ ，MN MG ∴= ，MAF QV 为等边三角形，MA MF ∴= ，MN MA MG MF ∴=﹣﹣ ，AN FG ∴= ，AB BC AB BN AN +=+=Q ，FG EF EG EF DE =+=+ ，AB BC EF DE ∴+=+ ．20.如图所示，一个六边形的六个内角都是120︒ ，其中连续四边的长依次是1995、、、 ．求这个六边形的周长为____.答案：42解析：首先延长并反向延长AB CD EF ，， ，两两相交于点G H I 、、 ，可得GHI GBC V V ， 是等边三角形，同理：HAF DEI V V ， 是等边三角形，即可求得AF 与EF的长，继而求得答案.解：如图，延长并反向延长AB CD EF ，， ，两两相交于点G H I 、、，Q 六边形ABCDEF 的每个内角都是120︒，6060G H I GCB GBC ∴∠=∠=∠=︒∠=∠=︒， ，GHI GBC ∴V V ， 是等边三角形，同理：HAF DEI V V ， 是等边三角形，95BG GC BC DE DI EI ∴======， ，99523GI GC CD DI ∴=++=++= ，23GH GI HI ∴=== ，13AH GH BG AB ∴=--= ，13AF AH FH ∴=== ，5EF HI EI FH ∴=--= ，∴ 六边形ABCDEF 的周长113559942AB AF EF DE CD BC =+++++=+++++= ．。
中考数学二轮复习 专题练习(上)常用辅助线—构造等边三角形 新人教版-新人教版初中九年级全册数学试题
等边三角形1.公园里有一块形如四边形ABCD 的草地，测得10BC CD ==米，120B C ∠=∠=︒，45A ∠=︒．请你求出这块草地的面积？答案：见解析 解析：延长DC AB 、交于E ，连结DB ，∵120ABC BCD ∠=∠=︒，∴60EBC ECB ∠=∠=︒， ∴EBC ∆是等边三角形，∵DC CB =，∴30CDB DBC ∠=∠=︒， ∴90DBA ∠=︒，BD =， ∵45A ∠=︒，∴AB =∴(211502ABDS ∆==，11110222BCD BDE S S ∆∆==⨯⨯⨯=∴这块草地的面积为(150+平方米．DCBAEABCD2.如图：已知10AB =,点C D 、在线段AB 上且2AC DB ==；P 是线段CD 上的动点,分别以AP PB 、为边在线段AB 的同侧作等边AEP 和等边PFB ,连结EF ,设EF 的中点为G ；当点P 从点C 运动到点D 时,则点G 移动路径的长是____．答案：3解：如图，分别延长PP、PP 交于点P ．∵∠P ＝∠PPP ＝60°，∴PP ∥PP ，∵∠P ＝∠PPP ＝60°，∴PP ∥PP ，∴四边形PPPP 为平行四边形，∴PP 与PP互相平分．∵P 为PP 的中点，∴P 正好为PP 中线PP ．∵PP ＝10－2－2＝6，∴PP＝3，即P 的移动路径长为33.四边形ABCD ，有BC CD =，120B C ∠=∠=︒，45A ∠=︒．请你求D ∠=____︒.答案：75 解析：延长DC AB 、交于E ，连结DB ，∵120ABC BCD ∠=∠=︒，∴60EBC ECB ∠=∠=︒， ∴EBC ∆是等边三角形，∵DC CB =，∴30CDB DBC ∠=∠=︒， ∴90DBA ∠=︒，∵45A ∠=︒，∴904545ADB ∠=︒-︒=︒， ∴453075ADC ADB BDC ∠=∠+∠=︒+︒=︒4.如图，四边形ABCD 中，AC BD ， 是对角线，ABC 是等边三角形．3035ADC AD BD ∠=︒==，， ，则CD 的长为____.DCBAEABCD答案：4解析：首先以CD 为边作等边CDE ，连接AE ，利用全等三角形的判定得出BCD ACE ≌ ，进而求出DE 的长即可．解：如图，以CD 为边作等边CDE ，连接AEBCD BCA ACD DCE ACD ACE ∠=∠+∠=∠+∠=∠ ，∴ 在BCD 和ACE 中， AC BC ACE BCD CD CE =⎧⎪∠=∠⎨⎪=⎩BCD ACE SAS ∴≌（）， BD AE ∴= ．又30ADC ∠=︒ ，90ADE ∴∠=︒ ．在Rt ADE 中，53AE AD ==， ，于是4DE == ，4CD DE ∴==．5.如图所示，在ABC 中，AB AC D E =，、是ABC 内两点，AD 平分60BAC EBC E ∠∠=∠=︒．，若62BE DE ==，，则BC 的长度是__.答案：8解析：作出辅助线后根据等腰三角形的性质得出62BE DE ==，，进而得出BEM 为等边三角形，EFD 为等边三角形，从而得出BN 的长，进而求出答案． 解：延长ED 交BC 于M ，延长AD 交BC 于N ，作DF BC 于F ，AB AC AD =，平分BAC ∠ ， AN BC BN CN ∴⊥=， ，60EBC E ∠=∠=︒ ，BEM ∴为等边三角形， EFD ∴为等边三角形，62BE DE ==， ，4DM ∴= ，BEM 为等边三角形，60EMB ∴∠=︒ ， AN BC ⊥ ， 90DNM ∴∠=︒ ， 30NDM ∴∠=︒ ， 2NM ∴= ， 4BN ∴= ， 28BC BN ∴== ，6.如图，六边形ABCDEF 中，每一个内角都是1201230828AB BC CD DE ︒====，，，，．求这个六边形的周长为_____.答案：116解析：凸六边形ABCDEF ，并不是一规则的六边形，但六个角都是120︒ ，所以通过适当的向外作延长线，可得到等边三角形，进而求解．解：如图，分别作直线AF ED BC 、、 的延长线和反向延长线使它们交于点G H P 、、 ．六边形ABCDEF 的六个角都是120°，∴ 六边形ABCDEF 的每一个外角的度数都是60°． PGH BGA DHC EFP ∴、、、 都是等边三角形． 128GC BC DH CH ∴====， ．1230850GH ∴=++=，5028814FE PE PH ED DH ==--=--=，50141224AF PG PF AG =--=--=．∴ 六边形的周长为：24123082814116+++++= ．7.如图，已知120ABC ∠=︒ ，BD 平分60ABC DAC ∠∠=︒， ，若23AB BC ==， ，则BD 的长是_____.答案：5解析：在CB 的延长线上取点E ，使BE AB =，连接AE ，则可证得ABE 为等边三角形，再结合条件可证明ABD AEC ≌ ，可得BD CE = ，再利用线段的和差可求得CE ，则可求得BD .解：在CB 的延长线上取点E ，使BE AB =，连接AE ，120ABC ∠=︒ ，18060ABE ABC ∴∠=∠=︒﹣ ，BE AB = ，ABE ∴ 为等边三角形，60AE AB BAE E ∴=∠=∠=︒， ， 60DAC ∠=︒ ，DAC BAE ∴∠= ，BAD BAC DAC EAC BAC BAE ∠=∠+∠∠=∠+∠， ， BAD EAC ∴∠=∠ ，BD 平分ABC ∠ ，，ABD E ∴∠=∠ ，在ABD 和AEC 中，BAD EAC AB AEABD E ∠=∠⎧⎪=⎨⎪∠=∠⎩， ABD AEC ASA ∴≌（）， BD CE ∴= ，325CE BE BC AB BC =+=+=+= ，5BD ∴= ，8.如图，在ABC 中，AB AC D E =，、 是ABC 内两点，AD 平分60BAC EBC E ∠∠=∠=︒， ，若602BE cm DE cm ==， ，则BC =____cm ．答案：62解析：作出辅助线后根据等腰三角形的性质得出62BE DE ==， ，进而得出BEM 为等边三角形，EFD 为等边三角形，从而得出BN 的长，进而求出答案． 解：延长ED 交BC 于M ，延长AD 交BC 于N ，作DFBC ，AB AC = ，AD 平分BAC ∠ ， AN BC BN CN ∴⊥=， ， 60EBC E ∠=∠=︒ ，BEM ∴ 为等边三角形， EFD ∴ 为等边三角形，602BE DE ==， ， 58DM ∴= ，BEM 为等边三角形，60EMB ∴∠=︒ ， AN BC ⊥ ， 90DNM ∴∠=︒ ，30NDM ∴∠=︒ ，29NM ∴= ，31BN ∴= ，262BC BN ∴== ，故答案为62．9.如图，过边长为1的等边ABC 的边AB 上一点P ，作PE AC ⊥ 于E Q ， 为BC 延长线上一点，当PA CQ = 时，连PQ 交AC 边于D ，则DE 的长为____.（注：若答案不是整数，请化为小数）答案：解析：过P 作PF BC 交AC 于F ，得出等边三角形APF ，推出AP PF QC == ，根据等腰三角形性质求出EF AE = ，证PFD QCD ≌ ，推出FD CD = ，推出12DE AC =即可．解：过P 作PF BC 交AC 于F ．PF BC ，ABC 是等边三角形，PFD QCD APF ∴∠=∠， 是等边三角形，AP PF AF ∴== ，PE AC ⊥ ，AE EF ∴= ，AP PF AP CQ ==， ，PF CQ ∴= ．在PFD 和QCD 中，PFD QCD PDF QDC PF CQ ∠=∠⎧⎪∠=∠⎨⎪=⎩，PFD QCD AAS ∴≌（） ，FD CD ∴= ，AE EF = ，EF FD AE CD ∴+=+ ，12AE CD DE AC ∴+== ， 1AC = ，10.52DE ∴== ．10.如图，ABC 中，AB AC AD =， 平分BAC D E ∠，、 是ABC 内两点，且60ECB E ∠=∠=︒ ，若82CE DE ==， ，则BC =_____.答案：10解析：延长ED 交BC 于M ，延长AD 交BC 于N ，根据等腰三角形的性质得出82CE DE ==， ，进而得出CEM 为等边三角形，从而得出BN 的长，进而求出答案． 解：延长ED 交BC 于M ，延长AD 交BC 于N ，AB AC AD =， 平分BAC ∠ ，AN BC BN CN ∴⊥=， ，60ECB E ∠=∠=︒ ，CEM ∴ 为等边三角形，82CE DE ==， ，6DM ∴= ， CEM 为等边三角形，60EMC ∴∠=︒ ，AN BC ⊥ ，90DNM ∴∠=︒ ，30NDM ∴∠=︒ ，3NM ∴= ，835CN ∴==﹣ ，5BN ∴=，210BC BN ∴== ．故答案为：10．11.如图，凸四边形ABCD 满足条件：60120AB AD BAD BCD =∠=︒∠=︒，， 那么AC ____BC CD +．（填“大于”或“小于”或“等于”）答案：等于解析：延长DC 到点E ，使得BC CE =，连接BE 和BD ，根据已知条件和所作辅助线可得ABD 与BCE 均为等边三角形，证明ABC 和DBE 全等即可证明；解：延长DC 到点E ，使得BC CE =，连接BE 和BD .∵120BCD ∠=︒∴18012060BCE ∠=︒-︒=︒又BC CE =，60AB AD BAD =∠=︒，ABD ∴ 与BCE 均为等边三角形60BD AB BE BC ABD EBC ∴==∠=∠=︒，，ABD DBC EBC DBC ∴∠+∠=∠+∠,即ABC DBE ∠=∠在ABC 和DBE 中AB BD ABC DBE BC BE =∠=∠=⎧⎪⎨⎪⎩，∴ABC DBE ≌∴BD DE =∵DE CD EC CD BC =+=+AC BC CD ∴=+ ．故答案为：相等12.已知：如图，等边ABC 中，1AB P =， 是AB 边上一动点，作PE BC ⊥ ，垂足为E ；作EF AC ⊥ ，垂足为F ；作FQ AB ⊥ ，垂足为Q ．（1）设BP x AQ y ==， ，求y 与x 之间的函数关系式；（2）当点P 和点Q 重合时，求线段EF 的长；（3）当点P 和点Q 不重合，但线段PE FQ 、 延长线相交时，求它们与线段EF 围成的三角形周长的取值X 围．答案：见解析解析：（1）由已知等边ABC 中，可得每个角都是60︒ ，由作PE BC ⊥ ，垂足为E ；作EF AC ⊥ ，垂足为F ；作FQ AB ⊥ ，垂足为Q ，得三个直角三角形且都有30︒ 的角，据此用x 可表示出BE CE CF ，， ，相继表示出AF AQ ， ，求出y 与x 之间的函数关系式．（2）由已知可列出方程组结合已知求出EF 的长．（3）当线段PE FQ 、 相交时，根据已知得到它们与线段EF 围成的三角形三个角都是60︒ 解：（1）ABC 是等边三角形，1AB = ．601A B C BC CA AB ∴∠=∠=∠=︒===， ．又90BEP CFE FQA BP x ∠=∠=∠=︒=， ．11122BE x CE x ∴==-， ，1111111242424CF x AF x x =-=--=+，（）． 11112224AQ AF x ∴==+（） ， 1184y x ∴=+ ．（2）由方程组11184x y y x +=⎧⎪⎨=+⎪⎩得23x = ． ∴ 当点P 和点Q 重合时，23x =，1124EF x ∴==-=）．（3）设线段EP FQ 、 的延长线相交于点M ，EF AC ⊥ ，390QFE ∴∠+∠=︒ ，FQ AB ⊥ ，390A ∴∠+∠=︒ ，60A QFE ∴∠=∠=︒ ，190C ∠+∠=︒ ，1290∠+∠=︒ ，260C ∴∠=∠=︒ ，MEF ∴ 是等边三角形，且当点P 和点Q 重合时，EF 最短为3.且当点P 和点B 重合时，EF 最长为2m ≤．13.如图，在四边形ABCD 中，60120AB AD BAD BCD =∠=︒∠=︒，， ，连接AC BD ， 交于点E ．（1）若2BC CD == ，M 为线段AC 上一点，且12AM CM =：： ，连接BM ，求点C 到BM 的距离．（2）证明：BC CD AC += ．答案：见解析解析：（1）由条件可以证明ABC ADC ≌，可以得出30BAC DAC ∠=∠=︒ ，6090ACB ACD AEB ∠=∠=︒∠=︒， ，求出90ABC ∠=︒ ，由勾股定理可以求出4AC AB ==，，由12AM CM =：： 可以求得AM CM 、 的值，在Rt BEC 中由勾股定理可以求出CE BE 、 的值，从而求出BM 的值，过点C 作CF MB ⊥ 于F ，利用三角形的面积相等建立等量关系就可以求出结论．（2）要证BC DC AC += ，延长BC 到E ，使CE CD = ，则求AC BE = 即可．由60AB AD ABD =∠=︒， ，得ABD 是等边三角形，进而得60ADB AD BD ∠=︒=，，又有120BCD ∠=︒ ，则DCE 是等边三角形，所以得ACD BDE ≌ ，则AC BE BC CD ==+ ．解：（1）60AB AD BAD =∠=︒， ，ABD ∴ 是等边三角形，60ABD ADB ∴∠=∠=︒ ．BC CD = ，ABC ADC ∴≌ ，3060BAC DAC ACB ACD ∴∠=∠=︒∠=∠=︒， ． 9090AEB BEC ABC ∴∠=∠=︒∠=︒， ， 112CE BC ∴==，324BE AC BC ===， ． 12AM CM =：： ，43AM ∴=，83CM = ， 53EM ∴= ，在Rt BEM 中由勾股定理得BM == 过点C 作CF BM ⊥ 于点F ．22BM CFCM BE⋅⋅∴= ．83322⨯∴= ，CF ∴= ．即点C 到BM的距离43913．（2）证明：延长BC 到点F ，使CF CB = ，连接DF ，，60AB AD ABD =∠=︒，ABD ∴ 是等边三角形，60ADB AD BD ∴∠=︒=， ，BC CD ∴= ，CF CD ∴= ．120BCD ∠=︒ ，18060DCF BCD ∴∠=︒∠=︒﹣ ，DCF ∴ 是等边三角形，60CDF ADB DC DF ∴∠=∠=︒=， ，ADC BDF ∴∠=∠ ，又AD BD = ，ACD BDF ∴≌ ，AC BF BC CF ∴==+ ，即AC BC CD =+ ．14.已知：如图，在等边三角形ABC 中，点D 是AC 边上的一个动点（D 与A C ， 不重合），延长AB 到E ，使BE CD = ，连接DE 交BC 于点F ．（1）求证：DF EF = ；（2）若ABC 的边长为10 ，设CD x BF y ==， ，求y 与x 的函数关系式，写出自变量x 的取值X 围．答案：见解析解析：（1）过D 作DM AB 交BC 于M ，则CDM 为等边三角形，得CD DM = ，而BE CD = ，得到DM BE = ，易证得FDM FEB ≌ ，根据全等三角形的性质即可得到结论；（2）由（1）得FDM FEB ≌ ，得到MF BF y == ，易得CM CD x == ，而10BC = ，即有10x y y ++= ，即可得到y 与x 间的函数关系式．解：（1）证明：过D 作DM AB 交BC 于M ，CDM A CMD ABC ∴∠=∠∠=∠， ，又∵在等边三角形ABC 中，60A ABC C ∠=∠=∠=︒ ，CDM CMD C ∴∠=∠=∠ ，CDM ∴ 是等边三角形，CD DM ∴= ，又CD BE = ，BE DM ∴= ，DM AE ，MDF E ∴∠=∠ ，在DMF 和EBF 中，MDF E ∠=∠ ，DFM EFB ∠=∠ ，DM BE = ，DMF EBF AAS ∴≌（）， DF EF ∴= ；（2）由（1）得DMF EBF ≌ ，BF MF y ∴== ，由（1）得CDM 是等边三角形，CM CD x ∴== ，又10CM MF FB BC ++== ，210y x ∴+= ， 即152010x y x =-（＜＜）．15.如图，在四边形ABCD 中，2604AB AD A BC CD ==∠=︒==，， ．（1）求ADC ∠ 的度数．（2）求四边形ABCD 的面积．答案：见解析解析：（1）连接BD ，根据260AB AD A ==∠=︒，，得出ABD 是等边三角形，求得2BD = ，然后根据勾股定理的逆定理判断三角形BDC 是直角三角形，从而求得150ADC ∠=︒ ；（2）根据四边形的面积等于三角形ABD 和三角形BCD 的和即可求得；解：（1）连接BD ，260AB AD A ==∠=︒， ，ABD ∴ 是等边三角形，260BD ADB ∴=∠=︒，，4BC CD == ，则222222242020BD CD BC +=+===，（ ， 222BD CD BC ∴+= ，90BDC ∴∠=︒ ，150ADC ∴∠=︒ ；（2）1111••22244222222ABD BDC S S S AD AD BD DC =+=+=⨯⨯⨯+⨯⨯=+16.已知：如图，四边形ABCD 中，6030ADC ABC AD CD ∠=︒∠=︒=，， ．（1）连接AC ACD ， 的形状是？（2）求证：222BD AB BC =+ ．答案：见解析解析：（1）根据全等三角形的判定定理“有一内角为60︒ 的等腰三角形是等边三角形”推知ACD 是等边三角形．（2）如图，以BC 为边向形外作等边BCE ，连接AE ．构造全等三角形（BCD ECA ≌ ），然后根据全等三角形的性质、勾股定理证得结论．解：（1）如图，连接AC ．60ADC AD CD ∠=︒=， ，ACD ∴ 是等边三角形；故答案是：等边三角形；（2）如图，以BC 为边向形外作等边BCE ，连接AE ．由（1）知，ACD 是等边三角形，则60DC AC EC BC ACD BCE ==∠=∠=︒，， ，在BCD 与ECA ，∵DC AC DCB ACE BC EC =⎧⎪∠=∠⎨⎪=⎩，BCD ECA SAS ∴≌（）， AE BD ∴= ，90ABE ∠=︒ ，∴ 在Rt ABE 中，有222AB BE AE += ，即222AB BC BD += ．17.如图，在ABC 中，AB AC D =， 是三角形外一点，且60ABD BD DC AB ∠=︒+=， ．求证：ACD ∠= ____°．答案：60解析：首先延长BD 至E ，使CD DE = ，连接AE AD ， ，由BD DC AB += ，易得ABE 是等边三角形，继而证得ACD ADE ≌ ，则可证得：60ACD E ∠=∠=︒ ． 证明：延长BD 至E ，使CD DE = ，连接AE AD ，，BD CD AB BE BD DE +==+， ，BE AB ∴= ，60ABD ∠=︒ ，ABE ∴ 是等边三角形，60AE AB AC E ∴==∠=︒， ，在ACD 和ADE 中，AC AE CD DE AD AD =⎧⎪=⎨⎪=⎩，ACD ADE SSS ∴≌（）， 60ACD E ∴∠=∠=︒ ．18.如图，凸六边形ABCDEF 的六个角都是120︒ ，边长28116AB cm BC cm CD cm DE cm ====，，， ，求出这个六边形的周长为____cm .答案：46解析：凸六边形ABCDEF ，并不是一规则的六边形，但六个角都是120︒ ，所以通过适当的向外作延长线，可得到等边三角形，进而求解．解：如图，分别作直线AB CD EF 、、 的延长线使它们交于点G H P 、、 ．因为六边形ABCDEF 的六个角都是120︒，所以六边形ABCDEF 的每一个外角的度数都是60︒ ．所以三角形APF 、三角形BGC 、三角形DHE 、三角形GHP 都是等边三角形． 所以86GC BC cm DH DE cm ====， ．所以811625GH cm =++= ，252815FA PA PG AB BG cm ==--=--= ，251564EF PH PF EH cm =--=--= ．所以六边形的周长为2811641546cm +++++= ．19.如图，在六边形ABCDEF 中，A B C D E F ∠=∠=∠=∠=∠=∠ ．（1）试说明MAF 为等边三角形；（2）请探索AB BC EF DE ，，， 之间的关系（等量关系或位置关系）并说明理由．答案：见解析解析：（1）根据多边形的内角和定理求出120A B C D E F ∠=∠=∠=∠=∠=∠=︒ ，求出60MAF MFA ∠=∠=︒ ，得出等边三角形MAF ，推出MA MF = ，同理求出NBC MNG EDG 、、 是等边三角形，推出BN BC DE EG ==， ，求出AN FG = ，即可求出答案．解：（1）作直线AB 、直线EF 、直线CD AB ， 和EF 交于M AB ， 和CD 交于N EF ， 和CD 交于G ，A B C D E F ∠=∠=∠=∠=∠=∠ ，62180A B C D E F ∠+∠+∠+∠+∠+∠=-⨯︒（） ，120A B C D E F ∴∠=∠=∠=∠=∠=∠=︒ ，18012060MAF MFA ∴∠=∠=︒-︒=︒ ，MF MA ∴= ，MAF ∴为等边三角形．（2）AB BC EF DE +=+ ，理由是：120ABC BCD ∠=∠=︒ ，18012060NBC NCB ∴∠=∠=︒︒=︒﹣ ，NB NC ∴= ，BNC ∴ 是等边三角形，60BC BN N ∴=∠=︒， ，同理60DE EG G =∠=︒， ，60G N ∴∠=∠=︒ ，MN MG ∴= ， MAF 为等边三角形，MA MF ∴= ，MN MA MG MF ∴=﹣﹣ ，AN FG ∴= ，AB BC AB BN AN +=+= ，FG EF EG EF DE =+=+ ，AB BC EF DE ∴+=+ ．20.如图所示，一个六边形的六个内角都是120︒ ，其中连续四边的长依次是1995、、、 ．求这个六边形的周长为____.答案：42解析：首先延长并反向延长AB CD EF ，， ，两两相交于点G H I 、、 ，可得GHI GBC ， 是等边三角形，同理：HAF DEI ， 是等边三角形，即可求得AF 与EF 的长，继而求得答案.解：如图，延长并反向延长AB CD EF ，， ，两两相交于点G H I 、、，六边形ABCDEF 的每个内角都是120︒，6060G H I GCB GBC ∴∠=∠=∠=︒∠=∠=︒， ，GHI GBC ∴， 是等边三角形，同理：HAF DEI ， 是等边三角形，95BG GC BC DE DI EI ∴======， ，99523GI GC CD DI ∴=++=++= ，23GH GI HI ∴=== ，13AH GH BG AB ∴=--= ，13AF AH FH ∴=== ，5EF HI EI FH ∴=--= ，∴ 六边形ABCDEF 的周长113559942AB AF EF DE CD BC =+++++=+++++= ．。
人教版中考数学二轮复习专题练习上常用辅助线-构造等边三角形
6.构造等边三角形1.公园里有一块形如四边形ABCD 的草地，测得10BC CD ==米，120B C ∠=∠=︒，45A ∠=︒．请你求出这块草地的面积？DCBA答案：见解析 解析：EABCD延长DC AB 、交于E ，连结DB ，∵120ABC BCD ∠=∠=︒，∴60EBC ECB ∠=∠=︒， ∴EBC ∆是等边三角形，∵DC CB =，∴30CDB DBC ∠=∠=︒， ∴90DBA ∠=︒，BD =， ∵45A ∠=︒，∴AB =∴(211502ABDS ∆==，11110222BCD BDE S S ∆∆==⨯⨯⨯=∴这块草地的面积为(150+平方米．2.如图：已知10AB=,点C D、在线段AB上且2AC DB==；P是线段CD上的动点,分别以AP PB、为边在线段AB的同侧作等边AEP 和等边PFB,连结EF,设EF的中点为G；当点P从点C运动到点D时,则点G移动路径的长是____．A BC DPEFG答案：3解析：分别延长AE BF、交于点H，易证四边形EPFH为平行四边形，得出G为中点，则的运行轨迹为三角形的中位线．再求出的长，运用中位线的性质求出的长度即可．解：如图，分别延长交于点．，，，，四边形为平行四边形，与互相平分．为的中点，正好为中点，即在的运动过程中，始终为的中点，所以的运行轨迹为三角形的中位线．，∴，即的移动路径长为3.四边形ABCD，有BC CD=，120B C∠=∠=︒，45A∠=︒．请你求D∠=____︒.DCBA答案：75 解析：EABCD延长DC AB 、交于E ，连结DB ，∵120ABC BCD ∠=∠=︒，∴60EBC ECB ∠=∠=︒， ∴EBC ∆是等边三角形，∵DC CB =，∴30CDB DBC ∠=∠=︒， ∴90DBA ∠=︒，∵45A ∠=︒，∴904545ADB ∠=︒-︒=︒， ∴453075ADC ADB BDC ∠=∠+∠=︒+︒=︒4.如图，四边形ABCD 中，AC BD ， 是对角线，ABC 是等边三角形．3035ADC AD BD ∠=︒==，， ，则CD 的长为____.答案：4解析：首先以CD为边作等边CDE，连接AE，利用全等三角形的判定得出BCD ACE≌，进而求出DE的长即可．解：如图，以CD为边作等边CDE，连接AEBCD BCA ACD DCE ACD ACE∠=∠+∠=∠+∠=∠，∴在BCD和ACE中，AC BCACE BCDCD CE=⎧⎪∠=∠⎨⎪=⎩BCD ACE SAS∴≌（），BD AE∴=．又30ADC∠=︒，90ADE∴∠=︒．在Rt ADE中，53AE AD==，，于是224DE AE AD=-=，4CD DE∴==．5.如图所示，在ABC中，AB AC D E=，、是ABC内两点，AD平分60BAC EBC E∠∠=∠=︒．，若62BE DE==，，则BC的长度是__.答案：8解析：作出辅助线后根据等腰三角形的性质得出62BE DE ==，，进而得出BEM 为等边三角形，EFD 为等边三角形，从而得出BN 的长，进而求出答案． 解：延长ED 交BC 于M ，延长AD 交BC 于N ，作DF BC 于F ，AB AC AD =，平分BAC ∠ ， AN BC BN CN ∴⊥=， ， 60EBC E ∠=∠=︒ ，BEM ∴为等边三角形， EFD ∴为等边三角形，62BE DE ==， ，4DM ∴= ，BEM 为等边三角形，60EMB ∴∠=︒ ， AN BC ⊥ ， 90DNM ∴∠=︒ ， 30NDM ∴∠=︒ ，2NM ∴= ， 4BN ∴= ， 28BC BN ∴== ，6.如图，六边形ABCDEF 中，每一个内角都是1201230828AB BC CD DE ︒====，，，，．求这个六边形的周长为_____.答案：116解析：凸六边形ABCDEF ，并不是一规则的六边形，但六个角都是120︒ ，所以通过适当的向外作延长线，可得到等边三角形，进而求解．解：如图，分别作直线AF ED BC 、、 的延长线和反向延长线使它们交于点G H P 、、 ．六边形ABCDEF 的六个角都是120°，∴ 六边形ABCDEF 的每一个外角的度数都是60°． PGH BGA DHC EFP ∴、、、 都是等边三角形． 128GC BC DH CH ∴====， ．1230850GH ∴=++=，5028814FE PE PH ED DH ==--=--=，50141224AF PG PF AG =--=--=．∴ 六边形的周长为：24123082814116+++++= ．7.如图，已知120ABC ∠=︒ ，BD 平分60ABC DAC ∠∠=︒， ，若23AB BC ==， ，则BD 的长是_____.答案：5解析：在CB 的延长线上取点E ，使BE AB =，连接AE ，则可证得ABE 为等边三角形，再结合条件可证明ABD AEC ≌ ，可得BD CE = ，再利用线段的和差可求得CE ，则可求得BD .解：在CB 的延长线上取点E ，使BE AB =，连接AE ，120ABC ∠=︒ ，18060ABE ABC ∴∠=∠=︒﹣ ，BE AB = ，ABE ∴ 为等边三角形，60AE AB BAE E ∴=∠=∠=︒， ， 60DAC ∠=︒ ，DAC BAE∴∠=，BAD BAC DAC EAC BAC BAE∠=∠+∠∠=∠+∠，，BAD EAC∴∠=∠，BD平分ABC∠，，ABD E∴∠=∠，在ABD和AEC中，BAD EACAB AEABD E∠=∠⎧⎪=⎨⎪∠=∠⎩，ABD AEC ASA∴≌（），BD CE∴=，325CE BE BC AB BC=+=+=+=，5BD∴=，8.如图，在ABC中，AB AC D E=，、是ABC内两点，AD平分60BAC EBC E∠∠=∠=︒，，若602BE cm DE cm==，，则BC= ____cm．答案：62解析：作出辅助线后根据等腰三角形的性质得出62BE DE==，，进而得出BEM为等边三角形，EFD为等边三角形，从而得出BN的长，进而求出答案．解：延长ED交BC于M，延长AD交BC于N，作DF BC，=，AD平分BAC∠，AB AC，，∴⊥=AN BC BN CN∠=∠=︒，EBC E60∴为等边三角形，BEM∴为等边三角形，EFD，，==BE DE602DM∴=，58BEM为等边三角形，∴∠=︒，60EMB⊥，AN BC∴∠=︒，DNM90∴∠=︒，NDM30∴=，NM29∴=，BN31∴==，BC BN262故答案为62．9.如图，过边长为1的等边ABC 的边AB 上一点P ，作PE AC ⊥ 于E Q ， 为BC 延长线上一点，当PA CQ = 时，连PQ 交AC 边于D ，则DE 的长为____.（注：若答案不是整数，请化为小数）答案：0.5 解析：过P 作PFBC 交AC 于F ，得出等边三角形APF ，推出AP PF QC == ，根据等腰三角形性质求出EF AE = ，证PFD QCD ≌ ，推出FD CD = ，推出12DE AC =即可．解：过P 作PFBC 交AC 于F ．PF BC ，ABC 是等边三角形， PFD QCD APF ∴∠=∠， 是等边三角形，AP PF AF ∴== ，PE AC ⊥ ，AE EF ∴= ，AP PF AP CQ ==， ，PF CQ∴=．在PFD和QCD中，PFD QCDPDF QDCPF CQ∠=∠⎧⎪∠=∠⎨⎪=⎩，PFD QCD AAS∴≌（），FD CD∴=，AE EF=，EF FD AE CD∴+=+，12AE CD DE AC∴+==，1AC=，10.52DE∴==．10.如图，ABC中，AB AC AD=，平分BAC D E∠，、是ABC内两点，且60ECB E∠=∠=︒，若82CE DE==，，则BC=_____.答案：10解析：延长ED交BC于M，延长AD交BC于N，根据等腰三角形的性质得出，，进而得出CEM为等边三角形，从而得出BN的长，进而求出答案．==CE DE82解：延长ED交BC于M，延长AD交BC于N，∠，=，平分BACAB AC AD∴⊥=，，AN BC BN CNECB E∠=∠=︒，60∴为等边三角形，CEM，，==82CE DE∴=，6DMCEM为等边三角形，60∴∠=︒，EMC⊥，AN BC∴∠=︒，90DNM∴∠=︒，NDM30∴=，NM3﹣，∴==CN835∴=，5BN∴==．BC BN210故答案为：10．11.如图，凸四边形ABCD 满足条件：60120AB AD BAD BCD =∠=︒∠=︒，， 那么AC ____BC CD +．（填“大于”或“小于”或“等于”）答案：等于解析：延长DC 到点E ，使得BC CE = ，连接BE 和BD ，根据已知条件和所作辅助线可得ABD 与BCE 均为等边三角形，证明ABC 和DBE 全等即可证明；解：延长DC 到点E ，使得BC CE = ，连接BE 和BD .∵120BCD ∠=︒∴18012060BCE ∠=︒-︒=︒又BC CE = ，60AB AD BAD =∠=︒，ABD ∴ 与BCE 均为等边三角形60BD AB BE BC ABD EBC ∴==∠=∠=︒，，ABD DBC EBC DBC ∴∠+∠=∠+∠ ,即ABC DBE ∠=∠在ABC 和DBE 中AB BDABC DBEBC BE=∠=∠=⎧⎪⎨⎪⎩，∴ABC DBE≌∴BD DE=∵DE CD EC CD BC=+=+AC BC CD∴=+．故答案为：相等12.已知：如图，等边ABC中，1AB P=，是AB边上一动点，作PE BC⊥，垂足为E；作EF AC⊥，垂足为F；作FQ AB⊥，垂足为Q．（1）设BP x AQ y==，，求y与x之间的函数关系式；（2）当点P和点Q重合时，求线段EF的长；（3）当点P和点Q不重合，但线段PE FQ、延长线相交时，求它们与线段EF围成的三角形周长的取值范围．答案：见解析解析：（1）由已知等边ABC中，可得每个角都是60︒，由作PE BC⊥，垂足为E；作EF AC⊥，垂足为F；作FQ AB⊥，垂足为Q，得三个直角三角形且都有30︒的角，据此用x 可表示出BE CE CF ，， ，相继表示出AF AQ ， ，求出y 与x 之间的函数关系式．（2）由已知可列出方程组结合已知求出EF 的长．（3）当线段PE FQ 、 相交时，根据已知得到它们与线段EF 围成的三角形三个角都是60︒ 解：（1）ABC 是等边三角形，1AB = ．601A B C BC CA AB ∴∠=∠=∠=︒===， ．又90BEP CFE FQA BP x ∠=∠=∠=︒=， ．11122BE x CE x ∴==-， ，1111111242424CF x AF x x =-=--=+，（）． 11112224AQ AF x ∴==+（） ， 1184y x ∴=+ ．（2）由方程组11184x y y x +=⎧⎪⎨=+⎪⎩得23x = ． ∴ 当点P 和点Q 重合时，23x =，11333243EF CF x ∴==-=（） ．（3）设线段EP FQ 、 的延长线相交于点M ，EF AC ⊥ ，390QFE ∴∠+∠=︒ ，FQ AB ⊥ ，390A ∴∠+∠=︒ ，60A QFE ∴∠=∠=︒ ，190C ∠+∠=︒ ，1290∠+∠=︒ ，260C ∴∠=∠=︒ ，MEF ∴ 是等边三角形，且当点P 和点Q 重合时，EF 最短为33. 且当点P 和点B 重合时，EF 最长为32 3332m ∴<≤ ．13.如图，在四边形ABCD 中，60120AB AD BAD BCD =∠=︒∠=︒，， ，连接AC BD ， 交于点E ．（1）若2BC CD == ，M 为线段AC 上一点，且12AM CM =：： ，连接BM ，求点C 到BM 的距离．（2）证明：BC CD AC += ．答案：见解析解析：（1）由条件可以证明ABC ADC ≌，可以得出30BAC DAC ∠=∠=︒ ，6090ACB ACD AEB ∠=∠=︒∠=︒， ，求出90ABC ∠=︒ ，由勾股定理可以求出423AC AB ==，，由12AM CM =：： 可以求得AM CM 、 的值，在Rt BEC 中由勾股定理可以求出CE BE 、 的值，从而求出BM 的值，过点C 作CF MB ⊥ 于F ，利用三角形的面积相等建立等量关系就可以求出结论．（2）要证BC DC AC += ，延长BC 到E ，使CE CD = ，则求AC BE = 即可．由60AB AD ABD =∠=︒， ，得ABD 是等边三角形，进而得60ADB AD BD ∠=︒=，，又有120BCD ∠=︒ ，则DCE 是等边三角形，所以得ACD BDE ≌ ，则AC BE BC CD ==+ ．解：（1）60AB AD BAD =∠=︒， ，ABD ∴ 是等边三角形，60ABD ADB ∴∠=∠=︒ ．BC CD = ，ABC ADC ∴≌ ，3060BAC DAC ACB ACD ∴∠=∠=︒∠=∠=︒， ．9090AEB BEC ABC ∴∠=∠=︒∠=︒， ，112CE BC ∴==，324BE AC BC ===， ． 12AM CM =：： ，43AM ∴=，83CM = ， 53EM ∴= ，在Rt BEM 中由勾股定理得 225213(3)()3BM =+= 过点C 作CF BM ⊥ 于点F ．22BM CF CMBE⋅⋅∴= ．213833322CF ⨯∴= ，439CF ∴= ．即点C 到BM 的距离43913．（2）证明：延长BC 到点F ，使CF CB = ，连接DF ，，60AB AD ABD =∠=︒，ABD ∴ 是等边三角形，60ADB AD BD ∴∠=︒=， ，BC CD ∴= ，CF CD ∴= ． 120BCD ∠=︒ ，18060DCF BCD ∴∠=︒∠=︒﹣ ，DCF ∴ 是等边三角形，60CDF ADB DC DF ∴∠=∠=︒=， ，ADC BDF ∴∠=∠ ，又AD BD = ，ACD BDF ∴≌ ，AC BF BC CF ∴==+ ，即AC BC CD =+ ．14.已知：如图，在等边三角形ABC 中，点D 是AC 边上的一个动点（D 与A C ， 不重合），延长AB 到E ，使BE CD = ，连接DE 交BC 于点F ．（1）求证：DF EF = ；（2）若ABC 的边长为10 ，设CD x BF y ==， ，求y 与x 的函数关系式，写出自变量x 的取值范围．答案：见解析解析：（1）过D 作DM AB 交BC 于M ，则CDM 为等边三角形，得CD DM = ，而BE CD = ，得到DM BE = ，易证得FDM FEB ≌ ，根据全等三角形的性质即可得到结论；（2）由（1）得FDM FEB ≌ ，得到MF BF y == ，易得CM CD x == ，而10BC = ，即有10x y y ++= ，即可得到y 与x 间的函数关系式．解：（1）证明：过D 作DM AB 交BC 于M ，CDM A CMD ABC ∴∠=∠∠=∠， ，又∵在等边三角形ABC 中，60A ABC C ∠=∠=∠=︒ ，CDM CMD C ∴∠=∠=∠ ，CDM ∴ 是等边三角形，CD DM ∴= ，又CD BE = ，BE DM ∴= ，DM AE ，MDF E ∴∠=∠ ，在DMF 和EBF 中，MDF E ∠=∠ ，DFM EFB ∠=∠ ，DM BE = ，DMF EBF AAS ∴≌（）， DF EF ∴= ；（2）由（1）得DMF EBF ≌ ，BF MF y ∴== ，由（1）得CDM 是等边三角形，CM CD x ∴== ，又10CM MF FB BC ++== ，210y x ∴+= ，即152010x y x =-（＜＜）．15.如图，在四边形ABCD 中，260254AB AD A BC CD ==∠=︒==，，， ．（1）求ADC ∠ 的度数．（2）求四边形ABCD 的面积．答案：见解析解析：（1）连接BD ，根据260AB AD A ==∠=︒， ，得出ABD 是等边三角形，求得2BD = ，然后根据勾股定理的逆定理判断三角形BDC 是直角三角形，从而求得150ADC ∠=︒ ；（2）根据四边形的面积等于三角形ABD 和三角形BCD 的和即可求得；解：（1）连接BD ，260AB AD A ==∠=︒， ，ABD ∴ 是等边三角形，260BD ADB ∴=∠=︒，，254BC CD ==， ，则22222224202520BD CD BC +=+===，（） ， 222BD CD BC ∴+= ，90BDC ∴∠=︒ ，150ADC ∴∠=︒ ；（2）131131••2224432222ABD BDC S S S AD AD BD DC =+=+=⨯⨯⨯+⨯⨯=+．16.已知：如图，四边形ABCD 中，6030ADC ABC AD CD ∠=︒∠=︒=，， ．（1）连接AC ACD ， 的形状是？（2）求证：222BD AB BC =+ ．答案：见解析解析：（1）根据全等三角形的判定定理“有一内角为60︒的等腰三角形是等边三角形”推知ACD是等边三角形．（2）如图，以BC为边向形外作等边BCE，连接AE．构造全等三角形（BCD ECA≌），然后根据全等三角形的性质、勾股定理证得结论．解：（1）如图，连接AC．60ADC AD CD∠=︒=，，ACD∴是等边三角形；故答案是：等边三角形；（2）如图，以BC为边向形外作等边BCE，连接AE．由（1）知，ACD是等边三角形，则60DC AC EC BC ACD BCE==∠=∠=︒，，，在BCD与ECA，∵DC ACDCB ACEBC EC=⎧⎪∠=∠⎨⎪=⎩，BCD ECA SAS∴≌（），AE BD∴=，90ABE∠=︒，∴在Rt ABE中，有222AB BE AE+=，即222AB BC BD+=．17.如图，在ABC中，AB AC D=，是三角形外一点，且60ABD BD DC AB∠=︒+=，．求证：ACD∠= ____°．答案：60解析：首先延长BD至E，使CD DE=，连接AE AD，，由BD DC AB+=，易得ABE是等边三角形，继而证得ACD ADE≌，则可证得：60ACD E∠=∠=︒．证明：延长BD至E，使CD DE=，连接AE AD，，BD CD AB BE BD DE+==+，，BE AB∴=，60ABD∠=︒，ABE∴是等边三角形，60AE AB AC E∴==∠=︒，，在ACD和ADE中，AC AECD DEAD AD=⎧⎪=⎨⎪=⎩，ACD ADE SSS∴≌（），60ACD E ∴∠=∠=︒ ．18.如图，凸六边形ABCDEF 的六个角都是120︒ ，边长28116AB cm BC cm CD cm DE cm ====，，， ，求出这个六边形的周长为____cm .答案：46解析：凸六边形ABCDEF ，并不是一规则的六边形，但六个角都是120︒ ，所以通过适当的向外作延长线，可得到等边三角形，进而求解．解：如图，分别作直线AB CD EF 、、 的延长线使它们交于点G H P 、、 ．因为六边形ABCDEF 的六个角都是120︒，所以六边形ABCDEF 的每一个外角的度数都是60︒ ．所以三角形APF 、三角形BGC 、三角形DHE 、三角形GHP 都是等边三角形． 所以86GC BC cm DH DE cm ====， ．所以811625GH cm =++= ，252815FA PA PG AB BG cm ==--=--= ，251564EF PH PF EH cm =--=--= ．所以六边形的周长为2811641546cm +++++= ．19.如图，在六边形ABCDEF 中，A B C D E F ∠=∠=∠=∠=∠=∠ ．（1）试说明MAF 为等边三角形；（2）请探索AB BC EF DE ，，， 之间的关系（等量关系或位置关系）并说明理由．答案：见解析解析：（1）根据多边形的内角和定理求出120A B C D E F ∠=∠=∠=∠=∠=∠=︒ ，求出60MAF MFA ∠=∠=︒ ，得出等边三角形MAF ，推出MA MF = ，同理求出NBC MNG EDG 、、 是等边三角形，推出BN BC DE EG ==， ，求出AN FG = ，即可求出答案．解：（1）作直线AB 、直线EF 、直线CD AB ， 和EF 交于M AB ， 和CD 交于N EF ， 和CD 交于G ，A B C D E F ∠=∠=∠=∠=∠=∠ ，62180A B C D E F ∠+∠+∠+∠+∠+∠=-⨯︒（） ，120A B C D E F ∴∠=∠=∠=∠=∠=∠=︒ ，18012060MAF MFA ∴∠=∠=︒-︒=︒ ，MF MA ∴= ，MAF ∴为等边三角形．（2）AB BC EF DE +=+ ，理由是：120ABC BCD ∠=∠=︒ ，18012060NBC NCB ∴∠=∠=︒︒=︒﹣ ，NB NC ∴= ，BNC ∴ 是等边三角形，60BC BN N ∴=∠=︒， ，同理60DE EG G =∠=︒， ，60G N ∴∠=∠=︒ ，MN MG ∴= ，MAF 为等边三角形，MA MF ∴= ，MN MA MG MF ∴=﹣﹣ ，AN FG ∴= ，AB BC AB BN AN +=+= ，FG EF EG EF DE =+=+ ，AB BC EF DE ∴+=+ ．20.如图所示，一个六边形的六个内角都是120︒ ，其中连续四边的长依次是1995、、、 ．求这个六边形的周长为____.答案：42解析：首先延长并反向延长AB CD EF ，， ，两两相交于点G H I 、、 ，可得GHI GBC ， 是等边三角形，同理：HAF DEI ， 是等边三角形，即可求得AF 与EF的长，继而求得答案.解：如图，延长并反向延长AB CD EF ，， ，两两相交于点G H I 、、，六边形ABCDEF 的每个内角都是120︒，6060G H I GCB GBC ∴∠=∠=∠=︒∠=∠=︒， ，GHI GBC ∴， 是等边三角形，同理：HAF DEI ， 是等边三角形，95BG GC BC DE DI EI ∴======， ，99523GI GC CD DI ∴=++=++= ，23GH GI HI ∴=== ，13AH GH BG AB ∴=--= ，13AF AH FH ∴=== ，5EF HI EI FH ∴=--= ，∴ 六边形ABCDEF 的周长113559942AB AF EF DE CD BC =+++++=+++++= ．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
PFD QCD，A APF 是等边三角形， AP PF AF ， PE AC ， AE EF ， AP PF，AP CQ ，
PF CQ ．
在 A PFD 和 AQCD 中， PFD QCD PDF QDC ， PF CQ A PFD≌A（Q）CD AAS ，
CD DE 4 ．
5.如图所示，在 A ABC 中， AB AC，D、 E 是 A ABC 内两点， AD 平分 BAC．EBC E 60 ，若 BE 6，DE 2 ，则 BC 的长度是__.
答案：8
解析：作出辅助线后根据等腰三角形的性质得出 BE 6，DE 2 ，进而得出 A BEM 为 等边三角形， A EFD 为等边三角形，从而得出 BN 的长，进而求出答案． 解：延长 ED 交 BC 于 M ，延长 AD 交 BC 于 N ，作 DF A BC 于 F ，
BCD BCA ACD DCE ACD ACE ，
在 A BCD 和 A ACE 中， AC BC ACE BCD CD CE
A BCD≌A（A）CE SAS ， BD AE ． 又ADC 30 ， ADE 90 ． 在 RtA ADE 中， AE 5，AD 3 ， 于是 DE AE2 AD2 4 ，
间的函数关系式．
（2）由已知可列出方程组结合已知求出 EF 的长． （3）当线段 PE、FQ 相交时，根据已知得到它们与线段 EF 围成的三角形三个角都是 60 解：（1）A ABC 是等边三角形， AB 1 ． A B C 60，BC CA AB 1 ． 又BEP CFE FQA 90，BP x ．
E B
∴ DBA 90 ， BD 10 3 ，
∵ A 45 ，∴ AB 10 3 ，
∴ SABD
1 2
10
3
2
150 ， SBCD
1 2 SBDE
1 1 10 10 22
3 25
3，
∴这块草地的面积为 150 25 3 平方米．
2.如图：已知 AB 10 ,点 C、D 在线段 AB 上且 AC DB 2 ； P 是线段 CD 上的动点, 分别以 AP、PB 为边在线段 AB 的同侧作等边 A AEP 和等边 A PFB ,连结 EF ,设 EF 的中 点为 G ；当点 P 从点 C 运动到点 D 时,则点 G 移动路径的长是____．
答案：10
解析：延长 ED 交 BC 于 M ，延长 AD 交 BC 于 N ，根据等腰三角形的性质得出 CE 8，DE 2 ，进而得出 ACEM 为等边三角形，从而得出 BN 的长，进而求出答
案．
解：延长 ED 交 BC 于 M ，延长 AD 交 BC 于 N ，
AB AC，AD 平分 BAC ， AN BC，BN CN ， ECB E 60 ， ACEM 为等边三角形， CE 8，DE 2 ， DM 6 ， ACEM 为等边三角形，
，
ABD E ， 在 A ABD 和 A AEC 中，
BAD EAC
AB
AE
，
ABD E
A ABD≌A（A）EC ASA ， BD CE ， CE BE BC AB BC 3 2 5 ， BD 5 ，
8.如图，在 A ABC 中， AB AC，D、 E 是 A ABC 内两点， AD 平分 BAC，EBC E 60 ，若 BE 60cm，DE 2cm ，则 BC ____ cm ．
．
六边形 ABCDEF 的六个角都是 120°， 六边形 ABCDEF 的每一个外角的度数都是 60°．
A PGH、A B、G、A A DHC A EFP 都是等边三角形． GC BC 12，DH CH 8 ． GH 12 30 8 50，FE PE PH ED DH 50 28 8 14， AF PG PF AG 50 14 12 24 ．
的三角形周长的取值范围．
答案：见解析
解析：（1）由已知等边 A ABC 中，可得每个角都是 60 ，由作 PE BC ，垂足为 E ；作 EF AC ，垂足为 F ；作 FQ AB ，垂足为 Q ，得三个直角三角形且 都有 30 的角，据此用 x 可表示出 BE，C，E CF ，相继表示出 AF，AQ ，求出 y 与 x 之
FD CD ， AE EF ， EF FD AE CD ， AE CD DE 1 AC ，
2 AC 1 ， DE 1 0.5 ．
2
10.如图， A ABC 中， AB AC，AD 平分 BAC，D、 E 是 A ABC 内两点，且 ECB E 60 ，若 CE 8，DE 2 ，则 BC _____.
答案：等于
解析：延长 DC 到点 E ，使得 BC CE ，连接 BE 和 BD ，根据已知条件和所作辅 助线可得 A ABD 与 A BCE 均为等边三角形，证明 A ABC 和 A DBE 全等即可证明；
解：延长 DC 到点 E ，使得 BC CE ，连接 BE 和 BD . ∵ BCD 120 ∴ BCE 180 120 60 又 BC CE ， AB AD，BAD 60 A ABD 与 A BCE 均为等边三角形 BD AB，B，E BC ABD EBC 60 ABD DBC EBC DBC ,即 ABC DBE 在 A ABC 和 A DBE 中
D C
B
D C E
B
4.如图，四边形 ABCD 中， AC，BD 是对角线， A ABC 是等边三角形． ADC 30，A，D 3 BD 5 ，则 CD 的长为____.
答案：4
解析：首先以 CD 为边作等边 ACDE ，连接 AE ，利用全等三角形的判定得出 A BCD≌A ACE ，进而求出 DE 的长即可． 解：如图，以 CD 为边作等边 ACDE ，连接 AE
6.如图，六边形 ABCDEF 中，每一个内角都是 120，A，B，，12 BC 30 CD 8 DE 28 ．求这个六边 形的周长为_____.
答案：116
解析：凸六边形 ABCDEF ，并不是一规则的六边形，但六个角都是120 ，所以通过适
当的向外作延长线，可得到等边三角形，进而求解．
解：如图，分别作直线 AF、E、D BC 的延长线和反向延长线使它们交于点 G、H、 P
六边形的周长为： 24 12 30 8 28 14 BD 平分 ABC，DAC 60 ，若 AB 2，BC 3 ，则 BD 的长是_____.
答案：5
解析：在 CB 的延长线上取点 E ，使 BE AB ，连接 AE ，则可证得 A ABE 为等边 三角形，再结合条件可证明 A ABD≌A AEC ，可得 BD CE ，再利用线段的和差可求 得 CE ，则可求得 BD . 解：在 CB 的延长线上取点 E ，使 BE AB ，连接 AE ，
F G E
A CP
DB
答案：3
解析：分别延长 AE、BF 交于点 H ，易证四边形 EPFH 为平行四边形，得出 G 为PH中点，
则G的运行轨迹为三角形HCD的中位线MN．再求出CD的长，运用中位线的性质求出MN的长度 即可．
解：如图，分别延长AE、BF交于点H．
∵ ∠A＝∠FPB＝60°， ∴ AH ∥ PF， ∵ ∠B＝∠EPA＝60°， ∴ BH ∥ PE， ∴ 四 边形EPFH为平行四边形， ∴ EF与HP互相平分． ∵ G为EF的中点， ∴ G正好为PH中点， 即在P的运动过程中，G始终为PH的中点，所以G的运行轨迹为三角形HCD的中位线MN． ∵ CD＝10－2－2＝6，∴MN＝3，即G的移动路径长为3
6.构造等边三角形
1.公园里有一块形如四边形 ABCD 的草地，测得 BC CD 10 米， B C 120 ， A 45 ．请你求出这块草地的面积？
D
C
答案：见解析 解析：
A
B
D C
A
延长 DC、AB 交于 E ，连结 DB ， ∵ ABC BCD 120 ，∴ EBC ECB 60 ， ∴ EBC 是等边三角形， ∵ DC CB ，∴ CDB DBC 30 ，
ABC 120 ， ABE 180﹣ABC 60 ， BE AB ， A ABE 为等边三角形， AE AB，BAE E 60 ， DAC 60 ， DAC BAE ， BAD BAC DAC，EAC BAC BAE ， BAD EAC ， BD 平分 ABC ，
3.四边形 ABCD ，有 BC CD ， B C 120 ， A 45 ．请你求 D ____ .
A
答案：75 解析：
A
延长 DC、AB 交于 E ，连结 DB ， ∵ ABC BCD 120 ，∴ EBC ECB 60 ， ∴ EBC 是等边三角形， ∵ DC CB ，∴ CDB DBC 30 ， ∴ DBA 90 ， ∵ A 45 ，∴ ADB 90 45 45 ， ∴ ADC ADB BDC 45 30 75
答案不是整数，请化为小数）
答案：0.5
解析：过 P 作 PF A BC 交 AC 于 F ，得出等边三角形 APF ，推出 AP PF QC ，根据等腰三角形性质求出 EF AE ，证 A PFD≌AQCD ，推出 FD CD ，推出 DE 1 AC 即可．
2
解：过 P 作 PF A BC 交 AC 于 F ．
EMC 60 ， AN BC ， DNM 90 ， NDM 30 ， NM 3 ， CN 8﹣3 5 ， BN 5， BC 2BN 10 ．
故答案为：10．
11.如图，凸四边形 ABCD 满足条件： AB AD，，BAD 60 BCD 120 那么 AC ____ BC CD ．（填“大于”或“小于”或“等于”）
AB BD ABC DBE ， BC BE ∴ A ABC≌A DBE ∴ BD DE ∵ DE CD EC CD BC AC BC CD ．
故答案为：相等