一元一次方程的解法(去分母)
含分母的一元一次方程解法步骤
含分母的一元一次方程解法步骤含分母的一元一次方程是指方程中存在形如1/x的项，解这种方程需要特别的方法。
下面将介绍一种解法步骤。
解法步骤如下：1. 清除分母。
首先，我们需要将方程中的分母消去，以便得到一个等价的无分母方程。
为了实现这一点，我们可以将方程两边乘以分母的最小公倍数，这样就可以消去分母。
假设方程中有两个分母为a和b的项，那么我们可以将方程两边乘以ab来消去分母。
如果方程中有多个分母项，那么我们需要找到它们的最小公倍数来进行消去。
2. 整理方程。
在消去分母后，我们得到一个等价的无分母方程。
现在，我们需要整理方程，将所有项移到等号的一侧，并将方程化简为标准形式ax + b = 0，其中a和b是已知的系数。
3. 求解方程。
根据一元一次方程的定义，我们知道方程的解就是使得方程成立的变量的取值。
对于标准形式的一元一次方程，我们可以通过移项的方法求解。
首先，我们将常数项b移到等号的另一侧，得到ax = -b。
然后，我们可以通过除以系数a来求解x的值，即x = -b/a。
这就是方程的解。
4. 验证解。
最后，我们需要验证求得的解是否符合原始方程。
将求得的解代入原始方程中，计算两边的值是否相等。
如果相等，那么解是正确的。
如果不相等，那么解是错误的，我们需要重新检查解的求解过程。
以上就是含分母的一元一次方程解法的步骤。
通过清除分母、整理方程、求解方程和验证解，我们可以准确地求解这类方程。
这种解法在实际问题中也具有一定的应用，可以帮助我们解决含有分母的一元一次方程。
七年级数学上册第3章一元一次方程3.3一元一次方程的解法第2课时用去分母解方程课件新版湘教版
知识点 解含分母的一元一次方程
1. 把方程 3x＋2x－3 1＝－x＋2 1去分母，正确的是 (C)
A．3x＋2(2x－1)＝－3(x＋1) B．18x＋2(2x－1)＝－3x＋1 C．18x＋2(2x－1)＝－3(x＋1) D．3x－2×2x－1＝－3x＋1
2. 下列方程去分母后，所得结果错误的有( B )
规律 ．
，
第
10
个方程
【解析】根据题意得第 n 个方程为nx＋n＋x 1＝2n＋1，
解为 x＝n(n＋1)，所以第 10 个方程为1x0＋1x1＝21，其解
为 x＝10×11＝110.
2. 某同学在解方程2x－3 1＝x＋3 a－2 去分母时，方程 右边的－2 没有乘 3，其他步骤正确，这时求得的方程的 解为 x＝2，试求 a 的值，并求出原方程的正确的解．
解：设甲、乙两地的路程为 x km， 列方程为x5－x7＝20， 解得 x＝350. 答：略．
1. 有一系列方程：第 1 个方程是 x＋2x＝3，解为 x
＝2；第 2 个方程是2x＋3x＝5，解为 x＝6；第 3 个方程是3x
＋ 是
4x1x＝0＋71，x1＝解2为1 ，x其＝解12为；
…根据 x＝110
法．请用这种方法解方程： 5(2x＋3)－34(x－2)＝2(x－2)－12(2x＋3)．
解：移项、合并同类项得121(2x＋3)＝141(x－2)， 约分、去分母得 2(2x＋3)＝x－2， 去括号，得 4x＋6＝x－2， 移项、合并同类项，得 3x＝－8， 两边都除以 3，得 x＝－83.
10. 从甲地到乙地，公共汽车原需行驶 7 h，开通高 速公路后，车速平均每小时增加了 20 km，只需 5 h 即可 到达，求甲、乙两地的路程．
2 一元一次方程的解法-课时4 “去分母”解一元一次方程
10x
3中的分母化成整数，得
2
= 30
D.将方程5% ⋅ x = 2 × 3%变形，得5x = 200 × 3
【解析】 将方程0.001 −
x
意；将方程
0.2
=
x
100
= 5去分母，得0.1 − x = 500，B项不符合题
10x
3中的分母化成整数，得
2
= 3，C项不符合题意；将方
程5% ⋅ x = 2 × 3%变形，得5x = 2 × 3，D项不符合题意。
C.2x − 2 − x = 1
D.2x − 2 − x = 4
【解析】 方程的两边都乘4，得2x − 2 − x = 4。
1
2
3
4
5
6
7
在去分母时，方程两边同乘各分母的最小公倍数，不要漏乘不含分母的
项，同时要把分子作为一个整体加上括号，原因是分数线具有括号的作用。
1
2
3
4
5
6
7
x−2
x+1
2
2.[2024邯郸期末]若代数式
活应用，各个步骤的目的都是为使方程向x = a的形式转化。
1
2
3
4
5
6
7
知识点2 “去分母”解一元一次方程的实际应用
6.一题多解[2023哈尔滨十七中月考]登山是一种简单易行的健身运动，山
中森林覆盖率高，负氧离子多，能使人身心愉悦地进行体育锻炼。张老师
和李老师登一座山，张老师每分钟登高10米，并且先出发30分钟，李老师
C.去括号，得x − 24 = 7
4 5x−120
D.括号内先通分，得 ⋅
5
4
8
利用去分母解一元一次方程
一个数，它的三分之二，它的一半，它的七分之 一，它的全部，加起来总共是33，求这个数.
讲授新课
一 解含分母的一元一次方程
例题Biblioteka 解方程：3x 1 2 3x 2 2x .
2
10 5
1. 方程 3 5x 7 x 17 去分母正确的是
()
2
4
A. 3－2(5x+7) = －(x+17)
B. 12－2(5x+7) = －x+17
C. 12－2(5x+7) = －(x+17)
D. 12－10x+14 = －(x+17)
观察与思考
下列方程的解法对不对？如果不对，你能找出错在 哪里吗？
解方程： 2x 1 x 2 1
32
解：去分母，得 4x－1－3x + 6 = 1 移项，合并同类项，得 x=4
典例精析
例1 解下列方程：
(1) x 1 1 2 2 x ；
2
4
(2)3x x 1 3 2x 1 .
3. 去分母与去括号这两步分开写，不要跳步， 防止忘记变号.
课堂小结
不要漏乘不含 分母的项
乘以所有分母 的最小公倍数
不要漏乘， 注意符号
等式的性质2 去分母
等式的性质2 系数
化为1
解一元一次方 程的一般步骤 去括号
移项
等式的性质1
合并同 类项
移项要变号
复习----去括号
解一元一次方程去分母
你来精心选一选
2 y 1 5 y 2 3 y 1 D 解方程 1去分母时 , 正确的是 (___) 3 6 4
( A)4(2 y 1) 2 5 y 2 3 y 1 12 ( B)4(2 y 1) 2(5 y 2) 3(3 y 1) 1 (C )4(2 y 1) 2(5 y 2) 3(3 y 1) 12
X-1 =
2
4x+2 -2(x-1) 5
5x+1 (２ ) 4
2x-1 4
=2 - Y-2 2
(３) Y+4 -Y+5= Y+3 3 3
丢番图的墓志铭:
―坟中安葬着丢番图,多么令人惊讶,它忠实地记录 了所经历的道路.上帝给予的童年占六分之一.又 过十二分之一,两颊长胡.再过七分之一,点燃结婚 的蜡烛.五年之后天赐贵子,可怜迟到的宁馨儿,享 年仅及其父之半,便进入冰冷的墓.悲伤只有用数论 的研究去弥补,又过四年,他也走完了人生的旅途.‖
合并同类项，得 25x=23 23 系数化为1，得 x 25
慧眼找错： 小马虎解方程时有一个地方错了，
请你指出来，并改正。
2x 1 x 2 (1) 1 3 3
解:去分母,得 2x-1=x+2-1 移项,得 2x-x=2-1+1 合并同类项,得 x=2 x=0
慧眼找错： 小马虎解方程时有一个地方错了，
请你指出来，并改正。
x 1 x 2 4 x (2) 3 6 2
解:去分母,得 2x-1-x+2=12-x 移项,得 2x-x+x=12+1-2 合并,得 2x=11 系数化为1,得 x= 11
2
x=4
第二节 一元一次方程的解法(含答案)...七年级数学 学而思
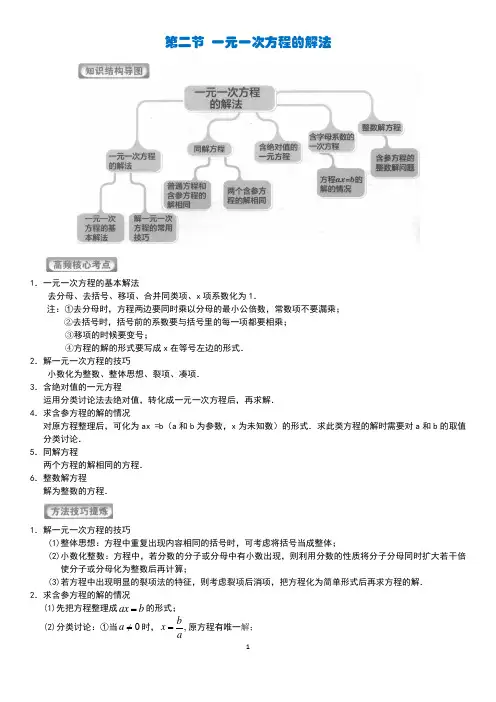
第二节 一元一次方程的解法1．一元一次方程的基本解法去分母、去括号、移项、合并同类项、x 项系数化为1．注：①去分母时，方程两边要同时乘以分母的最小公倍数，常数项不要漏乘；②去括号时，括号前的系数要与括号里的每一项都要相乘；③移项的时候要变号；④方程的解的形式要写成x 在等号左边的形式． 2．解一元一次方程的技巧小数化为整数、整体思想、裂项、凑项． 3．含绝对值的一元方程运用分类讨论法去绝对值，转化成一元一次方程后，再求解． 4．求含参方程的解的情况对原方程整理后，可化为ax =b （a 和b 为参数，x 为未知数）的形式．求此类方程的解时需要对a 和b 的取值分类讨论． 5．同解方程两个方程的解相同的方程． 6．整数解方程解为整数的方程．1．解一元一次方程的技巧(1)整体思想：方程中重复出现内容相同的括号时，可考虑将括号当成整体；(2)小数化整数：方程中，若分数的分子或分母中有小数出现，则利用分数的性质将分子分母同时扩大若干倍使分子或分母化为整数后再计算；(3)若方程中出现明显的裂项法的特征，则考虑裂项后消项，把方程化为简单形式后再求方程的解． 2．求含参方程的解的情况(1)先把方程整理成b ax =的形式； (2)分类讨论：①当0=/a 时，,abx =原方程有唯一解；②当0=a 且0=b 时．原方程有无数解： ③当a 0=且，0=/b 原方程无解． 3．同解方程问题(1)普通方程和含参方程的解相同：①解出普通方程的解；②将普通方程的解代入含参方程中； ③求出参数值；(2)两个含参方程的解相同：①将其中一个方程的解用参数表示出来；②将①中的解代入另一个方程中，消去未知数； ③求出参数值． 4．方程的 整数解问题①将方程整理成b ax =的形式； ②解方程，得⋅=ab x ③求出满足条件的参数值，常用枚举法或分离常数法．例1．解方程：⋅-=--05.035.22.04x x检测1．（四川雁江区期末）解方程：.2.15.023.01=+--x x 例2．解方程：.2016201720161262=⨯++++xx x x ΛΛ检测2．解方程：⋅=⨯++⨯+⨯+⨯2019120192017755331x x x x ΛΛ 例3．（广东普宁市期末）阅读下列解方程的过程，并完成(1)(2)小题的解答．解方程：.2|1|=-x解：当,01<-x 即1<x 时，原方程可化为：,2)1(=--x 解得,1-=x当≥-1x ,0即1≥x 时，原方程可化为：,21=-x 解得,3=x 综上所述，方程2|1|=-x 的解为1-=x 或.3=x (1)解方程：;8|32|=+x (2)解方程：.1|1||32|=--+x x检测3．解方程：.1|21|=--x x例4．(1)已知关于x 的方程)2(2)1(2--=-+m m x 的解比方程1)1(41)1(5+-=-+x x 的解大2，求m 的值；(2)已知方程1324+=+x m x 和方程1623+=+x m x 的解相同． ①求m 的值； ②求20202019)572()2(-⋅+m m 的值．检测4．（湖北黄冈期末）如果方程22834+-=--x x 的解与方程126)13(4-+=+-a x a x 的解相同，求式子a a 1-的值．例5．已知关于x 的方程b x ax -=+56有无数个解，试求b a +2的值．检测5．讨论关于x 的方程b x x a +-=-12的解的情况，其中a ，b 为已知数．例6．已知关于x 的方程),2(2)1(--=+x k x k 求当k 是取什么整数值时，方程的解是整数．检测6．（北京海淀区期末）已知关于x 的方程x kx -=7有正整数解，则整数k 的值为 例7．我们规定，若关于x 的一元一次方程b ax =的解为a b -则称该方程为定解方程，例如：293=x 的解为,23329=-则该方程293=x 就是定解方程．请根据上边规定解下列问题： (1)若x 的一元一次方程m x =2是定解方程，则=m(2)若x 的一元一次方程a ab x +=2是定解方程，它的解为a ，则=a (3)若x 的一元一次方程m mn x +=2和n mn x +=-2是定解方程，求代数式]2)[(21])[(3)24(222n m mn m m mn m ++-++++-的值，检测7．（福建永春县期末）对于两个不相等的有理数a ，b ，我们规定符号},max{b a 表示a ，b 中的较大值，如：,4}4,2max{=按照这个规定解决下列问题： =--}2,3max{)1((2)方程23},max{+=-x x x 的解为第二节 一元一次方程的解法（建议用时 35分钟）实战演练1．(1)（湖南株洲中考）在解方程21331+=+-x x x 时，方程两边同时乘以6，去分母后，正确的是( ) )13(3612.+=+-x x x A )13(36)1(2.+=+-x x x B )13(3)1(2.C +=+-x x x )1(3)1.(+=+-x x x D(2)（四川富顺县模拟）下列解方程过程中，变形正确的是( )A ．由312=-x 得132-=xB ．由2.11.01314++=+x x 得12110314++=+x x C ．由7675=-x 得7675-=xD.由123=-xx 得632=-x x2．已知,1=/a 则关于x 的方程a x a -=-1)1(的解是( )0.=x A 1.=x B 1.-=x C D ．无解3．（山东滕州市期末）规定一种计算法则为,c b d a db ca ⨯-⨯=如--⨯=-)2(12201,202-=⨯依此法则计算2423-=-x 中的x 值为4．a ．b 互为相反数，c ，d 互为倒数，则关于x 的方程02)1(3)(2=--++x x cd x b a 的解为=x 5．马小哈在解一元一次方程923)x (+=-•x 时，一不小心将墨水泼在作业本上了，其中未知数x 前的系数看不清了，他便问邻桌，邻桌不愿意告诉他，并用手遮住解题过程，但邻桌的最后一步“所以，原方程的解为x=-2”（邻桌的答案是正确的）露在手外被马小哈看到了，马小哈由此就知道了被墨水遮住的系数，请你帮马小哈算一算，被墨水遮住的系数是6．已知关于x 的方程439+=-kx x 有整数解，那么满足条件的整数k 有 个 7．（四川岳池县期末）解方程：.14126110312-+=+--x x x 8．解方程：.02}2]2)231(31[31{31=----x9．解方程：⋅+=-++03.002.001.0355.09.05.0xx x10．已知方程,21)20191(541=-+x 求代数式)20191(203-+x 的值．11．（江苏东台市期末）我们定义一种新运算：ab b a b a +-=2*（等号右边为通常意义的运算）：(1)计算：)3(*2-的值；(2)解方程：.*21*3x x =12．解方程：.2020202032132121=+++++++++++ΛΛx x x x 13．（山东牡丹区期末）阅读下面的解题过程：解方程：.2|3|=+x解：当03≥+x 时，原方程可化成为,23=+x 解得,1-=x 经检验1-=x 是方程的解；当,03<+x 原方程可化为，,2)3(=+-x 解得,5-=x 经检验5-=x 是方程的解．所以原方程的解是.5,1-=-=x x 解答下面的两个问题： (1)解方程：;04|23|=--x(2)探究：当a 为何值时，方程,|2|a x =-①无解；②只有一个解；③有两个解．14．当m 为何值时，关于x 的方程524+=-x m x 的解比1)2(3)(2--=-x m x 的解小2． 15．（湖南祁阳县期末）方程0)1(32=+-x 的解与关于x 的方程x k xk 2232=--+的解互为倒数，求k 的值． 16．已知：关于x 的方程b x a x a 3)5()1(2+-=-有无数多解，求a ，b 的值 17.解方程：.121115236362-=---xx x拓展创新18．若a ，b ，c 是正数，解方程：.3=--+--+--bac x a c b x c b a x 拓展1．若a ，b ，c 是正数，解方程：⋅++=-+-+-)111(222Cb a b cab xa bc a x c abc x拓展2．若a ，b ，c ，d 是正数且,1=abcd 解方程：⋅+++=+++)1111(||||||||2222dC b a d x abc b x acd a x bcd c x abd极限挑战19.若,1=abc 解方程：.1121212=++++++++c ca cxb bc bx a ab ax课堂答案培优答案11。
3-3-2 一元一次方程的解法(二)去分母(教学课件)-七年级数学上册同步备课系列(人教版)
1
1
42 x 42 x 42 x 42 x 42 33
3
2
7
即
28x＋21x＋6x＋42x=1386
合并同类项，得
化系数为1，得
1386
答：这个数为x=
97
.
97x=1386
1386
x=
97
自学导航
3x 1
3x 2 2 x 3
2
.
解方程：
2
10
5
迁移应用
3.解下列方程:
3−1
(1)
2
=
4+2
3−1 3+
2−1
2+1
；(2)1= ；(3)
-x=
；
5
4
2
3
4
3−2
(4)
-(2-x)=x.
2
解：(1)去分母(方程两边乘10)，得5(3x-1)=2(4x+2).
去括号，得15x-5=8x+4.
移项,得15x-8x=4+5.
合并同类项,得7x=9.
D.-10
+1 2−
-4
2.若式子 与 的值的和等于2，则x的值为______.
3
2
迁移应用
+3 2−3
3.已知 比
的值大1,求2-a的值.
4
7
+3 2−3
解:根据题意,得 =1.
4
7
去分母,得7(a+3)-4(2a-3)=28.
去括号,得7a+21-8a+12=28.
移项,得7a-8a=28-21-12.
数学人教版七年级上册解一元一次方程——去分母教案
《一元一次方程的解法----去分母》教案湖北省松滋市沙道观初级中学——周友芬教学目标1、知识目标：（1）.掌握解一元一次方程中“去分母”的方法，并能解这种类型的方程；（2）.了解一元一次方程解法的一般步骤。
（3）.会处理分母中含有小数的方程。
2、能力目标：经历“把实际问题抽象为方程”的过程，发展用方程方法分析问题、解决问题的能力。
3、情感目标：（1）.通过具体情境引入新问题（如何去分母），激发学生的探究欲望；（2）.通过埃及古题的情境感受数学文明。
（3）.多表扬、多鼓励、营造学生快乐学习的课堂氛围。
教学重点：通过"去分母"解一元一次方程。
教学难点：探究通过“去分母”的方法解一元一次方程（①不漏乘不含分母的项②注意给分子添加括号。
）教学活动流程：活动1:复习回顾——活动2：典故引入解含有分母且方程一边是多项式的一元一次方程——活动3：突破难点，去分母时多项式一边要添括号——活动4：典例精讲，分子是多项式去分母时要添括号——活动5：突破多项式分子添括号难点，评选最优互助组——活动6：如何查错。
——活动7：学生练习演板, 学生点评。
——活动8：归纳总结解方程的一般步骤和各步变形时的注意点——活动9：实战演练竞赛快准解方程——活动10：拓展，解含小数的方程——活动11：反馈化整得——活动12：教学小结——活动13：在乐曲中完成作业第98页练习，习题第3题。
教学设计一、复习回顾1、解方程①7X=6X-4 ；②8-2(X-7)=X-(X-4)鼓励两名同学板演，其余同学在练习本上自主完成解题，看哪组同学全对的人数最多。
从简单到复杂，巩固所学的解方程知识为去分母做铺垫，并让学生回忆解一元一次方程的基本程序。
①去括号②移项③合并同类项④两边同除以未知数的系数1、求下列各组数的最小公倍数：10,5与15 4，6与9二、典故导入，激情引趣，探索新知：1、国伦敦博物馆保存着一部极其珍贵的文物----纸莎草文书.这是古代埃及人用象形文字写在一种特殊的草上的著作,至今已有三千七百多年.书中记载了许多与方程有关的数学问题.其中有如下一道著名的求未知数的问题:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33.试问这个数是多少?【师】你能帮古人解决这个问题吗？【生】设未知数列方程来求这个数。
新沪科版7年级上册数学教学课件 3.2 1元1次方程及其解法 第2课时 利用去分母解1元1次方程
课堂总结
解一元一次方程的一般步骤
去括号
移项
合并同类项
系数化为1
去分母
怎么去分母：方程两边都各乘分母的最小公倍数
去分母的依据：等式的性质2
去分母的注意点：
随堂练习
1.解下列方程：
【教材101 练习 第1题】
（1） ；
解：去分母，得3(2x+1)-5(x+1)=0. 去括号，得6x+3-5x-5=0. 移项，得6x-5x=-3+5. 合并同类项，得x=2.
（2） ；
3.2 一元一次方程及其解法利用去分母解一元一次方程
沪科版七年级上册
情境导入
请你列出方程算一算，丢番图去世时的年龄？
点击图片播放视频
解：设丢番图去世时的年龄为x岁，得出方程
你能解出这道方程吗?
把你的解法与其他同学交流一下，看谁的解法好.
像上面这样的方程中有些系数是分数，如果能化去分母，把系数化为整数，则可以使解方程中的计算更方便些.
探索新知
例3：解方程： .
【教材P100 例3】
思考：1.若使方程各项的系数变成整数，方程两边应该同乘以什么数？
2.去分母时要注意什么问题？
解：去分母，得12x-2(10x+1)=3(2x+1)-12.
去括号，得12x-20x-2=6x+3-12.
解：去分母，得10y-5(y-1)=-2(y+2). 去括号，得10y-5y+5=-2y-4. 移项，得10y-5y+2y=-4-5. 合并同类项，得7y=-9.两边同除以7，得y= .
第三章 3.3.2利用去分母解一元一次方程
15x 3x 4x 2 6 5 20
合并同类项
16x 7
系数化为1
7
x
16
注意:(1)为什么方程
的两边每一项都要
剩以10，小心不要
漏乘；
(2)为什么去分母后
分子要添括号，是
不是所有的分子都
必须填括号
例题讲解
例.解下列方程：
x 1
2 x
(1)
1 2
2
4
解：去分母(方程两边乘4)，得
2(x+1) －4=8+ (2 －x)
去括号，得
2x+2 －4=8+2 －x
移项，得 2x+x =8+2 －2+4
合并同类项，得 3x = 12
系数化为1，得x = 4
观察思考
方程右边的“1”
去分母时漏乘最
下列方程的解法对不对？如果不对，你能找出错在哪里吗？
小公倍数6
加起来总共是33，求这个数.
它的三分之二＋它的一半＋它的七分之一＋它的全部＝33
1
1
2
x
x
x
x
2
7
3
根据题意可列方程
解：设这个数为x ，
2
1
1
x x x x 33
3
2
7
探究
2
1
1
x x x x 33
3
2
7
解：合并同类项，得
能不能化去分母，
把系数化为整数，
使计算变得简便呢?
)
解：原方程可变形为
去括号，得9x＋15＝4x－2.(
(
)，得9x－4x＝－15－2.(
3.3.3_一元一次方程的解法(去分母、去括号)
中考 试题
例1
3 的倒数与 2a- 9 互为相反数，那么a的值为（ C a 3 A. 3 B. - 3 C.3 D.-3 2 2
分析
解
解方程即可求出a的值.
）.
3 因为 a 的倒数是 a ，根据“互为相反数之和等于0”可得a + 2a3 9 ， 3 3
由已知条件可得 a + 2a-9 =0 ，去分母，得a+2a-9=0， 3 3 合并同类项，得3a=9，系数化为1，得a=3. 故，应选择C.
9
9 因此，原方程的解是 x = 7 .
7x = 9
说一说
解一元一次方程有哪些基本步骤？
一元一次方程
去分母，去括号， 移项，合并同类项得 ax=b(a，b是常数，a≠0)
两边都除以a得
b x=a
练习
1. 下面各题中的去分母对吗？如不对，请改正.
5x （1） 3 - 2 x- 3 = 2，去分母，得5x-2x+3 = 2； 5
本节内容 3.3.3
一元一次方程的解法
去括号、去分母
动脑筋
刺绣一件作品，甲单独绣需要15天完成，乙单 独绣需要12天完成. 现在甲先单独绣1天，接着乙又 单独绣4天，剩下的工作由甲、乙两人合绣. 问再合 绣多少天可以完成这件作品？
本问题涉及的等量关系有： 甲完成的工作量 + 乙完成的工作量 = 总工作量. 因此，设工作总量为1，则甲每天完成工作总量 1 1 的 15 ，乙每天完成工作总量的 12 . 如果剩下的工作两人合绣x天就可完成， 1 那么甲共绣了(x+1)天，完成的工作量为 15( x +1) ； 1 乙共绣了(x+4)天，完成的工作量为 12( x + .
北师大版(2024)数学七年级上册5.2.4 利用去分母解一元一次方程 (共22张PPT)
去括号，得
3x+3=4x-4
移项，合并同类项，得 x=7;
课堂练习
(5) 2x 1 x 2 1;
3
4
(6) 1 ( x 1) 2 1 ( x 2).
2
5
去分母，得
4(2x-1)=3(x+2)-12 去分母，可得 5(x-1)=20-2(x+2)
去括号，得
8x-4=3x+6-12 去括号，得
5x-5=20-2x-4
第五章 一元一次方程
2 一元一次方程的解法 第4课时 利用去分母解一元一次方程
学习目标 新课引入 获取新知 例题讲解 课堂练习 课堂小结 课后作业
学习目标
1.掌握解一元一次方程中“去分母”的方法.（重点） 2.掌握含分母的一元一次方程的解法并归纳解一元 一次方程的步骤.（难点）
情境引入
例题讲解
合并同类项 系数相加，不漏项
系数化为1 分子、分母不要写倒了
课堂小结 这节课，你有什么困惑？
移项，合并同类项，得5x=-2;
移项，合并同类项，得7x=21
系数化为1，得
x=-2;
5
系数化为1，得
x=3.
课堂小结 这节课，你有什么收获？
课堂小结
去分母
用去分母解 一元一次 方程的步骤
去括号 移项
1.不要漏乘不含分母的项 2. 分子是多项式应添括号 1.不要漏乘括号中的每一项 2.括号前是“－”号，要变号 移项要变号
解：去分母，得 4x－1－3x + 6 = 1.
移项，合并同类项，得
约去分母 3 后，(2x－1)×2 在去括号时出错.
x = 4.
去括号符号错误.
正确解法：
3.3 一元一次方程的解法三去分母
（4）50%(3x -1)-20%(2-x)=x .
（1） y 1 = 1 2 y 2 4 y 1 × 4 = 1 2 y× 4 去分母，得 解: 4 2 (y -1)×2 = 1-2y 去括号，得 移项，得 化简，得 2y-2 = 1-2y 2y +2y = 2+1 4y = 3 y= 3
结
束
中考 试题
例1
3 的倒数与 2a - 9 互为相反数，那么a的值为（ C a 3
A. 3
D.-3
分析
解
3 a + 2a - 9 因为 a 的倒数是 a ，根据“互为相反数之和等于 0” 可得 ， 3 3 3
解方程即可求出a的值.
由已知条件可得 a + 2a -9 =0 ，去分母，得a+2a-9=0， 3 3 合并同类项，得3a=9，系数化为1，得a=3. 故，应选择C.
9 9. 因此，原方程的解是 x = 7
7x = 9
说一说
解一元一次方程有哪些基本步骤？
一元一次方程
去分母，去括号， 移项，合并同类项得 ax=b(a，b是常数，a≠0)
两边都除以a得
b x=a
练习
1. 下面各题中的去分母对吗？如不对，请改正.
5x - 3 = 2，去分母，得5x-2x+3 = 2； （1） 3 - 2 x 5
4
方程两边同除以 4，
5x （2） 5 +3 x = 3 3 2
解:
去分母，得
5 +3 x 3 5 x × 6 × 6 = 2 3
(5+3x)×3 = (3+5x)×2 去括号，得 移项，得 化简，得 15+9x = 6+10x 9x -10x = 6-15 -1x = -9 x=9
6..一元一次方程的解法--去括号去分母(青岛版)
D.4x+2-10x+1=6
3.解为x=-3的方程是(
D
)
A.2x-6=0
B.3(x-2)-2(x-3)=5x
C. 5x 3=6
D. x 1 3 2x 5
2
4
6
2
4.若式子 1 (x-1)与 1 (x+2)的值相等,则x的值是
( B )2
3
A.6
B.7
C.8
D.-1
5.指出下列解方程哪步变形是错误的，并指出错误 的原因。
去括号，得3-0.4x-2=0.2x
移项，得 0.4x 0.2x 3 2
移项，得 -0.4x-0.2x=-3+2
合并同类项，得 0.2x 5
两边同除以-0.2得 x 25
合并同类项，得 -0.6x=-1
∴ x5 3
1.计算（1） 4x + 3(2x-3) = 12- (x-2) x= 23
11
1
1
（2） 6( 2 x - 4) + 2x = 7-( 3 x - 1)
x=6
解一元一次方程 的步骤有：
去括号 移项 合并同类项 系数化为1
典例解析
题例2： 2、解方程 3 x 1 2 3 x 2 2 x 3
2
10
5
想一想 若是方程的系数变成整系数方程，
方程两边应该同乘以什么数?
解方程：6x-7=4x-1 1、一元一次方程的解法我们学了哪几步？
移项
6x－4x=-1＋7
合并同类项
2x=6
系数化为1
X=3
2、移项，合并同类项，系数化为1，要注意什么？ ①移项时要变号.（变成相反数） ②合并同类项时，只是把同类项的系数相加作为所得 项的系数，字母部分不变.
解一元一次方程之去分母-化小数系数为整数系数
• 最终解得
$x = frac{3}{8}$
Part
05
注意事项与常见错误
去分母的注意事项
确定公分母
在去除分母之前，首先要确定所有项 的最小公倍数作为公分母，确保每一 项都能整除。
扩大倍数
简化过程
在去除分母后，要对方程进行简化， 合并同类项，使方程更易于求解。
将每一项都乘以公分母，从而将分数方程转 化为整式方程。注意在扩大倍数时要确保每 一项都乘以相同的数，以保持方程的平衡。
将方程两边同时乘以该整数，从而消去小数系数。
最小公倍数法
找出方程中所有小数系数的分母，并求出它们的最小公倍数 。
将方程两边同时乘以该最小公倍数，从而将小数系数化为整 数系数。
分数的基本性质法
利用分数的基本性质，即分数的 分子和分母同时乘以或除以同一 个不为零的数，分数的值不变。
将方程中的小数系数写成分数的 形式，并找到分子和分母的最大
单一去分母的示例
• 分析
方程中有分母，需要先去除分母。 找到分母4和3的LCM，即12，然后
将方程两边都乘以12。
• 解法
$12 times frac{3x+2}{4} - 12 times frac{2x-1}{3} = 12 times 2$
• 化简得
$9x + 6 - 8x + 4 = 24$
忽略简化过程
在去除分母或化小数系数为整数系数后，学生可能会忽略简化方程的步骤。纠正方法是强调简化方程的 重要性，并指导学生如何合并同类项和进行其他必要的简化操作。
Part
06
总结与拓展
去分母和化小数系数为整数系数的意义
简化计算过程
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解一元一次方程的步骤: (1) 去分母
（2）去括号 （3）移项 （4）合并同类项 （5）系数化为1
练一练
解下列方程:
（1）y 1 y 2
24
（2）2
5
x
-
x
+ 2
3
=
2
（3）1- 3x - 7 = x +17
45
（4）y
y
1 2
2
y
5
2
（5）3x 1 2 3x 1 2x 3
2பைடு நூலகம்
10 5
一元一次方程的解法（去分母）
一、知识回顾： 1. 解一元一次方程有哪些步骤？ 答：1.去括号；
2.移项； 3.合并； 4.系数化为1.
2.解方程：31(
2
x
5)
1(x 4
3)
1 12
解：去分母，得
1 2[31( 2 x 5 ) ]
12[41(x
3)
1] 12
4(2x-5)=3(x-3)-1
去括号，得 8x-20=3x-9-1
移项，得
8x-3x=-9-1+20
合并同类项，得 5x=10
系数化为1，得 x=2
例1:解方程:
3y 1 3
143y 6
解：去分母，得
3y 3
1
6
14
6
3y
6
2(3y1) 143y
去括号，得 6y 2 143y
移 项，得 6y 3y 142
合并，得
3y 12
系数化为1，得 y 4
例2 解下列方程： x 3 2x x
解：去分母，得
52
2x-5(3-2x)=10x
去括号，得 2x-15+10x=10x
移项，得 2x+10x-10x=15
合并，得
2x=15
系数化为1，得
x=7.5
去分母时须注意:
（1）确定各分母的最小公倍数；
（2）不要漏乘没有分母的项；
（3）分数线有括号作用，去掉分母 后，若分子是多项式，要加括号， 视多项式为一整体。
作业：
1.把课本第102页第3题写到作业本 上。
2.写《启东作业本》第59、60页。 3.写《课时作业》第29页。
议一议
解方程：00..10x3
0.9
0.2x 0.5
1
解：
10x 9 2x 1 35
510x 3(9 2x) 15
50x 27 6x 15 50x 6x 15 27 56x 42
x3 4
课堂小结
解一元一次方程的步骤: (1) 去分母 （等式的性质2）
（2）去括号 （去括号法则） （3）移项 （等式的性质1） （4）合并同类项（合并同类项法则） （5）系数化为1 （等式的性质2）