七年级尺规作图
北师大版七年级数学下册尺规作图课件
决
2.
2.家 庭 作 业 ：
（
1
）
P
2
随
2
堂
练
习
；
（2） 配 套 练 习 （ 同 步 到 本 节 ） ；
（ 3） 完 成 导 学 案 （ 同 步 到 本 节 ） ；
（ 4） 预 习 下 一 节 ， 背 诵 并 默 写 平 方 差 公 式 .
立足教育
首创未来
第二章 相交线与平行线
§2.4尺规作图
1．在具体情境中，理解尺规作图的定 义，会用尺规作一个角等于已知角．
2．通过对角的和、差、倍的关系的分析， 能用尺规作已知角的和、差、倍．
第一环节
如图2-24，要在长方
走进生活 引入课题 形木板上截一个平行四边
形，使它的一组对边在长
方形木板的边缘上，另一
• 请过C点画出与 组对边中的一条边为AB.
圆规
基本工具： 无刻度直尺
尺 规
基本步骤：三弧两线
作 角
圆心 画弧必备条件：
半径
应用： 分类讨论思想
第六环节
布置作业，能力延伸
1.课 堂 作 业 ：
（ 1） 平 方 差 公 式 文 字 语 言 表 达 2遍 ，
平 方 差 公 式 符 号 表 示 1遍 ；
（
2
）
P2
习
2
题
1
.1
0
知
识
技
能
1
，
问
题
解
1
2
巩固练习
用尺规作图比较两个角的大小. B
D’
O DA
BE’
C
O’ C’
AF’
图案设计 第三环节
七年级下册尺规作图专题复习课件
C
• 连接AC，BC。
b
a
• 则△ABC就是所求作的三角形。
A
c
B
题目四:已知两边及夹角作三角形
• 已知：如图，线段m，n, ∠ . • 求作：△ABC，使∠A=∠ ，AB=m，AC=n.
• 作法：
• 作∠A=∠ ；
n
m
C
• 在AB上截取AB=m ,AC=n；
n
• 连接BC。
α
• 则△ABC就是所求作的三角形。
题目一：作一条线段等于已知线段
• 已知：如图，线段a .求作：线段AB，使AB = a .
• 作法：
• 作射线AP；
a
• 在射线AP上截取AB=a .
• 则线段AB就是所求作的图形。 A
B
P
题目二：作一个角等于已知角
• 已知：如图，∠AOB。 • 求作：∠A’O’B’，使A’O’B’=∠AOB • 作法： （1）作射线O’A’； （2）以O为圆心，任意长度为半径画弧，交OA于M，交OB于N； （3）以O’为圆心，以OM的长为半径画弧，交O’A’于M’； （4）以M’为圆心，以MN的长为半径画弧，交前弧于N’； （5）连接O’N’并延长到B’。则∠A’O’B’就是所求作的角。
变式2：经过直线外一点作已知直线 的垂线
【考点练习】
• 例1、如图:107国道OA和320国道OB在某市相交于点O,在 ∠AOB的内部有工厂C和D,现要修建一个货站P,使P到OA、 OB的距离相等且PC=PD,用尺规作出货站P的位置(不写作 法,保留作图痕迹,写出结论)
A D
107国道
C
O
320国道 B
• 例7、如图，A、B两村在一条小河的的同一侧， 要在河边建一水厂向两村供水．
七年级下学期尺规作图题练习(最新整理)
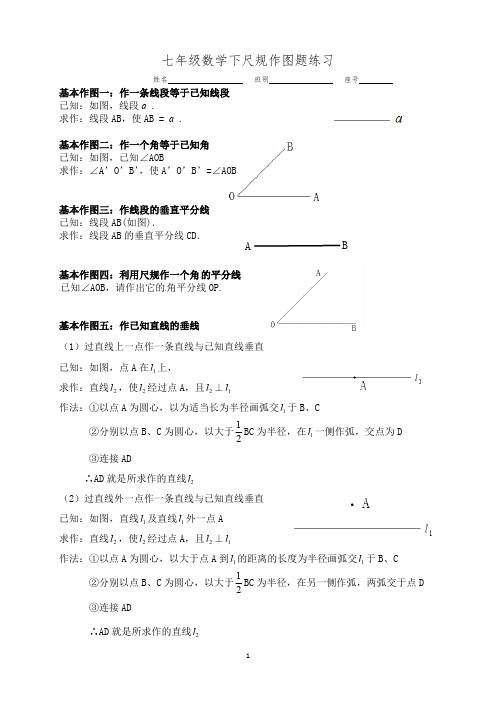
七年级数学下尺规作图题练习姓名 班别 座号基本作图一：作一条线段等于已知线段已知：如图，线段a .求作：线段AB ，使AB = a .基本作图二：作一个角等于已知角已知：如图，已知∠AOB求作：∠A’O’B’，使A’O’B’=∠AOB基本作图三：作线段的垂直平分线已知：线段AB(如图)．求作：线段AB 的垂直平分线CD ．基本作图四：利用尺规作一个角的平分线已知∠AOB ，请作出它的角平分线OP.基本作图五：作已知直线的垂线（1）过直线上一点作一条直线与已知直线垂直已知：如图，点A 在上，1l 求作：直线，使经过点A ，且⊥2l 2l 2l 1l 作法：①以点A 为圆心，以为适当长为半径画弧交于B 、C1l ②分别以点B 、C 为圆心，以大于BC 为半径，在一侧作弧，交点为D 211l ③连接AD∴AD 就是所求作的直线2l （2）过直线外一点作一条直线与已知直线垂直已知：如图，直线及直线外一点A1l 1l 求作：直线，使经过点A ，且⊥2l 2l 2l 1l 作法：①以点A 为圆心，以大于点A 到的距离的长度为半径画弧交于B 、C1l 1l ②分别以点B 、C 为圆心，以大于BC 为半径，在另一侧作弧，两弧交于点D 21③连接AD ∴AD就是所求作的直线2l A BB练习：1、请在图中作出△ABC 的2、请在图中作出△ABC 的BC 边上的中点E.角平分线BD （要求保留作图痕迹）. （要求保留作图痕迹）.3、已知：如图，∠AOB 内有两定点C 、D求作：一点P 使PC=PD ，且P 到∠AOB 的两边之距相等要求：用尺规作图，不写作法，但要保留作图痕迹4、张庄A 、李庄B 位于河沿L 的同侧，现在河沿L 上修一泵站C 向张庄A 、李庄B 供水，问泵站修在河沿L 的什么地方，所用水管最少？5、过点C 作一条线平行于AB6、已知：如图，∠，∠，线段m .αβ求作：△ABC ，使∠A=∠，∠B=∠,AB=m .αβ“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
尺规作图(第一节)
• 高斯（Johann Carl Friedrich Gau (Gauss)，1777年4月30日－1855年2月23 日），生于布伦瑞克，卒于哥廷根，德国 著名数学家、物理学家、天文学家、大地 测量学家。高斯被认为是最重要的数学家， 并有「数学王子」的美誉 • 给我最大快乐的 不是已懂的知识 而是不 断的学习 不是已经达到的高度 而是继续不 断地攀登 高斯
古希腊的三大几何难题
• 1.三等分角问题：将任一个给定的角三等分。 • 2.立方倍积问题：求作一个正方体的棱长， 使这个正方体的体积是已知正方体体积的 二倍。 • 3.化圆为方问题：求作一个正方形，使它 的面积和已知圆的面积相等
高斯的发现
• 最先突破的是德国数学家高斯（17771855）1796年年仅19岁的高斯宣布他发 现了正十七边形的作图方法时，在数学界 引起巨大的震憾。
尺规作图是起源于古希腊的数学课题。 只使用圆规和直尺，并且只准许使用有限 次，来解决不同的平面几何作图题。 最先大概是恩诺皮德斯(Oenopides，约公元 前465年)提出的，以后又经过柏拉图(Plato，公元 前427—347)大力提倡.柏拉图非常重视数学，强调 学习几何对训练逻辑思维能力的特殊作用，主张对 作图工具要有限制，反对使用其他机械工具作图. 之后，欧几里得(Euclid，约公元前330—275)又把 它总结在《几何原本》一书中
最后的胜利
• 1837年，23岁的旺策尔（Wantzel）（法， 1814-1848年）以他的睿智和毅力实现了自 己的梦想，证明了立方倍积与三等分任意 角不可能用尺规作图法解决。 • 1882年，德国数学家林德曼（Linderman） 证明了π的超越性，从而解决了化圆为方的 问题。
这两项简单平凡的工具推动了几千年数学 的发展。我们在对利用尺规作图来解决三大难题 的同时，也得出了很多好的副产品，特别是开创 了对圆锥曲线的研究，发现了一批著名的曲线， 等等.不仅如此，三大问题还和近代的方程论、群 论等数学分支发生了关系.
2019-2020学年七年级数学上册《4.2.3-尺规作图》教案-(新版)新人教版
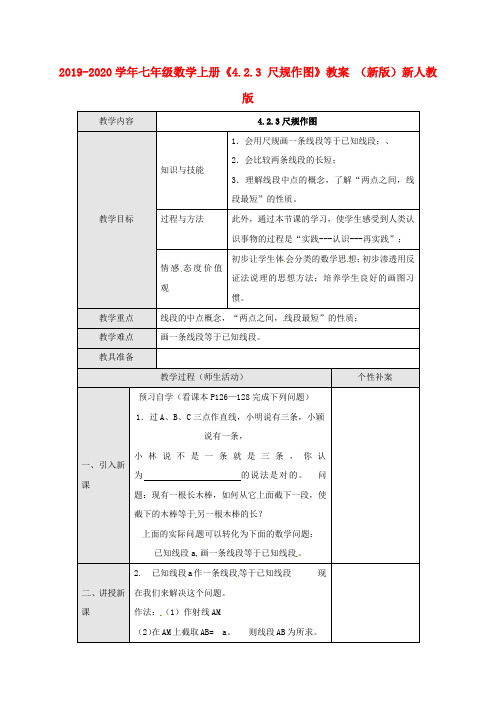
2019-2020学年七年级数学上册《4.2.3 尺规作图》教案（新版）新人教版教学内容 4.2.3尺规作图教学目标知识与技能1．会用尺规画一条线段等于已知线段；、2．会比较两条线段的长短；3．理解线段中点的概念，了解“两点之间，线段最短”的性质。
过程与方法此外，通过本节课的学习，使学生感受到人类认识事物的过程是“实践---认识---再实践”；情感态度价值观初步让学生体会分类的数学思想；初步渗透用反证法说理的思想方法；培养学生良好的画图习惯。
教学重点线段的中点概念，“两点之间，线段最短”的性质；教学难点画一条线段等于已知线段。
教具准备教学过程（师生活动）个性补案一、引入新课预习自学（看课本P126—128完成下列问题）1．过A、B、C三点作直线，小明说有三条，小颖说有一条，小林说不是一条就是三条，你认为的说法是对的。
问题：现有一根长木棒，如何从它上面截下一段，使截下的木棒等于另一根木棒的长？上面的实际问题可以转化为下面的数学问题：已知线段a,画一条线段等于已知线段。
二、讲授新课2. 已知线段a作一条线段等于已知线段现在我们来解决这个问题。
作法：（1）作射线AM（2）在AM上截取AB= a。
则线段AB为所求。
应用：已知线段a、b，求作线段AB=a+b。
解：（1）作射线AM；（2）在AM上顺次截取AC=a，CB= b。
则AB= a+b 为所求。
做一做：作线段AB=a-b。
3．比较两条线段的长短两条线段可能相等，也可能不相等，那么怎样比较两条线段的长短呢？我们先来回答下面的问题。
怎样比较两个同学的身高？一是用尺子测量；二是站在一起比（脚在同一高度）。
如果把两个同学看成两条线段，那么比较两条线段就有两种方法。
（1）用刻度尺分别量出两条线段的长度从而进行比较。
（2）把一条线段移到另一条线段上，使一端对齐，从而进行比较。
三、课堂练习1．比较线段a和b的长短，其结果一定是（）．A．a=b B．a>b C．a<b D．a>b或a=b或a<b 2．画线段AB=50mm，在线段AB上取一点C，使得5AC=2AB，在AB的延长线上取一点D，使得AB=10BD，那么CD=______mm．3．如右上图，AC=CD=DE=EB，图中和线段AD长度相等的线段是________．4．把弯曲的河道改直后，缩短了河道的长度，这是因为5．已知，如图，AB＝16㎝，C是BC的中点，且AC=10㎝，D是AC的中点，E是BC的中点，求线段DE的长四、布置作业课本128页练习五、板书设计1.会用尺规画一条线段等于已知线段；、2.会比较两条线段的长短；3.理解线段中点的概念，了解“两点之间，线段最短”的性质。
七年级下册尺规作图复习课件讲课稿
• 作法：
• 作∠A=∠ ；
n
m
C
• 在AB上截取AB=m ,AC=n；
n
• 连接BC。
α
• 则△ABC就是所求作的三角形。
α A
m
B
题目九：已知两角及夹边作三角形。
• 已知：如图，∠ ，∠ ，线段m .
• 求作：△ABC，使∠A=∠ ，∠B=∠ , AB=m.
• 作法：
• 作线段AB=m；
• 在AB的同旁作∠A=∠ ，作∠B=∠ ，
A D
107国道
C
O
320国道 B
• 例2、三条公路两两相交，交点分别为A，B， C，现计划建一个加油站，要求到三条公路 的距离相等，问满足要求的加油站地址有几 种情况？用尺规作图作出所有可能的加油站 地址。
A
B
C
• 例3、过点C作一条线平行于AB。
C
A
B
• 例3：已知线段AB和CD，如下图，求作一 线段，使它的长度等于AB＋2CD.
• ∠A与∠B的另一边相交于C。
• 则△ABC就是所求作的图形（三角形）。
m
C
α
β
α
A
β B
【考点练习】
• 例1、如图:107国道OA和320国道OB在某市相交于点O,在 ∠AOB的内部有工厂C和D,现要修建一个货站P,使P到OA、 OB的距离相等且PC=PD,用尺规作出货站P的位置(不写作 法,保留作图痕迹,写出结论)
• 作法：
• （１）分别以M、N为圆心，大于 画弧，两弧相交于P，Q；
• （２）连接PQ交MN于O．
的相同线段为半径
P
• 则点O就是所求作的ＭＮ的中点。
M
O
七年级数学下册课件(北师大版)用尺规作三角形
解：如图，A 为汽车站的位置，B 为桥的位置，这三个
场所构成一个等腰三角形．
6 综合与实践”学习活动准备制作一组三角形，记这些三
角形的三边分别为a，b，c，并且这些三角形三边的长度
为大于1且小于5的整数个单位长度．
(1)用记号(a，b，c )(a ≤b ≤c )表示一个满足条件的三角
形，如(2，3，3)表示边长分别为2，3，3个单位长度的 一个三角形，请列举出所有满足条件的三角形；
(2)用直尺和圆规作出三边满足a< b<c 的三角形(用给
定的单位长度，不写作法，保留作图痕迹)．
解：(1)共九种：(2，2，2)，(2，2，3)，(2，3，3)， (2，3，4)，(2，4，4)，(3，3，3)，(3，3，4)， (3，4，4)，(4，4，4)．
(2)只有a＝2，b＝3，c＝4的一个三角形．如图， △ABC 即为满足条件的三角形．
知识点 2 用尺规作三角形 做一做 1.已知三角形的两边及其夹角，求作这个三角形.
已知：线段a，c，∠α (如图).
求作：△ABC，使BC＝a，AB＝c，∠ABC＝∠α.
作法与示例：
作法
(1)作一条线段BC＝a；
示范
(2)以B 为顶点，以BC 为一边 作角∠DBC＝ ∠α；
(3)在射线BD上截取线段BA ＝c；
(1)已知，即将条件具体化； (2)求作，即具体叙述所作图形应满足的条件； (3)分析，即寻找作图方法(通常画出草图)； (4)作法，即根据分析所得的作图方法，作出正式图
形，并依次叙述作图过程； (5)说明，即验证所作图形的正确性．其中(3)在草稿
纸上进行，(5)通常省略不写．
例4 如图，△ABC 是不等边三角形，DE＝BC，以D，E 为两个顶 点作位置不同的三角形，使所作的三角形与△ABC 全等，则
人教版七年级数学上册第4章第5课时《尺规作图(一)—作线段》(教师版)
人教版七年级数学上册第4章第5课时《尺规作图（一）—作线段》（教师版）一、教学目标1.通过本课的学习，学生能够了解尺规作图的基本概念和相关术语。
2.学生能够运用尺规作图的方法，准确地作出给定长度的线段。
3.学生能够理解尺规作图在实际生活中的应用。
二、教学重点1.掌握尺规作图的基本概念和常用术语。
2.掌握作线段的具体方法。
三、教学难点1.理解尺规作图的原理和方法。
2.掌握作图过程中的注意事项。
四、教学准备1.教师准备：黑板、粉笔、尺子、圆规等。
2.学生准备：课本、练习册、尺子、圆规等。
五、教学过程1. 导入新知教师可以通过以下问题引导学生思考：•你们在生活中已经接触过尺规作图吗？它有什么作用？•有哪些常见的几何图形可以用尺规来作图？2. 提出问题教师出示一张纸条，上面写着一段线段的长度m。
请学生思考如何使用尺规来作出这个线段。
3. 讲解尺规作图的基本概念和术语教师通过黑板示意图和实际操作的方式，向学生讲解尺规作图的基本概念和术语，如尺规的构造、尺规的刻度、尺规的使用方法等。
4. 指导学生作图教师向学生演示如何使用尺规作出一段给定长度的线段。
然后，让学生按照教师的示范进行操作。
教师可以提醒学生注意尺规的刻度对齐、线段的精确度等问题。
5. 练习与巩固让学生在练习册上完成若干道作图题，巩固学习成果。
教师可以在完成后进行讲解和指导。
6. 拓展应用教师可以以实际生活中的例子，让学生思考尺规作图的应用，如建筑中的测量、工程施工中的标定等。
六、课堂小结本节课主要学习了尺规作图的基本概念和作线段的方法。
通过实践操作，学生掌握了使用尺规作图的基本技巧。
同时，通过拓展应用，学生理解了尺规作图在实际生活中的重要性。
七、作业布置1.完成练习册上的相关练习。
2.思考并写出一篇关于尺规作图的应用的短文。
以上为本课教学内容的大致安排和教学步骤。
教师可以根据实际情况进行调整和补充，以达到教学目标和效果。
最新北师大版七年级数学下册尺规作图
α七年级下册数学尺规作图1、已知：a求作：AB ，使AB=a2、已知：∠α求作：∠AOB ，使∠AOB=∠α3、已知三角形的两边及其夹角,求作这个三角形.已知：线段a ，c ，∠α。
求作：ΔABC ，使得BC= a ，AB=c ，∠ABC=∠α。
4、已知三角形的两角及其夹边,求作这个三角形.已知：角∠α，∠β，线段c 。
求作：ΔABC ，使得∠A=∠α，∠B=∠β，AB=c 。
5、已知：线段a ，b ，c 。
求作：ΔABC ，使得AB=c ，AC=b ，BC=a 。
ααα6、已知∠α，线段a ，用尺规作一个三角形，使其一个内角等于∠α，；另一个内角等于 2∠α，且这两个内角的夹边等于a 。
7、用尺规作一个直角三角形，使其中一个锐角为∠α，这个锐角和直角的夹边为a 。
8、如图，要在街道旁修建一个奶站，向居民区A 、B 提供牛奶，奶站应建在什么地方才能使A 、B 到它的距离相等？9、如图所示，要在街道旁修建一个奶站，向居民区A 、B 提供牛奶，奶站应建在什么地方，才能使A 、B 到它的距离之和最短？10、如图，一张纸上有A、B、C、D这四个点，请找出一点M，使得MA=MB且MC=MD。
11、A，B，C这3个村庄的位置如图所示，每两个村庄之间有公路相连，村民希望共同投资建一个货运中转站，使中转站的位置到3个村庄的距离相等，请你用尺规确定中转站的位置。
12、某部门想在S区建一个农贸市场，使它到公路、铁路距离相等，且离公路与铁路交叉处500m，这个集贸市场应建于何处（在图上标出它的位置，比例尺为1：20000）？（尺规作图，不写作法，保留作图痕迹）13、直线OA，OB表示两条相互交叉的公路，点M、N表示两个蔬菜基地。
现在建立一个蔬菜批发市场P，要求它到两条公路的距离相等，且到两个蔬菜基地的距离也相等，请用尺规作图说明市场的位置。
14、有公路l1同侧、l2异侧的两个城镇A，B，如下图．电信部门要修建一座信号发射塔，按照设计要求，发射塔到两个城镇A，B的距离必须相等，到两条公路l1，l2的距离也必须相等，发射塔C 应修建在什么位置？请用尺规作图找出所有符合条件的点，注明点C 的位置．（保留作图痕迹，不要求写出画法）15、小明的爸爸准备根据图纸制作一种三角形的零件，却不小心将图纸弄脏了，图纸上只能看清两个顶点A 、C ，已知A ∠是顶角。
七年级下学期尺规作图练习
七年级数学下尺规作图练习
姓名班别座号
题目1：已知三边作三角形
已知：如图，线段a，b，c.
求作：△ABC，使AB = c，AC = b，BC = a.
作法：
（1）作线段AB = c；
（2）以A为圆心b为半径作弧，
以B为圆心a为半径作弧与
前弧相交于C；
（3）连接AC，BC.
则△ABC就是所求作的三角形.
题目2：已知两边及夹角作三角形
已知：如图，线段m，n, ∠α.
求作：△ABC，使∠A=∠α，AB=m，AC=n.
作法：
（1）作∠A=∠α；
（2）在AB上截取AB= m,AC= n；
（3）连接BC.
则△ABC就是所求作的三角形.
题目3：已知两角及夹边作三角形
已知：如图，∠α，∠β，线段m .
求作：△ABC，使∠A=∠α，∠B=∠β,AB=m.
作法：
（1）作线段AB=m；
（2）在AB的同旁作∠A=∠α，作∠B=∠β，
∠A与∠B的另一边相交于C .
则△ABC就是所求作的图形（三角形）.
练习：
1、张庄A、李庄B位于河沿L的同侧，现在河沿
L上修一泵站C向张庄A、李庄B供水，问泵站修
在河沿L的什么地方，所用水管最少？
C
A
2、过点C作一条线平行于AB
3、己知一个三角形三条边分别为a，b，c求作这个三角形.
4、已知：如图，线段a、b和∠α
求作：△ABC，使BC=a，AB=b，a、b两边的夹角为∠α
5、已知：如图，∠α，∠β，线段c .
求作：△ABC，使∠A=∠α，∠B=∠β,AB=c.。
七年级下册数学尺规作图
尺规作图【知识要点】一．关于尺规作图：尺规作图是指只用圆规和没有刻度的直尺来作图.1.作一条线段等于已知线段：（1）首先用直尺作一条射线;（2）其次以射线的端点为圆心，以已知线段的长度为半径画弧，交射线于一点，该交点和端点之间的线段就是所求作的线段.2.作一个角等于已知角：3.作线段的中点：4.作中垂线：5.作直角：6.作角平分线：7.等分角或等分线段：8.过直线外一点作已知直线的平行线或垂线.二．尺规作图的规范语言1.用直尺作图的几何语言：（1）过点〤，点〤作直线〤〤；或作直线〤〤;或作射线〤〤;(2) 连结两点〤〤；或连结〤〤；(3) 延长〤〤到点〤；或延长（反向延长）〤〤到点〤，使〤〤=〤〤;或延长〤〤交〤〤于点〤.2.用圆规作图的几何语言：（1）在〤〤上截取〤〤=〤〤；（2）以点〤为圆心，〤〤的长为半径作圆（或弧）；（3）以点〤为圆心，〤〤的长为半径作弧，交〤〤于点〤；(4) 分别以点〤，点〤为圆心，以〤〤，〤〤的长为半径作弧，两弧相交于点〤，〤.3.尺规作图题的步骤要求：一般的几何作图题要有已知，求作，作法，证明等几个步骤，但一般只要求前两步.切记要保留作图痕迹.【典型例题】例1 如图，已知直线AB 和直线AB 外的一点P ，作一条经过点P 的直线CD ，使CD ∥AB ．例2 已知如图，α∠和β∠，求作:AOB ∠，使∠AOB=∠α+∠β．例3 已知，如图线段AB ，求作线段AB 的垂直平分线．例4 如图，已知∠AOB ，求作∠AOB 的平分线． ABOA BaβABP ·例5. 已知三角形的两个角分别等于∠a 、∠β，这两角所夹的边等于c 如图，按下列步骤作出这个三角形.例6．如图，一束光线AO 照在镜面BC 上，OE 是法线（与镜面垂直），入射光线与法线的夹角叫入射角，反射光线与法线的夹角叫反射角，在镜面反射中，入射角与反射角相等.利用尺规，你能在图中作出反射光线吗？试试看！【初试锋芒】1．作一条线段c b a AB -+=．2.作一条线段AB=2（a －b ）． aβcab cA BOCEab3．（2008 杭州）如图所示，已知∠α、∠β，用直尺和圆规求作一个∠γ.使得βαγ∠-∠=∠21（只须作出正确图形、保留作图痕迹，不必写出作法）.【大展身手】一．选择1．尺规作图的画图工具是（ ）A. 刻度尺，量角器B. 三角板，量角器 C ．直尺，量角器 D. 没有刻度尺的直尺和圆规 2.下面属于尺规作图的是（ ）A ．用量角器画出AOB ∠等于已知角α∠ B ．用圆规和直尺作线段AB 等于已知线段aC ．用三角板作已知直线AB 的垂线D ．用刻度尺画线段ＡＢ＝２cm 3.下列作图语句正确的是（ ）A. 作射线的垂直平分线B. 延长线段ＡＢ到Ｃ，使ＡＣ＝BCC. 作AOB ∠，使AOB ∠=α∠ D ．以点O 为圆心作弧 二．作图1.（2005年 四川）如右图,内宜高速公路OA 和自雅路OB 在我市相交于O,在AOB ∠内部有两个镇C,D 若要修一个大型农贸市场P,使P 到OA,OB 的距离相等,且使PC=PD,用尺规作出市场P 的位置 (不写作法,保留作图痕迹)DCB OA2. 作三角形的 (1) 角平分线;(2)中线;(3)高线(只保留作图痕迹,不写作法)(1) (2) (3)。
尺规作图方法大全[技巧]
![尺规作图方法大全[技巧]](https://img.taocdn.com/s3/m/5b411c1417fc700abb68a98271fe910ef12daec3.png)
aM七年级数学期末复习资料（七）尺规作图【知识回顾】1、尺规作图的定义：尺规作图是指用没有刻度的直尺和圆规作图。
最基本,最常用的尺规作图,通常称基本作图。
一些复杂的尺规作图都是由基本作图组成的。
2、五种基本作图：1、作一条线段等于已知线段；2、作一个角等于已知角；3、作已知线段的垂直平分线；4、作已知角的角平分线；5、过一点作已知直线的垂线；（1）题目一：作一条线段等于已知线段。
已知：如图，线段a .求作：线段AB ，使AB = a .作法：（1） 作射线AP ；（2） 在射线AP 上截取AB=a .则线段AB 就是所求作的图形。
（2）题目二：作已知线段的中点。
已知：如图，线段MN.求作：点O ，使MO=NO （即O 是MN 的中点）. 作法：（１）分别以M 、N 为圆心，大于的相同线段为半径画弧，两弧相交于P ，Q ；（２）连接PQ 交MN 于O ．则点O 就是所求作的ＭＮ的中点。
（3）题目三：作已知角的角平分线。
已知：如图，∠AOB ，求作：射线OP, 使∠AOP ＝∠BOP （即OP 平分∠AOB ）。
作法：（1）以O 为圆心，任意长度为半径画弧，分别交OA ，OB 于M ，N ；（2）分别以M 、Ｎ为圆心，大于 的线段长为半径画弧，两弧交∠AOB 内于Ｐ；③②①BBAP（3） 作射线OP 。
则射线OP 就是∠AOB 的角平分线。
（4）题目四：作一个角等于已知角。
已知：如图，∠AOB 。
求作：∠A ’O ’B ’，使A ’O ’B ’=∠AOB作法： （1）作射线O ’A ’；（2）以O 为圆心，任意长度为半径画弧，交OA 于M ，交OB 于N ；（3）以O ’为圆心，以OM 的长为半径画弧，交O ’A ’于M ’；（4）以M ’为圆心，以MN 的长为半径画弧，交前弧于N ’；（5）连接O ’N ’并延长到B ’。
则∠A ’O ’B ’就是所求作的角。
（5）题目五：经过直线上一点做已知直线的垂线。
七年级尺规作图知识点
七年级尺规作图知识点尺规作图是数学中重要的一部分，它是一种把各种几何形状通过尺子和圆规进行构造的方法。
这种构造方法有时比较麻烦，因为要准确地测量和绘制各个点的位置。
在七年级的数学学习中，尺规作图是必须掌握的知识点之一，下面我们来看一下尺规作图的具体知识点：1. 直线的作图在尺规作图中，直线的作图是一个基本的步骤。
通过尺规测量和定位两个点的位置，并使用直尺连接两个点，就可以得到一条直线。
另外，如果要通过一条直线作图得到另一个角度，也可以使用尺规来测量和绘制。
例如，如果要在一条直线上作一条平分线，就需要在直线上作一个垂线，该垂线将直线平分。
垂线可以通过尺规来测量和绘制。
2. 角的作图在尺规作图中，角的作图是另一个基本的步骤。
角可以通过尺规来测量和绘制。
例如，如果要作一条相等角度的线段，需要先在一条直线上作一个角，然后使用尺规来测量这个角的大小，并将其应用于另一个角度上。
3. 三角形的作图三角形的作图是尺规作图中的重要部分。
必须通过尺规来测量和绘制各点的位置。
例如，如果要作三角形的高，需要在三角形的顶点上作一个垂线。
垂线可以通过尺规来测量和绘制。
另外，如果要作一个等腰三角形，需要先在一条直线上作一个角，然后将其应用于另一个角度上。
4. 正方形和长方形的作图作正方形和长方形的步骤与作三角形类似，需要通过尺规来测量和绘制各点的位置。
例如，如果要作一个正方形，需要先画一个正方形的边长，然后使用尺规中的标准措施来完成每个角度的角。
另外，如果要作一个长方形，则需要在一条直线上作一条边长，然后在另一条边长上作一个垂线。
垂线可以通过尺规来测量和绘制。
总结：以上就是七年级尺规作图的主要知识点，当然，这些知识点只是尺规作图的基础。
在实际应用中，一些更高级的技能和知识也非常重要，例如比例，图形相似性等等。
但在掌握了这些基础知识点之后，可以更好地理解尺规作图的原理，从而更好地完成更高级的绘制工作。
七年级数学同步拔高第四讲《尺规作图》讲义
第四讲尺规作图（讲义）一、知识点睛1．五种基本作图：①作一条线段等于已知线段；②作一个角等于已知角；③作已知线段的垂直平分线；④作已知角的角平分线；⑤过平面内一点，作已知直线的垂线．书写作法时注意：________________，________________．2．应用作图：①______________________，设计作图方案；②调用__________________完成图形．二、精讲精练1.作一条线段等于已知线段．已知：如图，线段a．求作：线段AB，使AB=a．作法：（1）作射线AP；（2）以为圆心，为半径作弧，交射线AP于点B；___________即为所求．2.作一个角等于已知角．已知：如图，∠ABC．求作：∠DEF，使∠DEF=∠ABC．作法：（1）作射线EF；（2）以_____为圆心，______为半径作弧，交BA于点M，交BC于点N；（3）以____为圆心，_____为半径作弧，交EF于点P；（4）___________，___________作弧，交前弧于点D；（5）作射线ED．∠DEF______________．证明：连接_____，_____．在______和______中___________()___________()___________()⎧⎪⎨⎪⎩已作已作已作∴_______________（）∴_______________3.作已知线段的垂直平分线．已知：线段MN ．求作：直线AB ，使AB 垂直平分MN．作法：（1）分别以_______，______为圆心，___________为半径作弧，两弧相交于点A 和点B ；（2）_______________________________________．_______________________________________．4.作已知角的角平分线．已知：如图，∠AOB ．求作：射线OP ，使∠AOP =∠BOP （即OP 平分∠AOB）．作法：（1）________________，________________作弧，交OA 于点M ，交OB 于点N ；（2）分别以_______，_______为圆心，_________为半径作弧，两弧在交于点P ；（3）_____________________________________．_____________________________________．5.（1）过直线上一点，作已知直线的垂线．已知：A为直线MN上一点．求作：直线AB，使AB⊥MN．作法：（1）___________________________________________ ______________________________________；（2）__________________________________________ ______________________________________；（3）________________________________________．___________________________________________．5.（2）过直线外一点，作已知直线的垂线．已知：A为直线MN外一点．求作：直线AB，使AB⊥MN．作法：（1）__________________________________________ _______________________________________；（2）__________________________________________；_______________________________________；（3）__________________________________________；（4）__________________________________________．____________________________________．6.已知三边作三角形．已知：如图，线段a，b，c．求作：△ABC，使AB=c，AC=b，BC=a．作法：（1）作线段__________；（2）___________________作弧，_______________作弧与前弧相交于点B；（3）连接AB，BC．__________________．7.过直线外一点作已知直线的平行线．已知：如图，A是直线MN外一点．求作：直线AB，使AB∥MN．作法：（1）过点A作_____________________________；（2）过点A作_____________________________．直线AB即为所求．8.已知两边及夹角作三角形．已知：如图，线段m，n，∠α．求作：△ABC，使∠A=∠α，AB=m，AC=n．作法：（1）___________________；（2）在射线______上截取__________，在射线______上截取____________；（3）连接BC．___________________．9.以下叙述的作图方法中能够实现的有____________．①过点A作直线BC的垂线；②过点A作线段BC的垂直平分线；③作∠AOB的平分线；④延长AB交CD的中点于E；⑤延长AB使AB⊥CD．10.电信部门要修建一座电视信号发射塔，如下图，按照设计要求，发射塔到两个城镇A，B的距离必须相等，到两条高速公路m，n的距离也必须相等，发射塔P应修建在什么位置？11.为打造“宜居城市”，某市拟在新竣工的矩形广场的内部修建一个音乐喷泉，要求音乐喷泉M到广场的两个入口A，B的距离相等，且到广场管理处C的距离等于A和B之间距离的一半，A，B，C的位置如图所示．请在题目给的原图上利用尺规作图作出音乐喷泉M的位置．12.请画出草图，解决下列问题：（1）已知：在△ABC中，CE平分∠ACB交AB于E，过点E 作ED∥AC交BC于D，过D作DF∥CE交AB于F，则∠EDF和∠BDF的数量关系是______________________．（2）在△ABC中，BD平分∠ABC交AC于点D，过D作DE∥BC交AB于点E，则∠AED和∠EDB的数量关系是____________________________．（3）已知：在△ABC中，BO平分∠ABC，CO平分∠ACB，BO与CO交于点O，过点O作DE∥BC交AB于D，交AC 于E，则DE_____BD+CE（选填“>”、“<”或“=”）（4）已知：在Rt△ABC中，∠C=90º，BD平分∠B交AC于点D，在AB边上取一点E，使BE=BC，连结ED．则∠BED=_________．三、回顾与思考________________________________________________________ ________________________________________________________ ________________________________________________________。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
尺规作图
1.下列作图属于尺规作图的就是( )
A.画线段MN=3cm
B.用量角器画出∠AOB的平分线
C.用三角尺作过点A垂直于直线L的直线
D.已知∠α,用没有刻度的直尺与圆规作∠AOB,使∠AOB=2∠α
2.下列尺规作图的语句正确的就是( )
A.延长射线AB到点C
B.延长直线AB到点C
C.延长线段AB到点C,使BC=AB
D.延长线段AB到点C,使AC=BC
3.下列尺规作图的语句错误的就是( )
A.作∠AOB,使∠AOB=3∠α
B.以点O为圆心作弧
C.以点A为圆心,线段a的长为半径作弧
D.作∠ABC,使∠ABC=∠α+∠β
4.如图所示,过点P画直线a的平行线b的作法的依据就是( )
A.两直线平行,同位角相等
B.同位角相等,两直线平行
C.两直线平行,内错角相等
D.内错角相等,两直线平行
5.如图所示,已知线段a,b,c (a>b+c),求作线段AB,使AB=a－b－c.下面利用尺规作图正确的就是
( )
6.如图所示,AF=_____ __.(用a,b,c表示)
7.画线段AB;延长线段AB到点C,使BC=2AB;反向延长AB到点D,使AD=AC,则线段CD=______AB.
8.已知∠AOB=22、5°,分别以射线OA,OB为始边,在∠AOB的外部作∠AOC=∠AOB,∠BOD=2∠AOB,则OC与OD的位置关系就是______.
9.如图所示,求作一个角等于已知角∠AOB.
作法:(1)作射线_______;
(2)以______为圆心,以_____为半径画弧,交OA于点C,交OB于点D;
(3)以______为圆心,以_____为半径画弧,交O′B′于点D′;
(4)以点D′为圆心,以______为半径画弧,交前面的弧于点C′;
(5)过______作射线O′A′.
∠A′O′B′就就是所求作的角.
10.如图所示,已知线段a,b,c,利用尺规作一条线段,使它等于a+b－2c,并写出作法.
c
b a
11.如图所示,已知线段a 与b ,直线AB 与CD 相交于点O.利用尺规,按下列要求作图:(1)在射线OA,OB 上分别作线段OA′,OB′,使它们都与线段a 相等;(2)在射线OC,OD 上分别作线段OC′,OD′,使它们都与线段b 相等;(3)依次连接A′,C′,B′,D′,A ′.
您得到了一个怎样的图形? (不写作法,保留作图痕迹)
12.如图所示,利用尺规作∠A′O′B′=3∠AOB.
13.如图所示,已知∠α与∠β,按要求作图: (1)利用尺规作∠BOD=∠α+2∠β.
(2)利用尺规作∠AOB,使∠AOB=∠α－∠β.
(3)利用尺规作∠AOB,使∠AOB=2(∠α－∠β).
14.如图所示,在一个三角形支架上要加一根横杆DE,使DE ∥BC,请您用尺规作出DE 的位置.(不写作
D B
法,保留作图痕迹),并说说您的根据.
15.已知直线L及L
外一点,按下列要求写出画法,并保留画图痕迹.在下图中,只用圆规在直线L外画出
一点P,使得点A,P所在直线与直线L平行.
1、下列作图属于尺规作图的就是( )
A、用量角器,画出∠MON的平分线OQ
B、作∠AOB,使∠AOB=2α
C、画线段MN=6cm
D、用三角尺过点P作AB的垂线
2、下列各作法中,正确的就是( )
A、以点O为圆心,以任意长为半径画弧,交线段OA于点B
B、以∠AOB的边OB为一边作∠BOC
C、以点O为圆心画弧,交射线OA于点B
D、在线段AB的延长线上截取线段BC=3cm
3、如图,已知∠AOB及其两边上的点C、D,
①过点C作直线CE∥OB
②过点D作直线DF∥OA,CE、DF交于点P
③探究∠DPC与∠AOB的大小关系、
4、某大饭店的墙砖掉了一块(如图①中阴影部分),工人师傅想在一块完整的壁砖上裁下一块补上,请您帮助工人师傅在图②的壁砖上裁下一块与墙上掉的完全一样可以不?若行,请用尺规作图画出来、
5、已知∠α与线段a,b,如图所示、按照下列程序作图:
(1)作∠DBE=∠α;
a
b
b
a (2)以B 为圆心,a 为半径画弧,交BD 于A; (3)以B 为圆心,
b 为半径画弧,交BE 于C;
(4)连接AC 、 问所得到的就是什么图形?
6、 如图所示,就是某施工队的一张破损的图纸,已知a 、b 就是一个角的两边(这个角的其它部分已丢失),现在要在图纸上量出这个角的度数,请您帮助她们解决这个问题、
7、一张地图上有A 、B 、C 三个城市,但在地图上C 城市被墨迹污染了,如图所示,只知道∠BAC=∠α,∠ABC=∠β,您能用尺规帮她在图中确定C 城市的具体位置不?
B
α
β。