高考数学2.3 连续型随机变量的数学期望与方差
《概率论与数理统计》笔记

《概率论与数理统计》笔记一、课程导读“概率论与数理统计”是研究随机现象的规律性的一门学科在自然界,在人们的实践活动中,所遇到的现象一般可以分为两类:确定性现象随机现象➢确定性现象在一定的条件下,必然会出现某种确定的结果.例如,向上抛一枚硬币,由于受到地心引力的作用,硬币上升到某一高度后必定会下落.我们把这类现象称为确定性现象(或必然现象).同样,任何物体没有受到外力作用时,必定保持其原有的静止或等速运动状态;导线通电后,必定会发热;等等也都是确定性现象.➢随机现象在一定的条件下,可能会出现各种不同的结果,也就是说,在完全相同的条件下,进行一系列观测或实验,却未必出现相同的结果.例如,抛掷一枚硬币,当硬币落在地面上时,可能是正面(有国徽的一面)朝上,也可能是反面朝上,在硬币落地前我们不能预知究竟哪一面朝上.我们把这类现象称为随机现象(或偶然现象).同样,自动机床加工制造一个零件,可能是合格品,也可能是不合格品;射击运动员一次射击,可能击中10环,也可能击中9环8环……甚至脱靶;等等也都是随机现象.➢统计规律性对随机现象,从表面上看,由于人们事先不能知道会出现哪一种结果,似乎是不可捉摸的;其实不然.人们通过实践观察到并且证明了,在相同的条件下,对随机现象进行大量的重复试验(观测),其结果总能呈现出某种规律性.例如,多次重复抛一枚硬币,正面朝上和反面朝上的次数几乎相等;对某个靶进行多次射击,虽然各次弹着点不完全相同,但这些点却按一定的规律分布;等等.我们把随机现象的这种规律性称为统计规律性.●应用例子➢摸球游戏中谁是真正的赢家在街头巷尾常见一类“摸球游戏”.游戏是这样的:一袋中装有16个大小、形状相同,光滑程度一致的玻璃球.其中8个红色、8个白色.游戏者从中一次摸出8个,8个球中.当红白两种颜色出现以下比数时.摸球者可得到相应的“奖励”或“处罚”:注:表中“-2”表示受罚2元解: 此游戏(实为赌博),从表面上看非常有吸引力,5种可能出现的结果.有4种可得奖.且最高奖达10元.而只有一种情况受罚.罚金只是2元.因此就吸引了许多人特别是好奇的青少年参加.结果却是受罚的多,何以如此呢?其实.这就是概率知识的具体应用:现在是从16个球中任取8个.所有可能的取法为816C 种.即基本事件总数有限.又因为是任意抽取.保证了等可能性.是典型的古典概型问题.由古典概率计算公式.很容易得到上述5种结果.其对应的概率分别是:3807048730121800099460000155404848385828681878.C C C P(E);.C C 2C P(D);.C C 2C P(C);.C C 2C P(B);.C 2P(A)816816816816816==========假设进行了1000次摸球试验, 5种情况平均出现的次数分别为:0、10、122、487、381次,经营游戏者预期可得2×381-(10×0+1×10+0.5×122+0.2×487) =593.6(元). 这个例子的结论可能会使我们大吃一惊,然而正是在这一惊之中.获得了对古典概率更具体、更生动的知识.➢ 戏院设座问题乙两戏院在竞争500名观众,假设每个观众完全随意地选择一个戏院,且观众之间选择戏院是彼此独立的,问每个戏院至少应该设多少个座位才能保证观众因缺少座位而离开的概率小于5%?解 由于两个戏院的情况相同,故只需考虑甲戏院即可。
高中数学中的概率统计计算期望与方差的技巧

高中数学中的概率统计计算期望与方差的技巧概率统计是高中数学中的重要内容,计算期望与方差是其中的关键技巧。
本文将介绍几种常见的计算期望与方差的技巧,以帮助读者更好地理解和应用这些知识。
一、离散型随机变量的期望与方差计算对于离散型随机变量X,其概率分布列为P(X=x),而期望和方差的计算公式如下:1. 期望计算期望E(X)表示随机变量X的平均值,计算公式为:E(X) = Σ[x * P(X=x)]其中,Σ表示对所有可能取值的求和。
通过遍历所有可能取值,将取值与其对应的概率相乘,再求和,即可得到期望值。
2. 方差计算方差Var(X)表示随机变量X的离散程度,计算公式为:Var(X) = Σ[(x - E(X))^2 * P(X=x)]同样,通过遍历所有可能取值,将每个取值减去期望值,再平方,再与其对应的概率相乘,最后再求和,即可得到方差值。
这种计算方法适用于离散型随机变量的期望和方差计算,例如投掷一枚骰子的结果、抽取一副扑克牌的点数等情况。
二、连续型随机变量的期望与方差计算对于连续型随机变量X,其概率密度函数为f(x),而期望和方差的计算公式如下:1. 期望计算期望E(X)的计算公式为:E(X) = ∫(x * f(x))dx其中,∫表示对整个定义域的积分。
通过对概率密度函数乘以x后再积分,即可得到期望值。
2. 方差计算方差Var(X)的计算公式为:Var(X) = ∫[(x - E(X))^2 * f(x)]dx同样,通过对概率密度函数乘以(x - E(X))的平方后再积分,即可得到方差值。
这种计算方法适用于连续型随机变量的期望和方差计算,例如正态分布、指数分布等情况。
三、应用技巧下面将介绍一些计算期望与方差时的常用技巧:1. 期望的线性性质如果X和Y是两个随机变量,a和b为常数,则有:E(aX + bY) = aE(X) + bE(Y)这是期望的线性性质,利用这个性质可以简化复杂随机变量的期望计算。
高中高三数学《随机变量和数学期望》教案、教学设计

(3)针对不同难度的练习题,进行分层教学,使学生在逐步克服难点的过程中,提高自己的数学素养。
3.教学策略和手段:
(1)运用信息技术,如多媒体、网络资源等,为学生提供丰富的学习材料,提高课堂教学效果。
2.教学过程:
(1)教师发放练习题,要求学生在规定时间内完成。
(2)学生独立完成练习题,教师巡回指导,解答学生疑问。
(3)教师选取部分学生作品进行展示,分析解题思路和技巧,并进行点评。
(五)总结归纳
1.教学内容:对本节课所学内容进行总结,巩固学生对随机变量和数学期望的理解。
2.教学过程:
(1)教师引导学生回顾本节课所学的主要内容,如随机变量的概念、分类、表示方法,数学期望的定义、性质和计算方法等。
4.小组合作完成一道综合应用题,要求学生在解决实际问题的过程中,运用随机变量和数学期望的知识。此题目旨在培养学生的合作意识和运用数学工具解决实际问题的能力。
5.针对课堂所学内容,教师编制一份测试卷,包括选择题、填空题、解答题等,全面检测学生对本章知识的掌握程度。
作业布置要求:
1.学生应在规定时间内独立完成作业,遇到问题可请教同学或老师,培养自主解决问题的能力。
(2)以小组合作的形式,让学生探讨随机变量的表示方法,如分布列、概率密度函数等,培养他们的合作意识和解决问题的能力。
(3)通过典型例题,引导学生掌握数学期望的定义和性质,学会运用数学期望进行计算。
2.对于难点内容的教学设想:
(1)针对分布列和概率密度函数的理解,设计直观的图表和动画,帮助学生形象地理解抽象概念。
4.引导学生关注社会热点问题,运用所学知识为社会发展贡献力量,培养他们的社会责任感和使命感。
随机变量的数学期望

20
20
i = 1,2,L,10.
得
E ( X ) = E ( X 1 + X 2 + L + X 10 )
= E ( X 1 ) + E ( X 2 ) + L + E ( X 10 )
9 20 = 10 1 − = 8.784(次 ). 10
一、数学期望的概念
1. 离散型随机变量的数学期望
义 设离散型随机变量 X 的分布律为 定 P { X = xk } = pk , k = 1,2,L.
若级数 ∑ xk pk 绝对收敛 , 则称级数 ∑ xk pk
k =1 k =1 ∞ ∞
为随机变量 X 的数学期望 , 记为 E ( X ). 即 E ( X ) = ∑ xk pk .
的值. 求a与b的值 与 的值
解: 由题意知
∫
+∞
−∞
ห้องสมุดไป่ตู้
a f (x)d x = ∫ (ax +b)d x = +b =1 , 0 2
1 +∞ 1
a b 7 E(X) = ∫ xf (x)d x = ∫ x(ax +b)d x = + = −∞ 0 3 2 12
解方程组得 a=1, b=1/2.
随机变量函数的数学期望
+∞ −∞
x 2 f ( x)dx = ∫
b
a
1 2 a 2 + ab + b 2 x dx = b−a 3
市场上对某种产品每年的需求量为X 例5 市场上对某种产品每年的需求量为 吨 , X~U ( 2000,4000 ), 每出售一吨可赚 万元 ,售 每出售一吨可赚3万元 不出去,则每吨需仓库保管费1万元, 不出去,则每吨需仓库保管费1万元,问应该生 产这种商品多少吨, 才能使平均利润最大? 产这种商品多少吨, 才能使平均利润最大?
数学期望(均值)、方差和协方差的定义与性质

均值、方差和协方差的定义和基本性质1 数学期望(均值)的定义和性质定义:设离散型随机变量X 的分布律为{}, 1,2,k k P X x p k === 若级数1k k k xp ∞=∑绝对收敛,则称级数1k k k xp ∞=∑的和为随机变量X 的数学期望,记为()E X 。
即()1k k k E X x p ∞==∑。
设连续型随机变量X 的概率密度为()f x ,若积分()xf x dx ∞−∞⎰ 绝对收敛,则称积分()xf x dx ∞−∞⎰的值为随机变量X 的数学期望,记为()E X 。
即 ()()E X xf x dx ∞−∞=⎰ 数学期望简称期望,又称为均值。
性质:下面给出数学期望的几个重要的性质(1)设C 是常数,则有()E C C =;(2)设X 是一个随机变量,C 是常数,则有()()E CX CE X =;(3)设X 和Y 是两个随机变量,则有()()()E X Y E X E Y +=+,这一性质可以推广至任意有限个随机变量之和的情况;(4)设X 和Y 是相互独立的随机变量,则有()()()E XY E X E Y =。
2 方差的定义和性质定义:设X 是一个随机变量,若(){}2E X E X −⎡⎤⎣⎦存在,则称(){}2E X E X −⎡⎤⎣⎦为X的方差,记为()D X 或()Var X ,即性质:下面给出方差的几个重要性质(1)设C 是常数,则有()0D C =;(2)设X 是一个随机变量,C 是常数,则有()()2D CX C D X =,()()D X C D X +=;(3)设X 和Y 是两个随机变量,则有()()()()()()(){}2D X Y D X D Y E X E X Y E Y +=++−−特别地,若X 和Y 相互独立,则有()()()D X Y D X D Y +=+ (4)()0D X =的充分必要条件是以概率1取常数()E X ,即(){}1P X E X ==。
数学期望和方差

数学期望和方差
第四章 数学期望和方差
分布函数能够完整地描述随机变量的统计特 性,但在实际问题中,随机变量的分布函数较 难确定,而它的一些数字特征较易确定.并且 在很多实际问题中,只需知道随机变量的某些 数字特征也就够了.
另一方面,对于一些常用的重要分布,如二 项分布、泊松分布、指数分布、正态分布等, 只要知道了它们的某些数字特征,就能完全确 定其具体的分布.
8 8
9 10 11 12 7 15 10 10 50
则这 50 个零件的平均直径为
8 8 9 7 1015 1110 1210 50 10.14cm
第四章
数学期望和方差
换个角度看,从这50个零件中任取一个,它 的尺寸为随机变量X , 则X 的概率分布为 X P 8
x
| x| 但 | x | f ( x ) dx dx 发散. 2 (1 x )
它的数学期望不存在.
注:虽然f(x)是偶函数,但不能用定理1.1.
第四章
数学期望和方差
§4.2 数学期望的性质
设已知随机变量X的分布,我们需要计算的不 是X的数学期望, 而是X的某个函数的数学期望, 比如说g(X)的数学期望. 那么应该如何计算呢? 更一般的,已知随机向量(X1 , X2 …,Xn ) 的联合分布, Y= g(X1, X2 …,Xn ) 是 (X1 , X2 …,Xn ) 的函数, 需要计算Y 的数学期 望,应该如何计算呢? 我们下面就来处理这个 问题.
8 50
12
9
7 50
10
15 50
12
11
10 50
12
10 50
则这 50 个零件的平均直径为
高三数学下册《随机变量和数学期望》教案、教学设计

-撰写一份小组报告,阐述研究过程、结果及意义。
4.写一篇学习心得,要求学生反思本节课的学习内容,包括以下要点:
-随机变量和数学期望在实际问题中的应用。
-学习过程中遇到的困难和解决方法。
-对随机变量和数学期望的理解,以及如何将其运用到生活中。
作业要求:
1.学生需按时完成作业,保持作业整洁、字迹清晰。
五、作业布置
为了巩固学生对随机变量和数学期望的理解,以及提升他们解决实际问题的能力,特布置以下作业:
1.请学生完成教材第chapter页的习题,包括以下题目:
-第1题:理解随机变量的概念,并能正确表示给定随机现象的随机变量。
-第2题:根据实际情境,推导并分析随机变量的分布列。
-第3题:计算给定随机变量的数学期望,并解释其物理意义。
高三数学下册《随机变量和数学期望》教案、教学设计
一、教学目标
(一)知识与技能
1.理解随机变量的概念,掌握离散型随机变量及其分布列的性质,能正确运用随机变量描述实际问题。
2.掌握数学期望的定义,理解数学期望的物理意义,能运用数学期望计算随机变量的平均取值。
3.学会运用方差描述随机变量的取值波动程度,理解方差的性质和意义,能计算简单随机变量的方差。
2.教学过程:
(1)教师引导:通过本节课的学习,我们知道随机变量是用来描述随机现象的数学模型,分布列反映了随机变量取值的概率分布,而数学期望和方差则分别反映了随机变量取值的集中趋势和波动程度。
(2)学生分享:邀请学生分享他们在学习过程中的心得体会,以及如何运用所学知识解决实际问题。
(3)教师总结:强调本节课的重点和难点,鼓励学生在课后继续巩固所学知识,为后续学习打下基础。
连续型随机变量的数学期望与方差
(1)D( )
E[
E( )]2
[x
E( )]2
p( x)dx
(2)方差的简便计算公式
D( )=E( 2) E(2 )
x2 p(x)dx
x p( x)dx
例2 随机变量的概率密度函数
6x(1 x),当0 x 1
p(x)
0
当x 0或x 1时
求随机变量的方差。
12
4、方差的性质 设 k ,b,c均为常数,则有
E( ) xp(x)dx
15
2、数学期望的性质
(1)EaX b aEX b
(2)EaX aEX
(3)EX b EX b
(4)Eb b
(5)EX Y EX EY
(6)E( f ( )) f (x)p(x)dx
(6)E f ( ) f (xk )PK
k
16
(二)连续型随机变量ξ取值的方差
(1)D(c) 0
(2)D(k ) k 2D( ) (3)D( b) D( )
(4)D(k b) k 2D( )
13
下页
三、练习
• 课本第90页 第6题
14
四、小结 (一)连续型随机变量ξ取值的数学期望
1、连续型随机变量的数学期望的定义 p(x) 设连续型随机变量 的密度函数为
若积分 xp(x绝)d对x 收敛,则 的数学期望为:
x0 x1 x2 L xn
xi xi1 xi
b i
【xi
,
xi
)
+1
y p(x)
o
x0b0 x1 xi bi xi1
xn x
6
连续型随机变量ξ的概率分布
ξ 【x0 , x1)【x1, x2)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、标准差的定义 D( )
4
随 3、方差的常用的计算公式
机 变 量
x1
x2
[ E( )]2 [x1 E( )]2 [x2 E( )]2
P
p1
p2
··· xn
···[xn E( )]2
··· pn
(1)D( ) E[ E( )]2 [x1 E( )]2 P1 [x2 E( )]2 P2 [xn E( )]2 Pn
2020年5月3日星期日
1
一、复习
(一)离散型随机变量取值的数学期望
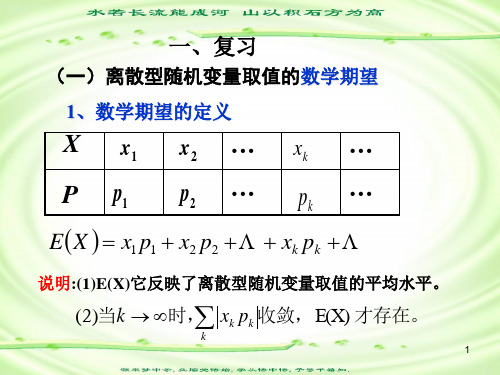
1、数学期望的定义
X x1 x2 ··· xk ···
P p1 p2 ··· pk ···
EX x1 p1 x2 p2 xk pk
说明:(1)E(X)它反映了离散型随机变量取值的平均水平。
(2)当k 时, xk pk 收敛,E(X) 才存在。
19
4、方差的性质 设 k ,b,c均为常数,则有
(1)D(c) 0
(2)D(k ) k 2D( ) (3)D( b) D( )
(4)D(k b) k 2D( )
20
下页
五、作业
• 课本第90页 第5题
21
1、方差的定义
D( ) E[ E( )]2
(刻画了随机变量ξ与其均值 E(的) 平均偏离程度)
2、标准差的定义
D( )
18
3、方差的常用的计算公式
(1)D( )
E[
E( )]2
[x
E( )]2
p( x)dx
(2)方差的简便计算公式
D( )=E( 2) E(2 )
x2 p(x)dx
x p( x)dx
x0 x1 x2 L xn
xi xi1 xi
b i
【xi
,
xi
)
+1
y p(x)
o
x0b0 x1 xi bi xi1
xn x
7
连续型随机变量ξ的概率分布
ξ 【x0 , x1)【x1, x2)
L
P p(b0 )x0 p(b1)x1
L
【xn1, xn)
p(bn 1 )xn 1
离散型随机变量η的概率分布表:
(1)D(c) 0
(2)D(k ) k 2D( ) (3)D( b) D( )
(4)D(k b) k 2D( )
14
下页
三、练习
• 课本第90页 第6题
15
四、小结 (一)连续型随机变量ξ取值的数学期望
1、连续型随机变量的数学期望的定义 p(x) 设连续型随机变量 的密度函数为
若积分 xp(x绝)d对x 收敛,则 的数学期望为:
(3)EX b EX b
(4)Eb b
(5)EX Y EX EY
(6)E( f ( )) f (x)p(x)dx
(6)E f ( ) f (xk )PK
k
10
(二)连续型随机变量ξ取值的方差
1、方差的定义
D( ) E[ E( )]2
(刻画了随机变量ξ与其均值 E(的) 平均偏离程度)
E( ) xp(x)dx
16
2、数学期望的性质
(1)Ea3)EX b EX b
(4)Eb b
(5)EX Y EX EY
(6)E( f ( )) f (x)p(x)dx
(6)E f ( ) f (xk )PK
k
17
(二)连续型随机变量ξ取值的方差
设连续型随机变量 的密度函数为 p(x)
若积分 xp(x绝)d对x 收敛,则 的数学期望为:
E( ) xp(x)dx
例1 随机变量的概率密度函数
p(
x)
6x(1 x),当0 x 1
0
当x 0或x 1时
求随机变量的数学期望。
9
2、数学期望的性质
(1)EaX b aEX b
(2)EaX aEX
(2)方差的简便计算公式
D( )=E( 2) E(2 )
5
4、方差的性质
(1)D(c) 0
(3)D( b) D( )
(2)D(k ) k 2D( ) (4)D(k b) k 2D( )
6
二、新课
(一)连续型随机变量ξ取值的数学期望
设连续型的概率密度函数y p(x)
在x轴上取很密的分点: y
η
b0
b1
L
P p(b0 )x0 p(b1)x1
L
bn1
p(bn 1 )xn 1
n
E 与E 很接近,E = bi p(bi )xi
i 1
n
nn ,maxxi0 lim 如果 bi p(bi )xi的极限存在 n
i 1
bi p(bi )xi
xp(x)dx
E
i1
8
1、连续型随机变量的数学期望的定义
2、标准差的定义
D( )
11
3、方差的常用的计算公式
(1)D(
)
E[
E(
)]2
[x
E(
)]2
p( x)dx
根据数学期望(6)E( f ( ))
f (x)p(x)dx
(2)方差的简便计算公式
D( )=E( 2) E(2 )
x2 p(x)dx
x p( x)dx
12
3、方差的常用的计算公式
(1)D( )
E[
E( )]2
[x
E( )]2
p( x)dx
(2)方差的简便计算公式
D( )=E( 2) E(2 )
x2 p(x)dx
x p( x)dx
例2 随机变量的概率密度函数
6x(1 x),当0 x 1
p(x)
0
当x 0或x 1时
求随机变量的方差。
13
4、方差的性质 设 k ,b,c均为常数,则有
k
2
2、数学期望的性质
(1)EaX b aEX b (2)EaX aEX (3)EX b EX b
(4)Eb b X b P1
(5)EX Y EX EY
(6)E f ( ) f (xk )PK 3 k
(二)离散型随机变量取值的方差 1、方差的定义
D( ) E[ E( )]2
