稳态对流扩散方程边值问题的一种有限元求解方法
对流-扩散问题的galerkin部分迎风有限元方法

对流-扩散问题的galerkin部分迎风有限元方法
对流-扩散问题是一类重要的偏微分方程问题,它描述了一种物质在流动过程中同时受到对流和扩散两种影响的变化规律。
针对这类问题,可以采用各种数值方法进行求解。
其中,Galerkin部分迎风有限元方法是一种有效的求解方法。
Galerkin部分迎风有限元方法的核心思想是结合galerkin方法和部分迎风格式,利用有限元方法离散空间和时间,同时使用部分迎风领域的数值通量来处理对流项,提高数值格式稳定性和精度。
它的基本步骤如下:
1. 将原对流-扩散方程进行有限元离散,得到离散后的方程;
2. 对原对流项采用部分迎风格式进行数值通量的计算;
3. 对原扩散项使用标准有限元格式进行离散;
4. 将离散后的对流项和扩散项合并,得到一个离散方程组;
5. 对离散方程组进行时间离散,一般采用隐式格式或半隐式格式进行求解。
Galerkin部分迎风有限元方法具有较好的精度和稳定性,特别适用于高对流性问题的求解。
但是,它的计算量比较大,需要进行较为复杂的数值计算。
因此,
在实际应用中需要结合具体问题的特点进行选择。
第五章对流扩散问题(一维稳态对流扩散问题)
第五章 对流扩散问题———一维稳态对流扩散问题
a P P a E E a W W
中心节点系数
相邻节点系数
aP aE , a W aP aE a W (Fe Fw )
考虑到连续方程
Fe-Fw=0
满足相邻系 数之和准则
a P aE a W
扩散项和以前的处理方法一样,即有:
(u) e e (u) w w e ( E P ) ( x ) e w ( P E ) ( x ) w
而控制容积界面上的变量值取其相应上风侧网格 节点上的值。即:
第五章 对流扩散问题———一维稳态对流扩散问题
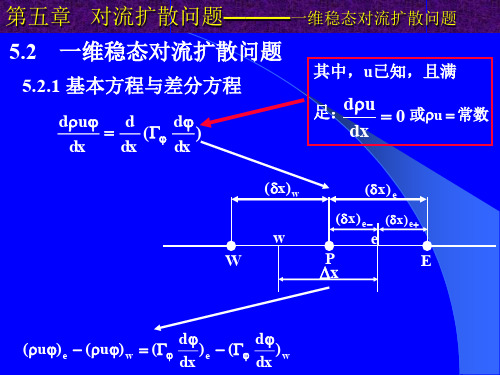
第五章 对流扩散问题———一维稳态对流扩散问题 5.2 一维稳态对流扩散问题
5.2.1 基本方程与差分方程
du d d ( ) dx dx dx
(x)w
其中,u已知,且满
d u 足: 0 或u 常数 dx
( x ) e
( x ) e ( x ) e
w W
e P x
a P P a E E a W W
aE 1 4 1 2 4 aW 1 3 2 a P 1 3 4 4 2
2P E 3W
De Dw 1 Fe Fw 4
E 200, W 100
E 100 W 200
2 P 0.25E 1.75 W
De D w 1 Fe Fw 1.5
E 200, W 100
E 100 W 200
P 187.5
P 112.5
某问题 结果合理
第五章 对流扩散问题———一维稳态对流扩散问题
对流方程及其解法

对流方程及其解法对流方程是描述流体运动的最基本方程之一,涉及热、动量、物质等的传递现象,对于各种物理问题的研究都具有重要意义。
本文将从对流方程的基本形式和意义出发,探讨其常见解法及相关应用。
一、对流方程的基本形式与意义对流方程是描述流体中质量、热量和动量传递的方程,其基本形式可以写作:$$ \frac{\partial\phi}{\partial t} + (\mathbf{v}\cdot\nabla)\phi =\nabla\cdot(\Gamma\nabla\phi) $$其中,$\phi$为描述流体量的变量,如温度、密度、浓度等;$\mathbf{v}$为流体的流速,$\Gamma$为扩散系数。
对该方程的解析求解较为困难,故通常采用数值方法进行求解。
下面介绍几种常见的数值解法。
二、有限差分法有限差分法是在连续方程的基础上,利用有限差分代替导数,将微分方程变为代数方程组,从而利用计算机求解的方法。
其基本思想是将求解区域划分为有限个网格,对每个网格内的量用差分代替导数,从而得到有限差分方程。
以简单的二维对流扩散为例,其对流方程为:$$ \frac{\partial\phi}{\partial t} + u\frac{\partial\phi}{\partial x} + v\frac{\partial\phi}{\partial y} = \Gamma\frac{\partial^2\phi}{\partial x^2} + \Gamma\frac{\partial^2\phi}{\partial y^2} $$其中,$u$和$v$分别代表$x$和$y$方向的流速。
对该方程进行离散,假设$\phi_{i,j}$为$x=i\Delta x$,$y=j\Delta y$处的$\phi$值,则可以得到:$$ \frac{\phi^{k+1}_{i,j} - \phi^k_{i,j}}{\Delta t} +u\frac{\phi^k_{i+1,j} - \phi^k_{i-1,j}}{2\Delta x} +v\frac{\phi^k_{i,j+1} - \phi^k_{i,j-1}}{2\Delta y} $$$$ = \frac{\Gamma\Delta t}{(\Delta x)^2}(\phi^k_{i+1,j} -2\phi^k_{i,j} + \phi^k_{i-1,j}) + \frac{\Gamma\Delta t}{(\Deltay)^2}(\phi^k_{i,j+1} - 2\phi^k_{i,j} + \phi^k_{i,j-1}) $$其中,$k$为时刻,$\Delta x$和$\Delta y$分别为$x$和$y$方向的网格间距。
稳态热传导问题有限元法

6. 稳态热传导问题的有限元法本章的内容如下:6.1热传导方程与换热边界6.2稳态温度场分析的一般有限元列式 6.3三角形单元的有限元列式 6.4温度场分析举例6.1热传导方程与换热边界在分析工程问题时,经常要了解工件内部的温度分布情况,例如发动机的工作温度、金属工件在热处理过程中的温度变化、流体温度分布等。
物体内部的温度分布取决于物体内部的热量交换,以及物体与外部介质之间的热量交换,一般认为是与时间相关的。
物体内部的热交换采用以下的热传导方程(Fourier 方程)来描述,Q z T z y T y x T x t T c+⎪⎭⎫⎝⎛∂∂∂∂+⎪⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂=∂∂z y x λλλρ (6-1)式中ρ为密度,kg/m 3; c 为比热容,K)J/(kg ⋅;z y x λλλ,,为导热系数,)k m w ⋅;T 为温度,℃;t 为时间,s ;Q 为内热源密度,w/m 3。
对于各向同性材料,不同方向上的导热系数相同,热传导方程可写为以下形式,Q zTy T x T t T c 222222+∂∂+∂∂+∂∂=∂∂λλλρ(6-2)除了热传导方程,计算物体内部的温度分布,还需要指定初始条件和边界条件。
初始条件是指物体最初的温度分布情况,() z y,x,T T 00t ==(6-3)边界条件是指物体外表面与周围环境的热交换情况。
在传热学中一般把边界条件分为三类。
1)给定物体边界上的温度,称为第一类边界条件。
物体表面上的温度或温度函数为已知,s s T T =或),,,(t z y x T T s s =(6-4)2)给定物体边界上的热量输入或输出,称为第二类边界条件。
已知物体表面上热流密度,s sz z y y x xq n z T n y T n x T =∂∂+∂∂+∂∂)(λλλ或),,,()(t z y x q n zT n y T n x T s sz z y y x x=∂∂+∂∂+∂∂λλλ(6-5)3)给定对流换热条件,称为第三类边界条件。
对流扩散方程的求解

对流扩散方程的求解
个人收集整理-ZQ
对流扩散问题地有效数值解法一直是计算数学中重要地研究内容,求解对流扩散方程地数值方法主要是有限差分法()、有限元法()、有限体积法()、有限解析法()、边界元法()、谱方法() 等多种方法.但是对于对流占优问题,用通常地差分法或有限元法进行求解将出现数值震荡.为了克服数值震荡,年代,.和等提出特征修正技术求解对流扩散占优地对流扩散问题,与其它方法相结合,提出了特征有限元方法、特征有限差分方法、特征混合元方法;和提出过一种沿流线方向附加人工黏性地间断有限元法,称为流线扩散方法().有限差分法、有限元法、有限体积法是工程应用中地主要方法.
对流扩散方程地特点
对流扩散方程右端第一项为扩散项,左端第二项则是对流项.由于其方程本身地特点,给建立准确有效地数值求解方法带来一定地困难.对流和扩散给流体中由流体携带地某种物理量地变化过程,可以通过一个无量纲地特征参数(数)来描述,数地定义为:ν.这里是来流速度,是特征长度,是物质地扩散系数.如果数较小,即对流效应相对较弱,这类问题中,扩散占主导地位,方程是椭圆型或抛物线型;如果数较大,即溶质分子地扩散相对于流体速度而言是缓慢地,这类问题中,对流占优,方程具有双曲型方程地特点.对于对流占优问题地求解,采用常规地有限元方法,为了避免求解结果产生数值振荡,获得稳定解,则应使每个单元地局部数,ν≤,这里为单元地最大尺寸,为单元中地最大速度分量值.因此,用本文方法求解对流占优对流扩散问题,要得到稳定解,则要通过加密有限元网格来实现.资料个人收集整理,勿做商业用途
1 / 1。
tvd格式_对流扩散方程_解释说明

tvd格式对流扩散方程解释说明1. 引言1.1 概述对流扩散方程是描述物质传输中对流和扩散过程的数学模型,广泛应用于自然科学和工程领域。
为了准确地求解对流扩散方程,需要选择适当的数值方法。
TVD(Total Variation Diminishing)格式是一种被广泛应用于求解对流扩散方程的数值方法,具有一阶或高阶精度、小量级能量损失等优点。
1.2 文章结构本文分为五个部分来讨论TVD格式与对流扩散方程。
首先,在引言部分概述了文章的背景和主要内容。
其次,在第二部分将简要介绍TVD格式和对流扩散方程,并探讨了TVD格式在解决对流扩散方程中的应用。
接下来,在第三部分详细介绍了TVD格式的原理和推导过程,还讨论了TVD限制器的作用和选择方法。
第四部分将通过数值实验和应用案例的分析,深入研究TVD格式的效果,并探讨其在实际问题中的应用意义。
最后,在第五部分总结本文研究工作并给出未来研究方向展望。
1.3 目的本文的主要目的是介绍TVD格式在求解对流扩散方程中的应用,并探讨其原理和推导过程。
希望通过数值实验和应用案例分析,验证TVD格式的有效性,同时提出改进方法。
本文还将总结研究工作的贡献点,并展望未来在这一领域的深入研究方向。
通过本文的撰写,旨在增加人们对TVD格式与对流扩散方程相关知识的了解,并为相关领域研究者提供参考和启示。
以上是“1. 引言”部分内容,包括概述、文章结构以及目的三个小节。
下文将继续详细阐述其他部分内容。
2. TVD格式与对流扩散方程2.1 TVD格式简介TVD(Total Variation Diminishing)格式是求解对流扩散方程的一种数值方法。
它在处理具有激烈变化、激波或阶跃的解时表现出色,并且能够有效地抑制数值耗散和震荡现象。
TVD格式广泛应用于流体力学、传热学等领域中。
2.2 对流扩散方程概述对流扩散方程是描述一维物理过程中物质输运的数学模型。
它由对流项和扩散项组成,其中对流项描述了物质通过速度场的输运,而扩散项则描述了物质因浓度或温度差异而发生的不规则传播。
二维稳态线性对流扩散方程的Galerkin有限元方法

[, l 12
、
有 限元法 [ 、 限体积法[ 。 。 有 , 引 ,
Glk a ri 限元 法 是求解 数学 物理 问题 的一类 重要数 值方 法 , 于 1 1 e n有 它 9 5年提 出后 , 在力 学 、 物
理 及工程 计算 中扮 演 了重要 的角色 ,其 理论在 14 9 0年代 末 已由以 SCM k l .. i i h n为代表 的前 苏联 数学 家建 立 。有 限元法 源 自 G l k a ri , e n法 它是 G l k a ri e n法的特款 。有 限元 法最早于 14 9 3年 由. ’orn 提 R C uat 出。 主要 思想是用分片线性 函数构造 G l kn 影空 间。其 后经过众 多工程 师 、 学家和数 学家 的努 a ri 投 e 力
关键词 : 对流扩散 方程 ; 态; 稳 有限元 ; 误差 ; 随算子 伴
中图分类号 : 2 1 2 0 4. 8
文献标识码 : A
文章编号 :0 17 1 (0 10 — 83 0 10 - 19 2 1 )6 0 2— 7
Th lr i i i e e tM e h d f r Two d me so a t b e s t e Ga e k n F l t Elm n t o o le - i n i n l a l-t e S a Li e r Co v c in d fu i n Eq a in n a n e t - i so u to o
第五章对流扩散问题(假扩散)
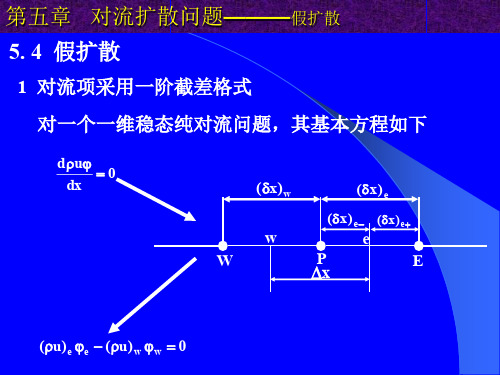
该问题的数值解如下:
1 n i
u t n u t n (1 ) i i 1 x x
MUD : du d ux d (( ) ) dx dx 2 dx
第五章 对流扩散问题———假扩散
由图可以看出,在区间 P 2 ,中心差分格式预报的 P 值优于迎风格式的预报值。对比这两种格式,其扩散项 的处理是完全相同的,所不同的仅仅是对流项的处理上 ,在中心差分格式中对流项的差分格式具有二阶精度, 而在迎风格式中对流项的差分格式只具有一阶精度。在 区间 P 2 ,两种格式预报 P值所表现出的差异性恰恰是 这两种格式精度不同的体现。观察上图,迎风格式所预 报的 P值具有该高不高和该低不低的特点,这一特点正 是由一阶精度迎风格式所引起的扩散系数为 ux / 2 的 假扩散项造成的。也反映了假扩散项的影响。
n n ux ut 2 n ( ) i u( ) i (1 )( 2 ) i O( x 2 , t 2 ) t x 2 x x
由此可以看出,我们前边得到的差分方程所逼近的是 一个非稳态对流扩散问题,而非原型问题所要求的非 稳态对流问题。
第五章 对流扩散问题———假扩散
1 n (1 P
ut n ut n ) P W x x
用编号法表示
1 n i
1 n , n 在点 (i, n) i i 1
u t n u t n (1 ) i i 1 x x
做Taylor展开
n n u 2 n 1 2 n ( ) i u( ) i ( 2 ) i x ( 2 ) i t O( x 2 , t 2 ) t x 2 x 2! t
第五章 对流扩散问题———假扩散
将 i 1 和 i 1 台劳 级数展开代入
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
于是,有限元法是在 vh ∈ v1h 的条件下寻找近似的函数 u,与(4)相比较,下面也是解决问题的一种方
法:
求uh
∈
vh
,
使得
对uh
∈
vh , 都有
a (uh , vh
)
=
1
∫0
f
(x)v
(
x) dx
恒成立
(6)
在实际计算当中我们利用如下两个求积准则来离散变分问题(6): 1) 梯形法法(求积)准则:
−ε∆u + λ= ∇u f ,=u u ( x) , x ∈ Rn , λ ∈ Rn
(1)
其中 λ 为给定的常向量,(1)是 n 维稳态对流扩散方程,当 n = 1 时,我们得到:
−ε
∂2u ∂x2
+
λ
∂u ∂x
= f ( x),
(2)
方程(2)是一维稳态对流扩散方程的一个基本形式,解决实际问题的时候还要加上边界条件才能模拟 实际问题。因此对于方程(2),我们附加边界条件,于是得到对流扩散方程的边值问题:
Received: Feb. 3rd, 2016; accepted: Feb. 22nd, 2016; published: Feb. 29th, 2016 Copyright © 2016 by authors and Hans Publishers Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). /licenses/by/4.0/
β
∫α
g
( x) dx
2.2. 有限元法设计的基本思路
有限元法首先根据变分原理或方程余量与权函数正交化原理,建立与微分方程初边值问题等价的积 分表达式[2]。
对积分表达式,通过采用不同的权函数和插值函数形式,可构成不同的有限元法。有限元法有一鲜 明特点:通常把计算域剖分为有限个互不重叠且相互连接的单元,再在每个单元内选择基函数,用单元 基函数的线形组合来逼近未知函数在单元中的真解。如果整个计算域上总体的基函数可以由每个单元基 函数组成,那么整个计算域内的解可以看作是由所有单元上的近似解构成。在有限元法中,单元基函数 通过插值函数来构造。而插值函数分通常分为两大类,一类只要求插值多项式本身在插值点取已知值, 称为拉格朗日多项式插值;另一种不仅要求插值多项式本身,还要求它的导数值在插值点取已知值,称 为哈密特多项式插值[2] [3] [8]。
(
a,
b
)
= v v ∈H01 (
a,
b
)
,
v
(
a
)
= 0, v (b) = 0
于是,利用变分法,求解关于方程(3)的边界问题就等价于下面形式的变分问题:
求u
∈
H
1 0
(
0,1)
,
使得
对∀v ∈V , 都有
a (u, v)
=
1
∫0
f
( x) v ( x) dx
恒成立
(4)
这里
V
表示
H
1 0
Keywords
Steady Convection-Diffusion Equation, Boundary Value Problem, Finite Element Method, Nonuniform Grids, Boundary Layer
稳态对流扩散方程边值问题的一种有限元求解 方法
邱 俊,姚世举,王汉权
为进一步离散变分问题(4),下面先做单元剖分:给定一正整数 n,我们把区间[0,1]分成 n + 1 个子区
间
Ii
。再对给定的正整数
,我们假设
P
(
Ii
)
为定义在区间
Ii
上的次数不超过
的多项式所形成的集合。
vh 也是一定义在区间[0,1]上的函数组成的集合,图 1 是关于函数空间 vh 的两个实例。
(0,1)
,[0,1]
→
R
,积分函数
1
∫0
v
2
和
1
∫0
v′ 2
在边界条件 v= (0)
v= (1)
0 上有意义,我们
要求解函空间数 v,而 a 是定义在双线性空间V ×V 上的一个函数,具体表示如下:
= a (u, v)
ε
1
∫0
u′
(
x
)
v′
(
x
)
dx
+
λ
1
∫0
u
′
(
x
)
v
(
x
)
dx
(5)
可以证明:问题(4)的解正好是问题(3)的解,问题(3)的解正好是(4)的解。
2. 有限元方法概述
常见的离散偏微分方程的数值方法有:有限元法、有限差分法和有限体积法。下面我们简单介绍有 限元法的思想、有限元法的解题步骤。
2.1. 有限元法简介
有限元法(finite element method)的含义:有限元方法是一种高效能、常用的离散计算方法,它的基础 是变分原理和加权余量法,选择特殊的基函数,其基本求解思想是把计算域划分为有限个互不重叠的单 元,在每个单元内,选择一些合适的节点作为求解函数的插值点,将微分方程中的变量改写成由各变量 或其导数的节点值与所选用的插值函数组成的线性表达式,借助于变分原理或加权余量法,将微分方程 离散求解,从而使一个连续的无限自由度问题变成离散的有限自由度问题。有限元法有许多优点,包括 适用于较一般的区域,也适用于较复杂的区域和不同粗细的网格,离散方程一般都满足积分守恒[5] [7]。
Abstract
In this article, we aim to design a finite element method for solving the boundary value problem of the steady convection-diffusion equation. This boundary value problem is different from the general one, in which there is a small term in the equation, which will make us difficult to design a higher-order numerical method for such problem. We first design two standard finite element methods (including linear and quadratic finite element method) to solve this boundary value problem; we next use these two methods to obtain the approximated solution, and compare the approximated solution with the analytical one in Matlab; we finally propose suggestions to improve these two standard finite element methods based on nonuniform grids, in order to find a better approximation to the boundary value problem of the convection-diffusion equation.
132
邱俊 等
−ε
∂2u ∂x2
+
λ
∂u= ∂x
f ( x), x ∈[0,1]
(3)
= u (0) 0= ,u (1) 0.
其中 ε 为大于零的微小常数, λ 为已知常数,方程(3)就是本文要研究的对流扩散方程,它是求解很多复 杂微分问题的基础。并且小参数 ε 很小时会给一般的数值计算方法带来困难。
本文正是通过偏微分方程中的对流扩散方程的有限元方法来如何模拟实际的科学研究和工程技术中 的一些问题。对流扩散方程被广泛地应用于许多自然现象的表达之中,例如水和大气中的污染物质浓度 的扩散、海水盐度、流体流动与传热、电化学反应等,还应用于环境科学、能源开发、电子科技等[5]。
一般的稳态对流扩散方程方程形式如下[6]:
关键词
稳态对流扩散方程,边值问题,有限元法,非均匀网格,边界层
1. 引言
理论和实验是分不开的,彼此相互联系,现实中有很多不能用科学技术马上解决的实际问题,只有 通过数值模拟得到实际应用所需要的数值结果,揭示其本质规律,从而来解决实际问题[1] [2]。数值模拟 在各门自然科学(物理学、气象学、地质学和生命科学)和技术科学与工程科学(核技术、航空航天和打下 土木工程等等)中起着巨大的作用,在很多重要的领域成为不可缺少的工具。而科学与工程计算中最重要 的内容就是求解在科学研究和工程技术中出现的各种各样的偏微分方程或方程组,而有限元方法就是在 解决这些问题的基础上产生的[2] [3]。
摘要
在本文中,我们为稳态对流扩散方程边值问题设计一种有限元法。对流扩散方程边值问题与普通的边值 问题不同,方程之中含有一个微小元项,它会给高阶数值方法的设计带来困难。我们首先通过设计典型 的有限元法(包括线性元和二次元)来求解该边值问题,然后用MATLAB画图来比较近似解与精确解之间 的实际差距,分析这两种典型的有限元法在求解该边值问题过程中所出现的问题;最后提出建议通过基 于非均匀网格来改进这两种典型的有限元法,以便更好地求解这类稳态对流扩散方程边值问题。
