六年级数学巧用“单位1”(转化与统一)(可编辑修改word版)
数学中 “单位1” 的巧用

数学中“单位1” 的巧用笔者在几年小学毕业班数学教学实践中,深刻认识到:分数、百分数、工程问题,是小学生最难理解和难于掌握的内容,而这三种内容的应用题又是小学生更难的,而又必须掌握的知识之一。
而单位“1”好比是解答这难题的一把金钥匙,利用得当可帮助学生理解题意、掌握解题思路、发展思维,提高学生解题能力和技巧,可起到事半功倍的作用。
因此,教师在教学中引导学生掌握单位“1”的运用方法很有必要。
首先要让学生认清单位“1”,它不同于自然数中的“1”,它可表示数字“1”,更重要的是它在分数、百分数、比类,工程问题应用题中表示“一个单位、一个整体”,这在教学中就叫单位“1”或“整体1”。
故单位“1”可表示“一个总量、一个部分、一项工程的总量、一批物件”等。
所有单位“1”的量叫标准量,与它相比的叫比较量,在解答应用题时,如单位“1”的量已知,就用单位“1”的量乘以所求量对应的分率;如求单位“1”的量,就用已知量除以已知量的对应分率。
由于用单位“1”计算方法固定,故只要选好单位“1”,就可知计算方法,这就解决了学生不知用什么方法计算这一难题。
而选择单位“1”一般以“总量、不变量、两者相比的后项、几分之几的对象”为单位“1”。
下面谈谈单位“1”的运用。
一、单位“1”在分数应用题中的运用这类应用题一般把总量看作单位“1”。
例(1):一堆煤有5 0吨,用去3/5后,还剩多少吨?分析:本题应把总量一堆煤看作单位“1”,用去的单位“1”的3/5,剩下的占单位“1”的(1-3/5)(剩下量对应分率),由于单位“1”量已知而用乘法,求剩下量列式为:5 0×(1-3/5)。
例(2):一堆煤,第一次运走总吨数的1/3,第二次运走总吨数的1/4,还剩65吨没运,求这堆煤有多少吨?分析:本题与例(1)一样把总量看作单位“1”,剩下的占单位“1”的(1 -1/3-1/4),但这题求单位“1”的量而用除法,列式为:65÷(1-1/3-1/ 4)=156吨。
(非常典型)六年级数学:巧妙转化单位“1”和“一分数应用题题多解

六年级数学分数应用题中非常重要的就是单位“1”的确定,一般情况下,我们会根据关键词,如“是、比、占、相当于”和“分率”之间的量,来确定单位“1”。
但是,这只是对于一般简单分数应用题,如果对于较复杂的分数应用题,这样确定单位“1”就没有这么简单。
同样,学生进入六年级后,随着学习内容的增加,获得的解题经验也随之增长。
如何促进学生多角度解决问题,如何深入思考解决问题,如何面对一个问题做到“一题多解”,下面我结合具体例题讲解如何对于分数应用题“一题多解”。
例1:某班共有学生51人,男生人数的34等于女生的23。
这个班男女生各有多少人?方法1:根据“男生人数的34等于女生的23”这一等量关系式,可以用方程来解题:对于学生来说,把哪个未知量转化为已知量(写解设),如何利用已知条件建立等量关系是学生不愿意用方程来解题的关键。
解:设男生人数是x人,女生有(51-x)人。
3 4x=(51-x)×233 4x=51×23-x×23(34+23)x=34X=34÷1712X=24女生:51-24=27(人)比。
应用“按比分配”解决问题。
男生人数×34=女生×23男生人数:女生人数=23:34男生人数:女生人数=8:98+9=17男生:51×817=24(人)女生:51×917=27(人)比。
应用“份数法”解决问题。
男生人数×34=女生×23男生人数:女生人数=23:34男生人数:女生人数=8:9 51÷(8+9)=3(人)男生:3×8=24(人)女生:3×9=27(人)方法4:设男生人数为单位“1”,则女生人数是男生人数的:34÷23=98男生:51÷(1+98)=24(人)女生:51-24=27(人)同理也可以设女生人数为单位“1”,则男生人数是女生人数的:23÷34=89女生:51÷(1+89)=27(人)男生:51-27=24(人)巩固练习:1、图书馆买来科技书和文艺书共340本,文艺书的本数的13和科技书的45相等。
六年级数学上册分数应用题转化单位1的五种解题方法
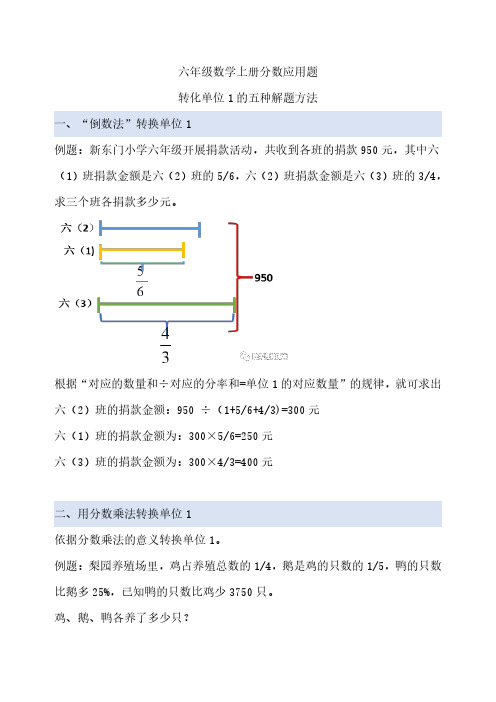
六年级数学上册分数应用题转化单位1的五种解题方法一、“倒数法”转换单位1例题:新东门小学六年级开展捐款活动,共收到各班的捐款950元,其中六(1)班捐款金额是六(2)班的5/6,六(2)班捐款金额是六(3)班的3/4,求三个班各捐款多少元。
根据“对应的数量和÷对应的分率和=单位1的对应数量”的规律,就可求出六(2)班的捐款金额:950÷(1+5/6+4/3)=300元六(1)班的捐款金额为:300×5/6=250元六(3)班的捐款金额为:300×4/3=400元二、用分数乘法转换单位1依据分数乘法的意义转换单位1。
例题:梨园养殖场里,鸡占养殖总数的1/4,鹅是鸡的只数的1/5,鸭的只数比鹅多25%,已知鸭的只数比鸡少3750只。
鸡、鹅、鸭各养了多少只?以养殖总数为单位1,依据分数乘法的意义,鹅占养殖总数的1/4×1/5=1/20,鸭占养殖总数的1/20×(1+25%)=1/16。
鸡、鹅、鸭的分率如下图:这样,鸡与鸭就统一单位1了,都是以养殖总数为单位1的,用鸡与鸭的数量差与分率差相除,就能求出养殖总数了:3750÷(1/4-1/16)=20000只。
鸡的只数:20000×1/4=5000只鹅的只数:20000×1/20=1000只鸭的只数:20000×1/16=1250只三、用份数法转换单位1例题:乌江泥厂有甲、乙、丙、丁四个车间,甲车间人数是其他三个车间的1/4,乙车间人数是其他三个车间的4/11,丙车间人数是其他三个车间的1/2,已知丁车间有60人,该厂有职工多少人?我们可以用全厂职工总数为单位1,用份数法,分别求出甲、乙、丙三车间人数各占全厂职工总数的几分之几,然后,再求出丁车间人数占全厂职工总数的几分之几。
三个车间的分率转换如下:甲车间人数是全厂职工的1÷(1+4)=1/5,乙车间人数占全厂职工的4÷(4+11)=4/15丙车间人数占全厂职工的1÷(1+2)=1/3.现在,本题的数量关系已简化成下图:看图可知,60人的对应分率为1-1/5-4/15-1/3。
六年级秋季第4讲:巧用单位1

六年级秋季第四讲:巧用单位“1”姓名:在应用分数乘法、除法,百分数的乘法、除法解决问题时,都会遇到单位“1”的问题,根据题目条件正确使用单位“1”,能使解答的思路更清晰,方法更简捷。
但很多同学不能正确的找到单位“1”,不会应用单位“1”解决问题,在此,就单位“1”的问题做一下研究。
找单位“1”的方法。
一般情况下,题目都会告诉我们“一个量的几分之几,一个量的百分之几。
”这里的一个量就是本题的单位“1”,我们要弄清楚这里的“几分之几、百分之几”是那个量的,只要找出这个量,就找出了单位“1”。
例如:鸡是鸭的1/6。
这里的指的1/6是“鸭只数的1/6”,由此,我们可以说:鸭的只数就是本题的单位“1”。
正确分析单位“1”是已知量还是未知量,确定解决方法。
在一道题目中,如果单位“1”是已知量,该题用“乘法”做,如果单位“1”是未知量,该题用“除法”解决。
例1、某超市运来白菜1500kg,运来的土豆是白菜的35,超市运来土豆多少千克?例2、某超市运来白菜1500kg,是运来的土豆的35,超市运来土豆多少千克?例3、某养殖场养鸡480只,养的鸭是鸡的56,又是鹅的47,该养殖场养鹅多少只?例4、4个苹果的重量等于3个梨子的重量,一个梨子比一个苹果重10克,一个梨子和一个苹果各重多少克?例5、工地上运来水泥36吨,运来的水泥比黄沙少35,工地上运来黄沙多少吨?例6、红绸带比绿绸带长19,绿绸带比红绸带短多少?例7、小敖看一本书,计划每天看15页,12天看完。
结果每天比计划多看20%,这样几天可看完?例8、柯南看一本书贞探小说,第一天看了全书的41还多10页,第二天看了全书的52少8页,这时还剩26页。
这本书一共有多少页?例9、工程队修一落千丈条公路,第一天修了全长的51,第二天与第一天所修的长度比是4:3。
这时还剩下600米没修,这条公路全长多少米?例10、甲、乙、丙三个修路队修一条公路,已知甲队修了这条公路全长的52,乙队修了剩下的31,丙队修了甲队已修的32,这时还剩120米。
转化单位“1”—2022-2023学年六年级数学思维拓展(学生版)

2022-2023学年小学六年级思维拓展专题 转化单位“1”知识精讲把不同的数量当作单位“1”,得到的分率可以在一定的条件下转化。
如果甲是乙的ab,乙是丙的cd,则甲是丙的acbd;如果甲是乙的ab,则乙是甲的ba;如果甲的ab等于乙的cd,则甲是乙的cd÷ab=bcad,乙是甲的ab÷ab=adbc。
我们必须重视转化训练。
通过转化训练,既可理解数量关系的实质,又可拓展我们的解题思路,提高我们的思维能力。
典例分析【典例01】甲数是乙数的23,乙数是丙数的34,甲、乙、丙的和是216,甲、乙、丙各是多少?解法一:把丙数看所单位“1”那么甲数就是丙数的34×23=12,丙:216÷1+34+34×23=96乙:96×34=72甲:72×23=48解法二:可将“乙数是丙数的34”转化成“丙数是乙数的43”,把乙数看作单位“1”。
乙:216÷23+1+43=72甲:72×23=48丙:72÷34=96解法三:将条件“甲数是乙数的23”转化为“乙数是甲数的32”,再将条件“乙数是丙数的34”转化为“丙数是乙数的43”,以甲数为单位“1”。
甲:216÷1+32+32×43=48乙:48×32=72丙:72×43=96答:甲数是48,乙数是72,丙数是96。
【典例02】红、黄、蓝气球共有62只,其中红气球的35等于黄气球的23,蓝气球有24只,红气球和黄气球各有多少只?解法一:将条件“红气球的35等于黄气球的23”转化为“黄气球的只数是红气球的35÷23=910”。
先求红气球的只数,再求出黄气球的只数。
红气球:(62-24)÷1+35÷23=20(只)黄气球:62-24-20=18(只)解法二:将条件“红气球的35等于黄气球的23”转化为“红气球的只数是黄气球的23÷35= 109”。
单位1的应用题解题技巧六年级

单位1的应用题解题技巧六年级
单位“1”是数学中常用的一个概念,用来表示整体或者比较的标准。
在六年级的应用题中,单位“1”的概念经常被使用。
掌握单位“1”的应用题的解题技巧,对于提高解题效率和正确率都非常重要。
解题技巧:
1. 确定单位“1”的量:在题目中,通常会给出某个量作为比较的标准,这个量就是单位“1”。
例如,“某商品打八折出售,比原价便宜了20%”,这里的“原价”就是单位“1”。
2. 找出数量与单位“1”的关系:找出题目中数量与单位“1”之间的关系,如倍数、分数等。
3. 建立数学方程:根据数量与单位“1”的关系,建立相应的数学方程。
4. 解方程求解:解方程求出未知量。
例题解析:
例1. 一个商场销售的某种商品如果按原价的八折出售,比原价便宜了20%。
已知该商品的原价为200元,求打折后的售价。
解:设打折后的售价为x元。
根据题意,得 x = 200 × 0.8 = 160。
答:打折后的售价为160元。
例2. 一个果园里有三种水果树,其中苹果树占了40%,梨树占了35%,桃树占了25%,已知果园里共有果树100棵,求三种树各有多少棵。
解:苹果树有 100 × 40% = 40棵;
梨树有 100 × 35% = 35棵;
桃树有 100 × 25% = 25棵。
答:苹果树有40棵,梨树有35棵,桃树有25棵。
小六解应用题之单位”1“的转换
名思教育-----我的成功不是偶然的
海到无边天作岸,山高绝顶我为峰 课题
分数、百分数的应用题 教学目标 1.能够理清题目中的具体数量与抽象分率之间的关系 2.学会将不同的单位“1”转化成统一的单位“1”
3.抓住不变量解题
重难点透视
不同单位“1”向同一单位“1”的转化和抓住不变量为单位“1”,
将已知条件转化为不变量的几分之几是本节课的重难点。
一、用对应法解题
分数应用题中的量率对应,是解答分数应用题的根本思想。
在这一练习中药先画线段图,再解答。
例: 一辆汽车从甲地开往乙地,行驶了全程的8
5,超过中点的1.2千米,甲乙两地全程是多少千米?本题目的关键是要找出1.2千米占全程的几分之几。
画出图段 观察量率对应关系。
二、复杂的题目中常常含有几个不同的单位“1”,根据题目的具体情况,将不同单位“1”转化成 统一的单位“1”
例:兄弟两人各有人民币若干元,其中弟弟的钱数是兄的5
4,如果弟给兄4元,则弟的钱数是兄的 3
2,求兄弟两人原来各有多少元? 兄弟两人的总钱数不变,把它看做单位“1”。
将题中的分率转化成总钱数的分率。
三、抓住不变量
在较复杂的分数应用题中有许多数量前后发生变化,一个数量的变化,往往引起另一个数量的变化,但总存在着不变量。
解题时要抓住不变量,将变量转化为以不变量为单位“1”的分率。
六年级奥数单位1的妙用
学生课程讲义单位“1”的妙用解答分数应用题,关键要通过分析数量关系,弄清每一道题把什么看作单位“1”,找出解题的数量关系式,再根据分数与除法的关系或一个数乘以分数的意义列式解答。
知识、规律、方法在解答时,有的分数应用题常常会出现几个不同的单位“1”,一般都要经过分析,转化成统一的单位“1”,然后进行解答。
例1.甲、乙两数之和为180,甲数的14等于乙数的15,问甲、乙两数各是多少?拓展一甲、乙两数相差30,其中甲数的310与乙数的13相等,求这两个数的和是多少?拓展二上元水果店运来的苹果比橘子多1筐,其中苹果筐数的37与橘子筐数的12相同,上元水果店一共运来苹果和橘子多少筐?拓展三学校有皮球和足球共100个,皮球个数的13比足球个数的110多16个,学校有皮球和足球各多少个?例2.某工厂的甲、乙、丙三个车间向灾区捐款,甲车间捐款数是另外两个车间捐款数的23,乙车间捐款数是另外两个车间捐款数的3,已知丙车间捐款180元,这三个车间共捐款多少元?拓展一兄弟四人合修一条路,结果老大修了另外三人总数的一半,老二修了另外三人总数的13,老三修了另外三人总数的14,老四修了91米,问这条路全长多少米?拓展二把一堆皮球分装在四个盒子中,其中15放入甲盒,13放入乙盒。
放入丙盒的皮球是甲、乙两盒皮球总数的34,丁盒放入10个皮球,这堆皮球一共有多少个?拓展三有红黄两种颜色的小球共140个,拿出红球的14,再拿出7个黄球,剩下的红球和黄球正好一样多。
原来红球和黄球各有多少个?例3.把一批面粉分给三个工厂,甲厂先分得这批面粉的25,乙厂分得余下的25,最后丙厂分得14.4吨,这批面粉重多少吨?拓展一某校四、五、六三个年级共有学生618人,其中五年级人数比四年级多10%,六年级人数比五年级少10%,求各年级有学生多少人?拓展二有甲、乙两个粮库,原来甲粮库存粮的吨数是乙粮库的57。
如果从乙粮库调6吨粮食到甲粮库,甲粮库存粮的吨数是乙粮库的45。
小学数学解题方法——转化法(3)单位“1”的转化精选全文
可编辑修改精选全文完整版方法点一画图转化单位“1”例1 乙数是甲数的,丙数是乙数的,丙数是甲数的几分之几?方法指导可以用画格子图法理解甲数和丙数的关系。
如图,把甲数看作一个整体,用长方形表示。
把长方形平均分成3份,乙数占其中的2份,如图一所示。
再把阴影部分平均分成5份,丙数占其中的4份,如图二所示。
从图中可以看出,丙数是甲数的。
正确解答答:丙数是甲数的。
例2 某工程队计划修一条长800米的水渠,第一周修了全长的,第二周修的相当于第一周的,第二周修了多少米?方法指导观察下图可以发现,第二周修的水渠长度是这条水渠全长的,用水渠的总长800乘即可求出第二周修的水渠长度。
正确解答答:第二周修了160米。
方法点二列表转化单位“1”例3 甲数是乙数的,乙数是丙数的,甲、乙、丙三个数的和是216,甲、乙、丙三个数各是多少?方法指导解这道题的关键是确定谁是单位“1”,然后判断216里有几个单位“1”。
思路一把丙数看作单位“1”。
思路二把乙数看作单位“1”思路三把甲数看作单位“1”。
正确解答解法一解法二解法三答:甲数是48,乙数是72,丙数是96。
例4已知甲校学生数是乙校学生数的,甲校的女生数是甲校学生数的,乙校的男生数是乙校学生数的,那么两校女生总数占两校学生总数的几分之几?方法指导思路一把乙校学生数看作单位“1”。
思路二把甲校学生数看作单位“1”。
观察上表可知,两校的女生总数可以用表示,两校的总人数可以用表示,用除以,即可求出两校女生总数占两校学生总数的几分之几。
正确解答解法一解法二答:两校女生总数占两校学生总数的。
方法点三利用不变量转化单位“1”例5有两筐橘子,乙筐橘子质量是甲筐的,从甲筐取出5千克橘子放入乙筐后,乙筐的橘子质量是甲筐的。
甲、乙两筐橘子共重多少千克?方法指导根据已知条件“从甲筐取出5千克橘子放入乙筐后”,可以知道甲、乙两筐橘子的数量都发生了变化,但是甲、乙两筐橘子的总质量没有发生变化。
把两筐橘子的总质量看作单位“1”,则原来甲筐里的橘子占这两筐橘子总质量的,取出5千克橘子后,甲筐里剩下的橘子占这两筐橘子总质量的。
六年级奥数转化单位1与简便运算
1.
14 15
×8
2.
2 25
×126
3. 35×1316
4. 73×7745
5.
1997 1998
×1999
【例题 2】
计算:73115 ×18 16 1
原式=(72+15 )×8 =72×1 +16 ×1
传播优秀 Word 版文档 ,希望对您有帮助,可双击去除!
=9+125 2
=915
练习 2 计算下面各题: 1. 64117 ×19
【例题 5】甲数是乙数的 2/3,乙数是丙数的 3/4,甲、乙、丙的和是 216,甲、乙、丙各 是多少?
传播优秀 Word 版文档 ,希望对您有帮助,可双击去除!
解法一:把丙数看所单位“1” 那么甲数就是丙数的 3/4×2/3=1/2, 丙:216÷(1+3/4+3/4×2/3)=96 乙:96×3/4=72 甲:72×2/3=48
2. 22210 ×211
11 3. 7 ×576
13 14 4. 413 ×4 +514 ×5
【例题 3】
计算:15 ×27+35 ×41 33
原式=5 ×9+5 ×41 =35 ×(9+41) =35 ×50=30
练习 3 计算下面各题:
1.
1 4
×39+34
×27
2.
1 6
×35+56
×17
3.
1.有一批货物,第一天运了这批货物的 1/4,第二天运的是第一天的 3/5,还剩 90 吨没 有运。这批货物有多少吨?
2.修路队在一条公路上施工。第一天修了这条公路的 1/4,第二天修了余下的 2/3,已知 这两天共修路 1200 米,这条公路全长多少米?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分数应用题解决策略(五)
-----转化单位“1”统一单位“1”量率对应
班级:姓名:
一、填空。
1 3 ()1、有一批货物,第一天运了这批货物的4,第二天运的是第一天的5。
第二天运的是这批货物的()。
3 4 ()
2、一辆汽车第一天行了全程的8,第二天行了余下的5,第二天行了全程的()。
1
3、一本书,上午读了10,下午读了60页,这时已读页数和未读页数比是1:3。
这时已读页数占这本书
()()
的(),下午读了 60 页占这本书的()。
5 3 ()
4、苹果的质量是梨子的6,香蕉质量是苹果的4。
香蕉的质量是梨子的()。
3 1 ()
5、有两筐苹果,甲筐苹果的8等于乙筐苹果数的2。
甲筐苹果数相当于乙筐苹果数的()。
二、应用。
1 1
1、一条绳子,第一次剪去全长的3,第二次剪去余下的5,第一次比第二次多剪24米。
求这条绳子的全长。
2 1
2、六(19)班男生比全班人数的5多12人,女生人数占男生人数的2,六(19)班共有学生多少人?
5 3
3、苹果的质量是梨子的6,香蕉的质量是苹果的4。
梨子和香蕉共有 78 千克,苹果有多少千克?
2 1
4、一根绳子,先用去40米,又用去余下长度的5,这时余下的绳子正好是原来总长度的3.这根绳子原来长多少米?
1
5、六年级三个班的同学一起向希望工程捐款。
一班捐款数是其他两个班的4,二班捐款数是其他两个班2
的5.二班比一班多捐款108元,三班捐款多少元?
5 2
6、幼儿园为大中小三个班分得一批图书,大班分得这批图书的12,中班分得中、小两班图书总数的5还多 60 本,小班分得 150 本。
三个班一共分得多少本?
8
7、筑路队 4 天修完一条路,第一天修了全长的25,后三天修的长度比为 6:7:4,最后一天比第一天少
修 8 千米。
这条公路全长多少千米?
2
9、一批肥皂,第一天卖了总数的11,第二天比第一天多卖 8 箱,这时卖过的箱数与剩下的箱数的比是
4:5,这批肥皂一共有多少箱?
10、图书柜中有科技书和文艺书共 250 本,如果科技书借出原来各有多少本?1
9,还比文艺书多 5 本,科技书与文艺书
1 1
11、某校有书 2900 册,分别放在三个书架上,已知甲书架比乙书架多2,丙书架比甲书架少4。
求三个书架各放了多少本书?
2 1
12、工程队修一条路,每天修 25 米,修了 4 天,后来又修了全长的5,还剩全长的5没有修。
这条路共有多长?
1 1
13、有一堆西瓜,上午卖掉了 8 2千克,下午卖掉了剩下的3,这样一天共卖掉 44kg,这堆西瓜原来有多少千克?
7 1
14、一桶油,用去它的8,又装进 12.5kg,这时的油占原来油量的3,这桶油原来有多少千克?
1 1
15、妈妈分糖,哥哥得到其中的2还多 5 块,弟弟得到了剩下的2也多 5 块,正好分完。
妈妈共有多少块糖?(找到弟弟占总量的分率,再列方程,答案是;30 块)
1
16、小英三天读完一本书,第一天读了这本书的4多 6 页,第二天读了这本书的一半,第三天读的是第
2
一天的3,这本书共有多少页?
2
17、三个车间共做一批玩具,一车间做了总数的7,二车间做了 1600 个,三车间做的是一、二车间总和的一半,这批玩具共有多少个?
1
18、A、B、C、D、E 是五个连续的偶数,C 比 A、E 总数的4多 18,这五个偶数的和是多少?。
