《机械原理》(于靖军版)第11章习题答案
机械原理习题册答案

参考答案 第一章 绪论一,填空题1.1 能量,物料,信息1.2运动,动力 1.3制造,运动,装配 二、选择题2.1 D 2.2 B 三,简答题第二章 机械的结构分析二、综合题1.n = 7 ,p l = 9 ,p h = 121927323=-⨯-⨯=--=h l P P n F从图中可以看出该机构有2个原动件,而由于原动件数与机构的自由度数相等,故该机构具有确定的运动。
2. (a )D 、E 处分别为复合铰链(2个铰链的复合);B 处滚子的运动为局部自由度;构件F 、G 及其联接用的转动副会带来虚约束。
n = 8 ,p l = 11 ,p h = 1111128323=-⨯-⨯=--=h l P P n F3. (c )n = 6 ,p l = 7 ,p h = 313726323=-⨯-⨯=--=h l P P n F(e )n = 7 ,p l = 10 ,p h = 0101027323=-⨯-⨯=--=h l P P n F 4. (a )n = 5 ,p l = 7 ,p h = 010725323=-⨯-⨯=--=h l P P n FⅡ级组 Ⅱ级组 因为该机构是由最高级别为Ⅱ级组的基本杆组构成的,所以为Ⅱ级机构。
(c )n = 5 ,p l = 7 ,p h = 010725323=-⨯-⨯=--=h l P P n FⅢ级组因为该机构是由最高级别为Ⅲ级组的基本杆组构成的,所以为Ⅲ级机构。
5. n = 7 ,p l =10 ,p h = 0101027323=-⨯-⨯=--=h l P P n FⅡ级组 Ⅲ级组当以构件AB 为原动件时,该机构为Ⅲ级机构。
Ⅱ级组 Ⅱ级组 Ⅱ级组当以构件FG 为原动件时,该机构为Ⅱ级机构。
可见同一机构,若所取的原动件不同,则有可能成为不同级别的机构。
6. (a )n = 3 ,p l = 4 ,p h = 101423323=-⨯-⨯=--=h l P P n F因为机构的自由度为0,说明它根本不能运动。
机械原理课后习题答案部分

机械原理课后习题答案部分第二章2-1 何谓构件?何谓运动副及运动副元素?运动副是如何进行分类的?答:参考教材5~7页。
2-2 机构运动简图有何用处?它能表示出原机构哪些方面的特征?答:机构运动简图可以表示机构的组成和运动传递情况,可进行运动分析,也可用来进行动力分析。
2-3 机构具有确定运动的条件是什么?当机构的原动件数少于或多于机构的自由度时,机构的运动将发生什么情况?答:参考教材12~13页。
2-5 在计算平面机构的自由度时,应注意哪些事项?答:参考教材15~17页。
2-6 在图2-22所示的机构中,在铰链C、B、D处,被连接的两构件上连接点的轨迹都是重合的,那么能说该机构有三个虚约束吗?为什么?答:不能,因为在铰链C、B、D中任何一处,被连接的两构件上连接点的轨迹重合是由于其他两处的作用,所以只能算一处。
2-7 何谓机构的组成原理?何谓基本杆组?它具有什么特性?如何确定基本杆组的级别及机构的级别? 答:参考教材18~19页。
2-8 为何要对平面高副机构进行“高副低代"?“高副低代”应满足的条件是什么?答:参考教材20~21页。
2-11 如图所示为一简易冲床的初拟设计方案。
设计者的思路是:动力由齿轮1输入,使轴A连续回转;而固装在轴A上的凸轮2与杠杆3组成的凸轮机构将使冲头上下运动以达到冲压目的。
试绘出其机构运动简图,分析其是否能实现设计意图?并提出修改方案。
解:1)取比例尺绘制机构运动简图。
2)分析其是否可实现设计意图。
F=3n-( 2P l +P h –p’ )-F’=3×3-(2×4+1-0)-0=0此简易冲床不能运动,无法实现设计意图。
3)修改方案。
为了使此机构运动,应增加一个自由度。
办法是:增加一个活动构件,一个低副。
修改方案很多,现提供两种。
※2-13图示为一新型偏心轮滑阎式真空泵。
其偏心轮1绕固定轴心A转动,与外环2固连在一起的滑阀3在可绕固定轴心C 转动的圆柱4中滑动。
机械设计第十一章课后习题答案

械设计第十一章课后习题答案11-1 解1)由公式可知:轮齿的工作应力不变,则则,若,该齿轮传动能传递的功率11-2解由公式可知,由抗疲劳点蚀允许的最大扭矩有关系:设提高后的转矩和许用应力分别为、当转速不变时,转矩和功率可提高69%。
11-3解软齿面闭式齿轮传动应分别验算其接触强度和弯曲强度。
(1)许用应力查教材表11-1小齿轮45钢调质硬度:210~230HBS取220HBS;大齿轮ZG270-500正火硬度:140~170HBS,取155HBS。
查教材图11-7,查教材图11-10 , 查教材表11-4取,故:(2)验算接触强度,验算公式为:其中:小齿轮转矩载荷系数查教材表11-3得齿宽中心距齿数比则:、,能满足接触强度。
(3)验算弯曲强度,验算公式:其中:齿形系数:查教材图11-9得、则:满足弯曲强度。
11-4解开式齿轮传动的主要失效形式是磨损,目前的设计方法是按弯曲强度设计,并将许用应力降低以弥补磨损对齿轮的影响。
(1)许用弯曲应力查教材表11-1小齿轮45钢调质硬度:210~230HBS取220HBS;大齿轮45钢正火硬度:170~210HBS,取190HBS。
查教材图11-10得,查教材表11-4 ,并将许用应用降低30% 故(2)其弯曲强度设计公式:其中:小齿轮转矩载荷系数查教材表11-3得取齿宽系数齿数,取齿数比齿形系数查教材图11-9得、因故将代入设计公式因此取模数中心距齿宽11-5解硬齿面闭式齿轮传动的主要失效形式是折断,设计方法是按弯曲强度设计,并验算其齿面接触强度。
(1)许用弯曲应力查教材表11-1,大小齿轮材料40Cr 表面淬火硬度:52~56HRC,取54HRC。
查教材图11-10得,查材料图11-7得。
查教材表11-4 ,因齿轮传动是双向工作,弯曲应力为对称循环,应将极限值乘70%。
故(2)按弯曲强度设计,设计公式:其中:小齿轮转矩载荷系数查教材表11-3得取齿宽系数齿数,取齿数比齿形系数应将齿形系数较大值代入公式,而齿形系数值与齿数成反比,将小齿轮的齿形系数代入设计公式,查教材图11-9得因此取模数(3)验算接触强度,验算公式:其中:中心距齿宽,取满足接触强度。
机械原理课后答案
习题解答第一章绪论1-1 答:1 )机构是实现传递机械运动和动力的构件组合体。
如齿轮机构、连杆机构、凸轮机构、螺旋机构等。
2 )机器是在组成它的实物间进行确定的相对运动时,完成能量转换或做功的多件实物的组合体。
如电动机、内燃机、起重机、汽车等。
3 )机械是机器和机构的总称。
4 )a. 同一台机器可由一个或多个机构组成。
b. 同一个机构可以派生出多种性能、用途、外型完全不同的机器。
c. 机构可以独立存在并加以应用。
1-2 答:机构和机器,二者都是人为的实物组合体,各实物之间都具有确定的相对运动。
但后者可以实现能量的转换而前者不具备此作用。
1-3 答:1 )机构的分析:包括结构分析、运动分析、动力学分析。
2 )机构的综合:包括常用机构设计、传动系统设计。
1-4 略习题解答第二章平面机构的机构分析2-1 ~2-5 (答案略)2-6(a) 自由度F=1 (b) 自由度F=1(c) 自由度F=12-7题2 -7 图F =3 × 7 -2 × 9 -2 =12 -8a) n =7 =10 =0 F =3×7-2×10 =1b) B 局部自由度n =3 =3 =2 F=3×3 -2×3-2=1c) B 、D 局部自由度n =3 =3 =2 F=3×3 -2×3-2 =1d) D( 或C) 处为虚约束n =3 =4 F=3×3 -2×4=1e) n =5 =7 F=3×5-2×7=1f) A 、B 、C 、E 复合铰链n =7 =10 F =3×7-2×10 =1g) A 处为复合铰链n =10 =14 F =3×10 -2×14=2h) B 局部自由度n =8 =11 =1 F =3×8-2×11-1 =1i) B 、J 虚约束C 处局部自由度n =6 =8 =1 F =3×6 -2×8-1=1j) BB' 处虚约束A 、C 、D 复合铰链n =7 =10 F =3×7-2×10=1 k) C 、D 处复合铰链n=5 =6 =2F =3×5-2×6-2 =1l) n =8 =11 F =3×8-2×11 =2m) B 局部自由度I 虚约束4 杆和DG 虚约束n =6 =8 =1 F =3×6-2×8-1 =12-9a) n =3 =4 =1 F =3 × 3 -2 × 8 -1 =0 不能动。
第十一章课后题及答案(邱俊)

十一章习题及答案11-1. 举出日常生活中和机械工程中应用飞轮调速的例子,并说明其原理。
飞轮调速原理:是利用飞轮具有的储存与释放动能的功能。
飞轮具有较大的转动惯量,在机械系统获得盈功时,吸收储存多余的能量,而在出现亏功时释放其能量,以弥补能量的不足,从而使机械系统的角速度变化幅度得以缓减,即达到调节作用。
11-2. 设起重机的电动机特性曲线可近似用抛物线代替,若其等效驱动力矩为21450.34040.01ed M ωω=--,等效阻力矩和等效转动惯量为常数,分别为223er M N m =, 2e kgm1J = ,若电动机在t 0=10sec 的角速度为0100/rad s ω=。
试分析电机主轴从t 0开始的角速度ω与角加速度ε随时间t 的变化关系。
解:由于()()ed er ed M M J dtωωω-=,将式中变量分离后,得/[()()]e ed er dt J d M M ωωω=-积分得 0()()e e d e rd t t J M Mωωωωω=+-⎰2100101450.34040.01223d t ωωωω=+---⎰()10010 1.154arctan 0.0120.196t ωω=-+162.390.9t a n (/t ω=-21450.34040.01223780.3404(162.390.9tan(/1.154))0.01(162.390.9tan(/1.154))d dtt t ωεωω==---=----31.85tan(0.867)21.1t ε=+11-3. 牛头刨床主运动机构中含一导杆机构,如图11.18所示。
已知2100l m m =,当AB AC⊥时,430ϕ=︒,导杆4对轴C 的转动惯量20.08C J kg m =⋅,其他构件的质量和转动惯量忽略不计;作用在导杆4的阻力矩为410M N m =⋅。
若取曲柄2为等效构件,求该机构的等效阻力矩er M 和等效转动惯量e J 。
机械原理课后习题答案
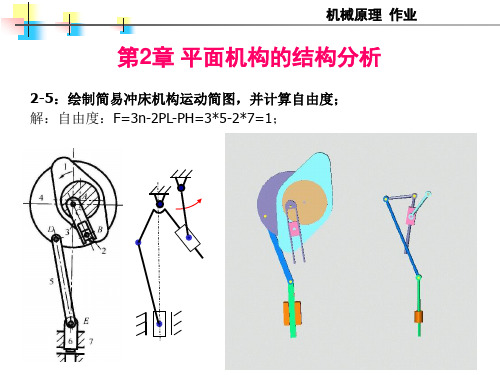
inva )
=6.8mm
分度圆半径r=mz/2=10*18/2=90mm
齿槽宽:ea=2π ra/z-sa
分度圆齿厚s=π m/2=15.7mm
=28.1mm
齿顶圆半径ra=r+ha*m=90+10=100mm
基圆半径rb=rcosα=90cos200=84.57mm
inv200=0.0148
齿顶圆压力角
第2章 平面机构的结构分析
2-7:计算自由度,指出所有的复合铰链、局部自由度和虚约束,判定运动 是否确定; 解:自由度:
a) F=3n-2PL-PH=3*3-2*4=1;确定 b) F=3n-2PL-PH=3*6-2*8=2;不确定 c) F=3n-2PL-PH=3*4-2*5-1=1;确定 d) F=3n-2PL-PH=3*4-2*5-1=1;确定
从而lAB+lBC, lBC-lAB可求得,最后确定lAB和lBC; 设计步骤:
①取一点A,并定D点; ②以D为圆心,作圆; 根据CD摆角15°定C1,C2点; ③ 量取lAC1,lAC2
lAB+lBC=430 lBC-lAB=348
C2 15° 15°C1
B A
lAB=41
A
B1
D
lBC=389
B2
虚约束
局部自由度
复合铰链
a)
b)
c)
d)
机械原理 作业
第2章 平面机构的结构分析
2-8:计算自由度;确定机构所含杆组的数目与级别;确定机构级别。画出 瞬时替代机构; 解:自由度:
a) F=3n-2PL-PH=3*7-2*10=1;Ⅱ级 b) F=3n-2PL-PH=3*6-2*8-1=1;Ⅲ级
机械原理课后习题答案

《机械原理》课后习题答案第2章(P27)2-2 计算下列机构的自由度,如遇有复合铰链、局部自由度、虚约束等加以说明。
(a)n=3,p l=3 F=3*3-2*3=3(b)n=3,p l=3,p h=2 F=3*3-2*3-2=1 (B处有局部自由度)(c)n=7,p l=10 F=3*7-2*10=1(d)n=4,p l=4,p h=2 F=3*4-2*4-2=2 (A处有复合铰链)(e)n=3,p l=4 F=3*3-2*4=1 (A或D处有虚约束)(f)n=3,p l=4 F=3*3-2*4=1 (构件4和转动副E、F引入虚约束)(g)n=3,p l=5 F=(3-1)*3-(2-1)*5=1 (有公共约束)(h)n=9,p l=12,p h=2 F=3*9-2*12-2=1 (M处有复合铰链,C处有局部自由度)2-3 计算下列机构的自由度,拆杆组并确定机构的级别。
(a)n=5,p l=7 F=3*5-2*7=1由于组成该机构的基本杆组的最高级别为Ⅱ级杆组,故此机构为Ⅱ级机构。
(b)n=5,p l=7 F=3*5-2*7=1此机构为Ⅱ级机构。
(c)n=5,p l=7 F=3*5-2*7=1拆分时只须将主动件拆下,其它构件组成一个Ⅲ级杆组,故此机构为Ⅲ级机构。
2-4 验算下列运动链的运动是否确定,并提出具有确定运动的修改方案。
(a)n=3,p l=4,p h=1 F=3*3-2*4-1=0 该运动链不能运动。
修改方案如下图所示:(b)n=4,p l=6 F=3*4-2*6=0 该运动链不能运动。
修改方案如下图所示:或第3章(P42)3-2 下列机构中,已知机构尺寸,求在图示位置时的所有瞬心。
(a)(b)(c)(a) v3=v P13=ω1P14P13μl3-6 在图示齿轮连杆机构中,三个圆互作纯滚,试利用相对瞬心P13来讨论轮1与轮3的传动比i13。
第5章(P80)5-2 一铰接四杆机构(2)机构的两极限位置如下图:(3)传动角最大和最小位置如下图:5-3题略解:若使其成为曲柄摇杆机构,则最短杆必为连架杆,即a 为最短杆。
机械原理课后习题答案.pdf

[解]
(1)取μι作机构运动简图;
μl
=
0.002
m mm
C3
lBC =
l
2 AB
+
l
2 AC
−
l AB
⋅ lAB
⋅ cos135
= 302 + 1002 − 30 ×100 × cos135 = 123 (mm)
B
D
2
1 ω1
A
ϕ1
4
E
(2)速度分析 取C为重合点:C( C2, C3)
vB → vC 2 → vD ,vE → ω2
p(c3)
ω2
2
D
c2
2) 求aC2
aC 2 = aB
+ aCn 2B
+
at C 2B
=
aC 3
+
aCk
2C 3
+ aCr 2C 3
方向: B→A C→B ⊥CB
0 ⊥CБайду номын сангаас向下 ∥BC e
大小: √ √
?
0√
?
E
d
b
其中:
an C 2B
= ω2 2
lBC
=
2.02
4
C P34
1
A P12
题3-1 试求图示各机构在图示位置时全部瞬心。
b) P13
P34 B
3
P 23 →∞
2
P12
A
4
C P14→∞
P24
1
题3-1 试求图示各机构在图示位置时全部瞬心。
c)
P13 P14 C
4
→∞ P 34
M
vM
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11-1 一对渐开线齿轮廓如题图11-1所示,两渐开线齿廓啮合于K 点,试求:
(1) 当绕点O 2转动的齿廓为主动及啮合线如下图中N 2N 1时,确定两齿廓的转动方向; (2)用作图法标出渐开齿廓G 1上的点a 2、b 2相共轭的点a 1、b 1,标出渐开线齿廓G 2上与
点d 1相共轭的点d 2;
(3)用阴影线标出两条渐开线齿廓的齿廓工作段;
(4)在图上标出这对渐开线的节圆和啮合角α',并说明啮合角与节圆压力角之间的关系。
1
题图11-1
齿廓工作段分别为:b 1d 1、b 2d 2
(4)啮合角和节圆压力角相等
11-2 一对渐开线外啮合直齿圆柱齿轮机构,两轮的分度圆半径分别为r 1=30mm ,r 2=54mm ,
α=20°,试求:
(1)当中心距a'=86mm 时,啮合角α'等于多少?两个齿轮的节圆半径r 1'和r 2'各为多少? (2)当中心距改变为a '=87mm 时,啮合角α'和节圆半径r 1'、r 2'又等于多少? (3)以上两种中心距情况下的两对节圆半径的比值是否相等,为什么? 解:(1) α'=23.39° r 1'=30.71mm r 2'=55.29mm (2) α'=24.87° r 1'=31.07mm r 2'=55.93mm (3) 相等 都等于两齿轮基圆半径的比值
11-3 已知一对渐开线外啮合标准直齿圆柱齿轮机构,α=20°,h a *=1,m =4mm ,z 1=18,z 2=41。
试求:
(1)两轮的几何尺寸和标准中心距a ,以及重合度ε;
(2)按比例作图,画出理论啮合线21N N ,在其上标出实际啮合线12B B ,并标出一对齿啮
合区和两对齿啮合区,以及节点P 的位置。
解:(1)各个几何尺寸按公式即可计算 其中 a =118mm ε=1.63
(2)
B 2E 、B 1D 为单啮合区 DE 为双啮合区
11-4 有一齿条刀具,m =2 mm ,α=20°,h a *=1。
刀具在切制齿轮时的移动速度v =1mm/s 。
试求:
(1)用这把刀具切制z =14的标准齿轮时,刀具中线离轮坯中心的距离L 为多少?轮坯每分
钟的转数应为多少?
(2)若用这把刀具切制z =14的变位齿轮时,其变位系数x =0.5,则刀具中线离轮坯中心的
距离L 应为多少?轮坯每分钟的转数应为多少? 解:(1)L =14mm n=0.682(r/min) (2)L =
1
2
mz mx +=15mm n =0.637(r/min) 11-5有一标准直齿圆柱齿轮与齿条传动,已知z 1=20,m =10mm ,α=20°,h a *=1,若安装时将分度圆与中线移开5mm ,试用图解法求:(1)实际啮合线段12B B 长度;(2)重合度ε;(3)顶隙c 。
解:r 1=100mm h a =10mm r a1=110mm '
20αα== r b1=94mm 如图所示,齿条移动之后,啮合线不变,齿条的齿顶线向下移动了5mm ,可计算的AP =5mm ,所以量的1238B B mm = 则可计算出 ε=1.29 c = c *m +5=7.5mm
11-6 一对标准安装的直齿圆柱标准齿轮外啮合传动。
已知其实际啮合线长度1224.6505B B =mm ,重合度ε=1.67,啮合角α'=20°。
(1)试求这对齿轮的模数m 。
(2)若该对齿轮的传动比i 12=3,标准安装中心距a =200mm ,求两个齿轮的齿数z 1,z 2; (3)现若齿轮其它参数不变,将中心距改为a '=210mm 。
求这对齿轮的节圆半径r 1'、r 2'及啮合角α'。
解:(1)m =5
(2)z1=20 z2=60
(3)r1'=52.5mm r2'=157.5mm
(4)α'=26.5°
11-7 一对在仪器中工作的渐开线齿廓标准直齿圆柱齿轮,已知m=2mm,α=20°,h a*=1。
经过精密测量,中心距为a=101mm,传动比i12=1.5。
问
(1)根据上述已知条件,判断该二齿轮是否符合正确安装?请给出详细计算说明。
(2)若其中小齿轮齿数为40,请计算啮合角α',以及两个齿轮的齿顶圆压力角αa1、αa2。
(计算结果保留四位小数)
(3)计算ε。
该对齿轮是否满足连续传动条件?
解:(1)假设符合正确安装计算出z1=40.4 z2=60.6 齿数不是整数不符合正确安装(2)α'=21.5°αa1=26.5°αa2=24.6°
(3)直接带入公式计算ε=1.27 所以满足传动条件
11-8 一对渐开线直齿圆柱齿轮传动中,主动轮1作逆时针转动。
已知标准中心距a=126mm,z1=17,z2=25,α=20°,h a*=1,要求:
(1)确定模数m;
(2)按长度比例尺
12mm/mm
μ=画出两齿轮的啮合图,并确定理论啮合线
12
N N位置;(3)在图上标出节点P和啮合角α';
(4)确定齿顶圆半径;
(5)在图上标出齿顶压力角αa1、αa2(以中心角表示);
(6)确定实际啮合线
12
B B位置;
(7)求重合度ε(有关寸可直接由图上量取)。
解:(1)m=6mm
r1=51mm r b1=47.9mm r a1=57mm r2=75mm r b2=70.5mm r a2=81mm
(7)量得
1227.7
B B mm
=ε=1.56
11-9一渐开线直齿圆柱标准齿轮和一标准直齿条标准安装并啮合传动,已知参数如下:齿轮齿数z=20,压力角α=20°,模数m=5mm,齿顶高系数h a*=1,试做简图说明并计算:(1)齿轮以200r/min的转速旋转时,齿条移动的线速度?
(2)齿条外移1mm时齿轮的节圆半径和啮合角α'?
(3)齿条外移1mm时齿条顶线与啮合线的交点B2到节点P的距离?
解:(1) v=1000
3
pi(mm /s)
(2)节圆半径为50mm α'=20°
m
(3)PB’=11.695mm
11-10 在相距160mm的O1、O2两轴间,欲采用两个渐开线标准直齿圆柱齿轮作外啮合传动,设m=8mm,z1=18,z2=21,α=20°,h a*=1,c*=0.25,要求:
(1)求两个齿轮分度圆、基圆、节圆、齿顶圆,齿根圆半径(或直径)。
(2)准确作图标出理论啮合线端点、实际啮合线端点、节点,量出实际啮合线段长,判断能否连续转动。
(3)在图上表示顶隙并计算顶隙的实际值。
(4)计算啮合角。
(5)填空或把不对的划出:这一对齿轮是(有侧、无侧)隙的;在中心距、齿数、模数不变的条件下,欲实现无侧隙,须采用传动;为此,可将其中一个齿轮设计成变位的,或两个齿轮都变位而变位系数和(大于、等于、小于)零。
解(1)带入公式计算即可。
(2)求出ε>1.08,能实现连续传动
(3)6mm
(4)α'=23.6°
(5)有变位正大于。
