立体几何证明垂直专项含练习题及答案
专题4：立体几何中垂直关系的证明基础练习题
12．证明见解析
【分析】
在等腰三角形PAB中， 是 的中点，可得 ，利用线面垂直的判定定理可证 平面 ，利用线面垂直的性质定理，即可得证.
【详解】
证明：∵ 是 的中点， ，
∴ ，
∵ 底面 ，
∴ ，
又∵ ，即
∴ 平面 ，
∴ ，
∵ 平面 ， 平面 ，
∴ 平面 ，
∵ 平面 ，
∴ .
8．证明见解析
【分析】
由平面 ⊥平面 得到 ⊥平面 ，进一步得到 ⊥ ，再结合直径所对圆周角为直角得到 ⊥ ， ⊥平面 ，从而得到证明.
【详解】
由题设知，平面 ⊥平面 ，交线为 .
因为 ⊥ ， 平面 ，所以 ⊥平面 ，故 ⊥ .
因为 为 上异于 ， 的点，且 为直径，所以 ⊥ .
又 = ，所以 ⊥平面 .
∴点O为三角形ABC的垂心，∴BO⊥AC
又因PO⊥AC，所以AC⊥PBO
故PB⊥AC
考点：证明异面直线垂直．
7．见解析
【分析】
由已知中P为正方形ABCD所在平面外一点，PA⊥面ABCD，结合正方形的几何特征，我们易得到BC⊥平面PAB，由线面垂直的性质得到BC⊥AE，结合已知中AE⊥PB，及线面垂直的判定定理，得到AE⊥平面PBC，最后再由线面垂直的判定定理，即可得到AE⊥PC．
【点睛】
此题考查线面垂直的性质和判定的综合应用，利用线面垂直得线线垂直.
5．证明见解析
【分析】
先证直线 平面 ，再证平面 ⊥平面 .
【详解】
证明:∵ 是圆的直径， 是圆上任一点， ， ，
平面 ， 平面 ，
，又 ，
平面 ，又 平面 ，
平面 ⊥平面 .
【点睛】
立体几何第六讲面面垂直练习题(含答案)
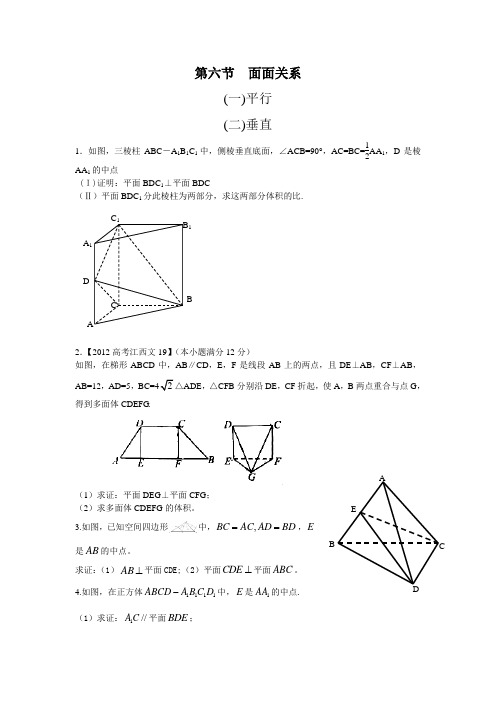
第六节 面面关系(一)平行 (二)垂直1．如图，三棱柱ABC －A 1B 1C 1中，侧棱垂直底面，∠ACB=90°，AC=BC=12AA 1，D 是棱AA 1的中点(Ｉ)证明：平面BDC 1⊥平面BDC（Ⅱ）平面BDC 1分此棱柱为两部分，求这两部分体积的比.2．【2012高考江西文19】（本小题满分12分）如图，在梯形ABCD 中，AB ∥CD ，E ，F 是线段AB 上的两点，且DE ⊥AB ，CF ⊥AB ，AB=12，AD=5，BC=42△ADE ，△CFB 分别沿DE ，CF 折起，使A ，B 两点重合与点G ，得到多面体CDEFG .（1）求证：平面DEG ⊥平面CFG ； （2）求多面体CDEFG 的体积。
3.如图，已知空间四边形中，,BC AC AD BD ==，E是AB 的中点。
求证：（1）⊥AB 平面CDE;（2）平面CDE ⊥平面ABC 。
4.如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点. （1）求证：1//A C 平面BDE ；B 1C BADC 1A 1AEDBCA AC⊥平面BDE.（2）求证：平面15.已知四棱锥P—ABCD，底面ABCD是菱形，∠PDDAB,60平面ABCD，PD=AD，=⊥︒点E为AB中点，点F为PD中点.（1）证明平面PED⊥平面PAB；（2）求二面角P—AB—F的平面角的余弦值第六节 面面关系答案（一）平行 （二）垂直1.【命题意图】本题主要考查空间线线、线面、面面垂直的判定与性质及几何体的体积计算，考查空间想象能力、逻辑推理能力，是简单题.【解析】（Ⅰ）由题设知BC ⊥1CC ,BC ⊥AC ，1CC AC C ⋂=,∴BC ⊥面11ACC A , 又∵1DC ⊂面11ACC A ，∴1DC BC ⊥,由题设知01145A DC ADC ∠=∠=,∴1CDC ∠=090,即1DC DC ⊥,又∵DC BC C ⋂=, ∴1DC ⊥面BDC , ∵1DC ⊂面1BDC ， ∴面BDC ⊥面1BDC ；（Ⅱ）设棱锥1B DACC -的体积为1V ，AC =1，由题意得，1V =1121132+⨯⨯⨯=12，由三棱柱111ABC A B C -的体积V =1，∴11():V V V -=1:1， ∴平面1BDC 分此棱柱为两部分体积之比为1:1.2.【解析】（1）由已知可得AE=3，BF=4，则折叠完后EG=3，GF=4，又因为EF=5，所以可得EG GF ⊥又因为CF EGF ⊥底面,可得CF EG ⊥，即EG CFG ⊥面所以平面DEG ⊥平面CFG . （2）过G 作GO 垂直于EF ，GO 即为四棱锥G-EFCD 的高，所以所求体积为11125520335DECF S GO ⋅=⨯⨯⨯=正方形3.证明：（1）BC AC CE AB AE BE =⎫⇒⊥⎬=⎭同理，AD BD DE AB AE BE =⎫⇒⊥⎬=⎭又∵CE DE E ⋂= ∴AB ⊥平面CDE （2）由（1）有AB ⊥平面CDE又∵AB ⊆平面ABC ， ∴平面CDE ⊥平面ABC 4.证明：（1）设AC BD O ⋂=，∵E 、O 分别是1AA 、AC 的中点，∴1A C ∥EO又1AC ⊄平面BDE ，EO ⊂平面BDE ，∴1A C ∥平面BDE （2）∵1AA ⊥平面ABCD ，BD ⊂平面ABCD ，1AA BD ⊥ 又BD AC ⊥，1AC AA A⋂=，∴BD ⊥平面1A AC ，BD ⊂平面BDE ，∴平面BDE ⊥平面1A AC5.（1）证明：连接BD.ADB DAB AD AB ∆∴︒=∠=,60, 为等边三角形.E 是AB 中点，.DE AB ⊥∴⊥PD 面ABCD ，AB ⊂面ABCD ，.PD AB ⊥∴⊂DE 面PED ，PD ⊂面PED ，⊥∴=AB D PD DE , 面PED. ⊂AB 面PAB ，⊥∴PED 面面PAB.（2）解：⊥AB 平面PED ，PE ⊂面PED ，.PE AB ⊥∴ 连接EF ，⊂EF PED ，.EF AB ⊥∴PEF ∠∴为二面角P —AB —F 的平面角. 设AD=2，那么PF=FD=1，DE=3. 在,1,2,7,===∆PF EF PE PEF 中,147572212)7(cos 22=⨯-+=∠∴PEF 即二面角P —AB —F 的平面角的余弦值为.1475立体几何练习题1.设α、β、γ为两两不重合的平面，l 、m 、n 为两两不重合的直线，给出下列四个命题： 若α⊥γ，β⊥γ，则α∥β；②若m ⊂α，n ⊂α，m ∥β，n ∥β，则α∥β；③若α∥β，l ⊂α，则l ∥β；④若α∩β=l ，β∩γ=m ，γ∩α=n ，l ∥γ，则m ∥n ． 其中真命题的个数是( ) A ．1 B ．2 C ．3 D ．42.正方体ABCD ﹣A 1B 1C 1D 1中，BD 1与平面ABCD 所成角的余弦值为（） A ．B ．CD ．3.三棱柱ABC ﹣A 1B 1C 1中，AA 1=2且AA 1⊥平面ABC ，△ABC 是 边长为的正三角形，该三棱柱的六个顶点都在一个球面上，则这个球的体积为（） A ． 8πB ．C ．D ． 8π4.三个平面两两垂直，它们的三条交线交于点O ，空间一点P 到三个平面的距离分别为3、4、5，则OP 长为（）A ． 5B ． 2C ． 3D ． 55.如图，四棱锥S ﹣ABCD 的底面为正方形，SD ⊥底面ABCD ，则下列结论中不正确的是（） A ． AC⊥SB B ．AB∥平面SCDC ． SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角 D ． AB 与SC 所成的角等于DC 与SA 所成的角6.如图，四棱锥P ﹣ABCD 的底面为正方形，PD ⊥底面ABCD ，PD=AD=1，设点CG 到平面PAB 的距离为d 1，点B 到平面PAC 的距离为d 2，则有（ ） A ． 1＜d 1＜d 2 B ． d 1＜d 2＜1C ． d 1＜1＜d 2D ． d 2＜d 1＜17.在锐角的二面角βα--EF ，A EF ∈，AG α⊂， 45=∠GAE ，若AG 与β所成角为 30，则二面角βα--EF 为__________. 8.给出下列四个命题：(1)若平面α上有不共线的三点到平面β的距离相等，则βα//； (2)两条异面直线在同一平面内的射影可能是两条平行直线；(3)两条异面直线中的一条平行于平面α，则另一条必定不平行于平面α； (4)b ,a 为异面直线，则过a 且与b 平行的平面有且仅有一个． 其中正确命题的序号是_______________________9.已知正方体 1111ABCD A B C D -中，点E 是棱 11A B 的中点，则直线AE 与平而 11BDD B 所成角的正弦值是_________.EFA Gαβ10.已知直三棱柱111ABC A B C -中，090ABC ∠=，122AC AA ==，2AB =，M 为1BB 的中点，则1B 与平面ACM 的距离为______11.边长分别为a 、b 的矩形，按图中所示虚线剪裁后，可将两个小矩形拼接成一个正四棱锥的底面，其余恰好拼接成该正四棱锥的4个侧面，则ba的取值范围是 ． 12.已知矩形ABCD 的长4AB =，宽3AD =，将其沿对角线BD 折起，得到四面体A BCD -，如图所示， 给出下列结论：①四面体A BCD -体积的最大值为725； ②四面体A BCD -外接球的表面积恒为定值；③若E F 、分别为棱AC BD 、的中点，则恒有EF AC ⊥且EF BD ⊥； ④当二面角A BD C --为直二面角时，直线AB CD 、所成角的余弦值为1625； ⑤当二面角A BD C --的大小为60︒时，棱AC 的长为145． 其中正确的结论有 (请写出所有正确结论的序号)． 13.如图，在直三棱柱ABC ﹣A 1B 1C 1中，∠BAC=90°，AB=BB 1，直线B 1C 与平面ABC 成30°角．（I ）求证：平面B 1AC⊥平面ABB 1A 1；（II ）求直线A 1C 与平面B 1AC 所成角的正弦值．14.如图，在三棱锥P ﹣ABC 中，D ，E ，F 分别为棱PC ，AC ，AB 的中点．已知PA⊥AC，PA=AB=6，BC=8，DF=5． （1）若PB⊥BC，证明平面BDE⊥平面ABC ． （2）求直线BD 与平面ABC 所成角的正切值．15.如图，长方体ABCD ﹣A 1B 1C 1D 1中，AB=AD=1，AA 1=2，点P 为DD 1的中点． （1）求证：直线BD 1∥平面PAC ；4343AB CD4334DCBA（2）求证：平面PAC⊥平面BDD1B1；（3）求CP与平面BDD1B1所成的角大小．16.如图，四棱锥P﹣ABCD的底面是正方形，PD⊥底面ABCD，点E在棱PB上（1）求证：AC⊥平面PDB（2）当PD=AB且E为PB的中点时，求AE与平面PDB所成的角的大小．17.在四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠ADC=45°，AD=AC=1，O为AC中点，PO⊥平面ABCD，PO=2，M为PD中点．（Ⅰ）求证：PB∥平面ACM；（Ⅱ）求证：AD⊥平面PAC；（Ⅲ）求二面角M﹣AC﹣D的正切值．18.如图所示，在四棱锥P﹣ABCD中，底面ABCD为矩形，PA⊥平面ABCD，点E在线段PC上，PC⊥平面BDE．（1）证明：BD⊥平面PAC；（2）若PA=1，AD=2，求二面角B﹣PC﹣A的正切值．19.如图，直三棱柱ABC﹣A1B1C1中，CA⊥CB，AA1=AC=CB=2，D是AB的中点．（1）求证：BC1∥平面A1CD；（2）求证：A1C⊥AB1；（3）若点E在线段BB1上，且二面角E﹣CD﹣B的正切值是，求此时三棱锥C﹣A1DE的体积．20.如图，四棱锥S﹣ABCD的底面是正方形，每条侧棱的长都是底面边长的倍，P为侧棱SD上的点．（1）求证：AC⊥SD；（2）若SD⊥平面PAC，求二面角P﹣AC﹣D的大小；（3）在（2）的条件下，侧棱SC上是否存在一点E，使得BE∥平面PAC．若存在，求SE：EC的值；若不存在，试说明理由．试卷答案1.B：解：若α⊥γ，β⊥γ，则α与β可能平行也可能相交，故①错误；由于m，n不一定相交，故α∥β不一定成立，故②错误；由面面平行的性质定理，易得③正确；由线面平行的性质定理，我们易得④正确；故选B2.D考点：棱柱的结构特征．专题：空间角．分析：找出BD1与平面ABCD所成的角，计算余弦值．解答：解：连接BD，；∵DD1⊥平面ABCD，∴BD是BD1在平面ABCD的射影，∴∠DBD1是BD1与平面ABCD所成的角；设AB=1，则BD=，BD1=，∴cos∠DBD1===；故选：D．点评：本题以正方体为载体考查了直线与平面所成的角，是基础题．3.C考点：球的体积和表面积．专题：计算题；空间位置关系与距离．分析：根据题意，正三棱柱的底面中心的连线的中点就是外接球的球心，求出球的半径即可求出球的体积．解答：解：由题意可知：正三棱柱的底面中心的连线的中点就是外接球的球心，因为△ABC是边长为的正三角形，所以底面中心到顶点的距离为：1；因为AA1=2且AA1⊥平面ABC，所以外接球的半径为：r==．所以外接球的体积为：V=πr3=π×（）3=．故选：C．点评：本题给出正三棱柱有一个外接球，在已知底面边长的情况下求球的体积．着重考查了正三棱柱的性质、正三角形的计算和球的体积公式等知识，属于中档题．4.D考点：平面与平面垂直的性质．专题：计算题；空间位置关系与距离．分析：构造棱长分别为a，b，c的长方体，P到三个平面的距离即为长方体的共顶点的三条棱的长，OP为长方体的对角线，求出OP即可．解答：构造棱长分别为a，b，c的长方体，P到三个平面的距离即为长方体的共顶点的三条棱的长，则a2+b2+c2=32+42+52=50因为OP为长方体的对角线．所以OP=5．故选：D．点评：本题考查点、线、面间的距离计算，考查计算能力，是基础题．5.D考点：直线与平面垂直的性质．专题：综合题；探究型．分析：根据SD⊥底面ABCD，底面ABCD为正方形，以及三垂线定理，易证AC⊥SB，根据线面平行的判定定理易证AB∥平面SCD，根据直线与平面所成角的定义，可以找出∠ASO是SA与平面SBD所成的角，∠CSO是SC与平面SBD所成的角，根据三角形全等，证得这两个角相等；异面直线所成的角，利用线线平行即可求得结果．解答：解：∵SD⊥底面ABCD，底面ABCD为正方形，∴连接BD，则BD⊥AC，根据三垂线定理，可得AC⊥SB，故A正确；∵AB∥CD，AB⊄平面SCD，CD⊂平面SCD，∴AB∥平面SCD，故B正确；∵SD⊥底面ABCD，∠ASO是SA与平面SBD所成的角，∠DSO是SC与平面SBD所成的，而△SAO≌△CSO，∴∠ASO=∠CSO，即SA与平面SBD所成的角等于SC与平面SBD所成的角，故C正确；∵AB∥CD，∴AB与SC所成的角是∠SCD，DC与SA所成的角是∠SAB，而这两个角显然不相等，故D不正确；故选D．点评：此题是个中档题．考查线面垂直的性质定理和线面平行的判定定理，以及直线与平面所成的角，异面直线所成的角等问题，综合性强．6.D考点：点、线、面间的距离计算．专题：综合题；空间位置关系与距离；空间角．分析：过C做平面PAB的垂线，垂足为E，连接BE，则三角形CEB为直角三角形，根据斜边大于直角边，再根据面PAC和面PAB与底面所成的二面角，能够推导出d2＜d1＜1．解答：解：过C做平面PAB的垂线，垂足为E，连接BE，则三角形CEB为直角三角形，其中∠CEB=90°，根据斜边大于直角边，得CE＜CB，即d2＜1．同理，d1＜1．再根据面PAC和面PAB与底面所成的二面角可知，前者大于后者，所以d2＜d1．所以d2＜d1＜1．故选D．点评：本题考查空间距离的求法，解题时要认真审题，仔细解答，注意空间角的灵活运用．7.48.(2)(4)10.111.1 (,) 212.②③④13.考点：平面与平面垂直的判定；直线与平面所成的角．专题：证明题．分析：（I）欲证平面B1AC⊥平面ABB1A1，关键是寻找线面垂直，而AC⊥平面ABB1A1，又AC⊂平面B1AC，满足面面垂直的判定定理；（II）过A1做A1M⊥B1A1，垂足为M，连接CM，∠A1CM为直线A1C与平面B1AC所成的角，然后在三角形A1CM 中求出此角的正弦值即可．解答：解：（I）证明：由直三棱柱性质，B1B⊥平面ABC，∴B1B⊥AC，又BA⊥AC，B1B∩BA=B，∴AC⊥平面ABB1A1，又AC⊂平面B1AC，∴平面B1AC⊥平面ABB1A1．（II）解：过A1做A1M⊥B1A1，垂足为M，连接CM，∵平面B1AC⊥平面ABB1A，且平面B1AC∩平面ABB1A1=B1A，∴A1M⊥平面B1AC．∴∠A1CM为直线A1C与平面B1AC所成的角，∵直线B1C与平面ABC成30°角，∴∠B1CB=30°．设AB=BB1=a，可得B1C=2a，BC=，∴直线A1C与平面B1AC所成角的正弦值为点评：本题主要考查了平面与平面垂直的判定，以及直线与平面所成的角，考查空间想象能力、运算能力和推理论证能力．14.考点：直线与平面所成的角；平面与平面垂直的判定．专题：空间位置关系与距离；空间角．分析：（1）由已知得DE⊥AC，DE2+EF2=DF2，从而DE⊥平面ABC，由此能证明平面BDE⊥平面ABC．（2）由DE⊥平面ABC，得∠DBE是直线BD与平面ABC所成的角，由此能求出直线BD与平面ABC所成角的正切值．解答：（1）证明：∵在三棱锥P﹣ABC中，D，E，F分别为棱PC，AC，AB的中点．PA⊥AC，PA=AB=6，BC=8，DF=5，∴DE⊥AC，DE=3，EF=4，DF=5，∴DE2+EF2=DF2，∴DE⊥EF，又EF∩AC=F，∴DE⊥平面ABC，又DE⊂平面BDE，∴平面BDE⊥平面ABC．（2）∵DE⊥平面ABC，∴PA⊥平面ABC，∴PA⊥AB，∵PB⊥BC，∴AB⊥BC，∴AC==10，∴，由DE⊥平面ABC，得∠DBE是直线BD与平面ABC所成的角，tan∠DBE==．∴直线BD与平面ABC所成角的正切值为．点评：本题考查平面与平面垂直的证明，考查直线与平面所成角的正切值的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．15.考点：直线与平面平行的判定；平面与平面垂直的判定；直线与平面所成的角．专题：证明题．分析：（1）设AC和BD交于点O，由三角形的中位线的性质可得PO∥BD1，从而证明直线BD1∥平面PAC．（2）证明AC⊥BD，DD1⊥AC，可证AC⊥面BDD1B1，进而证得平面PAC⊥平面BDD1B1 ．（3）CP在平面BDD1B1内的射影为OP，故∠CPO是CP与平面BDD1B1所成的角，在Rt△CPO中，利用边角关系求得∠CPO的大小．解答：（1）证明：设AC和BD交于点O，连PO，由P，O分别是DD1，BD的中点，故PO∥BD1，∵PO⊂平面PAC，BD1⊄平面PAC，所以，直线BD1∥平面PAC．（2）长方体ABCD﹣A1B1C1D1中，AB=AD=1，底面ABCD是正方形，则AC⊥BD，又DD1⊥面ABCD，则DD1⊥AC．∵BD⊂平面BDD1B1，D1D⊂平面BDD1B1，BD∩D1D=D，∴AC⊥面BDD1B1．∵AC⊂平面PAC，∴平面PAC⊥平面BDD1B1 ．（3）由（2）已证：AC⊥面BDD1B1，∴CP在平面BDD1B1内的射影为OP，∴∠CPO是CP与平面BDD1B1所成的角．依题意得，，在Rt△CPO中，，∴∠CPO=30°∴CP与平面BDD1B1所成的角为30°．点评：本题考查证明线面平行、面面垂直的方法，求直线和平面所称的角的大小，找出直线和平面所成的角是解题的难点，属于中档题．16.考点：直线与平面所成的角；直线与平面垂直的判定．专题：综合题；空间位置关系与距离；空间角．分析：（1）根据题意证明AC⊥BD，PD⊥AC，可得AC⊥平面PDB；（2）设AC∩BD=O，连接OE，根据线面所成角的定义可知∠AEO为AE与平面PDB所的角，在Rt△AOE中求出此角即可．解答：（1）证明：∵四边形ABCD是正方形，∴AC⊥BD，∵PD⊥底面ABCD，∴PD⊥AC，又BD∩PD=D∴AC⊥平面PDB，（3分）（2）设AC∩BD=O，连接OE，由（1）知AC⊥平面PDB于O，∴∠AEO为AE与平面PDB所的角，（5分）又O，E分别为DB、PB的中点，∴OE∥PD，OE=PD，在Rt△AOE中，OE=PD=AB=AO，∴∠AEO=45°，（7分）即AE与平面PDB所成的角的大小为45°．（8分）点评：本题主要考查了直线与平面垂直的判定，以及直线与平面所成的角，考查空间想象能力、运算能力和推理论证能力，属于中档题．17.考点：与二面角有关的立体几何综合题；直线与平面平行的判定；直线与平面垂直的判定．专题：计算题．分析：（Ⅰ）连接OM，BD，由M，O分别为PD和AC中点，知OM∥PB，由此能够证明PB∥平面ACM．（Ⅱ）由PO⊥平面ABCD，知PO⊥AD，由∠ADC=45°，AD=AC=1，知AC⊥AD，由此能够证明AD⊥平面PAC．（Ⅲ）取DO中点N，连接MN，由MN∥PO，知MN⊥平面ABCD．过点N作NE⊥AC于E，由E为AO中点，连接ME，由三垂线定理知∠MEN即为所求，由此能求出二面角M﹣AC﹣D的正切值．解答：（Ⅰ）证明：连接OM，BD，∵M，O分别为PD和AC中点，∴OM∥PB，∵OM⊂平面ACM，PB⊄ACM平面，∴PB∥平面ACM…．（4分）（Ⅱ）证明：由已知得PO⊥平面ABCD∴PO⊥AD，∵∠ADC=45°，AD=AC=1，∴AC⊥AD，∵AC∩PO=O，AC，PO⊂平面PAC，∴AD⊥平面PAC．…..（8分）（Ⅲ）解：取DO中点N，连接MN，则MN∥PO，∴MN⊥平面ABCD过点N作NE⊥AC于E，则E为AO中点，连接ME，由三垂线定理可知∠MEN即为二面角M﹣AC﹣D的平面角，∵MN=1，NE=∴tan∠MEN=2…..（13分）点评：本题考查直线与平面平行、直线现平面垂直的证明，考查二面角的正切值的求法，解题时要认真审题，仔细解答，注意三垂直线定理的合理运用．18.考点：二面角的平面角及求法；直线与平面垂直的判定．专题：空间位置关系与距离；空间角；立体几何．分析：（1）由题设条件及图知，可先由线面垂直的性质证出PA⊥BD与PC⊥BD，再由线面垂直的判定定理证明线面垂直即可；（2）由图可令AC与BD的交点为O，连接OE，证明出∠BEO为二面角B﹣PC﹣A的平面角，然后在其所在的三角形中解三角形即可求出二面角的正切值．解答：（1）∵PA⊥平面ABCD∴PA⊥BD∵PC⊥平面BDE∴PC⊥BD，又PA∩PC=P∴BD⊥平面PAC（2）设AC与BD交点为O，连OE∵PC⊥平面BDE∴PC⊥平面BOE∴PC⊥BE∴∠BEO为二面角B﹣PC﹣A的平面角∵BD⊥平面PAC∴BD⊥AC∴四边形ABCD为正方形，又PA=1，AD=2，可得BD=AC=2，PC=3∴OC=在△PAC∽△OEC中，又BD⊥OE，∴∴二面角B﹣PC﹣A的平面角的正切值为3点评：本题考查二面角的平面角的求法及线面垂直的判定定理与性质定理，属于立体几何中的基本题型，二面角的平面角的求法过程，作，证，求三步是求二面角的通用步骤，要熟练掌握19.考点：棱柱、棱锥、棱台的体积；空间中直线与直线之间的位置关系；直线与平面平行的判定．专题：综合题；空间位置关系与距离；空间角．分析：（1）连接AC1交A1C于点F，由三角形中位线定理得BC1∥DF，由此能证明BC1∥平面A1CD．（2）利用线面垂直的判定定理证明A1C⊥平面AB1C1，即可证明A1C⊥AB1；（3）证明∠BDE为二面角E﹣CD﹣B的平面角，点E为BB1的中点，确定DE⊥A1D，再求三棱锥C﹣A1DE 的体积．解答：（1）证明：连结AC1，交A1C于点F，则F为AC1中点，又D是AB中点，连结DF，则BC1∥DF，因为DF⊂平面A1CD，BC1⊄平面A1CD，所以BC1∥平面A1CD．…（3分）（2）证明：直三棱柱ABC﹣A1B1C1中，因为AA1=AC，所以AC1⊥A1C…（4分）因为CA⊥CB，B1C1∥BC，所以B1C1⊥平面ACC1A1，所以B1C1⊥A1C…（6分）因为B1C1∩AC1=C1，所以A1C⊥平面AB1C1所以A1C⊥AB1…（8分）（3）在直三棱柱ABC﹣A1B1C1中，AA1⊥CD，因为AC=CB，D为AB的中点，所以CD⊥AB，CD⊥平面ABB1A1．所以CD⊥DE，CD⊥DB，所以∠BDE为二面角E﹣CD﹣B的平面角．在Rt△DEB中，．由AA1=AC=CB=2，CA⊥CB，所以，．所以，得BE=1．所以点E为BB1的中点．…（11分）又因为，，，A1E=3，故，故有DE⊥A1D所以…（14分）点评：本题主要考查直线与平面平行、垂直等位置关系，考查线面平行、二面角的概念、求法、三棱锥C﹣A1DE的体积等知识，考查空间想象能力和逻辑推理能力，是中档题．20.考点：直线与平面平行的判定；直线与平面垂直的判定；与二面角有关的立体几何综合题．专题：计算题；证明题；压轴题．分析：（1）连BD，设AC交于BD于O，由题意知SO⊥平面ABCD．以O为坐标原点，分别为x轴、y轴、z轴正方向，建立坐标系O﹣xyz，设底面边长为a，求出高SO，从而得到点S与点C 和D的坐标，求出向量与，计算它们的数量积，从而证明出OC⊥SD，则AC⊥SD；（2）根据题意先求出平面PAC的一个法向量和平面DAC的一个法向量，设所求二面角为θ，则，从而求出二面角的大小；（3）在棱SC上存在一点E使BE∥平面PAC，根据（Ⅱ）知是平面PAC的一个法向量，设，求出，根据可求出t的值，从而即当SE：EC=2：1时，，而BE不在平面PAC内，故BE∥平面PAC解答：证明：（1）连BD，设AC交于BD于O，由题意知SO⊥平面ABCD．以O为坐标原点，分别为x轴、y轴、z轴正方向，建立坐标系O﹣xyz如图．设底面边长为a，则高．于是，，，，故OC⊥SD从而AC⊥SD（2）由题设知，平面PAC的一个法向量，平面DAC的一个法向量．设所求二面角为θ，则，所求二面角的大小为30°．（3）在棱SC上存在一点E使BE∥平面PAC．由（Ⅱ）知是平面PAC的一个法向量，且设，则而即当SE：EC=2：1时，而BE不在平面PAC内，故BE∥平面PAC点评：本题主要考查了直线与平面平行的判定，以及空间两直线的位置关系的判定和二面角的求法，涉及到的知识点比较多，知识性技巧性都很强．。
立体几何线面平行垂直、面面平行垂直专题练习(高三党必做)
立体几何线面平行垂直、面面平行垂直专题一、解答题（本大题共27小题，共324.0分）1.如图，四棱锥P-ABCD中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点．（1）证明：MN∥平面PAB；（2）求直线AN与平面PMN所成角的正弦值．2.如图，四棱锥P-ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB＝AD，∠BAD＝∠ABC＝90°，E是PD的中点．BC＝12(1)证明：直线CE∥平面PAB；(2)点M在棱PC上，且直线BM与底面ABCD所成角为45°，求二面角M-AB-D的余弦值．3.如图，在三棱柱ABC-A1B1C1中，BB1⊥平面ABC，∠BAC=90°，AC=AB=AA1，E是BC的中点．（1）求证：AE⊥B1C；（2）求异面直线AE与A1C所成的角的大小；（3）若G为C1C中点，求二面角C-AG-E的正切值．4.如图所示，在四棱锥P-ABCD中，底面四边形ABCD是菱形，AC∩BD=O，△PAC是边长为2的等边三角形，PB=PD=√6，AP=4AF．（Ⅰ）求证：PO⊥底面ABCD；（Ⅱ）求直线CP与平面BDF所成角的大小；（Ⅲ）在线段PB上是否存在一点M，使得CM∥平面BDF如果存在，求BM的值，如果不存在，请说明理BP由．5.如图，在直三棱柱ABC-A1B l C1中，AC=BC=√2，∠ACB=90°．AA1=2，D为AB的中点．（Ⅰ）求证：AC⊥BC1；（Ⅱ）求证：AC1∥平面B1CD：（Ⅲ）求异面直线AC1与B1C所成角的余弦值．6.如图，正三棱柱ABC-A1B1C1中，AB=AA1=2，点P，Q分别为A1B1，BC的中点．（1）求异面直线BP与AC1所成角的余弦值；（2）求直线CC1与平面AQC1所成角的正弦值．7.如图，在四棱锥P-ABCD中，底面ABCD为正方形，平面PAD⊥平面ABCD，点M在线段PB上，PD∥平面MAC，PA=PD=√6，AB=4．（1）求证：M为PB的中点；（2）求二面角B-PD-A的大小；（3）求直线MC与平面BDP所成角的正弦值．8.如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．（1）证明：PB∥平面AEC；（2）设AP=1，AD=√3，三棱锥P-ABD的体积V=√3，求A到平面PBC的距4离．9.如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AD⊥AB，AB∥DC，AD＝DC＝AP＝2，AB＝1，点E为棱PC的中点．（Ⅰ）证明：BE⊥DC；（Ⅱ）求直线BE与平面PBD所成角的正弦值；（Ⅲ）若F为棱PC上一点，满足BF⊥AC，求二面角F-AB-P的余弦值．10.如图，已知四棱锥P-ABCD，△PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点．（Ⅰ）证明：CE∥平面PAB；（Ⅱ）求直线CE与平面PBC所成角的正弦值．11.如图，正三角形ABE与菱形ABCD所在的平面互相垂直，AB=2，∠ABC=60°，M是AB的中点，N是CE的中点．（I）求证：EM⊥AD；（II）求证：MN∥平面ADE；（III）求点A到平面BCE的距离．12.已知几何体ABCDEF中，AB∥CD，AD⊥DC，EA⊥平面ABCD，FC∥EA，AB=AD=EA=1，CD=CF=2．（Ⅰ）求证：平面EBD⊥平面BCF；（Ⅱ）求点B到平面ECD的距离．13.如图，四棱锥P-ABCD中，底面ABCD为矩形，PD⊥底面ABCD，AD=PD=2，E、F分别为CD、PB的中点．（1）求证：EF∥平面PAD；（2）求证：平面AEF⊥平面PAB；（3）设AB=√2AD，求直线AC与平面AEF所成角θ的正弦值．14.如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，∠ADC=45∘，AD=AC=2，O为AC的中点，PO⊥平面ABCD且PO=6，M为BD的中点．(1)证明：AD⊥平面PAC；(2)求直线AM与平面ABCD所成角的正切值．15.如图，正三棱柱ABC-A1B1C1中，AB=2，AA1=√2，点D为A1C1的中点．（I）求证：BC1∥平面AB1D；（II）求证：A1C⊥平面AB1D；（Ⅲ）求异面直线AD与BC1所成角的大小．16.如图，P-ABD和Q-BCD为两个全等的正棱锥，且A，B，C，D四点共面，其中AB=1，∠APB=90°．（Ⅰ）求证：BD⊥平面APQ；（Ⅱ）求直线PB与平面PDQ所成角的正弦值．17.如图，在三棱柱ABC-A1B1C1中，平面A1ACC1⊥底面ABC，AB=BC=2，∠ACB=30°，∠C1CB=60°，BC1⊥A1C，E为AC的中点，侧棱CC1=2．（1）求证：A1C⊥平面C1EB；（2）求直线CC1与平面ABC所成角的余弦值．18.如图，在三棱锥P-ABC中，平面PAB⊥平面ABC，AB=6，BC=2√3，AC=2√6，D为线段AB上的点，且AD=2DB，PD⊥AC．（1）求证：PD⊥平面ABC；，求点B到平面PAC的距离．（2）若∠PAB=π419.如图，三棱柱ABC-A1B1C1中，A1A⊥平面ABC，△ABC为正三角形，D是BC边的中点，AA1=AB=1．（1）求证：平面ADB1⊥平面BB1C1C；（2）求点B到平面ADB1的距离．20.如图，在三棱锥P-ABC中，点D，E，F分别为棱PC，AC，AB的中点，已知PA⊥平面ABC，AB⊥BC，且AB=BC．（1）求证：平面BED⊥平面PAC；（2）求二面角F-DE-B的大小；（3）若PA=6，DF=5，求PC与平面PAB所成角的正切值．21.如图,在四棱锥P—ABCD中,PD⊥平面ABCD,AD⊥CD,DB平分∠ADC,E为PC的中点,AD＝CD＝1,DB=2√2.(1)证明PA∥平面BDE;(2)证明AC⊥平面PBD;(3)求直线BC与平面PBD所成的角的正切值.22.如图所示，在四棱台ABCD-A1B1C1D1中，AA1⊥底面ABCD，四边形ABCD为菱形，∠BAD=120°，AB=AA1=2A1B1=2．（Ⅰ）若M为CD中点，求证：AM⊥平面AA1B1B；（Ⅱ）求直线DD1与平面A1BD所成角的正弦值．=√2.23.如图，在直三棱柱ABC−A1B1C1中，∠ACB=90°，E为A1C1的中点，CC1C1E（Ⅰ）证明：CE⊥平面AB1C1；（Ⅱ）若AA1=√6，∠BAC=30°，求点E到平面AB1C的距离．24.如图，在四棱锥E-ABCD中，底面ABCD是边长为√2的正方形，平面AEC⊥平面CDE，∠AEC=90°，F为DE中点，且DE=1．（Ⅰ）求证：BE∥平面ACF；（Ⅱ）求证：CD⊥DE；（Ⅲ）求FC与平面ABCD所成角的正弦值．25.已知：平行四边形ABCD中，∠DAB=45°，AB=√2AD=2√2，平面AED⊥平面ABCD，△AED为等边三角形，EF∥AB，EF=√2，M为线段BC的中点．（1）求证：直线MF∥平面BED；（2）求证：平面BED⊥平面EAD；（3）求直线BF与平面BED所成角的正弦值．26.如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，侧棱PA=PD=√2，底面ABCD为直角梯形，其中BC∥AD，AB⊥AD，AC=√2，AB=BC=1，E为AD中点．（Ⅰ）求证：PE⊥平面ABCD；（Ⅱ）求异面直线PB与CD所成角的余弦值；（Ⅲ）求平面PAB与平面PCD所成的二面角．27.如图，已知多面体ABCA1B1C1，A1A，B1B，C1C均垂直于平面ABC，∠ABC=120°，A1A=4，C1C=1，AB=BC=B1B=2．（1）证明：AB1⊥平面A1B1C1；（2）求直线AC1与平面ABB1所成的角的正弦值．答案和解析1.【答案】（1）证明：法一、如图，取PB 中点G ，连接AG ，NG ，∵N 为PC 的中点， ∴NG ∥BC ，且NG =12BC ，又AM =23AD =2，BC =4，且AD ∥BC ， ∴AM ∥BC ，且AM =12BC ，则NG ∥AM ，且NG =AM ，∴四边形AMNG 为平行四边形，则NM ∥AG ， ∵AG ⊂平面PAB ，NM ⊄平面PAB ， ∴MN ∥平面PAB ； 法二、在△PAC 中，过N 作NE ⊥AC ，垂足为E ，连接ME ， 在△ABC 中，由已知AB =AC =3，BC =4，得cos ∠ACB =42+32−322×4×3=23，∵AD ∥BC ，∴cos ∠EAM =23，则sin ∠EAM =√53，在△EAM 中，∵AM =23AD =2，AE =12AC =32，由余弦定理得：EM =√AE 2+AM 2−2AE ⋅AM ⋅cos∠EAM =√94+4−2×32×2×23=32，∴cos ∠AEM =(32)2+(32)2−42×32×32=19，而在△ABC 中，cos ∠BAC =32+32−422×3×3=19，∴cos ∠AEM =cos ∠BAC ，即∠AEM =∠BAC ， ∴AB ∥EM ，则EM ∥平面PAB ．由PA ⊥底面ABCD ，得PA ⊥AC ，又NE ⊥AC ， ∴NE ∥PA ，则NE ∥平面PAB ． ∵NE ∩EM =E ，∴平面NEM ∥平面PAB ，则MN ∥平面PAB ；（2）解：在△AMC 中，由AM =2，AC =3，cos ∠MAC =23，得CM 2=AC 2+AM 2-2AC •AM •cos ∠MAC =9+4−2×3×2×23=5．∴AM 2+MC 2=AC 2，则AM ⊥MC ， ∵PA ⊥底面ABCD ，PA ⊂平面PAD ，∴平面ABCD ⊥平面PAD ，且平面ABCD ∩平面PAD =AD ， ∴CM ⊥平面PAD ，则平面PNM ⊥平面PAD ．在平面PAD 内，过A 作AF ⊥PM ，交PM 于F ，连接NF ，则∠ANF 为直线AN 与平面PMN 所成角．在Rt△PAC中，由N是PC的中点，得AN=12PC=12√PA2+PC2=52，在Rt△PAM中，由PA•AM=PM•AF，得AF=PA⋅AMPM =√42+22=4√55，∴sin∠ANF=AFAN =4√5552=8√525．∴直线AN与平面PMN所成角的正弦值为8√525．【解析】本题考查直线与平面平行的判定，考查直线与平面所成角的求法，考查数学转化思想方法，考查了空间想象能力和计算能力，是中档题．（1）法一、取PB中点G，连接AG，NG，由三角形的中位线定理可得NG∥BC，且NG=12BC，再由已知得AM∥BC，且AM=12BC，得到NG∥AM，且NG=AM，说明四边形AMNG为平行四边形，可得NM∥AG，由线面平行的判定得到MN∥平面PAB；法二、证明MN∥平面PAB，转化为证明平面NEM∥平面PAB，在△PAC中，过N作NE⊥AC，垂足为E，连接ME，由已知PA⊥底面ABCD，可得PA∥NE，通过求解直角三角形得到ME∥AB，由面面平行的判定可得平面NEM∥平面PAB，则结论得证；（2）由勾股定理得CM⊥AD，进一步得到平面PNM⊥平面PAD，在平面PAD内，过A作AF⊥PM，交PM于F，连接NF，则∠ANF为直线AN与平面PMN所成角．然后求解直角三角形可得直线AN与平面PMN所成角的正弦值．2.【答案】（1）证明：取PA的中点F，连接EF，BF，因为E是PD的中点，所以EF∥AD，EF=12AD，AB=BC=12AD，∠BAD=∠ABC=90°，∴BC∥AD，EF∥BC,EF=BC,∴四边形BCEF是平行四边形，可得CE∥BF，BF⊂平面PAB，CE⊄平面PAB，∴直线CE∥平面PAB;（2）解:如图所示，取AD中点O，连接PO，CO，由于△PAD为正三角形，则PO⊥AD，因为侧面PAD为等边三角形且垂直于底面ABCD，平面PAD∩平面ABCD=AD，所以PO⊥平面ABCD，所以PO⊥CO. 因为AO=AB=BC=12AD，且∠BAD=∠ABC= 90∘，所以四边形ABCO是矩形，所以CO⊥AD，以O为原点，OC为x轴，OD为y轴，OP为z轴建立空间直角坐标系,不妨设AB=BC=12AD=1，则OA=OD=AB=CO=1.又因为△POC为直角三角形，|OC|=√33|OP|，所以∠PCO=60∘.作MN⊥CO，垂足为N，连接BN，因为PO ⊥CO ，所以MN //PO ，且PO ⊥平面ABCD ，所以MN ⊥平面ABCD ，所以∠MBN 即为直线BM 与平面ABCD 所成的角, 设CN =t ，因为∠PCO =60∘，所以MN =√3t ，BN =√BC 2+CN 2=√t 2+1. 因为∠MBN =45∘，所以MN =BN ，即√3t =√t 2+1，解得t =√22，所以ON =1−√22，MN =√62，所以A (0,−1,0)，B (1,−1,0)，M (1−√22,0,√62)，D (0,1,0)，则AB ⃗⃗⃗⃗⃗ =(1,0,0)，AD⃗⃗⃗⃗⃗⃗ =(0,2,0)，AM ⃗⃗⃗⃗⃗⃗ =(1−√22,1,√62). 设平面MAB 和平面DAB 的法向量分别为n 1⃗⃗⃗⃗ =(x 1,y 1,z 1)，n 2⃗⃗⃗⃗ =(x 2,y 2,z 2), 则{AB ⃗⃗⃗⃗⃗ ·n 1⃗⃗⃗⃗ =0AM ⃗⃗⃗⃗⃗⃗ ·n 1⃗⃗⃗⃗ =0，即{x 1=0(1−√22)x 1+y 1+√62z 1=0， 可取z 1=−2，则n 1⃗⃗⃗⃗ =(0,√6,−2), 同理可得n 2⃗⃗⃗⃗ =(0,0,1)，所以.因为二面角M -AB -D 是锐角，所以其余弦值为√105.【解析】本题考查直线与平面平行的判定定理的应用，空间向量求二面角夹角，考查空间想象能力以及计算能力，属于中档题．（1）取PA 的中点F ，连接EF ，BF ，通过证明CE ∥BF ，利用直线与平面平行的判定定理证明即可．（2）取AD 中点O ，连接PO ，CO ，作MN ⊥CO ，垂足为N ，以O 为原点，OC 为x 轴，OD 为y 轴，OP 为z 轴建立空间直角坐标系，即可求出二面角M -AB -D 的余弦值．3.【答案】证明：（1）因为BB 1⊥面ABC ，AE ⊂面ABC ，所以AE ⊥BB 1,由AB =AC ，E 为BC 的中点得到AE ⊥BC , ∵BC ∩BB 1=B ，BC 、BB 1⊂面BB 1C 1C ， ∴AE ⊥面BB 1C 1C ，,∴AE ⊥B 1C ；解：（2）取B 1C 1的中点E 1，连A 1E 1，E 1C ，则AE ∥A 1E 1， ∴∠E 1A 1C 是异面直线AE 与A 1C 所成的角， 设AC =AB =AA 1=2，则由∠BAC =90°， 可得A 1E 1=AE =√2，A 1C =2√2，E 1C 1=EC =12BC =√2，∴E 1C =√E 1C 12+C 1C 2=√6，∵在△E 1A 1C 中，cos ∠E 1A 1C =2+8−62⋅√2⋅2√2=12， 所以异面直线AE 与A 1C 所成的角为π3；（3）连接AG ，设P 是AC 的中点，过点P 作PQ ⊥AG 于Q ，连EP ，EQ ，则EP ⊥AC ，又∵平面ABC ⊥平面ACC 1A 1,平面ABC ∩平面ACC 1A 1=AC ∴EP ⊥平面ACC 1A 1， 而PQ ⊥AG ∴EQ ⊥AG ．∴∠PQE 是二面角C -AG -E 的平面角， 由(2)假设知：EP =1，AP =1， Rt △ACG ∽Rt △AQP ，PQ =CG·AP AG=1√5，故tan ∠PQE =PEPQ =√5，所以二面角C -AG -E 的平面角正切值是√5.【解析】本题考查异面直线的夹角，线线垂直的判定，属于中档题，熟练掌握线面垂直，线线垂直与面面垂直之间的转化及异面直线夹角及二面角的定义，是解答本题的关键，属于较难题.（1）由BB 1⊥面ABC 及线面垂直的性质可得AE ⊥BB 1，由AC =AB ，E 是BC 的中点，及等腰三角形三线合一，可得AE ⊥BC ，结合线面垂直的判定定理可证得AE ⊥面BB 1C 1C ，进而由线面垂直的性质得到AE ⊥B 1C ；（2）取B 1C 1的中点E 1，连A 1E 1，E 1C ，根据异面直线夹角定义可得，∠E 1A 1C 是异面直线A 与A 1C 所成的角，设AC =AB =AA 1=2，解三角形E 1A 1C 可得答案． （3）连接AG ，设P 是AC 的中点，过点P 作PQ ⊥AG 于Q ，连EP ，EQ ，则EP ⊥AC ，由直三棱锥的侧面与底面垂直，结合面面垂直的性质定理，可得EP ⊥平面ACC 1A 1，进而由二面角的定义可得∠PQE 是二面角C -AG -E 的平面角．4.【答案】（Ⅰ）证明：因为底面ABCD 是菱形，AC ∩BD =O ，所以O 为AC ，BD 中点．-------------------------------------（1分）又因为PA =PC ，PB =PD ，所以PO ⊥AC ，PO ⊥BD ，---------------------------------------（3分）所以PO ⊥底面ABCD ．----------------------------------------（4分）（Ⅱ）解：由底面ABCD 是菱形可得AC ⊥BD ， 又由（Ⅰ）可知PO ⊥AC ，PO ⊥BD ．如图，以O 为原点建立空间直角坐标系O -xyz ．由△PAC 是边长为2的等边三角形，PB =PD =√6，可得PO =√3，OB =OD =√3．所以A(1，0，0)，C(−1，0，0)，B(0，√3，0)，P(0，0，√3)．---------------------------------------（5分）所以CP ⃗⃗⃗⃗⃗ =(1，0，√3)，AP ⃗⃗⃗⃗⃗ =(−1，0，√3)． 由已知可得OF ⃗⃗⃗⃗⃗ =OA⃗⃗⃗⃗⃗ +14AP ⃗⃗⃗⃗⃗ =(34，0，√34)-----------------------------------------（6分） 设平面BDF 的法向量为n −=（x ，y ，z ），则{√3y =034x +√34z =0令x =1，则z =−√3，所以n ⃗ =（1，0，-√3）．----------------------------------------（8分） 因为cos ＜CP ⃗⃗⃗⃗⃗ ，n ⃗ ＞=CP ⃗⃗⃗⃗⃗ ⋅n ⃗⃗|CP ⃗⃗⃗⃗⃗ ||n ⃗⃗ |=-12，----------------------------------------（9分） 所以直线CP 与平面BDF 所成角的正弦值为12，所以直线CP 与平面BDF 所成角的大小为30°．-----------------------------------------（10分）（Ⅲ）解：设BMBP =λ（0≤λ≤1），则CM ⃗⃗⃗⃗⃗⃗ =CB ⃗⃗⃗⃗⃗ +BM ⃗⃗⃗⃗⃗⃗ =CB ⃗⃗⃗⃗⃗ +λBP ⃗⃗⃗⃗⃗ =(1，√3(1−λ)，√3λ)．---------------------------------（11分）若使CM ∥平面BDF ，需且仅需CM −⋅n ⃗ =0且CM ⊄平面BDF ，---------------------（12分） 解得λ=13∈[0，1]，----------------------------------------（13分） 所以在线段PB 上存在一点M ，使得CM ∥平面BDF ． 此时BM BP =13．-----------------------------------（14分）【解析】（Ⅰ）证明PO ⊥底面ABCD ，只需证明PO ⊥AC ，PO ⊥BD ；（Ⅱ）建立空间直角坐标系，求出直线CP 的方向向量，平面BDF 的法向量，利用向量的夹角公式可求直线CP 与平面BDF 所成角的大小；（Ⅲ）设BMBP =λ（0≤λ≤1），若使CM ∥平面BDF ，需且仅需CM −⋅n ⃗ =0且CM ⊄平面BDF ，即可得出结论．本题考查线面垂直，考查线面平行，考查线面角，考查向量知识的运用，正确求出向量的坐标是关键．5.【答案】解：（I ）证明：∵CC 1⊥平面ABC ，AC ⊂平面ABC ，∠ACB =90°， ∴CC 1⊥AC ，AC ⊥BC ，又BC ∩CC 1=C ，∴AC ⊥平面BCC 1，BC 1⊂平面BCC 1， ∴AC ⊥BC 1．（II ）证明：如图，设CB 1∩C 1B =E ，连接DE ， ∵D 为AB 的中点，E 为C 1B 的中点，∴DE ∥AC 1， ∵DE ⊂平面B 1CD ，AC 1⊄平面B 1CD ， ∴AC 1∥平面B 1CD ．（III ）解：由DE ∥AC 1，∠CED 为AC 1与B 1C 所成的角，在△CDE 中，DE =12AC 1=12√AC 2+CC 12=√62， CE =12B 1C =12√BC 2+BB 12=√62，CD =12AB =12√AC 2+BC 2=1，cos ∠CED =CE 2+DE 2−CD 22×CE×DE=32+32−12×√62×√62=23，∴异面直线AC 1与B 1C 所成角的余弦值为23．【解析】本题考查线线垂直的判定、线面平行的判定、异面直线及其所成的角． （I ）先证线面垂直，再由线面垂直证明线线垂直即可； （II ）作平行线，由线线平行证明线面平行即可；（III ）先证明∠CED 为异面直线所成的角，再在三角形中利用余弦定理计算即可． 6.【答案】解：如图，在正三棱柱ABC -A 1B 1C 1中， 设AC ，A 1C 1的中点分别为O ，O 1， 则，OB ⊥OC ，OO 1⊥OC ，OO 1⊥OB ，故以{OB ⃗⃗⃗⃗⃗⃗ ，OC ⃗⃗⃗⃗⃗ ，OO 1⃗⃗⃗⃗⃗⃗⃗⃗ }为基底， 建立空间直角坐标系O -xyz ，∵AB =AA 1=2，A （0，-1，0），B （√3，0，0）， C （0，1，0），A 1（0，-1，2），B 1（√3，0，2），C 1（0，1，2）．（1）点P 为A 1B 1的中点．∴P(√32，−12，2)，∴BP ⃗⃗⃗⃗⃗ =(−√32，−12，2)，AC 1⃗⃗⃗⃗⃗⃗⃗ =(0,2,2)． |cos <BP ⃗⃗⃗⃗⃗ ,AC 1⃗⃗⃗⃗⃗⃗⃗ >|=|BP ⃗⃗⃗⃗⃗ ⋅AC 1⃗⃗⃗⃗⃗⃗⃗⃗||BP ⃗⃗⃗⃗⃗ |⋅|AC 1⃗⃗⃗⃗⃗⃗⃗⃗ |=|−1+4|√5×2√2=3√1020．∴异面直线BP 与AC 1所成角的余弦值为：3√1020； （2）∵Q 为BC 的中点．∴Q （√32，12，0）∴AQ ⃗⃗⃗⃗⃗ =(√32，32，0)，AC 1⃗⃗⃗⃗⃗⃗⃗ =(0,2,2),CC 1⃗⃗⃗⃗⃗⃗⃗ =(0,0,2)，设平面AQC 1的一个法向量为n⃗ =（x ，y ，z ）， 由{AQ ⃗⃗⃗⃗⃗ ·n ⃗ =√32x +32y =0AC 1⃗⃗⃗⃗⃗⃗⃗ ·n⃗ =2y +2z =0，可取n⃗ =（√3，-1，1）， 设直线CC 1与平面AQC 1所成角的正弦值为θ， sinθ=|cos|=|CC 1⃗⃗⃗⃗⃗⃗⃗ ⋅n ⃗ ||CC 1⃗⃗⃗⃗⃗⃗⃗ |⋅|n⃗ |=2√5×2=√55， ∴直线CC 1与平面AQC 1所成角的正弦值为√55．【解析】本题考查了向量法求空间角，属于中档题．设AC ，A 1C 1的中点分别为O ，O 1，以{OB ⃗⃗⃗⃗⃗⃗ ，OC ⃗⃗⃗⃗⃗ ，OO 1⃗⃗⃗⃗⃗⃗⃗⃗ }为基底，建立空间直角坐标系O -xyz ，（1）由|cos ＜BP ⃗⃗⃗⃗⃗ ，AC 1⃗⃗⃗⃗⃗⃗⃗ ＞|=|BP ⃗⃗⃗⃗⃗⃗ ⋅AC 1⃗⃗⃗⃗⃗⃗⃗⃗||BP ⃗⃗⃗⃗⃗⃗ |⋅|AC 1⃗⃗⃗⃗⃗⃗⃗⃗ |可得异面直线BP 与AC 1所成角的余弦值；（2）求得平面AQC 1的一个法向量为n⃗ ，设直线CC 1与平面AQC 1所成角的正弦值为θ，可得sinθ=|cos ＜CC 1⃗⃗⃗⃗⃗⃗⃗ ，n⃗ ＞|=|CC 1⃗⃗⃗⃗⃗⃗⃗ ⋅n ⃗⃗ ||CC 1⃗⃗⃗⃗⃗⃗⃗ |⋅|n ⃗⃗ |，即可得直线CC 1与平面AQC 1所成角的正弦值．7.【答案】（1）证明：如图，设AC ∩BD =O ，∵ABCD 为正方形，∴O 为BD 的中点，连接OM ，∵PD ∥平面MAC ，PD ⊂平面PBD ，平面PBD ∩平面AMC =OM ， ∴PD ∥OM ，则BOBD =BM BP，即M 为PB 的中点；（2）解：取AD 中点G ， ∵PA =PD ，∴PG ⊥AD ，∵平面PAD ⊥平面ABCD ，且平面PAD ∩平面ABCD =AD ， ∴PG ⊥平面ABCD ，则PG ⊥AD ，连接OG ，则PG ⊥OG ，由G 是AD 的中点，O 是AC 的中点，可得OG ∥DC ，则OG ⊥AD ．以G 为坐标原点，分别以GD 、GO 、GP 所在直线为x 、y 、z 轴距离空间直角坐标系， 由PA =PD =√6，AB =4，得D （2，0，0），A （-2，0，0），P （0，0，√2），C （2，4，0），B （-2，4，0），M （-1，2，√22），DP ⃗⃗⃗⃗⃗ =(−2，0，√2)，DB⃗⃗⃗⃗⃗⃗ =(−4，4，0)． 设平面PBD 的一个法向量为m ⃗⃗⃗ =(x ，y ，z)，则由{m ⃗⃗⃗ ⋅DP ⃗⃗⃗⃗⃗ =0m⃗⃗⃗ ⋅DB ⃗⃗⃗⃗⃗⃗ =0，得{−2x +√2z =0−4x +4y =0，取z =√2，得m ⃗⃗⃗ =(1，1，√2)． 取平面PAD 的一个法向量为n ⃗ =(0，1，0)．∴cos ＜m ⃗⃗⃗ ，n ⃗ ＞=m ⃗⃗⃗ ⋅n ⃗⃗ |m ⃗⃗⃗ ||n ⃗⃗ |=12×1=12． ∴二面角B -PD -A 的大小为60°；（3）解：CM ⃗⃗⃗⃗⃗⃗ =(−3，−2，√22)，平面BDP 的一个法向量为m ⃗⃗⃗ =(1，1，√2)．∴直线MC 与平面BDP 所成角的正弦值为|cos ＜CM ⃗⃗⃗⃗⃗⃗ ，m ⃗⃗⃗ ＞|=|CM ⃗⃗⃗⃗⃗⃗⋅m ⃗⃗⃗|CM ⃗⃗⃗⃗⃗⃗ ||m ⃗⃗⃗ ||=|−2√9+4+12×1|=2√69．【解析】本题考查线面角与面面角的求法，训练了利用空间向量求空间角，属中档题．（1）设AC ∩BD =O ，则O 为BD 的中点，连接OM ，利用线面平行的性质证明OM ∥PD ，再由平行线截线段成比例可得M 为PB 的中点；（2）取AD 中点G ，可得PG ⊥AD ，再由面面垂直的性质可得PG ⊥平面ABCD ，则PG ⊥AD ，连接OG ，则PG ⊥OG ，再证明OG ⊥AD ．以G 为坐标原点，分别以GD 、GO 、GP 所在直线为x 、y 、z 轴距离空间直角坐标系，求出平面PBD 与平面PAD 的一个法向量，由两法向量所成角的大小可得二面角B -PD -A 的大小；（3）求出CM⃗⃗⃗⃗⃗⃗ 的坐标，由CM ⃗⃗⃗⃗⃗⃗ 与平面PBD 的法向量所成角的余弦值的绝对值可得直线MC 与平面BDP 所成角的正弦值．8.【答案】解：（Ⅰ）证明：设BD 与AC 的交点为O ，连结EO ， ∵ABCD 是矩形， ∴O 为BD 的中点 ∵E 为PD 的中点， ∴EO ∥PB ．EO ⊂平面AEC ，PB ⊄平面AEC ∴PB ∥平面AEC ；（Ⅱ）∵AP =1，AD =√3，三棱锥P -ABD 的体积V =√34，∴V =16PA ⋅AB ⋅AD =√36AB =√34，∴AB =32，PB =√1+(32)2=√132．作AH ⊥PB 交PB 于H ， 由题意可知BC ⊥平面PAB ， ∴BC ⊥AH ，故AH ⊥平面PBC ．又在三角形PAB 中，由射影定理可得：AH =PA⋅AB PB=3√1313A 到平面PBC 的距离3√1313．【解析】本题考查直线与平面垂直，点到平面的距离的求法，考查空间想象能力以及计算能力．（Ⅰ）设BD 与AC 的交点为O ，连结EO ，通过直线与平面平行的判定定理证明PB ∥平面AEC ；（Ⅱ）通过AP =1，AD =√3，三棱锥P -ABD 的体积V =√34，求出AB ，作AH ⊥PB 角PB于H ，说明AH 就是A 到平面PBC 的距离．通过解三角形求解即可． 9.【答案】证明：（I ）∵PA ⊥底面ABCD ，AD ⊥AB ， 以A 为坐标原点，建立如图所示的空间直角坐标系，∵AD =DC =AP =2，AB =1，点E 为棱PC 的中点． ∴B （1，0，0），C （2，2，0），D （0，2，0）， P （0，0，2），E （1，1，1）∴BE⃗⃗⃗⃗⃗ =（0，1，1），DC ⃗⃗⃗⃗⃗ =（2，0，0） ∵BE ⃗⃗⃗⃗⃗ •DC ⃗⃗⃗⃗⃗ =0， ∴BE ⊥DC ；（Ⅱ）∵BD ⃗⃗⃗⃗⃗⃗ =（-1，2，0），PB ⃗⃗⃗⃗⃗ =（1，0，-2），设平面PBD 的法向量m⃗⃗⃗ =（x ，y ，z ）， 由{m ⃗⃗⃗ ⋅BD ⃗⃗⃗⃗⃗⃗ =0m⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗ =0，得{−x +2y =0x −2z =0， 令y =1，则m⃗⃗⃗ =（2，1，1）， 则直线BE 与平面PBD 所成角θ满足： sinθ=m⃗⃗⃗ ⋅BE ⃗⃗⃗⃗⃗⃗ |m ⃗⃗⃗ |⋅|BE ⃗⃗⃗⃗⃗⃗ |=2√6×√2=√33， 故直线BE 与平面PBD 所成角的正弦值为√33．（Ⅲ）∵BC⃗⃗⃗⃗⃗ =（1，2，0），CP ⃗⃗⃗⃗⃗ =（-2，-2，2），AC ⃗⃗⃗⃗⃗ =（2，2，0）， 由F 点在棱PC 上，设CF⃗⃗⃗⃗⃗ =λCP ⃗⃗⃗⃗⃗ =（-2λ，-2λ，2λ）（0≤λ≤1）， 故BF ⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ +CF⃗⃗⃗⃗⃗ =（1-2λ，2-2λ，2λ）（0≤λ≤1）， 由BF ⊥AC ，得BF ⃗⃗⃗⃗⃗ •AC ⃗⃗⃗⃗⃗ =2（1-2λ）+2（2-2λ）=0， 解得λ=34，即BF ⃗⃗⃗⃗⃗ =（-12，12，32）， 设平面FBA 的法向量为n ⃗ =（a ，b ，c ）， 由{n ⃗ ⋅AB ⃗⃗⃗⃗⃗ =0n ⃗ ⋅BF ⃗⃗⃗⃗⃗ =0，得{a =0−12a +12b +32c =0令c =1，则n⃗ =（0，-3，1）， 取平面ABP 的法向量i =（0，1，0）， 则二面角F -AB -P 的平面角α满足： cosα=|i ⋅n ⃗⃗ ||i|⋅|n ⃗⃗ |=3√10=3√1010，故二面角F -AB -P 的余弦值为：3√1010【解析】本题考查的知识点是空间二面角的平面角，建立空间直角坐标系，将二面角问题转化为向量夹角问题，是解答的关键．（I ）以A 为坐标原点，建立空间直角坐标系，求出BE ，DC 的方向向量，根据BE ⃗⃗⃗⃗⃗ •DC ⃗⃗⃗⃗⃗ =0，可得BE ⊥DC ；（II ）求出平面PBD 的一个法向量，代入向量夹角公式，可得直线BE 与平面PBD 所成角的正弦值；（Ⅲ）根据BF ⊥AC ，求出向量BF ⃗⃗⃗⃗⃗ 的坐标，进而求出平面FAB 和平面ABP 的法向量，代入向量夹角公式，可得二面角F -AB -P 的余弦值． 10.【答案】证明：（Ⅰ）取AD 的中点F ，连接EF ，CF ，∵E 为PD 的中点，∴EF ∥PA ，EF ∥平面PAB ，在四边形ABCD 中，BC ∥AD ，AD =2DC =2CB ，F 为中点，∴四边形CBAF 为平行四边形，故CF ∥AB ，CF ∥平面PAB ，∵CF ∩EF =F ，EF ∥平面PAB ，CF ∥平面PAB ， ∴平面EFC ∥平面ABP ， ∵EC ⊂平面EFC ， ∴EC ∥平面PAB ．解：（Ⅱ）连接BF ，过F 作FM ⊥PB 于M ，连接PF ， ∵PA =PD ，∴PF ⊥AD ，∵DF ∥BC ，DF =BC ，CD ⊥AD ，∴四边形BCDF 为矩形，∴BF ⊥AD ， 又AD ∥BC ，故PF ⊥BC ，BF ⊥BC ，又BF ∩PF =F ,BF 、PF ⊂平面PBF ，BC ⊄平面PBF ， ∴BC ⊥平面PBF ，∴BC ⊥PB ，设DC =CB =1，由PC =AD =2DC =2CB ，得AD =PC =2， ∴PB =√PC 2−BC 2=√4−1=√3， BF =PF =1，∴MF =√12−(√32)2=12，又BC ⊥平面PBF ，∴BC ⊥MF ，又PB ∩BC =B ,PB 、BC ⊂平面PBC ，MF ⊄平面PBC ， ∴MF ⊥平面PBC ，即点F 到平面PBC 的距离为12，∵MF =12，D 到平面PBC 的距离应该和MF 平行且相等，均为12， E 为PD 中点，E 到平面PBC 的垂足也为所在线段的中点，即中位线， ∴E 到平面PBC 的距离为14，在△PCD 中,PC =2,CD =1,PD =√2，,故由余弦定理得CE =√2， 设直线CE 与平面PBC 所成角为θ，则sinθ=14CE=√28．【解析】本题考查线面平行的证明，考查线面角的正弦值的求法，考查空间中线线、能力，考查数形结合思想、化归与转化思想，属于中档题．（Ⅰ）取AD的中点F，连结EF，CF，推导出EF∥PA，CF∥AB，从而平面EFC∥平面ABP，由此能证明EC∥平面PAB．（Ⅱ）连结BF，过F作FM⊥PB于M，连结PF，推导出四边形BCDF为矩形，从而BF⊥AD，进而AD⊥平面PBF，由AD∥BC，得BC⊥PB，再求出BC⊥MF，由此能求出sinθ．11.【答案】证明：（Ⅰ）∵EA=EB，M是AB的中点，∴EM⊥AB，∵平面ABE⊥平面ABCD，平面ABE∩平面ABCD=AB，EM⊂平面ABE，∴EM⊥平面ABCD，∵AD⊂平面ABCD，∴EM⊥AD；（Ⅱ）取DE的中点F，连接AF，NF，∵N是CE的中点，∴NF=//12CD，∵M是AB的中点，∴AM=//12CD，∴NF=//AM，∴四边形AMNF是平行四边形，∴MN∥AF，∵MN⊄平面ADE，AF⊂平面ADE，∴MN∥平面ADE；解：（III）设点A到平面BCE的距离为d，由（I）知ME⊥平面ABC，BC=BE=2，MC=ME=√3，则CE=√6，BN=√BE2−EN2=√102，∴S△BCE=12CE⋅BN=√152，S△ABC=12BA×BC×sin60°=√3，∵V A-BCE=V E-ABC，即13S△BCE×d=13S△ABC×ME，解得d=2√155，故点A到平面BCE的距离为2√155．【解析】本题考查线线垂直、线面平行的证明，考查点到平面的距离的求法，涉及到力、数据处理能力，考查数形结合思想，是中档题．（Ⅰ）推导出EM ⊥AB ，从而EM ⊥平面ABCD ，由此能证明EM ⊥AD ；（Ⅱ）取DE 的中点F ，连接AF ，NF ，推导出四边形AMNF 是平行四边形，从而MN ∥AF ，由此能证明MN ∥平面ADE ；（III ）设点A 到平面BCE 的距离为d ，由V A -BCE =V E -ABC ，能求出点A 到平面BCE 的距离．12.【答案】（I ）证明：∵AB ∥CD ，AD ⊥DC ，AB =AD =1，CD =2，∴BD =BC =√2， ∴BD 2+BC 2=CD 2， ∴BD ⊥BC ，∵EA ⊥平面ABCD ，BD ⊂平面ABCD ， ∴EA ⊥BD ，∵EA ∥FC ， ∴FC ⊥BD ，又BC ⊂平面BCF ，FC ⊂平面BCF ，BC ∩CF =C ， ∴BD ⊥平面FBC ， 又BD ⊂平面BDE ，∴平面BDE ⊥平面BCF ．（II ）解：过A 作AM ⊥DE ，垂足为M ， ∵EA ⊥平面ABCD ，CD ⊂平面ABCD ， ∴EA ⊥CD ，又CD ⊥AD ，EA ∩AD =A ， ∴CD ⊥平面EAD ，又AM ⊂平面EAD ， ∴AM ⊥CD ，又AM ⊥DE ，DE ∩CD =D ， ∴AM ⊥平面CDE ，∵AD =AE =1，EA ⊥AD ，∴AM =√22，即A 到平面CDE 的距离为√22，∵AB ∥CD ，CD ⊂平面CDE ，AB ⊄平面CDE ， ∴AB ∥平面CDE ，∴B 到平面CDE 的距离为√22．【解析】（I ）先计算BD ，BC ，利用勾股定理的逆定理证明BD ⊥BC ，再利用EA ⊥平面ABCD 得出AE ⊥BD ，从而有CF ⊥BD ，故而推出BD ⊥平面FBC ，于是平面EBD ⊥平面BCF ；（II ）证明AB ∥平面CDE ，于是B 到平面CDE 的距离等于A 到平面CDE 的距离，过A 作AM ⊥DE ，证明AM ⊥平面CDE ，于是AM 的长即为B 到平面CDE 的距离． 本题考查了线面垂直、面面垂直的判定与性质，空间距离的计算，属于中档题． 13.【答案】证明：方法一：（1）取PA 中点G ，连结DG 、FG ． ∵F 是PB 的中点， ∴GF ∥AB 且GF =12AB ，又底面ABCD 为矩形，E 是DC 中点， ∴DE ∥AB 且DE =12AB∴GF ∥DE 且GF =DE ，∴EF ∥DG∵DG ⊂平面PAD ，EF ⊄平面PAD ， ∴EF ∥平面PAD ．（2）∵PD ⊥底面ABCD ，AB ⊂面ABCD ∴PD ⊥AB又底面ABCD 为矩形 ∴AD ⊥AB 又PD ∩AD =D ∴AB ⊥平面PAD ∵DG ⊂平面PAD ∴AB ⊥DG∵AD =PD ，G 为AP 中点 ∴DG ⊥AP又AB ∩AP =A ， ∴DG ⊥平面PAB又由（1）知EF ∥DG ∴EF ⊥平面PAB ，又EF ⊂面AEF ∴平面AEF ⊥平面PAB ．证法二：（1）以D 为坐标原点，DA 、DC 、DP 所在直线分别为x 轴、y 轴、z 轴，建立如图所示空间直角坐标系．设AB =a ． ∵AD =PD =2，∴A （2，0，0），B （2，a ，0），C （0，a ，0），P （0，0，2）， ∵E 、F 分别为CD ，PB 的中点 ∴E （0，a2，0），F （1，a2，0）．∴EF ⃗⃗⃗⃗⃗ =(1，0，1)， ∵DP ⃗⃗⃗⃗⃗ +DA ⃗⃗⃗⃗⃗ =（0，0，2）+（2，0，0）=（2，0，2）， ∴EF ⃗⃗⃗⃗⃗ =12（DP ⃗⃗⃗⃗⃗ +DA ⃗⃗⃗⃗⃗ ）=12DP ⃗⃗⃗⃗⃗ +12DA ⃗⃗⃗⃗⃗ ， 故EF ⃗⃗⃗⃗⃗ 、DP ⃗⃗⃗⃗⃗ 、DA ⃗⃗⃗⃗⃗ 共面， 又EF ⊄平面PAD ∴EF ∥平面PAD ．（2）由（1）知EF ⃗⃗⃗⃗⃗ =(1，0，1)，AB ⃗⃗⃗⃗⃗ =(0，a ，0)，AP⃗⃗⃗⃗⃗ =(−2，0，2)． ∴EF ⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ =0，EF ⃗⃗⃗⃗⃗ •AP ⃗⃗⃗⃗⃗ =-2+0+2=0， ∴EF ⃗⃗⃗⃗⃗ ⊥AB ⃗⃗⃗⃗⃗ ，EF ⃗⃗⃗⃗⃗ ⊥AP ⃗⃗⃗⃗⃗ ， 又AB ∩AP =A ，∴EF ⊥平面PAB ， 又EF ⊂平面AEF ，∴平面AEF ⊥平面PAB ， （3）AB =2√2由（1）知，∴AE ⃗⃗⃗⃗⃗ =（-2，√2，0），EF⃗⃗⃗⃗⃗ =（1，0，1）设平面AEF 的法向量n ⃗ =(x ，y ，z)，则{n⃗ ⋅AE ⃗⃗⃗⃗⃗ =0n ⃗ ⋅EF ⃗⃗⃗⃗⃗ =0即−2x +√2y =0令x =1，则y =√2，z =-1， ∴n⃗ =（1，√2，-1）， 又AC⃗⃗⃗⃗⃗ =（-2，2√2，0）， ∴cos ＜AC⃗⃗⃗⃗⃗ ，n ⃗ ＞=−2+4+02√12=√36， ∴sinθ=|cos ＜AC⃗⃗⃗⃗⃗ ，n ⃗ ＞|=√36．【解析】方法一；（1）取PA 中点G ，连结DG 、FG ，要证明EF ∥平面PAD ，我们可以证明EF 与平面PAD 中的直线AD 平行，根据E 、F 分别是PB 、PC 的中点，利用中位线定理结合线面平行的判定定理，即可得到答案． （2）根据线面垂直的和面面垂直的判断定理即可证明．方法二：（1）求出直线EF 所在的向量，得到EF ⃗⃗⃗⃗⃗ =12（DP ⃗⃗⃗⃗⃗ +DA ⃗⃗⃗⃗⃗ ）=12DP ⃗⃗⃗⃗⃗ +12DA ⃗⃗⃗⃗⃗ ，即可证明EF ∥平面PAD ．（2）再求出平面内两条相交直线所在的向量，然后利用向量的数量积为0，根据线面垂直的判定定理得到线面垂直，即可证明平面AEF ⊥平面PAB（3）求出平面的法向量以及直线所在的向量，再利用向量的有关运算求出两个向量的夹角，进而转化为线面角，即可解决问题．本题考查了本题考查的知识点是直线与平面平行的判定，面面垂直，直线与平面所成的角，解决此类问题的关键是熟练掌握几何体的结构特征，进而得到空间中点、线、面的位置关系，利于建立空间之间坐标系，利用向量的有关知识解决空间角与空间距离以及线面的位置关系等问题，属于中档题．14.【答案】解：（1）证明：∵PO ⊥平面ABCD ，且AD ⊂平面ABCD ， ∴PO ⊥AD ， ∵∠ADC =45°且AD =AC =2， ∴∠ACD =45°， ∴∠DAC =90°， ∴AD ⊥AC ，∵AC ⊂平面PAC ，PO ⊂平面PAC ，且AC ∩PO =O ， ∴由直线和平面垂直的判定定理知AD ⊥平面PAC ． （2）解：取DO 中点N ，连接MN ，AN ， 由PO ⊥平面ABCD ，得MN ⊥平面ABCD ， ∴∠MAN 是直线AM 与平面ABCD 所成的角， ∵M 为PD 的中点， ∴MN ∥PO ，且MN =12PO =3， AN =12DO =√52，在Rt △ANM 中，tan ∠MAN =MNAN =3√52=6√55， 即直线AM 与平面ABCD 所成角的正切值为6√55．【解析】（1）由PO ⊥平面ABCD ，得PO ⊥AD ，由∠ADC =45°，AD =AC ，得AD ⊥AC ，从而证明AD ⊥平面PAC ．（2）取DO 中点N ，连接MN ，AN ，由M 为PD 的中点，知MN ∥PO ，由PO ⊥平面出直线AM 与平面ABCD 所成角的正切值．本题考查直线与平面垂直的证明，考查直线与平面所成角的正切值的求法．解题时要认真审题，仔细解答，注意合理地化空间问题为平面问题． 15.【答案】证明：（I ）在三棱柱ABC -A 1B 1C 1中，连接A 1B ，交AB 1于O 点，连接OD∵在△A 1BC 1中，A 1D =DC 1，A 1O =OB ， ∴OD ∥BC 1，又∵OD ⊂平面AB 1D ，BC 1⊄平面AB 1D ； ∴BC 1∥平面AB 1D ；（II ）在三棱柱ABC -A 1B 1C 1中，A 1A ⊥平面A 1B 1C 1； ∵B 1D ⊂平面A 1B 1C 1； ∴A 1A ⊥B 1D在△A 1B 1C 1中，D 为A 1C 1的中点 ∴B 1D ⊥A 1C 1又∵A 1A ∩A 1C 1=A 1，A 1A ，A 1C 1⊂平面AA 1C 1C ， ∴B 1D ⊥平面AA 1C 1C ， 又∵A 1C ⊂平面AA 1C 1C ， ∴B 1D ⊥A 1C又∵A 1D AA 1=AA1AC =√22∴∠DA 1A =∠A 1AC =90°∴△DA 1A ∽△A 1AC ，∠ADA 1=∠CA 1A∵∠DA 1C +∠CA 1A =90° ∴∠DA 1C +∠ADA 1=90°∴A 1C ⊥AD又∵B 1D ∩AD =D ，B 1D ，AD ⊂平面AB 1D ； ∴A 1C ⊥平面AB 1D ；解：（III ）由（I ）得，OD ∥BC 1， 故AD 与BC 1所成的角即为∠ADO在△ADO 中，AD =√3，OD =12BC 1=√62，AO =12A 1B =√62，∵AD 2=OD 2+AO 2，OD =AO∴△ADO 为等腰直角三角形故∠ADO =45°即异面直线AD 与BC 1所成角等于45°【解析】（I ）连接A 1B ，交AB 1于O 点，连接OD ，由平行四边形性质及三角形中位线定理可得OD ∥BC 1，进而由线面平行的判定定理得到BC 1∥平面AB 1D ；（II ）由直棱柱的几何特征可得A 1A ⊥B 1D ，由等边三角形三线合一可得B 1D ⊥A 1C 1，进而由线面垂直的判定定理得到B 1D ⊥平面AA 1C 1C ，再由三角形相似得到A 1C ⊥AD 后，可证得A 1C ⊥平面AB 1D ．（III ）由（I ）中OD ∥BC 1，可得异面直线AD 与BC 1所成角即∠ADO ，解△ADO 可得答案．本题考查的知识点是直线与平面垂直的判定，异面直线及其所成的角，直线与平面平行的判定，（I ）的关键是证得OD ∥BC 1，（II ）的关键是熟练掌握线面垂直与线线垂直之间的转化，（III ）的关键是得到异面直线AD 与BC 1所成角即∠ADO ．16.【答案】（Ⅰ）证明：由P -ABD ，Q -BCD 是相同正三棱锥，且∠APB =90°，分别过P 、Q 作PE ⊥平面ABD ，QF ⊥平面BCD ，垂足分别为E 、F ，则E 、F 分别为底面正三角形ABD 与BCD 的中心． 连接EF 交BD 于G ，则G 为BD 的中点，连接PG 、QG ，则PG ⊥BD ，QG ⊥BD ，又PG ∩QG =G ，∴BD ⊥平面PQG ，则BD ⊥PQ ， 再由正三棱锥的性质可得PA ⊥BD ， 又PQ ∩PA =P ，∴BD ⊥平面APQ ；（Ⅱ）∵正三棱锥的底面边长为1，且∠APB =90°，∴PQ =EF =2EG =2×13AG =2×13×√32=√33， PE =√(√22)2−(√33)2=√66，则V B−PQD =13×12×√33×√66×1=√236．△PDQ 底边PQ 上的高为√(√22)2−(√36)2=√156，∴S △PDQ =12×√33×√156=√512．设B 到平面PQD 的距离为h ，则13×√512ℎ=√236，得h =√105．∴直线PB 与平面PDQ 所成角的正弦值为√105√22=2√55．【解析】（Ⅰ）由题意分别过P 、Q 作PE ⊥平面ABD ，QF ⊥平面BCD ，可得E 、F 分别为底面正三角形ABD 与BCD 的中心．连接EF 交BD 于G ，可得PG ⊥BD ，QG ⊥BD ，由线面垂直的判定及性质可得BD ⊥PQ ，再由正三棱锥的性质可得PA ⊥BD ，则BD ⊥平面APQ ；（Ⅱ）由已知求得PQ ，PE 的长，求得四面体B -PQD 的体积，利用等积法求出B 到平面PQD 的距离，则直线PB 与平面PDQ 所成角的正弦值可求．本题考查直线与平面所成的角，考查线面垂直的判定，考查空间想象能力和思维能力，训练了利用等积法求多面体的体积，是中档题． 17.【答案】（1）证明：如图：∵AB =BC ，E 为AC 的中点，∴BE ⊥AC ，∵平面A 1ACC 1⊥平面ABC ，平面A 1ACC 1∩平面ABC =AC ， ∴BE ⊥平面A 1ACC 1，∵A 1C ⊂平面A 1ACC 1，∴BE ⊥A 1C ．（2）解：∵面A1ACC1⊥面ABC，∴C1在面ABC上的射影H在AC上，∴∠C1CA为直线C1C与面ABC所成的角．过H作HM⊥BC于M，连C1M，在Rt△C1CM中，CM=CC1cos∠C1CM=2cos60°=1．在Rt△CMH中，CH=CMcos∠ACB =2√33．∴在Rt△C1CH中，cos∠C1CH=CHCC1=23√32=√33．∴直线C1C与面ABC所成的角的余弦值为√33.【解析】（1）证明BE⊥平面A1ACC1，可得BE⊥A1C，即可证明：A1C⊥平面C1EB；（2）判断∠C1CA为直线C1C与面ABC所成的角．过H作HM⊥BC于M，连C1M，即可求直线CC1与平面ABC所成角的余弦值．本题考查线面垂直的判定与性质，考查线面角，考查学生分析解决问题的能力，属于中档题．18.【答案】证明：（1）连接CD，据题知AD=4，BD=2，∵AC2+BC2=AB2，∴∠ACB=90°，∴cos∠ABC=2√36=√33，∴CD2=4+12−2×2×2√3cos∠ABC=8，∴CD=2√2，∴CD2+AD2=AC2，∴CD⊥AB，又∵平面PAB⊥平面ABC，平面PAB∩平面ABC=AB，CD⊂平面ABC,∴CD⊥平面PAB，∵PD⊂平面PAB，∴CD⊥PD，∵PD⊥AC，CD∩AC=C，CD、AC⊂平面ABC,∴PD⊥平面ABC．解：（2）∵∠PAB=π4，∴PD=AD=4，∴PA=4√2，在Rt△PCD中，PC=√PD2+CD2=2√6，∴△PAC是等腰三角形，∴S△PAC=8√2，设点B到平面PAC的距离为d，由V B-PAC=V P-ABC，得13S△PAC×d=13S△ABC×PD，∴d==3，故点B到平面PAC的距离为3．【解析】本题考查线面垂直的证明，考查点到平面的距离的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题．（1）连接CD，推导出CD⊥AB，CD⊥PD，由此能证明PD⊥平面ABC．（2）设点B到平面PAC的距离为d，由V B-PAC=V P-ABC，能求出点B到平面PAC的距离．19.【答案】解：（1）证明：∵ABC-A1B1C1中，A1A⊥平面ABC，又BB 1⊂平面BB 1C 1C ， ∴平面BB 1C 1C ⊥平面ABC ，∵△ABC 为正三角形，D 为BC 的中点， ∴AD ⊥BC ，又平面BB 1C 1C ∩平面ABC =BC ， ∴AD ⊥平面BB 1C 1C ， 又AD ⊂平面ADB 1，∴平面ADB 1⊥平面BB 1C 1C ；（2）由（1）可得△ADB 1为直角三角形， 又AD =√32，B 1D =√52，∴S △ADB 1=12×AD ×B 1D =√158，又S △ADB =12S △ABC =√38，设点B 到平面ADB 1的距离为d ， 则V B−ADB 1=V B 1−ADB ， ∴13S △ADB 1⋅d =13S △ADB ⋅BB 1， ∴点B 到平面ADB 1的距离d =S △ADB ⋅BB 1S △ADB 1=√3√15=√55．【解析】本题考查面面垂直的证明，考查点到平面的距离的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，考查数形结合思想，是中档题.（1）推导出BB 1⊥平面ABC ，从而平面BB 1C 1C ⊥平面ABC ，推导出AD ⊥BC ，从而AD ⊥平面BB 1C 1C ，由此能证明平面ADB 1⊥平面BB 1C 1C ；（2）设点B 到平面ADB 1的距离为d ，由V B−ADB 1=V B 1−ADB ，能求出点B 到平面ADB 1的距离.20.【答案】证明：（1）∵PA ⊥平面ABC ，BE ⊂平面ABC ， ∴PA ⊥BE ．∵AB =BC ，E 为AC 的中点， ∴BE ⊥AC ，又PA ⊂平面PAC ，AC ⊂平面PAC ，PA ∩AC =A ， ∴BE ⊥平面PAC ，又BE ⊂平面BED ， ∴平面BED ⊥平面PAC ．（2）∵D ，E 是PC ，AC 的中点， ∴DE ∥PA ，又PA ⊥平面ABC ，∴DE ⊥平面ABC ，∵EF ⊂平面ABC ，BE ⊂平面ABC ， ∴DE ⊥EF ，DE ⊥BE ．∴∠FEB 为二面角F -DE -B 的平面角．∵E ，F 分别是AC ，AB 的中点，AB =AC ， ∴EF =12BC =12AB =BF ，EF ∥BC ．又AB ⊥BC ，∴BF ⊥EF ，∴△BEF 为等腰直角三角形，∴∠FEB =45°． ∴二面角F -DE -B 为45°．∴PA⊥BC，又BC⊥AB，PA⊂平面PAB，AB⊂平面PAB，PA∩AB=A，∴BC⊥平面PAB．∴∠CPB为直线PC与平面PAB所成的角．∵PA=6，∴DE=12PA=3，又DF=5，∴EF=√DF2−DE2=4．∴AB=BC=8．∴PB=√PA2+AB2=10．∴tan∠CPB=BCPB =4 5．【解析】（1）通过证明BE⊥平面PAC得出平面BED⊥平面PAC；（2）由DE∥PA得出DE⊥平面ABC，故DE⊥EF，DE⊥BE，于是∠FEB为所求二面角的平面角，根据△BEF为等腰直角三角形得出二面角的度数；（3）证明BC⊥平面PAB得出∠CPB为所求角，利用勾股定理得出BC，PB，即可得出tan∠CPB．本题考查了线面垂直，面面垂直的判定，空间角的计算，做出空间角是解题关键，属于中档题．21.【答案】解：（1）证明：设AC∩BD=H，连接EH，在△ADC中，因为AD=CD，且DB平分∠ADC，所以H为AC的中点，又有题设，E为PC的中点，故EH∥PA，又HE⊂平面BDE，PA⊄平面BDE，所以PA∥平面BDE（2）证明：因为PD⊥平面ABCD，AC⊂平面ABCD，所以PD⊥AC由（1）知，BD⊥AC，PD∩BD=D，故AC⊥平面PBD（3）由AC⊥平面PBD可知，BH为BC在平面PBD内的射影，所以∠CBH为直线与平面PBD所成的角．由AD⊥CD，AD=CD=1，DB=2√2，可得DH=CH=√22，BH=3√22在Rt△BHC中，tan∠CBH=CHBH =13，所以直线BC与平面PBD所成的角的正切值为13．【解析】（1）欲证PA∥平面BDE，根据直线与平面平行的判定定理可知只需证PA与平面BDE内一直线平行，设AC∩BD=H，连接EH，根据中位线定理可知EH∥PA，而又HE⊂平面BDE，PA⊄平面BDE，满足定理所需条件；（2）欲证AC⊥平面PBD，根据直线与平面垂直的判定定理可知只需证AC与平面PBD内两相交直线垂直，而PD⊥AC，BD⊥AC，PD∩BD=D，满足定理所需条件；（3）由AC⊥平面PBD可知，BH为BC在平面PBD内的射影，则∠CBH为直线与平面PBD所成的角，在Rt△BHC中，求出此角即可．本小题主要考查直线与平面平行．直线和平面垂直．直线和平面所成的角等基础知识，考查空间想象能力、运算能力和推理能力．。
第8章立体几何专题4 垂直的证明-人教A版(2019)高中数学必修(第二册)常考题型专题练习
垂直的证明【方法总结】1、证明线面垂直的方法：①利用线面垂直定义：如果一条直线垂直于平面内任一条直线，则这条直线垂直于该平面；②用线面垂直判定定理：如果一条直线与平面内的两条相交直线都垂直，则这条直线与平面垂直；③用线面垂直性质：两条平行线中的一条垂直于一个平面，则另一条也必垂直于这个平面．2、证明线线（或线面）垂直有时需多次运用线面垂直的定义和线面垂直的判定定理，实现线线垂直与线面垂直的相互转化．3、证明面面垂直一般要先找到两个面的交线，然后再在两个面内找能与交线垂直的直线，最后通过证明线面垂直证明面面垂直。
【分类练习】考向一线面垂直例1、在四棱锥P ABCD -中，PA ⊥底面ABCD ，//AB CD ，AB BC ⊥，1AB BC ==，2DC =，点E 在PB 上求证：CA ⊥平面PAD ；【答案】(1)证明见解析；(2)2.【解析】(1)过A 作AF ⊥DC 于F ,则CF =DF =AF ,所以∠DAC =90°,即AC ⊥DA ，又PA ⊥底面ABCD ，AC ⊂面ABCD ，所以AC ⊥PA ，因为PA 、AD ⊂面PAD ，且PA ∩AD =A ，所以AC ⊥平面PAD .例2、如图，长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形，点E 在棱AA 1上，BE ⊥EC 1.（1）证明：BE ⊥平面EB 1C 1；解析：（1）由已知得，11B C ⊥平面11ABB A ，BE ⊂平面11ABB A ，故11B C ⊥BE ．又1BE EC ⊥，所以BE ⊥平面11EB C ．例3、如图，在三棱柱111ABC A B C -中，1CC ⊥平面ABC ，D ，E ，F ，G 分别为1AA ，AC ，11A C ，1BB 的中点求证：AC ⊥平面BEF ；【解析】(1)在三棱柱111ABC A B C -中，∵1CC ⊥平面ABC ，∴四边形11A ACC 为矩形．又E ，F 分别为AC ，11A C 的中点，∴AC ⊥EF ．∵AB BC =．∴AC ⊥BE ，∴AC ⊥平面BEF ．例4、如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，CD ⊥AD ，BC ∥AD ，12BC CD AD ==.（Ⅰ）求证：BD ⊥平面PAB ；【解析】因为PA ⊥平面ABCD ，BD ⊂平面ABCD ，所以BD ⊥PA .所以222AD AB BD =+，所以BD AB ⊥.因为PA AB A = ，所以BD ⊥平面PAB .【巩固练习】1、如图，在三棱柱ABC－A 1B 1C 1中，AB＝AC，A 1在底面ABC 的射影为BC 的中点，D 是B 1C 1的中点．证明：A 1D⊥平面A 1BC；【答案】见解析【解析】证明：设E 为BC 的中点，连接A 1E，AE.由题意得A 1E⊥平面ABC，所以A 1E⊥AE.因为AB＝AC，所以AE⊥BC.故AE⊥平面A 1BC.连接DE，由D，E 分别为B 1C 1，BC 的中点，得DE∥B 1B 且DE＝B 1B，从而DE∥A 1A 且DE ＝A 1A，所以AA 1DE 为平行四边形．于是A 1D∥AE.因为AE⊥平面A 1BC，所以A 1D⊥平面A 1BC.2．（2019·上海格致中学高三月考）如图，在四棱锥P ABCD -中，底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，PD DC =，E 是PC 的中点，作EF PB ⊥交PB 于点F .（1）证明：PA ∥平面EDB ；（2）证明：PB ⊥平面EFD .【答案】（1）详见解析；（2）详见解析.【解析】（1）设AC 与BD 相交于O ，连接OE ，由于O 是AC 中点，E 是PC 中点，所所以PA ∥平面EDB .（2）由于PD ⊥底面ABCD ，所以PD BC ⊥，由于,BC CD PD CD D ⊥⋂=，所以BC ⊥平面PCD ，所以BC DE ⊥.由于DP DC =且E 是PC 中点，所以DE PC ⊥，而PC BC C ⋂=，所以DE ⊥平面PBC ，所以DE PB ⊥.依题意EF PB ⊥，DE EF E = ，所以PB ⊥平面EFD .3．（2019·江苏高三月考）如图，在四棱锥P ABCD -中，四边形ABCD 是平行四边形，AC ，BD 相交于点O ，OP OC =，E 为PC 的中点，PA PD ⊥.（1）求证：//PA 平面BDE ；（2）求证：PA ⊥平面PCD【答案】（1）详见解析（2）详见解析【解析】（1）连结OE .因为四边形ABCD 是平行四边形，AC ，BD 相交于点O ，所以O 为AC 的中点.因为E 为PC 的中点，所以//OE PA .因为OE ⊂平面BDE ，PA ⊄平面BDE ，所以//PA 平面BDE .（2）因为OP OC =，E 为PC 的中点，所以OE PC ⊥.由（1）知，//OE PA ，所以PA PC ⊥.因为PA PD ⊥，PC ，PD ⊂平面PCD ，PC PD P ⋂=，所以PA ⊥平面PCD .考向二面面垂直例1、如图，在四棱锥P ABCD -中，已知底面ABCD 为矩形，且AB =，1BC =，E ，F 分别是AB ，PC 的中点，PA DE ⊥.(1)求证：//EF 平面PAD ；(2)求证：平面PAC ⊥平面PDE ．【答案】（1）详见解析（2）详见解析【解析】证明：(1)取PD 中点G ，连AG ，FG ，F ，G 分别是PC ，PD 的中点又E 为AB 中点//AE FG ∴，AE FG=四边形AEFG 为平行四边形//EF AG ∴，又EF ⊄平面PAD ，AG ⊂平面PAD//EF ∴平面PAD(2)设AC DE H= 由AEH CDH ∆∆ 及E 为AB 中点又BAD ∠为公共角GAE BAC∴∆∆ 90AHE ABC ∴∠=∠=︒即DE AC ⊥又DE PA ⊥，PA AC A= DE ⊥平面PAC ，又DE ⊂平面PDE∴平面PAC ⊥平面PDE例2、如图，边长为2的正方形ABCD 所在的平面与半圆弧 CD所在平面垂直，M 是 CD 上异于C ，D 的点．(1)证明：平面AMD ⊥平面BMC ；【解析】(1)由题设知，平面CMD ⊥平面ABCD ，交线为CD ．因为BC ⊥CD ，BC ⊂平面ABCD ，所以BC ⊥平面CMD ，故BC ⊥DM ．因为M 为 CD上异于C ，D 的点，且DC 为直径，所以DM ⊥CM ．又BC CM =C ，所以DM ⊥平面BMC ．而DM ⊂平面AMD ，故平面AMD ⊥平面BMC ．例3、如图，在梯形ABCD 中，AB ∥CD ，AD=DC=CB=a ，∠ABC=3π，平面ACFE ⊥平面ABCD ，四边形ACFE 是矩形，AE=AD ，点M 在线段EF 上。
高中数学立体几何平行、垂直位置关系证明题专项练习(带答案)
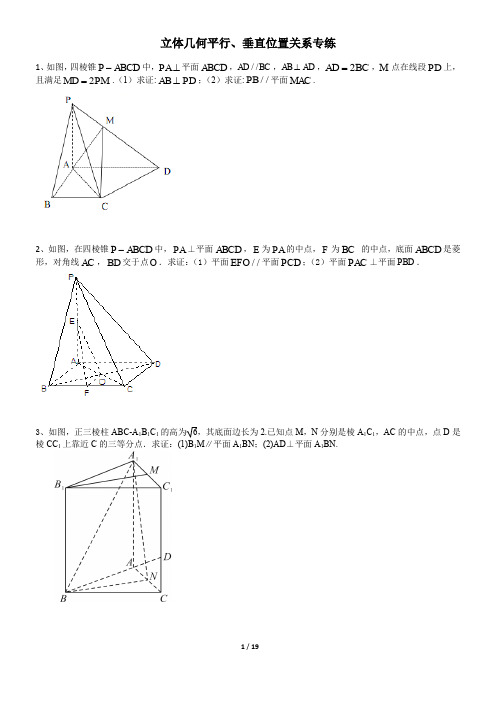
立体几何平行、垂直位置关系专练1、如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，//AD BC ，AB AD ⊥，2AD BC =，M 点在线段PD 上，且满足2MD PM =.（1）求证:AB PD ⊥；（2）求证://PB 平面MAC .2、如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，E 为PA 的中点，F 为BC 的中点，底面ABCD 是菱形，对角线AC ，BD 交于点O ．求证：（1）平面//EFO 平面PCD ；（2）平面PAC ⊥平面PBD ．3、如图，正三棱柱ABC-A 1B 1C 1的高为6，其底面边长为2.已知点M ，N 分别是棱A 1C 1，AC 的中点，点D 是棱CC 1上靠近C 的三等分点．求证：(1)B 1M ∥平面A 1BN ；(2)AD ⊥平面A 1BN.4、如图，等边三角形ABC与直角梯形ABDE所在平面垂直，BD∥AE，BD＝2AE，AE⊥AB，M为AB的中点．(1)证明：CM⊥DE；(2)在边AC上找一点N，使CD∥平面BEN.5、如图，矩形ABCD所在平面与三角形ABE所在平面互相垂直，AE＝AB，M，N，H分别为DE，AB，BE 的中点．求证：(1)MN∥平面BEC；(2)AH⊥CE.6、如图，在三棱台ABCDEF中，CF⊥平面DEF，AB⊥BC.(1)设平面ACE∩平面DEF＝a，求证：DF∥a；(2)若EF＝CF＝2BC，试问在线段BE上是否存在点G，使得平面DFG⊥平面CDE？若存在请确定点G的位置；若不存在，请说明理由．7、在三棱锥S ABC -中，平面SAB ⊥平面SBC ，AB BC ⊥，AS AB =，过A 作AF SB ⊥，垂足为F ，点E ，G 分别是棱SA ，SC 的中点．（1）求证：平面EFG ∥平面ABC ．（2）求证：BC SA ⊥．8、如图，在直三棱柱111ABC A B C -中，AB BC ⊥，点D 为棱1C C 的中点，1AC 与1A D 交于点E ，1BC 与1B D 交于点F ，连结EF .求证：（1）//AB EF ；（2）平面11A B D ⊥平面11B BCC .9、【2019年高考江苏卷】如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A 1B 1∥平面DEC 1；（2）BE ⊥C 1E ．点，平面PAB ⊥底面ABCD ，90PAB ∠= ．求证：（1）//PB 平面AEC ；（2）平面PAC ⊥平面ABCD ．11、2.（2020·江苏省镇江高三二模）如图，三棱锥P ABC -中，点D ，E 分别为AB ，BC 的中点，且平面PDE ⊥平面ABC ．()1求证：//AC 平面PDE ；()2若2PD AC ==，PE =PBC ⊥平面ABC .12、（2020·江苏省建湖高级中学高三月考）如图，在四面体ABCD 中，,90AD BD ABC =∠= ，点,E F 分别为棱,AB AC 上的点，点G 为棱AD 的中点，且平面//EFG 平面BCD ．（1）求证：12EF BC =；（2）求证：平面EFD ⊥平面ABC ．点，PA ⊥平面ABCD .（1）求证：//PB 平面AEC ；（2）若四边形ABCD 是矩形且PA AD =，求证：AE ⊥平面PCD .14、（2020·江苏省高三二模）如图，在三棱柱111ABC A B C -中，侧面11ABB A ⊥底面ABC ，AB AC ⊥，E ，F 分别是棱AB ，BC 的中点.求证：（1）11AC ∥平面1B EF ；（2）1AC B E ⊥.15、（2020·江苏省连云港高三）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，平面PAD ⊥平面ABCD ，PA PD ⊥，PA PD =，E 、F 分别为AD 、PB 的中点.（Ⅰ）求证：PE BC ⊥；（Ⅱ）求证：平面PAB ⊥平面PCD ；（Ⅲ）求证：//EF 平面PCD .16、（2020·江苏省苏州高三）如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A1B 1∥平面DEC 1；（2）BE ⊥C 1E ．17、（2020·江苏省通州高三）如图，在三棱柱111ABC A B C -中，侧棱垂直于底面1,2,1,,AB BC AA AC BC E F ⊥===分别是11,AC BC 的中点．（1）求证: 平面ABE ⊥平面11B BCC ；（2）求证:1C F ∥平面ABE ；18、（2020·江苏省高三三模）如图，三棱柱111ABC A B C -中，1BC B C =，O 为四边形11ACC A 对角线交点，F 为棱1BB 的中点，且AF ⊥平面11BCC B .（1）证明：//OF 平面ABC ；（2）证明：四边形11ACC A 为矩形.参考答案1．如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，//AD BC ，AB AD ⊥，2AD BC =，M 点在线段PD 上，且满足2MD PM =.（1）求证:AB PD ⊥；（2）求证://PB 平面MAC .【解析】（1）∵四棱锥P ABCD -中，PA ⊥平面ABCD ，AB 平面ABCD ， ∴AB PA ⊥，又AB AD ⊥，,PA AD ⊂平面PAD ，PA AD A ⋂=， ∴AB ⊥面PAD .PD ⊂面PAD ，∴AB PD ⊥. （2）连结BD AC O ⋂=，连结MO ， ∵//AD BC ，2AD BC =，2DO BO ∴=,∵在PBD ∆中，2DM MP =，2DO BO =∴//PB MO ， 又PB ⊄面MAC ，MO ⊂面MAC ，∴//PB 面MAC .2．如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，E 为PA 的中点，F 为BC 的中点，底面ABCD 是菱形，对角线AC ，BD 交于点O ．求证：（1）平面//EFO 平面PCD ；（2）平面PAC ⊥平面PBD ． 【详解】（1）因为在ΔPAC 中，E 为PA 的中点，O 为AC 的中点， 所以//EO PC又EO ⊄平面PCD ，PC ⊂平面PCD ， 所以//EO 平面PCD同理可证，//FO 平面PCD ，又EO FO O = ，EO ⊂平面EFO ,FO ⊂平面EFO 所以平面//EFO 平面PCD ．（2）因为PA ⊥平面ABCD ，BD ⊂平面ABCD ， 所以PA BD ⊥因为底面ABCD 是菱形，所以AC BD ⊥，又,,PA AC A PA PAC AC PAC =⊂⊂ 平面平面所以BD ⊥平面PAC 。
高中数学立体几何平行、垂直位置关系证明题专项练习(带答案)
立体几何平行、垂直位置关系专练1、如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，//AD BC ，AB AD ⊥，2AD BC =，M 点在线段PD 上，且满足2MD PM =.（1）求证:AB PD ⊥；（2）求证://PB 平面MAC .2、如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，E 为PA 的中点，F 为BC 的中点，底面ABCD 是菱形，对角线AC ，BD 交于点O ．求证：（1）平面//EFO 平面PCD ；（2）平面PAC ⊥平面PBD ．3、如图，正三棱柱ABC-A 1B 1C 1的高为6，其底面边长为2.已知点M ，N 分别是棱A 1C 1，AC 的中点，点D 是棱CC 1上靠近C 的三等分点．求证：(1)B 1M ∥平面A 1BN ；(2)AD ⊥平面A 1BN.4、如图，等边三角形ABC与直角梯形ABDE所在平面垂直，BD∥AE，BD＝2AE，AE⊥AB，M为AB的中点．(1)证明：CM⊥DE；(2)在边AC上找一点N，使CD∥平面BEN.5、如图，矩形ABCD所在平面与三角形ABE所在平面互相垂直，AE＝AB，M，N，H分别为DE，AB，BE 的中点．求证：(1)MN∥平面BEC；(2)AH⊥CE.6、如图，在三棱台ABCDEF中，CF⊥平面DEF，AB⊥BC.(1)设平面ACE∩平面DEF＝a，求证：DF∥a；(2)若EF＝CF＝2BC，试问在线段BE上是否存在点G，使得平面DFG⊥平面CDE？若存在请确定点G的位置；若不存在，请说明理由．7、在三棱锥S ABC -中，平面SAB ⊥平面SBC ，AB BC ⊥，AS AB =，过A 作AF SB ⊥，垂足为F ，点E ，G 分别是棱SA ，SC 的中点．（1）求证：平面EFG ∥平面ABC ．（2）求证：BC SA ⊥．8、如图，在直三棱柱111ABC A B C -中，AB BC ⊥，点D 为棱1C C 的中点，1AC 与1A D 交于点E ，1BC 与1B D 交于点F ，连结EF .求证：（1）//AB EF ；（2）平面11A B D ⊥平面11B BCC .9、【2019年高考江苏卷】如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A 1B 1∥平面DEC 1；（2）BE ⊥C 1E ．点，平面PAB ⊥底面ABCD ，90PAB ∠= ．求证：（1）//PB 平面AEC ；（2）平面PAC ⊥平面ABCD ．11、2.（2020·江苏省镇江高三二模）如图，三棱锥P ABC -中，点D ，E 分别为AB ，BC 的中点，且平面PDE ⊥平面ABC ．()1求证：//AC 平面PDE ；()2若2PD AC ==，PE =PBC ⊥平面ABC .12、（2020·江苏省建湖高级中学高三月考）如图，在四面体ABCD 中，,90AD BD ABC =∠= ，点,E F 分别为棱,AB AC 上的点，点G 为棱AD 的中点，且平面//EFG 平面BCD ．（1）求证：12EF BC =；（2）求证：平面EFD ⊥平面ABC ．点，PA ⊥平面ABCD .（1）求证：//PB 平面AEC ；（2）若四边形ABCD 是矩形且PA AD =，求证：AE ⊥平面PCD .14、（2020·江苏省高三二模）如图，在三棱柱111ABC A B C -中，侧面11ABB A ⊥底面ABC ，AB AC ⊥，E ，F 分别是棱AB ，BC 的中点.求证：（1）11AC ∥平面1B EF ；（2）1AC B E ⊥.15、（2020·江苏省连云港高三）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，平面PAD ⊥平面ABCD ，PA PD ⊥，PA PD =，E 、F 分别为AD 、PB 的中点.（Ⅰ）求证：PE BC ⊥；（Ⅱ）求证：平面PAB ⊥平面PCD ；（Ⅲ）求证：//EF 平面PCD .16、（2020·江苏省苏州高三）如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A1B 1∥平面DEC 1；（2）BE ⊥C 1E ．17、（2020·江苏省通州高三）如图，在三棱柱111ABC A B C -中，侧棱垂直于底面1,2,1,,AB BC AA AC BC E F ⊥===分别是11,AC BC 的中点．（1）求证: 平面ABE ⊥平面11B BCC ；（2）求证:1C F ∥平面ABE ；18、（2020·江苏省高三三模）如图，三棱柱111ABC A B C -中，1BC B C =，O 为四边形11ACC A 对角线交点，F 为棱1BB 的中点，且AF ⊥平面11BCC B .（1）证明：//OF 平面ABC ；（2）证明：四边形11ACC A 为矩形.参考答案1．如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，//AD BC ，AB AD ⊥，2AD BC =，M 点在线段PD 上，且满足2MD PM =.（1）求证:AB PD ⊥；（2）求证://PB 平面MAC .【解析】（1）∵四棱锥P ABCD -中，PA ⊥平面ABCD ，AB 平面ABCD ， ∴AB PA ⊥，又AB AD ⊥，,PA AD ⊂平面PAD ，PA AD A ⋂=， ∴AB ⊥面PAD .PD ⊂面PAD ，∴AB PD ⊥. （2）连结BD AC O ⋂=，连结MO ， ∵//AD BC ，2AD BC =，2DO BO ∴=,∵在PBD ∆中，2DM MP =，2DO BO =∴//PB MO ， 又PB ⊄面MAC ，MO ⊂面MAC ，∴//PB 面MAC .2．如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，E 为PA 的中点，F 为BC 的中点，底面ABCD 是菱形，对角线AC ，BD 交于点O ．求证：（1）平面//EFO 平面PCD ；（2）平面PAC ⊥平面PBD ． 【详解】（1）因为在ΔPAC 中，E 为PA 的中点，O 为AC 的中点， 所以//EO PC又EO ⊄平面PCD ，PC ⊂平面PCD ， 所以//EO 平面PCD同理可证，//FO 平面PCD ，又EO FO O = ，EO ⊂平面EFO ,FO ⊂平面EFO 所以平面//EFO 平面PCD ．（2）因为PA ⊥平面ABCD ，BD ⊂平面ABCD ， 所以PA BD ⊥因为底面ABCD 是菱形，所以AC BD ⊥，又,,PA AC A PA PAC AC PAC =⊂⊂ 平面平面所以BD ⊥平面PAC 。
高中数学必修二立体几何面面垂直与二面角专题练习(含答案)
面面垂直与二面角一．选择题（共12小题）1．如图梯形ABCD中，AD∥BC，∠ABC=90°，AD：BC：AB=2：3：4，E，F分别是AB，CD的中点，将四边形ADFE沿直线EF进行翻折，给出四个结论：①DF⊥BC；②BD⊥FC；③平面DBF⊥平面BFC；④平面DCF⊥平面BFC．则在翻折过程中，可能成立的结论的个数为（）A．1B．2C．3D．42．如图，已知四边形ABCD是边长为1的正方形，MD⊥平面ABCD，NB⊥平面ABCD，且MD=NB=1，E为MC的中点，则下列结论不正确的是（）A．平面BCE⊥平面ABNB．MC⊥ANC．平面CMN⊥平面AMND．平面BDE∥平面AMN3．下列命题中错误的是（）A．如果α⊥β，那么α内一定存在直线平行于平面βB．如果α⊥β，那么α内所有直线都垂直于平面βC．如果平面α不垂直平面β，那么α内一定不存在直线垂直于平面βD．如果α⊥γ，β⊥γ，α∩β=l，那么l⊥γ4．如图，棱长为1的正方体ABCD﹣A1B1C1D1中，P为线段A1B上的动点，则下列结论中正确的个数为（）①DC1⊥D1P ②平面D1A1P⊥平面A1AP③∠APD1的最大值为90°④AP+PD1的最小值为⑤C1P与平面A1B1B所成角正弦值的取值范围是[，]A．1B．2C．3D．45．如图，在正方体ABCDA1B1C1D1中，E为BC1的中点，则DE与平面ABC1D1所成角的正弦值为（）A．B．C．D．6．二面角的棱上有A、B两点，直线AC、BD分别在这个二面角的两个半平面内，且都垂直于AB，已知AB=2，AC=3，BD=4，CD=，则该二面角的大小为（）A．30°B．45°C．60°D．120°7．正四棱锥（顶点在底面的射影是底面正方形的中心）的体积为12，底面对角线的长为2，则侧面与底面所成的二面角为（）A．30°B．45°C．60°D．90°8．在正三棱柱ABC﹣A1B1C1中，D是AC的中点，AB1⊥BC1，则平面DBC1与平面CBC1所成的角为（）A．30°B．45°C．60°D．90°9．如图，在长方体ABCD﹣A1B1C1D1中，AB=2，，AA1=1，则二面角C﹣B1D﹣C1的大小的余弦值为（）A．B．C．D．10．如图，60°的二面角的棱上有A，B两点，直线AC，BD分别在这个二面角的两个半平面内，且都垂直于AB．已知AB=4，AC=6，BD=8，则CD的长为（）A．B．7C．2D．911．如图，M，N是圆锥底面圆O上不同两点，且M，N，O不共线，设AN与底面所成角为α，二面角A﹣MN﹣O的平面角为β，ON与平面AMN所成角为γ，则（）A．β＞α＞γB．β＞γ＞αC．α＞β＞γD．α＞γ＞β12．如图，P是△ABC边AB上一点，将△ACP沿CP折成直二面角A'﹣CP﹣B，要使|A'B|最短，则CP是（）A．△ABC中AB边上的中线B．△ABC中AB边上的高线C．△ABC中∠ACB的平分线D．要视△ABC的具体情况而定二．解答题（共18小题）13．如图，在四棱锥P﹣ABCD中，底面ABCD是边长为2的正方形，△PAD为等边三角形，E，M分别是AD，PD的中点，PB=2．（Ⅰ）求证：平面PBE⊥平面ABCD；（Ⅱ）求点P到平面ACM的距离．14．如图，在三棱锥P﹣ABC中，PA⊥AB，PA⊥BC，AB=BC，D为线段AC的中点，E为线段PC 上一点．〔Ⅰ）求证：PA⊥BD；（Ⅱ）求证：平面BDE⊥平面PAC．15．如图，BD是圆O的直径，C是圆周上不同于B，D的任意一点，AB⊥平面BCD，E为AB 的中点．（1）求证：OE∥平面ACD；（2）求证：平面ACD⊥平面ABC．16．在正方体ABCD﹣A1B1C1D1中，点E为CC1的中点．（1）求证：平面AA1CC1⊥平面BDB1D1；（2）求直线BE与平面ACC1A1所成角的余弦值．17．如图1，梯形ABCD满足：AB∥CD，AD⊥AB，AD=DC=2AB=2，E是BA延长线上一点，AE=2．现将△EDA沿直线DA翻折，记翻折后的点E为点P．若PC=2，M为PC的中点，如图2．（Ⅰ）求证：平面ABM⊥平面PBD；（Ⅱ）求直线BC与平面PBD所成的角的正弦值．18．已知三棱锥A﹣BCD中，△BCD是等腰直角三角形，且BC⊥CD，BC=4，AD⊥平面BCD，AD=2．（Ⅰ）求证：平面ABC⊥平面ADC（Ⅱ）若E为AB的中点，求点A到平面CDE的距离．19．如图（1）在直角梯形ABCD中，∠BAD=90°，AB∥CD，CD=2AB=2AD=4，E为CD中点，现将△CEB沿BE折起，使得AC=4，得到如图（2）几何体，记线段CB的中点为F．（1）求证：平面CED⊥平面ABED（2）求点F到平面ACD的距离．20．如图所示，在多面体ABCDEF中，四边形ABCD是正方形，AB=2EF=2，EF∥AB，EF⊥FB，∠BFC=90°，BF=FC，H为BC的中点．（1）求证：FH∥平面BDE；（2）求证：平面BDE⊥平面ACF．21．如图，在正三棱柱（底面为正三角形的直棱柱）ABC﹣A1B1C1中，已知AB=AA1=2，点Q为BC的中点．（Ⅰ）求证：平面AQC1⊥平面B1BCC1；（Ⅱ）求点B到平面AQC1的距离．22．如图，在正三棱柱ABC﹣A1B1C1中，底面边长和侧棱长都是4，D是CC1的中点，求：（1）三棱锥D﹣ABC的体积；（2）二面角D﹣AB﹣C的大小．23．如图，四棱锥P﹣ABCD的底面是正方形，PD⊥底面ABCD，PD=DC，E是PC的中点．（1）证明：平面PAB⊥平面PAD；（2）求二面角P﹣AB﹣D的大小．24．三棱柱ABC﹣A1B1C1的底面ABC是等边三角形，BC的中点为O，A1O⊥底面ABC，AA1与底面ABC所成的角为，点D在棱AA1上，且AD=，AB=2．（1）求证：OD⊥平面BB1C1C；（2）求二面角B﹣B1C﹣A1的平面角的余弦值．25．如图，在四棱锥P﹣ABCD中，底面ABCD是菱形且∠ABC=120°，点E是棱PC的中点，平面ABE与棱PD交于点F．（1）求证：EF∥CD；（2）若PA=PD=AD=2，且平面PAD⊥平面ABCD，求锐二面角P﹣AF﹣E的余弦值．26．四棱锥P﹣ABCD中，底面ABCD是平行四边形，BC=2AB，∠ABC=60°，PA=PB，点M为AB 的中点．（Ⅰ）在棱PD上作点N，使得AN∥平面PMC（Ⅱ）若PB⊥AC，且直线PC与平面PAB所成的角是45°，求二面角M﹣PC﹣A的余弦值27．如图，在直三棱柱ABC﹣A1B1C1中，E、F分别为A1C1、BC的中点AB=BC=2，C1F⊥AB．（1）求证：平面ABE⊥平面B1BCC1；（2）若直线C1F和平面ACC1A1所成角的正弦值等于，求二面角A﹣BE﹣C的平面角的正弦值．28．已知PA⊥菱形ABCD所在平面，PA=，G为线段PC的中点，E为线段PD上一点，且=2．（1）求证：BG∥平面AEC；（2）若AB=2，∠ADC=60°，求二面角G﹣AE﹣C的余弦值．29．在多面体ABCDEF中，底面ABCD是梯形，四边形ADEF是正方形，AB∥DC，AB=AD=1，CD=2，AC=EC=．（1）求证：平面EBC⊥平面EBD；（2）设M为线段EC上一点，3=，求二面角M﹣BD﹣E的平面角的余弦值．30．如图所示，在四棱锥P﹣ABCD中，底面四边形ABCD是边长为的正方形，，PC=4，点E为PA中点，AC与BD交于点O．（Ⅰ）求证：OE⊥平面ABCD；（Ⅱ）求二面角B﹣PA﹣D的余弦值．参考答案一．选择题（共12小题）1．解：因为BC∥AD，AD与DF相交不垂直，所以BC与DF不垂直，则①错误；设点D在平面BCF上的射影为点P，当BP⊥CF时就有BD⊥FC，而AD：BC：AB=2：3：4，可使条件满足，所以②正确；当点P落在BF上时，DP⊂平面BDF，从而平面BDF⊥平面BCF，所以③正确；因为点D的投影不可能在FC上，所以平面DCF⊥平面BFC不成立，即④错误．故选：B．2．解：分别过A，C作平面ABCD的垂线AP，CQ，使得AP=CQ=1，连接PM，PN，QM，QN，将几何体补成棱长为1的正方体．∵BC⊥平面ABN，BC⊂平面BCE，∴平面BCE⊥平面ABN，故A正确；连接PB，则PB∥MC，显然PB⊥AN，∴MC⊥AN，故B正确；取MN的中点F，连接AF，CF，AC．∵△AMN和△CMN都是边长为的等边三角形，∴AF⊥MN，CF⊥MN，∴∠AFC为二面角A﹣MN﹣C的平面角，∵AF=CF=，AC=，∴AF2+CF2≠AC2，即∠AFC≠，∴平面CMN与平面AMN不垂直，故C错误；∵DE∥AN，MN∥BD，∴平面BDE∥平面AMN，故D正确．故选：C．3．解：如果α⊥β，则α内与两平面的交线平行的直线都平行于面β，故可推断出A命题正确．B选项中α内与两平面的交线平行的直线都平行于面β，故B命题错误．C根据平面与平面垂直的判定定理可知C命题正确．D根据两个平面垂直的性质推断出D命题正确．故选：B．4．解：对于①，∵A1D1⊥DC1，A1B⊥DC1，∴DC1⊥面A1BCD1，D1P⊂面A1BCD1，∴DC1⊥D1P，①正确对于②，∵平面D1A1P即为平面D1A1BC，平面A1AP 即为平面A1ABB1，切D1A1⊥平面A1ABB1，∴平面D1A1BC，⊥平面A1ABB1，∴平面D1A1P⊥平面A1AP，∴②正确；对于③，当0＜A1P＜时，∠APD1为钝角，∴③错；对于④，将面AA1B与面A1BCD1沿A1B展成平面图形，线段AD1即为AP+PD1的最小值，在△D1A1A中，∠D1A1A=135°利用余弦定理解三角形得AD1=，即AP+PD1≥，∴④不正确．对于⑤，C1P与平面A1B1B所成角正弦值为，∵，∴C1P与平面A1B1B所成角正弦值的取值范围是[，]，故⑤正确．故选：C．5．解：以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，设正方体ABCDA1B1C1D1中棱长为2，D（0，0，0），E（1，2，1），A（2，0，0），B（2，2，0），C1（0，2，2），=（1，2，1），=（0，2，0），=（﹣2，2，2），设平面ABC1D1的法向量=（x，y，z），则，取x=1，得=（1，0，1），设DE与平面ABC1D1所成角为θ，则sinθ===，∴DE与平面ABC1D1所成角的正弦值为．故选：D．6．解：由已知可得：，，，∴=+2=32+22+42+2×3×4cos＜，＞=，∴cos＜＞=﹣，即＜＞=120°，∴二面角的大小为60°，故选：C．7．解：正四棱锥的体积为12，底面对角线的长为2，底面边长为2，底面积为12，所以正四棱锥的高为3，则侧面与底面所成的二面角的正切tanα==，则二面角等于60°，故选：C．8．在正三棱柱ABC﹣A1B1C1中，D是AC的中点，AB1⊥BC1，则平面DBC1与平面CBC1所成的角为（）A．30°B．45°C．60°D．90°解：以A为坐标原点，、的方向分别为y轴和z轴的正方向建立空间直角坐标系．设底面边长为2a，侧棱长为2b，则A（0，0，0），C（0，2a，0），D（0，a，0），B（a，a，0），C1（0，2a，2b），B1（a，a，2b）．=（），=（﹣，a，2b），=（，0，0），=（0，a，2b），由AB1⊥BC1，得•=2a2﹣4b2=0，即2b2=a2．设=（x，y，z）为平面DBC1的一个法向量，则•=0，•=0．即，又2b2=a2，令z=1，解得=（0，﹣，1）．同理可求得平面CBC1的一个法向量为=（1，，0）．设平面DBC1与平面CBC1所成的角为θ，则cos θ==，解得θ=45°．∴平面DBC1与平面CBC1所成的角为45°．故选：B．9．解：建立空间直角坐标系，如图所示；长方体ABCD﹣A1B1C1D1中，AB=2，，AA1=1，∴A（0，0，0），C（2，，0），D（0，，0），B1（2，0，1），C1（2，，1）；∴=（﹣2，，﹣1），=（﹣2，0，0），=（0，，0）；设平面CB1D的法向量为=（x，y，z），则，即，令y=1得=（0，1，）；同理，设平面C1B1D的法向量为=（x，y，z），则，即，令x=1，则=（1，0，﹣2）；∴cos＜，＞===﹣，∴二面角C﹣B1D﹣C1的余弦值为﹣cos＜，＞=．故选：A．10．解：∵CA⊥AB，BD⊥AB，∴，．∵，∴=+++2+2+2═62+42+82+2×6×8cos120°=68，∴CD=2故选：C．11．解：连接OA，OM，取MN的中点H，连接OH，AH，过O作OD⊥AH，垂足为D，连接ND，由AO⊥底面，可得∠ANO=α，由OH⊥MN，AO⊥底面，由三垂线定理可得MN⊥AH，可得∠AHO=β，由OD⊥AH，MN⊥平面AHO，可得OD⊥MN，OD⊥平面AMN，可得∠OND=γ，且α，β，γ均为锐角，则sinα=，sinβ=＞=sinα，即β＞α；=•=＞1，即有β＞γ，tanα=，tanγ=，设AO=h，ON=r，OH=d，可得OD=，DN=，则tanα=，tanγ=，tan2α﹣tan2γ=＞0，可得tanα＞tanγ，即有α＞γ，即为β＞α＞γ．故选：A．12．解：如图所示，作A′E⊥CP，垂足为E．∵直二面角A'﹣CP﹣B，∴A′E⊥平面BCP．时AC=b，BC=a，∠ACB=α．设∠ACP=θ．则A′E=bsinθ，CE=bcosθ．BE2=b2cos2θ+a2﹣2abcosθcos（α﹣θ），∴A′B2=（A′E）2+BE2=b2sin2θ+b2cos2θ+a2﹣2abcosθcos（α﹣θ）=b2+a2﹣2abcosθcos（α﹣θ），∵cosθcos（α﹣θ）=cosθ（cosαcosθ+sinαsinθ）=cosαcos2θ+sinαsin2θ=c osα+sinαsin2θ=+cos（α﹣2θ）．∴A′B2=b2+a2﹣abcosα﹣abcos（α﹣2θ），当且仅当cos（α﹣2θ）=1时，即α=2θ时，即CP为∠ACB的平分线时，|A'B|最短．故选：C．二．解答题（共18小题）13．（Ⅰ）证明：由题意知，正△PAD边长为2，∵E为AD的中点，∴PE⊥AD，PE=，在正方形ABCD中，E为AD的中点，边长为2，则BE=，在△PBE中，BE2+PE2=8=PB2，∴PE⊥BE，又BE∩AD=E，∴PE⊥平面ABCD，∵PE⊂P平面ABCDM，∴平面PBE⊥平面ABCD；（Ⅱ）由题意知V P﹣ACM=V C﹣APM，△PAD为等边三角形，则AM=，∴S△APM=，∵PE⊥平面ABCD，∴PE⊥CD，∵CD⊥AD．∴CD⊥平面PAD，故CD为三棱锥C﹣PAB的高，∴CD⊥PD，在正方形ABCD中，AC=2，则在△ACM中，满足8=AC2=AM2+CM2，∴△ACM为直角三角形，∴AM⊥MC，∴S△ACM=|AM|•|CM|=，设点P到平面ACM的距离为d，由V P﹣ACM=V C﹣APM，得×d×S△ACM=×CD×S△APM，解得d=14．证明：（Ⅰ）∵在三棱锥P﹣ABC中，PA⊥AB，PA⊥BC，AB∩BC=B，∴PA⊥平面ABC，∵D为线段AC的中点，∴BD⊂平面ABC，∴PA⊥BD．（Ⅱ）∵AB=BC，D为线段AC的中点，∴BD⊥AC，∵PA⊥BD，PA∩AC=A，∴BD⊥平面PAC，∵BD⊂平面BDE，∴平面BDE⊥平面PAC．15．．证明：（1）∵BD是圆O的直径，E为AB的中点，∴OE∥AD，∵OE⊄平面ACD，AD⊂平面ACD，∴OE∥平面ACD．（2）∵BD是圆O的直径，∴BC⊥DC，∵AB⊥平面BCD，CD⊂平面BCD，∴AB⊥CD，∵AB∩BC=B，∴平面ACD⊥平面ABC．16．证明：（1）正方体ABCD﹣A1B1C1D1中，有AA1⊥平面ABCD，又BD⊂平面ABCD，∴AA1⊥BD，又由正方形ABCD，可知AC⊥BD，AA1∩AC=A，∴BD⊥平面ACC1A1，又BD⊂平面BDD1B1，∴平面AA1C1C⊥平面BDD1B1．（6分）解：（2）记AC与BD交点为O，连接OE，∵BD⊥平面ACC1A1，∴∠OEB即为直线BE与平面ACC1A1所成角，设正方体棱长AB=2，则OB=，BE=，OE=，则有cos=，直线BE与平面ACC1A1所成角的余弦值为．（12分）17．（Ⅰ）证明：在△ADE中，AD=AE=2，得DE=2，即PD=．在△PDC中，DC=2，PC=2，可得PC2=PD2+DC2，∴∠CDP=90°，即CD⊥PD．又CD⊥AD，∴CD⊥平面PAD．取PD中点N，则MN是△PCD的中位线，∴MN∥CD，MN=．又AB∥CD，AB=，∴AB∥MN，AB=MN，即四边形ABMN为平行四边形．又AN是等腰直角三角形PAD斜边PD的中线，∴PD⊥AN，又CD⊥平面PAD，∴AB⊥平面PAD，AB⊥PD．∴PD⊥平面ABM，又PD⊂平面PBD，∴平面ABM⊥平面PBD；（Ⅱ）解：在△MNB中，作MH⊥NB于H，则MH⊥平面PBD，由已知可得MN=1，MB=，又NB=，∴，即点M到平面PDB的距离为．又由于M是PC的中点，∴点C到平面PBD的距离h=．求得BC=，设直线BC与平面PBD所成的角为θ，则s inθ=．18．（Ⅰ）证明：∵AD⊥平面BCD，BC⊂平面BCD，∴AD⊥BC，又∵BC⊥CD，CD∩AD=D，∴BC⊥平面ACD，又BC⊂平面ABC，∴平面ABC⊥平面ACD．…（5分）（Ⅱ）解：由已知可得，取CD中点为F，连结EF，∵，∴△ECD为等腰三角形，∴，，…（8分）由（Ⅰ）知BC⊥平面ACD，∴E到平面ACD的距离为：，∴S△ACD=4，…（10分）设A到平面CED的距离为d，有，解得，∴A到平面CDE的距离是．…（12分）19．（1）证明：由条件可知BA=DE，BA∥DE，∠BAD=90°，∴四边形ABED为正方形，∴BE⊥EC，BE⊥ED，EC⊥ED=E，⇒BE⊥平面DEC．又BE⊂平面ABCD，所以平面CED⊥平面ABCD．（2）AD∥BE，∴AD⊥平面DEC，∴∠ADC=90°，∴∠CED=120°，△CED为等腰三角形．过点E作EM⊥CD，∴M为CD中点⇒ME=1 ∴ME⊥CD，ME⊥AD⇒ME⊥平ACD．又F为BC的中点，∴．20．证明：（1）设BD与AC交于点O，连接OE、OH．∵O、H分别为AC，BC中点，∴OH∥AB，OH=AB，∴EF∥AB，EF=AB，∴OH=EF，OH∥EF，∴四边形OEFH为平行四边形，∴FH∥OE，又∴FH⊄平面BDE，OE⊂平面BDE，∴FH∥平面BDE．（2）∵EF∥AB，EF⊥FB，AB∩FB=B，∴EF⊥平面ABF，∵FB⊂平面ABF，∴AB⊥FB，∵AB⊥BC，BC∩FB=B，∴AB⊥平面BCF，∵FH⊂BCF，∴AB⊥FH，∵FH⊥BC，AB∩BC=B，∴FH⊥平面ABCD，又FH∥OE，∴OE⊥平面ABCD，∵AC⊂平面ABCD，∴OE⊥AC，∵AC⊥BD，AC∩BD=O，∴AC⊥平面BDE，又AC⊂平面ACF，∴平面BDE⊥平面ACF．21．解：（I）证明：由题意知，AB=AC，Q为BC的中点，∴AQ⊥BC；由B1B⊥平面ABC，得B1B⊥AQ；∵BC，B1B⊂平面B1BCC1，且BC∩B1B=B，∴AQ⊥平面B1BCC1，又∵AQ⊂平面AC1Q，∴平面AC1Q⊥平面B1BCC1；……（6分）（II）设点B到平面AQC1的距离为d，在正三棱柱ABC﹣A1B1C1中，CC1⊥平面ABQ，∴CC1为三棱锥C1﹣ABQ的高；由（I）知，AQ⊥平面B1BCC1，则AQ⊥QC1，∴；∴，；又，∴，即，解得．……（12分）22．解：（1）∵三棱柱ABC﹣A1B1C1为正三棱柱，且底面边长和侧棱长都是4，D是CC1的中点，∴，三棱锥D﹣ABC的高为DC=2．∴三棱锥D﹣ABC的体积V=；（2）取AB中点G，连接DG，CG，则AB⊥平面DGC，∴∠DGC为二面角D﹣AB﹣C的平面角，在Rt△DCG中，DC=2，CG=，∴tan∠DGC=，则．即二面角D﹣AB﹣C的大小为．23．证明：（1）∵四棱锥P﹣ABCD的底面是正方形，PD⊥底面ABCD，PD=DC，E是PC的中点．∴AB⊥AD，AB⊥PD，又AD∩PD=D，∴AB⊥平面PAD，∵AB⊂平面PAB，∴平面PAB⊥平面PAD．解：（2）以D为原点，DA为x轴，DC为y轴，DP为z轴，建立空间直角坐标系，设PD=DC=DP=2，则A（2，0，0），P（0，0，2），D（0，0，0），B（2，2，0），=（﹣2，0，2），=（0，2，0），设平面PAB的法向量=（x，y，z），则，取x=1，得=（1，0，1），平面ABD的法向量=（0，0，1），设二面角P﹣AB﹣D的大小为θ，则cosθ===，θ=45°，∴二面角P﹣AB﹣D的大小为45°．24．（1）证明：连接AO，∵A1O⊥底面ABC，AO，BC⊂底面ABC，∴BC⊥A1O，A1O⊥AO，且AA1与底面ABC 所成的角为∠A1AO，即．在等边三角形ABC中，易求得AO=．在△AOD中，由余弦定理，得，∴OD2+AD2=3=OA2，即OD⊥AA1．又∵AA1∥BB1，∴OD⊥BB1．∵AB=AC，OB=OC，∴AO⊥BC，又∵BC⊥A1O，AO∩A1O=O，∴BC⊥平面AA1O，又∵OD⊂平面AA1O，∴OD⊥BC，又BC∩BB1=B，∴OD⊥平面BB1C1C．（2）如下图所示，以O为原点，分别以OA，OB，OA1所在的直线为x，y，z轴建立空间直角坐标系，则故由（1）可知，∴可得点D的坐标为，∴平面BB1C1C的一个法向量是．设平面A1B1C的法向量=（x，y，z），由得，令，则y=3，z=﹣1，则，∴，易知所求的二面角为钝二面角，∴二面角B﹣B1C﹣A1的平面角的余弦角值是．25．解：（1）∵底面ABCD是菱形，∴AB∥CD，又∵AB⊄面PCD，CD⊂面PCD，∴AB∥面PCD，…（2分）又∵A，B，E，F四点共面，且平面ABEF∩平面PCD=EF，∴AB∥EF，即可得EF∥CD…（5分）（2）取AD中点G，连接PG，GB，∵PA=PD，∴PG⊥AD，又∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，∴PG⊥平面ABCD，∴PG⊥GB，在菱形ABCD中，∵AB=AD，∠DAB=60°，G是AD中点，∴AD⊥GB，…（6分）如图，建立空间直角坐标系G﹣xyz，设PA=PD=AD=2，则G（0，0，0），A（1，0，0），B（0，，0），C（﹣2，，0），D（﹣1，0，0），P（0，0，）又∵AB∥EF，点E是棱PC中点，∴点F是棱PD中点，E（﹣1，，），F（﹣，0，），，，设平面AFE的法向量为=（x，y，z），则有⇒，不妨令x=3，则平面AFE的一个法向量为．∵BG⊥平面PAD，∴是平面PAF的一个法向量，cos==∴锐二面角P﹣AF﹣E的余弦值为．．…（12分）26．解：（Ⅰ）：点N为PD中点．下证：取PD中点N，PC中点Q，连结AN，QN，MQ，在△PCD中，N，Q分别是所在边PD，PC的中点，则NQ∥CD且．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（1分）因为点M为AB中点，AB=CD，所以NQ∥AM且NQ=AM．﹣﹣﹣﹣﹣﹣﹣﹣﹣（2分）所以四边形AMQN是平行四边形，所以AN∥MQ．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（3分）又因为AN⊄平面PMC，MQ⊂平面PMC，所以AN∥平面PMC．﹣﹣﹣﹣﹣﹣﹣﹣﹣（4分）（Ⅱ）在△ABC中，BC=2AB，∠ABC=60°，设AB=a，则BC=2a，由余弦定理有：，则BC2=AB2+AC2，由勾股定理的逆定理可得：AC⊥AB．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（5分）又因为PB⊥AC，PB∩AB=B，PB，AB⊂平面PAB，所以AC⊥平面PAB．因为PM⊂平面PAB，所以AC⊥PM．因为PA=PB，点M为线段AB的中点，所以PM⊥AB，因此PM，AB，AC两两垂直．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（6分）以A为原点，分别以AB，AC所在直线为x，y轴，建立空间直角坐标系．因为直线PC与平面PAB的所成角是45°，所以∠CPA=45°，所以Rt△CAP是等腰直角三角形，所以．﹣﹣﹣﹣﹣﹣﹣﹣﹣（7分）则A（0，0，0），，，，，．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（8分）设平面PMC的一个法向量为=（x，y，z），则即得，同理可得，平面PAC的一个法向量为，﹣﹣﹣﹣﹣﹣﹣﹣（10分）则．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（11分）由图可得所求二面角的平面角为锐角，所以二面角M﹣PC﹣A的余弦值为．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（12分）27．（1）证明：在直三棱柱中，CC1⊥AB，又C1F⊥AB，且CC1∩C1F=C1，∴AB⊥平面B1BCC1，又∵AB⊂平面EBA，∴平面ABE⊥平面B1BCC1；（2）解：由（1）可知，AB⊥BC，以B点为坐标原点，为x轴正方向，为y轴正方向，为z轴正方向建立坐标系．设AA1=a，则B（0，0，0），C（2，0，0），A（0，2，0），B1（0，0，a），C1（2，0，a），A1（0，2，a），E （1，1，a），F（1，0，0）．直线FC1的方向向量，平面ACC1A1的法向量．可知||=，∴a=2．，，，设平面ABE的法向量，由，取z=﹣1，可得．设平面CBE的法向量，由，取z=﹣1，可得．记二面角A﹣BE﹣C的平面角为θ，∴|cosθ|=||=，则sin．故二面角A﹣BE﹣C的平面角的正弦值为．28．（1）证明：取PE的中点F，连接GF，BF，∵G为PC的中点，∴GF∥CE，∴GF∥平面AEC．连接BD交AC与点O，连接OE．∵E为DF的中点，∴BF∥OE，∴BF∥平面AEC．∵BF∩GF=F，∴平面BGF∥平面AEC．又BG⊄平面BGF，∴BG∥平面AEC；（2）解：如图，建立空间直角坐标系O﹣xyz．则则O（0，0，0），A（﹣1，0，0），C（1，0，0），P（﹣1，0，），D（0，，0），E（，，），G（0，0，2），∴=（，，），=（2，0，0），=（1，0，），设平面AEC的法向量为，则，∴，即，不妨设得=（0，，），设平面AEG的法向量为，则，∴，即，不妨设z2=1得=（，0，1），∴=．由图可知，二面角G﹣AE﹣C为锐角，则二面角G﹣AE﹣C的余弦值为．29．证明：（1）∵AD=1，CD=2，AC=，∴AD2+CD2=AC2，∴△ADC为直角三角形，且AD⊥DC，同理∵ED=1，CD=2，EC=，∴ED2+CD2=EC2，∴△EDC为直角三角形，且ED⊥DC，又四边形ADEF是正方形，∴AD⊥DE，又∵AB∥DC，∴DA⊥AB．在梯形ABCD中，过点作B作BH⊥CD于H，∴四边形ABHD是正方形，∴∠ADB=45°．在△BCH中，BH=CH=1，∴∠BCH=45°．BC=，∴∠BDC=45°，∴∠DBC=90°，∴BC⊥BD．∵ED⊥AD，ED⊥DC，AD∩DC=D．AD⊂平面ABCD，DC⊂平面ABCD．∴BD⊥平面ABCD，又∵BC⊂平面ABCD，∴ED⊥BC，因为BD∩ED=D，BD⊂平面EBD，ED⊂平面EBD．∴BC⊥平面EBD，BC⊂平面EBC，∴平面EBC⊥平面EBD．解：（2）以D为原点，DA，DC，DE所在直线为x，y，z轴建立空间直角坐标系，如图，D（0，0，0），E（0，0，1），B（1，1，0），C（0，2，0）．令M（0，y0，z0），则=（0，y0，z0﹣1），=（0，2，﹣1），∵3=，∴（0，3y0，3z0﹣3a）=（0，2，﹣1），∴M（0，，）．=（1，1，0），=（0，），∵BC⊥平面EBD，∴=（﹣1，1，0）是平面EBD的一个法向量．设平面MBD的法向量为=（x，y，z）．则．令y=1，得=（﹣1，1，1），∴cos＜＞===，∴二面角M﹣BD﹣E的平面角的余弦值为．30．证明：（I）底面四边形ABCD是边长为的正方形，，PC=4，在△PBC中，∵PB2=PC2+BC2，∴PC⊥BC，同理可得BC⊥CD，而BC∩CD=C，BC、CD⊂平面ABCD，∴PC⊥平面ABCD，在△PAC中，由题意知O、E分别为AC、PA中点，则OE∥PC，而PC⊥平面ABCD，∴OE⊥平面ABCD．解：（II）由（I）知：OE⊥平面ABCD，故可建立空间直角坐标系O﹣xyz，如图所示，A（1，0，0），B（0，1，0），D（0，﹣1，0），P（﹣1，0，4），∴=（﹣2，0，4），=（﹣1，1，0），=（﹣1，﹣1，0），设、=（a，b，c）分别为平面PAB和平面PAD的一个法向量，则，，∴，，不妨设z=c=1，则=（2，2，1），=（2，﹣2，1），∴cos＜＞===，由图知二面角B﹣PA﹣D为钝二面角，∴二面角的B﹣PA﹣D的余弦值为﹣．。
高二数学垂直试题答案及解析
高二数学垂直试题答案及解析1.在△ABC中，AB=AC=5，BC=6，PA⊥平面ABC，PA=8，则P到BC的距离是（）A．B．C．D．【答案】B【解析】如图：取BC的中点为E,连结AE及PE,由AB=AC=5知:,又因为PA⊥平面ABC，所以，从而有，所以线段PE的长就是P到BC的距离；在中有AE=4，又PA=8，在中有，故选B．【考点】线面的垂直及点到直线的距离．2.在类比此性质，如下图，在四面体P－ABC 中，若PA、PB、PC两两垂直，底面ABC上的高为h，则得到的正确结论为________________．【答案】【解析】如图所示，两两垂直，则平面，所以,在直角三角形中有,平面,则,又,故平面,那么,在直角三角形中，,可得.【考点】线面垂直的判定与性质.3.如图,已知长方形中,, ,为的中点．将沿折起，使得平面平面．(1)求证：；(2)若点是线段的中点，求二面角的余弦值．【答案】（1）见解析（2）【解析】(1)根据面面垂直可得线面垂直,进而得到线线垂直．根据矩形的边长,可证明,根据平面平面,且为交线,可证平面,进而得到．(2)要求二面角首先得找到二面角的平面角,根据是线段的中点,取的中点,则,根据(1)可知平面,过做,则可证明即二面角的平面角,根据已知条件可求出该角的余弦值．(1)即．平面平面,平面,(2)取的中点,则,由(1)知平面,平面．过做,连接．因为,,所以平面,则．所以根据二面角的平面角定义可知,即二面角的平面角，由已知【考点】线线垂直的证明,找二面角的平面角以及求角．4.如图，在四棱锥中，，，为正三角形，且平面平面．（1）证明：；（2）求二面角的余弦值．【答案】（1）证明见解析；（2）．【解析】（1）取的中点，然后利用矩形及正三角形的性质可证明，，从而可证明结果；（2）可考虑分别以，为轴，轴，轴建立空间直线坐标系，通过求两个平面的法向量的夹角来求二面角的余弦值．或考虑通过过点作，然后证明为所求二面角的一个平面角，再在中进行计算．（1）证明：取的中点，连接，∵为正三角形，∴．又∵在四边形中，，∴,且，∴四边形ABCO为平行四边形，∴，∴，∴．（2）(法一)：由（1）知，且平面平面∴平面，所以分别以，为轴，轴，轴建立如图，所示的直角坐标系，并设，则，,∴，，，，，∴，,,．设平面，平面的法向量分别为，则∴∴分别取平面，平面的一个法向量，∴，∴二面角的余弦值为．(法一)：由（1）知，且平面平面，∴平面，过点作，垂足为，连接，则，于是为所求二面角的一个平面角，设，则，，，∴∴二面角的余弦值为．【考点】1、空间直线与平面的垂直关系；2、空间向量的应用；3、二面角．5.如图，正方形所在的平面与平面垂直，是和的交点，，且．（1）求证：平面；（2）求二面角的大小．【答案】(1)详见解析;(2）.【解析】（1）要证AM⊥平面EBC，关键是寻找线线垂直，利用四边形ACDE是正方形，可得AM⊥EC．利用平面ACDE⊥平面ABC，BC⊥AC，可得BC⊥平面EAC，从而有BC⊥AM．故可证；（2）先求出二面角A-EB-C的平面角．再在Rt△EAB中，利用AH⊥EB，有AE•AB=EB•AH．设EA=AC=BC=2a可得AB＝2a，EB＝2a，∴AH＝＝．从而可求二面角A-EB-C的平面角 .证明：（1）∵四边形是正方形，∵平面平面，又∵，平面．平面，．平面． 6分（2）过作于，连结．平面，．平面．是二面角的平面角．∵平面平面，平面．．在中，，有．设可得，，．．．∴二面角等于． 12分.【考点】1.用空间向量求直线与平面的夹角； 2.用空间向量求平面间的夹角.6.如图所示，已知AB为圆O的直径，点D为线段AB上一点，且，点C为圆O上一点，且．点P在圆O所在平面上的正投影为点D，PD=DB．（1）求证：；（2）求二面角的余弦值．【答案】(1)证明见解析;(2)．【解析】（1）先利用平面几何知识与线面垂直的性质证线线垂直，由线线垂直得到线面垂直，再由线面垂直得到线线垂直；（2）作出二面角的平面角，证明符合二面角的定义，再在三角形中求二面角的平面角,从而求出所求的二面角．试题解析：(1)如图,连接，由知，点为的中点，又∵为圆的直径，∴，由知，，∴为等边三角形，从而．∵点在圆所在平面上的正投影为点，∴平面，又平面，∴，由得，平面，又平面，∴．（2）方法1:（综合法）如图,过点作，垂足为，连接,由（1）知平面，又∵平面，∴，又∵，∴平面，又∵平面，∴，∴为二面角的平面角．由（Ⅰ）可知，，∴，则，∴在中，，∴，即二面角的余弦值为．方法2:（坐标法）以为原点，、和的方向分别为轴、轴和轴的正向，建立如图所示的空间直角坐标系,设，由，得，，，∴，，，，∴，，，由平面，知平面的一个法向量为．设平面的一个法向量为，则，即，令，则，，∴，设二面角的平面角的大小为，则，∴二面角的余弦值为．【考点】1.直线与平面垂直的判定；2.二面角的平面角及求法．7.如图,直棱柱中,分别是的中点,.⑴证明:;⑵求EC与平面所成角的正弦值.【答案】(1)见解析；（2）sin∠ECD=.【解析】（1）线线垂直转化为线面垂直的思想.（2）通过证明线面垂直，找到了线面所成的角，再根据所给的线段的关系求出EC与平面所成角的正弦值.试题解析：⑴由,知,又,故,,故;⑵设,故可得,,,故,故,又由⑴得,故,故所求角的平面角为,故.【考点】1.线线垂直的证明.2.直线与平面所成的角的计算.8.设是两条直线，是两个平面，下列能推出的是( )A．B．C．D．【答案】C【解析】∵∥，且，∴，又∵，∴，选项C正确.【考点】线线垂直的判定.9.在平面几何里，有勾股定理：“设△ABC的两边AB，AC互相垂直，则AB2+AC2=BC2.”拓展到空间，类比平面几何的勾股定理，研究三棱锥的面面积与底面面积间的关系。
立体几何最典型的平行与垂直题型归纳(带答案)(1)
专题:立体几何最典型的平行与垂直题型归纳1．四面体ABCD 中，△ ABC 是正三角形，△ ACD 是直角三角形，∠ ABD ＝∠ CBD，AB＝BD ，则四面体的四个表面中互相垂直的平面有（）对．2．如图，在四棱锥P﹣ABCD 中，PA⊥底面ABCD ，四边形ABCD 为长方形，AD＝2AB，点E、F 分别是线段PD、PC 的中点．（Ⅰ）证明：EF∥平面PAB；（Ⅱ）在线段AD 上是否存在一点O，使得BO⊥平面PAC，若存在，请指出点O 的位置，⊥底面ABCD ，且PA＝AD＝2，AB＝BC＝1，M 为PD 的中点．Ⅰ）求证：CM ∥平面PAB；Ⅱ）求证：CD ⊥平面PAC．AD ∥BC ，∠ BAD ＝90°，PA4．如图，△ ABC 为正三角形，AE 和CD 都垂直于平而ABC，F 是BE 中点，AE＝AB＝2，CD＝1．1）求证：DF ∥平面ABC；2）求证：AF ⊥DE；3）求异面直线AF 与BC 所成角的余弦值．5．如图，在四棱锥A﹣BCDE 中，平面ABC⊥平面BCDE ，∠ CDE ＝∠ BED ＝90°，AB＝CD＝2，DE＝BE＝1，AC＝．（1）证明：D E⊥平面ACD ；2）求棱锥C﹣ABD 的体积．6．如图，在四棱锥P﹣ABCD 中，底面ABCD 是矩形，PA⊥平面ABCD，PA＝AD＝2，AB ＝1，M 为线段PD 的中点．I）求证：BM ⊥PDII ）求直线CM 与PB 所成角的余弦值．7．如图，在正三棱柱ABC﹣A1B1C1 中，所有棱长都等于2．（1）当点M 是BC 的中点时，求异面直线AB1和MC1所成角的余弦值；专题 :立体几何最容易错的最难的平行与垂直问题汇编1．如图，在三棱柱 ABC ﹣A 1B 1C 1中，侧棱垂直于底面，∠ ACB ＝90°， 2AC ＝AA 1，D ，M 分别是棱 AA 1， BC 的中点．证明：2）若∠ ABC ＝120°，AE ⊥EC ，AB ＝2，求点 G 到平面 AED 的距离．3．如图，在四棱锥 P ﹣ ABCD 中，平面 PAD ⊥平面 ABCD ，PA ⊥PD ，PA ＝PD ，AB ⊥AD ， AB ＝1，AD ＝2，AC ＝CD ＝ ．（ 1）求证： PD ⊥平面 PAB ；1）证明：平面 PAB ⊥平面 PAD；AB ∥CD ，且∠ BAP ＝∠ CDP ＝90BE ⊥平面 ABCD ．1）证明：平面 AEC ⊥平面 BED ．2）若 PA ＝PD ＝AB ＝DC ，∠APD ＝90°，且四棱锥 P ﹣ABCD 的体积为 ，求该四棱 1）证明： AC ⊥BD ；（2）已知△ ACD 是直角三角形， AB ＝BD ，若 E 为棱 BD 上与 D6．如图，在四棱锥 A ﹣EFCB 中，△ AEF 为等边三角形，平面 AEF ⊥平面 EFCB ，EF ＝ 2，四边形 EFCB 是高为 的等腰梯形， EF ∥BC ，O 为 EF 的中点．AD ＝CD ． 求 O 到平面 ABC 的距离．专题:立体几何最典型的平行与垂直题型归纳1．四面体ABCD 中，△ ABC 是正三角形，△ ACD 是直角三角形，∠ ABD ＝∠ CBD，AB＝BD ，则四面体的四个表面中互相垂直的平面有（）对．A ．0 B．1 C． 2 D． 3【解答】解：取AC 的中点E，连接BE，DE，∵∠ ABD＝∠ CBD ，∴ BD 在平面ABC 上的射影在直线BE 上，∵△ ACD 是直角三角形，∴∠ ADC＝90°，设 AB ＝ 2，则 BE ＝ ，DE ＝ AC ＝1，BD ＝2，2 2 2∴DE 2+BE 2＝ BD 2，即 DE ⊥BE ，又 BE ⊥ AC ，DE ∩AC ＝E ，∴ BE ⊥平面 ACD ，∴平面 ABC ⊥平面 ACD ．∵ D 在平面 ABC 上的射影为 E ， B 在平面 ACD 上的射影为 E ，∴平面 ABD 与平面 ABC 不垂直，平面 BCD 与平面 ABC 不垂直，平面 ABD 与平面 ACD 不垂直，平面 BCD 与平面 ACD 不垂直， 过A 作 AF ⊥BD ，垂足为 F ，连接 CF ，由△ ABD ≌△ CBD 可得 CF ⊥BD ，故而∠ AFC 为二面角 A ﹣BD ﹣C 的平面角， ∵ AD ＝＝ ， ∴ cos ∠ ABD ∴ CF ＝ AF ＝∴ cos ∠ AFC ＝∴∠ AFC ≠ 90°，∴平面 ABD 与平面 BCD 不垂直．F 分别是线段 PD 、PC 的中点．证明： EF ∥平面 PAB ；BO ⊥平面 PAC ，若存在，请指出点 O 的位置， 并证明 BO ⊥平面 PAC ；若不存在，请说明理由．2．如图， 在四棱锥 P ﹣ABCD 中， PA ⊥底面 ABCD ，四边形 ABCD 为长方形， AD ＝ 2AB ，在线段 AD 上是否存在一点 O ，使得，∴ sin ∠ ABD＝∵EF ∥CD ，∴ EF ∥AB ，∴ EF ∥平面 PAB ． ⋯（6 分）此时点 O 为线段 AD 的四等分点，满足 ，⋯（ 8 分） ∵长方形ABCD 中，∴△ ABO ∽△ ADC ， ∴∠ ABO+∠CAB ＝∠ DAC + ∠CAB ＝90°，∴AC ⊥BO ，（10 分） 又∵ PA ⊥底面 ABCD ，BO? 底面ABCD ， ∴PA ⊥BO ， ∵PA ∩AC ＝A ，PA 、AC? 平面 PACABCD 为长方形，∴CD ∥AB ，∠ BAO ＝∠ ADC ＝ 90°，四边形 ABCD 为直角梯形， AD∥BC ，∠ BAD＝，PA 又∵ EF? 平面 PAB ， AB? 平面 PAB ，Ⅱ） 在线段 AD 上存在一点 O ，使得 BO ⊥平面 PAC ，⊥底面ABCD ，且PA＝AD＝2，AB＝BC＝1，M为PD 的中点．（Ⅰ）求证：CM ∥平面PAB；（Ⅱ）求证：CD ⊥平面PAC．解答】证明：（I ）取PA 的中点E，连接ME 、BE，∵ ME ∥AD，ME AD，∴ ME ∥BC，ME＝BC，∴四边形BCME 为平行四边形，∴ BE∥CM ，∵BE? 平面PAB，CM?平面PAB，∴ CM∥平面PAB；（II ）在梯形ABCD 中，AB＝BC＝1，AD＝2，∠ BAD＝90° 过C作CH⊥AD于H，∴AC ＝CD＝2 2 2∵AC2+CD2＝AD2，∴ CD⊥AC又∵ PA⊥平面ABCD ，CD ?平面ABCD，∴ CD⊥PA∵PA∩AC＝A，∴CD ⊥平面PAC4．如图，在三棱柱ABC﹣A1B1C1中，AB＝AC，A1在底面ABC的射影为BC的中点，D是B1C1 的中点，证明：A1D⊥平面A1BC．解答】 证明：设 E 为 BC 的中点，连接 A 1E ， DE ，AE ，由题意得 A 1E ⊥平面 ABC ，∴ A 1E ⊥AE ．∵ AB ＝ AC ， AE ⊥BC ，∴ AE ⊥平面 A 1BC ． 由 D ，E 分别为 B 1C 1，BC 的中点，得 DE ∥B 1B 且 DE ＝B 1B ， 从而 DE ∥A 1A 且 DE ＝A 1A ，∴四边形 A 1AED 为平行四边形，∴ A 1D ∥AE ．5．如图，△ ABC 为正三角形， AE 和 CD 都垂直于平而 ABC ，F 是 BE 中点， AE ＝AB ＝ 2，CD ＝ 1．（1）求证： DF ∥平面 ABC ；（2）求证： AF ⊥DE ；（3）求异面直线 AF 与 BC 所成角的余弦值．【解答】（1）证明：取 AC 中点 O ，过 O 作平面 ABC 的垂线交 DE连结 OB ，则 OG ⊥OB ， OG ⊥ OC ，∵△ ABC 是正三角形， O 是 AC 中点，∴ OB ⊥ OC ，以 O 为原点， OB 、OC 、OG 所在直线分别为 x 、y 、z轴，建立空间直角坐标系，又∵ AE ⊥平面 A 1BC ， ∴ A 1D ⊥平面 A 1BC∵F 是 BE 中点， AE ＝AB ＝ 2，CD ＝1，＝（﹣ ， 1， 0）， ＝（ 0，0， 1），∵CD ⊥平面 ABC ，∴ ＝（0，0，1）是平面 ABC 的一个法向量，又 DF? 平面 ABC ，∴ DF ∥平面 ABC ．2）证明：∵ ＝（ ）， ＝（ 0，﹣2，1），∴ ＝ 0﹣ 1+1＝0，∴AF ⊥DE ．（3）解：∵ ＝（ ）， ＝（﹣ ，1， 0），设 AF 、 BC 所成角为 θ，cos θ＝ ∴异面直线 AF 与 BC 所成角的余弦值6．如图，在四棱锥 P ﹣ABCD 中，底面 ABCD 是矩形， PA ⊥平面 ABCD ，PA ＝AD ＝2，AB ＝ 1，M 为线段 PD 的中点．（ I ）求证： BM ⊥PD（ II ）求直线 CM 与 PB 所成角的余弦值．∴ ＝（ ，0）， ＝（ ）， ＝（0，﹣ 2，1），∵ ＝ ， ∴，D （0，1，1），E （0，﹣1，∴A （0，﹣ 1，0），B（| | ＝【解答】（ I ）证明：连接 BD ，∵四棱锥 P ﹣ABCD 中，底面 ABCD 是矩形， PA ⊥平面 ABCD ，PA ＝AD ＝2，AB ＝1， ∴PB ＝BD ＝∵ M 为线段 PD 的中点，∴BM ⊥PD（II ）解：连接 AC ，与 BD 交于 O ，连接 OM ，则∵ M 为线段 PD 的中点，∴MO ∥PB∴直线 CM 与 PB 所成角的余弦值为7．如图，在正三棱柱 ABC ﹣A 1B 1C 1 中，所有棱长都等于 2．（ 1）当点 M 是 BC 的中点时，① 求异面直线 AB 1和 MC 1 所成角的余弦值；② 求二面角 M ﹣AB 1﹣C 的正弦值；（2）当点 M 在线段 BC 上（包括两个端点）运动时， 求直线 MC 1与平面 AB 1C 所成角的∴∠ CMO （或其补角）为直线 CM 与 PB 所成角，在△ MOC中， ∴ cos ∠ CMO＝CM ＝ ＝ ，． ．解答】 解：（1）取 AC 的中点为 O ，建立空间直角坐标系 O ﹣ xyz ，则 ，C （ 0，1，0），当 M 是 BC 的中点时，则 ． ①， 设异面直线 AB 1 和 MC 1 所成角为 θ，则 ＝ ＝ ．＝ ＝ ．② ， ， ，，令 x ＝ 2，∴ ，∴ ．设二面角 M ﹣ AB 1﹣ C 的平面角为 θ，则＝．所以 ．（ 2）当 M 在 BC 上运动时，设 ．设平面 MAB 1的一个法向量为 ，则 ．∴ 设平面 AB 1C 的一个法向量为 ，令 ，则 y ＝﹣ 1，z ＝﹣ 1，∴，，则正弦值的取值范围．设M（x，y，z），∴，∴ ，则，∴ ．设直线MC1 与平面AB1C 所成的角为θ ，则设，设t＝λ+1 ∈[1，2]，所以，t∈[1，2]．设，∴∵ ，∴ ，∴∴直线MC 1与平面AB1C 所成的角的正弦值的取值范围为6．如图，在四棱锥 A ﹣BCDE 中，平面 ABC ⊥平面 BCDE ，∠ CDE ＝∠ BED ＝90°， AB ＝CD ＝ 2，DE ＝BE ＝1，AC ＝ ．（ 1）证明： DE ⊥平面 ACD ；（ 2）求棱锥 C ﹣ ABD 的体积．【解答】 解：（ 1）在直角梯形 BCDE 中，∵DE ＝ BE ＝ 1， CD ＝ 2，∴ BC ＝＝ ， 又 AB ＝2， AC ＝ ，∴ AB 2＝AC 2+BC 2，即 AC ⊥ BC ，又平面 ABC ⊥平面 BCDE ，平面 ABC ∩平面 BCDE ＝BC ，AC? 平面 ABC ，∴AC ⊥平面 BCDE ，又 DE? 平面 BCDE ，∴AC ⊥ DE ，又 DE ⊥DC ，AC ∩CD ＝C ，∴ DE ⊥平面 ACD ．1．如图，在三棱柱 ABC ﹣A 1B 1C 1中，侧棱垂直于底面，∠ ACB ＝90°， 2AC ＝AA 1，D ，M分别是棱 AA 1， BC 的中点．证明：S △BCD ?AC ＝V C ﹣ABD ＝V A ﹣BCD ＝1)AM∥平面BDC12)DC1⊥平面BDC ．∴AD ∥ MN ，且 AD ＝ MN ；∴四边形 ADNM 为平行四边形，∴DN ∥AM ；又 DN? 平面 BDC 1，AM? 平面 BDC 1，∴ AM ∥平面 BDC 1⋯（ 6 分）（ 2）由已知 BC ⊥CC 1，BC ⊥AC ，又 CC 1∩ AC ＝ C ，∴ BC ⊥平面 ACC 1A 1，又 DC 1? 平面 ACC 1A 1，∴ DC 1⊥BC ；由已知得∠ A 1DC 1＝∠ ADC ＝45°，∴∠ CDC 1＝ 90°，∴DC 1⊥DC ；又 DC ∩BC ＝C ，∴ DC 1⊥平面 BDC ．⋯（ 12分）【解答】 证明：（ 1）如图所示，取 BC 1 的中点 N ，连接 DN ，MN ．则 MN ∥ CC 1，且 M N ＝ CC 1；又 AD ∥CC 1，且 ADV ＝ ，2．如图，四边形 ABCD 为菱形， G 为 AC 与 BD 的交点， BE ⊥平面 ABCD ．（ 1）证明：平面 AEC ⊥平面 BED ．因为 BE ⊥平面 ABCD ， AC? 平面 ABCD ，所以 AC ⊥BE ，⋯（ 2 分）又因为 DB ∩BE ＝B ，所以 AC ⊥平面 BED ．⋯（ 3分） 又 AC? 平面 AEC ，所以平面 AEC ⊥平面 BED ．⋯（ 5 分）2）取 AD 中点为 M ，连接 EM ．因为∠ ABC ＝ 120°．，AB ＝2，所以 AB ＝DB ＝ 2，AG ＝ ，DG ＝ 1，因为 AE ⊥EC ，所以 EG ＝＝ ，所以 BE ＝ ，⋯（ 6 分）所以 AE ＝DE ＝ ，又所以 AD 中点为 M ，所以 EM ⊥AD 且 EM ＝ ．设点 G 到平面 AED 的距离为为 h ， 则三棱锥 E ﹣ADG 的体积为求点 G 到平面 AED 的距离．为菱形，所以 AC ⊥BD ，⋯（ 1 分）即，解得 h ＝ ．PAD ⊥平面 ABCD ，PA ⊥PD ，PA ＝PD ，AB ⊥AD ，ABCD ，且平面 PAD ∩平面 ABCD ＝AD ，AB ⊥AD ，AB? 平面 ABCD ，∴ AB ⊥平面 PAD ，∵PD? 平面 PAD ，∴AB ⊥PD ，又 PD ⊥PA ，且 PA ∩AB ＝A ，∴ PD ⊥平面 PAB ；（ 2）解：取 AD 中点 O ，连接 PO ，则 PO ⊥ AD ， 又平面 PAD ⊥平面 ABCD ， ∴PO ⊥平面 ABCD ，∵PA ⊥PD ，PA ＝PD ，AD ＝2，∴ PO ＝1．10 分） 所以点 G 到平面 AED 的距离为AB ＝1，AD ＝2，AC ＝CD ＝ ．1）求证： PD ⊥平面PAB ；在△ ACD 中，由 AD ＝2，AC ＝CD ＝ ，可得 ．4．如图，在四棱锥 P ﹣ABCD 中， AB ∥CD ，且∠ BAP ＝∠ CDP ＝901）证明：平面 PAB ⊥平面 PAD ；P ﹣ABCD 中，∠ BAP ＝∠ CDP ＝ 90°，∴AB ⊥PA ，CD ⊥PD ，又 AB ∥ CD ，∴ AB ⊥PD ，∵PA ∩PD ＝P ，∴ AB ⊥平面 PAD ，∵AB? 平面 PAB ，∴平面 PAB ⊥平面 PAD ．解：（2）设 PA ＝PD ＝AB ＝DC ＝a ，取 AD 中点O ，连结 PO ，∵PA ＝PD ＝AB ＝DC ，∠ APD ＝90°，平面 PAB ⊥平面 PAD ，∵四棱锥 P ﹣ABCD 的体积为由 AB ⊥平面 PAD ，得 AB ⊥ AD ，∴V P ﹣ABCD ＝2）若 PA ＝PD ＝ AB ＝ DC ，∠ APD ＝90°，且四棱锥 P ﹣ ABCD 的体积为求该四棱 ∴ PO ⊥底面ABCD ， O P＝ ＝ ＝ ＝ ， 解得 a ＝2，∴ PA ＝PD ＝AB ＝DC ＝2，AD ＝BC ＝2 ，PO ＝ ， ∴ PB ＝ PC ＝ ＝2 ，∴该四棱锥的侧面积：S 侧＝ S △PAD +S △PAB +S △PDC +S △PBC＝+1）证明： AC ⊥ BD ；2）已知△ ACD 是直角三角形， AB ＝ BD ，若 E 为棱 BD 上与 D 不重合的点， ∵△ ABC 是正三角形， AD ＝CD ，∴DO ⊥AC ，BO ⊥AC ，∵DO ∩BO ＝O ，∴ AC ⊥平面 BDO ，∵BD? 平面 BDO ，∴AC ⊥BD ． 解：（2）法一：连结 OE ，由（ 1）知 AC ⊥平面 OBD ， ∵OE? 平面 OBD ，∴ OE ⊥ AC ， 设 AD ＝ CD ＝ ，则 OC ＝ OA ＝ 1， EC ＝ EA ，2 2 2 ∵AE ⊥CE ，AC ＝2，∴ EC 2+EA 2＝AC 2，∴ EC ＝ EA ＝ ＝ CD ，∴E 是线段 AC 垂直平分线上的点，∴ EC ＝EA ＝CD ＝ ，由余弦定理得：AE ⊥＝ 6+2 ．AD ＝CD ．∵BE＜＜BD＝2，∴BE＝1，∴ BE＝ED ，∵四面体ABCE 与四面体ACDE 的高都是点 A 到平面BCD 的高h，∵ BE＝ED ，∴ S△DCE＝S△BCE，∴四面体ABCE 与四面体ACDE 的体积比为1．法二：设AD＝CD＝，则AC＝AB＝BC＝BD＝2，AO＝CO＝DO＝1，∴ BO＝＝，∴ BO2+DO2＝BD2，∴ BO⊥DO，以O 为原点，OA 为x 轴，OB 为y 轴，OD 为z 轴，建立空间直角坐标系，则C（﹣1，0，0），D（0，0，1），B（0，，0），A（1，0，0），设E（a，b，c），，（0≤λ≤1），则（a，b，c﹣1）＝λ（0，，﹣1），解得E（0，，1﹣λ），∴ ＝（1，），＝（﹣ 1 ，），∵AE⊥EC，∴＝﹣1+3λ2+ （1﹣λ）2＝0，由λ∈[0 ，1]，解得，∴ DE＝BE，∵四面体ABCE 与四面体ACDE 的高都是点 A 到平面BCD 的高h，∵DE＝BE，∴ S△DCE＝S△BCE，∴四面体ABCE 与四面体ACDE 的体积比为1．AEF⊥平面EFCB，EF＝2，四边形EFCB 是高为的等腰梯形，EF∥BC，O 为EF 的中点．1）求证：AO⊥CF；O 为EF 的中点，所以AO⊥ EF ⋯（ 1 分）又因为平面AEF⊥平面EFCB，AO? 平面AEF，平面AEF ∩平面EFCB ＝EF ，所以AO ⊥平面EFCB，⋯（ 4 分）又CF? 平面EFCB ，所以AO⊥ CF ⋯（ 5 分）（2）解：取BC 的中点G，连接OG．由题设知，OG⊥BC ⋯（ 6 分）由（1）知AO⊥平面EFCB ，又BC? 平面EFCB ，所以OA⊥BC，因为OG∩OA＝O，所以BC⊥平面AOG⋯（8 分）过O 作OH⊥AG，垂足为H，则BC⊥ OH ，因为AG∩BC＝G，所以OH⊥平面ABC．⋯（10 分）因为，所以，即O 到平面ABC 的距离为．（另外用等体积法亦可）⋯（12 分）10．直三棱柱ABC﹣A1B1C1 中，若∠ BAC＝90°，AB＝AC＝AA1，则异面直线BA1 与B1C 所成角的余弦值为（A．0 B．C．。
高二数学：立体几何垂直的证明练习题
高二数学：立体几何垂直的证明练习题主编：贾海琴老师1、如图,.AB O PA O C O是圆的直径，垂直圆所在的平面，是圆上的点(I)求证:BC PAC⊥平面；(II)设//.∆为的中点，为的重心，求证：平面Q PA G AOC QG PBC2、如图,在在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2,AD=CD=7,PA=3,∠ABC=120°,G为线段PC上的点.证明:BD⊥面PAC ;3、如图.在直菱柱ABC-A1B1C1中,,AB=AC,D是BC的中点,点E在棱BB1上运动.证明:AD⊥C1E;4、如图,在四棱锥P ABCD -中,//AB CD ,AB AD ⊥,2CD AB =,平面PAD ⊥底面ABCD ,PA AD ⊥,E 和F 分别是CD 和PC 的中点,求证: (1)PA ⊥底面ABCD ;(2)//BE 平面PAD ;(3)平面BEF ⊥平面PCD5、如图,三棱柱111ABC A B C -中,CA CB =,1AB AA =,160BAA ∠=.证明:1AB AC ⊥; C 1B 1AA 1B C6、如图,四棱锥P ABCD -中,,AB AC AB PA ⊥⊥,,2AB CD AB CD =∥,,,,,E F G M N 分别为,,,,PB AB BC PD PC 的中点（1）求证:CE PAD ∥平面; （2）求证:EFG EMN ⊥平面平面7、如图,四棱锥P ABCD -的底面ABCD 是边长为2的菱形,60BAD ∠=.已知2,PB PD PA === .证明:PC BD ⊥8、如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,BC AB ⊥,AB AS =,过A 作SB AF ⊥,垂足为F ,点G E ，分别是棱SC SA ，的中点. 求证:（1）平面//EFG 平面ABC ;（2）SA BC ⊥.9、如图，三棱柱ABC －A 1B 1C 1中，侧棱垂直底面，∠ACB=90°，AC=BC=12AA 1，D 是棱AA 1的中点。
微专题3 立体几何中的平行与垂直问题(解析版)
微专题3 立体几何中的平行与垂直问题（解析版）题型一、线面平行与垂直证明直线与平面的平行与垂直问题，一定要熟练记忆直线与平面的平行与垂直判定定理和性质定理，切记不可缺条件。
直线与平面的平行有两种方法：一是在面内找线；二是通过面面平行转化。
直线与平面垂直关键是找两条相交直线。
例1、如图，在四棱锥P ABCD中，M，N分别为棱P A，PD的中点．已知侧面P AD⊥底面ABCD，底面ABCD是矩形，DA＝DP.求证：(1)MN∥平面PBC；MD⊥平面P AB.【证明】(1)在四棱锥P－ABCD中，M，N分别为棱P A，PD的中点，所以MN∥AD又底面ABCD是矩形，所以BC∥AD.所以MN∥BC.又BC⊂平面PBC，MN⊄平面PBC，所以MN∥平面PBC.(2)因为底面ABCD是矩形，所以AB⊥AD.又侧面P AD⊥底面ABCD，侧面P AD∩底面ABCD＝AD，AB⊂底面ABCD，所以AB⊥侧面P AD.又MD⊂侧面P AD，所以AB⊥MD.因为DA＝DP，又M为AP的中点，从而MD⊥P A.又P A，AB在平面P AB内，P A∩AB＝A，所以MD⊥平面P AB【类比训练】如图所示，在三棱柱ABCA1B1C1中，四边形AA1B1B为矩形，平面AA1B1B⊥平面ABC，点E，F分别是侧面AA1B1B，BB1C1C对角线的交点．(1) 求证：EF∥平面ABC；(2) 求证：BB1⊥AC.解答(1)在三棱柱ABCA1B1C1中，四边形AA1B1B，四边形BB1C1C均为平行四边形，E，F分别是侧面AA1B1B，BB1C1C对角线的交点，所以E，F分别是AB1，CB1的中点，所以EF∥AC.(4分)因为EF⊄平面ABC，AC⊂平面ABC，所以EF∥平面ABC.(8分)(2)因为四边形AA1B1B为矩形，所以BB1⊥AB.因为平面AA1B1B⊥平面ABC，且平面AA1B1B∩平面ABC＝AB，BB1⊂平面AA1B1B，所以BB1⊥平面ABC.(12分)因为AC⊂平面ABC，所以BB1⊥AC.(14分)例2、如图，在三棱柱ABCA1B1C1中，AB＝AC，A1C⊥BC1，AB1⊥BC1，D，E分别是AB1和BC的中点．求证：(1)DE∥平面ACC1A1；(2)AE⊥平面BCC1B1.解答(1)连结A1B，在三棱柱ABCA1B1C1中，AA1∥BB1且AA1＝BB1，所以四边形AA1B1B是平行四边形．又因为D是AB1的中点，所以D也是BA1的中点．(2分)在△BA1C中，D和E分别是BA1和BC的中点，所以DE∥A1C.又因为DE⊄平面ACC1A1，A1C⊂平面ACC1A1，所以DE∥平面ACC1A1.(6分)(2)由(1)知DE∥A1C，因为A1C⊥BC1，所以BC1⊥DE.(8分)又因为BC1⊥AB1，AB1∩DE＝D，AB1，DE⊂平面ADE，所以BC1⊥平面ADE.又因为AE⊂平在ADE，所以AE⊥BC1.(10分)在△ABC中，AB＝AC，E是BC的中点，所以AE⊥BC.(12分)因为AE⊥BC1，AE⊥BC，BC1∩BC＝B，BC1，BC⊂平面BCC1B1，所以AE⊥平面BCC1B1. (14分)【类比训练】三棱锥DABC中，已知AC⊥BC，AC⊥DC，BC＝DC，E，F分别为BD，CD的中点．求证：(1) EF∥平面ABC；(2) BD⊥平面ACE.解答(1)三棱锥DABC中，因为E为DB的中点，F为DC的中点，所以EF∥BC，(3分)因为BC⊂平面ABC，EF⊄平面ABC，所以EF∥平面ABC.(6分)(2)因为AC⊥BC，AC⊥DC，BC∩DC＝C，BC，DC⊂平面BCD所以AC⊥平面BCD，(8分)因为BD⊂平面BCD，所以AC⊥BD，(10分)因为DC＝BC，E为BD的中点，所以CE⊥BD，(12分)因为AC∩CE＝C，AC，CE⊂平面ACE，所以BD⊥平面ACE.(14分)题型二、线面与面面平行与垂直证明平面与平面的平行与垂直问题，一定要熟练记忆平面与平面的平行与垂直判定定理和性质定理，切记不可缺条件。
(完整版)立体几何证明垂直专项含练习题及答案.doc
精品字里行间精品文档立体几何证明 ------ 垂直一. 复习引入1.空间两条直线的位置关系有： _________,_________,_________三种。
2.（公理 4）平行于同一条直线的两条直线互相 _________.3.直线与平面的位置关系有 _____________,_____________,_____________三种。
4.直线与平面平行判定定理 : 如果 _________的一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行5.直线与平面平行性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么 _________________________.6.两个平面的位置关系 :_________,_________.7.判定定理 1：如果一个平面内有 _____________直线都平行于另一个平面，那么这两个平面平行 .8.线面垂直性质定理：垂直于同一条直线的两个平面 ________.9.如果两个平行平面同时和第三个平面相交，那么它们的________平行 .10.如果两个平面平行，那么其中一个平面内的所有直线都 _____于另一个平面 . 二．知识点梳理知识点一、直线和平面垂直的定义与判定定义语言描述如果直线l 和平面α内的任意一条直线都垂直，我们就说直线 l 与平面互相垂直，记作 l ⊥α图形判定一条直线与一个平面内的两条相交直线都垂直，则这条直线与该平面垂直 .条件 b 为平面α内的任一直线，而 l 对这l ⊥m， l ⊥n，m∩n＝B，m ，一直线总有 l ⊥αn结论l ⊥l ⊥要点诠释：定义中“平面内的任意一条直线”就是指“平面内的所有直线”，这与“无数条直线”不同（线线垂直线面垂直）知识点二、直线和平面垂直的性质性质语言描述一条直线垂直于一个平面，那么这条垂直于同一个平面的两条直线平行.直线垂直于这个平面内的所有直线图形条件结论知识点三、二面角Ⅰ .二面角：从一条直线出发的两个半平面所组成的图形叫二面角（dihedral angle）. 这条直线叫做二面角的棱，这两个半平面叫做二面角的面. 记作二面角－AB－. （简记P－AB－Q）二面角的平面角的三个特征:ⅰ.点在棱上ⅱ.线在面内ⅲ .与棱垂直Ⅱ .二面角的平面角：在二面角－l－的棱l上任取一点O，以点O为垂足，在半平面,内分别作垂直于棱 l 的射线 OA 和 OB ，则射线 OA 和 OB 构成的AOB叫做二面角的平面角.作用：衡量二面角的大小；范围：001800.知识点四、平面和平面垂直的定义和判定定义判定文字描述两个平面相交，如果它们所成的二面一个平面过另一个平面的垂线，则这角是直二面角，就说这两个平面垂两个平面垂直直.图形结果α∩β =lα-l-β=90oα⊥β（垂直问题中要注意题目中的文字表述，特别是“任何”“ 随意”“无数”等字眼）三．常用证明垂直的方法立体几何中证明线面垂直或面面垂直都可转化为线线垂直，而证明线线垂直一般有以下的一些方法：（ 1）通过“平移”。
立体几何经典试题（含答案）
1. 如图，三棱柱ABC －A 1B 1C 1中，侧棱垂直底面，∠ACB=90°，AC=BC=12AA 1，D 是棱AA 1的中点的中点(Ｉ)证明：平面BDC 1⊥平面BDC（Ⅱ）平面BDC 1分此棱柱为两部分，求这两部分体积的比. 【解析】（Ⅰ）由题设知BC BC⊥⊥1CC ,BC ,BC⊥⊥AC AC，，1CC AC C Ç=,∴BC ^面11ACC A , , 又又∵1DC Ì面11ACC A ，∴1DC BC ^,由题设知01145A DC ADC Ð=Ð=,∴1CDC Ð=090,即1DC DC ^, 又∵DC BC C Ç=, , ∴∴1DC ⊥面BDC , , ∵∵1DC Ì面1BDC ， ∴面BDC ⊥面1BDC ；（Ⅱ）设棱锥1B DACC -的体积为1V ，AC =1，由题意得，1V =1121132+´´´=12，由三棱柱111ABC A B C -的体积V =1，∴11():V V V -=1:1， ∴平面1BDC 分此棱柱为两部分体积之比为1:1. 2. 如图5所示，在四棱锥P ABCD -中，AB ^平面PAD ，//AB CD ，PD AD =，E 是PB 的中点，F 是CD 上的点且12DF AB =，PH 为△PAD 中AD 边上的高. （1）证明：PH ^平面ABCD ；（2）若1PH =，2AD =，1FC =，求三棱锥E BCF -的体积；的体积；（3）证明：EF ^平面PAB . B 1C B A D C 1A 1【解析】（1）证明：因为AB ^平面PAD ，所以PH AB ^。
因为PH 为△PAD 中AD 边上的高，边上的高， 所以PH AD ^。
因为AB AD A = ，所以PH ^平面ABCD 。
（2）连结BH ，取BH 中点G ，连结EG 。
高中数学必修2立体几何专题-线面垂直专题典型例题精选精讲
线面垂直的证明中的找线技巧◆通过计算,运用勾股定理寻求线线垂直１ 如图1,在正方体1111ABCD A B C D -中,M 为1CC 的中点,ＡＣ交BD 于点O ,求证:1A O ⊥平面ＭＢD .证明:连结MO ，1A M，∵D Ｂ⊥1A A ,D Ｂ⊥ＡC ，1A AAC A =，∴DB ⊥平面11A ACC ，而1AO ⊂平面11A ACC ∴ＤB ⊥1A O . 设正方体棱长为a ，则22132A O a =,2234MO a =.在Rt △11A C M 中,22194A M a =．∵22211A O MO A M +=，∴1AO OM ⊥． ∵OM ∩D Ｂ=O ，∴ 1A O ⊥平面MBD . 评注：在证明垂直关系时，有时可以利用棱长、角度大小等数据，通过计算来证明.◆利用面面垂直寻求线面垂直２ 如图2,P 是△A ＢC 所在平面外的一点,且PA ⊥平面ABC ,平面PAC ⊥平面PBC .求证：B Ｃ⊥平面ＰＡC .证明：在平面PAC 内作A Ｄ⊥PC 交ＰC 于Ｄ.因为平面PAC ⊥平面PB Ｃ，且两平面交于P Ｃ,AD ⊂平面PAC ,且A Ｄ⊥PC ， 由面面垂直的性质，得ＡD ⊥平面PB Ｃ． 又∵BC ⊂平面P ＢC ，∴AD ⊥BC .∵PA ⊥平面AB Ｃ，BC ⊂平面ABC ，∴PA ⊥ＢC .∵AD ∩PA =A ，∴BC ⊥平面PAC ．(另外还可证BC 分别与相交直线AD ，A Ｃ垂直,从而得到BC ⊥平面PAC ）.评注：已知条件是线面垂直和面面垂直,要证明两条直线垂直,应将两条直线中的一条纳入一个平面中,使另一条直线与该平面垂直，即从线面垂直得到线线垂直．在空间图形中,高一级的垂直关系中蕴含着低一级的垂直关系，通过本题可以看到，面面垂直⇒线面垂直⇒线线垂直．一般来说,线线垂直或面面垂直都可转化为线面垂直来分析解决,其关系为:线线垂直−−−→←−−−判定性质线面垂直−−−→←−−−判定性质面面垂直.这三者之间的关系非常密切,可以互相转化，从前面推出后面是判定定理，而从后面推出前面是性质定理．同学们应当学会灵活应用这些定理证明问题.下面举例说明．3 如图1所示，ABCD 为正方形，SA ⊥平面AB ＣD ,过A 且垂直于SC 的平面分别交SB SC SD ，，于E F G ，，．求证:AE SB ⊥,AG SD ⊥．证明：∵SA ⊥平面ＡBCD , ∴SA BC ⊥.∵AB BC ⊥，∴BC ⊥平面SAB ．又∵AE ⊂平面SAB ，∴BC AE ⊥．∵SC ⊥平面AEFG ,∴SC AE ⊥．∴AE ⊥平面ＳBC ．∴AE SB ⊥.同理可证AG SD ⊥．评注：本题欲证线线垂直，可转化为证线面垂直，在线线垂直与线面垂直的转化中,平面起到了关键作用，同学们应多注意考虑线和线所在平面的特征，从而顺利实现证明所需要的转化.４ 如图2，在三棱锥A －BCD 中，BC ＝AC ,AD =BD ,作BE ⊥CD ,E 为垂足，作ＡH ⊥B Ｅ于H ．求证：AH ⊥平面B ＣＤ.证明：取A Ｂ的中点Ｆ，连结CF ，ＤF . ∵ACBC =,∴CF AB ⊥．∵AD BD =,∴DF AB ⊥.又CF DF F =，∴AB ⊥平面ＣＤF ． ∵CD ⊂平面CD Ｆ，∴CD AB ⊥． 又CD BE ⊥，BE AB B =, ∴CD ⊥平面A ＢE ，CD AH ⊥．∵AH CD ⊥，AH BE ⊥,CD BE E =,∴ AH ⊥平面ＢCD ．评注:本题在运用判定定理证明线面垂直时,将问题转化为证明线线垂直;而证明线线垂直时，又转化为证明线面垂直．如此反复,直到证得结论.5 如图３，AB 是圆O 的直径,C 是圆周上一点，PA ⊥平面ABC .若AE ⊥PC ，E 为垂足,F 是P Ｂ上任意一点， 求证：平面AEF ⊥平面PBC ．证明：∵AB 是圆O 的直径,∴AC BC ⊥.∵PA ⊥平面AB Ｃ,BC⊂平面A ＢC ，∴PA BC ⊥．∴BC ⊥平面ＡPC . ∵BC ⊂平面P ＢC ，∴平面AP Ｃ⊥平面ＰＢC ．∵AE ⊥ＰC ，平面APC ∩平面P ＢC =P Ｃ， ∴AE ⊥平面PBC .∵AE ⊂平面AE Ｆ，∴平面AE Ｆ⊥平面PB Ｃ． 评注:证明两个平面垂直时，一般可先从现有的直线中寻找平面的垂线，即证线面垂直,而证线面垂直则需从已知条件出发寻找线线垂直的关系.6. 空间四边形ABCD 中,若ＡB ⊥CD ，BC ⊥AD,求证:ＡC ⊥ＢＤAD B O C证明：过A 作ＡO ⊥平面ＢＣD 于O 。
高中数学高考总复习立体几何各种平行与垂直的判断习题及详解
高中数学高考总复习立体几何各种平行与垂直的判断习题及详解一、选择题1．设b 、c 表示两条不重合的直线，α、β表示两个不同的平面，则下列命题是真命题的是( )A.⎭⎪⎬⎪⎫b ⊂αc ∥α⇒b ∥c B.⎭⎪⎬⎪⎫b ⊂αb ∥c ⇒c ∥α C.⎭⎪⎬⎪⎫c ∥αc ⊥β⇒α⊥βD.⎭⎪⎬⎪⎫c ∥αα⊥β⇒c ⊥β [答案] C[解析] 选项A 中的条件不能确定b ∥c ；选项B 中条件的描述也包含着直线c 在平面α内，故不正确；选项D 中的条件也包含着c ⊂β，c 与β斜交或c ∥β，故不正确．[点评] 线线、线面、面面平行或垂直的性质定理和判定定理是解决空间图形位置关系推理的重要依据，在推理中容易把平面几何中的一些结论引用到立体几何中造成错误．对空间中位置关系的考虑不周，也是造成判断错误的因素，所以做这类题目应当考虑全面．2．定点A 和B 都在平面α内，定点P ∉α，PB ⊥α，C 是α内异于A 和B 的动点，且PC ⊥AC .那么，动点C 在平面α内的轨迹是( )A ．一条线段，但要去掉两个点B ．一个圆，但要去掉两个点C ．一个椭圆，但要去掉两个点D ．半圆，但要去掉两个点 [答案] B[解析] 连接BC ，∵PB ⊥α，∴AC ⊥PB . 又∵PC ⊥AC ，∴AC ⊥BC .∴C 在以AB 为直径的圆上．故选B. 3．设α、β、γ为平面，给出下列条件： ①a 、b 为异面直线，a ⊂α，b ⊂β，a ∥β，b ∥α； ②α内不共线的三点到β的距离相等； ③α⊥γ，β⊥γ.其中能使α∥β成立的条件的个数是( ) A ．0 B ．1 C ．2D ．3[答案] B[解析]对于②，三个点不一定在同侧；对于③，面面的垂直关系不具有传递性．对于①，过b作平面γ∩α＝b′，则b∥b′，∵a与b异面，∴a与b′相交，容易证明b′∥β，又∵a∥β，∴α∥β，故只有①正确．4．a、b、c是三条直线，α、β是两个平面，b⊂α，c⊄α，则下列命题不成立的是() A．若α∥β，c⊥α，则c⊥βB．“若b⊥β，则α⊥β”的逆命题C．若a是c在α内的射影，b⊥a，则b⊥cD．“若b∥c，则c∥α”的逆否命题[答案] B[解析]一条直线垂直于两个平行平面中的一个，则垂直于另一个，故A正确；若c∥α，∵a是c在α内的射影，∴c∥a，∵b⊥a，∴b⊥c；若c与α相交，则c与a相交，由线面垂直的性质与判定定理知，若b⊥a，则b⊥c，故C正确；∵b⊂α，c⊄α，b∥c，∴c∥α，因此原命题“若b∥c，则c∥α”为真，从而其逆否命题也为真，故D正确．如图，α⊥β，α∩β＝l，b⊂α，b与l不垂直，则b与β不垂直，∴B不成立．5．(文)(2010·天津河东区)已知直线a⊂平面α，直线AO⊥α，垂足为O，P A∩α＝P，若条件p：直线OP不垂直于直线a，条件q：直线AP不垂直于直线a，则条件p是条件q的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件[答案] C故OP⊥a⇔AP⊥a，从而p⇔q.(理)(2010·河南新乡调研)设α、β、γ为平面，l、m、n为直线，则m⊥β的一个充分条件为()A．α⊥β，α∩β＝l，m⊥lB．n⊥α，n⊥β，m⊥αC．α∩γ＝m，α⊥γ，β⊥γD．α⊥γ，β⊥γ，m⊥α[答案] B[解析]如图①知A错；如图②知C错；如图③在正方体中，两侧面α与β相交于l，都与底面γ垂直，γ内的直线m⊥α，但m与β不垂直，故D错．6．如图，四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°.将△ADB 沿BD折起，使平面ABD⊥平面BCD，构成三棱锥A－BCD，则在三棱锥A－BCD中，下列命题正确的是()A．平面ABD⊥平面ABCB．平面ADC⊥平面BDCC．平面ABC⊥平面BDCD．平面ADC⊥平面ABC[答案] D[解析]∵在四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°，∴BD ⊥CD.又平面ABD⊥平面BCD，且平面ABD∩平面BCD＝BD，故CD⊥平面ABD，则CD⊥AB.又AD⊥AB，故AB⊥平面ADC.∴平面ABC⊥平面ADC.7．(文)(2010·重庆文)到两互相垂直的异面直线的距离相等的点()A．只有1个B．恰有3个C ．恰有4个D ．有无穷多个[答案] D[解析] 过两条互相垂直的异面直线的公垂线段中点且与两条直线都成45°角的直线上所有点到两条直线的距离都相等，故选D.(理)(2010·全国Ⅱ理)与正方体ABCD －A 1B 1C 1D 1的三条棱AB 、CC 1、A 1D 1所在直线的距离相等的点( )A ．有且只有1个B ．有且只有2个C ．有且只有3个D ．有无数个[答案] D[解析] 如图连结B 1D ，可知B 1D 上的点到AB 、CC 1、A 1D 1的距离均相等，故选D.8．(文)平行四边形ABCD 的对角线交点为O ，点P 在平面ABCD 之外，且P A ＝PC ，PD ＝PB ，则PO 与平面ABCD 的关系是( )A ．斜交B ．平行C ．垂直D ．无法确定[答案] C[解析] ∵P A ＝PC ，∴PO ⊥AC ，∵PB ＝PD ，∴PO ⊥BD ，∵AC ∩BD ＝O ，∴PO ⊥平面ABCD .(理)棱长都为2的直平行六面体(底面为平行四边形的棱柱)ABCD －A 1B 1C 1D 1中，∠BAD ＝60°，则对角线A 1C 与侧面DCC 1D 1所成角的正弦值为( )A.12B.22C.34D.38 [答案] C[解析] 如图所示，过点A 1作直线A 1M ⊥D 1C 1，交D 1C 1延长线于点M ，连结MC ，A 1C ，则可得A 1M ⊥面DD 1C 1C ，∠A 1CM 就是直线A 1C 与面DD 1C 1C 所成的角．∵所有棱长均为2，∠A 1D 1C 1＝120°，∴A 1M ＝A 1D 1sin60°＝3，又A 1C ＝AC 12＋CC 12＝(23)2＋22＝4， ∴sin ∠A 1CM ＝A 1M A 1C ＝34，故应选C.[点评] 求直线与平面所成角时，一般要先观察分析是否可以找(或作)出直线上一点到平面的垂线，若能找出则可以将线面角归结到一个直角三角形中求解．若不容易找出线面角，则可以考虑能否进行转化或借助于空间向量求解，请再练习下题：(2010·全国Ⅰ文)正方体ABCD －A 1B 1C 1D 1中BB 1与平面ACD 1所成角的余弦值为( ) A.23B.33C.23D.63[答案] D[解析] 解法1：设BD 与AC 交于点O ，连结D 1O ，∵BB 1∥DD 1，∴DD 1与平面ACD 1所成的角就是BB 1与平面ACD 1成的角．∵AC ⊥BD ，AC ⊥DD 1，DD 1∩BD ＝D ，∴AC ⊥平面DD 1B ，平面DD 1B ∩平面ACD 1＝OD 1，∴OD 1是DD 1在平面ACD 1内的射影，故∠DD 1O 为直线DD 1与平面ACD 1所成的角，设正方体的棱长为1，则DD 1＝1，DO ＝22，D 1O ＝62，∴cos ∠DD 1O ＝DD 1D 1O ＝63，∴BB 1与平面ACD 1所成角的余弦值为63. 解法2：因为BB 1∥DD 1，所以BB 1与平面ACD 1所成角和DD 1与平面ACD 1所成角相等，设DO ⊥平面ACD 1，由等体积法得VD －ACD 1＝VD 1－ACD ，即13S △ACD 1·DO ＝13S △ACD ·DD 1.设DD 1＝a ，则S △ACD 1＝12AC ·AD 1sin60°＝12×(2a )2×32＝32a 2，S △ACD ＝12AD ·CD ＝12a 2.所以DO ＝S △ACD ·DD 1S △ACD 1＝a 33a 2＝33a ，设DD 1与平面ACD 1所成角为θ，则sin θ＝DO DD 1＝33， 所以cos θ＝63.解法3：建立如图所示空间直角坐标系D －xyz ，设边长为1，BB 1→＝(0,0,1)，平面ACD 1的一个法向量n ＝(1,1,1)，∴cos 〈BB 1→，n 〉＝13·1＝33，∴BB 1与面ACD 1所成角的余弦值为63. 9．(文)(2010·鞍山一中模拟)已知直线l ⊥平面α，直线m ⊂平面β，给出下列命题： ①α∥β⇒l ⊥m ；②α⊥β⇒l ∥m ；③l ∥m ⇒α⊥β；④l ⊥m ⇒α⊥β，其中正确的是( ) A ．①②③ B ．②③④ C ．②④ D ．①③ [答案] D∵m ⊂β，∴此时推不出l ∥m ，故②错，排除A ，故选D. (理)若平面α与平面β相交，直线m ⊥α，则( ) A ．β内必存在直线与m 平行，且存在直线与m 垂直 B ．β内不一定存在直线与m 平行，不一定存在直线与m 垂直 C ．β内不一定存在直线与m 平行，但必存在直线与m 垂直 D ．β内必存在直线与m 平行，不一定存在直线与m 垂直 [答案] C[解析] 若β内存在直线与m 平行，则必有β⊥α，但α与β不一定垂直，故否定A 、D ；在β内必存在与m 在β内射影垂直的直线，从而此线必与m 垂直，否定B ，故选C.10．(文)(2010·芜湖十二中)已知两条不同的直线m 、n ，两个不同的平面α、β，则下列命题中的真命题是( )A ．若m ⊥α，n ⊥β，α⊥β，则m ⊥nB ．若m ∥α，n ∥β，α∥β，则m ∥nC ．若m ⊥α，n ∥β，α⊥β，则m ⊥nD ．若m ∥α，n ⊥β，α⊥β，则m ∥n[答案] A[解析]如图(1)，m⊥α，n⊥α满足n∥β，但m∥n，故C错；如图(2)知B错；如图(3)正方体中，m∥α，n⊥β，α⊥β，知D错．(理)(2010·浙江金华十校模考)设a，b为两条直线，α，β为两个平面，下列四个命题中真命题是()A．若a，b与α所成角相等，则a∥bB．若a∥α，b∥β，α⊥β，则a⊥bC．若a⊂α，b⊂β，a⊥b，则α⊥βD．若a⊥α，b⊥β，α⊥β，则a⊥b[答案] D[解析]正四棱锥P－ABCD中，P A、PC与底面ABCD所成角相等，但P A与PC相交，∴A错；如图(1)正方体中，a∥b∥c，满足a∥α，b∥β，α⊥β，故B错；图(2)正方体中，上、下底面为β、α，a、b为棱，满足a⊂α，b⊂β，a⊥b，但α∥β，故C错；二、填空题11．对于四面体ABCD，给出下列四个命题：①若AB＝AC，BD＝CD，则BC⊥AD；②若AB＝CD，AC＝BD，则BC⊥AD；③若AB ⊥AC ，BD ⊥CD ，则BC ⊥AD ； ④若AB ⊥CD ，AC ⊥BD ，则BC ⊥AD .其中真命题的序号是________．(把你认为正确命题的序号都填上) [答案] ①④[解析] 本题考查四面体的性质，取BC 的中点E ，则BC ⊥AE ，BC ⊥DE ，∴BC ⊥面ADE ，∴BC ⊥AD ，故①正确．设O 为A 在面BCD 上的射影，依题意OB ⊥CD ，OC ⊥BD ，∴O 为垂心，∴OD ⊥BC ，∴BC ⊥AD ，故④正确，②③易排除，故答案为①④.12．(文)P 为△ABC 所在平面外一点，P A 、PB 、PC 与平面ABC 所成角均相等，又P A 与BC 垂直，那么△ABC 形状可以是________．①正三角形 ②等腰三角形 ③非等腰三角形 ④等腰直角三角形(将你认为正确的序号全填上) [答案] ①②④[解析] 设点P 在底面ABC 上的射影为O ，由P A 、PB 、PC 与平面ABC 所成角均相等，得OA ＝OB ＝OC ，即点O 为△ABC 的外心，又由P A ⊥BC ，得OA ⊥BC ，即AO 为△ABC 中BC 边上的高线，∴AB ＝AC ，即△ABC 必为等腰三角形，故应填①②④.(理)如图将边长为1的正方形纸板ABCD 沿对角线AC 折起，使平面ACB ⊥平面ACD ，然后放在桌面上，使点B 、C 、D 落在桌面，这时点A 到桌面的距离为________．[答案]63[解析] 取AC 中点O ，∵OB ⊥AC ，OD ⊥AC ，OB ∩OD ＝O ，∴AC ⊥平面BOD ，∴∠BOD ＝90°.又∵BO ＝OD ＝22，∴BD ＝1，S △BOD ＝14， ∴V A －BCD ＝13S △BOD ·AC ＝212，设A 到桌面距离为h ，V A －BCD ＝13S △BCD ·h ＝13×34×h ＝212，∴h ＝63，即A 到桌面距离为63. 13．(2010·安徽淮北一中)已知四棱锥P －ABCD 的底面ABCD 是矩形，P A ⊥底面ABCD ，点E 、F 分别是棱PC 、PD 的中点，则①棱AB 与PD 所在的直线垂直； ②平面PBC 与平面ABCD 垂直； ③△PCD 的面积大于△P AB 的面积；④直线AE与直线BF是异面直线．以上结论正确的是________．(写出所有正确结论的编号)[答案]①③[解析]由条件可得AB⊥平面P AD，所以AB⊥PD，故①正确；∵P A⊥平面ABCD，∴平面P AB、平面P AD都与平面ABCD垂直，故平面PBC不可能与平面ABCD垂直，②错；S△PCD＝12CD·PD，S△P AB＝12AB·P A，由AB＝CD，PD>P A知③正确；由E、F分别是棱PC、PD的中点可得EF∥CD，又AB∥CD，所以EF∥AB，故AE与BF共面，故④错．14．(文)(2010·河北唐山)如图，在直四棱柱ABCD－A1B1C1D1中，∠ADC＝90°，且AA1＝AD＝DC＝2，M∈平面ABCD，当D1M⊥平面A1C1D时，DM＝________.[答案]2 2[解析]∵DA＝DC＝DD1且DA、DC、DD1两两垂直，故当点M使四边形ADCM为正方形时，D1M⊥平面A1C1D，∴DM＝2 2.(理)(2010·安徽巢湖市质检)已知正方体ABCD－A1B1C1D1的棱长为1，E，F，G分别是AB，BC，B1C1的中点．下列命题正确的是________(写出所有正确命题的编号)．①以正方体的顶点为顶点的三棱锥的四个面最多只有三个面是直角三角形；②P在直线FG上运动时，AP⊥DE；③Q在直线BC1上运动时，三棱锥A－D1QC的体积不变；④M是正方体的面A1B1C1D1内到点D和C1距离相等的点，则M点的轨迹是一条线段．[答案]②③④[解析]三棱锥A1－ABC的四个面都是Rt△，故①错；F在FG上运动时，PF⊥平面ABCD，∴PF⊥DE，又在正方体ABCD中，E、F为AB、BC中点，∴AF⊥DE，∴DE⊥平面P AF，∴DE⊥P A，故②真；VA－D1QC＝VQ－AD1C，∵BC1∥AD1，∴BC1∥平面AD1C，∴无论点Q在BC1上怎样运动，Q到平面AD1C距离都相等，故③真；到点D和C1距离相等的点在经过线段C1D的中点与DC1垂直的平面α上，故点M为平面α与正方体的面A1B1C1D1相交线段上的点，这条线段即A1D1.三、解答题15．(文)(2010·江苏，16)如图，四棱锥P －ABCD 中，PD ⊥平面ABCD ，PD ＝DC ＝BC ＝1，AB ＝2，AB ∥DC ，∠BCD ＝90°(1)求证：PC ⊥BC(2)求点A 到平面PBC 的距离．[解析] (1)∵PD ⊥平面ABCD ，BC ⊂平面ABCD ，∴PD ⊥BC . 由∠BCD ＝90°知，BC ⊥DC ， ∵PD ∩DC ＝D ，∴BC ⊥平面PDC ， ∴BC ⊥PC .(2)设点A 到平面PBC 的距离为h ， ∵AB ∥DC ，∠BCD ＝90°，∴∠ABC ＝90°， ∵AB ＝2，BC ＝1，∴S △ABC ＝12AB ·BC ＝1，∵PD ⊥平面ABCD ，PD ＝1， ∴V P －ABC ＝13S △ABC ·PD ＝13，∵PD ⊥平面ABCD ，∴PD ⊥DC ， ∵PD ＝DC ＝1，∴PC ＝2， ∵PC ⊥BC ，BC ＝1， ∴S △PBC ＝12PC ·BC ＝22，∵V A －PBC ＝V P －ABC ， ∴13S △PBC ·h ＝13，∴h ＝2， ∴点A 到平面PBC 的距离为 2.(理)如图，已知三棱锥A －BPC 中，AP ⊥PC ，AC ⊥BC ，M 为AB 的中点，D 为PB 中点，且△PMB 为正三角形．(1)求证：DM ∥平面APC ； (2)求证：平面ABC ⊥平面APC ；(3)若BC ＝4，AB ＝20，求三棱锥D －BCM 的体积．[解析] (1)∵M 为AB 中点，D 为PB 中点，∴DM ∥AP ，又DM ⊄平面APC ，AP ⊂平面APC .∴DM ∥平面APC .(2)∵△PMB 为正三角形，且D 为PB 中点，∴MD ⊥PB ，又由(1)知MD ∥AP ，∴AP ⊥PB又已知AP ⊥PC ，∴AP ⊥平面PBC ，∴AP ⊥BC ，又∵AC ⊥BC∴BC ⊥平面APC∴平面ABC ⊥平面APC .(3)∵AB ＝20，∴MP ＝10，∴PB ＝10又BC ＝4，PC ＝100－16＝221∴S △BDC ＝12S △PBC ＝14PC ·BC ＝14×4×221 ＝221又MD ＝12AP ＝12202－102＝5 3 ∴V D －BCM ＝V M －BCD ＝13S △BDC ·DM ＝13×221×5 3 ＝107.16．(文)如图，已知在直四棱柱ABCD －A1B 1C 1D 1中，AD ⊥DC ，AB ∥DC ，DC ＝DD 1＝2AD ＝2AB ＝2.(1)求证：DB ⊥平面B 1BCC 1；(2)设E 是DC 上一点，试确定E 的位置，使得D 1E ∥平面A 1BD ，并说明理由．[解析] (1)证明：∵AB ∥DC ，AD ⊥DC ，∴AB ⊥AD ，在Rt △ABD 中，AB ＝AD ＝1，∴BD ＝2，易求BC ＝2，又∵CD ＝2，∴BD ⊥BC .又BD ⊥BB 1，B 1B ∩BC ＝B ，∴BD ⊥平面B 1BCC 1.(2)DC 的中点即为E 点．∵DE ∥AB ，DE ＝AB ，∴四边形ABED 是平行四边形．∴AD 綊BE .又AD 綊A 1D 1，∴BE 綊A 1D 1，∴四边形A 1D 1EB 是平行四边形．∴D 1E ∥A 1B .∵D 1E ⊄平面A 1BD ，A 1B ⊂平面A 1BD .∴D 1E ∥平面A 1BD .(理)在三棱锥P －ABC 中，△P AC 和△PBC 是边长为2的等边三角形，AB ＝2，O 是AB 中点．(1)在棱P A 上求一点M ，使得OM ∥平面PBC ；(2)求证：平面P AB ⊥平面ABC ；(3)求二面角P －BC －A 的余弦值．[解析] (1)当M 为棱P A 的中点时，OM ∥平面PBC .证明如下：∵M 、O 分别为P A 、AB 中点，∴OM ∥PB又PB ⊂平面PBC ，OM ⊄平面PBC∴OM ∥平面PBC .(2)连结OC 、OP∵AC ＝CB ＝2，O 是AB 中点，AB ＝2，∴OC ⊥AB ，OC ＝1.同理，PO ⊥AB ，PO ＝1.又PC ＝2，∴PC 2＝OC 2＋PO 2＝2，∴∠POC ＝90°，∴PO ⊥OC .∵PO ⊥OC ，PO ⊥AB ，AB ∩OC ＝O ，∴PO ⊥平面ABC .∵PO ⊂平面P AB ，∴平面P AB ⊥平面ABC .(3)如图，建立空间直角坐标系O －xyz .则B (1,0,0)，C (0,1,0)，P (0,0,1)，∴BC →＝(－1,1,0)，PB →＝(1,0，－1)．由(2)知OP →＝(0,0,1)是平面ABC 的一个法向量．设平面PBC 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧ n ·BC →＝0n ·PB →＝0⇒⎩⎪⎨⎪⎧－x ＋y ＝0x －z ＝0， 令z ＝1，则x ＝1，y ＝1，∴n ＝(1,1,1)．∴cos 〈OP →，n 〉＝OP →·n |OP →|·|n |＝11×3＝33. ∵二面角P －BC －A 的平面角为锐角，∴所求二面角P －BC －A 的余弦值为33. 17．(文)如图，在△BCD 中，∠BCD ＝90°，BC ＝CD ＝1，AB ⊥平面BCD ，∠ADB ＝60°，E 、F 分别是AC 、AD 上的动点，且AE AC ＝AF AD ＝λ(0<λ<1)．(1)判断EF 与平面ABC 的位置关系并给予证明；(2)是否存在λ，使得平面BEF ⊥平面ACD ，如果存在，求出λ的值，如果不存在，说明理由．[分析] (1)EF 与平面ABC 相交于点E ，故其关系只能是垂直或斜交，由条件AE AC ＝AF AD＝λ易知，EF ∥CD ，由∠BCD ＝90°及AB ⊥平面BCD ，易证CD ⊥平面ABC .(2)∵EF ∥CD ，故问题相当于过点B 作一个平面与ACD 垂直，这样的平面一定存在，故只须计算出λ即可，由条件不难得到BE ⊥CD ，故只须BE ⊥AC .[解析] (1)EF ⊥平面ABC .证明：因为AB ⊥平面BCD ，所以AB ⊥CD ，又在△BCD 中，∠BCD ＝90°，所以BC ⊥CD ，又AB ∩BC ＝B ，所以CD ⊥平面ABC ，又在△ACD 中，E 、F 分别是AC 、AD 上的动点，且AEAC ＝AF AD＝λ(0<λ<1)，∴EF ∥CD ，∴EF ⊥平面ABC .(2)∵CD ⊥平面ABC ，BE ⊂平面ABC ，∴BE ⊥CD ，在Rt △ABD 中，∠ADB ＝60°，∴AB ＝BD tan60°＝6，则AC ＝AB 2＋BC 2＝7，当BE ⊥AC 时，BE ＝AB ×BC AC ＝67，AE ＝AB 2－BE 2＝367， 则AE AC ＝3677＝67，即λ＝AE AC ＝67时，BE ⊥AC ， 又BE ⊥CD ，AC ∩CD ＝C ，∴BE ⊥平面ACD ，∵BE ⊂平面BEF ，∴平面BEF ⊥平面ACD . 所以存在λ，且当λ＝67时，平面BEF ⊥平面ACD . [点评] 高考整体降低了对立体几何的考查要求，故线线、线面、面面的位置关系成了主要的考查点，其中平行、垂直的证明题与探索题是重点，同时也要注意由三视图与几何体的结合进行表面积与体积的计算等问题．(理)已知四棱锥P－ABCD 的三视图如下图所示，E 是侧棱PC 上的动点．(1)求四棱锥P －ABCD 的体积；(2)是否不论点E 在何位置，都有BD ⊥AE ？证明你的结论；(3)若点E 为PC 的中点，求二面角D －AE －B 的大小．[解析] (1)由三视图可知，四棱锥P －ABCD 的底面是边长为1的正方形，侧棱PC ⊥底面ABCD ，且PC ＝2.∴V P －ABCD ＝13S 正方形ABCD ·PC ＝13×12×2＝23， 即四棱锥P－ABCD 的体积为23.(2)不论点E 在何位置，都有BD ⊥AE .证明如下：连结AC ，∵ABCD 是正方形，∴BD ⊥AC .∵PC ⊥底面ABCD ，且BD ⊂平面ABCD ，∴BD ⊥PC .又∵AC ∩PC ＝C ，∴BD ⊥平面P AC .∵不论点E 在何位置，都有AE ⊂平面P AC .∴不论点E 在何位置，都有BD ⊥AE .(3)解法1：在平面DAE 内过点D 作DF ⊥AE 于F ，连结BF .∵AD ＝AB ＝1，DE ＝BE ＝12＋12＝2，AE ＝AE ＝3，∴Rt △ADE ≌Rt △ABE ，从而△ADF ≌△ABF ，∴BF ⊥AE .∴∠DFB 为二面角D －AE －B 的平面角．在Rt △ADE 中，DF ＝AD ·DE AE ＝1×23＝63， ∴BF ＝63. 又BD ＝2，在△DFB 中，由余弦定理得cos ∠DFB ＝DF 2＋BF 2－BD 22DF ·BF ＝－12， ∴∠DFB ＝2π3， 即二面角D －AE －B 的大小为2π3. 解法2：如图，以点C 为原点，CD ，CB ，CP 所在的直线分别为x ，y ，z 轴建立空间直角坐标系．则D (1,0,0)，A (1,1,0)，B (0,1,0)，E (0,0,1)，从而DA →＝(0,1,0)，DE →＝(－1,0,1)，BA→＝(1,0,0)，BE →＝(0，－1,1)．设平面ADE 和平面ABE 的法向量分别为n 1＝(x 1，y 1，z 1)，n 2＝(x 2，y 2，z 2)，由⎩⎪⎨⎪⎧n 1·DA →＝0n 1·DE →＝0⇒⎩⎪⎨⎪⎧ y 1＝0－x 1＋z 1＝0，取n 1＝(1,0,1)．由⎩⎪⎨⎪⎧n 2·BA →＝0n 2·BE →＝0⇒⎩⎪⎨⎪⎧ x 2＝0－y 2＋z 2＝0，取n 2＝(0，－1，－1)． 设二面角D －AE －B 的平面角为θ，则 cos θ＝n 1·n 2|n 1|·|n 2|＝－12·2＝－12， ∴θ＝2π3，即二面角D －AE －B 的大小为2π3.。
浙江专用2021届高考数学一轮复习专题八立体几何8.4直线平面垂直的判定与性质试题含解析
§8。
4 直线、平面垂直的判定与性质基础篇固本夯基【基础集训】考点一直线与平面垂直的判定与性质1。
已知m和n是两条不同的直线,α和β是两个不重合的平面,下面给出的条件中一定能推出m⊥β的是()A。
α⊥β且m⊂α B.α⊥β且m∥αC。
m∥n且n⊥β D.m⊥n且n∥β答案C2.下列命题中错误的是（）A.如果平面α外的直线a不平行于平面α，则平面α内不存在与a平行的直线B.如果平面α⊥平面γ，平面β⊥平面γ,α∩β=l,那么直线l⊥平面γC。
如果平面α⊥平面β,那么平面α内所有直线都垂直于平面βD.一条直线与两个平行平面中的一个平面相交，则必与另一个平面相交答案C3.如图，PA⊥圆O所在的平面,AB是圆O的直径，C是圆O上一点，E、F分别是A在PB、PC上的射影，给出下列结论：①AF⊥PB；②EF⊥PB;③AF⊥BC;④AE⊥平面PBC.其中正确命题的序号是.答案①②③4.《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑。
如图，在阳马P-ABCD中，侧棱PD⊥底面ABCD,且PD=CD，过棱PC的中点E，作EF⊥PB交PB于点F，连接DE,DF,BD，BE。
证明：PB⊥平面DEF.试判断四面体DBEF是不是鳖臑，若是,写出其每个面的直角（只需写出结论）;若不是，说明理由.解析因为PD⊥底面ABCD，所以PD⊥BC，由底面ABCD为长方形,得BC⊥CD,因为PD∩CD=D,所以BC⊥平面PCD,因为DE⊂平面PCD,所以BC⊥DE。
又因为PD=CD，点E是PC的中点,所以DE⊥PC.因为PC∩BC=C，所以DE⊥平面PBC。
因为PB⊂平面PBC,所以PB⊥DE.又PB⊥EF,DE∩EF=E，所以PB⊥平面DEF.由DE⊥平面PBC,PB⊥平面DEF，可知四面体BDEF的四个面都是直角三角形,即四面体DBEF是一个鳖臑,其四个面的直角分别为∠DEB,∠DEF，∠EFB,∠DFB.考点二平面与平面垂直的判定与性质5.如图，四棱锥P-ABCD中，PA⊥底面ABCD,底面ABCD为正方形，给出下列结论:①AD∥平面PBC;②平面PAC⊥平面PBD；③平面PAB⊥平面PAC；④平面PAD⊥平面PDC.其中正确结论的序号是.答案①②④6.如图，在三棱锥P-ABC中，PA⊥AB,PA⊥BC，AB⊥BC，PA=AB=BC=2,D为线段AC的中点，E为线段PC上一点.（1)求证：PA⊥BD；（2）求证:平面BDE⊥平面PAC;（3）当PA∥平面BDE时,求三棱锥E-BCD的体积。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
立体几何证明------垂直
一.复习引入
1.空间两条直线的位置关系有：_________,_________,_________三种。
2.（公理4）平行于同一条直线的两条直线互相_________.
3.直线与平面的位置关系有_____________,_____________,_____________三种。
4.直线与平面平行判定定理:如果_________的一条直线和这个平面内的一条直线平行，
那么这条直线和这个平面平行
5.直线与平面平行性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这
个平面相交，那么_________________________.
6.两个平面的位置关系:_________,_________.
7.判定定理1：如果一个平面内有_____________直线都平行于另一个平面，那么这两
个平面平行.
8.线面垂直性质定理：垂直于同一条直线的两个平面________.
9.如果两个平行平面同时和第三个平面相交，那么它们的________平行.
10.如果两个平面平行，那么其中一个平面内的所有直线都_____于另一个平面. 二．知识点梳理
知识点一、直线和平面垂直的定义与判定
定义判定
语言描述如果直线l和平面α内的任意一条直
线都垂直，我们就说直线l与平面
互相垂直，记作l⊥α一条直线与一个平面内的两条相交直线都垂直，则这条直线与该平面垂直.
图形
条件b为平面α内的任一直线，而l对这
一直线总有l⊥αl⊥m，l⊥n，m∩n＝B，m⊂α，n⊂α
结论l⊥αl⊥α
要点诠释：定义中“平面内的任意一条直线”就是指“平面内的所有直线”，这与“无数条直线”
不同（线线垂直线面垂直）
知识点二、直线和平面垂直的性质
性质
语言描述一条直线垂直于一个平面，那么这条
直线垂直于这个平面内的所有直线
垂直于同一个平面的两条直线平行.
图形
条件
结论
知识点三、二面角
Ⅰ.二面角：从一条直线出发的两个半平面所组成的图形叫二面角（dihedral angle ）. 这条直线叫做二
面角的棱，这两个半平面叫做二面角的面. 记作二面角AB αβ－－. （简记P AB Q －－）
二面角的平面角的三个特征:
ⅰ. 点在棱上 ⅱ. 线在面内 ⅲ.
与棱垂直
Ⅱ.二面角的平面角：在二面角αβ－l －的棱l 上任取一点O ，以点O 为垂足，在半平面,αβ内分别作垂直于棱l 的射线OA 和OB ，则射线OA 和OB 构成的AOB ∠叫做二面角的平面角. 作用：衡量二面角的大小；范围：000180θ<<.
知识点四、平面和平面垂直的定义和判定
定义 判定 文字描述 两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面垂直.
一个平面过另一个平面的垂线，则这
两个平面垂直 图形
结果
α∩β=l α-l-β=90o α⊥β
（垂直问题中要注意题目中的文字表述，特别是“任何”“ 随意”“无数”等字眼）
三．常用证明垂直的方法
立体几何中证明线面垂直或面面垂直都可转化为线线垂直，而证明线线垂直一般有以下的一些方法：
（1） 通过“平移”。
（3） 利用勾股定理。
（4） 利用直径所对的圆周角是直角
(1) 通过“平移”,根据若则a //b,且b⊥平面α,a⊥平面α
1．在四棱锥P-ABCD 中，△PBC 为正三角形，AB ⊥平面PBC ，AB ∥CD ，AB=2
1
DC ，中点为PD E . 求证：AE ⊥平面PDC.
2．如图，四棱锥P －ABCD 的底面是正方形，PA ⊥底面ABCD ， ∠PDA=45°，点E 为棱AB 的中点．求证：平面PCE ⊥平面PCD ；
（2）利用等腰三角形底边上的中线的性质
3、在三棱锥P ABC -中，2AC BC ==，90ACB ∠=，AP BP AB ==，PC AC ⊥． （Ⅰ）求证：PC AB ⊥；
（第2题
（3）利用勾股定理
4.如图，四棱锥P ABCD
-的底面是边长为1
的正方形，,1,
PA CD PA PD
⊥==
求证:PA⊥平面ABCD；
（4）利用直径所对的圆周角是直角
5、如图，AB是圆O的直径，C是圆周上一点，P A⊥平面ABC. （1）求证：平面P AC⊥平面PBC；
_D
_C
_B
_A
_P
A P
课堂及课后练习题：
1.判断下列命题是否正确，对的打“√”，错误的打“×”。
（1）垂直于同一直线的两个平面互相平行 （ ） （2）垂直于同一平面的两条直线互相平行 （ ）
（3）一条直线在平面内，另一条直线与这个平面垂直，则这两条直线垂直（ ）
2.已知直线
a,b
和平面α
，且,,a b a α⊥⊥则
b
与α
的位置关系是
________________________________________________.
3.如图所示，在四棱锥P ABCD -中，AB PAD ⊥平面,//AB CD ,PD AD =,E 是PB 的中点，F 是CD 上的点，且1
2
DF AB =
,PH 为PAD ∆中AD 边上的高。
（1）证明：PH ABCD ⊥平面；
4.如图所示, 四棱锥P -ABCD 底面是直角梯形,,2,BA AD CD AD CD AB PA ⊥⊥=⊥底面ABCD , E 为PC 的中点, P A ＝AD 。
证明: BE PDC ⊥平面;
C
A
D
B
O
E
5.如图，在三棱锥P ABC -中，⊿PAB 是等边三角形，∠P AC =∠PBC =90 º 证明：AB ⊥PC
6.如图，四面体ABCD 中，O 、E 分别是BD 、BC 的中点，
2, 2.CA CB CD BD AB AD ====== （1）求证：AO ⊥平面BCD ； （2）求异面直线AB 与CD 所成角的大小；
7.如图，四棱锥S ABCD -中，BC AB ⊥,BC CD ⊥，侧面SAB 为等边三角形，2,1AB BC CD SD ====． （Ⅰ）证明：SD SAB ⊥平面;
8.如图，在圆锥PO 中，已知PO =2，⊙O 的直径2AB =,C 是狐AB 的中点，D 为AC 的中点．证明：平面POD ⊥平面PAC ;
课堂及课后练习题答案： 1
（1） √ （2） √ （3）√ 2.b//b αα⊂或者 3.
证明：因为PH 为PAD ∆中AD 边上的高，所以PH AD ⊥，又因为AB PAD ⊥平面，所以AB PH ⊥，
=AB AD A ，所以PH ABCD ⊥平面
4.分析：取PD 的中点F ，易证AF//BE, 易证A F ⊥平面PDC ，从而BE PDC ⊥平面 .
5.证明：因为PAB ∆是等边三角形，90PAC PBC ∠=∠=︒, 所以Rt PBC Rt PAC ∆≅∆,可得AC BC =。
如图，取AB 中点D ，连结PD ,CD , 则PD AB ⊥,CD AB ⊥, 所以AB ⊥平面PDC ,
所以AB PC ⊥。
6.（1）证明：连结OC ,,.BO DO AB AD AO BD ==∴⊥ ,,.BO DO BC CD CO BD ==∴⊥ 在AOC ∆中，由已知可得1, 3.AO CO == 而2,AC =
222,AO CO AC ∴+=90,o AOC ∴∠=即.AO OC ⊥
,BD OC O = AO ∴⊥平面BCD
7.
（I ）取AB 中点E ，连结DE ，则四边形BCDE 为
矩形，DE=CB=2，连结SE ，则, 3.SE AB SE ⊥=
又SD=1，故222
ED SE SD =+，
所以DSE ∠为直角。
由,,AB DE AB SE DE
SE E ⊥⊥=，
得AB ⊥平面SDE ，所以AB SD ⊥。
SD 与两条相交直线AB 、SE 都垂直。
所以SD ⊥平面SAB 。