人教版七年级数学下册第十章数据的收集、整理与描述第二节直方图复习试题(含答案) (90)
人教版七年级数学下册第十章数据的收集、整理与描述第二节直方图习题(含答案) (60)

人教版七年级数学下册第十章数据的收集、整理与描述第二节直方图复习试题(含答案)一、单选题1.一组数据的最大值是97,最小值76,若组距为4,则可分为几组()A.4 B.5 C.6 D.7【答案】B【解析】根据题意,一组数据的最大值是97,最小值76,最大值与最小值的差为=5.25;则可分为6组.21;若组距为4,有214故选C.点睛:本题考查组数的确定方法,注意极差的计算与最后组数的确定,组数不要太少,也不能太多.2.小明在选举班委时得了28票,下列说法错误的是()A.不管小明所在的班级有多少学生,所有选票中选小明的选票频率不变B.不管小明所在的班级有多少学生,所有选票中选小明的选票频数不变C.小明所在班级的学生人数不少于28人D.小明的选票的频率不能大于1【答案】A【解析】【分析】根据频率=频数,即可解答.数据总和【详解】解:频率=频数数据总和,当全班人数变化时,所有选票中选小明的选票频率也随着变化;根据各小组频数之和等于数据总和,各小组频率之和等于1;可得B,C,D,都正确,A错误.故选A.【点睛】本题是对频率、频数灵活运用的综合考查,各小组频数之和等于数据总和,各小组频率之和等于1.频率、频数的关系:频率=频数数据总和.3.小亮把全班50名同学的期中数学测试成绩,绘成如图所示的条形图,其中从左起第一、二、三、四个小长方形高的比是1∶3∶5∶1.从中同时抽一份最低分数段和一份最高分数段的成绩的概率分别是().A.110、110B.110、12C.12、110D.12、12【答案】A【解析】试题分析:设第一个长方形的高为x,则第二、三、四个小长方形高分别为3x,5x,x,由题意得x+3x+5x+x=50,解得x=5,即最低分为5人,最高分为5人,根据概率公式从中同时抽一份最低分数段和一份最高分数段的成绩的概率分别是550=110、550=110.故选A.点睛:本题考查频率分布直方图的知识和概率公式,难度不大,注意掌握如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=mn.4.在全班45人中进行了你最喜爱的电视节目的调查活动,喜爱的电视剧有人数为18人,喜爱动画片有人数为15人,喜爱体育节目有人数为10人,则下列说法正确的是()A.喜爱的电视剧的人数的频率是1818+15+10B.喜爱的电视剧的人数的频率是1845C.喜爱的动画片的人数的频率是1818+10D.喜爱的体育节目的人数的频率是181514545--【答案】B【解析】试题分析:频率应为频数除以总数,所以喜欢看电视剧、动画片和体育节目的频率分别是1845、1545、1045,故选B.5.在-(-3),(-3)2,(-3)3,︱-3︱中,负数出现的频率为()A.25%B.50%C.75%D.100%【答案】A【解析】试题分析:-(-3)=3,(-3)2=9,(-3)3=-27,︱-3︱=3,所以负数出现的频率为25%,故选A.6.小文同学统计了他所在小区居民每天微信阅读的时间,并绘制了直方图.有以下说法:①小文同学一共统计了60人;②每天微信阅读不足20分钟的人数有8人;③每天微信阅读30~40分钟的人数最多;④每天微信阅读0-10分钟的人数最少.根据图中信息,上述说法中正确的是( )A.①②③④B.①②③C.②③④D.③④【答案】D【解析】①小文同学一共统计了4+8+14+20+16+12=74(人),则命题错误;②每天微信阅读不足20分钟的人数有4+8=12(人),故命题错误;③每天微信阅读30−40分钟的人数最多,正确;④每天微信阅读0−10分钟的人数最少,正确.故选D.点睛: 本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.7.要反映一个家庭在教育方面支出占总收入的比,宜采用()A.条形统计图B.扇形统计图C.折线统计图D.频数分布直方图【答案】B【解析】根据统计图的特点进行分析可得:扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;折线统计图表示的是事物的变化情况;条形统计图能清楚地表示出每个项目的具体数目.【解答】解:由统计图的特点,知要反映一个家庭在教育方面支出占总收入的比,宜采用扇形统计图.故选B.8.某班将安全知识竞赛成绩整理后绘制成直方图,图中从左至右前四组的百分比分别是4%、12%、40%、28%,第五组的频数是8,下列结论错误的是()A.该班有50名同学参赛B.第五组的百分比为16%C.成绩在70~80分的人数最多D.80分以上的学生有14名【答案】D【解析】A.8÷(1-4 %-12 %-40 %-28 %)=50(人),故正确;B. 1-4 %-12 %-40 %-28 %=16%,故正确;C.由图可知,成绩在70~80分的人数最多,故正确;D.50×(28 %+16 %)=22(人),故不正确;9.单位在植树节派出50名员工植树造林,统计每个人植树的棵树之后,绘制出如图所示的频数分布直方图(图中分组含最低值,不含最高值),则植树7棵及以上的人数占总人数的( )A .40%B .70%C .76%D .96%【答案】C【解析】 由图可得,植树7棵及以上的人数占总人数的5029650-=% ,故选D. 10.下列关于统计图的说法中,错误的是( )A .条形图能够显示每组中的具体数据B .折线图能够显示数据的变化趋势C .扇形图能够显示数据的分布情况D .直方图能够显示数据的分布情况【答案】C【解析】A. ∵条形图能够显示每组中的具体数据,故正确;B. ∵折线图能够显示数据的变化趋势,故正确;C. ∵扇形图能够显示部分与总体的关系,故不正确;D. ∵直方图能够显示数据的分布情况,故正确;。
人教版七年级数学下册第十章数据的收集、整理与描述第二节直方图习题(含答案) (100)
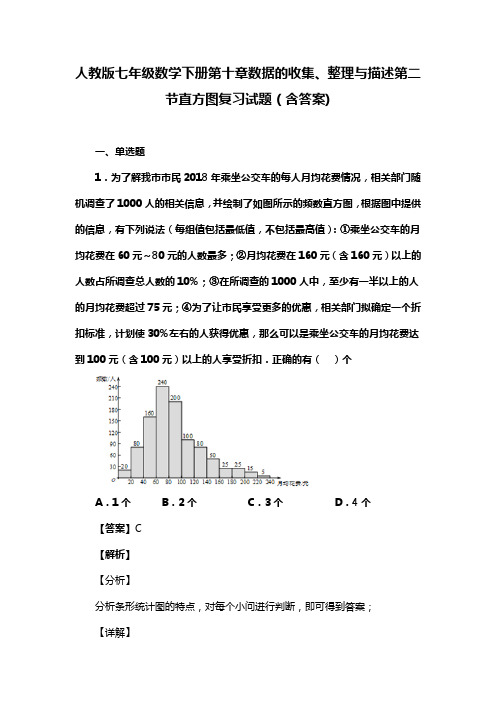
人教版七年级数学下册第十章数据的收集、整理与描述第二节直方图复习试题(含答案)一、单选题1.为了解我市市民2018年乘坐公交车的每人月均花费情况,相关部门随机调查了1000人的相关信息,并绘制了如图所示的频数直方图,根据图中提供的信息,有下列说法(每组值包括最低值,不包括最高值):①乘坐公交车的月均花费在60元~80元的人数最多;②月均花费在160元(含160元)以上的人数占所调查总人数的10%;③在所调查的1000人中,至少有一半以上的人的月均花费超过75元;④为了让市民享受更多的优惠,相关部门拟确定一个折扣标准,计划使30%左右的人获得优惠,那么可以是乘坐公交车的月均花费达到100元(含100元)以上的人享受折扣.正确的有()个A.1个B.2个C.3个D.4个【答案】C【解析】【分析】分析条形统计图的特点,对每个小问进行判断,即可得到答案;【详解】解:①根据题意,乘坐公交车的月均花费在60元~80元的人数最多,有240人;②月均花费在160元(含160元)以上的人数有70人,70100%7%1000⨯=;③在所调查的1000人中,80元以上有:200+100+80+50+25+25+15+5=500人,∴至少有一半以上的人的月均花费超过75元;④100030%300⨯=人,由表格可知,100元以上的有:100+80+50+25+25+15+5=300人,∴计划使30%左右的人获得优惠,那么可以是乘坐公交车的月均花费达到100元(含100元)以上的人享受折扣.∴正确的有:①③④;故选C.【点睛】本题主要考查了频数分布直方图,抽样调查以及用样本估计总体,一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.2.一次统计八(2)班若干名学生每分跳绳次数的频数分布直方图的次数(结果精确到个位)是()A.数据不全无法计算B.103C.104 D.105【答案】C【解析】【分析】根据频数分布直方图可知本次随机抽查的学生人数为:2+4+6+3=15(人);然后取每一小组中间的数值近似地作为该组内每位学生的每分钟跳绳次数,再用加权平均数求解即可.【详解】解:根据频数分布直方图可知本次随机抽查的学生人数为:2+4+6+3=15(人);所以这若干名学生每分钟跳绳次数的平均数=(62×2+87×4+112×6+137×2)÷15≈103.67≈104,故选C.【点睛】本题考查学生读取频数分布直方图的能力和利用统计图获取信息的能力.对此类问题,必须认真观察题目所给的统计图并认真的思考分析,才能作出正确的判断,从而解决问题.3.某校为了了解学生在校午餐所需的时间,抽查了20 名同学在校午餐所需的时间,获得如下数据(单位:分):10,12,15,10,16,18,19,18,20,34,22,25,20,18,18,20,15,16,21,16.若将这些数据分为5组,则组距是()A.4 分B.5 分C.6 分D.7 分【答案】B【解析】【分析】找出20个数据的最大值与最小值,求出它们的差,再除以5即得结果.【详解】解:根据题意得:(34-10)÷5=4.8.即组距为5分.故选B.【点睛】本题考查了频数分布表的相关知识,弄清题意,掌握求组距的方法是解题的关键.4.一个容量为80的样本最大值为143,最小值为50,取组距为10,则可以分成的组数是()A.8 B.9 C.10 D.11【答案】C【解析】【分析】计算最大值与最小值的差,除以组距即得组数,即:(143-50)÷10=9.3≈10.【详解】解:(143-50)÷10=9.3,故分成10组较好.故选:C.【点睛】考查频数分布表的制作方法,用最大值与最小值的差除以组距可得组数,不是整数用进一法取近似值确定组数.5.小红随机写了一串数“313233*********”,数字“3”出现的频数是( ) A.4 B.5 C.6 D.7【答案】D【解析】【分析】根据频数的概念:频数是表示一组数据中符合条件的对象出现的次数.【详解】∵一串数“313233*********”中,数字“3”出现了7次,∴数字“3”出现的频数为7.故选D.【点睛】此题考查频数与频率,解题关键在于掌握其概念6.有40 个数据,其中最大值为39,最小值为12,若取组距为4,则应分为()A.4 组B.5 组C.6 组D.7 组【答案】D【解析】【分析】根据组数=(最大值-最小值)÷组距计算即可,注意小数部分要进位.【详解】解:∵在样本数据中最大值与最小值的差为39-12=27,又∵组距为4,∴组数=27÷4=6.75,∴应该分成7组.故选:D.【点睛】本题考查的是组数的计算,属于基础题,熟记组数的计算方法是解决此题的关键.7.在“I LOVE MATHS.”这个句子的所有字母中,字母“e”出现的频数是()A.1 B.3 C.4 D.5【答案】A【解析】【分析】数出这个句子中字母“e”出现的次数即可.【详解】解:在“I LOVE MATHS”这个句子的所有字母中,字母“e”出现了1次,故字母“e”出现的频数为1.故选:A.【点睛】此题考查频数的定义,即每个对象出现的次数.8.小明随机写了一串数字“1,2,3,3,2,1,1,1,2,2,3,3,”,则数字3出现的频数()A.6 B.5 C.4 D.3【答案】C【解析】【分析】根据频数的定义可直接得出答案【详解】解:∵该串数字中,数字3出现了4次,∴数字3出现的频数为4.故选:C.【点睛】本题是对频数定义的考查,即频数是表示一组数据中符合条件的对象出现的次数.9.调查50名学生的年龄,列频数分布表时,这些学生的年龄落在5个小组中,第一、二、三、五组数据个数分别是2,8,15,5,则第四组的频数是()A.20 B.30 C.0.4 D.0.6【答案】A【解析】【分析】根据频数的定义:频数表是数理统计中由于所观测的数据较多,为简化计算,将这些数据按等间隔分组,然后按选举唱票法数出落在每个组内观测值的个数,称为(组)频数。
人教版七年级数学下册第十章数据的收集、整理与描述第二节直方图习题(含答案) (91)

人教版七年级数学下册第十章数据的收集、整理与描述第二节直方图复习试题(含答案)某校为了了解九年级学生的体能情况,随机抽取了30名学生测试11分钟仰卧起坐的次数,统计结果并绘制成如图所示的频数分布直方图.已知该校九年级共有150名学生,请据此估计,该校九年级1分钟仰卧起坐次数在3035次之间的学生人数大约是()A.20B.25C.50D.55【答案】B【解析】【分析】用样本中次数在30~35次之间的学生人数所占比例乘以九年级总人数可得.【详解】解:该校九年级1分钟仰卧起坐次数在30~35次之间的学生人数大约是530×150=25(人),故选:B.【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.12.如图是某班级的一次考试成绩(得分均为整数)的频数分布直方图(每组包含最小值,不包含最大值),则下列说法错误的是()A.得分在70~79分的人数最多B.该班的总人数为40C.人数最少的分数段的频数为2D.得分及格(≥60分)约有12人【答案】D【解析】【分析】观察条形图即可一一判断.【详解】A、得分在70~79分的人数最多,故正确;B、该班的总人数为40人,故正确;C、人数最少的得分段的频数为2,故正确;D、得分及格(≥60分)的有12+14+8+2=46人,故错误.故选:D.【点睛】本题考查频数分布直方图,解题的关键是读懂图象信息,属于中考常考题型.13.现有57本书,计划分给各学习小组,如每组6本则有剩余,每组7本却不够分,则学习小组共有()A.7个B.8个C.9个D.10个【答案】C【解析】【分析】设学习小组共有x个,利用每组6本则有剩余,每组7本却不够分列不等式组得6x<57<7x,然后解不等式组,确定它的整数解即可.【详解】解:设学习小组共有x个,根据题意得6x<57<7x,解得817<x<912,而x为整数,所以x=9.即学习小组共有9个.故选C.【点睛】本题考查了一元一次不等式的应用:对具有多种不等关系的问题,考虑列一元一次不等式组,并求解.14.一次数学测试后,某班60名学生的成绩被分为5组,第一至第四组的频数分别为8、10、16、14,则第五组的频率是()A.0.1 B.0.2 C.0.3 D.0.4【答案】B【解析】【分析】根据第1~4组的频数,求出第5组的频数,即可确定出其频率.【详解】解:∵第五组的频数为60-(8+10+16+14)=12,∴第五组频率是12÷60=0.2,故选B【点睛】此题考查了频数与频率,弄清题中的数据是解本题的关键.15.有50个数据,其中最大值为86,最小值为57,若取组距为6,则应该分的组数是().A.4 B.5 C.6 D.7【答案】B【解析】【分析】若(最大值-最小值)÷组距的结果为整数,则该整数就是分的组数;若该结果为小数,则整数部分加1就是分的组数.【详解】根据题意:(86-57)÷6=29÷6=54,6∴应该分的组数是5,故选B.【点睛】本题考查对数据进行整理的题目,解题关键在于掌握求组数的方法.16.一个样本中最大值是143,最小值是50,取组距为10,则可以分成()A.8组B.9组C.10组D.11组【答案】C【解析】【分析】根据题目中的数据可以求得极差,再根据组距,即可确定组数,本题得以解决.【详解】∵一个样本中最大值是143,最小值是50,∴极差是143-50=93,∵这组数据取组距为10,93÷10=9…3,∴这组数据可以分成10组,故选:C.【点睛】考查频数(率)分布表,解答本题的关键是明确题意,求出相应的组数.17.为了了解某校初三年级学生的运算能力,随机抽取了100名学生进行测试,将所得成绩(单位:分)整理后,列出下表:本次测试这100名学生成绩良好(大于或等于80分为良好)的人数是()A.22B.30C.60D.70【答案】D【解析】【分析】先根据表格得到成绩良好的频率,再用100×频率即可得解.【详解】解:由题意可知成绩良好的频率为0.3+0.4=0.7,则这100名学生成绩良好的人数是100×0.7=70(人).故选D.【点睛】本题主要考查频率与频数,解此题的关键在于熟练掌握其知识点,在题中准确找到需要的信息.18.陈老师对56名同学的跳绳成绩进行了统计,跳绳个数140个以上的有28名同学,则跳绳个数140个以上的频率为()A.0.4 B.0.2 C.0.5 D.2【答案】C【解析】【分析】根据频率的定义用28除以56即可求解.【详解】0.5,依题意跳绳个数140个以上的频率为2856=故选C.【点睛】此题主要考查频率的求解,解题的关键是熟知频率的求解公式.19.对某校600名学生的体重(单位:kg)进行统计,得到如图所示的频率分布直方图,学生体重在60kg以上的人数为()A.120 B.150 C.180 D.330【答案】B【解析】【分析】用总人数乘以对应频率即可得.【详解】解:学生体重在60kg以上的人数为600×(0.20+0.05)=150(人),故选:B.【点睛】本题主要考查频数(率)分布直方图,解题的关键是掌握频率=频数÷总数及样本估计总体思想的运用.二、解答题20.为了增强环境保护意识,6月5日“世界环境日”当天,若干名“环境小卫士”组成了“控制噪声污染”课题学习研究小组.该小组抽样调查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),将调查的数据进行处理(设所测数据均为正整数),得频数分布表如表:根据表中提供的信息解答下列问题:(1)频数分布表中的a=,b=,c=;(2)补全完整频数分布直方图(如图);(3)从这个统计中,你认为噪声污染的噪音声级分布情况怎样?~所【答案】(1)8;12;30%;(2)图见解析;(3)噪声声级89.5104.5~所占比例最小;噪声污染的频率随声级先增占比例最大;噪声声级44.559.5大再减小.【解析】【分析】(1)用总数乘以59.5--74.5的频率求出a,再用总人数减去其它段的频数求出b;用89.5--104.5的频数除以总数求出c;(2)利用(1)的结果补全即可;(3)根据直方图即可得出结论.【详解】解:(1)a=40×0.2=8,b=40-4-8-10-6=12,c=12÷40=0.3.故答案为:8;12;30%(2)补全频数分布直方图如图所示:~所占比例最大.(3)由直方图可知:①噪声声级89.5104.5~所占比例最小.②噪声声级44.559.5③噪声污染的频率随声级先增大再减小.【点睛】本题考查了频数(率)分布直方图,正确理解频数与频率成正比,频率分布直方图中长方形的高与频数即测量点数成正比,是解决问题的关键.。
人教版七年级数学下册第十章数据的收集、整理与描述第二节直方图复习试题(含答案) (80)

人教版七年级数学下册第十章数据的收集、整理与描述第二节直方图复习试题(含答案)某校开展捐书活动,七(1)班同学积极参与,现将捐书数量绘制成频数分布直方图(如图所示),如果捐书数量在3.5﹣4.5组别的人数占总人数的30%,那么捐书数量在4.5﹣5.5组别的人数是_____.【答案】16【解析】【分析】根据捐书数量在3.5-4.5组别的频数是12、频率是0.3,由频率=频数÷总数求得总人数,根据频数之和等于总数可得答案.【详解】解:∵被调查的总人数为12÷30%=40(人),∴捐书数量在4.5-5.5组别的人数是40-(4+12+8)=16(人),故答案为:16人.【点睛】本题主要考查频数(率)分布表,掌握频率=频数÷总数是解题的关键.92.(1)已知20个数据如下:25 21 23 25 27 29 25 24 30 2926 23 25 27 26 22 24 25 26 28对于这些数据编制频率分布表,其中25~27这一组的频率是________.(2)对60名学生的身高检测数据整理后,得出落在167~171cm之间的频率是0.3,那么落在这个区间的学生数是_____人.(3)把容量是50的样本分成6组,其中有1组的频数是14,有2组的频数是10,有2组的频率是0.14,则另一组的频数是__________,频率是_________.【答案】0.4 18 2 0.04【解析】【分析】(1)根据频率是指每个对象出现的次数与总次数的比值(或者百分比).即频率=频数÷数据总数即可算出答案;(2)根据频率=频数÷数据总数计算即可;(3)根据频率计算出频率是0.14两组的频数,进而可求出另一组的频数和频率.【详解】(1)∵25~27这一组共有8个数据,∴这一组的频率为:820=0.4,故答案为0.4(2)落在这个区间的学生数为:60×0.3=18(人)故答案为18(3)∵频率为0.14的这一组的频数为:50×0.14=7,∴另一组的频数为:50-14-2×10-2×7=2;频率为:250=0.04故答案为2;0.04【点睛】此题主要考查了频率,关键是掌握频率的计算公式.93.在画直方图时,数据越多则分成的组数也________,当数据的个数在100以内时,一般可分为________组.【答案】越多,5~12【解析】【分析】根据画频数分布直方图的原则来解答.【详解】将一批数据分组,一般数据越多,分的组数也越多,经验法则是:当数据在100个以内时,按照数据的多少,常分成5~12组.组距是指每个小组的两个端点之间的距离.【点睛】画直方图的原则是本题的考点,掌握基础知识是解题的关键.94.在对一些数据进行整理的频数分布表中,各组的频数之和等于________.【答案】总数【解析】【分析】根据频率、频数的概念可知答案【详解】在频率分布表中,频数之和等于总数;频率之和等于1;频率是频数和总数的比.故本题答案为:总数【点睛】本题考查频率、频数的概念;频率的计算方法:频率=频数÷总数;牢记基础知识是解题的关键.95.下表是某校八年级(8)班共50位同学身高情况的频数分布表,•则表中的组距是7,估计极差至多是27.频率是0.28的这一小组的组中值是___.【答案】163.【解析】【分析】先求出频率是0.28的一组的频数,再求出其组中值即可.【详解】.解:频率是0.28的一组的频数=50×0.28=14人,∴这一组是159.5﹣166.5组,∴组中值为159.5166.52=163.故本题答案为:163.【点睛】此题主要考查频率与频数的关系,解题的关键是根据频率求出频数.96.在前100个正整数中,3的倍数出现的频数是__,其频率是__,4的倍数出现的频率是___.【答案】频数是33,频率为0.33;频率为0.25.【解析】【分析】先数出在前100个正整数中,3的倍数的个数及4的倍数的个数,再进行求解.【详解】解:根据题意,得前100个正整数中,3的倍数有3 6 9 12 …99,共33个,故其频数是33,其频率为0.33;4的倍数有4 8 12 16…100,共25个,其频率为0.25.【点睛】此题主要考查频数与频率的关系,解题的关键是根据题意数出目标个数.97.经调查某村共有银行储户若干户,其中存款额2~3万元之间的储户的频率是0.2,而存款额为其余情况的储户的频数之和为40,则该村存款额2~3万元之间银行储户有___________ 户.【答案】10【解析】【分析】首先根据各个小组的频率和是1,得到存款额为其余情况的储户的频率,再根据总数=频数÷频率,求得总数,最后根据频数=频率×总数,求得频数.解:根据题意,得:存款额为其余情况的储户的频率=1-0.2=0.8,则银行储户的总数=40÷0.8=50户,则该村存款额2~3万元之间银行储户=50×0.2=10户.【点睛】,频数=频率×总数,总数=频数本题考查频率、频数的关系:频率=频数数据总和÷频率.注意:各组的频率和是1.98.一组数据分为5组,第一组的频率为0.15,第二组的频率为0.21,第三组的频率为0.29,第四组的频率为0.15,则第五组的频率是______.【答案】0.20.【解析】【分析】根据各组的频率的和是1即可求解.【详解】第五组的频率是:1-0.15-0.21-0.29-0.15=0.2.故答案为:0.20.【点睛】本题考查了频率的意义,关键是熟悉各组的频率的和是1的知识点.99.对100个数据分组频率分布表,各组的频数之和为__________,频率之和为_________.【答案】100; 1.【解析】利用频数及频率的意义即可得到结果.【详解】解:在对100个数据进行整理的频率分布表中,各组的频数之和等于100,频率之和等于1.故答案为:100;1.【点睛】此题考查了频数(率)分布表,弄清题意是解本题的关键.100.一个样本的容量为50,分组后落在某区间的频数是6,则该组的频率是_______.【答案】0.12.【解析】【分析】此题只需根据频率=频数÷总数,进行计算.【详解】解:根据题意,得该组的频率是6÷50=0.12.故答案为:0.12.【点睛】此题考查了频率、频数的关系:频率=频数÷数据总和.。
人教版七年级数学下册第十章数据的收集、整理与描述第二节直方图复习试题(含答案) (51)

人教版七年级数学下册第十章数据的收集、整理与描述第二节直方图复习试题(含答案)一、单选题1.如图是某班全体学生外出时选择乘车、步行、骑车人数的条形统计图和扇形统计图(两图都不完整),则下列结论中正确的是( )A.步行人数为30人B.骑车人数占总人数的10%C.该班总人数为50人D.乘车人数是骑车人数的40%【答案】C【解析】【分析】根据乘车的人数和所占的百分比求出总人数,用总人数乘以步行所占的百分比求出步行的人数,用骑车的人数除以总人数求出骑车人数占总人数的百分比,用乘车的人数除以骑车人数,求出乘车人数是骑车人数的倍数.【详解】A、步行的人数有:25×30%=15人,故本选项错误;50%=20%,故本选项错误;B、骑车人数占总人数10÷2550%C、该班总人数为25=50人,故本选项正确;50%D、乘车人数是骑车人数的25=2.5倍,故本选项错误;10故选:C.【点睛】本题考查了频数(率)分布直方图和扇形统计图,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.2.一个容量为63的样本,最大值为172,最小值为149,若取组距为3,则可以分成()A.6组B.7组C.8组D.9组【答案】C【解析】【分析】根据组数=(最大值﹣最小值)÷组距计算,注意小数部分要进位.【详解】在数据中,最大值为172,最小值为149,它们的差是172﹣149=23,若取组距为3,由于2327;故可以分成8组.33故选C.【点睛】本题考查了组数的计算,属于基础题,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.3.如图为某校782名学生小考成绩的次数分配直方图,若下列有一选项为图(一)成绩的累积次数分配直方图,则此图为何()A. B.C. D.【答案】A【解析】【分析】将一个变量的不同等级的相对频数用矩形块标绘的图表(每一矩形的面积对应于频数).因为本题求哪个是成绩的累积次数分配直方图,故累计次数做为纵坐标.【详解】关键知道,分数是横坐标,累计次数是纵坐标,符合题意的是A.故选A.【点睛】本题考查了频数直方图的画法以及对横纵坐标要求的理解.才能够正确选出答案.4.某学校有1000名九年级学生,要知道他们在学业水平考试中成绩为A 等、B等、C等、D等的人数各是多少,需要做的工作是()A.求平均成绩B.进行频数分布C.求极差D.计算方差【答案】B【解析】【分析】根据频数的概念知,把学生分成四等,进行的工作是计算频数的分布.【详解】由题意可知:成绩为A等、B等、C等、D等的人数各是多少,则是计算它们的频数.故选B.【点睛】本题考查了频数的概念:对总数据按某种标准进行分组,统计出各个组内含个体的个数.5.八年级某班45位同学中,4月份出生的频率是0.20,那么这个班4月份出生的同学有()A.8位B.9位C.10位D.11位【答案】B【解析】【分析】根据频率公式:频率 频数,即可求解.总数45×0.20=9(位).故选B.【点睛】本题考查了频率的计算公式,理解公式是关键.6.一次数学测试后,某班40名学生的成绩被分为5组,第1~4组的频数分别为12,10,6,8,则第5组的百分比是( )A.10% B.20% C.30% D.40%【答案】A【解析】【分析】根据第1~4组的频数,求出第5组的频数,即可确定出其百分比.【详解】根据题意得:40-(12+10+6+8)=40-36=4,则第5组所占的百分比为4÷40=0.1=10%,故选A.【点睛】此题考查了频数与频率,弄清题中的数据是解本题的关键.7.2018年11月贵阳市教育局对某校七年级学生进行体质监测共收集了200名学生的体重,并绘制成了频数分布直方图,从左往右数每个小长方形的长度之比为2:3:4:1,其中第三组的频数为()A.80人B.60人C.20人D.10人【解析】【分析】用200乘以第三组所占的比例即可得.【详解】=80,200×42341+++即第三组的频数为80,故选A.【点睛】本题考查了频数分布直方图,频数等知识点,熟练掌握频数分布直方图中每个小长方形的宽是相同的,各组的频数之比就是每个小长方形的长度之比是解题的关键.8.有100个数据,落在某一小组内的频数与总数之比是0.4,那么在这100个数据中,落在这一小组内的数据的频数是()A.100 B.40 C.20 D.4【答案】B【解析】【分析】根据频率、频数的关系:频率=频数÷数据总数,可得频数=频率×数据总数.【详解】∵一个有100个数据的样本,落在某一小组内的频率是0.4,∴在这100个数据中,落在这一小组内的频数是:100×0.4=40.故选B.【点睛】本题考查了频率、频数与数据总数的关系:频数=频率×数据总数.9.一次跳远比赛中,成绩在4.05米以上的有8人,频率为0.4,则参加比赛的共有()A.40人B.30人C.20人D.10人【答案】C【解析】【分析】根据频率、频数的关系:频率=频数÷数据总和,可得数据总和=频数÷频率.【详解】∵成绩在4.05米以上的频数是8,频率是0.4,∴参加比赛的运动员=8÷0.4=20.故选C.【点睛】考查频数与频率,掌握数据总和=频数÷频率是解题的关键.10.某校测量了初三(1)班学生的身高(精确到1cm),按10cm为一段进行分组,得到如图频数分布直方图,则下列说法正确的是()A.该班人数最多的身高段的学生数为7人;B.该班身高低于160.5cm的学生人数为15人;C.该班身高最高段的学生数为20人;D.该班身高最高段的学生数为7人【答案】D【解析】【分析】根据频数直方图的意义,表示每段中的人数,即可得到答案.【详解】解:由频数直方图可以看出:该班人数最多的身高段的学生数为20人;该班身高低于160.5cm的学生数为20人;该班身高最高段的学生数为7人;故选D.【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.。
人教版七年级数学下册第十章数据的收集、整理与描述第二节直方图习题(含答案) (89)

人教版七年级数学下册第十章数据的收集、整理与描述第二节直方图复习试题(含答案)为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下尚不完整的统计图表。
请根据以上图表,解答下列问题:(1)这次被调查的同学共有_____________人,a+b=______________,m=________;(2)求扇形统计图中扇形C的圆心角度数。
【答案】(1)50,28,8(2)144°【解析】【分析】(1)根据B组的频数是16,对应的百分比是32%,据此求得调查的总人数,利用百分比的意义求得b,然后求得a的值,m的值;(2)利用360°乘以对应的比例即可求解。
【详解】(1)调查的总人数是16÷32%=50(人),则b=50×16%=8,a=50-4-16-8-2=20,=8%,则m=8.A组所占的百分比是450a+b=8+20=28.故答案是:50,28,8;=144°。
(2)扇形统计图中扇形C的圆心角度数是360°×2050【点睛】本题考查了扇形统计图,观察统计表、扇形统计图获得有效信息是解题关键,扇形统计图直接反映部分占总体的百分比大小.92.在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量x(单位:个),并绘制了如下统计表和如图所示的频数分布直方图.“宇番2号”番茄挂果数量统计表请结合图表中的信息解答下列问题:(1)统计表中,a= ,b= ;(2)将频数分布直方图补充完整;(3)若绘制“宇番2号番茄挂果数量扇形统计图”,则挂果数量在“35≤x<45”所对应扇形的圆心角度数为°;(4)若所种植的“宇番2号”番茄有1 000株,则可以估计挂果数量在“55≤x<65”范围的番茄有株.【答案】(1)15,0.3;(2)补全的频数分布直方图见解析;(3)72°;(4)300 【解析】分析:(1)根据题意可以求得a的值、b的值;(2)根据(1)中a的值,可以将频数分布直方图补充完整;(3)根据挂果数量在“35≤x<45”所对应的频率,可以求得挂果数量在“35≤x<45”所对应扇形的圆心角度数;(4)根据频数分布直方图可以估计挂果数量在“55≤x<65”范围的番茄的株数.=0.3.详解:(1)a=60×0.25=15,b=1860(2)补全的频数分布直方图如图所示.(3)由题意可得,挂果数量在“35≤x<45”所对应扇形的圆心角度数为360°×0.2=72°.(4)由题意可得,挂果数量在“55≤x<65”范围的番茄约有1000×0.3=300(株).点睛:本题考查频数分布直方图、用样本估计总体、扇形圆心角的度数,解题的关键是明确题意,找出所求问题需要的条件.93.体育委员统计了全班同学60秒跳绳的次数,并列出下列人数次数分布表,回答下列问题:(1)全班有多少人?(2)组距、组数是多少?(3)跳绳次数在100≤x<140范围内同学有多少人,占全班的百分之几(精确到0.01%)?【答案】(1)53人;(2)组距为20,组数为6;(3)64%.【解析】分析:(1)把各组人数相加即可;(2)根据表格数据可知组距和组数;(3)根据表格可知人数是100≤x<120和120≤x<140两组人数的和,然后求百分比即可.详解:(1)全班总人数=2+5+21+13+8+4=53(人);(2)组距为20,组数为6;(3)∵跳绳次数在100≤x<140范围的同学有多34人,∴x=34,∴占全班的百分比=3453×100%≈64%.点睛:本题考查根据图表获取信息的能力及动手操作能力,弄清题意是解本题的关键.94.为了解我县中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,根据成绩分成如下四个组:A:60≤x<70,B:70≤x<80,C:80≤x<90,D:90≤x≤100,并制作出如下的扇形统计图和直方图. 请根据图表信息解答下列问题:(1)扇形统计图中的m=___,并在图中补全频数分布直方图;(2)小明的成绩是所有被抽查学生成绩的中位数,据此推断他的成绩在____组;(3)4个小组每组推荐1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中A,C两组学生的概率是多少?请列表或画树状图说明.【答案】144 C【解析】分析:(1)根据A:60≤x<70有30人,圆心角为36°,即可求出总数,再求出C:80≤x<90的人数,即可得出m的值;(2)因为抽查的总人数为300,故中位数为:第150个数和第151个数的平均数,这两个数都落在C组;(3)列表格求出概率即可.=300(人),C:80≤x<90的人数=300-30-详解:(1)30÷3636090-60=120(人),∴m=360°×120=144°.300补全图形如下:(2)因为抽查的总人数为300,故中位数为:第150个数和第151个数的平均数,这两个数都落在C组;(3)列表如下:由表可知共有12种等可能结果,抽到A、C组人的共有两种结果,∴P(AC)=212=16点睛:本题考查了列表法与树状图法、扇形统计图、条形统计图、用样本估计总体,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.95.为了考查一种零件的加工精度,从中抽出40只进行检测,其尺寸数据如下(单位:微米):161,165,164,166,160,158,163,162,168,159,147,165,167,151,164,159,152,159,149,172,162,157,162,169,156,164,163,157,163,165,173,159,157,169,165,154,153,163,168,169.试列出样本频数及频率分布表,绘制频数分布直方图.【答案】见解析【解析】分析:(1)计算最大值与最小值的差,(2)决定组距与组数,(3)决定分点,(4)列频数及频率分布表,(5)绘频数分布直方图.详解:(1)计算最大值与最小值的差:在样本数据中,最大值是173,最小值是147.它们的差是173-147=26(微米).(2)决定组距与组数:设组距为4微米,则最大值-最小值组距=264=6.5,∴组数为7.(3)决定分点:把起点数147减去末位的半个单位,即147-0.5=146.5.这样依次分为:146.5~150.5,150.5~154.5,…,166.5~170.5,170.5~174.5.(4)列频数及频率分布表:正正正正(5)绘频数分布直方图:点睛:本题考查了频数(率)分布直方图的绘制,通过直方图的绘制,掌握收集和处理数据的能力.96.6月5日是“世界环境日”,南宁市某校举行了“绿色家园”演讲比赛,赛后整理参赛同学的成绩,制作成直方图(如图).(1)全校共有多少人参加比赛?(2)组距是多少?组数是多少?(3)分数段在哪个范围内的人数最多?并求出该小组的频数、频率;(4)如果比赛成绩90分以上(含90分)可以获得奖励,那么获奖率是多少?【答案】(1) 24人.(2)组距是5,组数是4.(3) 85~90分,频数为10,频 .(4) 37.5%.率是512【解析】分析:(1)根据总人数=每个组人数之和计算;(2)根据直方图可得组距和组数;(3)根据直方图可得结论;(4)利用比赛成绩90分以上(含90分)的人数除以总数24即可得到结论.详解:(1)5+10+6+3=24(人).答:全校共有24人参加比赛.(2)组距是5,组数是4..(3)分数段在85~90分的人数最多,频数为10,频率是512(4)(6+3)÷24=37.5%.答:获奖率是37.5%.点睛:本题考查了频数(率)分布直方图以及利用样本估计总体的运用,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.97.小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t)并绘制了样本的频数分布表和频数分布直方图(如图).(1)请根据题中己有的信息补全频数分布表和频数分布直方图;(2)如果家庭月均用水量“大于或等于4t 且小于7t ”为中等用水量家庭,请你估计小王所居住的小区中等用水量家庭大约有多少户?(3)从月均用水量在2x 3≤<,8x 9≤<这两个范围内的样本家庭中任意抽取2个,请用列举法(画树状图或列表)求抽取出的2个家庭来自不同范围的概率.【答案】(1)15,30%,6;图见解析(2)279;(3)23【解析】分析:(1)根据第一组的频数是2,百分比是4%即可求得总人数,然后根据百分比的意义求解;(2)利用总户数450乘以对应的百分比求解;(3)在2≤x<3范围的两户用a 、b 表示,8≤x<9这两个范围内的两户用1,2表示,利用树状图法表示出所有可能的结果,然后利用概率公式求解.详解:(1)调查的总数是:2÷4%=50(户),x≤<部分调查的户数是:50×12%=6(户),则67x≤<的户数是:50−2−12−10−6−3−2=15(户),则45所占的百分比是:1550×100%=30%.故答案为15,30%,6;补全频数分布表和频数分布直方图,如图所示:(2)中等用水量家庭大约有450×(30%+20%+12%)=279(户);x≤<范围的两户用a、b表示,(3)在2389x ≤<这两个范围内的两户用1,2表示, 画树状图:则抽取出的2个家庭来自不同范围的概率是:82.123= 点睛:本题主要考查统计表和条形统计图,树状图求概率. 较为容易.注意频数,频率和总数之间的关系.98.近期,中宣部、国家发改委发出开展节俭养德全民节约行动的通知,在全社会营造厉行节约、拒绝浪费的浓厚氛围,我市某中学为了解该校学生家庭月均用电量情况,给学生布置了收集自己家中月均用电量数据的课外作业,学校随机抽取了1000名学生家庭月均用电量的数据,并将调查数据整理如下:(1)频数分布表中的m=_____,n=_____;(2)补全频数分布直方图;(3)被调查的1000名学生家庭月均用电量的众数落在哪一个范围?(4)求月均用电量小于150度的家庭数占被调查家庭总数的百分比.【答案】160 0.24【解析】试题分析:(1)根据抽查的总户数和频率=频数总数,即可求出答案; (2)根据图表所给的数据直接补全频数分布直方图; (3)根据众数的定义和统计表所给的数据即可求出答案;(4)把每月均用电量小于150度的家庭数加起来,再除以总户数,即可求出答案.试题解析:解:(1)m =1000×0.16=160,n =240÷1000=0.24.故答案为160、0.24;(2)补全条形图如下:(3)被调查的1000名学生家庭月均用电量的众数落在100≤a <150; (4)月均用电量小于150度的家庭数占被调查家庭总数的百分比为3002401201000++×100%=66%.点睛:本题考查了读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.99.(本题8分) 某校数学兴趣小组的成员小华对本班上学期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成如下频数分布表和频数分布直方图.请你根据图表提供的信息,解答下列问题:(1)频数分布表中a= ,b= ;(2)补全频数分布直方图;【答案】(1)8,0.08;(2)详见解析.【解析】分析:(1)、根据频数、频率、样本容量之间的关系即可得出答案;(2)、根据题意得出60—70分的频数,从而得出答案.详解:请你根据图表提供的信息,解答下列问题:(1)频数分布表中a= 8 ,b= 0.08 ;(2)补全频数分布直方图;如图所示.点睛:本题主要考查的频数、频率以及样本容量之间的关系,属于基础题型.理解三者之间的关系是解题的关键.100.“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表.请结合图表完成下列各题:(1)①表中a的值为;①把频数分布直方图补充完整;(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?【答案】(1)12;(2)详见解析;(3)44%.【解析】试题分析:(1)由参加决赛的学生总数50减去频数分布表中的已知频数即可得到a 的值;(2)根据(1)中求得的a的值将频数分布直方图规范的补充完整即可;(3)结合(1)中求得的a的值和频数分布表中的已知数据计算出不低于80分的学生人数,由这个人数÷50×100%即可得到优秀率.试题解析;(1)由题意可得:a=50-6-8-14-10=12;(2)频数分布直方图补充完整如下图所示:(3)由题意可得,这次比赛的优秀率为:12+10100%44%⨯=.50答:这次测试的优秀率为44%.。
人教版七年级数学下册第十章数据的收集、整理与描述第二节直方图复习试题(含答案) (95)

人教版七年级数学下册第十章数据的收集、整理与描述第二节直方图复习试题(含答案)如图,在频数直方图中,人数最少的一组的频数是____;69.5~79.5这一组的频数是____;数据分组时的组距为____.【答案】2 18 10【解析】【分析】由频数分布直方图可知所求答案.【详解】在频数直方图中,人数最少的一组的频数是2;69.5~79.5这一组的频数是18;数据分组时的组距为10.【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力,解本题的要点在于利用频数直方图获取所需要的数据.42.2018年6月6日是第二十三个全国爱眼日.某校为了做好学生的眼睛保护工作,对全体学生的裸眼视力进行了一次抽样调查,调查结果如图所示.根据学生视力合格标准,裸眼视力大于或等于5.0的为正常视力,那么该校正常视力的学生占全体学生的比值是_____.【答案】20%【解析】【分析】用裸眼视力大于或等于5.0的人数除以总人数可得答案.【详解】解:该校正常视力的学生占全体学生的比值是40++++2030506040=0.2=20%,故答案为20%.【点睛】本题考查了频数分布直方图的知识,解题的关键是仔细的读图并从中找到进一步解题的有关信息.43.如图,晓岚同学统计了她家5月份的长途电话明细清单,按通话时间画出频数分布直方图,则从图中的信息可知,她家通话时间不足10分钟的有_____次.【答案】43【解析】【分析】根据频数分布直方图直接解答.【详解】解:从图中的信息可知,她家通话时间不足10分钟的有25+18=43次,故答案为:43.【点睛】本题考查了频数分布直方图,弄清组距与各组的值是解题的关键.44.为了更好的刻画数据的总体的规律,我们还可以在得到的频数分布直方图上________,________,得到________图.【答案】取点连线频数分布折线【解析】【分析】根据画频数分布折线图的方法即可求解.【详解】解:为了更好的刻画数据的总体的规律,我们还可以在得到的频数分布直方图上取点,连线,得到频数分布折线图.故答案为取点,连线,频数分布折线图.【点睛】本题考查了频数分布折线图的画法及意义,一般利用直方图画频数分布折线图,在频数分布直方图中,把每个小长方形上面的一条边的中点顺次连接起来,得到频数分布折线图.注意:折线图要与横轴相交,方法是在直方图的左右两边各延伸一个假想组,并将频数折线两端连接到假想组中点,它主要显示数据的变化趋势.45.在对一个含有80个数据的样本绘制统计表时,发现其中一个小组的数据的个数占80的20%,那么这个小组含有________个数据.【答案】16【解析】【分析】用数据总数乘以此组所占的频率,即可求得该小组的频数即小组含有数据的个数.【详解】解:依题意,这个小组含有的数据为:80×20%=16(个).故答案为16.【点睛】本题主要考查了频率、频数和数据总数的关系,理解某一组的频率是该组频数与数据总数的比值,是解答此题的关键.46.对某班部分学生最近一次数学测试成绩(得分取整数)进行统计分析,将所有成绩由低到高分成五组,并绘制成如图所示的频数分布直方图,根据直方图提供的信息,在这次测试中,成绩为及格(60分以上,不含60分)的百分率为____.【答案】90%【解析】总人数为:5+9+15+14+7=50人;及格及以上人数为:9+15+14+7=45人;所以成绩为及格(60分以上,不含60分)的百分率为4590%.50故答案是:90%.47.对以下的实际问题,选用哪种常用统计图描述数据比较合适?请将你的选择填在题后的横线上.(1)某病人一昼夜的体温记录(单位:℃):36.9,36.5,36.8,37.5,37.5,36.5;___________(2)体育课上全班有10人跳长绳,15人在打篮球,剩余12人在打乒乓球;_____________(3)学校为七年级新生购进校服前,按身高分型号进行了登记.对女生的记录中,身高150cm以下记为S号,150~160cm记为M号,160~170cm记为L号,170cm以上记为XL号.___________【答案】折线图折线图直方图【解析】根据直方图可以从图中很容易看出各种数量的多少;折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况;直方图是数值数据分布的精确图形可得:(1)体温的变化情况,故选择折线统计图;(2)各部分的人数,故选择折线统计图;(3)各部分分布情况,故选择直方图;故答案是:折线图,折线图,直方图.48.频数分布直方图是以小长方形的_______来反映数据落在各个小组内的频数的大小.【答案】面积【解析】由题意,得小长方形的长为:频率组距,宽为:组距,∴小长方形的面积为:频率组距×组距=频率.∴小长方形的面积表示频率.故答案为:面积.49.若有一组数据最大值与最小值的差为23,取组距为3,则共可分为______组.【答案】8【解析】【分析】用最大值与最小值的差除以组距可得到组数.【详解】,所以可分8组.因为23÷3=723故答案为8【点睛】本题考核知识点:频数分布中的组数.解题关键点:理解组数的求法.50.如果将统计数据进行适当分组,那么落在各组里的数据的个数叫做_________.【答案】频数【解析】【分析】根据频数的定义填空即可.【详解】如果将统计数据进行适当分组,那么落在各组里的数据的个数叫做频数.故答案为频数【点睛】本题考核知识点:频数定义.解题关键点:熟记频数定义.。
人教版七年级数学下册第十章数据的收集、整理与描述第二节直方图习题(含答案) (50)

人教版七年级数学下册第十章数据的收集、整理与描述第二节直方图复习试题(含答案)一、单选题1.在频数分布直方图中()A.横轴必须从0开始,纵轴不受这个限制B.纵轴必须从0开始,横轴不受这个限制C.横轴与纵轴都必须从0开始D.横轴与纵轴都不必从0开始【答案】B【解析】试题解析:由于在频数分布直方图中,小长方形面积=组距×频数可知,纵轴必须从0开始,横轴不受这个限制.故选B.2.随着宜昌市精神文明建设的不断推进,市民八小时以外的时间越来越多,下面是某报记者在抽样调查了一些市民八小时以外用于读书的时间(单位:分钟)后,绘制的频数分布直方图,从左至右的前六个长方形所相对应的频率之和为0.95,最后一组的频数是10,则此次抽样调查的人数共有()A.200 B.100 C.500 D.10【答案】A【解析】试题解析:由题意可知:最后一组的频率=1-0.95=0.05,则由频率=频数÷总人数可得:总人数=10÷0.05=200人;故选A.3.武汉市某校在“创新素质实践行”活动中组织学生进行社会调查,并对学生的调查报告进行评比,下面是将某年级60篇学生调查报告的成绩进行整理,分成五组画出的频数分布直方图.已知从左至右5个小组的频数之比为1:3:7:6:3,则在这次评比中被评为优秀的调查报告(分数大于或等于80分为优秀,且分数为整数)占百分之()A.45 B.46 C.47 D.48【答案】A【解析】试题解析:由于:6391376320+=++++=45%. 故选A . 4.绘制频数分布直方图时,各小长方形面积占全体小长方形总面积的百分比刚好等于相应各组的( )A .组距B .平均值C .频数D .频率【答案】D【解析】试题解析:在频数直方图中纵坐标表示各组的频数/组距,横坐标表示组距, 则小长方形的高表示频数/组距,小长方形的长表示组距,则长方形的面积为长乘宽,即组距×频数/组距=频数;而全体小长方形总面积即样本容量;则各小长方形面积占全体小长方形总面积的百分比刚好等于相应各组的频率;故选D .5.为了绘制一批数据的频率分布直方图,首先要算出这批数据的变化范围,数据的变化范围是指数据的( )A .最大值B .最小值C .最大值与最小值的差D .个数 【答案】C【解析】【分析】【详解】解:根据频率直方图的是将数据将参量的数值范围等分为若干区间,统计该参量在各个区间上出现的频率,并用矩形条的长度表示频率的大小.即是按照数据的大小按序排列,故选C .6.小杰调查了本班同学体重情况,画出了频数分布直方图,那么下列结论不正确的是( )A .全班总人数为45人B .体重在50千克55~千克的人数最多C .学生体重的众数是14D .体重在60千克65~千克的人数占全班总人数的19【答案】C【解析】试题解析:由频数直方图可以看出:全班总人数为8+10+14+8+5=45人;A 正确;体重在50千克到55千克的人数最多为14人;故众数在50千克到55千克之间.B 正确,但C 错误;在体重在60千克到65千克的人数为5人,则占全班总人数的5÷45=19;D 正确.故选C .7.如图是九年级()1班同学的一次体检中每分钟心跳次数的频率分布直方图(次数均为整数).已知该班只有5位同学的心跳每分钟75次,请通过观察右图,指出下列说法中错误的是()A.数据75落在第2小组B.第4小组的频率为0.1C.数据75一定是中位数D.心跳每分钟75次的人数占该班体检人数的112【答案】C【解析】试题解析:A、∵69.5<75<79.5,∴数据75落在第2小组正确,故本选项错误;B、九年级(1)班同学总人数为:25+20+9+6=60,=0.1正确,故本选项错误;所以,第4小组的频率为660C、∵只有5位同学的心跳每分钟75次,20-5=15,25+15=40,25+5=30,∴数据75有可能是中位数,也有可能不是中位数,故本选项正确;D、心跳每分钟75次的人数占该班体检人数的51正确,故本选项错误.=6012故选C.点睛:本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题,要注意C选项中还有15人的心跳次数不是75.8.体育老师对九年级()1班学生“你最喜欢的体育项目是什么(只写一项)?”的问题进行了调查,把所得数据绘制成频数分布直方图(如图).由图可知,最喜欢篮球的学生的人数是()A.8 B.12 C.16 D.20【答案】D【解析】试题解析:由图可知,最喜欢篮球的学生的人数是20人,故选D.9.对赵中、安中的最近的联考二的数学测试成绩(得分为整数)进行统计,将所有成绩由低到高分成五组,并绘制成如图所示的频数分布直方图,根据直方图提供的信息,在这次测试中,成绩为A等(80分以上,不含80分)的百分率为()A.24%B.40%C.42%D.50%【答案】C【解析】试题解析:总人数是:5+9+15+14+7=50,则成绩为A等(80分以上,不含80分)的百分率是:14+7×100%=42%.50故选C.10.某校为了了解九年级500名学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起座的次数,并绘制成如图所示的频数分布直方图,请你根据图示计算,估计仰卧起座次数在15~20之间的学生有()A.50 B.85 C.165 D.200【答案】A【解析】3500=50,所以估计仰卧起座次数在15~20之间的学生有50人,故选30A.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版七年级数学下册第十章数据的收集、整理与描述第二
节直方图复习试题(含答案)
有100个数据,其中最大值为76,最小值为32,若取组距为5,对数据进行分组,则应分为______组.
【答案】9
【解析】
【分析】
根据频数分布直方图的组数的确定方法,用极差除以组距,然后根据组数比商的整数部分大1确定组数.
【详解】
解:∵极差为76-32=44,
∴由44÷5=8.8知可分9组,
故答案为:9.
【点睛】
本题考查了频数分布直方图的组数的确定,需要特别注意,组数比商的整数部分大1,不能四舍五入.
92.为了解某校九年级女生1分钟仰卧起坐的次数,从中随机抽查了50名女生参加测试,并绘制成频数分布直方图(如图).如果被抽查的女生中有90%的女生1分钟仰卧起坐的次数大于等于30且小于50,那么1分钟仰卧起坐的次数在40∼45的频数是______.
【答案】31
【解析】
【分析】
先求出1分钟仰卧起坐的次数大于等于30且小于50的女生人数,然后用次数大于等于30且小于50的女生人数减去次数30∼35的人数、35∼40的人数、45∼50的人数即可得解.
【详解】
解:∵1分钟仰卧起坐的次数大于等于30且小于50的女生:50×90%=45(人),
∴1分钟仰卧起坐的次数在40∼45的人数:45-3-5-6=31(人),
即1分钟仰卧起坐的次数在40∼45的频数是31,
故答案为31.
【点睛】
本题考查补全频数直方图.解决本题的关键是要懂得频率分布直方图的意义,了解频数分布直方图是一种以频数为纵向指标的统计图.
93.为了解小学生的体能情况,抽取了某小学同年级50名学生进行1分钟跳绳测试,将所得数据整理后,画出如图所示的频数分布直方图(各组只含最小值,不含最大值),已知图中从左到右各组的频率分别a, 0.3, 0.4, 0.2,设跳绳次
数不低于100次的学生有b人,则a,b的值分别是______.
【答案】0.1;30.
【解析】
【分析】
用总人数乘以第3、4组的频率和可得b的值,由频率之和等于1可得a的值.
【详解】
解:由题意知b=50×(0.4+0.2)=30,
a=1-(0.4+0.3+0.2)=0.1,
故答案为:0.1,30.
【点睛】
本题考查频数分布直方图,解答本题的关键是明确题意,利用数形结合的思想解答.
94.某班有48名同学,在一次英语单词竞赛成绩统计中,成绩在81~90这一分数段的人数所占的频率是0.25,那么成绩在这个分数段的同学有
_________名.
【答案】12
【解析】
【分析】
由题意直接根据频数=频率×总数,进而可得答案.
解:由题意可得成绩在81~ 90这个分数段的同学有48×0.25=12(名). 故答案为:12.
【点睛】
本题主要考查频数和频率,解题的关键是掌握频率等于频数除以总数进行分析计算.
95.已知一个样本中,样本容量为50,这50个数据分别落在5个小组内,第一、二、四、五小组的频数分别是2,10,10,20,则第三个小组的频率为________.
【答案】0.16
【解析】
【分析】
根据频数之和等于样本容量以及频率公式计算.
【详解】
解:由题意知:第三小组的频数()5021010208=-+++=,
其频率=频数÷样本容量8500.16=÷=.
故答案为:0.16.
【点睛】
本题考查频率的意义与计算:频率=频数÷样本总量.
96.已知某组数据的频数为56,频率为0.8,则样本容量为________.
【答案】70
【解析】
根据频率 频数
进行计算即可.
总数
【详解】
56÷0.8=70.
故答案为:70.
【点睛】
本题考查了频率,关键是掌握频率的计算公式.
97.在样本容量为60的一个样本中,某组数据的频率是0.4,则这组数据的频数是______________。
【答案】24
【解析】
【分析】
根据频率、频数的关系:频数=频率×数据总和,可得这一小组的频率.【详解】
∵容量是60的一个样本,分组后某一小组的频率是0.4,
∴样本数据在该组的频数=0.4×60=24.
故答案为:24.
【点睛】
此题考查频数与频率,解题关键在于明确频数=频率×数据总和这个关系.
98.在一次数学考试中,某班50名学生的成绩在100~110分这组的频率是0.2,则这组的频数是________.
【答案】10
【分析】
用总数×频率即可求出频数.
【详解】
⨯=
这组的频数是500.210
故答案为:10.
【点睛】
本题主要考查频数,掌握频数和频率之间的关系是解题的关键.
99.为了了解初三毕业班学生一分钟跳绳次数的情况,某校抽取了一部分初三毕业生进行一分钟跳绳次数的测试,将所得数据进行处理,共分成4组,频率分布表(不完整)如下表所示.如果次数在110次(含110次)以上为达标,那么估计该校初三毕业生一分钟跳绳次数的达标率约为_____.
【答案】92%
【解析】
【分析】
根据抽取的学生一分钟跳绳的达标率,即可估计该校初三毕业生一分钟跳绳
的达标率.
【详解】
解:∵样本容量为:3÷0.06=50,
∴该校初三毕业生一分钟跳绳次数的达标率约为5031
50
--
×100%=92%,
故答案为:92%
【点睛】
本题考查的是频数分布表的知识,准确读表、从中获取准确的信息是解题的关键,注意用样本估计总体的运用.
100.已知某组数据的频数为20,样本容量为50,则频率为______.
【答案】0.4
【解析】
【分析】
用频数20除以样本容量为50即可.
【详解】
20÷50=0.4.
故答案为:0.4.
【点睛】
本题考查了频率的计算方法,熟练掌握频率=频数÷总数是解答本题的关键.。
