【湘教版】九年级数学上册:第4章 锐角三角函数 单元目标检测试卷(含答案)
【九年级】九年级上册数学第4章锐角三角函数测试(湘教版带答案)

【九年级】九年级上册数学第4章锐角三角函数测试(湘教版带答案)来来源第4章锐角三角函数检测题(时间:90分钟,满分:100分)一、(每小题3分,共30分)1.计算:a.b.c.d.2.在△, ∠ = 90°,如果,,那么sin的值是()a.b.c.d.3.在△, ∠ = 90,然后是罪()a.b.c.d.4.在下列陈述中,正确的是()a.b、如果是锐角,那么c.对于锐角,必有D5.在△中,∠=90°,,则sin的值是()a、 b.c.1d。
6.已知在中,,则的值为()a、不列颠哥伦比亚省。
7.如图,一个小球由地面沿着坡度的坡面向上前进了10,此时小球距离地面的高度为()a、 b.2c.4d.8.如图所示,在钻石中,,,Tan的值∠ 是()a.b.2c.d.9.在△,,, 等于()a.b.1c.2d.310.如图所示,已知45°<a<90°,则以下公式为真()a.b.c、 d。
二、题(每小题3分,共24分)11.那么__12.若∠是锐角,cos=,则∠=_________.13.小兰想测量南塔的高度她抬头看了看塔顶,测量了30°的仰角,然后向塔的方向移动了50°,测量了60°的仰角,所以塔的高度大约是___________________14.等腰三角形的腰长为2,腰上的高为1,则它的底角等于________.15.大坝的横截面为梯形。
坝内坡度和坝外坡度是两个坡度角的总和16.△abc的顶点都在方格纸的格点上,则_.在图中,四边形18.如图,在△中,已知,,,则________.三、回答问题(共46分)19.(8分)计算下列各题:(1);(2).20.(6分)在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树的高度,设计的方案及测量数据如下:(1)在树前的平地上选择一个点,测量树顶与该点的仰角为35°;(2)在点和大树之间选择一点(、、在同一条直线上),测得由点看大树顶端的仰角恰好为45°;(3)两个测量点之间的距离为4.5请你根据以上数据求出大树的高度.(结果保留3个有效数字)21.(6点)已知:如图所示,在山脚处测得的山顶仰角为,沿坡度前进米,以坡度角到达(即。
【湘教版】九年级数学上册:第四章 锐角三角函数 单元检测题(含答案)

第四章 锐角三角函数检测题 (时间:90分钟,满分:100分)一.选择题(每小题3分,共30分) 1.计算:A. B.232+ C.23 D.231+2.在△中,∠=90°,如果,,那么sin 的值是( ). A.21B.55 C.33 D.233.(4分)如图,△ABC 中,∠B =90°,BC =2AB ,则cos A =( ) A. B. C. D.4.下列说法中,正确的是( ) A.B.若为锐角,则C.对于锐角,必有sin cos ββ<D.5.如图,在网格中,小正方形的边长均为1,点A ,B ,C 都在格点上,则∠ABC 的正切值是( )A.2B.C.D.6.已知在Rt ABC △中,390sin 5C A ∠==°,,则tan B 的值为( )A.43B.45C.54D.347.如图,一个小球由地面沿着坡度的坡面向上前进了10 m ,此第7题图A BC第10题图时小球距离地面的高度为( ) A.B.25m C.45m D.310m 8.如图,在菱形ABCD 中,,3cos 5A =,BE =2,则tan ∠DBE 的值是( )A.12B.2C.5D.59.在△中,,,,则等于( )A. B.1 C.2 D.3 10.如图,已知:45°<A <90°,则下列各式成立的是( ) A.sin A =cos AB. sin A ﹥cos AC. sin A ﹥tan AD. sin A ﹤cos A 二.填空题(每小题3分,共24分)11.在Rt ABC △中,90C ∠=,5AC =,4BC =,则tan A =______. 12.如图,△ABC 中,DE 是BC 的垂直平分线,DE 交AC 于点E ,连接BE ,若BE =9,BC =12,则cos C =___________.13.如图,小兰想测量南塔的高度, 她在A 处仰望塔顶,测得仰角为30°,再往塔的方向前进50 m 至B 处,测得仰角为60°,那么塔高约为 _________ m.(小兰身高忽略不计,732.13≈) 14.等腰三角形的腰长为2,腰上的高为1,则它的底角等于________ . 15.大坝的横断面是梯形,坝内斜坡的坡度,坝外斜坡的坡度,则两个坡角的和为 .16.如图,△ABC的顶点都在网格纸的格点上,则_ . 17. 如图,在四边形中,,,,,则__________.18. 如图,在△中,已知,,,则________. 三.解答题(共46分) 19.(8分)计算下列各题: (1) ()42460sin 45cos 22+- ; (2)2330tan 3)2(0-+--.20.(6分)如图,AD 是△ABC 的中线,tan B =,cos C =,AC =.求: (1)BC 的长;(2)sin ∠ADC 的值.20题图21.(6分)已知:如图,在山脚的处测得山顶的仰角为,沿着坡角为的斜坡前进m 到达处(即∠,m ),测得的仰角为,求山的高度.22.(6分)如图,为了测量某建筑物CD 的高度,先在地面上用测角仪自A 处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100 m ,此时自B 处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5 m ,请你计算出该建筑物的高度.(3≈1.732,结果精确到1 m )23.(6分)如图,在梯形中,∥,,.ABCD第21题图(1)求sin∠DBC的值;(2)若长度为,求梯形的面积.24.(6分)如图,在小山的东侧A处有一热气球,以每分钟30 m的速度沿着仰角为60°的方向上升,20 min后升到B处,这时热气球上的人发现在A的正西方向俯角为45°的C处有一着火点,求热气球的升空点A与着火点C的距离(结果保留根号).25.(8分)如图,平台AB高为12 m,在B处测得楼房CD顶部点D 的仰角为45°,底部点C的俯角为30°,求楼房CD的高度.( 1.7)第24题图BC A 东西45°60°参考答案1.B解析:方法1:∵∴,∴∴ 这个直角三角形的斜边长是3,故选B.方法2:设1x 和2x 是方程22870x x -+=的两个根,由一元二次方程根与系数的关系可得∴22221212127()24292x x x x x x +=+-=-⨯=,∴ 这个直角三角形的斜边长是3,故选B.2.B 解析:∵ 22141411104b ac -=-⨯⨯=-=,∴ 一元二次方程+x +=0有两个相等的实数根. 3.B 解析:设第一块木板的宽是,则第一块木板的长是,第二块木板的长是,第二块木板的宽是.根据题意,得3(22)2108x x x x --⋅=. 整理,得223540x x --=,因式分解,得(6)(29)0x x -+=,解得1296,2x x ==-. ∵ 292x =-不合题意,舍去.∴ 6x =. ∴ 第一块木板长,宽,第二块木板长,宽.4.B 解析:过作的平行线交于,则△∽△.∵ 是的中点,∴ ,,∴A BEF CD第4题答图G∴ AC =AF +FG +GC =4+8+8=20(cm ).故选B. 5.C 解析 :∵ AB AC =,∴ ABC ACB ∠=∠. 又∵ CBD A ∠=∠,∴ △ABC ∽△BCD . 同理可得△ABC ∽△BCD ∽△CDE ∽△DFE , ∴,,AB BC CD DE EF DEBC CD BD CD DE CE===,解得23423,,b b b CD DE EF a a a===.故选C.6. C 解析:根据题意,得AB ⊥PB ,∠ABP =90°,在Rt △ABP 中,∠PAB =55°,PA =2海里,cos AB PAB PA∠=,∴ cos AB PA PAB =⋅∠=2cos 55°海里,故选项C 正确.7.C 解析:平均成绩相同,方差反映数据的稳定性,方差越小成绩越稳定.8.A 解析:如图,过点A作因为22,所以.由勾股定理,得.又53, 所以所以 第8题答图所以所以9.D 解析:如图,过点C 作CD AB ⊥于点D .设AC x =海里.在△ACD 中,∠90ADC =︒,∠102030CAD =︒+︒=︒,第9题答图AC x =海里,∴ C D =12AC =12x 海里,AD =3CD =32x 海里. 在△BCD 中,∠90BDC =︒,∠802060CBD =︒-︒=︒, ∴ BD =33CD =36x 海里. ∵ AD BD AB +=,∴ 32x +36x 20=, 解得103x =,所以救援船航行的速度为2010330360÷=(海里/时). 10.B 解析:因为,,所以,所以A =90°-A ,所以A =45°. 11.2560x x -+= 12.0x =或3x =13.3tan 50° 解析:在Rt △ABC 中,∵∠C =90°,∠A =40°, ∴ ∠B =50°,∴ tan B =tan 50°=BCAC, ∴ AC =BC tan 50°=3 tan 50°.14. 3 4 解析:设方程的另一个根为a ,根据根与系数的关系得到a ×1=3,a +1=m , 解得a =3,m = 4. 15.3 解析:∵ ,∠为△和△的公共角,∴ △∽△,∴.在Rt △中,由勾股定理得,得. 又∵,,,∴,∴.16. 变大 解析:减少木工2名,增加电工.瓦工各1名后,14名员工的工资少了两个6 000,多了一个7 000和一个5 000,调整前后工程队员工月平均工资不变,均是6 000元,但调整后各数据与平均数的差的平方和变大了,所以方差变大了. 17. 135 解析:在Rt △ABD 中,∠BAD =90°,=, ∵ ∠ADB =30°,AB =45 m ,∴ =,∴ AD =45m.在Rt △ADC 中,∠ADC =90°,=, ∵ ∠CAD =60°,AD =45m ,∴=,∴ DC =135 m.18. 6 解析:如图,连接OA ,OB ,OC ,OD ,设DC ,AB 分别交y 轴于点F ,E ,则S △AOB =12OE ·AB =32OE =12a -12b ,S △COD =12OF ·CD =12×OF ×2=12a -12b ,∴ 325,OE OF OE OF ⎧=⎪⎨⎪+=⎩,解得2,3,OE OF =⎧⎨=⎩∴ 12a -12b =3,∴ a -b =6.19.解:(1)55sin 35sin 12145sin 222+++-2222(21)sin 35cos 352⨯--++22.(2)12︒-30tan 3+121-⎪⎭⎫ ⎝⎛-2133332-+⨯-=13-=. 20.解:设矩形猪舍垂直于住房墙的一边长为x m,则矩形猪舍的另一边长为(26-2x )m.根据题意,得x (26-2x )=80. 化简,得-13x +40=0. 解这个方程,得=5,=8.当x =5时,26-2x =16>12(舍去);当x =8时,26-2x =10<12.答:所建矩形猪舍的长为10 m,宽为8 m 时,猪舍面积为80 m 2. 21.解:(1)过点C 作CE ∥OA 交BD 于点E ,则△BCE ∽△BOD . 又C 为OB 的中点,所以BC OC =,所以1122CE OD AD ==. 再由CE ∥OA ,△ECP ∽△DAP ,所以2==CEADPC AP . (2)过C 作CE ∥OA 交BD 于点E ,设AD x =,则4OA OB x ==,3OD x =, 由△BCE ∽△BOD ,得1322CE OD x ==. 再由△ECP ∽△DAP ,得32==CE AD PE PD . 由勾股定理可知5BD x =,52DE x =,则32=-PD DE PD ,可得PD AD x ==, 则∠BPC =∠DPA =∠A ,所以tan ∠BPC =tan ∠A =21=AO CO . 22.(1)证明:AB ∥DC ,∴ ACF CAE =∠∠.在△CFO 和△AEO 中,∴ △≌△CFO AEO ,∴ OF OE =.又 OA OC =,∴ 四边形AECF 是平行四边形. EF AC ⊥,∴ 四边形AECF 是菱形.(2)解: 四边形AECF 是菱形,4EF =,∴ 114222OE EF ==⨯=. 在Rt AEO △中, 2tan 5OE OAE OA ==∠,∴ 5OA =, ∴ 22510AC AO ==⨯=.∴23.解:设B 处距离码头O x km. 在Rt △CAO 中,∠CAO =45°. ∵ tan ∠CAO =∴ CO =AO ·tan ∠CAO =(45×0.1+x )·tan 45°=4.5+x. 在Rt △DBO 中,∠DBO =58°.∵ tan∠DBO=,∴DO=BO·tan∠DBO=x·tan 58°.∵DC=DO CO,∴ 36×0.1= x·tan 58°(4.5+x),∴x=≈=13.5.因此,B处距离码头O大约13.5 km.24.解:(1)10÷25%=40;(2)补全条形统计图如下:第24题答图40×30%=12,40-10-15-12=3.(3)1 200× =90.答:估计全校最喜爱篮球的人数比最喜爱足球的人数多90人. 25.(1)证明:由题意可知∵∥∴∠∠,∠=∠∴△≌△∴.又∥∴四边形是平行四边形.∵,∴平行四边形是菱形.(2)解:∵四边形是菱形,∴.设,∵△的面积为24,△的周长为.(3)解:存在,过点作的垂线,交于点,点就是符合条件的点.证明如下:∵ ∠∠90°,∠∠ ∴ △∽△,∴ AE AO AP AE ,∴ . ∵ 四边形是菱形,∴ ∴∴。
第4章 锐角三角函数数学九年级上册-单元测试卷-湘教版(含答案)

第4章锐角三角函数数学九年级上册-单元测试卷-湘教版(含答案)一、单选题(共15题,共计45分)1、如图,⊙O是△ABC的外接圆,弦AC的长为3,sinB= ,则⊙O的半径为()A.4B.3C.2D.2、在中,,,,则的值是()A. B. C. D.3、如图,一艘轮船在A处测得灯塔P位于其北偏东60°方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30°方向上,此时轮船与灯塔P的距离是()A.15 海里B.30海里C.45海里D.30 海里4、如图,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是()A. B. C. D.5、如图,在中,,,,若是边上的动点,则的最小值()A. B.6 C. D.46、sin30°的值为()A. B. C. D.7、若cosα=,则锐角α的度数是()A.30°B.45°C.60°D.90°8、下列各数中是有理数的是()A. B.4π C.sin45° D.9、如图,在中,,则等于()A. B. C. D.10、已知等边三角形的外接圆半径为2,则该等边三角形的边长是( )A.2B.4C.D.211、如图,已知A,B,C,D是⊙O上的点,AB⊥CD,OA=2,CD=2 ,则∠D等于()A. B. C. D.12、如果一斜坡的坡比是1:2.4,那么该斜坡坡角的余弦值是()A. B. C. D.13、在Rt△ABC中,∠C=90°,若AB=4,sinA=,则斜边上的高等于()A. B. C. D.14、直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B 重合,折痕为DE,则tan∠CBE的值是()A. B. C. D.15、在中,,,,则的值是()A. B. C. D.二、填空题(共10题,共计30分)16、如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点.△ABC的顶点都在方格的格点上,则cosA=________.17、矩形的一条对角线长为26,这条对角线与矩形一边夹角的正弦值为,那么该矩形的面积为________.18、如图,在菱形中,,分别在边上,将四边形沿翻折,使的对应线段经过顶点,当时,的值为________.19、如图,斜坡AB的坡度i=1:3,该斜坡的水平距离AC=6米,那么斜坡AB的长等于________ 米.20、如图所示,正方形ABCD的边长为1,点E为AB的中点,以E为圆心,1为半径作圆,分别交AD,BC于M,N两点,与DC切于点P,则图中阴影部分面积是________.21、某斜坡坡角的正弦值,则该斜坡的坡度为________.22、如图所示,四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,若sin∠ACB=,则cos∠ADC=________.23、如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值是________.24、如图,在扇形OAB中,∠AOB=60°,扇形半径为r,点C在上,CD⊥OA,垂足为D,当△OCD的面积最大时,的长为________ .25、等腰三角形底边长10cm,周长为36cm,则一底角的正切值为________三、解答题(共5题,共计25分)26、计算:()﹣1﹣(2017﹣π)0﹣2sin45°+| ﹣1|27、如图,山顶建有一座铁塔,塔高米,测量人员在一个小山坡的P处测得塔的底部B点的仰角为,塔顶C点的仰角为已测得小山坡的坡角为,坡长米求山的高度精确到1米参考数据:28、如图,一艘货轮以40海里/小时的速度在海面上航行,当它行驶到处时,发现它的东北方向有一灯塔,货轮继续向北航行30分钟后到达点,发现灯塔在它北偏东方向,求此时货轮与灯塔的距离.(结果精确到0.1海里,参考数据:,)29、如图,河堤横断面为梯形,上底为,堤高为,斜坡的坡比为,斜坡的坡角为.求:河堤横截面的面积.30、如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1:,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC 宽30m,求高压电线杆CD的高度(结果保留三个有效数字,≈1.732)参考答案一、单选题(共15题,共计45分)1、C2、A3、B4、D5、B6、A7、C8、D9、C10、D11、C12、D13、B14、C15、B二、填空题(共10题,共计30分)16、17、18、19、21、22、23、24、25、三、解答题(共5题,共计25分)26、28、29、30、。
湘教版九年级数学上册第4章《锐角三角函数》检测试卷(含答案)
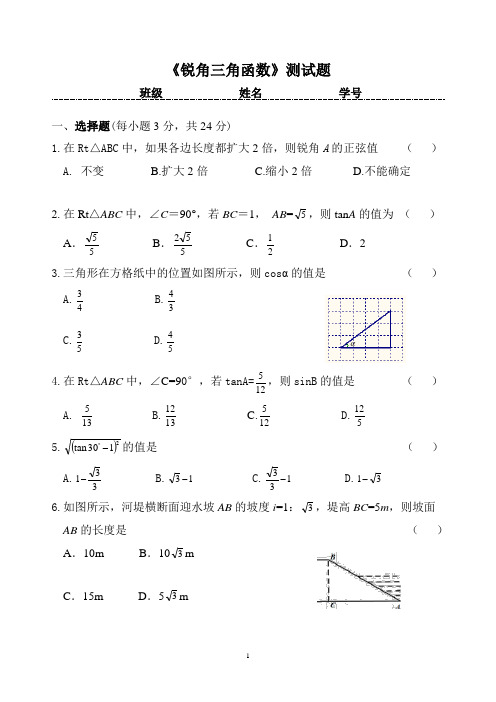
《锐角三角函数》测试题班级 姓名 学号一、选择题(每小题3分,共24分)1.在Rt △ABC 中,如果各边长度都扩大2倍,则锐角A 的正弦值 ( ) A. 不变 B.扩大2倍 C.缩小2倍 D.不能确定2.在Rt △ABC 中,∠C =90°,若BC =1, AB =5,则tan A 的值为 ( ) A .55 B .552 C .21D .2 3.三角形在方格纸中的位置如图所示,则cos α的值是 ( ) A.43 B.34C.53 D.544.在Rt △ABC 中,∠C=90°,若tanA=125,则sinB 的值是 ( ) A.135 B.1312 C.125 D.5125.()2130tan -︒的值是 ( ) A.331-B.13-C.133- D.31- 6.如图所示,河堤横断面迎水坡AB 的坡度i =1:3,堤高BC =5m ,则坡面AB 的长度是 ( ) A .10m B .103mC .15mD .53m7.如图,在Rt △ABC 中,∠ACB =90°,CD ⊥AB ,垂足为D .若AC =5,BC =2,则sin ∠ACD 的值为 ( )A .32B .552 C .25 D .358.将矩形纸片ABCD 按如图所示的方式折叠,AE 、EF 为折痕,∠BAE =30°,AB=3,折叠后,点C 落在AD 边上的C 1处,并且点B 落在EC 1边上的B 1处. 则BC 的长为 ( )A.3 B .2C .3D .32二、填空题(每小题3分,共30分)9.在Rt △ABC 中,∠C =90°,∠A ,∠B ,∠C 的对边分别为a ,b ,c ,则sinB= .10.在Rt △ABC 中,∠C =90°,∠A =60°,BC=3,则AC= . 11. 计算:︒︒︒︒+60604530tan sin tan cos = . 12. 如果α是锐角,且tan α=1,那么α= . 13. 在△ABC 中,∠A ,∠B 为锐角,sin A =21,tan B =33,则△ABC 的形状 为 .14. 如图,在菱形ABCD 中,D E ⊥AB ,垂足为E ,DE =6, sin A =53,则菱形ABCD 的周长是 .15.等腰三角形腰长为2cm ,底边长为23cm ,则顶角为 .16.边长为a 的等边三角形的高是 .17.在Rt △ABC 中,∠C =90°,BC=12,43=A tan ,则AB= . 18.如图,在平面直角坐标系中,已知点A(2,4), 连接OA ,则OA 与x 轴所成的锐角α的正弦值 为 .三、解答题(第19和20题每题8分,其余每题10分,共46分) 19. 计算:(1)186********+-+︒︒︒tan cos sin ;(2)()()2201452303-143-2-++︒︒sin tan .π20.如图,AD 是△ABC 的中线,31tan =B ,22cos =C ,2=AC .求: (1)BC 的长; (2)ADC ∠sin 的值.AB CD21.如图,某校数学兴趣小组的同学在测量建筑物AB 的高度时,在地面的C 处测得点A 的仰角为45°,向前走20米到达D 处,在D 处测得点A 的仰角为60°,求建筑物AB 的高度(得数保留根号).22.如图,在Rt △ABC 中,∠C =90°,∠A ,∠B ,∠C 的对边分别为a,b,c, (1)直接写出sinA 与cosB 的关系式; (2)求证:122=+B sin A sin ;(3)请你运用上述结论解决问题:在Rt △ABC 中,∠C =90°,135cos =B ,求B s i n 的值.45° 60°ABDCABabc23. 如图,一艘海监船位于灯塔P的东南方向,距离灯塔200海里的A处。
湘教版九年级数学上册《第四章锐角三角函数》单元评估检测试卷(有答案)

湘教版九年级数学上册 第四章 锐角三角函数 单元评估检测试卷一、单选题(共10题;共30分)1.tan60°的值等于( )A. B. C. D. 12333232.(2017•兰州)如图,一个斜坡长130m ,坡顶离水平地面的距离为50m ,那么这个斜坡与水平地面夹角的正切值等于( )A. B. C. D. 513121351213123. sin60°的值为( )A. B. C. D. 33222124.将一张矩形纸片ABCD (如图)那样折起,使顶点C 落在C'处,测量得AB=4,DE=8.则sin ∠C'ED 为( )A. 2B.C.D.1222325.在Rt △ABC 中,∠C=90°,若AB=2AC ,则sinA 的值是( )A. B. C. D. 31232336.计算:tan45°+sin30°=( )A. B. C. D. 22+32321+327.如图,为了测得电视塔的高度EC ,在D 处用高2米的测角仪AD ,测得电视塔顶端E 的仰角为45°,再向电视塔方向前进100米到达B 处,又测得电视塔顶端E 的仰角为60°,则电视塔的高度EC 为( )A. (50+152)米B. (52+150)米C. (50+150)米D. (52+152)米33338.在Rt △ABC 中,∠C=90°,AC=3,BC=4,那么cosB 的值是( )A. B. C. D. 453534439.已知Rt △ABC 中,∠C=90°,tanA=,BC=8,则AC 等于( )43A. 6 B. C. 10 D. 1232310.如图,已知在Rt △ABC 中,∠C=90°,BC=1,AC=2,则tanA 的值为( )A. 2B.C.D. 1255255二、填空题(共10题;共30分)11.在Rt △ABC 中,∠C=90°,AB=3,BC=2,则cosA 的值是________.12.如果沿斜坡AB 向上前进20米,升高10米,那么斜坡AB 的坡度为________.13.如果在平面直角坐标系xoy 中,点P 的坐标为(3,4),射线OP 与X 轴的正半轴所夹的角为α,那么α的余弦值等于________.14.如图,在等腰Rt △ABC 中,∠C=90°,AC=6,D 是AC 上一点,若tan ∠DBA= , 则AD 的长为15________.15.如图,在▱ABCD 中,AD=7,AB=2 ,∠B=60°.E 是边BC 上任意一点,沿AE 剪开,将△ABE 沿BC 方3向平移到△DCF 的位置,得到四边形AEFD ,则四边形AEFD 周长的最小值为________.16.热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m ,这栋高楼高________ m (结果保留根号).17.△ABC 之中, ∠BAC=90°,点D 在直线AB 上,连接DC ,若tanB= ,AB=3,AD=2,则△DBC 的面积为12________.18.如图,某人在塔顶的P 处观测地平面上点C 处,经测量∠ P=35°,则他从P 处观察C 处的俯角是________ 度.19.在Rt △ABC 中,∠C=90°,有两边长分别为3和4,则sinA 的值为________ .20.一次函数y= x+b (b <0)与y= x﹣1图象之间的距离等于3,则b 的值为________.4343三、解答题(共8题;共60分)21.如图,从热气球C 处测得地面A,B 两点的俯角分别为 , ,此时热气球C 处所在位置到地30°45°面上点A 的距离为400米.求地面上A ,B 两点间的距离.22.如图,水库大坝的横截面是梯形,坝顶宽5米,坝高20米,斜坡AB的坡比为1:2.5,斜坡CD的坡比为1:2,求大坝的截面面积23.如图,小明在操场上放风筝,已知风筝线AB长100 米,风筝线与水平线的夹角α=37°,小王拿风筝线的手离地面的高AD为1.5米,求风筝离地面的高度BE(精确到0.1米).24.位于合肥滨湖新区的渡江战役纪念馆,实物图如图1所示,示意图如图2所示.某学校数学兴趣小组3通过测量得知,纪念馆外轮廓斜坡AB的坡度i=1:,底基BC=50m,∠ACB=135°,求馆顶A离地面23BC的距离.(结果精确到0.1m,参考数据:≈1.41,≈1.73)25.如图,在数学活动课上,小丽为了测量校园内旗杆AB的高度,站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.已知旗杆与教学楼的距离BD=9m,请你帮她求出旗杆的高度(结果保留根号).26.在南部沿海某气象站A测得一热带风暴从A的南偏东30°的方向迎着气象站袭来,已知该风暴速度为每小时20千米,风暴周围50千米范围内将受到影响,若该风暴不改变速度与方向,问气象站正南方60千米处的沿海城市B是否会受这次风暴的影响?若不受影响,请说明理由;若受影响,请求出受影响的时间.27.如图,为了测量某风景区内一座塔AB的高度,小明分别在塔的对面一楼房CD的楼底C,楼顶D处,测得塔顶A的仰角为45°和30°,已知楼高CD为10m,求塔的高度(结果精确到0.1m).(参考数据:23≈1.41,≈1.73)28.如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB ,坡面AC的倾斜角为45° .为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i= :3 .若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:≈1.414,≈1.732)答案解析部分一、单选题1.【答案】D2.【答案】C3.【答案】B4.【答案】B5.【答案】C6.【答案】C7.【答案】A8.【答案】A9.【答案】A10.【答案】B二、填空题11.【答案】5312.【答案】1:313.【答案】14.【答案】215.【答案】2016.【答案】160 317.【答案】 154或3418.【答案】5519.【答案】或或或4535347420.【答案】﹣6 三、解答题21.【答案】解: 过点C 作 于点DCD ⊥AB由题意得 , ∠A =∠ECA =30°∠B =∠FCB =45°∵在Rt △ACD 中, , sinA =CD AC cosA =AD AC∴CD=AC = =400× =200(m)sinA 400sin30°12AD= AC = =400× =200 (m )cosA 400cos30°323∵在Rt △BCD 中, tanB= CDBD∴BD= = =200 (m)CD tanB 200tan45°∴AB=AD+BD= m (2003+200)答:地面上A ,B 两点间的距离为 m .(2003+200)22.【答案】解:∵斜坡AB 的坡度i=1:2.5,∴ ,BE AE =12.5∵斜坡CD 的坡度i=1:2,∴ ,CFDF =12∵BE=20米,∴AE=50米,DF=40米,∵EF=BC ,BC=5米,∴EF=5米,∴AD=AE+EF+DF=50+5+40=95米∴S 梯形ABCD = (AD+BC)×BE= ×100×20=1000(平方米)121223.【答案】解:∵AB=100米,α=37°,∴BC=AB•sinα=100sin37°,∵AD=CE=1.5米,∴BE=BC+CE=100×sin37°+1.5≈100×0.60+1.5=61.5(米),答:风筝离地面的高度BE 为:61.5米24.【答案】解:如解图,过点A 作AD ⊥BC 交BC 的延长线于点D .∵∠ACB=135°,∴△ADC 为等腰直角三角形,设AD=x ,则CD=x ,BD=50+x ,∵斜坡AB 的坡度i=1:,∴x :(50+x )=1:,整理得(﹣1)x=50,解得x=25(+1)≈68.3.答:馆顶A 离地面BC 的距离约为68.3 m .25.【答案】解:如图,在Rt △ACF 中,∵tan ∠ACF=,AF CF ∴tan30°=,AF 9∴ = ,AF 933∴AF=3 m ,3在Rt △BCF 中,∵∠BCF=45°,∴BF=CF=9m ,∴AB=AF+BF=3 +9(m ).326.【答案】解:根据题意画出图形,根据题意可知AB=60千米,∠BAF=30°过B 作BD ⊥AF 于点D ,作BE=BF=50千米,分别交AF 于点E 、F ∵ BD ⊥AF,AB=60千米,∠BAF=30°∴ 风暴离B 城市的最近距离为BD=AB×sin30°=30千米,∵ BD <50千米∴ 沿海城市B 会受到这次风暴的影响∵ BE=BF=50千米∴ 沿海城市B 受影响时风暴所走的路程为线段EF∵ BE=BF=50千米,BD=30千米,BD ⊥AF∴ DF=DE=502-302=40∴ EF=2DF=80千米∵ 风暴速度为每小时20千米∴ 受影响时间==4小时8020∴沿海城市B 会受到这次风暴的影响,受影响的时间为4小时。
第4章 锐角三角函数数学九年级上册-单元测试卷-湘教版(含答案)

第4章锐角三角函数数学九年级上册-单元测试卷-湘教版(含答案)一、单选题(共15题,共计45分)1、如果,那么的范围是()A. B. C. D.2、如图,△OAC按顺时针方向旋转,点O在坐标原点上,OA边在x轴上,OA=8,AC=4,把△OAC绕点A按顺时针方向转到△O′AC′,使得点O′的坐标是(4,)则在这次旋转过程中线段OC扫过部分(阴影部分)的面积为()A. B. C. D.3、在Rt△ABC中,已知∠B=90°,AC=10,AB=5,则∠A等于()A.45°B.30°C.60°D.50°4、sin30°的值等于()A. B. C. D.15、如图,已知点A(-1,0)和点B(1,2),在坐标轴上确定点P,使得△ABP为直角三角形,则满足这样条件的点P共有()A.2个B.3个C.6个D.7个6、如图1是一个手机的支架,由底座、连杆和托架组成(连杆始终在同一平面内),垂直于底座且长度为的长度为的长度可以伸缩调整.如图2,保持不变,转动,使得,假如时为最佳视线状态,则此时的长度为(参考数据:)()A. B. C. D.7、如图,将∠AOB放置在5×5的正方形网格中,则sin∠AOB的值是()A. B. C. D.8、在Rt△ABC中,∠C=90°,a=4,b=3,则sinA的值是()A. B. C. D.9、在Rt△ABC中,∠C=90°,BC=4,sinA= ,则AB的长为()A. B.6 C.12 D.810、如图,▱ABCO的顶点B、C在第二象限,点A(﹣3,0),反比例函数y=(k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )A.﹣4tanαB.﹣2sinαC.﹣4cosαD.﹣2tan11、如图,在RtΔABC中,∠C=90°,∠A=30°, E为AB上一点,且AE︰EB=4︰1,EF ⊥AC于F,连结FB,则tan∠CFB的值等于()A. B. C. D.12、在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA等于()A. B. C. D.13、在Rt△ABC中,∠ACB=90°,BC=1,AC=2,则下列结论正确的是()A.sinA=B.tanA=C.cosB=D.tanB=14、如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是()A.2B.C.D.15、如图,在地面上的点A处测得树顶B的仰角为α,AC=7米,则树高BC为(用含α的代数式表示()A.7sin 米B.7cos 米C.7tan 米D. 米二、填空题(共10题,共计30分)16、如图,已知A(1,5),直线l1:y=x,直线l2过原点且与x轴正半轴成60°夹角,在l1上有一动点M,在l2上有一动点N,连接AM、MN,则AM+MN的最小值为________。
第4章 锐角三角函数数学九年级上册-单元测试卷-湘教版(含答案)

第4章锐角三角函数数学九年级上册-单元测试卷-湘教版(含答案)一、单选题(共15题,共计45分)1、使有意义的锐角x的取值范围是()A.x=45°B.x≠45°C.45°<x<90°D.0°<x<45°2、如图所示,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上任意一点,则PK+QK的最小值为( )A.1B.C.2D. +13、cos60°的值等于()A.1B.C.D.4、如图,OA=4,线段OA的中点为B,点P在以O为圆心,OB为半径的圆上运动,PA的中点为Q.当点Q也落在⊙O上时,cos∠OQB的值等于()A. B. C. D.5、在Rt△ABC中,∠C=90°,sinA=,则tanA的值为()A. B. C. D.6、一副三角板按图所示的位置摆放,将△DEF绕点A(F)逆时针旋转60°后,测得CG=10cm,则两个三角形重叠(阴影)部分的面积为( )A.75cm 2B.25 cm 2C.(25+)cm 2D.(25+)cm 27、如图,在菱形ABCD中,DE⊥AB,cosA=,BE=2,则tan∠DBE的值()A. B.2 C. D.8、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D ,如果AC=3,AB=6,那么AD的值为()A. B. C. D.9、如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则sinB的值等于()A. B. C. D.10、如图,△ABC是锐角三角形,sinC= ,则sin A的取值范围是( )A.0<sinA<B. <SinA<1C. <sinA<D. <sinA<111、如图,巳知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为()A.3B.C.4D.12、如图,延长RT△ABC斜边AB到点D,使BD=AB,连接CD,若tan∠BCD=,则tanA=()A. B.1 C. D.13、已知锐角A的tanA<,则锐角A的取值范围是()A.0<A<60°B.60°<A<90°C.0<A<30°D.30°<A<90°14、已知α为锐角,tan(90°-α)=,则α的度数为()A.30°B.45°C.60°D.75°15、如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B、C之间的距离为()A.20海里B.10 海里C.20 海里D.30海里二、填空题(共10题,共计30分)16、如图,斜坡长为100米,坡角,现因“改小坡度”工程的需要,将斜坡改造成坡度的斜坡(、、三点在地面的同一条垂线上),那么由点到点下降了________米(结果保留根号)17、若cosA=0.6753,则锐角A=________ (用度、分、秒表示).18、如图,△ABC内接于⊙O,AB=BC,∠ABC=120°,AD为⊙O的直径,AD=6,那么BD=________19、+2sin30°-tan60°+tan45°=________.20、如图,在四边形ABCD中,∠B=∠D=90°,AB=3, BC=2,tanA=,则CD=________.21、如图,在边长为1的小正方形网格中,点A,B,C,D都在这些小正方形的顶点上,AB,CD相交于点O,则cos∠BOD=________.22、如图,,两点在以为直径的上,若,的半径为2,则的值为________.23、如图,在矩形中,,,将沿射线平移长度得到,连接,,则当是直角三角形时,a的长为________.24、如图,的顶点都是正方形网格中的格点,则________.25、如图,国庆节期间,小明一家自驾到某景区C游玩,到达A地后,导航显示车辆应沿北偏西60°方向行驶8千米至B地,再沿北偏东45°方向行驶一段距离到达景区C,小明发现景区C恰好在A地的正北方向,则B,C两地的距离为________.三、解答题(共5题,共计25分)26、计算:()﹣1+|1﹣|﹣2sin60°+(π﹣2016)0﹣.27、如图,在中,,点在边上,求的值。
度第一学期湘教版九年级数学上册_第_四章_锐角三角函数_单元检测试题(有答案)

2019-2019学年度第一学期湘教版九年级数学上册第四章锐角三角函数单元检测试题考试总分: 120 分考试时间: 120 分钟学校:__________ 班级:__________ 姓名:__________ 考号:__________一、选择题(共 10 小题,每小题 3 分,共 30 分)1.如图,在的正方形网格中,的值等于()A. B. C. D.2.在中,,已知和,则下列关系中正确的是()A. B.C. D.3.在坡角为的山坡上种树,要求株距离(相邻两树间的水平距离)是,则斜坡上相邻两树间的坡面距离是()A. B. C. D.4.若为锐角,且,则为()A. B. C. D.5.如图,要在宽为米的九州大道两边安装路灯,路灯的灯臂长米,且与灯柱成角,路灯采用圆锥形灯罩,灯罩的轴线与灯臂垂直,当灯罩的轴线通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱高度应该设计为()A.米B.米C.米D.米6.已知甲处看乙处为仰角,则乙处看甲处为()A.仰角B.俯角C.仰角D.俯角7.中,,若,则的值是()A. B. C. D.8.有一拦水坝的横断面是等腰梯形,它的上底长为米,下底长为米,高为米,那么此拦水坝斜坡的坡度和坡角分别是()A.,B.,C.,D.,9.已知、的半径分别是、,若两圆相交,则圆心距可能取的值是()A. B. C. D.10.为一建筑物的最高点,在地面上的投影为,从地面上的点,用测角仪测得点的仰角为,测角仪高,若,则建筑物的高可表示为()A. B.C. D.二、填空题(共 9 小题,每小题 3 分,共 27 分)11.如图,市东偏北方向有一旅游景点,在市东偏北的公路上向前行米到处,测得位于的北偏西,则景点到公路的距离为________米(结果保留根号).第 1 页12.如图所示,一艘轮船在处观测到北偏东方向上有一个灯塔,轮船在正东方向以每小时海里的速度航行小时后到达处,又观测到灯塔在北偏东方向上,则此时轮船与灯塔相距________海里.(结果保留根号)13.如图,小明在“五一”假期到郊外放风筝,风筝飞到处时的线长为,此时小明正好站在处,并测得,牵引底端离地面米,则此时风筝离地面的高度的高度约为________.(结果精确到,)14.如图,在中,,,点在上,,若,则________.15.某厂家心开发的一种电动车如图,它的大灯射出的光线、与地面所夹的锐角分别是和.大灯离地面的距离为,则该车大灯照亮地面的宽度是________.(不考虑其他因素)(参考数据:,,,).16.如图,坡上有一颗与水平面垂直的大树,台风过后,大树倾斜后折断倒在山坡上,大树顶部接触到坡面上的点.已知山坡的坡角,量得树干倾斜角,大树被折断部分和坡面所成的角且米.则这棵大树折断前的高度________米.17.已知:如图,在菱形中,,垂足为,对角线,,则________,________.18.如图,为测量一棵与地面垂直的树的高度,在距离树的底端米的处,测得树顶的仰角为,则树的高度为________米(用三角函数表示)19.如图,将的按下面的方式放置在一把刻度尺上:顶点与尺下沿的端点重合,与尺下沿重合,与尺上沿的交点在尺上的读数恰为.若按相同的方式将的放置在该刻度尺上,则与尺上沿的交点在尺上的读数约为________.(结果精确到,参考数据:,,)三、解答题(共 7 小题,每小题 9 分,共63分)20.如果是锐角,且,求,的值.21.计算:;先化简,再求值:,其中.22.去年某省将地处、两地的两所大学合并成一所综合大学,为了方便、两地师生的交往,学校准备在相距千米的、两地之间修筑一条笔直公路.如图中线段,经测量,在地北偏东方向,地西偏北方向的处有一个半径为千米的公园,问计划修筑的这条公路会不会穿过公园?为什么?23.距工厂大门正北的柱子上系着一条大狼狗,狼狗的活动范围是以为半径的圆的内部,一个小偷从大门向北走了,发现前面有狗,就沿北偏西的方向跑去,想避开狗过去偷东西.请问:小偷能躲开狗吗?24.小洪站在房屋上看房屋,从点看点的俯角为,看点的俯角为,若的长为米,求房屋和的高度(精确到米).以下参考数据可供使用,,,,.25.如图,李明在大楼米高(即米)的窗口处进行观测,测得山坡上处的俯角,山脚处的俯角,已知该山坡的坡度(即)为,点、、、、在同一个平面内.点、、在同一条直线上,且.山坡坡角(即)的度数等于________度;求的长(结果保留根号).26.如图是脚踏式垃圾桶,图是它的内部结构示意图.当用脚将点踩至地面点处时,水平横杆,竖杆就借助支点和活动轴心(点,点)移到,位置,并将水平桶盖顶至位置,即桶盖被打开.图中,垂足为点,设计要求是至少为.已知,,竖杆与垃圾桶左侧外壁之间的距离,水平横杆到地面的距离为.问:这个脚踩式垃圾桶符合设计要求吗?请说明理由.答案1.A2.B3.B4.C5.D6.B7.A8.C9.B10.C11.12.13.14.15.16.17.18.19.20.解:∵,∴,.21.解:原式;原式,第 3 页由,得到,则原式.22.解:过点作于,由题可知:,设千米,,所以,由,得到,又,所以为等腰直角三角形,则,∵ ,∴,∴.∴计划修筑的这条公路不会穿过公园.23.解:如图,,,圆的半径是,.则.过圆心作于点.∵ ,,,∴.∵ ,点距离的最短距离小于该圆的半径,∴小偷不能躲开狗.24.解:作于点,∴ 米,∵从点看点的俯角为,看点的俯角为,∴ ,,∵ 米,在中,米,∴ 米.∴房屋的高为米,的高为米.25.;由题意知过点的水平线为,,,∴ ,,∵ ,∴ ,∴ ,∴ ,∵在中,,∴,答:的长为米.26.解:作,,垂足为,,易证明 …,∴,∴∴∴ ,∴∴∴∴这个脚踩式垃圾桶符合设计要求.第 5 页。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新课程单元目标检测试卷
九年级数学(上)第4章:锐角三角函数
(时间:90分钟满分100分)
学校:___________班级:__________姓名:________得分:_______
一.填空题(每小题3分,共24分)
1.在△ABC中,∠C=90°, AB=10 , BC=6 ,则sinA=_____, tanB =_____ .
2.已知α是锐角,且sinα=5
13
,那么cos(90°-α)=______, tan α=______.
3.sin30
x-,则x的取值范围是________.
4. sin30°·cos60°=________.
5.若tan( 90°-α)则α=_______.
6.在△ABC中,若| 2cosA-1 |+tanB )2=0 , 则∠C=
_________.
7.已知矩形两个邻边的长分别是1则该矩形的两条对角线所夹的锐角是_______.
8.若某人沿坡度i=1:3的斜坡前进20米,则他所在的位置比原来的位置高______.
二.选择题(每小题4分,共32分)
1.在△ABC中,∠C=90°, cosA=3
5
,则tanB=( )
A.3
5 B.4
5
C.3
4
D.4
3
2.在Rt △ABC 中,∠C =90°,AB =10,tanB =1
2
,则ABC S =( )
A. 30
B. 40
C.3.有一拦水坝的横截面是等腰梯形,它的上底为6米,下底为10米,高为2 米,那么拦水坝斜坡的坡度和坡角分别是( )
A.
3,60°,30°° D. 3
,30° 4.点m(-sin60°, cos60°)关于x 轴的轴反射点的坐标是( )
,12) B. (-1
2)
C. (-
2,12) D.(-1
2
, -2) 5.已知三角形三边比是25 : 24 : 7 ,则最小角的余弦值是( ) A.
2425 B.7
25
C.724
D.247 6.若∠A 是锐角,且cosA =1
4
,则( )
A. 0°<∠A <30°
B. 30°<∠A <45°
C. 45°<∠A <60°
D. 60°<∠A <90° 三.解答题(每小题8分,共32分) 1.计算
(1)sin45°+tan30°cos60°
(2)tan60°sin60°-tan30°tan45°
2.如图,在Rt△ABC中,∠C=90°,∠B=30°,∠ADC=60°, BD=10,求AC的长.
3.为测量某塔AB的高,在离该塔底部20米处目测其顶,仰角为60°,目高1.5米,试求该塔的高度.
, 求这个三角形的4.在△ABC中,∠C=90°, BC=24cm , cosA=5
13
周长.
四.(12分):
已知α为锐角且cosα是方程2
2730
-+=的一个根,求
x x
-的值.
12sin30cosα
参考答案
一.填空题
1.35
.43
,2.
513.512,3.x ≥12,4.1
4
,5.30°6.60°7.60°8. 二.选择题:CDC BAD 三.解答题
1. ⑵32
2.AC=,
3.()
1.5米 4.可设AC=5x cm ,AB=13x cm ,则BC=12x cm ,由12x =24得x =2,∴AB=26,AC=10
∴△ABC 的周长为:10+24+26=60cm 四.提高题
解:由22730x x -+=得1213,2x x == 又∵0﹤cos α﹤1,∴cos α=12
=2。
