加权马尔可夫链在降水状况预测中的应用
基于改进FCM算法的加权马尔可夫链的年降水预测

基于改进FCM算法的加权马尔可夫链的年降水预测
苗正伟;徐利岗
【期刊名称】《灌溉排水学报》
【年(卷),期】2017(36)10
【摘要】应用改进的FCM(Fuzzy C-Means,模糊C均值聚类)算法对承德市1951—2015年的年降水序列进行模糊聚类,获得10个聚类中心和隶属度矩阵。
根据最大隶属原则确定每年的降水状态,采用规范化的各阶自相关系数为权重,建立了加权马尔可夫链模型。
以隶属度向量作为预测时的初始状态向量,通过该模型逐年
预测了承德市2004—2015年的降水状态,结果与实际情况一致。
引入模糊集中的级别特征值公式,并对该公式做出修正。
基于马尔可夫链的预测结果,应用修正后的级别特征值公式预测了2004—2015年的降水量,所有预测结果的相对误差都在7%以内,初步表明基于模糊聚类和加权马尔可夫链的降水预测模型是合理可行的。
【总页数】8页(P114-121)
【关键词】预测;降水;模糊聚类;FCM算法;加权马尔可夫链;承德
【作者】苗正伟;徐利岗
【作者单位】河北水利电力学院水利工程系;宁夏水利科学研究院
【正文语种】中文
【中图分类】P333
【相关文献】
1.张家口市年降水量的加权马尔科夫链预测 [J], 张良;郭世娟
2.南宁市年降水量的加权马尔科夫链预测研究 [J], 杜懿;麻荣永;赵立亚
3.基于加权马尔可夫链的榆林地区年降水状态预测研究 [J], 苗正伟;徐利岗
4.基于加权马尔可夫链的降水量预测模型研究 [J], 胡鑫
5.加权马尔可夫链在普洱市年降水量预测中的应用 [J], 栗静;王美玲;李琳静;邹进因版权原因,仅展示原文概要,查看原文内容请购买。
加权马尔可夫模型在降水预测中的应用

加权马尔可夫模型在降⽔预测中的应⽤
加权马尔可夫模型在降⽔预测中的应⽤
作者:甄英
作者机构:内江师范学院地理与资源科学学院,四川内江641199
来源:内江师范学院学报
ISSN:1671-1785
年:2014
卷:000
期:010
页码:23-27
页数:5
中图分类:P332.1
正⽂语种:chi
关键词:加权马尔可夫链;年降⽔量;预测;重庆市
摘要:依据1962-2011年重庆市年降⽔量资料,采⽤均值标准差法建⽴降⽔量丰枯级别,分为枯、偏枯、平、偏丰和丰5个⽔平年.以各阶⾃相关系数为权数,⽤加权马尔可夫链计算2012年重庆市降⽔量,通过验证发现计算出的状态与实际情况相符,预测降⽔量值与实测值误差为7.9%,说明该⽅法有效可⾏.进⼀步采⽤马尔可夫链的遍历性原理,计算重庆市近50年的年降⽔量极限分布,结果表明重庆市年降⽔量处于平⽔年的可能性最⼤,出现周期约为2.9年.。
论述马尔可夫模型地降水预测方法

随机过程与随机信号处理课程论文论述马尔可夫模型的降水预测方法摘要:预测是人们对未知事物或不确定事物行为与状态作出主观的判断。
中长期降水量的预测是气象科学的一个难点问题, 也是水文学中的一个重要问题。
今年来,针对降水预测的随机过程多采用随机过程中的马尔可夫链。
本文总结了降水预测的马尔可夫预测的多种方法和模型,对其中的各种方法的马尔可夫链进行了比较和分析,得出了一些有用的结论。
关键字:降水预测,随机过程,马尔可夫链,模拟前言:大气降水是自然界水循环的一个重要环节。
尤其在干旱半干旱地区, 降水是水资源的主要补给来源, 降水量的大小,决定着该地区水资源的丰富程度。
因此, 在水资源预测、水文预报中经常需要对降水量进行预报。
然而, 由于气象条件的变异性、多样性和复杂性, 降水过程存在着大量的不确定性与随机性, 因此到目前为止还难以通过物理成因来确定出未来某一时段降水量的准确数值。
在实际的降水预测中,有时不必预测出某一年的降水量,仅需预测出某个时段内降水的状况既可满足工作需要。
因此,预测的范围相应扩大,精度相应提高。
因此对降水的预测可采用随机过程的马尔可夫链来实现。
用随机过程中马尔可夫链进行预测是一种较为广泛的预测方法。
它可用来预测未来某时间发生的变化, 如预测运输物资需求量、运输市场等等。
马尔可夫链, 就是一种随机时间序列, 它表示若已知系统的现在状态, 则系统未来状态的规律就可确定, 而不管系统如何过渡到现在的状态。
我们在现实生活中, 有很多情况具有这种属性, 如生物群体的生长与死亡, 一群体增加一个还是减少一个个体, 它只与当前该生物群体大小有关, 而与过去生物群体大小无关。
]本文针对降水预测过程中采用马尔可夫链进行模拟进行了综述和总结。
主要的方法有利用传统的马尔可夫链的方法模拟;有采用加权的马尔可夫链模拟来进行预测;还有基于模糊马尔可夫链状模型预测的方法;还有通过聚类分析建立降水序列的分级标准来采用滑动平均的马尔可夫链模型来预测降水量;从这些方法中我们可以看出,马尔可夫链对降水预测有着重要的理论指导意义。
加权马尔可夫链在降水状况预测中的应用

第26卷第6期水利水电科技进展2006年12月V ol.26N o.6Advances in Science and T echnology of Water Res ources Dec.2006 基金项目:河海大学科技创新基金资助项目(2006408511)作者简介:夏乐天(1956—),男,浙江温州人,副教授,博士,从事应用概率统计及随机水文学研究。
E 2mail :math 2xia @ 加权马尔可夫链在降水状况预测中的应用夏乐天1,朱元生生2,沈永梅1(1.河海大学理学院,江苏南京 210098;2.河海大学水资源环境学院,江苏南京 210098)摘要:在介绍加权马尔可夫链预测方法的基础上,以郑州市1951~1994年降雨量资料为例,采用均值标准差分级法进行旱涝指标值分级,把这44年资料划分成雨涝、偏涝、正常、偏旱、干旱5种状态,应用加权马尔可夫链对该地区旱涝状态进行预测和分析,结果表明该方法预测结果与实际情况相吻合。
关键词:加权马尔可夫链;降雨量预测;郑州市中图分类号:P941 文献标识码:A 文章编号:1006Ο7647(2006)06Ο0020Ο04Application of w eighted Markov ch ain to prediction of precipitation//XI A Le 2tian 1,ZH U Y uan 2sheng 2,SHE N Y ong 2mei 1(1.College o f Sciences ,Hohai Univer sity ,Nanjing 210098,China ;2.College o f Water Resources and Environment ,Hohai Univer sity ,Nanjing 210098,China )Abstract :Based on the precipitation data for 195121994of Zhengzhou City ,the weighted Markov chain is applied to prediction and analysis of states of drought and water 2logging in this region ,in which the mean and standard deviation of in formation series are taken as the classification standard of precipitation states ,and the past 44years are classified into five classes according to the precipitation data ,i.e.water 2logging year ,weak water 2logging year ,normal year ,weak drought year ,and drought year.I t is concluded that the result of prediction by the present method agrees with the reality.K ey w ords :weighted Markov chain ;prediction of precipitation ;Zhengzhou City 马尔可夫链是状态和时间均离散的马尔可夫过程,简称“马氏链”。
蒙特卡洛与马尔可夫方法在降水预测中的应用
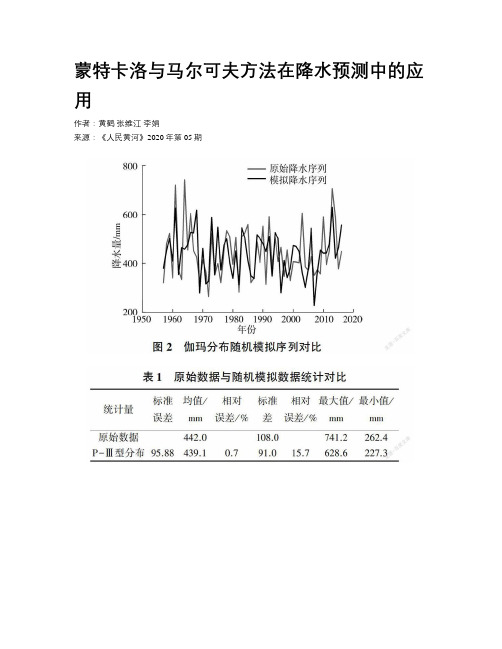
蒙特卡洛与马尔可夫方法在降水预测中的应用作者:黄鹤张维江李娟来源:《人民黄河》2020年第05期摘要:為了更深入地分析原州区的降水特征,为该区域水资源预测提供依据,基于原州区1957—2016年60 a降水资料,采用蒙特卡洛方法推求降水分布,采用K-S检验对模型进行显著性检验,采用基于欧氏距离的层次聚类方法进行状态划分,确定了原州区的降水分布,建立了适用于原州区的滑动平均加权马尔可夫预测模型。
根据已有数据验证了预测结果的有效性,再结合已确定的降水分布,通过K-S检验,检验了未来5 a降水预测的准确性。
结果表明:原州区降水分布符合P-Ⅲ型分布;马尔可夫模型适用于原州区降水预测,且未来5 a的降水预测结果是准确的,分别为508.5、520.8、554.9、451.0、466.6 mm。
关键词:蒙特卡洛方法;马尔可夫模型;随机模拟;降水预测;原州区;K-S检验中图分类号:TV11 文献标志码:Adoi:10.3969/j.issn.1000-1379.2020.05.004Abstract: In order to analyze the characteristics of precipitation in YuanzhouDistrict and provide a basis for water resources prediction in the region, based on the precipitation data from 1957 to 2016 of the district, the Monte Carlo method was used to estimate the precipitation distribution and the K-S test was used to model the significant test. It used the hierarchical clustering method based on Euclidean distance to divide the state, determined the precipitation distribution of the region and established a sliding average weighted Markov prediction model which was suitable for Yuanzhou District. Based on the existing data, the true validity of the prediction results was verified. Combined with the determined precipitation distribution, the accuracy of precipitation prediction for the next 5 years was tested by K-S test. Comparing with Pearson three-type distribution, the results show that the precipitation distribution in Yuanzhou District is more consistent with the log-normal distribution. The Markov model can be applied to the precipitation forecast in the region, and the prediction results of the sliding average precipitation in the next 5 years are real and effective,respectively 508.5, 520.8, 554.9, 451.0 and 466.6 mm.Key words: Monte Carlo method; Markov model; stochastic simulation; precipitation prediction; Yuanzhou District; K-S test1 引言由于客观世界中的一些现象可能与另一种现象存在着某种相似性,因此我们经常从一种现象出发来研究另一种现象。
马尔科夫链在天气预报中的应用

马尔科夫链在天气预报中的应用马尔科夫链在天气预报中的应用一、引言天气预报一直是人们生活中非常重要的信息之一,人们需要了解天气情况来进行出行计划、农作物种植、服装搭配等等。
然而,天气预报并非是一项简单的任务,因为天气是一个复杂的系统,涉及到多个因素的相互作用。
为了提高天气预报的准确性和可信度,科学家们一直在探索各种不同的模型和算法,其中马尔科夫链就是一种被广泛应用于天气预报中的方法。
二、马尔科夫链的基本概念马尔科夫链是一种数学模型,描述了一个系统在不同状态之间转移的概率。
具体而言,马尔科夫链假设当前状态的转移只与前一个状态有关,与更早的状态无关。
这种假设被称为马尔科夫性质。
马尔科夫链可以表示为一个状态空间和一个状态转移矩阵。
三、马尔科夫链在天气预报中的应用1.模型构建为了将马尔科夫链应用于天气预报中,首先需要构建一个合适的马尔科夫模型。
这可以通过收集历史天气数据来完成,包括温度、湿度、气压、风向等各种气象要素的观测值。
然后将这些观测值转化为天气状态,例如晴天、多云、阴天、雨天等。
接下来,可以通过计算状态之间的转移概率来构建状态转移矩阵。
2.状态转移一旦构建好了马尔科夫模型,就可以开始进行天气预报。
假设当前的天气状态为晴天,根据状态转移矩阵,可以计算出下一个天气状态是多云的概率、阴天的概率、雨天的概率等等。
这些概率可以作为天气预报的输出,告诉人们即将到来的天气情况。
3.模型评估为了评估马尔科夫链模型的准确性,可以使用历史数据进行模型验证。
将模型的预测结果与实际观测值进行比较,通过计算准确率、误差等指标,可以评估模型的预测能力。
四、马尔科夫链在天气预报中的优势和挑战1.优势马尔科夫链模型具有一定的优势,主要体现在以下几个方面:(1)相对简单:马尔科夫链模型的理论基础较为简单,容易理解和使用。
(2)实时性:马尔科夫链模型可以通过实时观测数据进行更新,使天气预报具有一定的实时性。
(3)适用性:马尔科夫链模型适用于不同的天气情况,包括晴天、雨天、阴天等。
马尔科夫链在年降水量预测中的应用

马尔科夫链在年降水量预测中的应用
李绍辉;孙学金
【期刊名称】《气象水文海洋仪器》
【年(卷),期】2015(032)002
【摘要】年降水量是目前水文和气象预测中非常重要的一项工作,是指导工农业生产以及经济发展策略的主要影响因素,其预测结果能够为气象、水文研究以及各种生产活动中决策的制定提供重要的数据支持.马尔科夫链是随机过程中的一种,在已知条件下对某个对象的未来进行预测,但是其未来产生的结果和过去所产生的结果之间相互独立,二者互补影响.这种随机过程的特征跟每年中降水量的特征完全相符,所以本文拟采用马尔科夫链,通过对降水量模型的构建,探讨了马尔科夫链在某个地区年降水量预测中的作用.
【总页数】3页(P84-86)
【作者】李绍辉;孙学金
【作者单位】解放军理工大学气象海洋学院,南京211101;解放军理工大学气象海洋学院,南京211101
【正文语种】中文
【中图分类】P49
【相关文献】
1.叠加马尔科夫链在年降水量预测中的应用 [J], 廖捷;胡豪然;陈功
2.加权马尔科夫链在济南市降水量预测中的应用 [J], 张杰;陶望雄;王青
3.灰色马尔科夫模型在年降水量预测中的应用 [J], 李智超
4.灰色-马尔科夫链在年降水量预测中的应用 [J], 魏代俊;谢民育
5.加权马尔科夫链在榆林市降水量预测中的应用 [J], 吴林川;孙婴婴
因版权原因,仅展示原文概要,查看原文内容请购买。
马尔可夫链在天气预测中的应用

马尔可夫链在天气预测中的应用马尔可夫链在天气预测中的应用一、引言天气对人类生活有着重要影响,了解未来的天气情况可以帮助人们做出相应的决策。
由于天气受到多种因素的影响,其变化具有一定的不确定性,因此天气预测一直是一项具有挑战性的任务。
随着计算机科学的发展,马尔可夫链成为了一种在天气预测中广泛应用的工具。
本文将介绍马尔可夫链的基本原理,并探讨其在天气预测中的应用。
二、马尔可夫链的基本原理马尔可夫链是一种数学模型,用于描述一系列随机事件的过程。
它满足所谓的马尔可夫性质,即当前事件的发生只与前一事件的状态有关,与更早的事件无关。
马尔可夫链有两个基本概念:状态和转移概率。
1. 状态状态是指描述系统在某一时刻所处的具体情况。
在天气预测中,状态可以表示为某一天的天气情况,例如晴天、阴天、雨天等。
2. 转移概率转移概率表示在当前状态下,系统转移到下一个状态的概率。
在天气预测中,转移概率可以表示为从某一天的天气情况到下一天天气情况的概率,例如从晴天转为阴天的概率。
利用马尔可夫链的概念,我们可以建立天气状态之间的转移模型,从而进行天气预测。
三、马尔可夫链在天气预测中的应用马尔可夫链在天气预测中的主要应用是基于历史数据进行未来的天气情况预测。
具体地说,我们可以通过统计过去一段时间内的天气情况,建立马尔可夫链模型,从而预测未来的天气情况。
1. 数据处理在进行天气预测之前,首先需要收集和处理大量的历史天气数据。
这些数据可以包括每天的天气情况、温度、湿度等信息。
通过对数据的分析和处理,我们可以得到天气状态之间的转移概率,即从当前状态转移到下一状态的概率。
2. 模型建立建立马尔可夫链模型涉及到两个方面的问题:状态的选择和转移概率的估计。
状态的选择是指确定天气的几种可能状态。
在天气预测中,状态可以根据具体需求而定,例如可以将天气分为晴天、阴天、雨天三种状态。
转移概率的估计是根据历史数据对转移概率进行估计。
通过统计每个状态转移到下一状态的频率,我们可以得到转移概率的估计值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第26卷第6期水利水电科技进展2006年12月V ol.26N o.6Advances in Science and T echnology of Water Res ources Dec.2006 基金项目:河海大学科技创新基金资助项目(2006408511)作者简介:夏乐天(1956—),男,浙江温州人,副教授,博士,从事应用概率统计及随机水文学研究。
E 2mail :math 2xia @ 加权马尔可夫链在降水状况预测中的应用夏乐天1,朱元生生2,沈永梅1(1.河海大学理学院,江苏南京 210098;2.河海大学水资源环境学院,江苏南京 210098)摘要:在介绍加权马尔可夫链预测方法的基础上,以郑州市1951~1994年降雨量资料为例,采用均值标准差分级法进行旱涝指标值分级,把这44年资料划分成雨涝、偏涝、正常、偏旱、干旱5种状态,应用加权马尔可夫链对该地区旱涝状态进行预测和分析,结果表明该方法预测结果与实际情况相吻合。
关键词:加权马尔可夫链;降雨量预测;郑州市中图分类号:P941 文献标识码:A 文章编号:1006Ο7647(2006)06Ο0020Ο04Application of w eighted Markov ch ain to prediction of precipitation//XI A Le 2tian 1,ZH U Y uan 2sheng 2,SHE N Y ong 2mei 1(1.College o f Sciences ,Hohai Univer sity ,Nanjing 210098,China ;2.College o f Water Resources and Environment ,Hohai Univer sity ,Nanjing 210098,China )Abstract :Based on the precipitation data for 195121994of Zhengzhou City ,the weighted Markov chain is applied to prediction and analysis of states of drought and water 2logging in this region ,in which the mean and standard deviation of in formation series are taken as the classification standard of precipitation states ,and the past 44years are classified into five classes according to the precipitation data ,i.e.water 2logging year ,weak water 2logging year ,normal year ,weak drought year ,and drought year.It is concluded that the result of prediction by the present method agrees with the reality.K ey w ords :weighted Markov chain ;prediction of precipitation ;Zhengzhou City 马尔可夫链是状态和时间均离散的马尔可夫过程,简称“马氏链”。
它的最基本特征是“马氏性”,也称“无后效性”,即在系统“现在”的状态已知的条件下,其“将来”的状态与“过去”的状态无关。
在现实生活中,很多情况都具有这种属性,例如生物群体的生长与死亡,单位时段内电话交换台来的呼叫次数等。
如果具有各种状态的某种事物或某种现象的时间序列可视为马尔可夫链,则根据n 时刻的状态即可预测n +1时刻的状态,这就是应用马尔可夫链模型解决各种预测问题的基本思想。
这一基本思想可以应用于天气预报、农作物年景预测、病虫害预测,也可应用于水文、地震和遗传学研究等。
本文以郑州市旱涝状态的预测为实例,介绍使用加权马尔可夫链模型进行旱涝状态预测的步骤和方法。
1 马尔可夫链与加权马尔可夫链预测111 马尔可夫链的定义及性质马尔可夫链的数学表述如下[1]:定义在概率空间(Ω,F ,P )上的随机序列{X (t ),t ∈T},其中参数集T ={0,1,2,…},状态空间E ={0,1,2,…},称为马尔可夫链,如果对任意的正整数l ,m ,k ,及任意的非负整数j l >…>j 2>j 1(m >j l ),i m +k ,i m ,i j l ,…,i j 2,i j 1∈E 有式(1)成立(这里要求式(1)的左端有意义)。
P X (m +k )=i m +k X (m )=i m ,X (j l )=j l ,…,X (j 2)=j 2,X (j 1)=j 1=P X (m +k )=i m +k X (m )=i m(1) 马尔可夫链的性质和有关结论很多,此处不一一叙述。
实际应用中,常记式(1)的右端P X (m +k )=i m +k X (m )=i m =P X m +k =j X m =i=p ij (m ;k )(i ,j ∈E ) 一般考虑齐次马尔可夫链,即对任意的m,k∈T,有p ij(m;k)=p ij(k) (i,j∈E)(2)式中:p ij(m;k)为系统在时刻m时处在状态i、经k 步状态转移到达状态j的概率;p ij(k)为系统从状态i、经k步状态转移到达状态j的概率,此时转移概率与初始时刻无关,k取1时p ij(1)记为p ij.齐次马尔可夫链完全由其初始分布{p0(i0),i0∈E}及其一步状态转移概率矩阵P=(p ij)i,j∈E所决定。
若已知时刻n时的绝对分布P(n)={p n(j), j∈E},则时刻n+1时的绝对分布P(n+1)=P(n)P=P(0)P n(3) 112 加权马尔可夫链预测对于一列相依的随机变量,用步长为1的马尔可夫链模型和初始分布推算出未来时段状态的绝对分布来做预测分析[2],即为传统的马尔可夫链预测方法之一,可称之为基于绝对分布的马尔可夫链预测方法。
该法默认所论马尔可夫链满足“齐次性”缺乏依据。
事实上,应用中所论及的随机变量序列,尽管满足“马氏性”,但“齐次性”一般都不满足。
另外,该法没有考虑对应各阶(各种步长)马尔可夫链的绝对分布在预测中所起的作用,因此没有充分利用已知数据资料的信息。
利用各阶马尔可夫链求得状态的绝对分布叠加来做预测分析[3],也是传统的马尔可夫链预测方法之一,可称之为叠加马尔可夫链预测方法。
该法尽管运用了各阶马尔可夫链状态的绝对分布叠加来预测状态,但没有考虑各阶马尔可夫链对应的绝对概率在叠加中所起的作用,即认为各阶马尔可夫链的绝对概率所起的作用是相同的,这显然不科学。
事实上,一个满足马氏性的相依时间序列,其各阶自相关性是不一样的。
一列相依的随机变量,其各阶自相关系数刻画了各种滞时的状态间相关关系的强弱。
因此,可考虑先分别依其前面若干时段的指标值状态对该时段指标值的状态进行预测,然后,按前面各年与该年相依关系的强弱加权求和,即可达到充分、合理地利用信息进行预测的目的。
这就是加权马尔可夫链预测的基本思想。
传统的马尔可夫链预测方法和现行的加权马尔可夫链预测方法[4Ο5]都没有考虑对指标值序列进行“马氏性”检验,这是一个欠缺,本文提出的加权马尔可夫链预测方法考虑到了这个问题,具体方法步骤如下:a.计算指标值序列均值 x和均方差s,建立指标值的分级标准(相当于确定马尔可夫链的状态空间),可根据资料序列的长短及具体问题的要求进行。
例如,可以样本均方差为标准[2Ο4](也可以用有序聚类的方法建立分级标准[5]等)将指标值分级,确定马尔可夫链的状态空间E={1,2,…,m}。
b.按步骤a所建立的分级标准确定资料序列中各时段指标值所对应的状态。
c.对步骤b所得的结果进行统计,可得不同滞时(步长)马尔可夫链的转移概率矩阵,它决定了指标值状态转移过程的概率法则。
d.进行“马氏性”检验。
e.计算各阶自相关系数r k(k∈E),计算公式如下:r k=∑n-kl=1(x l- x)(x l+k- x)∑nl=1(x l- x)2(4)式中:r k为第k阶(滞时为k年的)自相关系数;x l 为第l时段的指标值; x为指标值均值;n为指标值序列长度。
对各阶自相关系数规范化,即将w k=r k∑mk=1r k(5)作为各种滞时(步长)的马尔可夫链的权重(m为按预测需要计算到的最大阶数)。
f.分别以前面若干时段的指标值为初始状态,结合其相应的各阶转移概率矩阵即可预测出该时段指标值的状态概率P(k)i(i∈E),k为滞时(步长),k =1,2,…,m。
g.将同一状态的各预测概率加权和作为指标值处于该状态的预测概率,即P i=∑mk=1w k P(k)i (i∈E)(6) max{P i,i∈E}所对应的i即为该时段指标值的预测状态。
待该时段的指标值确定之后,将其加入到原序列之中,再重复步骤a~g,即可进行下时段指标值状态的预测。
h.可进一步对该马尔可夫链的特征(遍历性、平稳分布等)进行分析。
2 转移概率的计算、马氏性检验与指标值分级211 马尔可夫链转移概率的计算为了用马尔可夫链去做预测,需要根据实测资料估计出马尔可夫链的转移概率。
设x1,x2,…,x n 是所讨论的马尔可夫链的1个指标值序列,它包含m个状态,即状态空间E={1,2,…,m},用f ij表示指标值序列中从状态i经过一步转移到达状态j的频数(i,j∈E),转移的步长可以是1个时间单位,也可以是2个、3个,甚至m个时间单位,应用上遇到的马尔可夫链一般不满足“时齐”条件,因此仅需讨论一步转移概率。
由f ij(i,j∈E)组成的矩阵(f ij)i,j∈E称为转移频数矩阵。
将转移频数矩阵的第i行第j列元素f ij除以各行的总和所得的值称为转移概率,记为p ij(i,j∈E),即p ij=f ij∑m j=1f ij(7)实际上这是从状态i经过一步转移到达状态j的转移频率。
由频率的稳定性知,当式(7)的分母充分大时,转移频率近似等于转移概率,可用其估计转移概率。
因此为方便起见,这里就用转移概率的记号p ij 来表示转移频率,并且称它为转移概率,于是转移概率矩阵可表示为P=(p ij)i,j∈E(8)这里p ij(i,j∈E)同式(7)。
212 随机变量序列的马氏性检验检验随机序列是否具有马氏性,是应用马尔可夫链模型分析和解决实际问题的前提。
