天津市河北区2014届高三总复习质量检测(一)(2014河北区一模)文科数学 (清晰扫描,含答案)
2014年高考文科数学全国卷1(含详细答案)
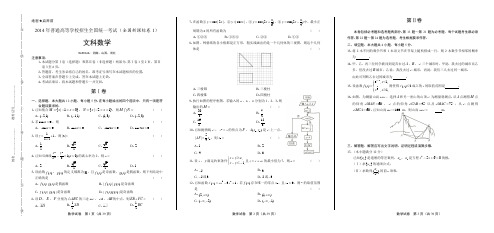
数学试卷 第1页(共39页) 数学试卷 第2页(共39页) 数学试卷 第3页(共39页)绝密★启用前2014年普通高等学校招生全国统一考试(全国新课标卷1)文科数学使用地区:河南、山西、河北注意事项:1.本试题分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至6页.2.答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置.3.全部答案在答题卡上完成,答在本试题上无效.4.考试结束后,将本试题和答题卡一并交回.第Ⅰ卷一、选择题:本大题共12小题,每小题5分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{|13}M x x =-<<,{|21}N x x =-<<,则M N = ( ) A .(2,1)- B .(1,1)- C .(1,3) D .(2,3)-2.若tan 0α>,则( )A . sin 0α>B .cos 0α>C . sin20α>D .cos20α> 3.设1i 1iz =++,则|z |=( )A .12B .22 C .32D .24.已知双曲线2221(0)3x y a a -=>的离心率为2,则a = ( )A .2B .62C .52D .1 5.设函数()f x ,()g x 的定义域都为R ,且()f x 是奇函数,()g x 是偶函数,则下列结论中正确的是( )A .()f x ()g x 是偶函数B .|()|f x ()g x 是奇函数C .()f x |()|g x 是奇函数D .|()()|f x g x 是奇函数6.设D ,E ,F 分别为ABC △的三边BC ,CA ,AB 的中点,则EB FC += ( )A .ADB .12AD C .BCD .12BC 7.在函数①cos |2|y x =,②|cos |y x =,③πcos(2)6y x =+,④πtan(2)4y x =-中,最小正周期为π的所有函数为( )A .①②③B .①③④C .②④D .①③8.如图,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是( )A .三棱锥B .三棱柱C .四棱锥D .四棱柱 9.执行如图的程序框图,若输入的a ,b ,k 分别为1,2,3.则输出的M =( )A .203B .72C .165D .15810.已知抛物线C :2y x =的焦点为F ,00(,)A x y 是C 上一点,05||4AF x =,则0x = ( )A .1B .2C .4D .811.设x ,y 满足约束条件,1,x y a x y +⎧⎨--⎩≥≤且z x ay =+的最小值为7,则a =( )A .5-B .3C .5-或3D .5或3-12.已知函数32()31f x ax x =-+,若()f x 存在唯一的零点0x ,且00x >,则a 的取值范围是( )A .(2,)+∞B .(1,)+∞C .(,2)-∞-D .(,1)-∞-第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答.第22题~第24题为选考题,考生根据要求作答. 二、填空题:本大题共4小题,每小题5分.13.将2本不同的数学书和1本语文书在书架上随机排成一行,则2本数学书相邻的概率为 .14.甲、乙、丙三位同学被问到是否去过A ,B ,C 三个城市时,甲说:我去过的城市比乙多,但没去过B 城市;乙说:我没去过C 城市;丙说:我们三人去过同一城市. 由此可判断乙去过的城市为 .15.设函数113e ,1,(),1,x x f x x x -⎧⎪=⎨⎪⎩<≥则使得()2f x ≤成立的x 的取值范围是 .16.如图,为测量山高MN ,选择A 和另一座山的山顶C 为测量观测点.从A 点测得M 点的仰角60MAN ∠=,C 点的仰角45CAB ∠=以及75MAC ∠=;从C 点测得60MCA ∠=.已知山高100BC = m ,则山高MN = m .三、解答题:解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)已知{}n a 是递增的等差数列,2a ,4a 是方程2560x x -+=的根. (Ⅰ)求{}n a 的通项公式; (Ⅱ)求数列{}2nn a 的前n 项和.姓名________________ 准考证号_____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第4页(共39页) 数学试卷 第5页(共39页) 数学试卷 第6页(共39页)18.(本小题满分12分)从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结(Ⅰ)在答题卡上作出这些数据的频率分布直方图:(Ⅱ)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);(Ⅲ)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?19.(本小题满分12分)如图,三棱柱111ABC A B C -中,侧面11BB C C 为菱形,1B C 的中点为O ,且AO ⊥平面11BB C C .(Ⅰ)证明:1B C AB ⊥;(Ⅱ)若1AC AB ⊥,160CBB ∠=,1BC =,求三棱柱111ABC A B C -的高.20.(本小题满分12分)已知点(2,2)P ,圆C :2280x y y +-=,过点P 的动直线l 与圆C 交于A ,B 两点,线段AB 的中点为M ,O 为坐标原点. (Ⅰ)求M 的轨迹方程;(Ⅱ)当||||OP OM =时,求l 的方程及POM △的面积.21.(本小题满分12分)设函数21()ln (1)2a f x a x x bx a -=+-≠,曲线()y f x =在点(1,(1))f 处的切线斜率为0.(Ⅰ)求b ;(Ⅱ)若存在01x ≥,使得0()1af x a <-,求a 的取值范围.请考生在第22、23、24三题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分,作答时请用2B 铅笔在答题卡上将所选题号后的方框涂黑. 22.(本小题满分10分)选修4—1:几何证明选讲如图,四边形ABCD 是O 的内接四边形,AB 的延长线与DC 的延长线交于点E ,且CB CE =.(Ⅰ)证明:D E ∠=∠;(Ⅱ)设AD 不是O 的直径,AD 的中点为M ,且MB MC =,证明:ADE △为等边三角形.23.(本小题满分10分)选修4—4:坐标系与参数方程已知曲线C :22149x y +=,直线l :2,22,x t y t =+⎧⎨=-⎩(t 为参数). (Ⅰ)写出曲线C 的参数方程,直线l 的普通方程;(Ⅱ)过曲线C上任意一点P 作与l 夹角为30的直线,交l 于点A ,求||PA 的最大值与最小值.24.(本小题满分10分)选修4—5:不等式选讲若0a >,0b >,且11a b+=(Ⅰ)求33a b +的最小值;(Ⅱ)是否存在a ,b ,使得236a b +=?并说明理由.3 / 132014年普通高等学校招生全国统一考试(全国新课标卷1)文科数学答案解析第Ⅰ卷一、选择题 1.【答案】B【解析】根据集合的运算法则可得:{|11}MN x x =-<<,即选B .【提示】集合的运算用数轴或者Venn 图可直接计算。
天津市河北区2014届高三总复习质量检测(一)文科数学试卷(带解析)

天津市河北区2014届高三总复习质量检测(一)文科数学试卷(带解析)1.己知集合{}{}|23|lg(2)0M x x N x x =-<<=+≥,则M N =I ( ). (A)(2,)-+∞ (B)[)1,3- (C)(]2,1-- (D)(2,3)- 【答案】B 【解析】 试题分析:由已知集合{}1N x x =-…,所以{}{}[)2311,3M N x x x x x =-<<-=-I I …,故正解答案选B.考点:1.集合运算;2.对数不等式.2.已知变量x ,y 满足约束条件110,1x y x x y +≤⎧⎪+≥⎨⎪-≤⎩,则目标函数z=2x +y 的最大值是( ).(A)-4 (B)0 (C)2 (D)4 【答案】C 【解析】试题分析:首先作出可行域110,1x y x+≤⎧⎪+≥≤区域,目标函数可化为2y x z =-+,所以作出直线y ()1,0时,所z 的最大值为max 2102z =⨯+=,故正解答案为C.考点:简单线性规划.3.)执行右边的程序框图,输出m 的值是( ).(A)3 (B)4 (C)5 (D)6【答案】A 【解析】试题分析:第一次执行循环体时:1m =,23a =,0ba=,选择“否”;第二次:2m =,228239a ⎛⎫=⨯= ⎪⎝⎭,293384b a =⨯=,选择“否”;第三次:3m =,328339a ⎛⎫=⨯= ⎪⎝⎭,89198b a =⨯=,选择“是”,故此输出m 的值为3.正解答案选A. 考点:1.程序框图;2.幂运算.4.“a>l ”是“函数()2f x ax =-(a >0且1a ≠)在区间(0,)+∞上存在零点”的( ). (A)充分而不必要条件 (B)必要而不充分条件 (C)充分必要条件 (D)既不充分也不必要条件 【答案】C 【解析】试题分析:令20ax -=,得2x a =,若1a >,则20a >,所以充分性成立;若函数()f x 在区间()0,+∞上存在零点时,则有20a >,显然存在2021a a<<⇒>,所以必要性成立.故正确答案为C.考点:1.充要条件;2.函数零点.5.一个几何体的三视图如图所示,则该几何体的体积是( ). (A)56 (B)103 (C)53(D)2【答案】B 【解析】试题分析:由三视图可知此几何体是由一个长为222的长方体过三个顶点切去一角的空间多面体,如图所示,则其体积为1110222222323V =⨯⨯=.故正确答案选B.2222考点:1.三视图;2.简单组合体体积. 6.在ABC ∆中,3,13,3BC AC B π===,则ABC ∆的面积是( ).(A)333 (C)332 (D)334【答案】A【解析】试题分析:由余弦定理得2222cos AC AB BC AB BC B =+-⋅∠,即2340AB AB --=,解得4AB =,所以113sin 433322ABC S AB BC B ∆=⋅⋅=⨯⨯=故正确答案为A. 考点:1.余弦定理;2.三角形面积.7.已知函数3log ,0()1(),03x x x f x x >⎧⎪=⎨≤⎪⎩.那么不等式()1f x ≥的解集为( ).(A) {}|30x x -≤≤ (B){}|30x x x ≤-≥或 (C){}|0x x ≤≤ (D){}|03x x x ≤≥或 【答案】D 【解析】试题分析:由已知得,①当0x >时,有3log 13x x ⇒厖;②当0x „时,有1103xx ⎛⎫⇒ ⎪⎝⎭厔,综①②得不等式的解集为{}|03x x x ≤≥或.故正确答案选D. 考点:1.对数、指数不等式;2.分类讨论思想.8.已知函数41()41x x f x -=+,若120,0x x >>,且12()()1f x f x +=,则12()f x x +的最小值为(). (A)14 (B)45(C)2 (D)4 【答案】B 【解析】试题分析:因为12()()1f x f x +=,所以1212414114141x x xx --+=++,整理得()1212444430x x x x ⋅-+-=,又1244x x +…124430x x ⋅-…,解得3,即12124449x x x x +⋅=?,因此()1212121241224114141915x x x x x x f x x +++-+==--=+++….故正确答案为B.考点:1.指数函数;2.基本不等式.9.复数11iz i-=+,则z =______________. 【答案】1 【解析】试题分析:因为()()()211111i i z i i i i --===-++-,所以1z ==.故正确答案为1. 考点:复数分母有理化、模.10.一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积为323π,那么这个三棱柱的体积是_____________.【答案】483 【解析】试题分析:由题意可得,球的半径为2R =,则正三棱柱的高为24h R ==,底面正三角形中心到各边的距离为2R =,所以底面边长为43,从而所求三棱柱的体积为()234344834V Sh ==⋅⋅=.故正确答案为483. 考点:1.球、三棱柱的体积;2.简单组合体.11.设F 是抛物线21:2(0)C y px p =>的焦点,点A 是抛物线1C 与双曲线22222:1(0,0)x y C a b a b-=>>的一条渐近线的一个公共点,且AF x ⊥轴,则双曲线的离心率为_______. 【答案】5 【解析】试题分析:由抛物线方程22y px =,可得焦点为,02p F ⎛⎫⎪⎝⎭,不妨设点A 在第一象限,则有,2p A p ⎛⎫⎪⎝⎭,代入双曲线渐近线方程b y x a =,得2b a =,则225c a b a =+=,所以双曲线离率为55ae ==.故正确答案为5. 考点:1.抛物线;2.双曲线.12.如图,AB 是半圆O 的直径,P 在AB 的延长线上,PD 与半圆O 相切于点C ,AD ⊥PD.若PC=4, PB=2,则CD=____________.【答案】125【解析】试题分析:连接OC ,则得直角三角形OPC ,设半圆的半径为r ,则有()22224r r +=+,解得3r =,又由CD CP AO OP =,得4123325CD =⋅=+.故正确答案为125.考点:1.圆的切线;2.平行线分线段成比例.13.己知0,0x y >>,若2287y xm m x y+>+恒成立,则实数m 的取值范围是___________. 【答案】81m -<< 【解析】试题分析:因为288y x x y +=…,所以287m m >+恒成立,即2780m m +-<恒成立,解得所求实数m 的范围为81m -<<.考点:1.基本不等式.14.已知a 、b 为非零向量,()m a tb t R =+∈,若1,2a b ==,当且仅当14t =时,m 取得最小值,则向量a 、b 的夹角为___________. 【答案】23π 【解析】 试题分析:设向量,a br r 的夹角为θ,则2222222cos 44cos 1m a tb a t a b t b t t θθ=+=++=++u r r r r r r r ,构造函数()2221144cos 14cos cos 124f t t t t θθθ⎛⎫=++=+-+ ⎪⎝⎭,因为当且仅当14t =时,m 取得最小值,所以当14t =时,函数()f t 有最小值,即111cos 0cos 422θθ+=⇒=-时,函数()f t 有最小值,又[]0,θπ∈,所以解得23πθ=.考点:1.向量;2.二次函数.15.已知实数{},2,1,1,2a b ∈--.(1)求直线y=ax+b 不经过第四象限的概率: (2)求直线y=ax+b 与圆221x y +=有公共点的概率. 【答案】(1)14;(2)34. 【解析】试题分析:(1)因为实数{},2,1,1,2a b ∈--,所以由,a b 构成的实数对总共有16种,又直线y ax b =+不过第四象限,即必须满足0a …且0b …,此时由,a b 构成的实数对总共有4种,故所求概率为41164=;(2)由圆方程221x y +=知圆心坐标为()0,0,半径为1,又直线与圆有公共点,即圆心到直线的距离d 不大于半径1,根据点到直线距离公式得1d =,整理得221b a +„,经检验满足此式的,a b 实数对共有12种,故所求概率为123164=. (1)由于实数(),a b 的所有取值为:()2,2--,()2,1--,()2,1-,()2,2-,()1,2--,()1,1--,()1,1-,()1,2-,()1,2-,()1,1-,()1,1,()1,2,()2,2-,()2,1-,()2,1,()2,2共16种. 2分设“直线y ax b =+不经过第四象限”为事件A ,若直线y ax b =+不经过第四象限,则必须满足0a …,0b ….则事件A 包含4个基本事件:()1,1,()1,2,()2,1,()2,2. 4分()41164P A ∴==,直线y ax b =+不经过第四象限的概率为14. 6分 (2)设“直线y ax b =+与圆221x y +=有公共点”为事件B ,1,即221b a +„. 9分所以事件B 包含12个基本事件:()2,2--,()2,1--,()2,1-,()2,2-,()1,1--,()1,1-,()1,1-,()1,1,()2,2-,()2,1-,()2,1,()2,2. 11分()123164P B ∴==,所以直线y ax b =+与圆221x y +=有公共点的概率为34. 13分 考点:1.古典概型;2.直线与圆.16.己知A 、B 、C 分别为△ABC 的三边a 、b 、c 所对的角,向量(sin ,sin ),m A B =(cos ,cos )n B A =,且sin2m n C ⋅=.(1)求角C 的大小:(2)若sinA ,sinC ,sinB 成等差数列,且18CA CB ⋅=u u u r u u u r,求边c 的长.【答案】(1)3π;(2)6. 【解析】试题分析:(1)由向量数量积坐标运算得()sin m n A B ⋅=+u r r,又,,A B C 三角形的三个内角,所以有()sin sin A B C +=,因此sin 2sin C C =,整理得1cos 2C =,所以所求角C 的大小为3π;(2)由等差中项公式得2sin sin sin C A B =+,根据正弦定理得2c a b =+,又18CA CB ⋅=u u u r u u u r,得cos 18ab C =,由(1)可得36ab =,根据余弦定理得()22222cos 3c a b ab C a b ab =+-=+-,即224336c c =-⨯,从而可解得6c ∴=.(1)()sin cos sin cos sin m n A B B A A B ⋅=+=+u r r2分 在ABC !中,由于()sin sin A B C +=,所以sin m n C ⋅=u r r.又sin m n C ⋅=u r r Q ,sin 2sin C C ∴=,sin 2sin C C ∴=,又sin 0C ≠,1cos 2C ∴=. 5分而0C π<<,3C π∴=. 7分(2)sin ,sin ,sin A C B Q 成等差数列,2sin sin sin C A B ∴=+,由正弦定理得2c a b =+. 9分18CA CB ⋅=u u u r u u u r Q ,cos 18ab C ∴=.由(1)知1cos 2C =,所以36ab =. 11分由余弦定理得()22222cos 3c a b ab C a b ab =+-=+-,224336c c ∴=-⨯,236c ∴=.6c ∴=. 13分考点:1.正弦、余弦定理;2.向量数量积.17.如图,在四棱锥P-ABCD 中,侧面PAD ⊥底面ABCD ,侧棱2PA PD ==,底面ABCD 为直角梯形,其中BC//AD ,AB ⊥AD ,AD=2,AB=BC=l ,E 为AD 中点. (1)求证:PE ⊥平面ABCD :(2)求异面直线PB 与CD 所成角的余弦值: (3)求点A 到平面PCD 的距离.【答案】(1)证明:在PAD ∆中,PA PD =,E 为AD 中点,PE AD ∴⊥.又侧面PAD ⊥底面ABCD ,平面PAD I 平面ABCD AD =,PE ⊂平面PAD ⊥.PE ∴⊥平面ABCD ;(2)63(3)233. 【解析】试题分析:(1)由题意可根据面面垂直的性质定理来证,已知侧面PAD ⊥底面ABCD ,并且相交于AD ,而PAD ∆为等腰直角三角形,E 为AD 中点,所以PE AD ⊥,即PE 垂直于两个垂直平面的交线,且PE ⊂平面PAD ,所以PE ⊥平面ABCD ;(2)连结BE ,由题意可知PBE ∠是异面直线PB 与CD 所成的角,并且三角形PBE 是直角三角形,EB ==,112PE AE AD ===,PB =,由余弦定理得cos3EB PBE PB ∠===;(3)利用体积相等法可得解,设点A 到平面PCD 的距离h ,即由P ACD A PCD V V --=,得1133ACD PCD S EP S h ∆∆⋅=⋅, 而在Rt PEC ∆中,PC =,所以PC CD DP ==,因此242PCD S ∆=⨯=,又112ACD S AD AB ∆=⋅=,1EP =,从而可得解. (1)证明:在PAD ∆中,PA PD =,E 为AD 中点,PE AD ∴⊥. 2分 又侧面PAD ⊥底面ABCD ,平面PAD I 平面ABCD AD =,PE ⊂平面PAD . PE ∴⊥平面ABCD . 4分(2)解:连结BE ,在直角梯形ABCD 中,BC AD P ,22AD AB BC ==,有ED BC P 且ED BC =.所以四边形EBCD 平行四边形,EB DC ∴P .由(1)知PE EB ⊥,PBE ∠为锐角,所以PBE ∠是异面直线PB 与CD 所成的角. 7分2,1AD AB BC ===Q ,在Rt AEB ∆中,1,1AB AE ==.EB ∴=.在Rt PEA ∆中,1,AP AE ==1EP ∴=.在Rt PBE ∆中,PB ==cos3EB PBE PB ∴∠===.所以异面直线PB 与CD 所成的角的余弦值为3. 9分(3)解:由(2)得CD EB ==在Rt PEC ∆中,PC =PC CD DP ∴==, 242PCD S ∆==. 设点A 到平面PCD 的距离h ,由P ACD A PCD V V --=,得1133ACD PCD S EP S h ∆∆⋅=⋅. 11分又112ACD S AD AB ∆=⋅=,解得h =分 考点:1.线面垂直;2.异面直线角;3.点到面距离.18.已知椭圆22221(0)x y a b a b+=>>的一个顶点为B(0,4),离心率5e =, 直线l 交椭圆于M,N 两点.(1)若直线l 的方程为y=x-4,求弦MN 的长:(2)如果∆BMN 的重心恰好为椭圆的右焦点F ,求直线l 的方程.【答案】(1;(2)65280x y --=. 【解析】试题分析:(1)由椭圆顶点()0,4B 知4b =,又离心率5c e a ==,且222a b c =+,所以220a =,从而求得椭圆方程为2212016x y +=,联立椭圆方程与直线4y x =-消去y 得29400x x -=,12400,9x x ==,再根据弦长公式12MN x =-,可求得弦MN的长;(2)由题意可设线段MN 的中点为()00,Q x y ,则根据三角形重心的性质知2BF FQ =u u u r u u u r,可求得Q 的坐标为()3,2-,又设直线MN 的方程为()()()112223,,,,y k x M x y N x y +=-,根据中点公式得12126,4x x y y +=+=-,又由点,M N 是椭圆上的点所以222211221,120162016x y x y +=+=,两式相减整理得1212121244665545y y x x k x x y y -+∴==-⋅=-⋅=-+-,从而可求出直线MN 的方程.(1)由已知4b =,且c a =,220a ∴=.所以椭圆方程为2212016x y +=. 4分 由2212016x y +=与4y x =-联立,消去y 得29400x x -=,12400,9x x ∴==. 6分129MN x ∴=-=. 7分 (2)椭圆右焦点F 的坐标为()2,0,设线段MN 的中点为()00,Q x y ,由三角形重心的性质知2BF FQ =u u u r u u u r,又()0,4B ,()()002,422,x y ∴-=-,故得003,2x y ==-.所以得Q的坐标为()3,2-. 9分设直线MN 的方程为()()()112223,,,,y k x M x y N x y +=-,则12126,4x x y y +=+=-,且222211221,120162016x y x y +=+=,两式相减得()()()()1212121202016x x x x y y y y +-+-+=. 11分1212121244665545y y x x k x x y y -+∴==-⋅=-⋅=-+-,故直线MN 的方程为65280x y --=.13分考点:1.椭圆方程;2.直线方程.19.已知函数1()()3x f x =,等比数列{}n a 的前n 项和为()f n c -,数列{}(0)n n b b >的前n 项为n S ,且前n 项和n S满足12)n n S S n --=+≥.(1)求数列{}n a 和{}n b 的通项公式: (2)若数列11n n b b +⎧⎫⎨⎬⎩⎭前n 项和为n T ,问使10052014nT >的最小正整数n 是多少? 【答案】(1)()213n n a n =-…,()211n b n n =-…;(2)252. 【解析】试题分析:(1)由已知得当2n …时,()()()12113n n n a f n c f n c a a -=----=-=-⎡⎤⎡⎤⎣⎦⎣⎦,则等比数列{}n a 的公比13q =,又()2121193a a q f c ∴=-==-⨯⎡⎤⎣⎦,解得121,3c a ==-,由等比数列通项公式11n n a a q -=可得所求数列{}n a的通项公式;由已知可先求出数列的通项公式,再求{}n b 的通项公式,因为11n n S S --=⇒==,1==,所以是首项为1,公差为1的等差数列,n =,即2n S n =,从而()1212n n n b S S n n -=-=-…,又11211b ==⨯-,故数列{}n b 的通项公式为()211n b n n =-…;(2)由数列11n n b b +⎧⎫⎨⎬⎩⎭的通项公式1111111212322121n b b b n n n n -⎛⎫=⋅=- ⎪---+⎝⎭可采用裂项求和法先求出前n 项和111111121335212121n n T n n n ⎡⎤⎛⎫⎛⎫⎛⎫∴=-+-+++= ⎪ ⎪ ⎪⎢⎥-++⎝⎭⎝⎭⎝⎭⎣⎦L ,从而可得1005100510051251201421201444n n T n n >⇒>⇒>=+,故满足条件的最小正整数n 是252. (1)因为等比数列{}n a 的前n 项和为()f n c =,则当2n …时,()()()12113n n n a f n c f n c a a -=----=-=-⎡⎤⎡⎤⎣⎦⎣⎦. 因为是等比数列,所以{}n a 的公比13q =. 2分 ()2121193a a q f c ∴=-==-⨯⎡⎤⎣⎦,解得121,3c a ==-.()213n na n ∴=-…. 4分 由题设知{}()0n n b b >的首项11b c ==,其前n 项和n S 满足)12n n S S n --=…,由11n n S S --==1==.所以是首项为1,公差为1的等差数列. 6分n =,2n S n =.()1212n n n b S S n n -=-=-Q …,又11211b ==⨯-. 故数列{}n b 的通项公式为()211n b n n =-…. 8分 (2)因为()211n b n n =-…,所以1111122121n b b b n n -⎛⎫=- ⎪-+⎝⎭. 10分 111111121335212121n n T n n n ⎡⎤⎛⎫⎛⎫⎛⎫∴=-+-+++= ⎪ ⎪ ⎪⎢⎥-++⎝⎭⎝⎭⎝⎭⎣⎦L . 12分 要使10052014n T >,则1005212014n n >+.所以1005125144n >=. 故满足条件的最小正整数n 是252. 14分 考点:1.数列通项公式;2.数列列前n 项和公式.20.已知()f x 是二次函数,不等式()0f x <的解集是(0,5),且()f x 在区间[-1,4]上的最大值是12.(1)求f(x)的解析式;(2)是否存在正整数m,使得方程37()0f x x+=在区间(,1)m m +内有且只有两个不等的实数根?若存在,求出所有m 的值;若不存在,请说明理由. 【答案】(1)()()()225210f x x x x x x R =-=-∈;(2)方程()32370210370f x x x x+=⇔-+=, 设()3221037h x x x =-+,则()()26202310h x x x x x '=-=-. 当100,3x ⎛⎫∈ ⎪⎝⎭时,()0h x '<,()h x 是减函数;当10,3x ⎛⎫∈+∞ ⎪⎝⎭时,()0h x '>,()h x 是增函数.因为()()101310,0,450327h h h ⎛⎫=>=-<=>⎪⎝⎭.所以方程()0h x =在区间103,3⎛⎫⎪⎝⎭,10,43⎛⎫⎪⎝⎭内分别有唯一实数根,而区间()0,3,()4,+∞内没有实数根.所以存在唯一的正数3m =,使得方程()370f x x+=在区间(),1m m +内有且只有两个不等的实数根. 【解析】试题分析:(1)由已知得0,5是二次函数()f x 的两个零点值,所以可设()()()50f x ax x a =->,开口方向向上,对称轴为52x =,因此()f x 在区间[]1,4-上的最大值是()16f a -=,则612a =,即2a =,因此可求出函数()f x 的解析式;(2)由(1)得()32370210370f x x x x+=⇔-+=,构造函数()3221037h x x x =-+,则方程()370f x x+=的实数根转化为函数()3221037h x x x =-+的零点,利用导数法得到函数()h x 减区间为100,3⎛⎫ ⎪⎝⎭、增区间为10,3⎛⎫+∞ ⎪⎝⎭,又有()310h =>,1010327h ⎛⎫=-< ⎪⎝⎭,()450h =>,发现函数()h x 在区间103,3⎛⎫ ⎪⎝⎭,10,43⎛⎫⎪⎝⎭内分别有唯一零点,而在区间()0,3,()4,+∞内没有零点,所以存在唯一的正数3m =,使得方程()370f x x+=在区间(),1m m +内有且只有两个不等的实数根.(1)因为()f x 是二次函数,且()0f x <的解集是()0,5, 所以可设()()()50f x ax x a =-> 2分所以()f x 在区间[]1,4-上的最大值是()16f a -=. 4分由已知,得612a =,2a ∴=.()()()225210f x x x x x x R ∴=-=-∈. 6分(2)方程()32370210370f x x x x+=⇔-+=, 设()3221037h x x x =-+,则()()26202310h x x x x x '=-=-. 10分 当100,3x ⎛⎫∈ ⎪⎝⎭时,()0h x '<,()h x 是减函数; 当10,3x ⎛⎫∈+∞⎪⎝⎭时,()0h x '>,()h x 是增函数. 10分 因为()()101310,0,450327h h h ⎛⎫=>=-<=>⎪⎝⎭. 所以方程()0h x =在区间103,3⎛⎫ ⎪⎝⎭,10,43⎛⎫⎪⎝⎭内分别有唯一实数根,而区间()0,3,()4,+∞内没有实数根. 12分所以存在唯一的正数3m =,使得方程()370f x x+=在区间(),1m m +内有且只有两个不等的实数根. 14分考点:1.函数解析式;2.函数零点.。
天津市河北区2014届高三总复习质量检测(三)文数 Word版含答案

天津市河北区2014届高三总复习质量检测(三)文数 本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,共150分,考试用时120分钟.第I 卷1至2页,第II 卷3至8页,第I 卷(选择题共40分)注意事项:1. 答第I 卷前,考生务必将自己的姓名、准考号、科目涂写在答题卡上,并在规定位置粘贴考试用条形码。
2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,在选涂其他答案标号。
答在试卷上的无效。
3. 本卷共8小题,每小题5分,共40分。
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.(1)复数(6)z i i =+在复平面内对应的点位于(A)第一象限 (B)第二象限(C)第三象限 (D)第四象限(2)已知集合{}{}|06,|23A x x B x x =<<=-< ,则 AB =(A) {}|16x x -<< (B) {}|15x x -<<(C) {}|03x x << (D) {}|05x x <<(3)执行如图所示的程序框图,输出的S 值为(A)9 (B) 19(C) 20 (D) 35(4)若 p q ⌝∨是假命题,则(A) p q ∧是假命题 (B) pVq 是假命题(C)p 是假命题 (D) q ⌝是假命题(5)已知一个四棱锥的三视图如图所示,则此四棱锥的四个侧面的面积中最大的是(A)3 (B) (C)6 (D)8(6)若双曲线 22:2(0)C x y m m -=>与抛物线216y x =的准线交于A ,B 两点且AB =,则m 的值是(A) 20 (B) 52(C) 80 (D) 116(7)函数 1()ln()f x x x=-的图象大致是(8)已知函数 2sin ()1x f x x =+.下列命题: ①函数 ()f x 的图象关于原点对称:②函数 ()f x 是周期函数;③当 2x π=时,函数f (x)取最大值:④函数()f x 的图象与函数 1y x= 的图象没有公共点. 其中正确命题的序号是(A)①③ (B)①②④(C)①④ (D)①③④第II 卷注意事项:1. 答卷前将密封线内的项目填写清楚。
2014年高考文科数学试题(天津卷)及参考答案

2014年普通高等学校招生全国统一考试(天津卷)文科数学一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. 1.i 是虚数单位,复数734ii+=+ A.1i - B.1i -+ C.17312525i + D.172577i -+ 2.设变量x 、y 满足约束条件20201x y x y y +-≥⎧⎪--≤⎨⎪≥⎩,则目标函数2z x y =+的最小值为A.2B.3C.4D.5 3.已知命题p :0x ∀>,总有(1)1xx e +>,则p ⌝为 A.00x ∃≤,使得00(1)1x x e +≤ B.00x ∃>,使得00(1)1x x e +≤ C.0x ∀>,总有00(1)1x x e+≤ D.0x ∀≤,总有00(1)1x x e +≤4.设2log a π=,12log b π=,2c π-=,则A.a b c >>B.b a c >>C.a c b >>D.c b a >>5.设{}n a 是首项为1a ,公差为1-的等差数列,n S 为其前n 项和,若1S 、2S 、4S 成等比数列,则1a =A.2B.-2C.21 D.21 6.已知双曲线22221(0x y a a b-=>,0)b >的一条渐近线平行于直线l :210y x =+,双曲线的一个焦点在直线l 上,则双曲线的方程为 A.221520x y -= B.221205x y -= C.2233125100x y -= D.2233110025x y -= 7.如图,ABC ∆是圆的内接三角形,BAC ∠的平分线交圆于点D ,交BC 于点E ,过点B 的圆的切线与AD 的延长线交于点F ,在上述条件下,给出下列四个结论:①BD平分CBF ∠;②2FB FD FA =⋅;③AE CE BE DE ⋅=⋅;④AF BD AB BF ⋅=⋅.则所有正确结论的序号是A.①②B.③④C.①②③D.①②④ 8.已知函数()3sin cos (0)f x x x ωωω=+>,x R ∈.在曲线()y f x =与直线1y =的交点中,若相邻交点距离的最小值为3π,则()f x 的最小正周期为 A.2πB.23πC.πD.2π二、填空题:本大题共6小题,每小题5分,共30分.9.某大学为了解在校本科生对参加某项社会实践活动的意向,拟采用分层抽样的方法,从该校四个年级的本科生中抽取一个容量为300的样本进行调查.已知该校一年级、二年级、三年级、四年级的本科生人数之比为4:5:5:6,则应从一年级本科生中抽取____名学生.10.一个几何体的三视图如图所示(单位:m ),则该几何体的体积为_________3m .11.阅读右边的框图,运行相应的程序,输出S 的值为________.12.函数2()lg f x x =的单调递减区间是______________.13.已知菱形ABCD 的边长为2,120BAD ∠=︒,点E 、F 分别在边BC 、DC 上,3BC BE =,DC DF λ=.若1AE AF ⋅=,则λ的值为________.14.已知函数2|54|(0)()2|2|(0)x x x f x x x ⎧++≤=⎨->⎩.若函数()||y f x a x =-恰有4个零点,则实数a 的取值范围为_______三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.(本小题满分13分)某校夏令营有3名男同学A 、B 、C 和3名女同学X 、Y 、Z ,其年级情况如下表:一年级 二年级 三年级 男同学 A B C 女同学 X Y Z现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同). ⑴用表中字母列举出所有可能的结果; ⑵设M 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件M 发生的概率.16.(本小题满分13分)在ABC ∆中,内角A 、B 、C 所对的边分别为a 、b 、c ,已知66a cb -=,sin 6sin B C =. ⑴求cos A 的值;⑵求cos(2)6A π-的值.17.(本小题满分13分)如图,四棱锥P ABCD -的底面ABCD 是平行四边形,2BA BD ==,2AD =,5PA PD ==,E 、F 分别是棱AD 、PC 的中点. ⑴证明://EF 平面PAB ;⑵若二面角P AD B --为60︒, ①证明:平面PBC ⊥平面ABCD ; ②求直线EF 与平面PBC 所成角的正弦值.18.(本小题满分13分)设椭圆22221(0)x y a b a b+=>>的左、右焦点分别为1F 、2F ,右顶点为A ,上顶点为B .已知123||||2AB F F =. ⑴求椭圆的离心率;⑵设P 为椭圆上异于其顶点的一点,以线段PB 为直径的圆经过点1F ,经过点2F 的直线l 与该圆相切于点M ,2||22MF =.求椭圆的方程.19.(本小题满分14分) 已知函数232()(0)3f x x ax a =->,x R ∈. ⑴求()f x 的单调区间和极值;⑵若对于任意的1(2x ∈,)+∞,都存在2(1x ∈,)+∞,使得12()()1f x f x ⋅=,求a 的取值范围.20.(本小题满分14分)已知q 和n 均为给定的大于1的自然数,设集合{0M =,1,2,...,1}q -,集合12{|A x x x x q ==++...1n n x q -+,i x M ∈,1i =,2,...,}n . ⑴当2q =,3n =时,用列举法表示集合A ;⑵设s 、t A ∈,12s a a q =++...1n n a q -+,12t b b q =++...1n n b q -+,其中i a 、i b M ∈,1i =,2,...,n .证明:若n n a b <,则t s <.参考答案一、选择题: 本大题共8小题,每小题5分,共40分.1.A2.B3.B4.C5.D6.A7.D8.C二、填空题:本大题共6小题,每小题5分,共30分.9.60 10.320π11.-4 12.)0,(-∞ 13.2 14.(1,2)三、解答题:本大题共6小题,共80分.15.(本小题满分13分)16.(本小题满分13分)17.(本小题满分13分)(2)18.(本小题满分13分)19.(本小题满分14分)20.(本小题满分14分)。
数学_2014年天津市河北区高考数学一模试卷(文科)(含答案)

2014年天津市河北区高考数学一模试卷(文科)一、选择题:本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项市符合题目要求的.1. 已知集合M ={x|−2<x <3},N ={x|lg(x +2)≥0},则M ∩N =( ) A (−2, +∞) B (−2, 3) C (−2, −1] D [−1, 3)2. 已知变量x ,y 满足约束条件{x +y ≤1x +1≥0x −y ≤1,则目标函数z =2x +y 的最大值是( )A −4B 0C 2D 43. 执行如图的程序框图,输出k 的值是( )A 3B 4C 5D 64. “a >1”是“函数f(x)=a x −2,(a >0且a ≠1)在区间(0, +∞)上存在零点”的( ) A 充分而不必要条件 B 必要而不充分条件 C 充分必要条件 D 既不充分也不必要条件5. 一个几何体的三视图如图所示,则几何体的体积是( )A 56 B 103 C 53 D 26. 在△ABC 中,BC =3,AC =√13,B =π3,则△ABC 的面积是( )A 3√3B 6√13C 3√32D 3√347. 已知函数f(x)={log 3x ,x >0(13)x ,x ≤0,那么不等式f(x)≥1的解集为( )A {x|−3≤x ≤0}B {x|x ≤−3或x ≥0}C {x|0≤x ≤3}D {x|x ≤0或x ≥3} 8. 已知函数f(x)=4x −14x +1,若x 1>0,x 2>0,且f(x 1)+f(x 2)=1,则f(x 1+x 2)的最小值为( )A 14B 45C 2D 4二、填空题:本大题共6小题,每小题5分,共30分. 9. 若复数z =1−i1+i ,则|z|=________.10. 一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积是323π,那么这个球的半径是________,三棱柱的体积是________.11. 设F 是抛物线C 1:y 2=2pr(p >0)的焦点,点A 是抛物线C 1与双曲线C 2:x 2a2−y 2b 2=1(a >0, b >0)的一条渐近线的一个公共点,且AF ⊥x 轴,则双曲线的离心率为________.12. 如图,AB 是半圆O 的直径,P 在AB 的延长线上,PD 与半圆O 相切于点C ,AD ⊥PD .若PC =4,PB =2,则CD =________. 13. 已知x >0,y >0,若2yx +8x y >m 2+7m 恒成立,则实数m 的取值范围是________.14. 已知a →、b →为非零向量,m →=a →+tb →(t ∈R),若|a →|=1,|b →|=2,当且仅当t =14时,|m →|取得最小值,则向量a →、b →的夹角为________.三、解答题:本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤. 15. 已知A ,B ,C 分别为△ABC 的三边a ,b ,c 所对的角,向量m →=(sinA,sinB),n →=(cosB,cosA),且m →⋅n →=sin2C . (1)求角C 的大小;(2)若sinA ,sinC ,sinB 成等差数列,且CA →⋅CB →=18,求边c 的长. 16. 已知实数a ,b ∈{−2, −1, 1, 2}(I)求直线y =ax +b 不经过第四象限的概率;(II)求直线y =ax +b 与圆x 2+y 2=1有公共点的概率.17. 如图,在四棱锥P −ABCD 中,侧面PAD ⊥底面ABCD ,侧棱PA =PD =√2,底面ABCD 为直角梯形,其中BC // AD ,AB ⊥AD ,AC =√2,AB =BC=1,E为AD中点.(1)求证:PE⊥平面ABCD;(2)求异面直线PB与CD所成角的余弦值;(3)求平面PAB与平面PCD所成的二面角.18. 已知椭圆x2a2+y2b2=1(a>b>0)的一个顶点为B(0, 4),离心率e=√55,直线l交椭圆于M、N两点.(1)若直线l的方程为y=x−4,求弦MN的长;(2)如果△BMN的重心恰好为椭圆的右焦点F,求直线l方程的一般式.19. 已知函数f(x)=(13)x,等比数列{a n}的前n项和为f(n)−c,数列{b n}{b n>0}的首项为c,且前n项和S n满足S n−S n−1=√S n+√S n−1(n≥2).(1)求数列{a n}和{b n}的通项公式;(2)若数列{1b n b n+1}前n项和为T n,问使T n>10052014的最小正整数n是多少?20. 已知f(x)是二次函数,不等式f(x)<0的解集是(0, 5),且f(x)在区间[−1, 4]上的最大值是12.(1)求f(x)的解析式;(2)是否存在自然数m,使得方程f(x)+37x=0在区间(m, m+1)内有且只有两个不等的实数根?若存在,求出m的值;若不存在,说明理由.2014年天津市河北区高考数学一模试卷(文科)答案1. D2. C3. A4. C5. B6. A7. D8. B9. 110. 2,48√311. √512. 12513. (−8, 1)14. 2π315. 解:(1)∵ m→=(sinA, sinB),n→=(cosB, cosA),∴ m→⋅n→=sin2C,即sinAcosB+sinBcosA=sin(A+B)=sinC=sin2C=2sinCcosC,∵ sinC ≠0, ∴ cosC =12,∵ C 为三角形内角, ∴ C =π3;(2)∵ sinA ,sinC ,sinB 成等差数列, ∴ 2sinC =sinA +sinB ,利用正弦定理化简得:2c =a +b , ∵ CA →⋅CB →=18,∴ abcosC =12ab =18,即ab =36,由余弦定理得c 2=a 2+b 2−2abcosC =a 2+b 2−ab =(a +b)2−3ab , 将a +b =2c ,ab =36代入得:c 2=4c 2−108,即c 2=36, 解得:c =6.16. 直线y =ax +b 不经过第四象限概率为14;y =ax +b 与圆x 2+y 2=1有公共点的概率为34.17. (1)证明:在△PAD 中PA =PD ,E 为AD 中点, ∴ PE ⊥AD又侧面PAD ⊥底面ABCD ,平面PAD ∩平面ABCD =AD ,PE ⊂平面PAD , 所以PE ⊥平面ABCD .(2)解:连结BE ,在直角梯形ABCD 中,BC // AD ,AD =2AB =2BC ,有ED // BC 且ED =BC ,∴ 四边形EBCD 是平行四边形, ∴ EB // DC由(1)知PE ⊥EB ,∠PBE 为锐角, ∴ ∠PBE 是异面直线PB 与CD 所成的角 ∵ AC =2,AB =BC =1,在Rt △AEB 中,AB =1,AE =1,∴ EB =√2,在Rt △PEA 中,AP =√2,AE =1,∴ EP =1,在Rt △PBE 中,PB =√EP 2+EB 2=√3, cos∠PBE =EB PB=√2√3=√63, ∴ 异面直线PB 与CD 所成的角的余弦值为√63.(3)解:以E 为原点,EC 为x 轴,ED 为y 轴,EP 为z 轴, 建立空直角坐标系,A(0, −1, 0),B(1, −1, 0),P(0, 0, 1), C(1, 0, 0),D(0, 1, 0), PA →=(0,1,1),PB →=(−1,1,1), PC →=(−1,0,1),PD →=(0,−1,1), 设平面PAB 的法向量n →=(x,y,z),则{n →⋅PB →=−x +y +z =0˙,取y =1,得n →=(0,1,−1), 设平面PCD 的法向量m →=(a,b,c),则{m →⋅PD →=−b +c =0˙,取a =1,得m →=(1,1,1), ∵ n →⋅m →=0,∴ 平面PAB 与平面PCD 所成的二面角为90∘.18. 由已知椭圆x 2a 2+y 2b 2=1(a >b >0)的一个顶点为B(0, 4), ∴ b =4, 又∵ 离心率e =ca =√55, 即c 2a 2=15,∴a 2−b 2a 2=15,解得a 2=20,∴ 椭圆方程为x 220+y 216=1;由4x 2+5y 2=80与y =x −4联立, 消去y 得9x 2−40x =0, ∴ x 1=0,x 2=409,∴ 所求弦长|MN|=√1+12|x 2−x 1|=40√29; 椭圆右焦点F 的坐标为(2, 0),设线段MN 的中点为Q(x 0, y 0),由三角形重心的性质知BF →=2FQ →,又B(0, 4), ∴ (2.−4)=2(x 0−2, y 0), 故得x 0=3,y 0=−2, 求得Q 的坐标为(3, −2);设M(x 1, y 1),N(x 2, y 2),则x 1+x 2=6,y 1+y 2=−4,且x 1220+y 1216=1,x 2220+y 2216=1,以上两式相减得(x 1+x 2)(x 1−x 2)20+(y 1+y 2)(y 1−y 2)16=0,∴ k MN =y 1−y2x 1−x 2=−45⋅x 1+x2y 1+y 2=−45⋅6−4=65,故直线MN 的方程为y +2=65(x −3),即6x −5y −28=0.19. 解:(1)∵ 函数f(x)=(13)x ,等比数列{a n }的前n 项和为f(n)−c ,∴ n ≥2时,a n =[f(n)−c]−[f(n −1)−c]=−23n , ∴ 等比数列{a n }的公比为q =13,∴ c =1,a 1=−23,∴ a n =−23n ;∵ 数列{b n }{b n >0}的首项为c ,且前n 项和S n 满足S n −S n−1=√S n +√S n−1(n ≥2). ∴ b 1=1,√S n −√S n−1=1,∴ {√S n }是首项为1,公差为1的等差数列, ∴ √S n =n ,∴ S n =n 2,∴ n ≥2时,b n =S n −S n−1=2n −1, ∵ b 1=1,∴ b n =2n −1; (2)1b n b n+1=12(12n−1−12n+1),∴ T n =12(1−13+13−15+...+12n−1−12n+1)=12(1−12n+1)=n2n+1,由T n >10052014,得n2n+1>10052014,解得n >251.25 ∴ T n >10052014的最小正整数n 是252.20. 解:(1)∵ f(x)是二次函数,且f(x)<0的解集是(0, 5), ∴ 可设f(x)=ax(x −5)(a >0).∴ f(x)在区间[−1, 4]上的最大值是f(−1)=6a . 由已知得6a =12,∴ a =2,∴ f(x)=2x(x −5)=2x 2−10x(x ∈R). (2)方程f(x)+37x=0等价于方程2x 3−10x 2+37=0.设ℎ(x)=2x 3−10x 2+37,则ℎ′(x)=6x 2−20x =2x(3x −10). 在区间x ∈(0,103)时,ℎ′(x)<0,ℎ(x)是减函数;在区间(−∞, 0),(103,+∞)上,ℎ′(x)>0,ℎ(x)是增函数, 故ℎ(0)是极大值,ℎ(103)是极小值.∵ ℎ(3)=1>0,ℎ(103)=−127<0,ℎ(4)=5>0,∴ 方程ℎ(x)=0在区间(3,103),(103,4)内分别有唯一实数根, 故函数ℎ(x)在(3, 4)内有2个零点.而在区间(0, 3),(4, +∞)内没有零点,在(−∞, 0)上有唯一的零点. 画出函数ℎ(x)的单调性和零点情况的简图,如图所示,∴ 存在惟一的自然数m =3,使得方程f(x)+37x=0在区间(m, m +1)内有且只有两个不同的实数根.。
天津市河北区-高三年级总复习质量检测(一).docx

天津市河北区2015-2016学年度高三年级总复习质量检测(一)数 学(文史类)第Ⅰ卷(选择题 共40分)3. 本卷共8小题,每小题5分,共40分。
参考公式:· 如果事件A ,B 互斥,那么P (A ∪B )=P (A )+P (B )· 如果事件A ,B 相互独立,那么P (AB )=P (A )⋅P (B )· 球的表面积公式 S =24R π球的体积公式 V =343R π其中R 表示球的半径一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. (1)已知集合={01234}U ,,,,,={123}A ,,,={24}B ,,则()U C A B =I(A ){2} (B ){24}, (C ){04}, (D ){4} (2)i 是虚数单位,复数34i12i+=- (A )12i + (B )12i - (C )12i -+ (D )12i --(3)执行如图所示的程序框图,则输出的结果是 (A )2016 (B )2 (C )12(D )1-(4)若1311321=()=log 2=log 32a b c ,,,则a b c ,,(A ) b c a >> (B )c a b >>(C ) a b c >> (D )a >(5)设x y ∈R ,,则“1x ≥且2y ≥”是“+3x y ≥”的(A )充分不必要条件 (B )必要不充分条件(C )充要条件 (D )既不充分也不必要条件(6)已知双曲线22221(00)x y =a >b >a b,-的一条渐近线平行于直线l :+2+5=0x y ,且双曲线的一个焦点在直线l 上,则双曲线的方程为(A )22=1205x y - (B )22=1520x y -(C )2233=125100x y - (D )2233=110025x y -(7)若函数()=sin +f x x x 的图象关于直线x =a 对称,则最小正实数a 的值为 (A )π6(B )π4(C )π3 (D )π2(8)已知函数2ln 0()410x x >f x =x +x +x ⎧⎪⎨⎪⎩,,,≤,若关于x 的方程2()()0f x bf x +c =-(b c ∈R ,)有8个不同的实数根,则b+c的取值范围是(A)(3)-,(B)(03]∞,(C)[03],(D)(03),第Ⅱ卷二、填空题:本大题共6小题,每小题5分,共30分. 把答案填在题中横线上.______________.(10)如图,已知切线PA切圆于点A,割线PBC分别交圆于点B C,,点D在线段BC上,且24,,,则线段AB的长为=∠=∠==DC BD BAD PAB PA PB_______________.(第9题图) (第10题图) (11)已知正数x y ,满足=x+y xy ,那么x+y 的最小值为 .(12)在区间[44]-,上随机地取一个实数x ,则事件“2230x x --≤”发生的概率是.(13)函数()e x f x =x 在点(1(1))f -,-处的切线方程为 .(14)已知ΔABC 中,AB =AC ,=4BC ,90BAC =∠︒,3BE EC =u u u r u u u r,若P 是BC 边上的动点,则AP AE ⋅u u u r u u u r的取值范围是______________.三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.得 分 评卷人 (15)(本小题满分13分)在锐角ABC ∆中,角A B C ,,的对边分别是a b c ,,,若7a 3b =, 7sin +sin =23B A(Ⅰ)求角A 的大小; (Ⅱ)求πsin(2)6B +的值.得 分 评卷人 (16)(本小题满分13分)1桶甲产品需耗A 原料3千克,B 原料1千克,生产1桶乙产品需耗A 原料1千克,B 原料3千克.每生产一桶甲产品的 利润为400元,每生产一桶乙产品的利润为300元,公司在生产这两种产品的计划中, 每天消耗A 、B 原料都不超过12千克.设公司计划每天生产x 桶甲产品和y 桶乙产品. (Ⅰ)用x ,y 列出满足条件的数学关系式,并在下面的坐标系中用阴影表示相应 的平面区域;(Ⅱ)该公司每天需生产甲产品和乙产品各多少桶时才使所得利润最大,最大利润是多少?(17)(本小题满分13分)如图,在四棱锥P ABCD -中,AB CD ∥,AB AD ⊥,22AB=AD=AP=CD=. (Ⅰ)若M 是棱PB 上一点,且2BM =PM ,求证:PD ∥平面MAC ;(Ⅱ) 若平面PAB ⊥平面ABCD ,平面PAD ⊥平面ABCD ,求证:PA ⊥平面ABCD ; PC 与平面ABCD 所成角的正切值.(18)(本小题满分13分)已知数列{}n a 是等差数列,n S 为{}n a 的前n 项和,且1028a =,8=92S ,数列{}n b 对任意*n ∈N ,总有1231=3+1n n b b b b b n ⋅⋅⋅L -成立. (Ⅰ)求数列{}n a 和{}n b 的通项公式; (Ⅱ)记2n n n na b c =⋅,求数列{}n c 的前n 项和n T .(19)(本小题满分14分)已知椭圆C :22221(0)x y +=a >b >ab的短轴长为2,离心率=2e .(Ⅰ)求椭圆C 的方程;(Ⅱ)若直线l :y =kx +m 与椭圆交于不同的两点A B ,,与圆2223x +y =相切 于点M .(i )证明:OA OB ⊥(O 为坐标原点); (ii )设AM λ=BM,求实数λ的取值范围.(20)(本小题满分14分)已知函数32()=f x ax x ax +-,其中a ∈R 且0a ≠. (Ⅰ)当1a=时,求函数()f x 的极值; (Ⅱ)求函数()3()ln f x g x =x x a-的单调区间; (Ⅲ)若存在(1]a ∈∞,--,使函数()()()[1](>1)h x =f x f x x b b '+∈,-,-在1x=-处 取得最小值,试求b 的最大值.河北区2015-2016学年度高三年级总复习质量检测(一)数 学 答 案(文)(9)16+π; (10) (11)4; (12)12; (13)1=ey -; (14)[26],.三、解答题:本大题共6小题,共80分. (15)(本小题满分13分)解:(Ⅰ)∵sinsin a b =A B ,∴sin sin b A B =a. …………2分 又a =3b =+sin =B A∴sin =A …………4分 又02A π<<,∴π=3A . …………6分(Ⅱ)由(Ⅰ)知, sin ==B A …………7分 又02B π<<,∴cos ==B …………9分 ∵sin2=2sin cos B B B 213cos2=12sin =14B B --, …………11分 ∴πππ1sin(2)=sin 2cos cos2sin =6667B B B ++- …………13分(16)(本小题满分13分) 解:(Ⅰ)设每天生产甲产品x 桶,乙产品y 桶,则x ,y 满足条件的数学关系式为3+12+31200x y x y x y ⎧⎪⎪⎨⎪⎪⎩,,≥,≥,≤≤ …… 3分 该二元一次不等式组表示的平面区域(可行域)如下…………7分 (Ⅱ)设利润总额为z 元,则目标函数为:400300z =x+y . ………8分 如图,作直线l :400300=0x+y ,即43=0x+y .当直线4=+3300zy x -经过可行域上的点A 时,截距300z 最大,即z 最大.解方程组3+=12+3=12x y x y ⎧⎨⎩,,得33x y ⎧⎨⎩==,即(33)A ,,………11分代入目标函数得max =2100z . ………12分答:该公司每天需生产甲产品3桶,乙产品3桶才使所得利润最大,最大利润为 2100元.…………13分 (17)(本小题满分13分) 证明:(Ⅰ)连结BD ,交AC 于点N ,连结MN .∵AB ∥CD ,2AB CD =, ∴2BN AB DN CD==. ∵2BM PM =, ∴2BM BN PM DN==. ∴MN ∥PD . ……2分又MN ⊂平面MAC ,PD ⊄平面MAC , ∴PD ∥平面MAC . …… 4分(Ⅱ)∵平面PAB ⊥平面ABCD ,平面PAB I 平面ABCD=AB ,AB AD ⊥,∴AD ⊥平面PAB . ∴AD PA ⊥. …… 6分同理可证AB PA ⊥. …… 7分又AB AD A =I ,∴PA ⊥平面ABCD . ……8分(Ⅲ)解:由(Ⅱ)知,PA ⊥平面ABCD∴PC 与平面ABCD 所成的角为PCA ∠. ……10分 在Rt PAC ∆中,∵2225PA AC AD +CD =,, ∴25tan 5PA PCA AC ∠===……12分 ∴PC 与平面ABCD 25. ……13分 (18)(本小题满分13分)解:(Ⅰ)设数列{}n a 的公差为d ,则10181=+9=2887=8+=922a a d S a d ⎧⎪⎨⨯⎪⎩.解得113a d ==,. ……2分∴32n a n =-. ……3分∵12313+1n n b b b b b =n ⋅⋅⋅L -, ① ∴1231=32(2n b b b b n n ⋅⋅L --≥). ② ①②两式相除得3132n n b n +=- (2)n ≥. ……5分 ∵当1n =时,14b =适合上式,∴3132n n b n +=-()n *∈N . ……6分 (Ⅱ)∵(31)221n n n nna b c ==n ⋅+, ……7分∴2311114710(31)2222n n T n =⨯+⨯+⨯+++L . ……8分2311111147(32)(31)22222n n n T n n +=⨯+⨯++-++L . ……9分两式相减得,2311333312()22222n n n n T ++=++++-L ……10分 1111[1()]3142231212n n n -+-+=+⨯-- ……11分173722n n ++=-. ……12分∴3772n nn T +=-. ……13分(19)(本小题满分14分) 解:(Ⅰ)∵22b =,∴1b =.…… 1分又c e a =,222a b c =+,∴ 22a =. ……3分∴ 椭圆C 的方程为 2212x y +=. …… 4分(Ⅱ)(i )∵直线l :y =kx +m 与圆2223x +y =相切,∴d ==222(1)3m k =+. ……5分 由2212y =kx +m x y ⎧⎪⎨+=⎪⎩, 消去y 并整理得,222(12)4220k x kmx m +++-=. 设11()A x y ,,22()B x y ,, 则12221224122212km x +x =+k m x x =+k ⎧⎪⎪⎨⎪⎪⎩--. …… 7分 ∵12121212()()OA OB =x x +y y =x x +kx +m kx +m ⋅u u u r u u u r.221212(1)()=+k x x +km x +x +m22222224(1)()1212m km=+k +km +m +k +k-- 2222223222(1)2201212m k +k k ===+k +k ----,∴OA OB ⊥. …… 9分(ii )∵直线l :y =kx+m 与椭圆交于不同的两点A B ,,∴222212121122x x +y =+y =,.∴AMλ==BM…… 11分由(Ⅱ)(i)知1212+=0x x y y,∴1212=x x y y-,222222121212==(1)(1)22x xx x y y--,即22122142=2+3xxx-.∴212+3==4xλ.…… 13分∵1x∴λ的取值范围是122λ≤≤.…… 14分(20)(本小题满分14分)解:(Ⅰ)当1a=时,32()+f x x x x=-,∴2()3+21(1)(31)f x x x x x'=-=+-.…… 2分令()0f x'=,得1x=-或13x=.列表讨论'()f x和()f x的变化情况:∴当1x=-时,()f x取得极大值(1)1f=-,当13x=时,()f x取得极15()327f=-. (4)小值分(Ⅱ)∵2()33()ln lnf xg x=x=ax x a xx a a+---,∴()g x的定义域为(0)+∞,,22323()21a x axg x=axax ax+'+=--2132()()2(0)a x xa a aax+=≠-.……5分(1)当0a>时,由()0g x'>,解得1xa>,由()0g x'<,解得10xa<<,∴()g x在1(0)a,上单调递减,在1()a+∞,上单调递增;……7分(2)当0a<时,由()0g x'>,解得32xa<<-,由()0g x'<,解得32xa>-,∴()g x在3(0)2a-,上单调递增,在3()2a-+∞,上单调递减.…9分(Ⅲ)∵2()=3+2f x ax x a'-,∴32()=+(3+1)+(2)h x ax a x a x a--.由题意知,()(1)h x h≥-在区间[1]b-,上恒成立.即2(+1)[(21)(13)]0x ax a x a+++-≥.①……10分当1x=-时,不等式①成立;当1x b-<≤时,不等式①可化为2(21)(13)0ax a x a+++-≥.②……11分令2()(21)(13)F x=ax+a+x+a-∵1a≤-,(1)40F a-=->,∴2()(21)(13)0F b ab a b a=+++-≥,……12分即2+231+1b bb a-≤-.由题意,只需2max+231()=1b bb a-≤-.b……13分又1b>-,∴1b-<∴maxb=.……14分。
天津市河北区2014届高三数学总复习质量检测 文(河北一模)

河北区2013 -2014学年度高三年级总复习质量检测(一)数学(文史类)本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共150分,考试用时120分钟.第I卷1至2页,第II卷3至8页,第I卷(选择题共40分)注意事项:1.答第I卷前,考生务必将自己的姓名、准考号、科目涂写在答题卡上,并在规定位置粘贴考试用条形码。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,在选涂其他答案标号。
答在试卷上的无效。
3.本卷共8小题,每小题5分,共40分。
参考公式:一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.(1)己知集合{}{}|23|lg(2)0M x x N x x=-<<=+≥,则M N =(A) (2,)-+∞ (B)[)1,3-(C) (]2,1--(D)(2,3)-(2)已知变量x,y满足约束条件110,1x yxx y+≤⎧⎪+≥⎨⎪-≤⎩,则目标函数z=2x +y的最大值是(A) -4 (B) 0(C)2 (D)4(3)执行右边的程序框图,输出m的值是(A)3 (B)4 (C)5 (D)6(4)“a>l”是“函数()2f x ax=-(a >0且1a≠)在区间(0,)+∞上存在零点”的。
(A)充分而不必要条件 (B)必要而不充分条件(C)充分必要条件 (D)既不充分也不必要条件(5) 一个几何体的三视图如右图所示,则该几何体的体积是(A)56 (B) 103 (C)53 (D)2 (6)在ABC ∆中,3,13,3BC AC B π===,则ABC ∆的面积是(A)33 (B)63(C)332 (D)334(7)已知函数log3,0()1(),03x x x f x x >⎧⎪=⎨≤⎪⎩.那么不等式()1f x ≥的解集为(A){}|30x x -≤≤ (B) {}|30x x x ≤-≥或 (C){}|0x x ≤≤ (D {}|03x x x ≤≥或(8)已知函数41()41x x f x -=+,若120,0x x >>,且12()()1f x f x +=, 则12()f x x +的最小值为(A)14 (B)45(C)2 (D)4第II 卷注意事项:1. 答卷前将密封线内的项目填写清楚。
天津市河北区2014届高三总复习质量检测(一)理科数学试卷(带解析)

天津市河北区2014届高三总复习质量检测(一)理科数学试卷(带解析)1.己知集合{}{}|23|lg(2)0M x x N x x =-<<=+≥,则MN =( ).(A)(2,)-+∞ (B)[)1,3- (C)(]2,1-- (D)(2,3)- 【答案】B 【解析】 试题分析:由已知集合{}1N x x =-…,所以{}{}[)2311,3MN x x x x x =-<<-=-…,故正解答案选B. 考点:1.集合运算;2.对数不等式.2.已知变量x ,y 满足约束条件110,1x y x x y +≤⎧⎪+≥⎨⎪-≤⎩,则目标函数z=2x +y 的最大值是( ).(A) -4 (B) 0 (C)2 (D)4 【答案】C 【解析】试题分析:首先作出可行域110,1x y x+≤⎧⎪+≥≤区域,目标函数可化为2y x z =-+,所以作出直线y ()1,0时,所z 的最大值为max 2102z =⨯+=,故正解答案为C.3.执行下边的程序框图,输出m 的值是( ).(A)3 (B)4 (C)5 (D)6 【答案】A 【解析】试题分析:第一次执行循环体时:1m =,23a =,0ba=,选择“否”;第二次:2m =,228239a ⎛⎫=⨯= ⎪⎝⎭,293384b a =⨯=,选择“否”;第三次:3m =,328339a ⎛⎫=⨯= ⎪⎝⎭,89198b a =⨯=,选择“是”,故此输出m 的值为3.正解答案选A. 考点:1.程序框图;2.幂运算.4.直线:10l mx y -+=与圆22:(1)5C x y +-=的位置关系是( ). (A)相切 (B)相离 (C)相交 (D)不确定 【答案】C 【解析】试题分析:由直线:10l mx y -+=,得()10y m x -=-,因此直线l 恒过点()0,1,又点()0,1是圆C 的圆心,所以直线l 与圆C 的位置关系是相交.故正确答案为C.考点:直线与圆5.一个几何体的三视图如图所示,则该几何体的体积是( ). (A)56 (B) 103 (C)53(D)2 【答案】B 【解析】试题分析:由三视图可知此几何体是由一个长为2点切去一角的空间多面体,如图所示,则其体积为111022323V =⨯⨯=.故正确答案选B.2222考点:1.三视图;2.简单组合体体积. 6.在ABC ∆中,3,3BC AC B π===,则ABC ∆的面积是( ).(A)【答案】A【解析】试题分析:由余弦定理得2222cos AC AB BC AB BC B =+-⋅∠,即2340AB AB --=,解得4AB =,所以11sin 4322ABC S AB BC B ∆=⋅⋅=⨯⨯=故正确答案为A. 考点:1.余弦定理;2.三角形面积.7.已知函数log3,0()1(),03x x x f x x >⎧⎪=⎨≤⎪⎩.那么不等式()1f x ≥的解集为( ).(A){}|30x x -≤≤ (B){}|30x x x ≤-≥或 (C){}|0x x ≤≤ (D){}|03x x x ≤≥或 【答案】D【解析】试题分析:由已知得,①当0x >时,有3log 13x x ⇒厖;②当0x …时,有1103xx ⎛⎫⇒ ⎪⎝⎭厔,综①②得不等式的解集为{}|03x x x ≤≥或.故正确答案选D. 考点:1.对数、指数不等式;2.分类讨论思想.8.已知函数41()41x x f x -=+,若120,0x x >>,且12()()1f x f x +=,则12()f x x +的最小值为( ). (A)14 (B)45(C)2 (D)4 【答案】B 【解析】试题分析:因为12()()1f x f x +=,所以1212414114141x x xx --+=++,整理得()1212444430x x x x ⋅-+-=,又1244x x +…124430x x ⋅-…,解得3,即124449x x x x+⋅=?,因此()1212121241224114141915x x x x x x f x x +++-+==--=+++….故正确答案为B.考点:1.指数函数;2.基本不等式.9.复数11iz i-=+,则z =______________. 【答案】1 【解析】试题分析:因为()()()211111i i z i i i i --===-++-,所以1z ==.故正确答案为1.考点:复数分母有理化、模.10.5(21)x -的展开式中3x 项的系数是____________(用数字作答). 【答案】80 【解析】试题分析:由题意得()()()55551552112rrrrr rr r T C x C x ----+=-=-⋅,令53r -=,解得2r =,代入上式得()23351280C -=.故正确答案为80.考点:二项式定理.11.在极坐标系中,圆心为(1,)2π,且过极点的圆的方程是____________.【答案】2sin ρθ= 【解析】试题分析:设圆上任一点P 的坐标为(),ρθ,连接圆心C 与极点O ,延长OC 交圆另一点A ,连接AP 得Rt OPA ∆,所以cos 22ρπθ⎛⎫=- ⎪⎝⎭,整理得所求圆的方程2sin ρθ=. 考点:圆的极坐标方程.12.如图,AB 是半圆D 的直径,P 在AB 的延长线上,PD 与半圆O 相切于点C ,AD ⊥PD.若PC=4,PB=2,则CD=____________.【答案】125【解析】试题分析:连接OC ,则得直角三角形OPC ,设半圆的半径为r ,则有()22224r r +=+,解得3r =,又由CD CP AO OP =,得4123325CD =⋅=+.故正确答案为125. 考点:1.圆的切线;2.平行线分线段成比例. 13.己知0,0x y >>,若2287y xm m x y+>+恒成立,则实数m 的取值范围是___________. 【答案】81m -<<【解析】试题分析:因为288y x x y +=…,所以287m m >+恒成立,即2780m m +-<恒成立,解得所求实数m 的范围为81m -<<. 考点:1.基本不等式.14.已知a 、b 为非零向量,()m a tb t R =+∈,若1,2a b ==,当且仅当14t =时,m 取得最小值,则向量a 、b 的夹角为___________. 【答案】23π 【解析】 试题分析:设向量,a b的夹角为θ,则2222222cos 44cos 1m a tb a t a b t b t t θθ=+=++=++,构造函数()2221144cos 14cos cos 124f t t t t θθθ⎛⎫=++=+-+ ⎪⎝⎭,因为当且仅当14t =时,m 取得最小值,所以当14t =时,函数()f t 有最小值,即111cos 0cos 422θθ+=⇒=-时,函数()f t 有最小值,又[]0,θπ∈,所以解得23πθ=.考点:1.向量;2.二次函数.15.己知A 、B 、C 分别为△ABC 的三边a 、b 、c 所对的角,向量(sin ,sin ),m A B =(cos ,cos )n B A =,且sin 2m n C ⋅=.(1)求角C 的大小:(2)若sinA ,sinC ,sinB 成等差数列,且18CA CB ⋅=,求边c 的长. 【答案】(1)3π;(2)6. 【解析】试题分析:(1)由向量数量积坐标运算得()sin m n A B ⋅=+,又,,A B C 三角形的三个内角,所以有()sin sin A B C +=,因此sin 2sin C C =,整理得1cos 2C =,所以所求角C 的大小为3π;(2)由等差中项公式得2sin sin sin C A B =+,根据正弦定理得2c a b =+,又18CA CB ⋅=,得c o s 18a b C=,由(1)可得36ab =,根据余弦定理得()22222cos 3c a b ab C a b ab =+-=+-,即224336c c =-⨯,从而可解得6c ∴=.(1)()sin cos sin cos sin m n A B B A A B ⋅=+=+ 2分 在ABC !中,由于()sin sin A B C +=,所以sin m n C ⋅=.又sin m n C ⋅=,sin 2sin C C ∴=,sin 2sin C C ∴=,又s i n 0C ≠,1cos 2C ∴=. 5分而0C π<<,3C π∴=. 7分(2)sin ,sin ,sin A C B 成等差数列,2sin sin sin C A B ∴=+,由正弦定理得2c a b =+.9分18CA CB ⋅=,cos 18ab C ∴=.由(1)知1cos 2C =,所以36ab =. 11分 由余弦定理得()22222cos 3c a b ab C a b ab =+-=+-,224336c c ∴=-⨯,236c ∴=.6c ∴=. 13分考点:1.正弦、余弦定理;2.向量数量积.16.某超市在节日期间进行有奖促销,凡在该超市购物满200元的顾客,将获得一次摸奖机会,规则如下:奖盒中放有除颜色外完全相同的1个红色球,1个黄色球,1个蓝色球和1个黑色球.顾客不放回的每次摸出1个球,直至摸到黑色球停止摸奖.规定摸到红色球奖励10元,摸到黄色球或蓝色球奖励5元,摸到黑色球无奖励. (1)求一名顾客摸球3次停止摸奖的概率;(2)记X 为一名顾客摸奖获得的奖金数额,求随机变量X 的分布列和数学期望. 【答案】(1)14; (2)所以随机变量X 的分布列为:,10EX =.【解析】 试题分析:(1)由题意知,事件“一名顾客摸球3次停止摸球”的基本事件为前两次摸到的球可能为红、黄、蓝球中的两种、第三次必是黑球,所以该事件个数为23A ,而事件总数是从四个球中不放回地选三个的总数为34A ,由古典概型的概率计算公式可求出所事件的概率;(2)由题意得,一名顾客摸球次数的可能性分别为1、2、3、4,由(1)的做法可得随机变量X 的所有取值为0、5、10、15、20,并分别求出相应的概率,从而可得到随机变量X 的分布列,并求出其数学期望.(1)设“一名顾客摸球3次停止摸奖”为事件A ,则()233414A P A A ==.故一名顾客摸球3次停止摸奖的概率为14. 4分(2)随机变量X 的所有取值为0、5、10、15、20. 6分()104P X ==,()2224156A P X A ===,()22234411106A P X A A ==+=,()1222341156C A P X A ⋅===,()33441204A P X A ===. 所以随机变量X 的分布列为:11分11111051015201046664EX =⨯+⨯+⨯+⨯+⨯= 13分考点:1.古典概型;2.随机变量布列、数学期望.17.如图,在四棱锥P-ABCD 中,侧面PAD ⊥底面ABCD,侧棱PA PD ==ABCD 为直角梯形,其中BC//AD ,AB ⊥AD ,AD=2,AB=BC=l ,E 为AD 中点.(1)求证:PE ⊥平面ABCD :(2)求异面直线PB 与CD 所成角的余弦值: (3)求平面PAB 与平面PCD 所成的二面角.【答案】(1)证明:在PAD ∆中,PA PD =,E 为AD 中点,PE AD ∴⊥.又侧面PAD ⊥底面ABCD ,平面PAD 平面ABCD AD =,PE ⊂平面PAD ⊥.PE ∴⊥平面ABCD ;(2(3【解析】试题分析:(1)由题意可根据面面垂直的性质定理来证,已知侧面PAD ⊥底面ABCD ,并且相交于AD ,而PAD ∆为等腰直角三角形,E 为AD 中点,所以PE AD ⊥,即PE 垂直于两个垂直平面的交线,且PE ⊂平面PAD ,所以PE ⊥平面ABCD ;(2)连结BE ,由题意可知PBE ∠是异面直线PB 与CD 所成的角,并且三角形PBE是直角三角形,EB ==112PE AE AD ===,PB ,由余弦定理得cos EB PBE PB ∠===;(3)利用体积相等法可得解,设点A 到平面PCD 的距离h ,即由P A C D AP C D V V--=,得1133ACD PCD S EP S h ∆∆⋅=⋅, 而在R t P E C ∆中,PC ,所以P C C D D P ==,因此2PCD S ∆==,又112A C D S A D AB ∆=⋅=,1EP =,从而可得解. (1)证明:在PAD ∆中,PA PD =,E 为AD 中点,PE AD ∴⊥. 2分 又侧面PAD ⊥底面ABCD ,平面PAD 平面ABCD AD =,PE ⊂平面PAD . PE ∴⊥平面ABCD . 4分(2)解:连结BE ,在直角梯形ABCD 中,BCAD ,22AD AB BC ==,有E D B C且ED BC =.所以四边形EBCD 平行四边形,EBDC ∴.由(1)知P E E B ⊥,PBE∠为锐角,所以PBE ∠是异面直线PB 与CD 所成的角. 7分2,1AD AB BC ===,在Rt AEB ∆中,1,1AB AE ==.EB ∴=.在Rt PEA ∆中,1,AP AE ==1EP ∴=.在Rt PBE ∆中,PB =cosEB PBE PB ∴∠===.所以异面直线PB 与CD 分(3)解:由(2)得CD EB ==在Rt PEC ∆中,PCPC CD DP ∴==, 2PCD S ∆==. 设点A 到平面PCD 的距离h ,由P ACD A PCD V V --=,得1133ACD PCD S EP S h ∆∆⋅=⋅. 11分又112ACD S AD AB ∆=⋅=,解得h =分 考点::1.线面垂直;2.异面直线角;3.点到面距离.18.已知椭圆22221(0)x y a b a b +=>>的一个顶点为B(0,4),离心率5e =, 直线l 交椭圆于M,N 两点.(1)若直线l 的方程为y=x-4,求弦MN 的长:(2)如果∆BMN 的重心恰好为椭圆的右焦点F ,求直线l 的方程.【答案】(1)9;(2)65280x y --=. 【解析】试题分析:(1)由椭圆顶点()0,4B 知4b =,又离心率c e a ==,且222a b c =+,所以220a =,从而求得椭圆方程为2212016x y +=,联立椭圆方程与直线4y x =-消去y 得29400x x -=,12400,9x x ==,再根据弦长公式12MN x =-,可求得弦MN 的长;(2)由题意可设线段MN 的中点为()00,Q x y ,则根据三角形重心的性质知2BF FQ =,可求得Q 的坐标为()3,2-,又设直线MN 的方程为()()()112223,,,,y k x M x y N x y +=-,根据中点公式得12126,4x x y y +=+=-,又由点,M N 是椭圆上的点所以222211221,120162016x y x y +=+=,两式相减整理得1212121244665545y y x x k x x y y -+∴==-⋅=-⋅=-+-,从而可求出直线MN 的方程.(1)由已知4b =,且c a =,220a ∴=.所以椭圆方程为2212016x y +=. 4分 由2212016x y +=与4y x =-联立,消去y 得29400x x -=,12400,9x x ∴==. 6分129MN x∴=-=. 7分(2)椭圆右焦点F的坐标为()2,0,设线段MN的中点为()00,Q x y,由三角形重心的性质知2BF FQ=,又()0,4B,()()002,422,x y∴-=-,故得003,2x y==-.所以得Q的坐标为()3,2-. 9分设直线MN的方程为()()()112223,,,,y k x M x y N x y+=-,则12126,4x x y y+=+=-,且222211221,120162016x y x y+=+=,两式相减得()()()()1212121202016x x x x y y y y+-+-+=. 11分1212121244665545y y x xkx x y y-+∴==-⋅=-⋅=-+-,故直线MN的方程为65280x y--=. 13分考点:1.椭圆方程;2.直线方程.19.已知函数1()()3xf x=,等比数列{}n a的前n项和为()f n c-,数列{}(0)n nb b>的前n项为nS,且前n项和nS满足12)n nS S n--=+≥.(1)求数列{}n a和{}n b的通项公式:(2)若数列11n nb b+⎧⎫⎨⎬⎩⎭前n项和为nT,问使10052014nT>的最小正整数n是多少?【答案】(1)()213n na n=-…,()211nb n n=-…;(2)252.【解析】试题分析:(1)由已知得当2n…时,()()()12113nn na f n c f n c a a-=----=-=-⎡⎤⎡⎤⎣⎦⎣⎦,则等比数列{}n a的公比13q=,又()2121193a a q f c∴=-==-⨯⎡⎤⎣⎦,解得121,3c a==-,由等比数列通项公式11nna a q-=可得所求数列{}n a的通项公式;由已知可先求出数列的通项公式,再求{}n b 的通项公式,因为11n n S S --=⇒==,1==,所以是首项为1,公差为1的等差数列,n =,即2n S n =,从而()1212n n n b S S n n -=-=-…,又11211b ==⨯-,故数列{}n b 的通项公式为()211n b n n =-…;(2)由数列11n n b b +⎧⎫⎨⎬⎩⎭的通项公式1111111212322121n b b b n n n n -⎛⎫=⋅=- ⎪---+⎝⎭可采用裂项求和法先求出前n 项和111111121335212121n n T n n n ⎡⎤⎛⎫⎛⎫⎛⎫∴=-+-+++= ⎪ ⎪ ⎪⎢⎥-++⎝⎭⎝⎭⎝⎭⎣⎦,从而可得1005100510051251201421201444n n T n n >⇒>⇒>=+,故满足条件的最小正整数n 是252. (1)因为等比数列{}n a 的前n 项和为()f n c =,则当2n …时,()()()12113n n n a f n c f n c a a -=----=-=-⎡⎤⎡⎤⎣⎦⎣⎦. 因为是等比数列,所以{}n a 的公比13q =. 2分 ()2121193a a q f c ∴=-==-⨯⎡⎤⎣⎦,解得121,3c a ==-.()213n nan ∴=-…. 4分 由题设知{}()0n n b b >的首项11b c ==,其前n项和n S满足)12n n S S n --=…,由11n n S S --=⇒=1==.所以是首项为1,公差为1的等差数列. 6分n =,2n S n =.()1212n n n b S S n n -=-=-…,又11211b ==⨯-. 故数列{}n b 的通项公式为()211n b n n =-…. 8分 (2)因为()211n b n n =-…,所以1111122121n b b b n n -⎛⎫=- ⎪-+⎝⎭. 10分 111111121335212121n n T n n n ⎡⎤⎛⎫⎛⎫⎛⎫∴=-+-+++= ⎪ ⎪ ⎪⎢⎥-++⎝⎭⎝⎭⎝⎭⎣⎦. 12分要使10052014n T >,则1005212014n n >+.所以1005125144n >=. 故满足条件的最小正整数n 是252. 14分考点:1.数列通项公式;2.数列列前n 项和公式. 20.已知函数2()ln ,f x x ax x a R =+-∈. (1)当a=l 时,求()f x 的单调区间;(2)若函数()f x 在[]1,2上是减函数,求实数a 的取值范围;(3)令2()()g x f x x =-,是否存在实数a ,当(]0,x e ∈(e 是自然对数的底数)时,函数g(x)最小值是3,若存在,求出a 的值;若不存在,说明理由.【答案】(1)单调递减区间为10,2⎛⎫ ⎪⎝⎭,单调递增区间为1,2⎡⎫+∞⎪⎢⎣⎭;(2)72a -…;(3)存在实数2a e =. 【解析】试题分析:(1)把1a =代入函数解析式得()2ln f x x x x =+-,且定义域为()0,+∞,利用导数法可求出函数的单调区间,由()()1211221x x f x x x x⎛⎫-+ ⎪⎝⎭'=+-=,分别解不等式()0f x '…,()0f x '…,注意函数定义域,从而可求出函数()f x 的单调区间;(2)此问题利用导数法来解决,若函数()f x 在[]1,2上是减函数,则其导函数()212120x ax f x x a x x+-'=+-=…在()1,2上恒成立,又因为()0,x ∈+∞,所以函数()221h x x ax =+-,必有()()1020h h ⎧⎪⎨⎪⎩……,从而解得实数a 的取值范围;(3)利用导数求极值的方法来解决此问题,由题意得()(]()ln 0,g x ax x x e =-∈,则()11ax g x a x x-'=-=,令()0g x '=,解得1x a =,通过对1a 是否在区间(]0,e 上进行分类讨论,可求得当10ea<<时,有()min 13g x g a ⎛⎫==⎪⎝⎭,满足条件,从而可求出实数a 的值.(1)当1a =时,()()2121121221x x x x f x x x x x⎛⎫-+ ⎪+-⎝⎭'=+-==. 2分因为函数()2ln f x x x x =+-的定义域为()0,+∞,所以当10,2x ⎛⎫∈ ⎪⎝⎭时,()0f x '…,当1,2x ⎡⎫∈+∞⎪⎢⎣⎭时,()0f x '….所以函数()f x 的单调递减区间为10,2⎛⎫ ⎪⎝⎭,单调递增区间为1,2⎡⎫+∞⎪⎢⎣⎭. 4分(2)()212120x ax f x x a x x+-'=+-=…在()1,2上恒成立. 令()221h x x ax =+-,有()()1020h h ⎧⎪⎨⎪⎩……, 6分得172a a -⎧⎪⎨-⎪⎩……,72a ∴-…. 8分(3)假设存在实数a ,使()(]()ln 0,g x ax x x e =-∈有最小值3,()11ax g x a x x-'=-=. 9分 当0a …时,()g x 在(]0,e 上单调递减, ()()min 13g x g e ae ∴==-=,4a e=(舍去); 10分 ②当10e a <<时,()g x 在10,a ⎛⎫ ⎪⎝⎭上单调递减,在1,e a ⎛⎫⎪⎝⎭上单调递增. ()min 11ln 3g x g a a ⎛⎫∴==+= ⎪⎝⎭,解得2a e =,满足条件; 12分③当1e a…时,()g x 在(]0,e 上单调递减, ()()min 13g x g e ae ∴==-=,4a e=(舍去). 13分综上,存在实数2a e =,使得当(]0,x e ∈时,()f x 有最小值3. 14分考点:1.导数性质;2.不等式求解;3.分类讨论.。
