第七章小结与思考(一)
苏科版2012-2013初一(下)备课组备课分工日期、章节明细表doc

樊新玲
许岑岑
第十、十一章综合复习
1
秦娟
陈尚高
期末总复习1
1
陈秀珍
王大勇
期末总复习2
1
江旭海
魏敏
期末总复习3
1
吴树荣
叶兴农
第19周
6月23~6月29
期末试卷评讲
1
江旭海
叶兴农
6月25、26、27、28期末考试
备注
6月30日放暑假,本学期共上课65天
说明:请每位老师提前一周备好课教案与配套课件
第八章小结与思考
2
秦娟
陈尚高
第6周
3月24~3月30
第九章从面积到乘法公式
2
3月27、28、29、30
小高考
9.1单项式乘单项式
1
许岑岑
樊新玲
9.2单项式乘多项式
1
许岑岑
樊新玲
9.3多项式乘多项式
1
许岑岑
樊新玲
第7周
3月31~4月6
9.4乘法公式(1)(2)(3)
3
叶兴农
吴树荣
4月4、5、6、7清明节
2
樊新玲
许岑岑
7.5三角形的内角和
3
陈尚高
秦娟
第3周
3月3~3月9
第七章复习
1
江旭海
魏敏
第七章小结与思考
2
江旭海
魏敏
第4周
3月10~3月16
第八章幂的运算
8.1同底数幂的乘法
1
毛云峰
郁胜军
8.2同底数幂的乘方
2
毛云峰
郁胜军
第5周
3月17~3月23
8.3同底数幂的除法
苏科版七年级上册数学:小结与思考》

还是过这一点能否分别画出这两条 直线的垂线吗?
a
a
B b
.M
A
b
Байду номын сангаас.D
C
M
温顾而知新
两种特殊 位置关系
图形
平行
A
Ba
C
Db
垂直
a
A.
C
A
B
. O
b
D
CB
D
定义
在同一平面内,不相交的 两条直线叫做平行线。
如果两条直线相交所成的四 个角中有一个角是直角,那 么这两条直线互相垂直。 点到直线的距离(垂线段最短)
A.大于acm
B.小于b cm
C.大于acm或小于b cm D.大于b cm且小于acm
课堂小结
通过本节课的复习,我对…有更深的了解。
升级挑战
如图,∠AOC与∠BOD都是直 角,且∠AOB:∠AOD=2:7。 求∠AOB的度数。
表示法
a∥b 或 AB∥CD
a⊥b 或 AB⊥CD
基本事实
过直线外一点有且只有一 条直线与这条直线平行。
过一点有且只有一条直线 与已知直线垂直。
想一想:
B
1.如右图,AC⊥BC,垂足为C,AC=6cm,
BC=8cm,AB=10cm,点A到BC所在直
线的距离是______cm,点A到 点B的距离
是 ____cm,点C到AB的距离是
cm.
C
A
2.在右图中,O是直线MN上的一点,∠1
和∠2满足什么条件时,能使OA⊥OB,
并说明理由。
M
N
你能用简便方法快速的画出过P点作
AP⊥ PQ,过Q点作BQ ⊥ PQ 吗?
第七章小结与思考(2)教学案
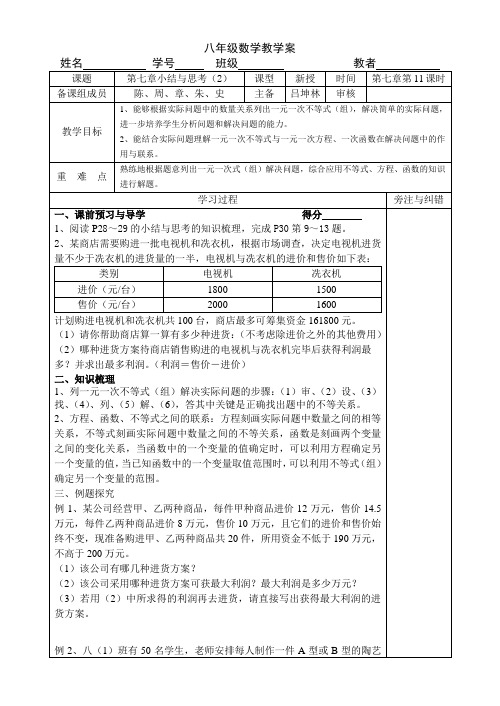
(1)求y与x函数关系式;
(2)如果这批农作物每天的需水量大于或等于4000kg,需要人工灌溉,那么应从第几天开始进行人工灌溉?
八年级数学教学案
姓名学号班级教者
课题
第七章小结与思考(2)
课型
新授
时间
第七章第11课时
备课组成员
陈、周、章、朱、史
主备
吕坤林
审核
教学目标
1、能够根据实际问题中的数量关系列出一元一次不等式(组),解决简单的实际问题,进一步培养学生分析问题和解决问题的能力。
2、能结合实际问题理解一元一次不等式与一元一次方程、一次函数在解决问题中的作用与联系。
四、巩固练习
课本P31第16、17题
《同步导学》P32第9题
教学后记:
0.4kg
1kg
(1)设制作B型陶艺品x件,求x的取值范围;
(2)请你根据学校现有材料,分别写出八(1)班制作A型和B型陶艺品的件数。
例3、“中国荷藕之乡乡”扬州宝应有着丰富的荷藕资源,某荷藕加工企业收购荷藕60吨,根据市场信息,如果对荷藕进行粗加工,每天可以加工8吨,每吨可获利1000元,如果对荷藕进行精加工,每天可加工0.5吨,每吨可获利5000元,由于受条件的限制,两种加工方式不能同时进行,为了保鲜的需要,该企业必须在一个月(30天)内将这批荷藕全部加工完毕,精加工的吨数x在什么范围内时,该企业加工这批荷藕的获利不低于8000元?
(3)若用(2)中所求得的利润再去进货,请直接写出获得最大利润的进货方案。
第七章第10课时锐角三角函数

第10课时 第七章 锐角三角函数——小结与思考(1)班级 学号 姓名知识要点:1.锐角三角函数的概念:2.特殊角的三角函数值:3. 锐角三角函数的性质:当角度在00~900间变化时,正弦、正切值随角度的增大(或减小)而 ,余弦值随角度的增大(或减小)而 . 0<sin α<1; 0<cos α<1; tan α>0. 4.解直角三角形的依据:(1)三边之间关系; (2)锐角之间的关系; (3)边、角之间的关系. 5、锐角α的正弦、余弦、正切之间的关系. 典型例题:例1、已知:如图,在Rt △ABC 中,∠C=900,若a=2b,求∠A 的锐角三角函数值例2、计算:(1)2·sin 2600-3·tan300-2·cos 2450(2)60tan 30tan 45cos 45tan 60cos 22020200+++例3、求下列各式中的锐角x :(1) 2cos x -1=0 (2) 3tan(x+100)-1=0例4、(1)Rt △ABC 中,∠C=900,BC=2, AC=6,解这个直角三角形.(2)Rt △ABC 中,∠C=900,∠B=300, c=10,解这个直角三角形.(3)如图,△ABC 中,∠B=300,∠C=450,AC=8,求BC 的长和△ABC 的面积.例5、某片绿地的形状如图所示,其中∠A=60°,AB ⊥BC ,CD ⊥AD ,•AB=•200m ,CD=100m ,求AD 、BC 的长(精确到1m1.732).例6、在矩形ABCD 中,AE ⊥BD 于E ,BE ∶ED=1∶3,试求tan ∠ADB 的值.课堂练习:1、已知角α为锐角,且23cos =α,则角α的大小为 .2、在ABC Rt ∆中,C ∠=90︒,AC=3,AB=5,则tan A 的值为 .3、在△ABC 中,,AB=AC=13,BC=10,则cos B 的值为 .4、已知角α为锐角,且3tan 4α=,则sin cos αα+= 。
九下第七章小结与思考

第7章 锐角三角函数复习[ 教案] 备课时间: 主备人:姓名_______________班级_________________学号_________________复习回顾:1.正弦,余弦,正切练习:如图,△ABC 中,AC=4,BC=3,BA=5,则sinA=______,sinB=______. cosA=______,cosB=______.tanA=______,tanB=______.2.三角函数的增减性正切值随着锐角的度数的增大而_____; 正弦值随着锐角的度数的增大而_____; 余弦值随着锐角的度数的增大而_____. 练习:已知:300<α<450,则:(1)sin α的取值范围:________; (2)cosα的取值范围:________; (3)tanα的取值范围:________. 3.特殊的三角函数的值练习计算:000245cos 30sin 460tan )1(-00030tan 130cos 130sin )2(++典型例题: 1. 如图,港口B 位于港口O 正西方向120海里外,小岛C 位于港口O 北偏西60°的方向.一艘科学考察船从港口O 出发,沿北偏东30°的OA 方向以20海里/小时的速度驶离港口O.同时一艘快艇从港口B 出发,沿北偏东30°的方向以60海里/小时的速度驶向小岛C ,在小岛C 用1小时装补给物资后,立即按原来的速度给考察船送去. (1) 快艇从港口B 到小岛C 需要多少时间?(2) 快艇从小岛C 出发后最少需要多少时间才能和考察船相遇?2.如图,A 、B 两地之间有一条河,原来从A 地到B 地需要经过DC ,沿折线A→D→C→B 到达,现在新建了桥EF ,可直接沿直线AB 从A 地到达B 地.已知BC=11km ,∠A=45°,∠B=37°.桥DC 和AB 平行,则现在从A 地到达B 地可比原来少走多少路程?(结果精确到0.1km)课后练习: 一、选择题:1.4121.已知在△ABC 中,∠C=90°,sinA=53,则tanB 的值为( ) A.34 B.54 C.45 D.432.如图,Rt △ABC 中,∠ACB=90°,CD ⊥AB 于点D.已知AC=5,BC=2,那么sin ∠ACD=( )A.552 B. 25 C. 35D. 323.△ABC 中,AB=AC=2,BC=B 的度数为( )A.30°B.60°C.90°D. 120° 二、填空题:4.在△ABC 中,∠A 、∠B 为锐角,且0)cos 21(1tan 2=-+-B A ,则∠C=________. 5.半径为10的圆的内接正六边形的边长为_____________. 6.一船向西航行,上午9时30分在小岛A 南偏东30°的B 处,已知AB 为60海里,上午11时整,船到达小岛A 的正南方向C则该船的航行速度为____________海里/时. 7.某中学升国旗时,李明同学站在离旗杆底部12m 该同学视线的仰角恰为45°,若他的双眼离地面1.5m ,则旗杆的高度是________m. 8.如图,一个小球由地面沿着坡度为i =1:2的坡面向上前进10米,此时小球距离地面的高度为_________米.9.如图,在菱形ABCD 中,DE ⊥AB ,垂足为E ,DE=6,sinA=53,则菱形ABCD 的面积是_____. 第8题 第9题 第10题 第11题 10. 如图,Rt △ABC 中,∠ACB=90°,∠A <∠B ,以AB 边上的中线CM 为折痕将△ACM 折叠,使点A 落在点D 处,如果CD 恰好与AB 垂直,则tanA=_______.11.四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图).如果小正方形面积为1,大正方形面积为25,直角三角形中较小的锐角为θ,那么=θcos . 三、计算题:E D C B A D CBA MDC BA12.002030sin 245cos 330tan 3-; 13. 20001)160(sin 60tan )14.3()21(-++---π四、解答题:14.Rt △ABC 中,∠C =900,∠A=60°,c=8,解这个直角三角形.15.某市在“旧城改造”中计划在市内一块如图所示的△ABC 空地上种植草皮以美化环境。
4.4小结与思考(1)

(2)每件服装的成本是多少?
(3)为保证不亏本,最多能打几折?
6. 旅游者游览某风景区,乘坐摩托艇顺水 而下,然后返回至登听处,已知水流速度为 2km/h,摩托艇在静水中的速度为18km/h, 为了使游览时间不超过3h,摩托艇驶出多 远就应掉头。
7、某同学在A、B两家超市发现他看中的随身听 的单价相同,书包单价也相同,随身听和书包单 价值和是452元,且随身听的单价比书包单价的 4倍少8元。 (1)求该同学看中的随身听和书包单价各是多 少元? (2)某一天该同学上街,恰好赶上商家促销, 超市A所有商品八折销售,超市B全场购物券满 100元返还购物券30元销售(不足100元不返还 券,购物券全场通用),但他只带了400元钱, 如果他只在一家购买看中的这两样商品,你能说 明他可以选择哪一家购买?若两家都可以,在哪 一家购买更省钱?
初中数学七年级上册 (苏科版)
4.4小结与思考(1)
(2)如果方程(m-1)x|m| + 2 =0是表示关于 x的一元一次方程,那么m= 。
例3 解下列方程
1. 学生问老师多少岁,老师说我像 你这么大 时你才2岁,你长到我这么大时,我就35岁了, 你算算老师、学生各多少岁? 2.用绳子量井深,把绳三折来量, 井外余绳 四尺,把绳四折来量,井外余绳一尺.求井深 及绳长.
8.一张长方形桌子可坐6人,按下图方式讲 桌子拼在一起。
。。。。。。
(1)一家餐厅有40张这样的长方形桌子,按照 上图方式拼成1张大桌子,共可坐多少人? (2)该家餐厅有n张这样的长方形桌子,按照 上图方式拼成1张大桌子,共可坐多少人?你有 哪些好的思考问题的方法?
3. 某商店以90元的相同价格卖出2件不同的 2件衬衫盈利了,还是亏损 了?
第七章小结与思考(1)教学案

旁注与纠错
一、课前预习与导学得分
1、解不等式,并把不等式的解集在数轴上表示出来:
≤-
2、若不等式组无解,确定a的取值范围。
3、不等式组解为x>y>0,化简︱a︱+︱3-a︱思路是什
么?
二、新课
(一)、复习与巩固
1、不等式6x-2≥3x+4的解集是_______;
2、不等式2<-3x<4的解集是_________;
7、若不等式组的整数解是关于x的方程 的根,求a的值
教学后记:
八年级数学教学案
姓名学号班级教者
课题
第七章小结与思考(1)
课型
新授
时间
第七章第10课时
备课组成员
陈、周、章、朱、史
主备
吕坤林
审核
教学目标
1、会列不等式;2、掌握不等式的两个性质并运用不等式的两个性质解一元一次不等式;3、会解一元一次不等式组,并会用数轴确定解集。
重难点
正确解出一元一次不等式(组),不等式两边都乘以(除以)同一个负数时不等号改变方向。
3、不等式1<2x-1<3的解集是_________;
4、设a<b,(1)的解集为_____(口诀是:___________)(2)的解集是______(口诀是:___________);
(3)的解集是_______(口诀是____________________);
(4)的解集ห้องสมุดไป่ตู้_____(口诀是________________)。
三、随堂演练
1、不等式组的解集是.
2、函数y=中,自变量 的取值范围是.
3、解下列不等式,并把它的解集在数轴上表示出来。
(1)2(x+1)-3(x+2)<0(2)<-2
第七章不等式小结与思考(一)导学案

第七章不等式小结与思考(二) (学案)学习过程:一、例题讨论:例1.已知关于x的不等式组21xxx a<⎧⎪>-⎨⎪<⎩无解,则a的取值范围是()A.a≤-1 B.-1<a<2 C.a≥2 D.a≤2例2、已知方程组331x y ax y a+=+⎧⎨-=-⎩的解是一对正数。
⑴求a的取值范围;⑵化简|2a+1|+|a-2|。
例3.七(2)班共有50名学生,老师安排每人制作一件A型或B型的陶艺品,学校现有甲种制作材料36kg,乙种制作材料29kg,制作A、B两种型号的陶艺品用料中下表:需甲种材料需乙种材料1件A型陶艺品0.9kg 0.3kg1件B型陶艺品0.4kg 1kg⑴设制作B型陶艺品x件,求x的取值范围。
⑵请你根据学校现有材料,分别写出七(2)班制作A型和B型陶艺品的件数。
二、课堂小结当堂检测1.关于x的不等式组1532223xxxx a+⎧>-⎪⎪⎨+⎪<+⎪⎩只有4个整数解,则a的取值范围是()A.-5≤a≤143-B.-5≤a<143-C.-5<a≤143-D.-5<a<143-2.若y=3x-2。
⑴求方程3x-2=0的解。
⑵求不等式3x-2≥0的解集。
⑶当y≤1时,求x的取值范围。
⑷当-1≤y≤1时,求x的取值范围。
⑸求图像与坐标轴围成的三角形的面积。
3.若干个苹果分给几个孩子,如果每人分3个,则余8个,每人分5个,则最后一人分得的数不足5个,问共有多少个孩子?多少个苹果?4.某煤矿现有100t煤炭要运往甲、乙两厂,通过了解获得甲、乙两厂的信息如下:厂别运费(元/t·km)路程(km)所需吨数(t)甲厂 1 150 不超过60乙厂 1.2 100 不超过80 要将100t煤炭全部运出,试写出总费用y(元)与运往甲厂x(t)煤炭之间的函数关系式。
如果你是该矿的矿主,请设计出合理的运送方案,使所需的总运费最低,并求出最低的总运费。
5.某学校去春游,若乘大客车,除一车坐8人外,其余每车均坐20人,若乘小客车,则除一车坐4人外,其余每车均坐12人,如果学生人数超过150人,且不超过250人,那么学生人数应是多少?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
sin A (3) tan A ; cos A
(4)sin A cos A 1.
2 2
α
三角函数
30°
1 2
3 2 3 3
45°
2 2
2 2
60°
3 2 1 2
sinα cosα tanα
1
3
1、计算:
(1) tan 60 4 sin 30 cos45
2 0 0
0
sin 30 1 (2) 0 0 1 cos30 tan30
4
A
基础训练:如图,△ABC中,AC=4,BC=3,
3 4 BA=5,则sinA=______,sinB=______. 5 5 4 3 cosA=______,cosB=______. B 5 5 c a 3 4 tanA=______,tanB=______. 4 C 3
b
A
(1)若∠A是锐角,则0<sinA<l,0<cosA<1 ; (2)若∠A+ ∠B=900, 则sinA=cosB ,cosA=sinB,tanA· tanB=1.
2、已知△ABC满足
3 12 sin A (cosB ) 0 2 2
0
则△ABC是______三角形.
正切值随着锐角的度数的增大而_____; 增大
正弦值随着锐角的度数的增大而_____; 增大
减小 余弦值随着锐角的度数的增大而_____.
1、比较大小: (1)sin250____sin430 (3)sin480____cos520
求∠B的度数以及边BC、AB的长.
16 3 , 3
8
今天你有什么收获?
请你谈谈对本节学习内容的 体会和感受.
例1.Rt△ABC中,∠C=90°,∠B=60°,两直角 边的和为14,求这个直角三角形的面积.
例2.如图,AC⊥BC,cos∠ADC=
4 , 5
∠B=30°AD=10,求 BD的长.
10 30°
1.Rt△ABC中,∠C=90°,∠A=30°,∠A、
∠B、∠C所对的边为a、b、c,则a:b:c=( )
A的对边 A的邻边 A的对边 斜边 A的邻边 斜边
a b a c b c
基础训练:如图,△ABC中,AC=4,BC=3,
3 4 BA=5,则sinA=______,sinB=______. 5 5 4 3 cosA=______,cosB=______. B 5 5 5 3 3 4 tanA=______,tanB=______. 4 C 3
B
c
A
a
b
C
如图(一),利用光线的平行和物体在地面的投影和物 体构成的两个直角三角形相似,从而求得物体的高度.
如图(二),我们可以利用 测角仪测出∠ECB的度数,用 皮尺量出CE的长度,而后按一 定的比例尺(例如1:500)画出图 形,进而求出物体的高度.
B
c
A
a
b
C
正切:tanA 三角函数 正弦:sinA 余弦:cosA
A.1:2:3 C.1: :2 3 B.1: 2 :3
D.1:2:3
2.在△ABC中,∠C=90°,AC=2.1cm, BC=2.8cm. 求:(1)△ABC的面积; (2)斜边AB的长;(3)高CD.
BD A2.8 C来自2.116 3 , 3.Rt△ABC中,∠C=90°,AC=8,∠A的平分线AD= 3
(2)cos70____cos80 (4)tan480____tan400
2、已知:300<α<450,则: (1)sin α的取值范围:________; (2)cosα的取值范围:________; (3)tanα的取值范围:________.
1、在直角三角形中,利用已知的元素求出所 有未知元素的过程,叫解直角三角形. 2、知道直角三角形中的2个元素(至少有一边), 可以求出其它三个元素.
