多元统计分析实验一
多元统计分析实验报告
第二部分:实验过程记录(可加页) (包括实验原始数据记录,实验现象记录,实验过程发现的问题
等) 操作步骤: 1、 执行“分析”—“比较均值”—“单因素方差分析” ; 2、 在弹出的单因素方差分析对话框中,将时期选为因子,将 X1、X2、X3、X4 选为因变量; 3、 单击“对比” ,选择“多项式” ,在后面的下拉菜单中选择“线性” ,然后继续; 4、 单击“两两比较” ,选择“LSD”和“S-N-K” ,显著性水平默认为 0.05,然后继续; 5、 单击“选项” ,选择“方差同质性检验”和“均值图” ,然后继续,点击“确定”后即可输出结果。
12
题目:研究者提出,随着时间的推移头骨尺寸会发生变化,这是外来移民与原住民人口民族融合的证据。表 6.13 是古埃及三个时期的男性头骨的四个观测值得观测数据,这是个观测变量是: X1=头骨最大的最大宽度 X2=头骨高度 X3=头骨底穴至齿槽的长度 X4=头骨鼻梁高度 对古埃及头骨数据构造单因子 MANOVA 表, a=0.05.并构造 95%联合置信区间来判断在三个时期中哪个分 令 量的均值发生了改变。同常的 MANOVA 假设对这些数据是不是合理的?请解释。 部分数据如下:
实验课程名称:多元统计分析-均值向量检验
实验项目名称 实 验 者 同 组 者
均值向量检验习题 均值向量检验习题 6.24
专业班级
实验成绩 实验成绩 组 别 年 月 日
实验日期
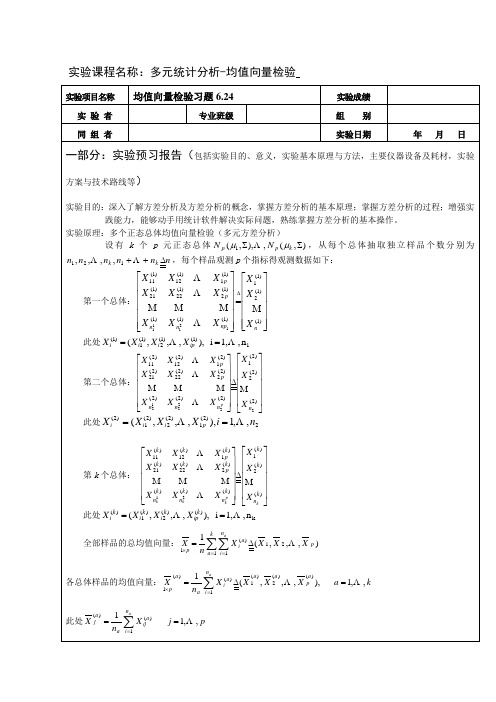
一部分:实验预习报告(包括实验目的、意义,实验基本原理与方法,主要仪器设备及耗材,实验
方案与技术路线等) 实验目的:深入了解方差分析及方差分析的概念,掌握方差分析的基本原理;掌握方差分析的过程;增强实 践能力,能够动手用统计软件解决实际问题,熟练掌握方差分析的基本操作。 实验原理:多个正态总体均值向量检验(多元方差分析) 设 有 k 个 p 元 正 态 总 体 N p ( µ1 , Σ), L , N p ( µ k , Σ) , 从 每 个 总 体 抽 取 独 立 样 品 个 数 分 别 为
多元统计分析 实验报告

多元统计分析实验报告1. 引言多元统计分析是一种用于研究多个变量之间关系的统计方法。
在实验中,我们使用了多元统计分析方法来探索一组数据中的变量之间的关系。
本报告将介绍我们的实验设计、数据收集和分析方法以及结果和讨论。
2. 实验设计为了进行多元统计分析,我们设计了一个实验,收集了一组相关变量的数据。
我们选择了X、Y和Z这三个变量作为我们的研究对象。
为了获得准确的结果,我们采用了以下实验设计:1.确定研究目的:我们的目标是探索X、Y和Z之间的关系,并确定它们之间是否存在任何相关性。
2.数据收集:我们通过调查问卷的方式收集了一组数据。
我们请参与者回答与X、Y和Z相关的问题,以获得关于这些变量的定量数据。
3.数据整理:在收集完数据后,我们将数据进行整理,将其转化为适合多元统计分析的格式。
我们使用Excel等工具进行数据整理和清洗。
4.数据验证:为了确保数据的准确性,我们对数据进行验证。
我们检查数据的有效性,比较数据之间的一致性,并排除任何异常值。
3. 数据分析在数据收集和整理完毕后,我们使用了一些常见的多元统计分析方法来分析我们的数据。
以下是我们使用的方法和步骤:1.描述统计分析:我们首先对数据进行了描述性统计分析。
我们计算了X、Y和Z的均值、标准差、最大值和最小值等。
这些统计量帮助我们了解数据的基本特征。
2.相关性分析:接下来,我们进行了相关性分析,以确定X、Y和Z之间是否存在相关关系。
我们计算了变量之间的相关系数,并绘制了相关系数矩阵。
这帮助我们确定变量之间的线性关系。
3.回归分析:为了更进一步地研究X、Y和Z之间的关系,我们进行了回归分析。
我们建立了一个多元回归模型,通过回归方程来预测因变量。
同时,我们还计算了回归系数和R方值,以评估模型的拟合度和预测能力。
4. 结果和讨论根据我们的实验设计和数据分析,我们得出了以下结果和讨论:1.描述统计分析结果显示,X的平均值为x,标准差为s;Y的平均值为y,标准差为s;Z的平均值为z,标准差为s。
(整理)多元统计分析上机实验.

多元统计分析上机实验指导第一部分 SPSS软件基本操作当用户安装SPSS软件后,点击快捷图标,将会出现以下界面:图1.1 启动SPSS后出现的对话框对话框包括一个六选一单选对话框和一个复选对话框,其内容为:●Run the tutorial 运行操作指南;●Type in data 输入数据选项,建立新的数据集时可选择此项;●Run an existing query 运行一个已经存在的数据文件选项;●Create new query using Database Wizard 用数据库处理工具建立新文件;●Open an existing date source 打开一个已经存在的数据文件;●Open another type of file 打开其他类型的文件。
●Don’t show this dialog in the future 是一复选对话框,选中该复选项后,下次启动SPSS时将不会显示对话框,直接显示数据编辑窗口。
如果只是利用该软件做一般性的统计分析,不做高级开发工作,可以在“Don’t show this dialog in the future”左方的小方块里打钩,以后启动SPSS时将不会显示对话框,直接显示数据编辑窗口。
§1.1 数据文件的建立SPSS 软件包的数据编辑主窗口类似于EXCEL ,数据文件的建立就是在数据编辑窗口中完成的。
数据编辑窗口可以显示两张表,分别是Data View (见图1.2)和Variable View (见图1.3),通过点击下端的2个同名窗口标签按钮实现相互切换。
数据编辑区是SPSS 的主要操作窗口,是一个二维平面表格,用于对数据进行各种编辑;标尺栏由纵向标尺栏和横向标尺栏,横向标尺栏显示数据变量,纵向标尺栏显示数据顺序(如时间顺序)。
Data View 表可以直接输入观测数据值或存放数据,表的左端列边框显示观测个体的序号,最上端行边框显示变量名。
多元统计分析-实验报告-计算协方差矩阵-相关矩阵-SAS

(一)院系:数学与统计学学院专业:__ _统计学年级: 2009级课程名称:统计分析学号:姓名:指导教师:2012年 4月 28 日(一)实验名称1.编程计算样本协方差矩阵和相关系数矩阵;2.多元方差分析MANOVA。
(二)实验目的1.学习编制sas程序计算样本协方差矩阵和相关系数矩阵;2.对数据进行多元方差分析。
(三)实验数据第一题:第二题:(四)实验内容1.打开SAS软件并导入数据;2.编制程序计算样本协方差矩阵和相关系数矩阵;3.编制sas程序对数据进行多元方差分析;4.根据实验结果解决问题,并撰写实验报告;(五)实验体会(结论、评价与建议等)第一题:程序如下:proc corr data=sasuser.shan cov;proc corr data=sasuser.shan nosimple cov;with x3 x4;partial x1 x2;run;结果如下:(1)协方差矩阵(2)相关系数矩阵第二题:程序如下:proc anova data=sasuser.huang; class kind; model x1-x4=kind; manova h=kind; run;结果如下:(1)分组水平信息(2)x1、x2、x3、x4的方差分析(3)多元方差分析根据多元分析结果,p指小于0.05,表明在0.05的显著水平下,四个变量有显著差异。
(注:文档可能无法思考全面,请浏览后下载,供参考。
可复制、编制,期待你的好评与关注!)。
多元统计分析实验报告计算协方差矩阵相关矩阵SAS

多元统计分析实验报告计算协方差矩阵相关矩阵SAS实验目的:通过对多元统计分析中的协方差矩阵和相关矩阵的计算,探究变量之间的相关性,并使用SAS进行实际操作。
实验步骤:1.数据准备:选择一个数据集,例如学生的成绩数据,包括数学成绩、语文成绩和英语成绩。
2.数据整理:将数据转化为矩阵形式,每一行代表一个学生,每一列代表一个变量(即成绩),记为X。
3. 计算协方差矩阵:根据公式计算协方差矩阵C,其中元素Cij表示变量Xi和Xj之间的协方差。
计算公式为Cij = cov(Xi, Xj) = E((Xi - u_i)(Xj - u_j)),其中E为期望值,u_i和u_j分别是变量Xi和Xj的均值。
4. 计算相关矩阵:根据协方差矩阵计算相关矩阵R,其中元素Rij表示变量Xi和Xj之间的相关性。
计算公式为Rij = cov(Xi, Xj) / (sigma_i * sigma_j),其中sigma_i和sigma_j分别是变量Xi和Xj的标准差。
5.使用SAS进行实际操作:使用SAS软件导入数据集,并使用PROCCORR和PROCPRINT命令进行协方差矩阵和相关矩阵的计算和输出。
实验结果:通过计算协方差矩阵和相关矩阵,可以得到变量之间的相关性信息。
协方差矩阵的对角线上的元素表示每个变量的方差,非对角线上的元素表示不同变量之间的协方差。
相关矩阵的对角线上的元素都是1,表示每个变量与自身的相关性为1,非对角线上的元素表示不同变量之间的相关性。
使用SAS进行实际操作后,我们可以得到一个包含协方差矩阵和相关矩阵的输出表格。
该表格可以帮助我们更直观地理解变量之间的相关性情况,从而为后续的统计分析提供参考。
实验总结:通过本次多元统计分析实验,我们了解了协方差矩阵和相关矩阵的计算方法,并使用SAS软件进行实际操作。
这些矩阵可以帮助我们评估变量之间的相关性,为后续的统计分析提供重要的基础信息。
在实际应用中,我们可以根据协方差矩阵和相关矩阵的结果,选择合适的统计方法和模型,并做出恰当的推断和决策。
多元统计分析实验教学上机指导书

《多元统计分析》实验教学上机指导书(共70页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--《多元统计分析》实验教学上机指导书数学与统计学学院信息与计算科学教研室第一章聚类分析一、实验目的与要求1.通过上机操作使学生掌握系统聚类分析方法在SAS和SPSS软件中的实现,熟悉系统聚类的用途和操作方法,了解各种距离,能按要求将样本进行分类;2.要求学生重点掌握该方法的用途,能正确解释软件处理的结果,尤其是冰柱图和树形图结果的解释;3.要求学生阅读一定数量的文献资料,掌握系统聚类分析方法在写作中的应用。
二、实验内容与步骤SAS部分(一)SAS程序语言简介SAS系统强大的数据管理能力、计算能力、分析能力依赖于作为其基础的SAS语言。
SAS语言是一个专用的数据管理与分析语言,它的数据管理功能类似于数据库语言(如FoxPro),但又添加了一般高级程序设计语言的许多成分(如分支、循环、数组),以及专用于数据管理、统计计算的函数。
SAS系统的数据管理、报表、图形、统计分析等功能都可以用SAS语言程序来调用,只要指定要完成的任务就可以由SAS系统按照预先设计好的程序去进行,所以SAS 语言和FoxPro等一样是一种第四代计算机语言。
SAS语言有它自己的对变量、常量、表达式的一系列规定,有一系列标准函数,有它自己的语句、语法,可以按一定规则构成SAS程序。
SAS语言程序由数据步(DATA步)和过程步(PROC步)组成。
数据步用来生成数据集、计算、整理数据,过程步用来对数据进行分析、报告。
SAS语言的基本单位是语句,每个SAS语句一般由一个关键字(如DATA,PROC,INPUT,CARDS,BY)开头,包含SAS名字、特殊字符、运算符等,以分号结束。
SAS关键字是用于SAS语句开头的特殊单词。
SAS名字在SAS程序中标识各种SAS成分,如变量、数据集、数据库,等等。
SAS 名字由1到8个字母、数字、下划线组成,第一个字符必须是字母或下划线。
《多元统计分析分析》实验报告

《多元统计分析分析》实验报告2012 年月日学院经贸学院姓名学号实验实验成绩名称一、实验目的(一)利用SPSS对主成分回归进行计算机实现.(二)要求熟练软件操作步骤,重点掌握对软件处理结果的解释.二、实验内容以教材例题7.2为实验对象,应用软件对例题进行操作练习,以掌握多元统计分析方法的应用三、实验步骤(以文字列出软件操作过程并附上操作截图)1、数据文件的输入或建立:(文件名以学号或姓名命名)将表7.2数据输入spss:点击“文件”下“新建”——“数据”见图1:图1点击左下角“变量视图”首先定义变量名称及类型:见图2:图2:然后点击“数据视图”进行数据输入(图3):图3完成数据输入2、具体操作分析过程:(1)首先做因变量Y与自变量X1-X3的普通线性回归:在变量视图下点击“分析”菜单,选择“回归”-“线性”(图4):图4将因变量Y调入“因变量”栏,将x1-x3调入“自变量”栏(图5):然后选择相关要输出的结果:①点击右上角“统计量(s)”:“回归系数”下选择“估计”;“残差”下选择“D.W”;在右上角选择输出“模型拟合度”、“部分相关和偏相关”“共线性诊断”(后两项是做多重共线性检验)。
选完后点击“继续”(见图6)②如果需要对因变量与残差进行图形分析则需要在“绘制”下选择相关项目(图7),一般不需要则继续③如果需要将相关结果如因变量预测值、残差等保存则点击“保存”(图8),选择要保存的项目④如果是逐步回归法或者设置不带常数项的回归模型则点击“选项”(图9)其他选项按软件默认。
最后点击“确定”,运行线性回归,输出相关结果(见表1-3)图5 图6图7图8图9回归分析输出结果:的协差阵也就是相关阵进行分解做因子分析或主成分分析),如果不需要对变量做标准化处理就选“协方差矩阵”;“输出”中的两项都选,要求输出没有旋转的因子解(主成分分析必选项)和碎石图(用图形决定提取的主成分或因子的个数);“抽取“下,默认的是基于特征值(大于1表示提取的因子或主成分至少代表1个单位标准差的变量信息,因为标准化后的变量方差为1,因子或者主成分作为提取的综合变量应该至少代表1个变量的信息),也可以自选提取的因子个数(即第二项),本例中做主成分回归,选择提取全部可能的3个主成分,所以自选个数填3。
多元统计分析多元统计分析1

多元统计分析是一门具有很强应用性的课程;它在自然科学 和社会科学等各个领域中得到广泛的应用;它包括了很多非常有 用的数据处理方法.
3.变量间的相互联系
(1) 相互依赖关系:分析一个或几个变量的变化是否依赖于另一些变 量的变化?如果是,建立变量间的定量关系式,并用于预测或控制---回 归分析.
(2) 变量间的相互关系: 分析两组变量间的相互关系---典型相关分 析等.
(3)两组变量间的相互依赖关系---偏最小二乘回归分析.
4.多元数据的统计推断 参数估计和假设检验问题.特别是多元正态分布的均值向量和协 方差阵的估计和假设检验等问题。
在实际问题中,很多随机现象涉及到的变量不只一个,而经常是 多个变量,而且这些变量间又存在一定的联系。
一、多元统计分析研究的对象和内容
我们先看一个例子,考察学生的学习情况时,就需了解学生在几 个主要科目的考试成绩。下表给出从中学某年级随机抽取的12名学生 中5门主要课程期末考试成绩。
序号 1 2 3 4 5 6 7 8 9 10 11 12
之后R.A.Fisher、H.Hotelling、S.N.Roy、许宝騄等人作了一系列 奠基的工作,使多元统计分析在理论上得到迅速的发展,在许多领域中 也有了实际应用.二十世纪50年代中期,随着电子计算机的出现和发展, 使得多元统计分析在地质、气象、医学、社会学等方面得到广泛的应 用.60年代通过应用和实践又完善和发展了理论,由于新理论、新方法的 不断出现又促使它的应用范围更加扩大.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
b.该统计量是F的上限,它产生了一个关于显著性级别的下限。
由上面的表可知,在多变量检验中,sig均小于0.05,即均值有显著性差异。
由成对比较的表格可知,对于儿童抚养比,东部和西部有显著性差异,对于废水排放量,东部和西部,中部和东部均有显著性检验。
三、指导教师评语及成绩:
评语:
成绩:指导教师签名:
人均S02排放量
.198
31
.003
.817
31
.000
*.这是真实显著水平的下限。
a. Lilliefors显著水平修正
因为样本量只有几十个属于小样本,选择sw统计量,可知,老年抚养比,儿童抚养比以及废水排放量属于正态分布,其余皆不属于正态分布。
2.在分析一般线性模型因变量为老年抚养比,儿童抚养比,人均废水排放量(即为上列sig大于0.05的变量)固定因子为地带两两比较:两两比较检验为地带选项:显示均值为地带,在比较主效应和方差齐性检验前面打勾确定,可以得到:
9.146
西部
-3.654
2.341
.130
-8.449
1.141
人均废水排放量
东部
西部
26.307*
5.212
.000
15.630
36.983
中部
20.262*
5.802
.002
8.377
32.146
西部
东部
-26.307*
5.212
.000
-36.983
-15.630
中部
-6.045
5.699
.298
批阅日期:
浙江财经大学东方学院
实验报告
项目名称实验一
所属课程名称多元回归统计
项目类型综合
实验(实训)日期2015/3/26
班级12统计2班
学号1220430219
姓名林俐
指导教师彭武珍
浙江财经学院东方学院教务部制
一、实验(实训)概述:
【目的及要求】
二、实验(实训)内容:
1.对上述指标数据进行正态分布检验,通过分析描述统计探索将所需要研究的指标放入因变量中绘制带检验的正态图,如图所示:
3.000
26.000
.000
Roy的最大根
82.500
714.996b
3.000
26.000
.000
地带
Pillai的跟踪
.562
3.520
6.000
54.000
.005
Wilks的Lambda
.452
4.219b
6.000
52.000
.002
Hotelling的跟踪
1.178
4.910
6.000
结果如下:
正态性检验
Kolmogorov-Smirnova
Shapiro-Wilk
统计量
df
Sig.
统计量
df
Sig.
人均GDP
.364
31
.000
.638
31
.000
第二产业比重
.176
31
.015
.835
31
.000
第三产业比重
.185
31
.008
.791
31
.000
人均消费支出
.253
31
.000
1.096
.700
-1.818
2.671
中部
-.169
1.220
.891
-2.668
2.329
西部
东部
-.427
1.096
.700
-2.671
1.818
中部
-.596
1.198
.623
-3.050
1.859
中部
东部
.169
1.220
.891
-2.329
2.668
西部
.596
1.198
.623
-1.859
主体间因子
值标签
N
地带
东部
东部
11
西部
西部
12
中部
中部
8
多变量检验a
效应
值
F
假设df
误差df
Sig.
截距
Pillai的跟踪
.988
714.996b
3.000
26.000
.000
Wilks的Lambda
.012
714.996b
3.000
26.000
.000
Hotelling的跟踪
82.500
714.996b
.562
3.520
6.000
54.000
.005
Wilks的lambda
.452
4.219a
6.000
52.000
.002
Hotelling的跟踪
1.178
4.910
6.000
50.000
.001
Roy的最大根
1.150
10.354b
3.000
27.000
.000
每个F检验地带的多变量效应。这些检验基于估算边际均值间的线性独立成对比较。
-17.719
5.629
中部
东部
-20.262*
5.802
.002-3ຫໍສະໝຸດ .146-8.377西部
6.045
5.699
.298
-5.629
17.719
基于估算边际均值
*.均值差值在.05级别上较显著。
b.对多个比较的调整:最不显著差别(相当于未作调整)。
多变量检验
值
F
假设df
误差df
Sig.
Pillai的跟踪
3.050
儿童抚养比
东部
西部
-7.919*
2.141
.001
-12.304
-3.534
中部
-4.265
2.383
.084
-9.146
.616
西部
东部
7.919*
2.141
.001
3.534
12.304
中部
3.654
2.341
.130
-1.141
8.449
中部
东部
4.265
2.383
.084
-.616
50.000
.001
Roy的最大根
1.150
10.354c
3.000
27.000
.000
a.设计:截距+地带
b.精确统计量
c.该统计量是F的上限,它产生了一个关于显著性级别的下限。
成对比较
因变量
(I)地带
(J)地带
均值差值(I-J)
标准误差
Sig.b
差分的95%置信区间b
下限
上限
老年抚养比
东部
西部
.427
.800
31
.000
老年抚养比
.121
31
.200*
.972
31
.576
儿童抚养比
.107
31
.200*
.963
31
.349
15岁以上人口文盲率
.276
31
.000
.493
31
.000
参与医疗保险人数占总人数比
.189
31
.007
.863
31
.001
人均废水排放量
.163
31
.035
.942
31
.091
