2019年高考数学压轴题专题01嵌套函数问题(解析版)

2．已知函数 y f ( x) 是定义域为 R 的偶函数 . 当 x 0 时， f (x)
5 sin( x) (0
42 ( 1 )x 1 (x 4
x 1)
，若关于
1)
x 的方程 [ f (x)]2 af (x) b 0（ a, b R ） , 有且仅有 6 个不同实数根，则实数 a 的取值范围是
_____.
【答案】 ( 5 , 9 ) ( 9 , 1)
24
4
【解析】作出 f (x)
5 sin( x) (0 x 1)
42
的图象如下， 又∵函数 y
( 1)x 1 (x 1)
4
f ( x) 是定义域为 R 的偶函数，
且关于 x 的方程 [ f ( x)] 2 af ( x) b 0 ， a, b R 有且仅有 6 个不同实数根，
【解析】由题意可得 y 0=sinx 0∈[-1 ， 1] ， f （ y 0） =ey0 +y0 -a ， ∵曲线 y=sinx 上存在点（ x0， y0）使得 f （f （ y0））=y0，∴存在 y 0∈ [0 ， 1] ，使 f （y 0） =y0 成立， 即 f （ x ） =x 在 [0 ， 1] 上有解，即 e x+x-x 2=a 在 [0 ，1] 上有解． 令 g（ x ） =ex+x-x 2，则 a 为 g（ x）在 [0 ， 1] 上的值域． ∵当 x∈ [0 ， 1] 时， g′（ x ）=ex+1-2x ＞0，故函数 g（ x）在 [0 ， 1] 上是增函数， 故 g（ 0）≤ g（ x）≤ g（ 1），即 1≤ a≤e， 故答案为： [1 ， e] ．
专题 01 嵌套函数问题
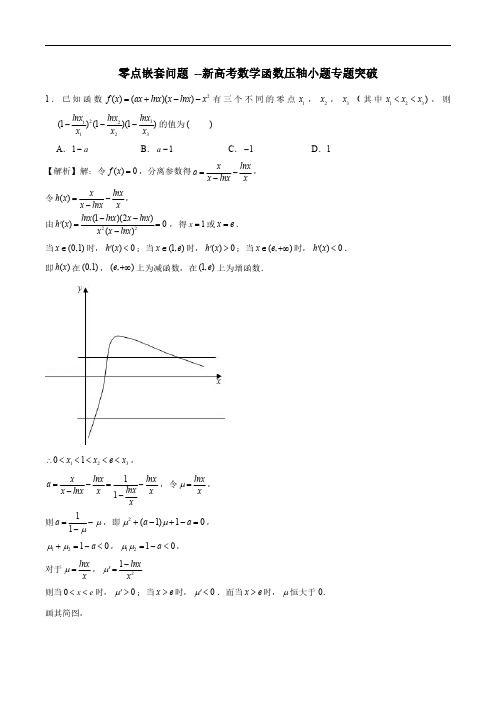
嵌套函数，就是指在某些情况下，您可能需要将某函数作为另一函数的参数使用，这一函数就是嵌套
函数 . 一般地，对于定义在区间 D 上的函数 y f (x) （ 1）若存在 x0 D , 使得 f (x0) x0, 则称 x0 是 函数 y f (x) 的一阶不动点 , 简称不动点； （2）若存在 x0 D , 使 f ( f ( x0)) x0 , 则称 x0 是函数 y f ( x) 的二阶不动点 , 简称稳定点 .
典例 3 已知函数 f x
x2 2ax a 1,x 0,
{
gx
ln x , x 0,
x2 1 2a . 若函数 y f g x 有 4 个
零点，则实数 a 的取值范围是 ________.
【答案】
51 ,1
1,
2
【解析】令 f t 0,t g x
当 1 a 0 时 f t 有两个零点 t1 1,t2 1，需 1 2a 1 a 1 当 1 a=0 时 f x 有三个零点， t1 1,t2 0, t3 =2 ， 1 2a
；
4
若 a2 x2 ax a 1 0 有实根且实根是方程 ax2 x 1 0 的根，则由方 ax2 x 1 0 ，
得 a2 x2 ax a ，代入 a2 x2 ax a 1 0 ，有 2ax 1 0 . 由此解得 x
1
，
2a
再代入得 1
1
3
1 0 ，由此 a ，故 a 的取值范围是
4a 2a
4
13 ,
.
44
1
（ 3）由题意： x0 是函数的稳定点 , 则 f ( f ( x0 )) x0 ，
① 若 f ( x0 )
x f ( x) 0 ，
是 R 上的单调增函数， [来源: 学 _科_网]
则 f ( f ( x0 )) f ( x0 ) ，所以 x0 f (x0) ，矛盾 .
② 若 x0 f (x0 ) ， f ( x) 是 R 上的单调增函数， 则 f ( x0 ) f ( f ( x0 )) ，所以 f ( x0 ) x0 ，矛盾
个零点，舍；
当 1 a 0 时，由于 1 2a 1
1 所以函数 y f g x 有 5
所以
4a2 4a 4 0 ，且 a a2 a 1 1 2a ，所以 5-1 a 1
2
2
综上实数 a 的取值范围是
51 ,1
1,
2
【名师指点】求解复合方程问题时，往往把方程
f [ g( x)] 0 分解为 f (t) 0 和 g (x) t 处理，先从方
【答案】 3
【解析】函数 f x
x3 ax2 bx c 有极值点 x1 ， x2 ，说明方程 f '( x) 3x2 2ax b 0的两根
2
为 x1 ， x2 ，∴方程 3 f x
2af x b 0 的解为 f (x) x1 或 f ( x) x2 ，若 x1 x2 ，即 x1 是极
大 值 点 ， x 2 是 极 小 值 点 ， 由 于 f x1 x1 ， ∴ x1 是 极 大 值 ， f ( x ) x1 有 两 解 ， x1 x2 ，
2 的两个不同的根为 － 1 和 2. 当 | d| ＜ 2 时， 因为 f ( － 1) －d＝ f (2) －d＝ 2－ d＞ 0， f (1) － d＝ f ( － 2) － d＝－ 2－ d＜0， 所以 － 2，－ 1,1,2 都不是 f ( x) ＝ d 的根．由 (1) 知 f ′ ( x) ＝3( x＋ 1)( x－ 1) ． ①当 x∈ (2 ， ＋∞ ) 时， f ′ ( x) ＞ 0， 于是 f ( x) 是单调增 函数 ， 从而 f ( x) ＞ f (2) ＝ 2， 此时 f ( x) ＝ d 无实根 ． 同理 ， f ( x) ＝ d 在( －∞ ，－ 2) 上无实根 ． ②当 x∈ (1,2) 时， f ′ ( x) ＞ 0， 于是 f ( x) 是单调增函数 ，又 f (1) － d＜ 0， f (2) － d＞0， y＝f ( x) － d 的 图象不间断 ， 所以 f ( x) ＝ d 在 (1,2) 内有唯一实根 ． 同理 ， f ( x) ＝d 在 ( － 2，－ 1) 内有唯一实根 ． ③当 x∈ ( － 1,1) 时， f ′ ( x) ＜ 0，故 f ( x) 是单调减函数 ，又 f ( － 1) － d＞ 0，f (1) －d＜ 0， y＝ f ( x) － d 的图象不间断 ， 所以 f ( x) ＝d 在 ( － 1,1) 内有唯一实根 ． 由上可知 ：当 | d| ＝2 时， f ( x) ＝ d 有两个不同的根 x1， x2 满足 | x1| ＝ 1，| x2| ＝ 2； 当 | d| ＜ 2 时， f ( x) ＝ d 有三个不同的根 x3， x4， x5 满足 | xi | ＜ 2， i ＝3,4,5.
f ( x) x2 f (x1) 只有一解，∴此时只有 3解，若 x1 x2 ，即 x1 是极小值点， x2 是极大值点，由于
f x1 x1 ，∴ x1 是极小值， f ( x) x1有 2 解， x1 x2 ， f (x) x2 f (x1) 只有一解， ∴此时只有 3
解.
类型三 嵌套函数中参数问题
明你的结论 .
【答案】没有 . f ( x) x ax2 (b 1)x c 0 无实数根，
(b 1)2 4ac 0 .
f ( f (x )) x 0 即为 a (ax 2 bx c)2 b( ax2 bx c) c x 0 ， a (ax2 bx c)2 ax2 ax2 b(ax2 bx c) c x 0 ， a (ax2 bx c x)(ax 2 bx c x) (b 1)ax2 ( b2 1)x c(b 1) 零点 ． 当 | c| ＝ 2 时， f ( t ) ＝ c 有两 个根 t 1， t 2 满足 | t 1| ＝ 1， | t 2| ＝ 2，而 f ( x) ＝ t 1 有三个不同的根 ， f ( x) ＝ t 2 有两个不同的根 ，故 y＝ h( x) 有 5 个零点 ． 当 | c| ＜ 2 时， f ( t ) ＝ c 有三个不同的根 t 3， t 4， t 5 满足 | t i | ＜2， i ＝ 3,4,5 ，而 f ( x) ＝ t i ( i ＝ 3,4,5) 有 三个不同的根 ，故 y＝ h( x) 有 9 个零点 ． 综上可知 ，当 | c| ＝2 时， 函数 y＝ h( x) 有 5 个零点 ；当 | c| ＜ 2 时， 函数 y＝h( x) 有 9 个零点 ． 4. 已知函数 f ( x) ax2 bx c (a 0) ，且 f ( x) x 没有实数根， f ( f ( x)) x 是 否有实数根？并证
若是，请证明你的结论；若不是，请说明的理由
.
【答案】（ 1）见解析（ 2）
13 , （ 3）是
44
【解析】解： （ 1）若 A ，则 A B 显然成立；若 A ，设 t A ，
f t t, f f t f t t ， t B ，故 A B .
（2） A
, ax 2 1 x 有实根， a
1 .又 A
B ，所以 a ax 2
∴ x2
ax b
0 的两根分别为 x1
5 ， 1 x2
5 或0
x1
1 ， 1 x2
5
，
4
4
4
由韦 达定理可得 x1 x2
a ，若 x1
5 ,1 x2
59
，则
5
5
a ，即
a
9
，
4
44
2
2
4
3
若0
x1 1，1 x2
5 ，则 1
4
9
9
a ，即
a
4
4
1 ，从而可知
5 a
2
99
或
a 1；
44
3．已知 a， b 是实数， 1 和 1是函数 f ( x) x3 ax2 bx 的两个极值点． （ 1）求 a 和 b 的值； （ 2）设函数 g( x) 的导函数 g ( x) f ( x) 2 ，求 g ( x) 的极值点； （ 3）设 h( x) f ( f (x)) c ，其中 c [ 2 ，2] ，求函数 y h(x) 的零点个数． 【答案】 (1) a＝ 0，b＝－ 3. (2) － 2. (3) 9 ． 【解析】 解：(1) 由题设知 f ′ ( x) ＝ 3x2＋ 2ax＋ b，且 f ′ ( － 1) ＝ 3－ 2a＋b＝ 0，f ′ (1) ＝ 3＋2a＋ b＝ 0， 解得 a＝ 0， b＝－ 3. ( 2) 由 (1) 知 f ( x) ＝ x3－3x. 因为 f ( x) ＋ 2＝( x－ 1) 2( x＋ 2) ，所以 g′ ( x) ＝ 0 的根为 x1＝ x2＝ 1，x3＝－ 2， 于是函数 g( x) 的极值点只可能是 1 或－ 2. 当 x＜－ 2 时， g′ ( x) ＜ 0；当－ 2＜ x＜ 1 时， g′ ( x) ＞ 0，故－ 2 是 g( x) 的极值点 ． 当－ 2＜ x＜1 或 x＞1 时， g′( x) ＞ 0，故 1 不是 g( x) 的极值点 ． 所以 g( x) 的极值点为 － 2. (3) 令 f ( x) ＝ t ，则 h( x) ＝ f ( t ) － c. 先讨论关于 x 的方程 f ( x) ＝ d 根的情况 ，d∈ [ － 2,2] ． 当 | d| ＝ 2 时，由 (2) 可知 ，f ( x) ＝－ 2 的两个不同的根为 1 和－ 2， 注意到 f ( x) 是奇函数 ，所以 f ( x) ＝