简单数阵图(精选.)
简单数阵图

简单数阵图一、知识点:一些数按照一定的规则,填在某一特定图形的规定位置上,这种图形,我们称它为“数阵图”,数阵图的种类繁多,绚丽多彩,这里只向大家介绍三种数阵图,即辐射型数阵图、封闭型数阵图和复合型数阵图。
在解答这类问题时,要善于确定所求的和与关键数字间的关系式,用试验的方法,找到相等的和与关键数字:要会对基本解中的数进行适当调整,得到其他的解,从而培养自己的观察能力,思维的灵活性和严密性。
二、典例剖析:1.辐射型数阵:辐射型数阵图只有一个重叠数,重叠次数是“直线条数”-1,即m-1。
对于辐射型数阵图,有已知各数之和+重叠数×重叠次数=直线上各数之和×直线条数。
由此得到:(1)若已知每条直线上各数之和,则重叠数等于(直线上各数之和×直线条数-已知各数之和)÷重叠次数。
(2)若已知重叠数,则直线上各数之和等于(已知各数之和+重叠数×重叠次数)÷直线条数。
(3)若重叠数与每条直线上的各数之和都不知道,则要从重叠数的可能取值分析讨论。
例1:把1~5这五个数分别填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于9。
同学们可能会觉得这道题太容易了,七拼八凑就写出了右上图的答案,可是却搞不清其中的道理。
下面我们就一起来分析其中的道理,只有弄懂其中的道理,才可能解出复杂巧妙的数阵问题。
分析与解:中间方格中的数很特殊,横行的三个数有它,竖列的三个数也有它,我们把它叫做“重叠数”。
也就是说,横行的三个数之和加上竖列的三个数之和,只有重叠数被加了两次,即重叠了一次,其余各数均被加了一次。
因为横行的三个数之和与竖列的三个数之和都等于9,所以(1+2+3+4+5)+重叠数=9+9,重叠数=(9+9)-(1+2+3+4+5)=3。
重叠数求出来了,其余各数就好填了(见上图)。
随堂练习:1、将2~8这7个数分别填在下图中的圆圈内,使每条线段上三个圆圈内数的和相等.2、把1~9这9个数字,分别填入下图的各圆圈内,使每条线上5个数的和相等.2、封闭型数阵:例2:将1~6分别填在图中,使每条边上的三个○内的数的和都等于9.分析:因为 1+2+3+4+5+6 = 21 ,而每条边上的三个数的和为9,则三条边上的和为 9×3 = 27 , 27-21 = 6 ,这个 6 就是由于三个顶点都被重复算了一次。
四年级下数学奥数-有趣的数阵图 全国通用( 17 张)

4
6
B3
5
C1
2~9填入左下图的八个○中,使得每条边上的三个数之和都等 于18。
4 A
5
9 B
四条边数字总和: 4×18=72
2-9九数之和:
6
2 2+3+4+5+6+7+8+9=44
A+B+C+D=72-44=28
C
3
D 故只能选,
8
7
4+9+8+7=28
将1~8这八个数分别填入右图的○里,使每条边上的三个数之 和都等于15。
6 31 5 4 72
将1-6这六个数字填入下图的圆圈中,使每个大 圆圈上4个数字之和为14。
3
1
2
4
6
5
把2~7这六个数填入右上图的○里,使每个圆 圈上的四个数之和都等于18。
将1、2、3、4、5、6填在下图中,使每条边上三个数之和等于9。
A:(48-45)÷3=1
练 1-9一数练之:和将:11~+27+入3+下4图+5的+6○+7内=,28使得每条边上的三个数字之6和都等于12。 4
横行、竖行五数和:24+24=48
7
8
9
四条线数之和: 12×4=48 1-9数之和:
1+2+3+4+5+6+7+8+9=45 A:(48-45)÷3=1 剩下的数字平均分成四组, 每组数字之和12-1=11 所以应为: 2+9、3+8、4+7、5+6。
将2-10这九个数填入下图圆圈内,使每条线上三个数字相加之和为 22.
二年级奥数数阵图
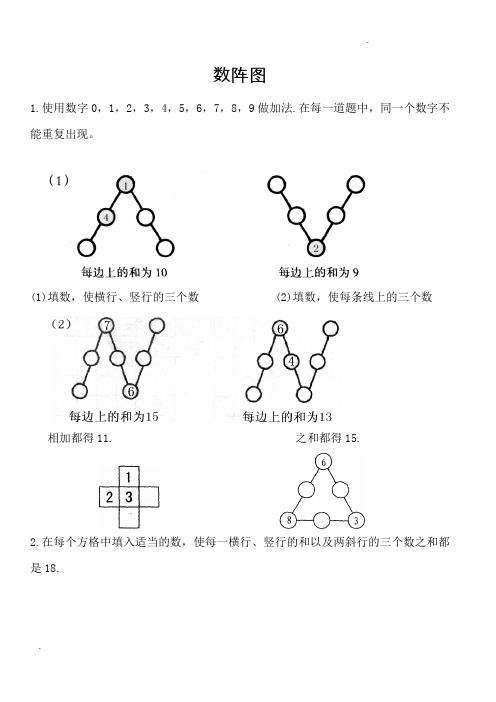
数阵图1.使用数字0,1,2,3,4,5,6,7,8,9做加法.在每一道题中,同一个数字不能重复出现。
(1)填数,使横行、竖行的三个数 (2)填数,使每条线上的三个数相加都得11. 之和都得15.2.在每个方格中填入适当的数,使每一横行、竖行的和以及两斜行的三个数之和都是18.在空格中填入适当的数,使横行和竖行或每条对角线上的三个数相加都等于15。
3.把3,4,5,6,7这五个数分别填入下面的空格里,使横行、竖行的三个数之和都等于14。
拓展练习(1)把2,3,4,5,6这五个数分别填入圆圈中,使每条线上三个数相加的和都等于12。
(2)把1,2,3,4,5,6分别填入○里,使每一个大椭圆上的四个数之和等于13.例4. 把1,3,5,7,9,11,13这七个数分别填入○里,使每条直线上的三个数相加的和都为17。
简单数阵图例1、把1—5 这五个数分别填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于9。
例2、把1—7这七个数分别填入图中的各○内,使每条线段上三个○内数的和等于10。
例3、在下图圆圈内分别填入数字1~9,使两条直线上五个数的和相等,和是多少?例4、把1~6这六个数分别填在下图中三角形三条边的六个○内,使每条边上三个○内数的和等于9。
例5、将2—9这八个数分别填入右图的○里,使每条边上的三个数之和都等于18。
例6、将1、2、3、4、5、6、7、8、9九个数字分别填入图中的小圆圈中,使三角形每边上四个数的和是17。
1、把2—6 这五个数分别填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于13。
2、在图中填入2—9,使每边3个数的和等于15。
3、将数字1—9分别填在图中的○内使每条线上五个○内数的和等于27。
4、把1、4、7、10、13、16、19七个数填入图中7朵花里,使每条线上三个数的和等于30。
简单的数阵图
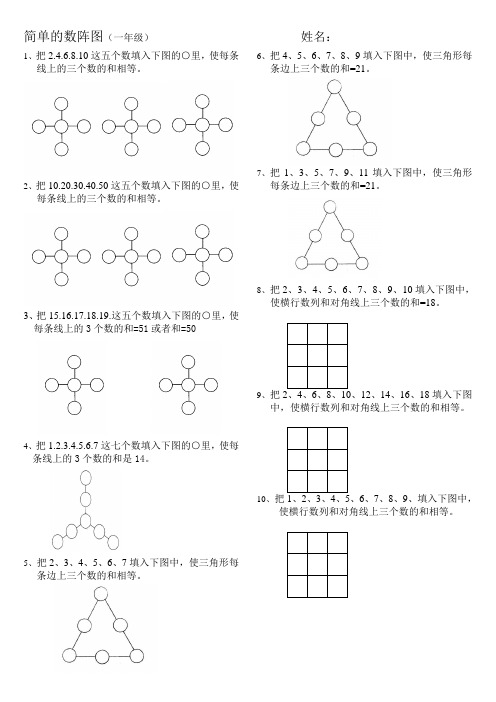
简单的数阵图(一年级)
1、把2.4.6.8.10这五个数填入下图的○里,使每条
线上的三个数的和相等。
2、把10.20.30.40.50这五个数填入下图的○里,使
每条线上的三个数的和相等。
3、把15.16.17.18.19.这五个数填入下图的○里,使
每条线上的3个数的和=51或者和=50
4、把1.2.3.4.5.6.7这七个数填入下图的○里,使每
条线上的3个数的和是14。
5、把2、3、4、5、
6、7填入下图中,使三角形每
条边上三个数的和相等。
姓名:
6、把4、5、6、
7、
8、9填入下图中,使三角形每
条边上三个数的和=21。
7、把1、3、5、7、9、11填入下图中,使三角形
每条边上三个数的和=21。
8、把2、3、4、5、6、7、8、9、10填入下图中,
使横行数列和对角线上三个数的和=18。
9、把、12、14、16、18填入下图
中,使横行数列和对角线上三个数的和相等。
10、把、6、7、8、9、填入下图中,
使横行数列和对角线上三个数的和相等。
小学数学数阵图

解题过程
边和X3 = a+b+c+d+e+f+g+2c 14X3 = 1+2+3+4+5+6+7+2c 42 = 28+2c 14 = 2c c= 7
2020/12/9
例1 (★★)
将1~7这七 个数字, 分别填入 2 图中各个 ○内,使 每条线段 上的三个 ○内数的 和都等于 14。
1
6
7
5
4
3
先填入边和,直线上微调,满足圆圈。
【超常大挑战】(★★★★★)
a ,b ,c ,d ,e, f, g ,h ,I ,处分别填入1至9, 如果每个圆环所填的数的和都相等, 那么这个相等的和最大是多少?最少是多少?
a+e+i+c+g+2(b+d+f+h)=和×5 45+b+d+f+h=和×5 b+d+f+h最大时为6,7,8,9 此时和为15 b+d+f+h最小时为1,2,3,4 和为11 当和为15时无解,和为14有解 最大为14,最小为11
行 业 PPT模 板 : /hangye/ PPT素 材 下 载 : /sucai/ PPT图 表 下 载 : /tubiao/ PPT教 程 : /powerpoint/ Excel教 程 : /excel/ PPT课 件 下 载 : /kejian/ 试 卷 下 载 : /shiti/
圈和X2=数字和+a+b 圈和X2=36+a+b 圈和等于21 a+b=6 则a 和b有两种可能1,5和2,4
(完整word版)简单数阵图

简单数阵图一、知识点:一些数按照一定的规则,填在某一特定图形的规定位置上,这种图形,我们称它为“数阵图”,数阵图的种类繁多,绚丽多彩,这里只向大家介绍三种数阵图,即辐射型数阵图、封闭型数阵图和复合型数阵图。
在解答这类问题时,要善于确定所求的和与关键数字间的关系式,用试验的方法,找到相等的和与关键数字:要会对基本解中的数进行适当调整,得到其他的解,从而培养自己的观察能力,思维的灵活性和严密性。
二、典例剖析:1.辐射型数阵:辐射型数阵图只有一个重叠数,重叠次数是“直线条数”-1,即m-1。
对于辐射型数阵图,有已知各数之和+重叠数×重叠次数=直线上各数之和×直线条数。
由此得到:(1)若已知每条直线上各数之和,则重叠数等于(直线上各数之和×直线条数-已知各数之和)÷重叠次数。
(2)若已知重叠数,则直线上各数之和等于(已知各数之和+重叠数×重叠次数)÷直线条数。
(3)若重叠数与每条直线上的各数之和都不知道,则要从重叠数的可能取值分析讨论。
例1:把1~5这五个数分别填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于9。
同学们可能会觉得这道题太容易了,七拼八凑就写出了右上图的答案,可是却搞不清其中的道理。
下面我们就一起来分析其中的道理,只有弄懂其中的道理,才可能解出复杂巧妙的数阵问题。
分析与解:中间方格中的数很特殊,横行的三个数有它,竖列的三个数也有它,我们把它叫做“重叠数”。
也就是说,横行的三个数之和加上竖列的三个数之和,只有重叠数被加了两次,即重叠了一次,其余各数均被加了一次。
因为横行的三个数之和与竖列的三个数之和都等于9,所以(1+2+3+4+5)+重叠数=9+9,重叠数=(9+9)-(1+2+3+4+5)=3。
重叠数求出来了,其余各数就好填了(见上图)。
随堂练习:1、将2~8这7个数分别填在下图中的圆圈内,使每条线段上三个圆圈内数的和相等.2、把1~9这9个数字,分别填入下图的各圆圈内,使每条线上5个数的和相等.2、封闭型数阵:例2:将1~6分别填在图中,使每条边上的三个○内的数的和都等于9.分析: 因为 1+2+3+4+5+6 = 21 ,而每条边上的三个数的和为9,则三条边上的和为 9×3 = 27 , 27-21 = 6 , 这个 6 就是由于三个顶点都被重复算了一次。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简单数阵图
一、知识点:
一些数按照一定的规则,填在某一特定图形的规定位置上,这种图形,我们称它为“数阵图”,数阵图的种类繁多,绚丽多彩,这里只向大家介绍三种数阵图,即辐射型数阵图、封闭型数阵图和复合型数阵图。
在解答这类问题时,要善于确定所求的和与关键数字间的关系式,用试验的方法,找到相等的和与关键数字:要会对基本解中的数进行适当调整,得到其他的解,从而培养自己的观察能力,思维的灵活性和严密性。
二、典例剖析:
1.辐射型数阵:
辐射型数阵图只有一个重叠数,重叠次数是“直线条数”-1,即m-1。
对于辐射型数阵图,有
已知各数之和+重叠数×重叠次数=直线上各数之和×直线条数。
由此得到:
(1)若已知每条直线上各数之和,则重叠数等于(直线上各数之和×直线条数-已知各数之和)÷重叠次数。
(2)若已知重叠数,则直线上各数之和等于(已知各数之和+重叠数×重叠次数)÷直线条数。
(3)若重叠数与每条直线上的各数之和都不知道,则要从重叠数的可能取值分析讨论。
例1:把1~5这五个数分别填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于9。
同学们可能会觉得这道题太容易了,七拼八凑就写出了右上图的答案,可是却搞不清其中的道理。
下面我们就一起来分析其中的道理,只有弄懂其中的道理,才可能解出复杂巧妙的数阵问题。
分析与解:中间方格中的数很特殊,横行的三个数有它,竖列的三个数也有它,我们把它叫做“重叠数”。
也就是说,横行的三个数之和加上竖列的三个数之和,只有重叠数被加了两次,即重叠了一次,其余各数均被加了一次。
因为横行的三个数之和与竖列的三个数之和都等于9,所以
(1+2+3+4+5)+重叠数=9+9,
重叠数=(9+9)-(1+2+3+4+5)=3。
重叠数求出来了,其余各数就好填了(见上图)。
随堂练习:
1、将2~8这7个数分别填在下图中的圆圈内,使每条线段上三个圆圈内数的和相等.
2、 把1~9这9个数字,分别填入下图的各圆圈内,使每条线上5个数的和相等
.
2、封闭型数阵:
例2:将1~6分别填在图中,使每条边上的三个○内的数的和都等于9.
分析: 因为 1+2+3+4+5+6 = 21 ,而每条边上的三个数的和为9,则三条边上的和为 9×3 = 27 , 27-21 = 6 , 这个 6 就是由于三个顶点都被重复算了一次。
所以三个顶点的和为 6 ,在 1-----6中,只能选1、2、3 填入三个顶点中,再将4、5、6填入另外的三个圈即可。
解: . a . b . c .
d .
e .
f .
1 6
2 4 5
3 1 5 3
4 2 6 2 6 1 5
3 4 2 4 3 1 5 6 3 5 1 6 2 4 3 4 2 6 1 5
随堂练习:
1、把3~8这6个数填在下图中的圆圈内,使每条线上的和都等于15。
2、把10~15这6个数字分别填放图中的各个圆圈内,使每边上的三个圆圈内数之和都等于36。
综合练习
1、将 10~20填入左下图的○内,其中15已填好,使得每条边上的三个数字之和都相等。
2、将1~7这七个数分别填入左下图中的○里,使每条直线上的三个数之和都等于12。
如果每条直线上的三个数之和等于10,那么又该如何填?
3、将1~9这九个数分别填入右图的小方格里,使横行和竖列上五个数之和相等。
(至少找出两种本质上不同的填法)
4、把1~10十个数分别填入下图的“六一”形十个空格内,使每行中数字和为12。
5、使每条线上的三个数之和都得15。
6、将1~8个数分别填入图中,使每个圆圈上五个数和分别为20,21,22.
7、将1~7这七个数分别填入下图的○里,使得每条直线上三个数之和与每个圆圈上的三个数之和都相等。
8、图中有10个小三角形和4个大三角形,将1~10填入每个小三角形,
使每个大三角形内的数字之和都等于25。
(以填好3个数)
9、将1~6六个数填入图中的圆圈中,要求四条直线上的数字之和都等于10。
10、如果将1—11这11个自然数填入下图的圆圈中,使每个菱形上的四个数之和都等于24。
最新文件仅供参考已改成word文本。
方便更改。
