李瀚荪《电路分析基础》(第4版)课后习题详解-第6章 一阶电路【圣才出品】
李瀚荪编《电路分析基础》(第4版)第一章课件精品名师资料

§1-1电路及集总电路模型
实际器件 理想元件 符号 图形 反映特性
电阻器 电容器 电感器
电阻元件 R 电容元件 C 电感元件 L
消耗电能 贮存电场能 贮存磁场能
§1-1电路及集总电路模型
开关 灯泡
Ri
US
Rf
10BASE-T wall plate
电 池
导线
电路图 (电路模型) 电气图
实际电路
§1-1电路及集总电路模型
§1-1电路及集总电路模型
低频信号发生器的内部结构
§1-1电路及集总电路模型
电容器
电池 晶体管 电阻器 运算放大器
线圈
§1-1电路及集总电路模型
电路的基本组成 电路:电工设备构成的整体,它为电流的流通提供路径 电路组成:主要由电源、中间环节、负载构成 • 电源(source):提供能量或信号(电池、发电机 、信号发生器) • 负载(load):将电能转化为其它形式的能量, 或对信号进行处理(电阻、电容、晶体管) • 中间环节(intermediate):一般由导线、开 关等构成,将电源与负载接成通路(传输线)
电压 u(t) ;
电荷 q(t) 与 磁链 ψ(t) ;
功率 p(t) 与 能量 w(t) 。
常用:电流、电压、功率
电流 (current)
P6
电荷在导体中的定向移动形成电流。 定义:单位时间内通过导体横截面的电 量定义为电流强度,简称电流 i ( t ) ,大 小为: d q(t ) i(t ) dt
电路理论
包括电路分析和电路综合两方面内容
输入 输出
电路
电路分析:已知 电路综合:已知 已知 求解 求解 已知
显然,电路分析是电路综合的基础。
李瀚荪《电路分析基础》(第4版)课后习题详解-第五章至第八章【圣才出品】

解:
(1)
,u
和 i 波形相同,但最大值、最小值并不同时发生。
5-2 考虑漏电现象,电容器可以用一个电容 C 与漏电阻 R 并联的电路作为模型。若某 电容器的模型中 C=0.1μF,R=150kΩ,外施电压如图 5-1 所示,试绘出电容器电流的波形。
图 5-1
1 / 129
圣才电子书 十万种考研考证电子书、题库视频学习平台
解: (1)
当 0<t<1s 时,
图 5-9
8 / 129
圣才电子书 十万种考研考证电子书、题库视频学习平台
(3)如 t 单位改为 ms 则
5-9 2mH 电感的电压如图 5-10 示,已知:i=0、t<-5ms。 (1)试绘出-5ms<t<20ms 期间电感电流波形(设电流、电压为关联参考方向); (2)在什么时刻电感中的储能为最大?储能的最大值是多少? (3)绘 t≥0 时该电感的等效电路。
解:
图 5-2
波形如图 5-2 所示。
5-3 0.1F 电容的电流如图 5-2 所示,若 u(0)=0,试绘出电容电压的波形。 解:
2 / 129
圣才电子书 十万种考研考证电子书、题库视频学习平台
波形如图 5-3 所示。
图 5-3 §5-3 电容电压的连续性质和记忆性质 5-4 流过 1.25μF 电容的电流波形(对所有 t)如图 5-4 所示,求 t>-1s,t>0 和 t >2s 时电容的等效电路。又,t=0+时等效电路如何?
4 / 129
圣才电子书
电压均为零。
十万种考研考证电子书、题库视频学习平台
(4)t=0+时,等效电路为 16V 电压源。
李瀚荪《电路分析基础》笔记和典型题(含考研真题)详解(分解方法及单口网络)

第4章分解方法及单口网络4.1 复习笔记一、分解的基本步骤1.划分原则一个元件的电压电流关系是由这个元件本身所确定的,与外接的电路无关。
从全面求解网络的角度来看,何处划分是随意的,视方便而定。
2.分解步骤分解的基本步骤为:(1)把给定网络划分为两个单口网络N1和N2;(2)分别求出N1和N2的VCR(计算或测量);(3)联立两者的VCR或由它们伏安特性曲线的交点,求得N1和N2的端口电压、电流;(4)分别求解N1和N2内部各支路电压、电流。
二、单口网络的电压电流关系1.单口网络的伏安关系VCR单口网络的伏安关系可用以下方式来描述:(1)具体的电路模型;(2)方程或曲线的形式;(3)等效电路。
2.单口网络VCR的求解方法(1)在单口网络两端外施电流源i求单口网络两端电压u;(2)在单口网络两端外施电压源u求单口网络两端电流i。
3.注意事项(1)单口网络的VCR与外接电路无关;(2)可以在最简单的外接电路情况下,求得单口网络的VCR;(3)外施电流源求电压法和外施电压源求电流法是求解VCR常用的方法.三、单口网络的置换-置换定理1.置换定理内容置换定理可表述为:若网络N由两个单口网络N1和N2连接组成,且已知端口电压和电流值分别为α和β,则N1(或N2)可以用一个电压为α的电压源或用一个电流为β的电流源置换,不影响N1(或N2)内各支路电压、电流原有数值。
2.置换过程的图示置换过程如图4-1所示。
(a)(b)N2为电压源所置换(c)N2为电流源所置换图4-1 置换定理四、单口网络的等效电路两单口网络等效是指一个单口网络N和另一个单口网络N'的电压、电流关系完全相同,即它们在u-i平面上的伏安特性曲线完全重叠。
1.等效串联电路(1)典型电路图串联等效电路的典型电路图如图4-2所示。
图4-2 串联等效电阻(2)串联等效的公式串联等效的公式为(3)串联等效的表述串联等效电路的电阻为各电阻之和。
2.等效并联电路(1)并列等效的公式等效并联电阻公式为(2)并联等效的表述并联等效电阻的倒数等于各电阻倒数之和。
电路分析基础第四版课后习题第四章第五章第六章答案
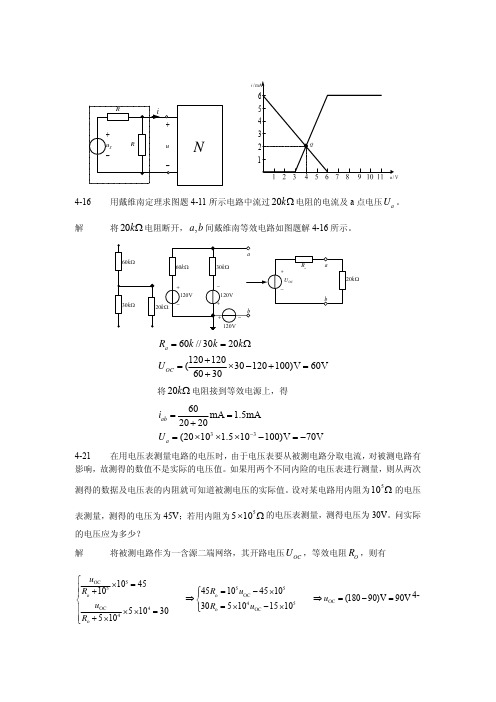
/i4-16 用戴维南定理求图题4-11所示电路中流过20k Ω电阻的电流及a 点电压。
a U 解将电阻断开,间戴维南等效电路如图题解4-16所示。
20k Ω,a bk Ω60//3020120120(30120100)V 60V6030a OCR k k k U ==Ω+=×−+=+ 将电阻接到等效电源上,得20k Ω3360mA 1.5mA2020(2010 1.510100)V 70V ab a i U −==+=×××−=− 4-21 在用电压表测量电路的电压时,由于电压表要从被测电路分取电流,对被测电路有影响,故测得的数值不是实际的电压值。
如果用两个不同内险的电压表进行测量,则从两次测得的数据及电压表的内阻就可知道被测电压的实际值。
设对某电路用内阻为的电压表测量,测得的电压为45V ;若用内阻为510Ω5510×Ω的电压表测量,测得电压为30V 。
问实际的电压应为多少? 解将被测电路作为一含源二端网络,其开路电压,等效电阻OC U O R ,则有5OC 555o o OC OC 454OCo OC 4o 10451045104510(18090)V 90V 30510151051030510u R R u u u R u R ⎧×=⎪⎧+=−×⎪⎪⇒⇒=⎨⎨=×−×⎪⎪⎩××=⎪+×⎩−=4-28 求图题4-20所示电路的诺顿等效电路。
已知:12315,5,10,R R R =Ω=Ω=Ω。
10V,1A S S u i ==解对图题4-20所示电路,画出求短路电流和等效内阻的电路,如下图所示SC i对左图,因ab 间短路,故0,0i i α==,10A 0.5A 155SC i ==+ 对右图,由外加电源法,106ab R α=Ω− 4-30 电路如图题4-22所示。
李瀚荪《电路分析基础》笔记和典型题(含考研真题)详解(集总参数电路中电压、电流的约束关系)

第1章1.1 复习笔记一、电路及集总电路模型1.基础元件图形实际电路是由电阻器、电容器、线圈、电源等部件和晶体管等器件相互连接组成的,各种部、器件可以用图形符号表示,如表1-1所示。
表1-1 部分电气图用图形符号2.集总电路(1)定义集总电路是指由集总参数元件组成的电路。
(2)应用条件当电路的尺寸远小于最高频率所对应的波长时,可以当做集总电路来处理。
二、电路变量电流、电压及功率1.电流(1)定义电流是指每单位时间内通过导体横截面的电荷量。
(2)表达式电流的表达式为(3)分类①恒定电流恒定电流是指大小和方向都不随时间变化的电流,简称直流。
②交变电流交变电流是指大小和方向都随时间作周期性变化的电流,简称交流。
2.电压(1)定义电路中a、b两点间的电压是指单位正电荷由a点转移到b点时所获得或失去的能量。
(2)表达式电压的表达式为(3)分类①恒定电压恒定电压是指大小和极性都不随时间而变动的电压,也叫直流电压。
②时变电压时变电压是指大小和极性都随时间变化的电压,也叫交流电压。
(4)关联参考方向:关联参考方向是指电流参考方向与电压参考方向一致,如图1-1所示。
图1-1 关联的参考方向3.功率(1)定义功率是指能量流动的速率。
(2)表达式功率的表达式为p(t)=u(t)i(t)(3)功率的正负功率的正负表示能力的吸收与产生,电压电流取关联参考方向时:①当功率为正,电路吸收能量,p值即为吸收能量的速率;②当功率为负,电路提供能量,p值为产生能量的速率。
三、基尔霍夫定律1.基尔霍夫电流定律(1)定律内容基尔霍夫电流定律可表述为:对于任一集总电路中的任一节点,在任一时刻,流出(或流进)该节点的所有支路电流的代数和为零。
(2)表达式基尔霍夫电流定律的数学表示式为(3)理论基础基尔霍夫电流定律的理论基础是电荷守恒法。
2.基尔霍夫电压定律(1)定律内容基尔霍夫电压定律可表述为:对于任一集总电路中的任一回路,在任一时刻,沿着该回路的所有支路电压降的代数和为零。
《电路分析基础》习题参考答案

3-5(1) , ;(2)u3=100sin(ωt+50°)V
3-6(1)i1=14.1 sin(ωt+50°)A;(2)u2=300 sin(ωt-60°)V
3-8(1)R;(2)L;(3)C;(4)L
3-9i=2.82sin (ωt-30°)A,Q=19.88var
第4章习题参考答案
4-1(a) , ;(b) ,
4-2Y=(0.06-j0.08) S,R=16.67Ω,L=0.04Ω
4-3
4-4
4-5 , , , ,
4-6 , , , ,
4-7 ,
4-8(a)30V;(b)2.24A;(c)14.49V
4-9(a)10V;(b)10A;(c)10V
4-10US=15.65V
2-17I1=4/5A,I2=-3/4A,I3=2A,I4=31/20A,I5=-11/4A
2-18I1=0.5A,I2=-0.25A
2-19I3=1A
2-20I5=-1A
2-21(1)I5=0A,Uab=0V;(2)I5=1A,Uab=11V。
2-22IL=2A
2-23IS=35/3A,R0=2Ω
第2章习题参考答案
2-12.4Ω,5A
2-2(1) 4V,2V,1V;(2) 40mA,20mA,10mA
2-31.5Ω,2A,1/3A
2-46Ω,36Ω
2-52A,1A
2-61A
2-72A
2-810A
2-9I1=1.4A,I2=1.6A,I3=0.2A
2-10I1=0A,I2=-3A,P1=0W,P2=-18W
3-10u=44.9sin (314t-135°) V,Q=3.18var
电路分析基础第六章(李瀚荪)

t
t0
t U S uC 1 解二: iC [U S U S (1 e )] R R t US e , t0 R
二、RL电路的零状态响应 t=0
iR
R IS
iL
L
+ uL _
已知:iL(0_ ) = 0,求 iL(t) , uL(t) , t 0 解:1. 定性分析
1. 定性分析
① t< 0 —充电 ② t = 0 —换路
③ t≥0 —放电
2. 定量分析
建立图(b)电路的一阶微分方程
u R uC 0
齐次方程通解: 根据初始条件 其解为:
duC RC uC 0 dt
uC (t ) Ke
uC (0 ) Ke
t RC
st
1 S=- RC
= 18e- 2500tV 18e- 2500t 6 ? 4 9
(t ? 0) 3e- 2500t A(t > 0)
uC (t ) 6 i1 (t ) = ? R 3+ 6
例3: 已知i (0 +) = 2A 求:i(t) , u(t) , t ≥ 0 3
i
0.5u
1
4H
+ u
_
u 3i (0.5u i) 1
t
6e 20 t V
( t 0)
duC U 0 t 6 20 t iC ( t ) C e e dt R 10 103 0.6e 20 t m A ( t 0)
电阻中的电流iR(t)可以用与iC(t)同样数值的电
流源代替电容,用电阻并联的分流公式求得 iR(t)
引例:求图示电路的一阶微分方程。
电路分析基础(四版)课后答案

I1 3 / /6 12 / /6 1 3A
再应用电阻并联分流公式, 得
I2
6 3
6
I1
2 3
3
2A
24
第1章 电路基本概念
I3
6 12
6
I1
13 3
1A
对节点a应用KCL, I=I2-I3=2-1=1 A
解答 题解1.7(c)图所示电路时, 不要设很多支路电流 建立很多的KCL、 KVL方程组, 然后联立求解。 这样求解 的思路能求解正确, 但费时费力, 不如应用串并联等效求 解简便。
所以
I 6 2 4A 2
20
第1章 电路基本概念
题解1.7图
21
第1章 电路基本概念 图(b)电路中, 设电流I1节点a及回路A, 如题解1.7图
(b)所示。 对节点a列写KCL方程, I1=1+I
对回路A列写KVL方程, -1+1×I+1×(I+1)=0
I=0
22
第1章 电路基本概念 当然, 本问亦可先将1 Ω电阻与1 V电压源的串联互换等
24
24 10 A
[8 / /8 2] / /[4 / /4 2] 2.4
再应用电阻并联分流公式, 得电流
因I与Us参考方向非关联, 所以电压源Us Ps=UsI=15×3=45 W
32
第1章 电路基本概念 1.10 求图示各电路中的电流I。
题解1.10图
33
第1章 电路基本概念 解 图(a):
I
100
2A
[50 / /50 6 / /30] / /60 / /20 40
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解: (1)
图 6-17
N1 内部可能为 3.3 kΩ 与电压源的串联组合。由于电容初始电压为零,充电电流的初 始值为
由此可知电压源电压
由于初始电流为负值,可知电压源的正极应处于图中所标 i(t)流入 N1。的位置。 (2)C 缩小为原有值的 1/5,为保持 τ 不变,R 应增为原值的 5 倍,即
11 / 58
图 6-15
图 6-16 解:断开电感支路,对断开支路后的电路求其戴维南等效电路。断开后
求 Ro 可开外施电源法。为此需令 4 A 电流源置零,在断开的支路处外施(测试)电 流源 i1,如图 6-16 所示,则
电源于 t=0 时作用于电路,故电感电流 i 的初始值为零,所求 i(t)、t≥0 属零状态 响应。稳态时,电感相当于短路,由戴维南等效电路可得稳态时电流为 56 V/14 Ω=4
解出
6-8 电路如图 6-13 所示,电压源于 t=0 时开始作用于电路,试求 i1(t),t≥0。已 知受控源参数 r=2 Ω。
8 / 58
圣才电子书
十万种考研考证电子书、题库视频学习平 台
图 6-13
图 6-14 解:从 ab 处断开 1 Ω 和 0.8 F 串联支路,求出开路电压 uoc,如图 6-14(a)所示。
圣才电子书
十万种考研考证电子书、题库视频学习平
台
为保持初始电流仍为 10 mA,电压源电压应增大为 5×33 V=165 V。参数值作如上
图 6-10
5 / 58
圣才电子书
十万种考研考证电子书、题库视频学习平 台
图 6-11 解: t<0 时开关未闭合,闭合时电容初始电压为零。运用戴维南定理可得如图 6-11(a) 所示的等效电路。其中 uoc 可求得如下:电容断开后,6 kΩ 电阻无电流,设剩下的回 路中电流为 i0,则
图 6-4
图 6-5
图 6-6 解: (1)对图题 6-4(a)所示电路,求开路电压 uoc 和短路电流 isc。开路时 u1=0,见 图 6-5,得 将 ab 短路,短路电流为 isc,可列出网孔方程
2 / 58
圣才电子书
十万种考研考证电子书、题库视频学习平,置换电路图如图 6-11(b)所示。
6 / 58
圣才电子书
对 i1 支路:
十万种考研考证电子书、题库视频学习平 台
又
6-6 电路如图 6-12 所示。(1)t=0 时 S1 闭合(S2 不闭合),求 i,t≥0;(2)若 t=0 时 S2 闭合(S1 不闭合),求 i,t≥0。
图 6-1
图 6-2
图 6-3 解: (1)对图 6-1(a)所示电路,见图 6-2 对图 6-1(b)所示电路,见图 6-3 (2)列出各电路的微分方程。图 6-1(a)有
1 / 58
圣才电子书
图 6-1(b)有
十万种考研考证电子书、题库视频学习平 台
6-2 对图 6-4 两电路,重复上题的要求。
求短路电流 isc,如图 6-14(b)所示。
等效电路如图 6-14(c)所示。由图 6-13 可知
9 / 58
圣才电子书
十万种考研考证电子书、题库视频学习平
台
又
所以
6-9 电路如图 6-15 所示,电源于 t=0 时开始作用于电路,试求 i(t), t≥0。
10 / 58
圣才电子书
十万种考研考证电子书、题库视频学习平
台
A,故得
6-10 电路如图 6-17(a)所示,已知 N1 仅含直流电源及电阻,电容 C=5μF,初始 电压为零。在 t=0 时开关闭合,闭合后的电流波形如图 6-17(b)所示。
(1)试确定 N1 的一种可能结构; (2)若 C 改为 1μF,是否可能通过改变 N1 而保持电流波形仍如图 6-17(b)所示, 若能,试确定 N1 的新结构形式。
对图 6-4(b)所示电路,见图 6-6,求 uab 即开路电压。以 b 为参考节点,列节点方 程
即 解得 将 ab 短路得短路电流 isc=10 mA 得 (2)列出各电路微分方程。对图 6-4(a)有
对图题 6-4(b)有
3 / 58
圣才电子书
十万种考研考证电子书、题库视频学习平 台
圣才电子书
十万种考研考证电子书、题库视频学习平 台
第 6 章 一阶电路
§6-1 分解方法在动态电路分析中的运用
6-1 图 6-1 两电路中,
L=2 mH,C=1μF。
(1)把各电路中除动态元件以外的部分化简为戴维南或诺顿等效电路;
(2)利用化简后的电路列出图中所注明输出量 u 或 i 的微分方程。
图 6-12 解: (1)S1 闭合,断开电感,得戴维南等效电路,其中
(2)S2 闭合,断开电感,得戴维南等效电路。
7 / 58
圣才电子书
十万种考研考证电子书、题库视频学习平 台
6-7 图 6-12 所示电路 t=0 时,S1、S2 同时闭合,求 i1 和 i2,t≥0。 解:S1、S2 同时闭合后,断开电感所得戴维南等效电路如图 6-13 所示。 由图 6-13(a)求开路电压 uoc,可得
十万种考研考证电子书、题库视频学习平 台
6-4 图 6-9 所示电路中,各电源均在 t=0 时开始作用于电路,求 i(t)。已知电容 电压初始值为零。
解:断开电容求戴维南等效电路
图 6-9
又 得 6-5 电路如图 6-10 所示,开关在 t=0 时闭合,求 t=15μs 时 us 及各支路电流。
§6-2 零状态响应
6-3 RC 电路如图 6-7(a)所示,若对所有 t,电压源 us 波形如图 6-7(b)所示, 试求 uC(t)、i(t),t≥0。
图 6-7 解: t≥0 时,电路如图 6-8 所示。由于 t≤0 时 us=0,故知 t>10 时,属零状态响应
又
图 6-8
4 / 58
圣才电子书
