海门中学热点专题1.三角与平面向量
三角函数解三角形平面向量ppt课件

[问题6] 下列四个命题:①若|a|=0,则a=0; ②若|a|=|b|,则a=b或a=-b;③若a∥b,则 |a|=|b|;④若a=0,则-a=0.其中正确命题是 ___④_____.
7.向量的数量积
|a|2=a2=a·a,
a·b=|a||b|cos θ=x1x2+y1y2,
cos θ=|aa|·|bb|=
正解 ∵0<α<π2且 cos α=17<cos π3=12, ∴π3<α<π2,又 0<β<π2, ∴π3<α+β<π,又 sin(α+β)=5143< 23, ∴23π<α+β<π.
∴cos(α+β)=- 1-sin2α+β=-1141,
sin α=
1-cos2α=47
3 .
∴cos β=cos[(α+β)-α]
又∵|c-a-b|2=c2-2c·(a+b)+2a·b+a2+b2=1,
∴2c·(a+b)=c2+1.
查缺补漏
1 2 3 =0,∴|a+b|= 2 , ∴c2+1=2 2 |c|cos θ(θ是c与a+b的夹角). 又-1≤cos θ≤1,∴0<c2+1≤2 2 |c|, ∴c2-2 2 |c|+1≤0, ∴ 2 -1≤|c|≤ 2+1. 答案 A
查缺补漏
1 2 3 4 5 6 7 8 9 10
5.函数 f(x)=Asin(2x+φ)(A,φ∈R)的部分
图象如图所示,那么 f(0)等于( )
[问题1] 已知角α的终边经过点P(3,-4),则sin α +cos α的值为___-__15___.
2.同角三角函数的基本关系式及诱导公式
(1)平方关系:sin2α+cos2α=1. (2)商数关系:tan α= sin α .
高考数学一轮复习之三角函数与平面向量

高考数学一轮复习之三角函数与平面向量
1.三角函数作为一种重要的基本初等函数,是中学数学的重要内容,也是高考命题的热点之一。
近几年对三角函数的要求基本未作调整,主要考察三角函数的定义、图象与性质以及同角三角函数的基本关系式、诱导公式、和角与倍角公式等。
高考对三角函数与三角恒等变换内容的考察,一是设置一道或两道客观题,考察三角函数求值、三角函数图象与性质或三角恒等变换等外容;二是设置一道解答题,考察三角函数的性质、三角函数的恒等变换或三角函数的实践运用,普通出如今前两个解答题的位置。
无论是客观题还是解答题,从难度来说均属于中高档标题,所占分值在20分左右,约占总分值的13.3%。
2.平面向量是衔接代数与几何的桥梁,是高考的重要内容之一。
高考常设置1个客观题或1个解答题,对平面向量知识停止片面的考察,其分值约为10分,约占总分的7%。
近年高考中平面向量与解三角形的试题是难易适中的基础题或中档题,一是直接考察向量的概念、性质及其几何意义;二是考察向量、正弦定理与余弦定理在代数、三角函数、几何等效果中的运用。
1.2021年高考试题预测
(1)剖析近几年高考对三角函数与三角恒等变换局部的命题特点及开展趋向,以下仍是今后高考的主要内容:
①三角函数的图象与性质是高考考察的中心内容,经过图象求解析式、经过解析式研讨函数性质是罕见题型。
②解三角函数标题的进程普通是经过三角恒等变换化简三角函数式,再研讨其图象与性质,所以熟练掌握三角恒等变换的方法和技巧尤为重要,比如升幂(降幂)公式、asinx+bcosx的常考内容。
③经过实践背景考察同窗们的数学建模才干和数学应意图识。
高一数学《三角函数与平面向量》精讲精练.doc
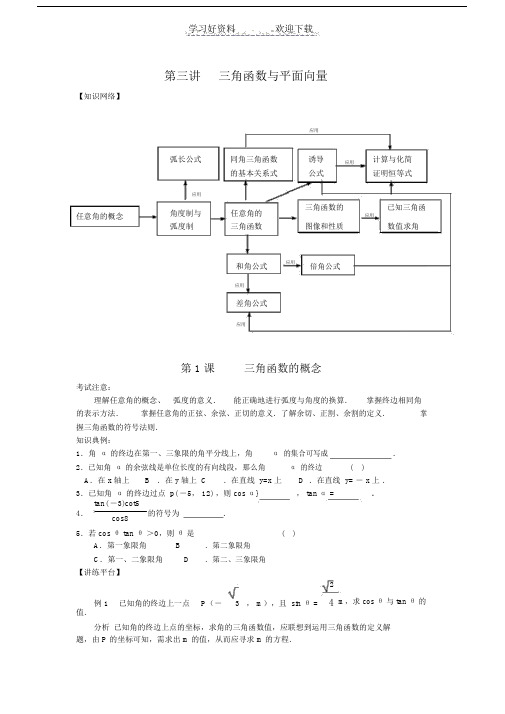
学习好资料 欢迎下载第三讲 三角函数与平面向量【知识网络】应用弧长公式同角三角函数诱导 应用计算与化简的基本关系式公式证明恒等式应用任意角的概念角度制与任意角的 三角函数的已知三角函应用弧度制图像和性质数值求角三角函数和角公式应用倍角公式应用差角公式应用第 1 课三角函数的概念考试注意:理解任意角的概念、 弧度的意义. 能正确地进行弧度与角度的换算. 掌握终边相同角的表示方法. 掌握任意角的正弦、余弦、正切的意义.了解余切、正割、余割的定义.掌握三角函数的符号法则.知识典例:1.角 α 的终边在第一、三象限的角平分线上,角 α 的集合可写成.2.已知角 α 的余弦线是单位长度的有向线段,那么角 α 的终边( )A .在 x 轴上B .在 y 轴上 C.在直线 y=x 上D .在直线 y= - x 上 . 3.已知角 α 的终边过点 p( -5, 12) ,则 cos α}, tan α =.4. tan( -3)cot5 .cos8 的符号为5.若 cos θ tan θ >0,则 θ是( )A .第一象限角 B.第二象限角 C .第一、二象限角D.第二、三象限角【讲练平台】2例 1 已知角的终边上一点 P (-3 , m ),且 sin θ =4 m ,求 cos θ 与 tan θ 的值.分析 已知角的终边上点的坐标,求角的三角函数值,应联想到运用三角函数的定义解题,由 P 的坐标可知,需求出 m 的值,从而应寻求 m 的方程.解 由题意知 r=3+m 2,则 sin θ =m=m 2 .r3+m2m2又∵ sin θ = 4 m , ∴ 3+ m 2 = 4 m . ∴ m=0, m=± 5 .当 m=0时, cos θ = - 1 , tan θ =0 ;当 m= 5 时, cos θ = - 6 , tan θ = - 154 3 ;当 m= - 5 时, cos θ = - 6 15 .,tan θ = 34点评 已知一个角的终边上一点的坐标,求其三角函数值,往往运用定义法( 三角函数 的定义 ) 解决.注意运用终边相同的角的表示方法表示有关象限角等; 已知角的终边上一点的坐标, 求三角函数值往往运用定义法;注意运用三角函数线解决有关三角不等式.1. 已知 α 是钝角,那么 α 是()2A .第一象限角B.第二象限角C .第一与第二象限角D.不小于直角的正角2. 角 α 的终边过点 P (- 4k ,3k ) (k <0} ,则 cos α 的值是( )3 43 4A . 5B . 5C .- 5D .-53.已知点 P(sin α -cos α,tan α ) 在第一象限, 则在[ 0,2π]内,α的取值范围是( )A . ( π ,3π) ∪ ( π , 5π ) B . ( π, π ) ∪ ( π, 5π) 2 4 4 4 24 π 3π5π 3π π π 3πC . ( 2 , 4)∪ ( 4 , 2)D . (4 , 2)∪( 4, π )3 44.若 sinx= - 5,cosx = 5 ,则角 2x 的终边位置在( )A .第一象限B .第二象限C .第三象限D .第四象限5.若 4π< α < 6π,且 α 与- 2π终边相同,则 α =.36. 角 α 终边在第三象限,则角 2α 终边在 象限.7.已知| tanx | =-tanx ,则角 x 的集合为.8.如果 θ是第三象限角,则 cos(sin θ) · sin(sin θ ) 的符号为什么?9.已知扇形 AOB 的周长是 6cm ,该扇形中心角是 1 弧度,求该扇形面积.第 2 课同角三角函数的关系及诱导公式掌握同角三角函数的基本关系式:sin 2α +cos 2α=1,sinα =tan α ,tan α cot α=1,cos α掌握正弦、 余弦的诱导公式. 能运用化归思想 (即将含有较多三角函数名称问题化成含有较 少三角函数名称问题)解题 .1. sin 2150°+sin 2135° +2sin210 ° +cos 2225°的值是( )A .1B .3C . 11D .944443 2.已知 sin( π +α )= - ,则( )54343A . cos α = 5B . tan α = 4C . cos α = - 5D . sin( π - α )= 54sin α - 2cos α3.已 tan α =3, 5cos α + 3sin α 的值为 . 4.化简 1+2sin( π -2)cos( π +2) =.4455.已知 θ是第三象限角,且 sin θ +cos θ= 9,那么 sin2 θ等于( )A .22B.-2 2C.2D.-233 33例 1 化简 sin(2 π - α )tan( π +α)cot(- α- π ).cos( π - α )tan(3 π - α )分析 式中含有较多角和较多三角函数名称,若能减少它们的个数,则式子可望简化.解( -sin α ) tan α [ -cot( α +π ) ] (-sin α )tan α (-cot α ) 原式 = (-cos α )tan( π - α ) = (-cos α )(-tan α)sin α · cos αsin α=.cos α=1点评 将不同角化同角, 不同名的三角函数化成同名的三角函数是三角变换中常用的方 法.1π π例 2若 sin θcos θ = 8 , θ ∈ (4 , 2 ) ,求 cos θ -sin θ 的值.分析已知式为 sin θ 、cos θ 的二次式, 欲求式为 sin θ 、cos θ 的一次式,为了运用条件,须将 cos θ -sin θ 进行平方.解 (cos θ - sin θ ) 2=cos 221 = 3 .θ+sin θ -2sin θ cos θ =1- 44π π∵θ ∈ ( 4 ,2),∴ cos θ <sin θ .∴cos θ - sin θ = - 3.2变式 1 条件同例, 求 cos θ +sin θ 的值.3 变式 2已知 cos θ - sin θ = -, 求 sin θ cos θ , sin θ +cos θ的值.2点评 sin θ cos θ, cos θ +sin θ , cos θ - sin θ三者关系紧密,由其中之一,可求其 余之二.1.在三角式的化简,求值等三角恒等变换中,要注意将不同名的三角函数化成同名的 三角函数.2.注意1 的作用:如1=sin2θ +cos2θ .3.要注意观察式子特征,关于sin θ 、 cos θ 的齐次式可转化成关于 tan θ 的式子.4.运用诱导公式,可将任意角的问题转化成锐角的问题.1. sin600 °的值是()1133 A . 2B.- 2 C. 2 D.-22. sin( π+α )sin (π - α )的化简结果为 ()4 411A . cos2 αB . 2cos2αC. sin2 αD.2sin2 α13.已知 sinx+cosx= 5, x ∈[ 0, π ],则 tanx 的值是( )3 4 434A .- 4B.- 3C.± 3D .-4或-34.已知 tan α =- 1,则2sin 1 2= .3α cos α +cos α1- 2sin10 ° cos10 °的值为.5.cos10°- 1- cos 2170°1+2sin α cos α1+ tan α6.证明cos 2α - sin 2α = 1 - tan α.2sin θ +cos θ7.已知 sin θ - 3cos θ =- 5,求 3cos2 θ +4sin2 θ 的值.8.已知锐角 α 、 β、 γ 满足 sin α +sin γ =sin β, cos α- cos γ =cos β ,求 α - β 的值.第 3 课两角和与两角差的三角函数(一)掌握两角和与两角差的正弦、余弦、正切公式,掌握二倍角的正弦、余弦、正切公式,能运用化归思想(将不同角化成同角等)解题. 1. cos105 °的值为()6 + 2 B6 - 2C2 - 6-6-2A ..4.4D .44π2.对于任何 α 、 β∈( 0, 2 ), sin( α+β ) 与 sin α +sin β的大小关系是 ( )A . sin( α +β ) > sin α +sin βB . sin( α +β ) <sin α +sin βC . sin( α +β )=sin α +sin βD .要以 α 、 β 的具体值而定3.已知 π< θ < 3π, sin2 θ=a ,则 sin θ +cos θ 等于 ( )2A . a+1B .- a+1C . a 2+1D .± a 2+11 14.已知 tan α =3, tan β =3,则 cot( α +2β )= .1 ,则 cos2x= .5.已知 tanx=211 ,求 cos( α -β ) 的值 . 例 1 已知 sin α -sin β =-, cos α - cos β =32分析 由于 cos( α - β )=cos α cos β+sin α sin β 的右边是关于 sin α 、 cos α、 sin β、 cos β 的二次式,而已知条件是关于 sin α 、 sin β、 cos α 、 cos β 的一次式,所以将已知式两边平方.解 1 ① cos α - cos β = 1∵ sin α -sin β =- ,,② 32① 2+② 2 ,得 2- 2cos( α - β )=13.3672∴ cos( α - β )= 59.点评 审题中要善于寻找已知和欲求的差异,设法消除差异.例 2 已知: sin( α +β)= - 2sin β .求证: tan α =3tan( α +β ) .分析 已知式中含有角 2α+β 和 β ,而欲求式中含有角 α和 α +β ,所以要设法将已知式中的角转化成欲求式中的角.解∵ 2α +β =( α +β)+ α , β=( α +β) - α ,∴ sin [ ( α +β )+ α ] =-2sin [ ( α +β ) - α ].∴ sin( α+β )cos α+cos( α+β )sin α =- 2sin( α+β )cos α+2cos( α +β )sinα.若 cos( α +β ) ≠0 , cos α ≠ 0,则 3tan( α +β )=tan α .点评 审题中要仔细分析角与角之间的关系,善于运用整体思想解题,此题中将 α +β看成一个整体1.已知 0< α < π< β < π, sin α = 3, cos( α +β )= - 4,则 sin β等于()255242424A . 0B .0 或25 C.25D.0 或- 25sin7 ° +cos15 °sin8 °2.cos7 °- sin15 ° sin8 °的值等于 ( )A .2+ 3B . 2+ 3C .2- 3D .2- 32 23. △ ABC 中, 3sinA+4cosB=6 , 4sinB+3cosA=1 ,则∠ C 的大小为()π 5π π 5π π 2π A . 6B.6 C.6或6 D .3 或3π 14.若 α 是锐角,且 sin( α - 6 )= 3,则 cos α 的值是.5. cos π cos 2πcos3π=.7 771 16.已知 tan θ = , tan φ = 2 3,且 θ 、 φ 都是锐角.求证: θ +φ =45°.7.已知cos( α -β)= - 4, cos(5α +β )=4,且(α -β)∈(π,π),α +β ∈(5 23π,22π),求 cos2 α、cos2 β的值.8.已知 sin( α +β)= 1,且 sin( π +α -β )=1 tan α2 3 ,求tan β.第四课平面向量基本概念一、 1. 向量是既有又有的量。
江苏省海门中学平面向量多选题试题含答案

江苏省海门中学平面向量多选题试题含答案一、平面向量多选题1.在OAB 中,4O OC A =,2O OD B =,AD 、BC 的交点为M ,过M 作动直线l分别交线段AC 、BD 于E 、F 两点,若OE OA λ=,(),0OB OF μλμ=>,则λμ+的不可能取到的值为( ) A .23+ B .33+ C .323+ D .423+ 【答案】ABC 【分析】先证明结论:当O 为直线EF 外一点时,E 、F 、M 三点共线(),OM xOE yOF x y R ⇔=+∈,1x y +=.计算出1377OM OA OB =+,设OM xOE yOF =+,结合OE OA λ=,(),0OB OF μλμ=>可得出13177x y λμ+=+=,然后将λμ+与1377λμ+相乘,展开后利用基本不等式求出λμ+的最小值,即可得出结论. 【详解】先证明结论:当O 为直线EF 外一点时,E 、F 、M 三点共线(),OM xOE yOF x y R ⇔=+∈,1x y +=.充分性:若E 、F 、M 三点共线,则存在k ∈R ,使得=EM k EF ,即()OM OE k OF OE -=-,所以,()1OM k OE kOF =-+,因为(),OM xOE yOF x y R =+∈,则()11x y k k +=-+=,充分性成立; 必要性:因为(),OM xOE yOF x y R =+∈且1x y +=,所以,()1OM xOE x OF =+-,即()OM OF x OE OF -=-,所以,FM xFE =, 所以,E 、F 、M 三点共线.本题中,取OC 的中点N ,连接DN ,如下图所示:D 、N 分别为OB 、OC 的中点,则DN //BC 且12DN BC =, 14OC OA =,67AC AN ∴=,即67AC AN =,//BC DN ,即//CM DN ,67AM AC AD AN ∴==,67AM AD ∴=, 12AD OD OA OB OA =-=-,6611377277OM OA AM OA AD OA OB OA OA OB ⎛⎫=+=+=+-=+ ⎪⎝⎭, E 、F 、M 三点共线,O 为直线EF 外一点,则(),OM xOE yOF x y R =+∈且1x y +=.OE OA λ=,(),0OB OF μλμ=>,则OM xOE yOF xOA yOB λμ=+=+,所以,1737x y λμ⎧=⎪⎪⎨⎪=⎪⎩,可得1737x y λμ⎧=⎪⎪⎨⎪=⎪⎩,由1x y +=可得13177λμ+=, 由基本不等式可得()131********μλλμλμλμλμ⎛⎫⎛⎫⎛⎫+=++=++≥ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=当且仅当μ=时,等号成立.所以,λμ+ABC 选项均不满足47λμ++≥. 故选:ABC. 【点睛】关键点点睛:解本题的关键在于以下两点:(1)利用三点共线的结论:当O 为直线EF 外一点时,E 、F 、M 三点共线(),OM xOE yOF x y R ⇔=+∈,1x y +=.利用该结论推出13177λμ+=; (2)利用基本不等式求出λμ+的最小值.2.下列命题中真命题的是( )A .向量a 与向量b 共线,则存在实数λ使a =λb (λ∈R )B .a ,b 为单位向量,其夹角为θ,若|a b -|>1,则3π<θ≤πC .A 、B 、C 、D 是空间不共面的四点,若AB •AC =0,AC •AD =0,AB •AD =0则△BCD 一定是锐角三角形D .向量AB ,AC ,BC 满足AB AC BC =+,则AC 与BC 同向 【答案】BC 【分析】对于A :利用共线定理判断 对于B :利用平面向量的数量积判断 对于C :利用数量积的应用判断 对于D :利用向量的四则运算进行判断 【详解】对于A :由向量共线定理可知,当0b =时,不成立.所以A 错误. 对于B :若|a b -|>1,则平方得2221a a b b -⋅+>,即12a b ⋅<,又1||2a b a b cos cos θθ⋅=⋅=<,所以3π<θ≤π,即B 正确.对于C :()()220BC BD AC AB AD AB AC AD AC AB AB AD AB AB ⋅=-⋅-=⋅-⋅-⋅+=>,0||BC BD cosB BC BD ⋅=⋅>,即B 为锐角,同理A ,C 也为锐角,故△BCD 是锐角三角形,所以C 正确.对于D :若AB AC BC =+,则AB AC BC CB -==,所以0CB =,所以则AC 与BC 共线,但不一定方向相同,所以D 错误. 故选:BC. 【点睛】(1)多项选择题是2020年高考新题型,需要要对选项一一验证;(2)要判断一个命题错误,只需举一个反例就可以;要证明一个命题正确,需要进行证明.3.已知直线1:310l mx y m --+=与直线2:310l x my m +--=相交于点P ,线段AB是圆()()22:114C x y +++=的一条动弦,G 为弦AB 的中点,AB =( )A .弦AB 的中点轨迹是圆B .直线12,l l 的交点P 在定圆()()22222x y -+-=上C .线段PG 长的最大值为1D .PA PB ⋅的最小值6+ 【答案】ABC 【分析】对于选项A :设()00,G x y ,利用已知条件先求出圆心到弦AB 的距离CG ,利用两点之间的距离公式即可得到结论;对于选项B :联立直线的方程组求解点P 的坐标,代入选项验证即可判断;对于选项C :利用选项A B 结论,得到圆心坐标和半径,利用1112max PG PG r r =++求解即可;对于选项D :利用平面向量的加法法则以及数量积运算得到23PA PB PG ⋅==-,进而把问题转化为求1112min PG PG r r =--问题,即可判断.【详解】对于选项A :设()00,G xy ,2AB =G 为弦AB 的中点, GB ∴=,而()()22:114C x y+++=, 半径为2,则圆心到弦AB 的距离为1CG ==,又圆心()1,1C --,()()2200111x y ∴+++=,即弦AB 的中点轨迹是圆. 故选项A 正确; 对于选项B : 由310310mx y m x my m --+=⎧⎨+--=⎩,得222232113211m m x m m m y m ⎧++=⎪⎪+⎨-+⎪=⎪+⎩, 代入()()2222x y -+-整理得2, 故选项B 正确;对于选项C :由选项A 知:点G 的轨迹方程为:()()22111x y +++=,由选项B 知:点P 的轨迹方程为:()()22222x y -+-=,()()11121,1,1,2,2,G r P r∴--=所以线段1112max 11PG PG r r =++=+=,故选项C 正确; 对于选项D :()()PA PB PG GA PG GB ⋅=+⋅+ ()2PG PG GA GB GA GB =+⋅++⋅ 22203PG PG GB PG =+⋅-=-,故()()2minmin3PA PBPG ⋅=-,由选项C 知:()()221112min 121212221PG PG r r =--=--+----=-,所以()()2min2213642PA PB⋅=--=-,故选项D 错误; 故选:A B C. 【点睛】关键点睛:本题考查了求圆的轨迹问题以及两个圆上的点的距离问题.把两个圆上的点的距离问题转化为两个圆的圆心与半径之间的关系是解决本题的关键.4.已知ABC 的面积为3,在ABC 所在的平面内有两点P ,Q ,满足20PA PC +=,2QA QB =,记APQ 的面积为S ,则下列说法正确的是( )A .//PB CQ B .2133BP BA BC =+ C .0PA PC ⋅< D .2S =【答案】BCD 【分析】本题先确定B 是AQ 的中点,P 是AC 的一个三等分点,判断选项A 错误,选项C 正确; 再通过向量的线性运算判断选项B 正确;最后求出2APQ S =△,故选项D 正确. 【详解】解:因为20PA PC +=,2QA QB =,所以B 是AQ 的中点,P 是AC 的一个三等分点,如图:故选项A 错误,选项C 正确;因为()121333BP BA AP BA BC BA BA BC =+=+-=+,故选项B 正确;因为112223132APQ ABCAB hS S AB h ⨯⨯==⋅△△,所以,2APQ S =△,故选项D 正确. 故选:BCD 【点睛】本题考查平面向量的线性运算、向量的数量积、三角形的面积公式,是基础题.5.已知向量(4,3)a k =,(4,3)b k =,则( ) A .若a b ⊥,则0k = B .若//a b ,则1k =C .若a b >,则1k <D .若a b a b +=-,则a b ⊥【答案】AD 【分析】先根据a b ⊥建立方程44330k k ⨯+⨯=解得0k =,判断选项A 正确;再根据//a b ,建立方程(4,3)(4,3)k k λ=解得1k =±,判断选项B 错误;接着根据a b >建立不等式4(3)(4)3k k +>+解得11k -<<,判断选项C 错误;最后根据a b a b +=-,化简整理得到a b ⊥,判断选项D 正确.【详解】解:因为(4,3)a k =,(4,3)b k =,a b ⊥,则44330k k ⨯+⨯=,解得0k =,故选项A 正确;因为(4,3)a k =,(4,3)b k =,//a b ,则λa b ,即(4,3)(4,3)k k λ=,解得1k =±,故选项B 错误;因为(4,3)a k =,(4,3)b k =,a b >,则>,解得11k -<<,故选项C 错误;因为(4,3)a k =,(4,3)b k =,a b a b +=-,则0a b ⋅=,0a ≠,0b ≠,所以a b ⊥,故选项D 正确. 故答案为:AD. 【点睛】本题考查利用向量垂直求参数、利用向量共线求参数、根据向量的模的大小关系求参数的范围、利用向量的运算判断向量垂直,是中档题.6.若平面向量,,a b c 两两夹角相等,,a b 为单位向量,2c =,则a b c ++=( ) A .1 B .2C .3D .4【答案】AD【分析】由平面向量,,a b c 两两夹角相等可知,夹角为0︒或120︒.分两种情况对三个向量的和的模长进行讨论,算出结果. 【详解】平面向量,,a b c 两两夹角相等,∴两两向量所成的角是0︒或120︒.当夹角为0︒时,,,a b c 同向共线,则4a b c ++=; 当夹角为120︒时,,a b 为单位向量,1a b ∴+= ,且a b +与c 反向共线,又2c =,1a b c ∴++=.故选:AD. 【点睛】本题考查了平面向量共线的性质,平面向量的模的求法,考查了分类讨论的思想,属于中档题.7.已知平行四边形的三个顶点的坐标分别是(3,7),(4,6),(1,2)A B C -.则第四个顶点的坐标为( ) A .(0,1)- B .(6,15)C .(2,3)-D .(2,3)【答案】ABC 【分析】设平行四边形的四个顶点分别是(3,7),(4,6),(1,2),(,)A B C D x y -,分类讨论D 点在平行四边形的位置有:AD BC =,AD CB =,AB CD =,将向量用坐标表示,即可求解. 【详解】第四个顶点为(,)D x y ,当AD BC =时,(3,7)(3,8)x y --=--,解得0,1x y ==-,此时第四个顶点的坐标为(0,1)-;当AD CB =时,(3,7)(3,8)x y --=,解得6,15x y ==,此时第四个顶点的坐标为(6,15); 当AB CD =时,(1,1)(1,2)x y -=-+,解得2,3x y ==-,此时第四个项点的坐标为(2,3)-. ∴第四个顶点的坐标为(0,1)-或(6,15)或(2,3)-. 故选:ABC . 【点睛】本题考查利用向量关系求平行四边形顶点坐标,考查分类讨论思想,属于中档题.8.设a 、b 是两个非零向量,则下列描述正确的有( ) A .若a b a b +=-,则存在实数λ使得λa bB .若a b ⊥,则a b a b +=-C .若a b a b +=+,则a 在b 方向上的投影向量为aD .若存在实数λ使得λa b ,则a b a b +=-【答案】AB 【分析】根据向量模的三角不等式找出a b a b +=-和a b a b +=+的等价条件,可判断A 、C 、D 选项的正误,利用平面向量加法的平行四边形法则可判断B 选项的正误.综合可得出结论. 【详解】当a b a b +=-时,则a 、b 方向相反且a b ≥,则存在负实数λ,使得λa b ,A选项正确,D 选项错误;若a b a b +=+,则a 、b 方向相同,a 在b 方向上的投影向量为a ,C 选项错误; 若a b ⊥,则以a 、b 为邻边的平行四边形为矩形,且a b +和a b -是这个矩形的两条对角线长,则a b a b +=-,B 选项正确. 故选:AB. 【点睛】本题考查平面向量线性运算相关的命题的判断,涉及平面向量模的三角不等式的应用,考查推理能力,属于中等题.二、立体几何多选题9.已知正方体1111ABCD A B C D -的棱长为2,点O 为11A D 的中点,若以O 为半径的球面与正方体1111ABCD A B C D -的棱有四个交点E ,F ,G ,H ,则下列结论正确的是( )A .11//A D 平面EFGHB .1AC ⊥平面EFGHC .11A B 与平面EFGH 所成的角的大小为45°D .平面EFGH 将正方体1111ABCD A B C D -分成两部分的体积的比为1:7 【答案】ACD 【分析】如图,计算可得,,,E F G H 分别为所在棱的中点,利用空间中点线面的位置关系的判断方法可判断A 、B 的正确与否,计算出直线AB 与平面EFGH 所成的角为45︒后可得C 正确,而几何体BHE CGF -为三棱柱,利用公式可求其体积,从而可判断D 正确与否. 【详解】如图,连接OA ,则2115OA AA =+=,故棱1111,,,A A A D D D AD 与球面没有交点.同理,棱111111,,A B B C C D 与球面没有交点. 因为棱11A D 与棱BC 之间的距离为26>BC 与球面没有交点.因为正方体的棱长为2,而26<球面与正方体1111ABCD A B C D -的棱有四个交点E ,F ,G ,H , 所以棱11,,,AB CD C C B B 与球面各有一个交点, 如图各记为,,,E F G H .因为OAE △为直角三角形,故22651AE OE OA -=-=,故E 为棱AB 的中点. 同理,,F G H 分别为棱11,,CD C C B B 的中点.由正方形ABCD 、,E F 为所在棱的中点可得//EF BC , 同理//GH BC ,故//EF GH ,故,,,E F G H 共面. 由正方体1111ABCD A B C D -可得11//A D BC ,故11//A D EF因为11A D ⊄平面EFGH ,EF ⊂平面EFGH ,故11//A D 平面EFGH ,故A 正确. 因为在直角三角1BA C 中,122A B =2BC = ,190A BC ∠=︒, 1A C 与BC 不垂直,故1A C 与GH 不垂直,故1A C ⊥平面EFGH 不成立,故B 错误.由正方体1111ABCD A B C D -可得BC ⊥平面11AA B B ,而1A B ⊂平面11AA B B , 所以1BC A B ⊥,所以1EF A B ⊥在正方形11AA B B 中,因为,E H 分别为1,AB BB 的中点,故1EH A B ⊥, 因为EFEH E =,故1A B ⊥平面EFGH ,所以BEH ∠为直线AB 与平面EFGH 所成的角,而45BEH ∠=︒, 故直线AB 与平面EFGH 所成的角为45︒,因为11//AB A B ,故11A B 与平面EFGH 所成的角的大小为45°.故C 正确. 因为,,,E F G H 分别为所在棱的中点,故几何体BHE CGF -为三棱柱, 其体积为111212⨯⨯⨯=,而正方体的体积为8, 故平面EFGH 将正方体1111ABCD A B C D -分成两部分的体积的比为1:7,故D 正确. 故选:ACD. 【点睛】本题考查空间中线面位置的判断、空间角的计算和体积的计算,注意根据球的半径确定哪些棱与球面有交点,本题属于中档题.10.已知正方体1111ABCD A B C D -棱长为2,如图,M 为1CC 上的动点,AM ⊥平面α.下面说法正确的是()A .直线AB 与平面α所成角的正弦值范围为32⎣⎦B .点M 与点1C 重合时,平面α截正方体所得的截面,其面积越大,周长就越大 C .点M 为1CC 的中点时,若平面α经过点B ,则平面α截正方体所得截面图形是等腰梯形D .已知N 为1DD 中点,当AM MN +的和最小时,M 为1CC 的中点 【答案】AC 【分析】以点D 为坐标原点,DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立空间直角坐标系D xyz -,利用空间向量法可判断A 选项的正误;证明出1AC ⊥平面1A BD ,分别取棱11A D 、11A B 、1BB 、BC 、CD 、1DD 的中点E 、F 、Q 、N 、G 、H ,比较1A BD 和六边形EFQNGH 的周长和面积的大小,可判断B 选项的正误;利用空间向量法找出平面α与棱11A D 、11A B 的交点E 、F ,判断四边形BDEF 的形状可判断C 选项的正误;将矩形11ACC A 与矩形11CC D D 延展为一个平面,利用A 、M 、N 三点共线得知AM MN +最短,利用平行线分线段成比例定理求得MC ,可判断D 选项的正误.【详解】对于A 选项,以点D 为坐标原点,DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立空间直角坐标系D xyz -,则点()2,0,0A 、()2,2,0B 、设点()()0,2,02M a a ≤≤,AM ⊥平面α,则AM 为平面α的一个法向量,且()2,2,AM a =-,()0,2,0AB =,2232cos ,,32288AB AMAB AM AB AM a a ⋅<>===⎢⋅⨯++⎣⎦, 所以,直线AB 与平面α所成角的正弦值范围为32⎣⎦,A 选项正确; 对于B 选项,当M 与1CC 重合时,连接1A D 、BD 、1A B 、AC ,在正方体1111ABCD A B C D -中,1CC ⊥平面ABCD ,BD ⊂平面ABCD ,1BD CC ∴⊥,四边形ABCD 是正方形,则BD AC ⊥,1CC AC C =,BD ∴⊥平面1ACC , 1AC ⊂平面1ACC ,1AC BD ∴⊥,同理可证11AC A D ⊥,1A D BD D ⋂=,1AC ∴⊥平面1A BD ,易知1A BD 是边长为22的等边三角形,其面积为()12322234A BD S =⨯=△,周长为22362⨯=.设E 、F 、Q 、N 、G 、H 分别为棱11A D 、11A B 、1BB 、BC 、CD 、1DD 的中点,易知六边形EFQNGH 是边长为2的正六边形,且平面//EFQNGH 平面1A BD ,正六边形EFQNGH 的周长为62,面积为()236233⨯⨯=,则1A BD 的面积小于正六边形EFQNGH 的面积,它们的周长相等,B 选项错误; 对于C 选项,设平面α交棱11A D 于点(),0,2E b ,点()0,2,1M ,()2,2,1AM =-,AM ⊥平面α,DE ⊂平面α,AM DE ∴⊥,即220AM DE b ⋅=-+=,得1b =,()1,0,2E ∴,所以,点E 为棱11A D 的中点,同理可知,点F 为棱11A B 的中点,则()2,1,2F ,()1,1,0EF =,而()2,2,0DB =,12EF DB ∴=,//EF DB ∴且EF DB ≠, 由空间中两点间的距离公式可得2222015DE =++=,()()()2222212205BF =-+-+-=,DE BF ∴=,所以,四边形BDEF 为等腰梯形,C 选项正确;对于D 选项,将矩形11ACC A 与矩形11CC D D 延展为一个平面,如下图所示:若AM MN +最短,则A 、M 、N 三点共线,11//CC DD ,2222222MC AC DN AD ∴===+, 11222MC CC =≠,所以,点M 不是棱1CC 的中点,D 选项错误. 故选:AC.【点睛】本题考查线面角正弦值的取值范围,同时也考查了平面截正方体的截面问题以及折线段长的最小值问题,考查空间想象能力与计算能力,属于难题.。
江苏省海门中学高三数学(苏教版)高考考点针对练习:解三角形

直击高考之解三角形◆考点剖析解三角形是传统的高中数学内容,也是历届高考数学的必考内容,常考题型有以选择题、填空题形式的小题,也有解答题形式的大题,试题特殊留意与三角变换、三角函数的图象与性质的融汇和整合,现举例解析如下:例1、(2010年北京卷)在ABC ∆中,若32,3,1π=∠==C c b ,则=a 。
分析:直接应用余弦定理建立方程即可获解:解:由余弦定理得C ab b a c cos 2222-+=,则)21(2132--+=a a ,即022=-+a a ,解之得:1=a 或2-=a (设去),故1=a 。
点评:本题考查余弦定理等学问点及方程思想的应用。
例2、(2010天津卷)在ABC ∆中,内角C B A ,,的对边分别是c b a ,,,若B C bc b a sin 32sin ,322==-,则=AA 、030B 、060C 、0120D 、0150分析:用正弦定理将B C sin 32sin =化为边的关系,再用余弦定理进行求解: 解:由正弦定理可将B C sin 32sin =化为b c 32=,将其代入bc b a 322=-可得b b b a 32322⨯=-,即b a 7=,再由余弦定理得:A bc c b a cos 2222-+=,将ba b c 7,32==代入并化简可得23cos =A ,则030=A ,应选答案A 。
点评:本题重点考查和检测正弦定理和余弦定理等学问点及整体代换的数学思想的应用。
例3、(2010全国课标卷)在ABC ∆中,D 为BC 上的一点,2,120,210==∠=AD ADB DC BD 。
若ADC ∆的面积为33-,求BAC ∠的值。
分析:可先设x DB =,用面积公式建立方程求出x ,再用余弦定理求出AC AB ,,最终求出BAC ∠的值。
解:(1)设x DB =,则x CD 2=,因0120=∠ADB ,故060=∠ADC ,由ADC ∆的面积为33-可得3360sin 22210-=⨯⨯x ,则13-=x ,在ADC ∆由中用余弦定理得:3122421)13(222)232(460cos 222222-=⨯-⨯⨯--+=⋅-+=DC AD DC AD AC ,即)13(631224-=-=AC ,在ADB ∆中用余弦定理得:6)21()13(22)13(4120cos 222222=-⨯-⨯--+=⋅-+=DB AD DB AD AB ,即6=AB ,在ABC∆中,21)13(662)13(93122462cos 2222=-⋅⋅---+=⋅-+=∠AC AB BC AC AB BAC ,所以060=∠BAC ,故求BAC ∠的值为060。
2020年高考数学一轮总复习三角函数、三角形、平面向量专题20平面向量的解题技法文(含解析)

专题16 平面向量的解题技法一、本专题要特别小心:1.平面向量的几何意义应用2. 平面向量与三角形的心3. 向量垂直的应用4.向量的数量积问题等综合问题5. 向量夹角为锐角、钝角时注意问题6.向量数量积在解析几何中应用7.向量数量积在三角形中的应用。
二.【学习目标】1.会用向量方法解决某些简单的平面几何问题.2.会用向量方法解决简单的力学问题与其他一些实际问题三.【方法总结】1.用向量解决平面几何问题的步骤(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;(2)通过向量运算,研究几何元素之间的关系,如距离、夹角等问题;(3)把运算结果“翻译”成几何关系.2.应用向量解决问题的关键是要构造合适的向量,观察条件和结构,选择使用向量的某些性质解决相应的问题,如用数量积解决垂直、夹角问题,用三角形法则、模长公式解决平面几何线段长度问题,用向量共线解决三点共线问题等,总之,要应用向量,如果题设条件中有向量,则可以联想性质直接使用,如果没有向量,则更需要有向量工具的应用意识,强化知识的联系,善于构造向量解决问题.3.几点注意事项(1)在处理三点共线问题时,转化为两个向量共线解决,需说明两个向量有公共点,两直线不能平行,只能重合.(2)在解决夹角问题时,应注意向量的方向,向量的夹角与所求角可能相等,也可能互补.(3)证明垂直问题一般要经过向量的运算得到数量积a·b=0,尽量用坐标运算.四.【题型方法】(一)平面向量的几何意义法例1. 如图,AB,CD是半径为1的圆O的两条直径,,则的值是()A.B.C.D.【答案】B【解析】,选B.练习1. 如图,平行四边形ABCD的对角线相交于点O,E是OD的中点,AE的延长线与CD相交于点若,,,则( )A. B. C. D.【答案】D【解析】,,,,为直角三角形,且,,平行行四边形ABCD的对角线相交于点O,E是OD的中点,,,∴,,,故选:D.练习2.已知D,E,F分别是△ABC的边BC,CA,AB的中点,且,,则①=--;②=+;③=-+;④++=0.其中正确的等式的个数为( )A.1 B.2 C.3 D.4【答案】D【解析】①如图可知=+=+=--=--,故①正确.②=+=+=+,故②正确.③=+=+=+(--)=-+,故③正确.④++=-++=-(+)++=-(+)++-+=0,故④正确.故选:D.(二)平面向量坐标法例2. 如图,圆是边长为的等边三角形的内切圆,其与边相切于点,点为圆上任意一点,,则的最大值为()A.B.C.2 D.【答案】C【解析】以D点为原点,BC所在直线为x轴,AD所在直线为y轴,建立坐标系,设内切圆的半径为1,以(0,1)为圆心,1为半径的圆;根据三角形面积公式得到,可得到内切圆的半径为可得到点的坐标为:故得到故得到,故最大值为:2.故答案为:C.练习1. 如图,在正方形ABCD中,E为AB的中点,P为以A为圆心、AB为半径的圆弧上的任意一点,设向量=λ+μ,则λ+μ的最小值为( )A.B.C.D.【答案】B【解析】以A为原点,以AB所在的直线为x轴,建立直角坐标系,设正方形ABCD的边长为1,则C(1,1),D(0,1),A(0,0),B(1,0).E为AB的中点,得设 P(cosθ,sinθ),∴=(1,1).再由向量=λ(,﹣1)+μ(cosθ,sinθ)=(+μcosθ,﹣λ+μsinθ )=(1,1),∴,∴.由题意得.,得=0,故λ+μ在[0,]上是增函数,当θ=0时,即cosθ=1,这时λ+μ取最小值为,当θ=时,即cosθ=0,这时λ+μ取最大值为,故λ+μ的取值范围为[,5]故选:B.练习2. 已知,,,,为外接圆上的一动点,且,则的最大值是()A.B.C.D.【答案】B【解析】以的中点为原点,以为轴,建立如图所示的平面直角坐标系,则外接圆的方程为,设的坐标为,过点作垂直轴,∵,∴,,∴,∴,∵,∴,,∵,∴∴,,∴,,∴,其中,,当时,有最大值,最大值为,故选:B.练习3.已知正方形ABCD的边长为1,动点P满足,若,则的最大值为A.B.C.D.【答案】C【解析】以A为原点建立如图所示的直角坐标系:则,,,,设, ,则由得,化简得:,又,,,,表示圆上的点到原点的距离得平方,其最大值等于圆心到原点的距离加半径的平方,即,故选:C.练习4.如图,原点是内一点,顶点在上, , , , , ,若,则()A.B.C.D.【答案】D【解析】建立如图所示的直角坐标系,则A(2,0),B(﹣,),C(﹣,﹣),因为,由向量相等的坐标表示可得:,得,即=,故选:D.练习5.点是平行四边形所在平面上一点,且,若,,,则__________.【答案】【解析】方法一:如图,以为轴建立直角坐标系,由题意可得各点坐标如下:,,,,设,因为,所以,所以解得即,所以,,所以.方法二:因为,所以,所以,所以;.所以(三)平面向量基本定理综合应用例3.已知A、B、P三点共线,O为任意一点,若求证;如图所示,已知中,点B关于点A的对称点为C,D在线段OB上,且,DC和OA相交于点设,.若,求实数的值.【答案】(1)见解析;(2)=【解析】证明:、B、P三点共线,可设,,又,,;解:由C、D、E三点共线,可设,,,又,,,,而,,,解得,故实数=.练习1. 如图,在中,D为BC的中点,G为AD的中点,过点G任作一直线MN分别交AB,AC于M,N 两点,若,,试问:是否为定值?【答案】见解析.【解析】设,,则,,.所以,.因为与共线,且不共线,所以有即,得,所以为定值.(四)向量综合例4.如图所示,在中,,点在线段上,设,,,则的最小值为()A.B.C.D.【答案】D【解析】.∵,,三点共线,∴.即.由图可知.∴.令,得,令得或(舍).当时,,当时,.∴当时,取得最小值.故选:D.练习1,。
三角形与平面向量结合问题

三角形与平面向量结合问题【典例1】【2021·宁夏长庆高级中学高三月考】已知向量()2sin ,1m A =,()sin ,3n A A =-,m n ⊥,其中A 是ABC 的内角. (1)求角A 的大小;(2)若角A ,B ,C 所对的边分别为a ,b ,c ,且2a =0AB BC ⋅>,求b c +的取值范围. 【思路引导】(1)由m n ⊥和三角恒等变换可得答案; (2)由0AB BC ⋅>和3A π=可得223B ππ<<,然后由正弦定理可得2sin sin 36b c B B B ππ⎛⎫⎛⎫+=+-=+ ⎪ ⎪⎝⎭⎝⎭,然后利用三角函数的知识可得答案.【典例2】【2021·江苏苏州市·星海实验中学高三月考】 已知O 内接ABC ,点D 为边BC 上一点,点E 为边AC 中点,AD 与BE 交于点P ,且4BP PE =.(Ⅰ)若AD xAB yAC =+(x ,y ∈R ),求y x -的值;(Ⅱ)若2AB AC ==,则AO AD ⋅是否为定值?若是,求出这个值;若不是,请说明理由. 【思路引导】(Ⅰ)根据平面向量基本定理,由向量的运算法则,先得到2255BP BC BA =+,设BC tBD =,根据三点共线的充要条件,得到32t =,再由向量运算法则,用AB 和AC 表示出AD ,结合题中条件,即可得出结果;(Ⅱ)根据向量数量积的几何意义,得到212AO AB AB ⋅=,212AO AC AC ⋅=,即可根据(Ⅰ)的结果,求出AO AD ⋅的值.【典例3】【2021·浙江省宁海中学高三月考】在ABC 中,角,,A B C 的对边分别是,,a b c ,sin sin 2B Cb a B +=,3BC =,如图所示,点D 在线段AC 上,满足AB AD =.(1)求A 的值;(2)若2BD CD =,求AB CB ⋅的值.【思路引导】(1)利用正弦定理边化角,结合诱导公式和二倍角公式可求得sin2A,进而得到A ; (2)在ABC 中利用余弦定理可求得DC ,从而求得cos B ,由平面向量数量积的定义可计算求得结果.【典例4】【陕西省安康市2019-2020学年高三上学期12月阶段性考试】在平面直角坐标系xOy 中,设ABC 的内角,,A B C 所对的边分别为,,a b c ,且3a b c +=,22sin 3sin sin C A B =.(1)求C ;(2)设()1,cos P A -,()cos ,1Q A -,且A C ≤,OP 与OQ 的夹角为θ,求cos θ的值. 【思路引导】(1)利用正弦定理得232c ab =.再由3a b c +=平方与余弦定理求得cos C 进而求得C 即可. (2)将(1)所得的3C π=代入条件即可求得30A =︒,90B =︒.再利用平面向量的公式求解cos θ即可.【典例5】【2019届重庆市巴蜀中学高三上学期第三次月考】 在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且12cos 2sin 22=+⎪⎭⎫⎝⎛+C B A ,a =1,b =2.(1)求∠C 和边c ;(2)若BC BM 4=,BA BN 3=,且点P 为△BMN 内切圆上一点,求222PC PB PA ++的最值. 【思路引导】(1)利用倍角公式和三角函数的诱导公式将12cos 2sin 22=+⎪⎭⎫⎝⎛+C B A 进行化简可得,一个关于C cos 的一元二次方程,进而可求解出C cos ,即可求出∠C 的大小;然后应用余弦定理即可求出边长c ;(2)建立坐标系,由已知向量的关系BC BM 4=,BA BN 3=可得,N M ,点的坐标,即可求出△BMN 的内切圆方程,运用参数方程[)πθθθ2,0,sin 1cos 1∈⎩⎨⎧+=+=y x ,将其代入所求式子222PC PB PA ++中并化简整理得)sin(324643211ϕθ+-+-,再由三角函数的值域为]1,1[-,故所求式子的最大值即可求出.【典例6】【2021·江苏淮安市·高三月考】如图,已知正方形ABCD 的边长为2,过中心O 的直线l 与两边AB CD 、分别交于交于点M N 、.(1)求BD DC →→⋅的值;(2)若Q 是BC 的中点,求QM QN ⋅的取值范围;(3)若P 是平面上一点,且满足()21OP OB OC λλ=+-,求PM PN ⋅的最小值.【思路引导】(1)把BC BD CD →→→=+代入BD DC →→⋅中,再由平面向量的数量积公式,即可求解; (2)由题可知点O 为线段MN 的中点,故根据向量的线性运算有22QO OM QO ON QM QN QO OM →→→→→→→→⎛⎫⎛⎫⋅=+⋅+=- ⎪ ⎪⎝⎭⎝⎭,进而求出向量,QO OM →→的模长范围,即可求解;(3)由22PO OM PO ON PM PN PO OM →→→→→→→→⎛⎫⎛⎫⋅=+⋅+=- ⎪ ⎪⎝⎭⎝⎭,进而求出向量,PO OM →→的模长范围,即可求得PM PN ⋅的最小值.【典例7】【广东省珠海市2019-2020学年高三上学期期末】已知A 、B 、C 是ABC ∆的内角,a 、b 、c 分别是其对边长,向量(),m a b c =+,()sin sin ,sin sin n B A C B =--,且m n ⊥.(1)求角A 的大小;(2)若2a =,求ABC ∆面积的最大值. 【思路引导】(1)由m n ⊥得出()()()sin sin sin sin 0a b B A c C B +-+-=,利用正弦定理边角互化思想以及余弦定理可得出cos A 的值,结合角A 的取值范围可得出角A 的大小;(2)利用余弦定理结合基本不等式可求出bc 的最大值,再利用三角形的面积公式可得出答案.1. 【2021·辽宁沈阳市高三年级模拟考试】()在ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,且(2cos cos ,1)m A C =-,(tan tan 1,1)n A C =-,m n ⊥.(1)求B 的大小;(2)若7b =,133sin sin 14A C +=,求ABC 的面积. 【思路引导】(1)由向量垂直可得0m n ⋅=,从而可求得答案. (2)由正弦定理结合条件可得13a c ,再由余弦定理可得出40ac =,从而可得面积.2. 【四川省德阳市2018届高三三校联合测试数学】在ABC ∆中,角A B C ,,所对的边分别为a b c ,,,且()cos 3cos a B c b A =-. (1)求cos A 的值;(2)若3b =,点M 在线段BC 上, 2AB AC AM +=, 32AM =求ABC ∆的面积.3. 【山西省太原市太原一中高三一模模拟】在锐角三角形ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,向量()cos ,cos m C A =与()2,n b c a =-平行.(Ⅰ)求角A 的大小; (Ⅱ)求b c的取值范围.【思路引导】(Ⅰ)由向量//m n 和正弦定理,求得sin 2sin cos 0B B A -⋅=,进而得到1cos 2A =,即可求解;(Ⅱ)根据ABC 为锐角三角形,求得62C ππ<<,利用三角恒等变换的公式,化简得到312b c =+,进而求得b c的取值范围.4. 【江苏省盐城市盐城中学2019-2020学年高三11月月考】如图,在ABC ∆中,120BAC ∠=︒,2AB =,1AC =,D 是边BC 上一点,2DC BD =.(1)求AD BC ⋅的值;(2)若()0AB tCD CD -⋅=,求实数t 的值. 【思路引导】(1)将,AD BC 都转化为用,AB AC 为基底表示,根据向量数量积的运算,求得AD BC ⋅的值. (2)将原方程()0AB tCD CD -⋅=转化为2AB CD t CD⋅=,同(1)的方法,将CD 转化为用,AB AC 为基底表示,根据向量数量积和模的运算,求出t 的值.5. 【湖南省张家界市2018届高三第三次模拟考】已知ABC ∆中,3B π=.(Ⅰ)若12AB AC ==,求ABC ∆的面积;(II )若4,,AB BM MN NC AN ====,求AM 的长.【思路引导】(1)由余弦定理得到BC =ABC 是直角三角形,根据公式求得面积;(2)设BM x =,则2BN x =,AN =,由余弦公式得到1BM =,AM =.6. 【2021·平罗中学高三期末】在ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,已知向量()3,m a c b =-,()cos ,cos n B C =-,且m n ⊥.(1)求sin B 的值;(2)若2b =,ABC ABC 的周长. 【思路引导】(1)利用向量的数量积以及正弦定理可得()3sin sin cos sin cos 0A C B B C --=,再由两角和的正弦公式以及三角形内角和性质即可求解.(2)利用余弦定理可得22243a c ac =+-,再由三角形的面积公式即可求解.7. 【辽宁省沈阳市交联体2018届高三上学期期中考试】已知函数2()cos 2cos 1f x x x x =--,()x R ∈(1)当[0,]2x π∈时,求函数()f x 的最小值和最大值;(2)设ABC ∆的内角,,A B C 的对应边分别为,,a b c ,且c =()0f C =,若向量(1,sin )m A =与向量(2,sin )n B =共线,求,a b 的值.【思路引导】(1)利用二倍角公式及化一公式,化简()f x 的表达式,再结合正弦函数的图象,在给定区域上求最值;(2)由()0f C =,解得C 角,利用共线条件及正弦定理得到b=2a ,再利用余弦定理解得,a b 的值.8. 在ABC ∆中,CA CB CA CB +=-. (1) 求角C 的大小;(2)若CD AB ⊥,垂足为D ,且4CD =,求ABC ∆面积的最小值.【思路引导】(1)由CA CB CA CB +=-,两边平方22CA CB CA CB +=-,整理可得0CA CB ⋅=,即CA CB ⊥,从而可得2C π∠=;(2)在直角ADC ∆与直角BDC ∆中中, 4sin sin CD AC A A== ,4sin sin CD BC B B== ,从而可得114481622sin sin sin cos sin2ABCS CA CB A B A A A∆=⋅=⋅⋅==,根据三角函数的有界性可得ABC ∆面积的最小值.9. 【2021·赣州市赣县第三中学高三月考】在ABC 中,角,,A B C 的对边分别为,,a b c ,已知向量(cos ,cos )m A B =,(,2)n a c b =-,且//m n .(1)求角A 的大小;(2)若4a =,且三角形周长为10时,求ABC 面积.【思路引导】(1)由平行向量的坐标关系,得到边角等量关系,利用正弦定理边化角,再由两角和的正弦公式化简,求出cos A ,即可求解;(2)由已知可得6b c +=,再由,a A 结合余弦定理,求出bc ,进而求出ABC 面积.10. 【2021·浙江省嵊州市高三上学期期末考试】 在三角形ABC 中,2,1,2AB AC ACD π==∠=,D 是线段BC 上一点,且12BD DC =,F 为线段AB 上一点.(1)若AD xAB yAC =+,求x y -的值; (2)求CF FA ⋅的取值范围;【思路引导】(1)根据平面向量基本定理,由题中条件,得到2133AD AB AC =+,从而可求出,x y 的值,进而可求得x y -的值; (2)根据题意先求出,33CAB BC π∠==,设AF x =,再由平面向量数量积运算,即可求得结果参考答案【典例1】【2021·宁夏长庆高级中学高三月考】已知向量()2sin ,1m A =,()sin ,3n A A =-,m n ⊥,其中A 是ABC 的内角. (1)求角A 的大小;(2)若角A ,B ,C 所对的边分别为a ,b ,c,且a =0AB BC ⋅>,求b c +的取值范围. 【思路引导】(1)由m n ⊥和三角恒等变换可得答案; (2)由0AB BC ⋅>和3A π=可得223B ππ<<,然后由正弦定理可得2sin sin 36b c B B B ππ⎛⎫⎛⎫+=+-=+ ⎪ ⎪⎝⎭⎝⎭,然后利用三角函数的知识可得答案.【解析】(1)因为()22sin sin 32sin cos 31cos 223m n A A A A A A A A ⋅=-=+-=-+-2sin 2206A π⎛⎫=--= ⎪⎝⎭,即有2262A k πππ-=+,(k Z ∈),3A k ππ=+,(k Z ∈),又A 为ABC 的内角,所以3A π=; (2)由0AB BC ⋅>,得B 为钝角,从而223B ππ<<由正弦定理,得21sin sin sin 3b cB C π===所以sin b B =,2sin sin 3c C B π⎛⎫==-⎪⎝⎭,则2sin sin 36b c B B B ππ⎛⎫⎛⎫+=+-=+⎪ ⎪⎝⎭⎝⎭又223B ππ<<,所以25366B πππ<+<,则32b c ⎫+∈⎪⎪⎝⎭【典例2】【2021·江苏苏州市·星海实验中学高三月考】已知O 内接ABC ,点D 为边BC 上一点,点E 为边AC 中点,AD 与BE 交于点P ,且4BP PE =. (Ⅰ)若AD xAB yAC =+(x ,y ∈R ),求y x -的值;(Ⅱ)若2AB AC ==,则AO AD ⋅是否为定值?若是,求出这个值;若不是,请说明理由.【思路引导】(Ⅰ)根据平面向量基本定理,由向量的运算法则,先得到2255BP BC BA =+,设BC tBD =,根据三点共线的充要条件,得到32t =,再由向量运算法则,用AB 和AC 表示出AD ,结合题中条件,即可得出结果;(Ⅱ)根据向量数量积的几何意义,得到212AO AB AB ⋅=,212AO AC AC ⋅=,即可根据(Ⅰ)的结果,求出AO AD ⋅的值.【解析】(Ⅰ)因为点E 为边AC 中点,AD 与BE 交于点P ,且4BP PE =,所以()4412255255BP BE BC BA BC BA ==⨯+=+, 又点D 为边BC 上一点,所以存在实数t ,使得BC tBD =,因此22225555BP BC BA tBD BA =+=+, 因为A ,P ,D 三点共线,所以22155t +=,则32t =, 即32BC BD =,所以()32AC AB AD AB -=-,整理得:1233AD AB AC =+, 又AD xAB yAC =+,所以1323x y ⎧=⎪⎪⎨⎪=⎪⎩,因此13y x -=; (Ⅱ)分别取AB ,AC 的中点M ,N ,连接OM ,ON ,则OM AB ⊥,ON AC ⊥, 所以212AO AB AB ⋅=,212AO AC AC ⋅=, 又2AB AC ==, 所以22121211333363AO AD AO AB AC AO AB AO AC AB AC ⎛⎫⋅=⋅+=⋅+⋅=+ ⎪⎝⎭44263=+=.【典例3】【2021·浙江省宁海中学高三月考】在ABC 中,角,,A B C 的对边分别是,,a b c ,sin sin 2B C b a B +=,3BC =,如图所示,点D 在线段AC 上,满足AB AD =.(1)求A 的值;(2)若2BD CD =,求AB CB ⋅的值.【思路引导】(1)利用正弦定理边化角,结合诱导公式和二倍角公式可求得sin 2A ,进而得到A ; (2)在ABC 中利用余弦定理可求得DC ,从而求得cosB ,由平面向量数量积的定义可计算求得结果.【解析】(1)由正弦定理得:sin sin sin sin 2B C B A B +=, B C A π+=-,sin sin cos 2222B C A A π+⎛⎫=-= ⎪⎝⎭, 又()0,B π∈,sin 0B ∴≠,cos sin 2sin cos 222A A A A ∴==, 0,22A π⎛⎫∈ ⎪⎝⎭,cos 02A ∴≠,1sin 22A ∴=, 26A π∴=,解得:3A π=. (2)AB AD =,3A π=,ABD ∴为等边三角形, 设DC x =,则2BD AB AD x ===,在ABC 中,由余弦定理得:2222222cos 4969BC AB AC AB AC A x x x =+-⋅=+-=,解得:377x =7AB ∴=,7=AC,222cos 214AB BC AC B AB BC +-∴==⋅,9cos 37AB CB AB BC B ∴⋅=⋅==. 【典例4】【陕西省安康市2019-2020学年高三上学期12月阶段性考试】在平面直角坐标系xOy 中,设ABC 的内角,,A BC 所对的边分别为,,a b c ,且a b +=,22sin 3sin sin C A B =.(1)求C ;(2)设()1,cos P A -,()cos ,1Q A -,且A C ≤,OP 与OQ 的夹角为θ,求cos θ的值.【思路引导】(1)利用正弦定理得232c ab =.再由a b +=平方与余弦定理求得cos C 进而求得C 即可. (2)将(1)所得的3C π=代入条件即可求得30A =︒,90B =︒.再利用平面向量的公式求解cos θ即可.解:(1)∵22sin 3sin sin C A B =∴23sin sin sin 2C A B =∴由正弦定理得232c ab =∵a b +=∴22223a b ab c ++= 根据余弦定理得:2222221cos 2222a b c c ab ab C ab ab ab +--==== ∴3C π=(2)由(1)知3C π=,代入已知,并结合正弦定理得3sin sin 21sin sin 2A B A B ⎧+=⎪⎪⎨⎪=⎪⎩,解得1sin 2A =或sin 1A =(舍去) 所以30A =︒,90B =︒ ∴2cos OP OQ A ⋅==而27||||11cos 4OP OQ A ⋅=+=+=∴22cos cos 1cos 4A A θ===+.【典例5】【2019届重庆市巴蜀中学高三上学期第三次月考】在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且12cos 2sin 22=+⎪⎭⎫⎝⎛+C B A ,a =1,b =2. (1)求∠C 和边c ;(2)若BC BM 4=,=且点P 为△BMN的最值.【思路引导】(1)利用倍角公式和三角函数的诱导公式将12cos 2sin 22=+⎪⎭⎫ ⎝⎛+C B A 进行化简可得,一个关于C cos 的一元二次方程,进而可求解出C cos ,即可求出∠C 的大小;然后应用余弦定理即可求出边长c ;(2)建立坐标系,由已知向量的关系4=,=可得,N M ,点的坐标,即可求出△BMN 的内切圆方程,运用参数方程[)πθθθ2,0,sin 1cos 1∈⎩⎨⎧+=+=y x ,+中并化简整理得)sin(324643211ϕθ+-+-,再由三角函数的值域为]1,1[-,故所求式子的最大值即可求出. 解:(1)因为12cos 2sin 22=+⎪⎭⎫ ⎝⎛+C B A , 所以C B A B A C cos )cos(2sin 212cos 2-=+=⎪⎭⎫ ⎝⎛+-=,所以01cos cos 22=-+C C ,所以1cos -=C 或21cos =C , 又因为),0(π∈C ,所以21cos =C ,所以3π=C .由余弦定理可得,3cos 222=-+=C ab b a c . 建立坐标系,由(1)A ()())1,0(,0,0,0,3C B ,由4=,BN = ()0,3),4,0(N M ,△BMN 的内切圆方程为:()()11122=-+-y x ,设),(y x P ,则令[)πθθθ2,0,sin 1cos 1∈⎩⎨⎧+=+=y x()()22222222213-+++++-=++y x y x y x PC PB PA ()θθcos 326sin 4321142323322-++-=+--+=y x y x ()324643211sin 324643211-+-≤+-+-=ϕθ【典例6】【2021·江苏淮安市·高三月考】如图,已知正方形ABCD 的边长为2,过中心O 的直线l 与两边AB CD 、分别交于交于点M N 、.(1)求BD DC →→⋅的值;(2)若Q 是BC 的中点,求QM QN ⋅的取值范围;(3)若P 是平面上一点,且满足()21OP OB OC λλ=+-,求PM PN ⋅的最小值.【思路引导】(1)把BC BD CD →→→=+代入BD DC →→⋅中,再由平面向量的数量积公式,即可求解;(2)由题可知点O 为线段MN 的中点,故根据向量的线性运算有22QO OM QO ON QM QN QO OM →→→→→→→→⎛⎫⎛⎫⋅=+⋅+=- ⎪ ⎪⎝⎭⎝⎭,进而求出向量,QO OM →→的模长范围,即可求解; (3)由22PO OM PO ON PM PN PO OM →→→→→→→→⎛⎫⎛⎫⋅=+⋅+=- ⎪ ⎪⎝⎭⎝⎭,进而求出向量,PO OM →→的模长范围,即可求得PM PN ⋅的最小值.【解析】(1)由题意可得:24BC CD DC CD BD DC →→→→→→⎛⎫⋅=+⋅=-=- ⎪⎝⎭; (2) 在正方形ABCD 中,过中心O 的直线l 与两边AB CD 、分别交于交于点M N 、.∴点O 为线段MN 的中点∴22QO OM QO ON QM QN QO OM →→→→→→→→⎛⎫⎛⎫⋅=+⋅+=- ⎪ ⎪⎝⎭⎝⎭. 又正方形ABCD 的边长为2,Q 是BC 的中点,1QO ∴=,12OM ≤≤10QM QN ∴-≤⋅≤.即QM QN ⋅的取值范围为[]1,0-.(3)由题可得22PO OM PO ON PM PN PO OM →→→→→→→→⎛⎫⎛⎫⋅=+⋅+=- ⎪ ⎪⎝⎭⎝⎭ 令2OT OP →→=,由()21OT OP OB OC λλ→→→→==+-,可知点T 在BC 上, 1OT ∴≥.从而1.2OP →≥1OM →≤≤2217244PM PN PO OM ⋅=-≥-=-. ∴PM PN ⋅的最小值为74-. 【典例7】【广东省珠海市2019-2020学年高三上学期期末】已知A 、B 、C 是ABC ∆的内角,a 、b 、c 分别是其对边长,向量(),m a b c =+,()sin sin ,sin sin n B A C B =--,且m n ⊥.(1)求角A 的大小;(2)若2a =,求ABC ∆面积的最大值.【思路引导】(1)由m n ⊥得出()()()sin sin sin sin 0a b B A c C B +-+-=,利用正弦定理边角互化思想以及余弦定理可得出cos A 的值,结合角A 的取值范围可得出角A 的大小;(2)利用余弦定理结合基本不等式可求出bc 的最大值,再利用三角形的面积公式可得出答案.解:(1)(),m a b c =+,()sin sin ,sin sin n B A C B =--,m n ⊥,()()()sin sin sin sin 0a b B A c C B ∴+-+-=,由正弦定理得()()()0b a b a c c b +-+-=,整理得222b c a bc +-=,2221cos 22b c a A bc +-∴==,0A π<<,3A π∴=;(2)在ABC ∆中,3A π=,2a =, 由余弦定理知2222242cos a b c bc A b c bc ==+-=+-,由基本不等式得2242bc b c bc +=+≥,当且仅当b c =时等号成立,4bc ∴≤,11sin 4222ABC S bc A ∆∴=≤⨯⨯=,因此,ABC ∆1. 【2021·辽宁沈阳市高三年级模拟考试】()在ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,且(2cos cos ,1)m A C =-,(tan tan 1,1)n A C =-,m n ⊥.(1)求B 的大小;(2)若7b =,sin sin 14A C +=,求ABC 的面积. 【思路引导】(1)由向量垂直可得0m n ⋅=,从而可求得答案.(2)由正弦定理结合条件可得13a c ,再由余弦定理可得出40ac =,从而可得面积.【解析】(1)由m n ⊥,则0m n ⋅=,即2cos cos (tan tan 1)1m n A C A C ⋅=--2sin sin 2cos cos 1A C A C =--2cos()1A C =-+-2cos 1B =-0=, 1cos 2B ∴=,又(0,)B π∈,3B π∴=(2)7sin sin sin sin 3ac b A C B π====sin 14A a ∴=,sin 14C =sin sinA C +==13a c +=. 又2222cos b a c ac B =+-,即22272cos 3a c ac π=+-,所以40ac =,11sin 40sin 103223ABC S ac B π∴==⨯⨯= 2. 【四川省德阳市2018届高三三校联合测试数学】在ABC ∆中,角A B C ,,所对的边分别为a b c ,,,且()cos 3cos a B c b A =-.(1)求cos A 的值;(2)若3b =,点M 在线段BC 上, 2AB AC AM +=, 32AM =,求ABC ∆的面积. 解:因为()cos 3cos a B c b A =- ,由正弦定理得: ()sin cos 3sin sin cos A B C B A =-即sin cos sin cos 3sin cos A B B A C A +=, sin 3sin cos C C A =在ABC ∆中, sin 0C ≠,所以1cos 3A = 2AB AC AM +=,两边平方得: 22224AB AC AB AC AM ++⋅=由3b =,32AM = 1cos 3A =得219234183c c ++⨯⨯⨯=⨯ 解得:79c c ==-或(舍);所以ABC ∆的面积122737223S =⨯⨯⨯= 3. 【山西省太原市太原一中高三一模模拟】 在锐角三角形ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,向量()cos ,cos m C A =与()2,n b c a =-平行.(Ⅰ)求角A 的大小;(Ⅱ)求bc 的取值范围.【思路引导】(Ⅰ)由向量//m n 和正弦定理,求得sin 2sin cos 0B B A -⋅=,进而得到1cos 2A =,即可求解;(Ⅱ)根据ABC 为锐角三角形,求得62C ππ<<,利用三角恒等变换的公式,化简得到312tan 2b c C =+,进而求得bc 的取值范围.【解析】(Ⅰ)由向量()cos ,cos m C A =与()2,n b c a =-平行,可得()cos 2cos 0a C b c A --=,又由正弦定理得sin cos 2sin cos sin cos 0A C B A C A -⋅+⋅=,即()sin 2sin cos 0A C B A +-⋅=,即sin 2sin cos 0B B A -⋅=.因为(0,)B π∈,可得sin 0B ≠,所以1cos 2A =, 又因为0A π<<,所以3A π=. (Ⅱ)因为ABC 为锐角三角形,可得(0,)22(0,)32C B C πππ⎧∈⎪⎪⎨⎪=-∈⎪⎩,解得62C ππ<<, 则231sin cos sin sin 31322sin sin sin 2C C C b B c C C C π⎛⎫-+ ⎪⎝⎭====+, 又因为,62C ππ⎛⎫∈ ⎪⎝⎭,所以()10,3tan C ∈,可得131222<+<,即122b c <<, 所以bc 的取值范围为1,22⎛⎫ ⎪⎝⎭. 4. 【江苏省盐城市盐城中学2019-2020学年高三11月月考】如图,在ABC ∆中,120BAC ∠=︒,2AB =,1AC =,D 是边BC 上一点,2DC BD =.(1)求AD BC ⋅的值;(2)若()0AB tCD CD -⋅=,求实数t 的值.【思路引导】(1)将,AD BC 都转化为用,AB AC 为基底表示,根据向量数量积的运算,求得AD BC ⋅的值. (2)将原方程()0AB tCD CD -⋅=转化为2AB CDt CD ⋅=,同(1)的方法,将CD 转化为用,AB AC 为基底表示,根据向量数量积和模的运算,求出t 的值.解:(1)D 是边BC 上一点,2DC BD =()1133BD BC AC AB ∴==- ()121333AD AB AC AB AB AC =+-=+ ()2133AD BC AB AC AC AB ⎛⎫∴⋅=+⋅- ⎪⎝⎭22121333AC AB AB AC =-+⋅ 18112cos120333=-+⨯⨯⨯︒18183333=--=-,故83AD BC ⋅=- (2)()0AB tCD CD -⋅=,2AB CDt CD ⋅∴=()2233CD CB AB AC ==-,214212cos1207BC =+-⨯⨯⨯︒= 2222839CD CB ⎛⎫== ⎪⎝∴⎭ 2233AB CD AB AB AC ⎛⎫⋅=⋅- ⎪⎝⎭22233AB AC AB =-⋅821012cos120333=-⨯⨯⨯︒=1514t ∴= 5. 【湖南省张家界市2018届高三第三次模拟考】已知ABC ∆中,3B π=.(Ⅰ)若12AB AC ==,求ABC ∆的面积;(II )若4,,AB BM MN NC AN ====,求AM 的长.【思路引导】(1)由余弦定理得到BC =ABC 是直角三角形,根据公式求得面积;(2)设BM x=,则2BN x =,AN =,由余弦公式得到1BM =,AM=.解析:(Ⅰ)由题意知,22212cosBC B +-= 12=,解得BC = ∴222AC BC AB +=,∴1122ABC S ∆=⨯=(Ⅱ)设BM x =,则2BN x =,AN =.在ABN ∆中,()()22242x =+ 242cos3x π-⋅⋅⋅,解得1x =或2x =-(舍去),∴1BM =.在ABM ∆中,AM ==.6. 【2021·平罗中学高三期末】在ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,已知向量()3,m a c b =-,()cos ,cos n B C =-,且m n ⊥.(1)求sin B 的值;(2)若2b =,ABC 的面积为4ABC 的周长. 【思路引导】(1)利用向量的数量积以及正弦定理可得()3sin sin cos sin cos 0A C B B C --=,再由两角和的正弦公式以及三角形内角和性质即可求解.(2)利用余弦定理可得22243a c ac =+-,再由三角形的面积公式即可求解. 【解析】(1)由m n ⊥,所以()3cos cos 0m n a c B b C ⋅=--=, 由正弦定理可得()3sin sin cos sin cos 0A C B B C --=, 即3sin cos sin cos sin cos A B C B B C --()3sin cos sin 0A B B C =-+=,又()sin sin B C A +=,所以3sin cos sin 0A B A -=, 又()0,A π∈,所以sin 0A ≠,所以1cos 3B =, 又()0,B π∈,所以sin B =. (2)根据余弦定理可知2222cos b a c ac B =+-,所以22243a c ac =+-,即()2843a c ac =+-,又ABC 的面积为64,所以11226sin 2234ac B ac =⨯=, 解得33ac =,所以()()2284423313a c ac +=+=+=+,解得31a c +=+,所以ABC 的周长为33+.7. 【辽宁省沈阳市交联体2018届高三上学期期中考试】 已知函数2()23sin cos 2cos 1f x x x x =--,()x R ∈ (1)当[0,]2x π∈时,求函数()f x 的最小值和最大值;(2)设ABC ∆的内角,,A B C 的对应边分别为,,a b c ,且3c =,()0f C =,若向量(1,sin )m A =与向量(2,sin )n B =共线,求,a b 的值.【思路引导】(1)利用二倍角公式及化一公式,化简()f x 的表达式,再结合正弦函数的图象,在给定区域上求最值;(2)由()0f C =,解得C 角,利用共线条件及正弦定理得到b=2a ,再利用余弦定理解得,a b 的值. 解:(1)当 ,即时,有最小值为当,即时,有最大值为(2)与向量共线由正弦定理得①,由余弦定理可得②①②联立可得8. 在ABC ∆中,CA CB CA CB +=-. (1) 求角C 的大小;(2)若CD AB ⊥,垂足为D ,且4CD =,求ABC ∆面积的最小值.【思路引导】(1)由CA CB CA CB +=-,两边平方22CA CB CA CB +=-,整理可得0CA CB ⋅=,即CA CB ⊥,从而可得2C π∠=;(2)在直角ADC ∆与直角BDC ∆中中, 4sin sin CD AC A A== ,4sin sin CD BC B B== ,从而可得114481622sin sin sin cos sin2ABCS CA CB A B A A A∆=⋅=⋅⋅==,根据三角函数的有界性可得ABC ∆面积的最小值. 解:(1)由CA CB CA CB +=-,两边平方22CA CB CA CB +=-, 即()()22CA CB CA CB +=-,得到20CA CB ⋅=,即CA CB ⊥.所以2C π∠=.(2)在直角ADC ∆中, 4sin sin CD AC A A == , 在直角BDC ∆中, 4sin sin CD BC B B== , 又0,2A π⎛⎫∈ ⎪⎝⎭,所以sin sin cos 2B A A π⎛⎫=-= ⎪⎝⎭,所以114481622sin sin sin cos sin2ABC S CA CB A B A A A∆=⋅=⋅⋅== , 由+2A B π=得,()20,A π∈,故(]sin20,1A ∈,当且仅当4A π=时,()max sin21A =,从而()min 16ABC S ∆= .9. 【2021·赣州市赣县第三中学高三月考】在ABC 中,角,,A B C 的对边分别为,,a b c ,已知向量(cos ,cos )m A B =,(,2)n a c b =-,且//m n .(1)求角A 的大小;(2)若4a =,且三角形周长为10时,求ABC 面积.【思路引导】(1)由平行向量的坐标关系,得到边角等量关系,利用正弦定理边化角,再由两角和的正弦公式化简,求出cos A ,即可求解;(2)由已知可得6b c +=,再由,a A 结合余弦定理,求出bc ,进而求出ABC 面积.【解析】(1)//m n ,所以cos (2)cos 0a B c b A --=,由正弦定理得sin cos (2sin sin )cos 0A B C B A --=,sin cos sin cos 2sin cos A B B A C A ∴+= sin()2sin cos A B C A ∴+=,由A B C π++=,sin 2sin cos C C A ∴=由于0C π<<,因此sin 0C >, 所以1cos 2A =,由于0A π<<,3A π∴= (2)4a =,且三角形周长为10,6b c ∴+=由余弦定理得2222cos a b c bc A =+-2222016()33b c bc b c bc bc ∴=+-=+-⇒=, 因此ABC 面积1120353sin 223S bc A ==⨯⨯=, 因此ABC 面积为533.10. 【2021·浙江省嵊州市高三上学期期末考试】 在三角形ABC 中,2,1,2AB AC ACD π==∠=,D 是线段BC 上一点,且12BD DC =,F 为线段AB 上一点.(1)若AD xAB yAC =+,求x y -的值; (2)求CF FA ⋅的取值范围;【思路引导】(1)根据平面向量基本定理,由题中条件,得到2133AD AB AC =+,从而可求出,x y 的值,进而可求得x y -的值;(2)根据题意先求出,3CAB BC π∠==,设AF x =,再由平面向量数量积运算,即可求得结果【解析】(1)因为12BD DC =,所以1()2AD AB AC AD -=-,得2133AD AB AC =+, 因为AD xAB yAC =+,所以21,33x y ==, 所以13x y -=, (2)因为在三角形ABC 中,2,1,2AB AC ACD π==∠=,所以,3CAB BC π∠==所以()CF FA CA AF FA CA FA AF FA ⋅=+⋅=⋅+⋅,AF x =,由题意得[0,2]x ∈,所以2cos CF FA CA FA AF FA CA FA CAB AF ⋅=⋅+⋅=⋅∠-,221112416x x x ⎛⎫=-=--+ ⎪⎝⎭, 因为[0,2]x ∈,所以21113,41616x ⎛⎫⎡⎤--+∈- ⎪⎢⎥⎝⎭⎣⎦,所以CF FA ⋅的取值范围为13,16⎡⎤-⎢⎥⎣⎦。
平面向量三角函数与解三角形第一讲平面向量课件文20191128290

避误 题时要特别注意两个向量夹角可能是 0 或 π 的情况,如 区 已知两个向量的夹角为钝角时,不仅要求其数量积小于
零,还要求不能反向共线
(二)创新考法
1.已知向量 a 与 b 的夹角为 θ,定义 a×b 为 a 与 b 的“向量
积”,且 a×b 是一个向量,它的长度|a×b|=|a||b|sin θ,若 u
答案:D
2.(2019·浙江宁波期末测试)已知向量O→A,O→B,满足|O→A|=1,
|O→B|=2,∠AOB=π3,M 为△OAB 内一点(包括边界),O→M=
xO→A+yO→B.若O→M·B→A≤-1,则以下结论一定成立的是( )
A.23≤2x+y≤2
B.12x≤y
C.-1≤x-3y
D.23≤x+y≤1
破解平面向量与“解析几何”相交汇问题的常用方法有两种: 一是“转化法”,即把平面向量问题转化为解析几何问题,利 用平面向量的数量积、共线、垂直等的坐标表示进行转化,再 利用解析几何的相关知识给予破解;二是“特值法”,若是选 择题,常可用取特殊值的方法来快速破解.
(2018·高考天津卷)如图,在平面四边形
解析:2a+b=(4,2),因为 答案:12
c∥(2a+b),所以
4λ=2,得
λ=12.
[类题通法] 1.应用平面向量基本定理表示向量的实质是利用 平行四边形法则或三角形法则进行向量的加、减或数乘运 算.一般将向量归结到相关的三角形中,利用三角形法则列出 三个向量之间的关系. 2.用平面向量基本定理解决问题的一般思路:先选择一组基 底,并运用该组基底将条件和结论表示成向量的形式,再通过 向量的运算来解决.注意同一个向量在不同基底下的分解是不 同的,但在每组基底下的分解都是唯一的.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
热点专题1. 三角与平面向量解题突破
1. 设函数()sin(2),[,]66f x x x a ππ=+∈-的值域是1[,1]2-,则实数a 的取值范围为 .[,]62
ππ
2. 如图,梯形ABCD 中,//AB CD ,6AB =,2AD DC ==,若12AC BD ⋅=-uu u r uu u r ,则AD BC ⋅=u u u r u u u r
.0
3.如图,在平面直角坐标系xOy 中,一单位圆的圆心的初始位置在)1,0(,此时圆上一点P 的位置在)0,0(,圆在x 轴上沿正向滚动. 当圆滚动到圆心位于)1,2(时,OP 的坐标为 . (2-sin 2,1-cos 2)
4. 已知π()3sin(2)6f x x =-
,若存在π
(0,)2α∈,使()()f x f x αα+=--
对一切实数x 恒成立,则α= .12
π 5.设ABC ∆的内角,,A B C 所对的边,,a b c 成等比数列,则sin sin B
A
的取值范围是 .5151(,)22-+ 6. 在ABC Rt ∆中,2==CB CA ,N M ,是斜边AB 上的两个动点,且2=MN ,则CN CM ⋅的取值范围
为 .⎣⎡⎦⎤
32,2
7. 若将函数)0)(4sin(>+=ωπ
ωx y 的图象向左平移π6个单位长度后,与函数cos()4y x p w =+的图象重合,则ω的最小值为_____________.3
8. 在ABC ∆中,角C B A ,,的对边分别为c b a ,,且2cos 2,c B a b =-若ABC ∆的面积为3
2
S c =,则ab 的最小值为_________.4
9. 已知O 是锐角△ABC 的外心,且θ=A ,若
AO m AC B
C
AB C B 2sin cos sin cos =+,则=m _____.θsin
10. 在ABC ∆中,角C B A ,,所对的边分别为c b a ,,且c b a b 2sin 2sin log log ,22<>,bc a c b 3222+=+,若
0<⋅BC AB ,则C B sin cos +的取值范围是______.36
22
(
,)
11.已知点)2,2(),0,4(),1,1(C B A -,区域D 由所有满足AC AB AP μλ+=)1,1(b a ≤<≤<μλ的点),(y x P 组成
的区域.若区域D 的面积为8,则b a +的最小值为 .4
12. 在△ABC 中,角C B A 、、所对的边分别为c b a 、、,且c A b B a 2
1
cos cos =
-,当)tan(B A -取最大值时,角C 的值为 . 2
π
13.已知正实数,a c 满足2
2
3a c ac +-=,则2a c +的最大值为 .27
14.设两个向量22
(2,cos )a λλθ=+- 和(,sin )2m b m θ=+ ,其中,,m R λθ∈.若2a b = ,则m
λ的取值范
D
A
B
C
第2
题
第3题
围是 .61m
λ
-≤≤
二、解答题:
15.在ABC ∆中,,,A B C 的对边分别为,,a b c ,且tan (2)tan b A c b B =-. (1)求角A 的大小;
(2)设AD BC ⊥,D 为垂足,若2b =,3c =,求AD AC ⋅u u u r u u u r
的值. 答案:(1)3
A π
∴=
;
(2) 2
27cos 7
AD AC AD AC C AD AD ⋅∠∴⋅=== .
16.如图,在xoy 平面上,点(1,0)A ,点B 在单位圆上,AOB θ∠=(0θπ<<)
(1)若点34(,)55
B -,求tan()4π
θ+的值;
(2)若OA OB OC += ,1813OB OC ⋅= ,求cos()3
π
θ-.
答案:(1)1tan 1
tan()41tan 7πθθθ++==-- ;
(2)5123
cos(
)cos
cos sin
sin 3
3
3
26
π
π
π
θθθ+-=+=
.
17.已知ABC ∆的内角A 的大小为 120,面积为3. (1)若22=AB ,求ABC ∆的另外两条边长;
(2)设O 为ABC ∆的外心,当21BC =时,求AO BC ⋅uuu r uu u r
的值. 解:(1)22222cos 428414BC a b c bc A b c ==+-=++=++=.
(2)由21BC =得22421b c ++=,即22
16170b b +-=,解得1b =或4.
设BC 的中点为D ,则AO AD DO =+uuu r uuu r uuu r
, 因为O 为△ABC 的外心,所以0DO BC ⋅=u u u r u u u r
,
于是()()
22
122b c AO BC AD BC AB AC AC AB -⋅=⋅=+⋅-=uuu r uu u r uuu r uu u r uu u r uuu r uuu r uu u r .
所以当1b =时,4c =,22
1522
b c AO BC -⋅==-uuu r uu u r ;
当4b =时,1c =,2215
22
b c AO BC -⋅==uuu r uu u r .
x
O
y B A
C 第16题图
18.在ABC ∆中,角A B C 、、的对边分别为a b c 、、,已知5
sin 13
B =
,且a b c 、、成等比数列. (1)求
11
tan tan A C
+的值; (2)若cos 12ac B =,求a c +的值.
解:(1)根据题意得,2
b a
c =.由正弦定理得2
sin sin sin B A C =,
11cos cos sin()
tan tan sin sin sin sin A C A C A C A C A C +∴
+=+=
sin 113
sin sin sin 5
B A
C B =
==,
(2)cos 12ac B = cos 0B ∴>5sin 13B =
,12cos 13
B ∴=. 212
13cos b ac B
∴==
=. 由余弦定理得22()22cos b a c ac ac B =+-- 37a c ∴+=
19.已知ABC ∆中,角C B A ,,的对边分别为c b a 、、,且2cos cos cos a B c B b C =+. (1)求角B 的大小; (2)设向量)2cos ,(cos A A m =,)5,12(-=n ,求当n m ⋅取最大值时,C tan 的值.
答案:(1)B =π
4
; (2)7.
20. 已知ABC ∆的三边长,1||,4||,13||===AC BC AB 动点M 满足,CB CA CM μλ+=且4
1=
λμ. (1)求||CM 最小值,并指出此时CM 与CB CA 、的夹角;
(2)是否存在两定点21F F 、使12||MF ||MF ||-
恒为常数K ?若存在,指出常数K 的值,若不存在,说明理由. 解:(1)由余弦定理得:
,
∴,
∵
∴
,
当且仅当时,等号成立,
∴最小值为.
此时设与的夹角分别是、,
当时,
∴,
又,∴.
同理可求,此时.
同理可求,当时,.
综上所得,此时与的夹角,与的夹角.
(2)以C为原点,以的平分线为轴建立平面直角坐标系,如图所示.
则,设,则,,
,∴,又,
又,消去得.
,存在两定点使恒为常数,.。
