时间序列分析上机指导
高效处理时间序列数据的技巧和方法

高效处理时间序列数据的技巧和方法时间序列数据是一种按时间顺序排列的数据,通常是用来描述某一现象在不同时间点上的变化情况。
时间序列数据在很多领域都有着重要的作用,比如金融、经济学、气象学、医学等领域都广泛使用时间序列数据进行分析和预测。
处理时间序列数据需要掌握一些高效的技巧和方法,本文将介绍一些处理时间序列数据的技巧和方法,以及它们在实际应用中的作用。
一、数据预处理在处理时间序列数据之前,首先要对原始数据进行预处理,以确保数据的准确性和可靠性。
数据预处理的步骤包括数据清洗、缺失值处理、异常值处理和数据重采样等。
1.数据清洗数据清洗是指对原始数据进行筛选和处理,去除不需要的数据或者错误的数据。
在处理时间序列数据时,数据清洗的过程包括去除重复数据、去除不必要的字段、对数据进行格式转换等。
清洗后的数据能够更好地反映原始数据的特征,同时也减少了数据处理的难度。
2.缺失值处理时间序列数据中经常会出现缺失值,这些缺失值可能是由于数据采集的问题或者数据损坏等原因造成的。
处理缺失值的方法包括删除缺失值、插值处理和填充处理等。
不同的处理方法会对后续的数据分析和建模产生不同的影响,因此需要根据实际情况选择合适的处理方法。
3.异常值处理异常值是指与其他数据明显不同的数值,可能是由于数据采集错误或者异常事件引起的。
处理异常值的方法包括删除异常值、替换异常值和转换异常值等。
对异常值进行处理可以减少对数据分析的干扰,使得分析结果更加准确。
4.数据重采样数据重采样是指将原始数据的时间间隔进行调整,使得数据变得更加平滑或者更加精细。
数据重采样的方法包括向前采样、向后采样、插值重采样和汇总重采样等。
选择合适的重采样方法可以更好地反映数据的变化趋势,提高数据分析的准确性。
二、特征提取在进行时间序列数据分析之前,需要对数据进行特征提取,以提取出数据的关键特征,为后续的建模和预测提供支持。
特征提取的方法包括统计特征提取、时域特征提取和频域特征提取等。
《时间序列分析》课程教学大纲

《时间序列分析》课程教学大纲一、课程基本信息二、课程教学目标本课程的目的是使学生掌握时间序列分析的基本理论和方法,让学生借助计算机的存储功能和计算功能来抽象掉其深奥的数学理论和复杂的运算,通过建模练习来掌握时间序列分析的基本思路和方法。
第一,通过这门课程的学习,培养学生对分析方法的理解,使学生初步掌握分析随机数据序列的基本思路和方法。
第二,通过这门课程的学习,使得学生能够运用时间序列分析知识和理论去分析、解决实际问题。
第三,通过这门课程的学习,提高学生利用时间序列的基本思想来处理实际问题,为后续学习打下方法论基础。
三、教学学时分配《时间序列分析》课程理论教学学时分配表《时间序列分析》课程实验内容设置与教学要求一览表四、教学内容和教学要求第一章时间序列分析简介(学时4)(一)教学要求通过本章内容的学习,了解时间序列的定义,理解时间序列的常用分析方法,掌握随机过程、平稳随机过程、非平稳随机过程、自相关基本概念。
(二)教学重点与难点教学重点:时间序列的相关概念。
教学难点:随机过程、系统自相关性。
(三)教学内容第一节引言第二节时间序列的定义(拟采用慕课或翻转课堂)第三节时间序列分析方法1.描述性时序分析2.统计时序分析第四节时间序列分析软件第五节上机指导1.创建时间序列数据集2.时间序列数据集的处理本章习题要点:1、基本概念和特征;2、软件基本操作。
第二章时间序列的预处理(学时6)(拟采用慕课或翻转课堂)(一)教学要求通过本章内容的学习,了解平稳时间序列的定义,理解平稳性和随机性检验的原理,掌握平稳性和随机性检验的方法。
(二)教学重点与难点教学重点:平稳时间序列的定义及统计性质。
教学难点:时间序列的相关统计量。
(三)教学内容第一节平稳性检验1.特征统计量2.平稳时间序列的定义3.平稳时间序列的统计性质4.平稳时间序列的意义5.平稳性的检验第二节纯随机性检验1.纯随机序列的定义2.白噪声序列的性质3.纯随机性的检验第二节上机指导1.绘制时序图2.平稳性与纯随机性检验本章习题要点:1、绘制给定时间序列的相关图;2、计算给定时间序列的相关统计量;3、检验序列的平稳性及纯随机性。
时间序列分析实验指导

时间序列分析实验指导时间序列分析是一种常用的统计方法,用于分析时间上的变化趋势和周期性变化。
它能够帮助我们预测未来的趋势和判断时间序列数据之间的因果关系。
本文将详细介绍进行时间序列分析的实验指导,包括实验准备、数据处理和模型建立等内容。
一、实验准备1. 确定实验目标:首先需要确定想要分析的时间序列的目标,如销售额、股票价格等。
明确实验目标有助于确定实验的方向和方法。
2. 数据采集:根据实验目标,选择合适的数据源,并采集相关数据。
常见的数据源包括数据库、API接口和互联网上的公开数据等。
3. 数据预处理:对采集到的数据进行预处理,包括数据清洗、填补缺失值和去除异常值等操作。
确保数据的准确性和一致性。
二、数据处理1. 数据可视化:将采集到的数据进行可视化,以便更好地理解数据的特征和变化趋势。
可以通过绘制时间序列图、箱线图和自相关图等方式进行数据可视化。
2. 数据平稳化:时间序列分析要求数据是平稳的,即均值和方差不随时间变化。
如果数据不平稳,需要进行平稳化处理。
常见的平稳化方法包括差分和对数变换。
3. 自相关性检验:利用自相关函数(ACF)和偏自相关函数(PACF)来检验数据的自相关性。
分析自相关系数的大小和延迟的时间间隔,判断是否存在显著的自相关关系。
4. 白噪声检验:利用残差的自相关函数和偏自相关函数来检验数据是否为白噪声。
如果数据是白噪声,说明数据中不存在周期性和趋势,不适合进行时间序列分析。
三、模型建立1. 模型选择:根据数据的特征和目标确定合适的时间序列模型。
常见的时间序列模型包括AR模型、MA模型、ARMA模型和ARIMA模型等。
2. 参数估计:对选择的模型进行参数估计,可以使用极大似然估计、最小二乘法或贝叶斯估计等方法。
3. 模型诊断:对模型进行诊断,判断模型的拟合程度和残差的性质。
可以使用残差自相关函数和偏自相关函数来检验模型的拟合优度。
4. 模型预测:利用已建立的模型对未来的数据进行预测。
时间序列分析实验报告

《时间序列分析》课程实验报告一、上机练习(P124)1.拟合线性趋势程序:data xiti1;input x@@;t=_n_;cards;;proc gplot data=xiti1;plot x*t;symbol c=red v=star i=join;run;proc autoreg data=xiti1;model x=t;output predicted=xhat out=out;run;proc gplot data=out;plot x*t=1 xhat*t=2/overlay;symbol2c=green v=star i=join;run;运行结果:分析:上图为该序列的时序图,可以看出其具有明显的线性递增趋势,故使用线性模型进行拟合:x t=a+bt+I t,t=1,2,3,…,12分析:上图为拟合模型的参数估计值,其中a=,b=,它们的检验P值均小于,即小于显著性水平,拒绝原假设,故其参数均显著。
从而所拟合模型为:x t=+.分析:上图中绿色的线段为线性趋势拟合线,可以看出其与原数据基本吻合。
2.拟合非线性趋势程序:data xiti2;input x@@;t=_n_;cards;;proc gplot data=xiti2;plot x*t;symbol c=red v=star i=none;run;proc nlin method=gauss;model x=a*b**t;parameters a= b=;=b**t;=a*t*b**(t-1);output predicted=xh out=out;run;proc gplot data=out;plot x*t=1 xh*t=2/overlay;symbol2c=green v=none i=join;run;运行结果:分析:上图为该时间序列的时序图,可以很明显的看出其基本是呈指数函数趋势慢慢递增的,故我们可以选择指数型模型进行非线性拟合:x t=ab t+I t,t=1,2,3,…,12分析:由上图可得该拟合模型为:x t=*+I t分析:图中的红色星号为原序列值,绿色的曲线为拟合后的拟合曲线,可以看出原序列值与拟合值基本上是重合的,故该拟合效果是很好的。
时间序列分析上机操作题
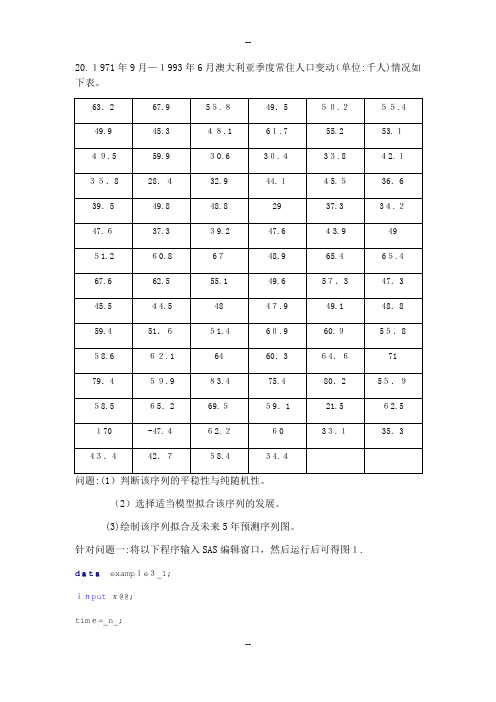
20.1971年9月—1993年6月澳大利亚季度常住人口变动(单位:千人)情况如下表。
问题:(1)判断该序列的平稳性与纯随机性。
(2)选择适当模型拟合该序列的发展。
(3)绘制该序列拟合及未来5年预测序列图。
针对问题一:将以下程序输入SAS编辑窗口,然后运行后可得图1.data example3_1;inputx@@;time=_n_;cards;63.26ﻩ7.95ﻩ5.8 49.5ﻩ50.255.4ﻩ49.9 45.348.1 61.755.2ﻩ 53.149.5ﻩ59.9ﻩ30.4ﻩ30.6ﻩ33.8 42.135.8ﻩ28.4ﻩ44.1ﻩ32.9ﻩ45.5 36.639.5 49.8 48.8 29 37.33ﻩ4.2 47.637ﻩ.339ﻩ.2 47.6 43.9ﻩ4951.2ﻩ60.8 67ﻩ 48.9 65.4ﻩ65.467.6 62.555.1 49.6ﻩ57.3 47.345.544.5ﻩ 4847.9 49.1 48.859.451ﻩ.651.4 60.9 60.9 55.8 58.662.1ﻩ64ﻩ 60.3 64.6ﻩ7179.459.983.4 75.4 80.255ﻩ.9 58.5 65.269.55ﻩ9.1 21.5 62.5 170 ﻩ-47.462.2ﻩ 60ﻩ33.135ﻩ.343.4ﻩ42.758ﻩ.434ﻩ.4;procgplotdata=example3_1;plotx*time=1;symbol1c=red I=join v=star;run;图1该序列的时序图由图1可读出:除图中170和-47.4这两个异常数据外,该时序图显示澳大利亚季度常住人口变动一般在在60附近随机波动,没有明显的趋势或周期,基本可视为平稳序列。
再接着输入以下程序运行后可输出五方面的信息。
具体见表1-表5.procarima data=example3_1;identifyVar=x nlag=8;run;表1 分析变量的描述性统计从表1可读出分析变量的名称、该序列的均值;标准差及观察值的个数(样本容量)。
时间序列分析实验指导范文

时间序列分析实验指导范文分析时间序列数据是一种常见的数据分析方法,它可以帮助我们识别和预测数据中的趋势和模式。
本实验将介绍如何进行时间序列分析,并使用ARIMA模型来预测未来的数据。
一、实验目的:掌握时间序列数据的分析方法,了解ARIMA模型的应用。
二、实验步骤:1. 数据准备从可靠的数据源获取时间序列数据,确保数据的完整性和准确性。
将数据保存为csv格式以便分析。
2. 数据预处理对时间序列数据进行必要的预处理,如去除缺失值、异常值处理等。
可以使用Python中的pandas库进行数据清洗。
3. 数据可视化使用Python中的matplotlib库绘制时间序列数据的折线图,观察数据的整体趋势和周期性。
4. 模型拟合利用ARIMA模型对时间序列数据进行拟合。
ARIMA模型包括自回归(AR)、差分(I)和移动平均(MA)三个组成部分。
根据数据的特点选择合适的参数来进行模型的训练。
5. 模型诊断对拟合的ARIMA模型进行诊断,检查模型的残差是否满足平稳性、独立性和正态分布性等假设。
可以绘制残差的自相关图和偏自相关图进行检验。
6. 模型预测使用训练好的ARIMA模型对未来的数据进行预测。
可以通过Python中的statsmodels库来实现。
7. 结果评估对模型预测的结果进行评估,比较预测值和实际值的差异。
可以计算预测误差的均方根误差(RMSE)或平均绝对误差(MAE)来评估模型的精度。
三、实验注意事项:1. 根据数据的性质选择合适的时间序列模型,不同的数据可能需要不同的模型来进行拟合和预测。
2. 在进行时间序列分析之前,需要对数据进行充分的了解,包括数据的来源、采集方法等,以确保数据的可靠性。
3. 在进行ARIMA模型的拟合时,可以通过调整模型的参数来提高模型的拟合度和预测精度。
四、实验总结:时间序列分析是一种常用的数据分析方法,可用于预测未来的数据趋势和模式。
通过本实验,我们学习了如何进行时间序列分析,并使用ARIMA模型对未来的数据进行预测。
应用时间序列分析上机实验-

应用时间序列分析上机实验教案第一次实验:(2014.9.22)Exercise 1.1要求:在R软件中命名、输入时间序列数据,并图示;案例:在R软件中将样本容量为10的数据:10,20,30,40,50,60,70,80,90,100赋值给变量X;命令:X<-c(10,20,30,40,50,60,70,80,90,100)Plot(X)运行结果:图1.1Exercise 1.2要求:在Exercise 1.1的图1.1中对X轴与Y轴重新标注;案例:在图1.1中将X轴标注为:“序号”,将Y轴标注为:“10-100的整10倍数”命令:X<-c(10,20,30,40,50,60,70,80,90,100) (略,若没有上前的命令,要写)plot(X,xlab='序号',ylab='10-100的整十倍数')注解:注意:1、xlab与ylab的标注是单引号;2、汉字不能用五笔输入法;运行结果:图1.2Exercise 1.3要求:将Exercise 1.2的图1.2转换为拆线图;案例:在图1.2中的plot命令中加入选项“type=’o’;命令:plot(X,xlab='序号',ylab='10-100的整十倍数',type=’o’)注解:没有“type=’o’”时,图形为点图,加入后将点连接为线,即拆线;运行结果:图1.3Exercise 1.4要求:改变Exercise 1.3的图1.3的高与宽及图中点的大小;案例:图1.4的高度为2.5,宽度为4.875,点大小为10;命令:win.graph(width=4.875, height=2.5,pointsize=10)plot(X,xlab='序号',ylab='10-100的整十倍数',type=’o’)注解:“width=4.875”--宽度为4.875,“height=2.5”--高度为2.5,“pointsize=10”--点大小为10;运行结果:图1.4Exercise 1.5要求:画出两个变量的散点图;案例:输入变量X、Y,画散点图;命令:X<-c(10,20,30,40,50,60,70,80,90,100)Y<-c(100,201,300,410,500,1200,710,820,900,1000)win.graph(width=4.875, height=4.5,pointsize=10)plot(X,Y)运行结果:图1.5Exercise 1.6要求:在Exercise 1.5的图1.5中加入X轴、Y轴标注;案例:将散点图1.5的X轴标注为“整十倍数”、Y轴标注为“奇异值”;命令:plot(X,Y,xlab='整十倍数',ylab='奇异值')运行结果:图1.6Exercise 1.7要求:从“*.TXT”文件中读取数据;案例:将1978-2012年我国的GDP时间序列数据赋给变量GDP;操作:先将数据源转换为“*.TXT”文件,比如:“GDP78-12.TXT”;保存于路径“E:\”下;在R 中修改当前目录于“E:\”;命令:点击“文件”/“改变当前目录”GDP<-read.table(“GDP78-12.txt”,head=TRUE)GDP运行结果:GDP1978年3,645.221979年4,062.581980年4,545.621981年4,891.561982年5,323.35...Exercise 1.8要求:利用scan( )函数从“*.TXT”文件中读取数据;案例:将100,200,300,400,500,600,700,1800,900,1000存于文件“1000.TXT”中,利用scan( )函数从文件“1000.TXT”中读取数据,赋于变量X1;操作:先将数据源保存于“1000.TXT”文件,比如:保存于路径“E:\”下(为方便起见,其它类同);在R中修改当前目录于“E:\”;命令:点击“文件”/“改变当前目录”X1<-scan(“1000.txt”);X1运行结果:[1] 100 200 300 400 500 600 700 1800 900 1000Exercise 1.9要求:在R中作出P1中图E1.1;操作:先打开library(TSA)---TSA是R的外部程序包,设定图宽、高等,调用数据--data(larain),作图plot(larain,ylab='Inches',xlab='Year',type='o')命令:library(TSA)win.graph(width=4.875, height=2.5,pointsize=8)data(larain); plot(larain,ylab='Inches',xlab='Year',type='o')运行结果:Exercise 1.10要求:在R中作出P2中图E1.2;操作:若第一次作图,先打开library(TSA),第二次即不需要,定图宽、高等,调用数据--data(larain),作图plot(larain,ylab='Inches',xlab='Year',type='o')命令:library(TSA)win.graph(width=3,height=3,pointsize=8)plot(y=larain,x=zlag(larain),ylab='Inches', xlab='Previous Year Inches')运行结果:注:字符用汉字:library(TSA)win.graph(width=3,height=3,pointsize=8)plot(y=larain,x=zlag(larain),ylab='英寸', xlab='上一年英寸')Exercise 1.11要求:在R中作出P2中图E1.3;命令:library(TSA)win.graph(width=4.875, height=2.5,pointsize=8)data(color)plot(color,ylab='Color Property',xlab='Batch',type='o') 运行结果:Exercise 1.12要求:在R中作出P3中图E1.4;命令:library(TSA)win.graph(width=3,height=3,pointsize=8)plot(y=color,x=zlag(color),ylab='Color Property', xlab='Previous Batch Color Property') 运行结果:。
SAS时间序列分析上机报告

SAS时间序列分析上机报告得到的结果如图⼀所⽰:图⼀时间序列editor窗中输⼊如下程序:(1) t t t X X ε+=-11.1data a; x1=0.5;n=-50;do i=-50 to 1000;a=rannor(32565);*随机正态,32565是种⼦; x=a+1.1*x1; x1=x; n=n+1;if i>0 then output ; end ; run ;proc print data =a; var x;proc gplot data =a;symbol i =spline c =red; plot x*n; run ;得到的结果如下图⼆所⽰:图⼆时间序列data a; x1=0.5;n=-50;do i=-50 to 1000;a=rannor(32565);*随机正态,32565是种⼦; x=a-1.1*x1; x1=x;n=n+1;if i>0 then output ; end ; run ;proc print data =a; var x;proc gplot data =a;symbol i =spline c =red; plot x*n; run ;(2) t t t X X ε+-=-11.1图三时间序列从上⾯的图形我们可以看到图⼀的所有值均在0左右波动,整个时间序列是平稳的,⽽图⼆和图三都是随着时间的推迟,越发偏离初始值,是不平稳的。
根据t t t X X εφ+=-11,只有11<φ,模型才是平稳的,显然后⾯两个模型不符合条件。
.模拟⾃回归模型t t t t X X X ε++=--213.05.0的程序如下:data a;x1=x;n=n+1;if i>0then output;end;run;proc print data=a;var x;proc gplot data=a;symbol i=spline c=red;plot x*n;run;得到的结果如下图四所⽰:图四A R(2)模拟图形8.针对第⼋题,我们利⽤⽤第七题的程序产⽣数据,在根据第⼋题的相关程序观察⾃相关函数和偏⾃相关函数的图像。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上机指导第五章5.8.1 拟合ARIMA模型由于ARMA模型是ARIMA模型的一种特例,所以在SAS系统中这两种模型的拟合都放在了ARIMA 过程中。
我们已经在第3章进行了ARMA模型拟合时介绍了ARIMA过程的基本命令格式。
再次以临时数据集example5_1的数据为例介绍ARIMA模型拟合与ARMA模型拟合的不同之处。
data example5_1;input x@@;difx=dif(x);t=_n_;cards;1.05 -0.84 -1.42 0.202.81 6.72 5.40 4.385.52 4.46 2.89 -0.43 -4.86 -8.54 -11.54 -16.22-19.41 -21.61 -22.51 -23.51 -24.49 -25.54 -24.06 -23.44-23.41 -24.17 -21.58 -19.00 -14.14 -12.69 -9.48 -10.29-9.88 -8.33 -4.67 -2.97 -2.91 -1.86 -1.91 -0.80proc gplot;plot x*t difx*t;symbol v=star c=black i=join;run;输出时序图显示这是一个典型的非平稳序列。
如图5-49所示时序图49 -序列x图5在原程序基础上添加同时考察查分后序列的平稳性,1阶差分运算,考虑对该序列进行相关命令,程序修改如下:data example5_1;input x@@;difx=dif(x);t=_n_;cards;1.05 -0.84 -1.42 0.202.81 6.72 5.40 4.385.52 4.46 2.89 -0.43 -4.86 -8.54 -11.54 -16.22-19.41 -21.61 -22.51 -23.51 -24.49 -25.54 -24.06 -23.44-23.41 -24.17 -21.58 -19.00 -14.14 -12.69 -9.48 -10.29-9.88 -8.33 -4.67 -2.97 -2.91 -1.86 -1.91 -0.80proc gplot;plot x*t difx*t;symbol v=star c=black i=join;proc arima;identify var=x(1);estimate p=1;forecast lead=5 id=t ;run;语句说明:(1)DATA步中的命令“difx=dif(x);”,这是指令系统对变量x进行1阶差分,差分后的序列值赋值给变量difx。
其中dif()是差分函数,假如要差分的变量名为x,常见的几种差分表示为:1阶差分:dif(x)2阶差分:dif(dif(x))k步差分:difk(x)(2)我们在GPLOT过程中添加绘制了一个时序图“difx*t”,这是为了直观考察1阶差分后序列的平稳性。
所得时序图如图5-50所示。
difx时序图50 图5-序列difx没有明显的非平稳特征。
时序图显示差分后序列,使用该命令可以识别查分后序列的平稳性、纯随机性和适;)”“identify var=x(3)(1支持多种形式的差SAS1x1x 当的拟合模型阶数。
其中()表示识别变量的阶差分后序列。
分序列识别:var=x(1),表示识别变量x的1阶查分后序列Δxt;var=x(1,1),表示识别变量x的2阶查分后序列Δ2xt;var=x(k),表示识别变量x的k步差分后序列Δkxt;var=x(k,s),表示识别变量x的k步差分后,再进行s步查分后序列ΔsΔkxt。
识别部分的输出结果显示1阶查分后序列difx为平稳非白噪声序列,且具有显著的自相关系数不截尾、偏自相关系数1截尾的性质。
(4)“estimate p=1;”对1阶差分后序列Δxt拟合AR(1)模型。
输出拟合结果显示常数项不显著,添加或修改估计命令如下:estimate p=1 nonit;这是命令系统不要常数项拟合AR(1)模型,拟合结果显示模型显著且参数显著。
如图5-51所示。
difx模型拟合结果图5-51 序列 1,1,0)模型,模型口径为:的拟合模型为ARIMA(输出结果显示,序列xtt/1-0.66933B xt=艾普龙Δ或等阶记为:t艾普龙xt=1.66933xt-1-0.66933xt-2+期预测。
xt作5(5)“forecast lead=5 id=t;”,利用拟合模型对序列建立数据集,绘制时序图一、data example5_2;input x@@;lagx=lag(x);t=_n_;cards;2.83 9.80 11.96 10.223.03 8.4613.26 19.57 13.77 16.18 16.84 8.4318.44 28.27 32.62 28.16 14.78 24.4833.01 50.66 43.70 38.36 44.46 25.2549.84 78.15 68.84 68.12 60.17 39.9777.88 62.23 91.49 103.20 104.53 118.18; 155.68 157.46 177.69 117.15 94.75 138.36proc gplot data=example5_2; plot x*t=1; symbol1 c=black i=join v=star;run;5输出时序图如-52所示。
x时序图图5-52 序列同时又有一定规有一个明显的随时间线性递增的趋势,时序图显示,序列X 律性的波动,所以不妨考虑使用误差自回归模型拟合该序列的发展。
二、因变量关于时间的回归模型=example5_2; data proc autoreg;dwprobmodel x=t/;run语句说明:“集数据对令data=example5_2;”指SAS系统临时autoreg1)(proc example5_2进行回归程序分析。
作为因作为自变量,变量系统以变量”指令dwprobmodel2)(“ x=t/ ;SAStx 变量,建立线性模型:u??bt?xa it检验统计量的分为点。
并给出残差序列 DW 本例中,序列x关于变量t的线性回归模型最小二乘估计输出结果如图5-53所示。
t的线性回归模型最小二乘估计结果序列x关于变量5图-53,输出概率显示残差序列显著正0.7628本例输出结果显示,DW统计量的值等于AUTOREG相关。
所以应该考虑对残差序列拟合自相关模型,修改程序如下:=example5_2; data proc autoreg=ml; method5backstep model x=t/nlag=run;阶的自相关图,并拟合Model语句是指令系统对线性回归模型的残差序列显示延迟5 5延迟阶自相关模型,特别注意,SAS输出的自回归模型结构为:????u?u?...u??tt?t551t?1即输出的自相关回归参数值与我们习惯定义的自回归参数值相差一个负号。
得阶数通常会指得大由于自相关延迟阶数的确定是由我们尝试选择的,所以nlag一些。
这就导致残差自回归模型中可能有部分参数不显著,指令系统使用逐步回归的方法筛选出显著自相关因子,并backstep,因而添加逐步回归选项使用极大似然的方法进行参数估计。
输出如下四方面的结果:54所示:因变量说明如图15-54 因变量说明5图- 2普通最小二乘估计结果、根号均DFE)、自由度(、均方误差(MSE)SSE)该部分输出信息包括差平方和(、总regress rsquare)信息量。
回归部分相关系数平方(SBC、Root MSE)方误差(.的相关系数平方(totel rsquare),DW统计量(durbin watson)及所有待参数的自由度、估计值、标准差、t值和统计量的P值。
如图5-55所示。
普通最小二乘估计结果-55 5图回归误差分析3逐步回归消除的不显著项报告、该部分共输出四方面的信息:残差序列自相关图、MSE)、自回归参数估计值。
初步均方误差(所示。
5本例该部分输出结果如图-565图-56 自回归误差分析输出结果逐步回归消除报告阶正相关性。
1本例输出的残差序列自相关图显示残差序列有非常显著的因延迟其他阶数的序列值均不具有显著的自相关性,阶的序列值显著自相关外,1显示除了.此延迟2阶-5阶的自相关项被剔除。
初步均方误差为??u?0.602573u t?1tt4、最终拟合模型该部分包括三方面的汇总信息:收敛状况、极大似然估计结果和回归系数估计。
57所示。
本例该部分输出结果如图5-5图-57 最终拟合模型输出结果本例得到最终拟合模型为:u2.7638t?x??tt???uu?0.6883?tt1?t数据OUTPUT为了得到直观的拟合效果,我们可以利用命令将拟合结果存入SAS集中,并对输出结果作图,相关命令如下:=example5_2; procautoreg data=ml;nlagmodel x=t/=5backstep method=trend;output out=out p=xp pm=example5_2; proc autoreg data;nointmethod=ml =model x=t/nlag5backstep=trend; =xp pmoutoutput =out p=out; data procgplot;overlay / 4 trend*t=3 xp*t=2 x*t=plot=black; =none csymbol2v=star i; 32l=wsymbol3v=none i=join c=red =; 2c=green w=symbol4v=none i=join;run语句说明:”,该命令是指令系统将部分结果输入临时=trend;p=out =xp pm“outputout;XP值),该拟合变量取名为选择输出的第一个信息为整体模型的拟合值数据集OUT,(P选项输出拟合残差项,值),还可以选择R选择输出的第二个信息为线性趋势拟合值(PM 本例不要求输出此项。
所示。
输出图像如图5-5858 拟合效果图图5-三、延迟因变量回归模型=example5_2; autoreg data proc=lagx;lagdepmodel x=lagx/;run 语句说明:,该语句指令系统使用延迟函数”步中添加命令“)首先在DATAlagx=lgax(x);(1 lagx,即阶延迟序列,并将该序列赋值给变量生成序列x的12t,??lagxx1?tt(2)系统建立带有延迟变量的回归模型”指令 x=lagx/“modellagdep=lagx;uxbx??a?ttt?1并通过LAGDEP选项指定被延迟的因变量名。
