专题五 切线的证明与计算
4.1 切线方程(精讲)(提升版)(原卷版)
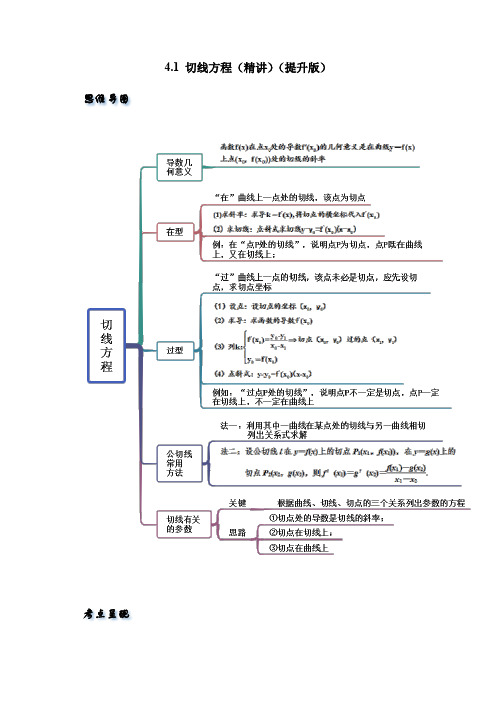
4.1 切线方程(精讲)(提升版)思维导图考点呈现考点一 斜率和倾斜角【例1-1】(2022·江苏淮安)已知函数()cos2(0,πf x x x =∈,)在0x x =处的切线斜率为85,则00co sin s x x -=( ) A .35 B .35C .355-D .355【例1-2】(2022·重庆一中)已知偶函数()f x ,当0x >时,()()212f x x f x '=-+,则()f x 的图象在点()()2,2f --处的切线的斜率为( ) A .3- B .3 C .5- D .5【一隅三反】1.(2022·辽宁)已知曲线()3cos1f x x =-在点()()1,1f 处的切线与直线:30l ax y --=垂直,则实数a 的值为______.2.(2022·湖南·长沙县第一中学模拟预测)函数()2ln 1sin y x x =++的图象在0x =处的切线对应的倾斜角为α,则sin2α=( ) A .310B .±310 C .35D .±35例题剖析3.(2022·湖南)已知P 是曲线)2:ln C y x x a x =++上的一动点,曲线C 在P 点处的切线的倾斜角为θ,若32ππθ≤<,则实数a 的取值范围是( )A .)⎡⎣B .)⎡⎣C .(,-∞ D .(-∞考点二 “在型”的切线方程【例2-1】(2022·广西)曲线31y x =+在点()1,a -处的切线方程为( ) A .33y x =+ B .31y x C .31y x =-- D .33y x =--【例2-2】(2022·广西·贵港市)已知曲线e ln x y ax x =+在点()1,e a 处的切线方程为3y x b =+,则( ) A .e a =,2b =- B .e a =,2b = C .1e a -=,2b =- D .1e a -=,2b =【一隅三反】1.(2022·河南)已知函数()()423f x x m =++的图象经过坐标原点,则曲线()y f x =在点()()1,1f --处的切线方程是( )A .872y x =-B .476y x =-C .872y x =+D .476y x =+2.(2022·安徽)已知()f x 为奇函数,且当0x >时()211e xf x x-=+,则曲线()y f x =在点11,22f ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭处的切线方程为( ) A .240x y ++= B .240x y -+= C .220x y -+= D .220x y ++=3.(2022·安徽·巢湖市)曲线22x ay x +=+在点()1,b 处的切线方程为60kx y -+=,则k 的值为( ) A .1- B .23-C .12D .14.(2022·湖北·武汉二中模拟预测)已知函数()1ln f x x x=-,直线y mx n =+是曲线()y f x =的一条切线,则2m n +的取值范围是( ) A .[)3,∞-+ B .2e 3,e -⎛⎤-∞ ⎥⎝⎦C .[)2ln 24,--+∞D .5ln 2,4⎡⎫-+∞⎪⎢⎣⎭考点三 “过型”的切线方程【例3】(2022·河南洛阳)已知函数()3221f x x x x =-++,则曲线()y f x =过坐标原点的切线方程为( ) A .y x = B .2y x =C .3y x =D .4y x =【一隅三反】1.(2022·广东·新会陈经纶中学)(多选)已知曲线3()21f x x =+.则曲线过点P (1,3)的切线方程为.( ) A .630x y --= B .3230x y -+=C .690x y +-=D .3290x y +-=2(2022·北京·汇文中学)228y x =+过点()12P ,的切线方程是__________.3.(2022·四川·广安二中)函数()2e x f x x =过点()0,0的切线方程为考点四 切线或切点数量问题【例4-1】(2022·河南洛阳)若过点()1,0P 作曲线3y x =的切线,则这样的切线共有( ) A .0条 B .1条C .2条D .3条【例4-2】(2022·全国·高三专题练习)若过点(,)a b 可以作曲线ln y x =的两条切线,则( ) A .ln a b < B .ln b a <C .ln b a <D .ln a b <【一隅三反】1.(2022·河南洛阳)若过点()1,0P 作曲线3y x =的切线,则这样的切线共有( ) A .0条 B .1条 C .2条 D .3条2.(2022·湖北·宜城市第一中学)若过点(),a b 可以作曲线()10y x x x=->的两条切线,则( ) A .0b a >> B .10a b a a-<<< C .10a b a a<-<< D .1a b a a>>-且0a >3.(2022·河南洛阳)若过点()1,P t 可作出曲线3y x =的三条切线,则实数t 的取值范围是( ) A .(),1-∞ B .()0,∞+ C .()0,1 D .{}0,14.(2022·全国·高考真题)若曲线()e x y x a =+有两条过坐标原点的切线,则a 的取值范围是________________.考点五 公切线【例5-1】(2022·安徽省舒城中学)已知直线l 是曲线e 1x y =-与ln 1y x =+的公共切线,则l 的方程为_____.【例5-2】(2022·江苏·南京外国语学校模拟预测)若两曲线y =x 2-1与y =a ln x -1存在公切线,则正实数a 的取值范围为( ) A .(]0,2e B .(]0,e C .[)2,e +∞ D .(],2e e【一隅三反】1.(2022·全国·模拟预测)若直线l 与曲线2y x 和2249x y +=都相切,则l 的斜率为______.2.(2022·河北保定·二模)(多选)若直线3y x m =+是曲线()30y x x =>与曲线()260y x nx x =-+->的公切线,则( ) A .2m =-B .1m =-C .6n =D .7n =3.(2022·安徽·合肥一六八中学)若直线y kx m =+是曲线ln(1)y x =-的切线,也是曲线3e x y -=的切线,则k =__________.考点六 切线与其他知识的运用【例6-1】(2022·湖北·黄冈中学)已知a ,b 为正实数,直线y x a =-与曲线ln()y x b =+相切,则14a b+的最小值为( )A .8B .9C .10D .13【例6-2】(2022·广东·深圳市光明区高级中学)已知函数()()2ln f x x x ax x a =-+∈R ,则曲线()y f x =在点()()1,1f 处的切线l 恒过定点_____________.【一隅三反】1.(2022·河北衡水)已知函数2ln ()2xf x x x=-在1x =处的切线为l ,第一象限内的点(,)P a b 在切线l 上,则1111a b +++的最小值为( )A B C D 2.(2022·安徽)对于三次函数()f x ,若曲线()y f x =在点(0,0)处的切线与曲线()y xf x =在点(1,2)处点的切线重合,则(2)f '=( )A .34-B .14-C .4-D .143.(2022·黑龙江·哈尔滨三中)若曲线e x y =过点(2,0)-的切线恒在函数212()e 31e e x f x a x x ⎛⎫=-+-+- ⎪⎝⎭的图象的上方,则实数a 的取值范围是__________.考点七 切线方程的运用【例7-1】(2022·全国·高三专题练习)设点P 在曲线y x =上,点Q 在曲线()ln 2y x =上,则PQ 的最小值为( )A .1ln 22- B )1ln 2- C .1ln 22+ D .)1ln 22+【例7-2】(2022·山东烟台·三模)已知函数()2ln ,021,0x x f x x x x ⎧>=⎨+-≤⎩,若方程()1f x ax =-有且仅有三个实数解,则实数a 的取值范围为( ) A .01a << B .02a << C .1a > D .2a >【一隅三反】1.(2022·江苏徐州)过平面内一点P 作曲线|ln |y x =的两条互相垂直的切线12,l l ,切点分别为12,P P (12,P P 不重合),设直线12,l l 分别与y 轴交于点A ,B ,则ABP △面积的取值范围为( ) A .10,2⎛⎤⎥⎝⎦B .()0,1C .1,12⎡⎫⎪⎢⎣⎭D .(0,2]2.(2022·全国·高三专题练习)已知函数()()e ln xf x x a x x =-+有两个零点,则实数a 的取值范围是______.3.(2022·云南曲靖·二模)设()'f x 是函数()f x 的导函数,()f x ''是函数()'f x 的导函数,若对任意R ()0,()0x f x f x '''∈><,恒成立,则下列选项正确的是( ) A .0(3)(3)(2)(2)f f f f ''<<-< B .0(3)(2)(2)(3)f f f f ''<-<< C .0(3)(2)(3)(2)f f f f ''<<<- D .0(2)(3)(3)(2)f f f f ''<<<-4.(2022·江西·新余市)若点A 在曲线ln 1y x =-上运动,点B 在直线2y x =+上运动,,A B 两点距离的最小值为______。
专题五 解析几何 文科数学

专题五 文科数学 解析几何1.(2011·朝阳期末)已知圆的方程为086222=++-+y x y x ,那么下列直线中经过圆心的直线方程为( B )(A )012=+-y x (B )012=++y x (C )012=--y x (D )012=-+y x2.(2011·朝阳期末)设椭圆的两个焦点分别为1F ,2F ,过2F 作椭圆长轴的垂线与椭圆相交,其中的一个交点为P ,若△12F P F 为等腰直角三角形,则椭圆的离心率是( A )(A )1-(B )12(C ) (D )23.(2011·朝阳期末)经过点(2, 3)-且与直线250x y +-=垂直的直线方程为 280x y -+= .4.(2011·朝阳期末)(本小题满分13分)已知点(4, 0)M ,(1, 0)N ,若动点P 满足6||M N M P P N ⋅=.(Ⅰ)求动点P 的轨迹C 的方程;(Ⅱ)设过点N 的直线l 交轨迹C 于A ,B 两点,若181275N A N B -⋅- ≤≤,求直线l 的斜率的取值范围.解:(Ⅰ)设动点(, )P x y ,则(4, )M P x y =- ,(3, 0)M N =- ,(1, )P N x y =--. …………………2分 由已知得22)()1(6)4(3y x x -+-=--,化简得223412x y +=,得22143xy+=.所以点P 的轨迹C 是椭圆,C 的方程为13422=+yx. ………………………6分(Ⅱ)由题意知,直线l 的斜率必存在,不妨设过N 的直线l 的方程为(1)y k x =-,设A ,B 两点的坐标分别为11(, )A x y ,22(, )B x y .由22(1),143y k x x y =-⎧⎪⎨+=⎪⎩消去y 得2222(43)84120k x k x k +-+-=. ………………8分因为N 在椭圆内,所以0∆>.所以212221228,34412.34kx x k k x x k ⎧+=⎪⎪+⎨-⎪=⎪+⎩………………………………………………………10分 因为2121212(1)(1)(1)(1)(1)NA NB x x y y k x x ⋅=--+=+--]1)()[1(21212++-+=x x x x k222222243)1(943438124)1(kk k kkkk ++-=+++--+=, …………12分所以22189(1)127345k k-+--+≤≤. 解得213k ≤≤.所以1k -≤或1k ≤≤. …………………………………………13分5.(2011·丰台期末)过点(34)-,且与圆22(1)(1)25x y -+-=相切的直线方程为 43240x y -+= . 6.(2011·丰台期末) (本小题满分14分)已知O 为平面直角坐标系的原点,过点(20)M -,的直线l 与圆221x y +=交于P ,Q 两点.(Ⅰ)若PQ =,求直线l 的方程;(Ⅱ)若12M P M Q =,求直线l 与圆的交点坐标.解:(Ⅰ)依题意,直线l 的斜率存在,因为 直线l 过点(2,0)M -,可设直线l :(2)y k x =+. 因为PQ =,圆的半径为1,P ,Q 两点在圆221x y +=上,所以圆心O到直线l12 =.又因为12 =,所以15k=±,所以直线l的方程为20x-+=或20x++=.………………………7分(Ⅱ)设11(,)P x y,22(,)Q x y,所以22(2,)M Q x y=+,11(2,)M P x y=+.因为2M Q M P=,所以212122(2)2x xy y+=+⎧⎨=⎩即21212(1)2x xy y=+⎧⎨=⎩(*);因为P,Q两点在圆上,所以2211222211x yx y⎧+=⎪⎨+=⎪⎩把(*)代入,得2211221114(1)41x yx y⎧+=⎪⎨++=⎪⎩,所以11788xy⎧=-⎪⎪⎨⎪=±⎪⎩,22144xy⎧=⎪⎪⎨⎪=±⎪⎩,所以P点坐标为7(88-或7(88--,,Q点坐标为1(44,或1(44-,.………………………14分7. (2011·东莞期末)已知双曲线22221x ya b-=的一条渐近线方程为12y x=,则该双曲线的离心率为( A)A.25B.3C.5D.28.(2011·东莞期末)(本小题满分14分)已知椭圆E 的中心在坐标原点O ,两个焦点分别为)0,1(-A 、)0,1(B ,一个顶点为)0,2(H .(1)求椭圆E 的标准方程;(2)对于x 轴上的点)0,(t P ,椭圆E 上存在点M ,使得MH MP ⊥,求t 的取值范围.解:(1)由题意可得,1c =,2a =,∴b =∴所求的椭圆的标准方程为:22143xy+=.(2)设),(00y x M )20±≠x (,则2200143x y +=. ①且),(00y x t MP --=,),2(00y x MH --=, 由MH MP ⊥可得0=⋅MH MP ,即∴0)2)((2000=+--y x x t . ②由①、②消去0y 整理得3241)2(0200-+-=-x x x t .∵20≠x , ∴23411)2(4100-=---=x x t .∵220<<-x ,∴ 12-<<-t .∴t 的取值范围为)1,2(--. 9. (2011·佛山一检)已知双曲线22221(0,0)x y a b ab-=>>与抛物线28y x =有一个公共的焦点F ,且两曲线的一个交点为P ,若5PF =,则双曲线的离心率为( A )A .2B .C 2D10. (2011·佛山一检)若点P 在直线03:1=++y x l上,过点P 的直线2l 与曲线22:(5)16C x y -+=相切于点M ,则PM 的最小值为( D )AB .2C .D .411. (2011·佛山一检)已知直线22x y +=分别与x 轴、y 轴相交于,A B 两点,若动点(,)P a b 在线段A B 上,则a b 的最大值为____12______.12.(2011·广东四校一月联考)过圆224x y +=外一点(4,2)P 作圆的两条切线,切点分别为,A B ,则ABP ∆的外接圆方程是( D )A .22(4)(2)1x y -+-=B .22(2)4x y +-=C .22(2)(1)5x y +++=D .22(2)(1)5x y -+-=13.(2011·广东四校一月联考)设θ是三角形的一个内角,且1sin cos 5θθ+=,则方程22sin cos 1x y θθ-=表示的曲线是( D ) A .焦点在x 轴上的双曲线 B .焦点在x 轴上的椭圆C .焦点在y 轴上的双曲线D .焦点在y 轴上的椭圆14.(2011·广东四校一月联考)(本小题满分14分)设(1,0)F ,M 点在x 轴的负半轴上,点P 在y 轴上,且,M P PN PM PF=⊥.(1)当点P 在y 轴上运动时,求点N 的轨迹C 的方程;(2)若(4,0)A ,是否存在垂直x 轴的直线l 被以A N 为直径的圆截得的弦长恒为定值?若存在,求出直线l 的方程;若不存在,请说明理由.解:(1)(解法一)MP PN =,故P 为M N 的中点. -------1分设(,)N x y ,由M 点在x 轴的负半轴上,则(,0),(0,),(0)2yM x P x -> -------2分又(1,0)F ,(,),(1,)22y y PM x PF ∴=--=--------4分又PM PF ⊥ ,204yPM PF x ∴⋅=-+= -------6分 所以,点N 的轨迹C 的方程为24(0)y x x => -------7分(解法二)MP PN =,故P为M N 的中点. -------1分设(,)N x y ,由M 点在x 轴的负半轴上,则(,0),(0,),(0)2yM x P x -> -------2分又由,M P PN PM PF =⊥ ,故FN FM = ,可得22FNFM=-------4分由(1,0)F ,则有222(1)(1)x y x -+=--,化简得:24(0)y x x => -------6分 所以,点N 的轨迹C 的方程为24(0)y x x => -------7分 (2)设A N 的中点为B ,垂直于x 轴的直线方程为x a =, 以A N 为直径的圆交l 于,C D 两点,C D 的中点为H .12CB AN ==412422x B H a x a +=-=-+ -------9分22222211[(4)](24)44CH CB BHx y x a ∴=-=-+--+221[(412)416](3)44a x a a a x a a=--+=--+ -------12分所以,令3a =,则对任意满足条件的x , 都有29123C H=-+=(与x 无关),-------13分即C D = -------14分15.(2011·广州期末)已知直线l 经过坐标原点,且与圆22430x y x +-+=相切,切点在第四象限,则直线l 的方程为( C )A.y = B.y = C.3y x =- D.3y x=16.(2011·广州期末)(本小题满分14分)图4已知椭圆(222:13x yE a a+=>的离心率12e =. 直线x t =(0t >)与曲线E 交于不同的两点,M N ,以线段M N 为直径作圆C ,圆心为C . (1)求椭圆E 的方程; (2)若圆C 与y轴相交于不同的两点,A B ,求A B C ∆的面积的最大值.(本小题主要考查椭圆、圆、直线与圆的位置关系等知识, 考查数形结合、化归与转化、函数与方程的数学思想方法,以及推理论证能力、运算求解能力和创新意识)(1)解:∵椭圆()222:133x yE a a+=>的离心率12e =,x=a∴12a=. …… 2分解得2a =.∴ 椭圆E 的方程为22143xy+=. …… 4分(2)解法1:依题意,圆心为.由22,1,43x t x y =⎧⎪⎨+=⎪⎩ 得221234t y -=.∴ 圆C的半径为2r =. …… 6分∵ 圆C 与y 轴相交于不同的两点,A B ,且圆心C 到y 轴的距离d t =,∴02t <<,即07t <<.∴弦长||A B ===. ……8分∴A B C ∆的面积12S =⋅ …… 9分)1=)2212712t +-≤7=. …… 12分=7t =时,等号成立.∴ A B C ∆的面积的最大值为7. …… 14分解法2:依题意,圆心为.由22,1,43x t x y =⎧⎪⎨+=⎪⎩ 得221234t y -=.∴ 圆C的半径为2r =. …… 6分 ∴ 圆C 的方程为222123()4tx t y --+=.∵ 圆C 与y 轴相交于不同的两点,A B ,且圆心C 到y 轴的距离d t =,∴02t <<,即07t <<.在圆C 的方程222123()4tx t y --+=中,令0x =,得2y =±,∴弦长||AB = 8分∴A B C ∆的面积12S =⋅ …… 9分)=)221272t +-≤7=. ……12分=7t =时,等号成立.∴ A B C ∆的面积的最大值为7. …… 14分17.(2011·哈九中高三期末)抛物线24x y =上一点到直线54-=x y 的距离最短,则该点的坐标是 ( )A .)2,1(B .)0,0(C .)1,21( D .)4,1(【答案】C【分析】根据题意,直线54-=x y 必然与抛物线24y x =相离,抛物线上的点到直线的最短距离就是与直线54-=x y 平行的抛物线的切线的切点。
高考数学备考艺体生辅导专题05《解析几何的第一问》(原卷版)

【高考备考艺体生文化课精选好题突围系列】专题五 解析几何的第一问圆的概念与方程【背一背基础知识】1. 标准方程:圆心坐标(,)a b ,半径r ,方程222()()x a y b r -+-=,一般方程:22x y Dx Ey ++++0F =(其中2240D E F +->);2.直线与圆的位置关系:相交、相切、相离 ,代数判断法与几何判断法; 3. 圆与圆的位置关系:相交、相切、相离、内含,代数判断法与几何判断法. 【讲一讲基本技能】 1. 必备技能:① 会用配方法把圆的一般方程化为标准方程;② 直线和圆的位置可用方程组的解来判断,但主要是应用圆心到直线的距离d 和圆半径r 比较,d r >⇔相离,d r =⇔相切,d r <⇔相交;③圆与圆的位置关系一般也是用圆心距12O O 与两圆的半径之和(或差)比较,12OO R r >+⇔相离,12OO R r =+⇔外切,12R r OO R r -<<+⇔相交,12OO R r =-⇔内切,12OO R r <-⇔内含. ④直线和圆的位置关系是这部分的重点考查内容.⑤对直线被圆截得弦长问题,求出圆的半径r ,圆心到直线的距离为d ,则直线被圆截得弦长为222r d -2.典型例题例1 在平面直角坐标系xOy 中,点)3,0(A ,直线42:-=x y l ,设圆C 的半径为1,圆心在l 上. 若圆心C 也在直线1-=x y 上,过点A 作圆C 的切线,求切线的方程;【分析】求圆的切线方程,一般设出直线方程为y kx b =+(斜率存在),再利用圆心到切线的距离等于圆的半径来求出其中的参数值. 【解析】例2 已知圆22:4230P x y x y +-+-=和圆外一点(4,8)M -.(1)过点M 作圆的割线交圆于,A B 两点,若||4AB =,求直线AB 的方程; (2)过点M 作圆的两条切线,切点分别为,C D ,求切线长及CD 所在直线的方程. 【答案】(1)4528440x y ++=或4x =;(2)27190x y --=.【分析】(1)先将圆的方程化成标准方程,求出圆心和半径,在根据弦长为4,结合垂径定理得到圆心到直线AB 的距离,则可以利用点到直线的距离公式求出直线AB 的斜率,求得直线方程;(2)利用切线的性质可知,切线长、半径、M 到圆心的距离满足勾股定理,则切线长可求;求出以PM 为直径的圆,与已知圆的方程,两式相减即可求得CD 所在的直线方程. 【解析】【练一练趁热打铁】1. 已知圆C 过点A (1,3),B (2,2),并且直线m: 320x y -=平分圆C 的面积. (Ⅰ)求圆C 的方程;2. 已知圆O 2:22460x y y +--=,求圆心在x-y-4=0,且过圆O 1与圆O 2交点的圆的方程。
中考数学二轮专题复习(专题五 开放探索问题)

下 页
返 回
步步高中考简易通
【例题1】 (2012· 浙江义乌)如图,在△ABC中,点D
专 题 解 读
是BC的中点,作射线AD,在线段AD及其延长 线上分别取点E、F,连接CE、BF.添加一个条
件,使得△BDF≌△CDE,并加以证明.你添
加的条件是________.(不添加辅助线).
专 题 突 破
∵点P(x,y)的坐标满足x+y=xy,∴x,y符号相
同,代入数字进行验证,符合条件的点的坐标有
(0,0),(2,2)等.故答案为:(0,0). 答案 (0,0)(答案不唯一)
上 页
下 页
返 回
步步高中考简易通
专 题 解 读
三、综合开放型
这类问题没有明确的条件和结论,并且符合条件的 结论具有多样性,需将已知的信息集中进行分析, 探索问题成立所必须具备的条件或特定的条件应该 有什么结论,通过这一思维活动得出事物内在联 系,从而把握事物的整体性和一般性.
课 时 跟 踪 检 测
专 题 突 破
上 页
下 页
返 回
步步高中考简易通
【例题5】 (2011· 青海)学校在艺术周上,要求学生制
专 题 解 读
作一个精美的轴对称图形,请你用所给出的几何图 形:○○△△ (两个圆,两个等边三角形,
课 时 跟 踪 检 测
两条线段)为构件,构思一个独特,有意义的轴对 称图形,并写上一句简要的解说词.
上 页
下 页
返 回
步步高中考简易通
专 题 解 读
【例题3】 (2012· 浙江丽水)写出一个比-3大的无理 数是________.
解析 根据这个数即要比-3 大又是无理数,解答出
课 时 跟 踪 检 测
专题五 第一讲 直线与圆
(x-1)2+y2=1
点评:本题主要考查平面图形的折叠问题、二面角以及利 用代入法求圆的方程等知识,涉及空间与平面直角坐标系 与斜坐标系的转化.综合性强、创新角度新颖.
已知圆C:x2+y2=12.直线l:4x+3y=25.圆C上任意一点 A到直线l的距离小于2的概率为________.
解析:如图,设与直线 4x+3y=25 距离为 2 且与该直线平行的直线与 圆交于 P、Q 两点.因为点 O 到直线 PQ 的距离 d=3.又 r=2 3,∴∠ OPQ=60° .若点 A 到直线 l 的距离小于 2,则点 A 只能在弧 PQ 上,∴ P= 60° 1 = . 360° 6
[考题
查漏补缺]
(2011· 重庆高考)设圆C位于抛物线y2=2x与直线x
=3所围成的封闭区域(包含边界)内,则圆C的半径能取到
的最大值为________.
[解析]
依题意,结合图形的对称性可知,要使满足题目约束条件
的圆的半径最大,需圆与抛物线及直线 x=3 同时相切,可设圆心 坐标是(a,0)(0<a<3), 则由条件知圆的方程是(x-a)2+y2=(3-a)2.
结论:
l1∥l2⇔k1=k2且b1≠b2;l1⊥l2⇔k1· 2=-1. k (2)若给定的方程是一般式,即l1:A1x+B1y+C1=0和l2: A2x+B2y+C2=0,则有下列结论: l1∥l2⇔A1B2-A2B1=0且B1C2-B2C1≠0;
l1⊥l2⇔A1A2+B1B2=0.
[做考题
查漏补缺]
答案:D
7.(2011· 湖北高考)过点(-1,-2)的直线 l 被圆 x2+y2-2x-2y +1=0 截得的弦长为 2,则直线 l 的斜率为________.
第一章点线面位置关系专题五共面问题微点1立体几何共面问题的解法【培优版】
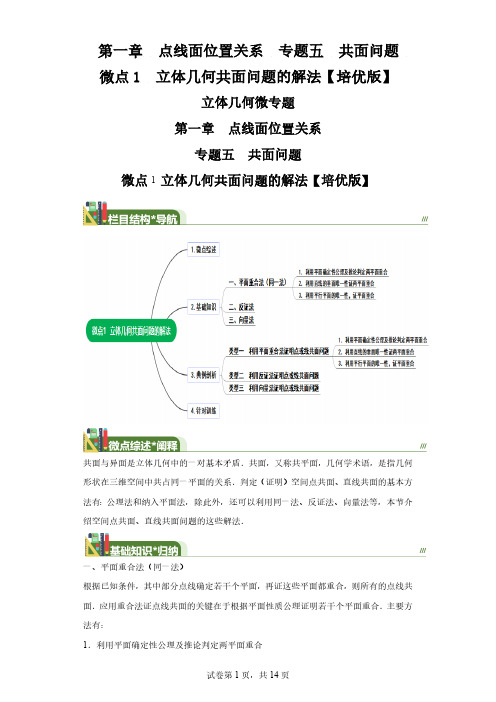
第一章点线面位置关系专题五共面问题微点1 立体几何共面问题的解法【培优版】立体几何微专题第一章点线面位置关系专题五共面问题微点1立体几何共面问题的解法【培优版】共面与异面是立体几何中的一对基本矛盾.共面,又称共平面,几何学术语,是指几何形状在三维空间中共占同一平面的关系.判定(证明)空间点共面、直线共面的基本方法有:公理法和纳入平面法,除此外,还可以利用同一法、反证法、向量法等,本节介绍空间点共面、直线共面问题的这些解法.一、平面重合法(同一法)根据已知条件,其中部分点线确定若干个平面,再证这些平面都重合,则所有的点线共面.应用重合法证点线共面的关键在于根据平面性质公理证明若干个平面重合.主要方法有:1.利用平面确定性公理及推论判定两平面重合2.利用直线的垂面唯一性证两平面重合3.利用平行平面的唯一性,证平面重合二、反证法三、向量法根据共面向量定理及其推论判定、证明点共面、直线共面.向量共面定理:向量,a b 不共线,向量p 与,a b 共面的充要条件是存在实数,(,)x y x y ∈R ,使p xa yb =+ .【推论】空间中一点O 和不共线的三点,,A B C ,则,,,P A B C OA A OP xOA yO P A B zO B AC OP AB AC C λμλμ⇔=+⇔=+⇔+++= ,且1x y z ++=.类型一 利用平面重合法(同一法)证明点或线共面问题1.利用平面确定性公理及推论判定两平面重合【典例1】求证:已知直线l 与三条平行线a 、b 、c 都相交(如图1),求证:l 与a 、b 、c 共面.图1【分析】设a ∩l =A ,b ∩l =B ,c ∩l =C ,由a ∥b ,得过a 、b 可以确定一个平面α.由b ∥c ,得过b 、c 可以确定一个平面β,由已知推导出α与β重合,从而能证明a 、b 、c 、l 共面.证明:如图2,设a ∩l =A ,b ∩l =B ,c ∩l =C ,∵a ∥b ,∴过a 、b 可以确定一个平面α.∵A ∈a ,B ∈b ,a 、b ⊂α,∴A ∈α,B ∈α,∴AB ⊂α,即l ⊂α.又∵b ∥c ,∴过b 、c 可以确定一个平面β,同理可证l ⊂β.∵α、β都过相交直线b 、l ,∴α与β重合,∴a 、b 、c 、l 共面.图2【点睛】共面问题的证明常有下列方法:(1)先作一个平面,再证明有关的点或线在这个平面内;(2)先过某些点或线作多个平面,再证明这些平面重合;(3)用反证法.本题采用方法2证明较好.【举一反三】(2023上·北京通州·高二统考期中)1.如图,在正方体1111ABCD A B C D -中,,,,E F G H 分别是棱AB ,11B C ,11C D ,1D D 的中点.(1)求证:,,,E F G H 四点共面;(2)求1B D 与平面EFGH 所成角的正弦值;(3)求点1B 到平面EFGH 的距离.【典例2】正方体1111ABCD A B C D -中,,,,,,E F G H I J 分别是它们所在棱的中点,求证:这六个中点共面.证明:如图6,联结FI ,易证EJ FI ∥,∴EJ 和FI 可确定一个平面,记作α.又联结GJ ,则GJ EF ∥,∴GJ 和EF 可确定一个平面β.但,αβ两平面内都含有不共线的三个点,,E F J ,过这三点的平面是存在且唯一的,∴,αβ两平面重合,同理可证,平面EFGH与,αβ都重合,由此可知,,,,,E F G H I J 六个中点共面.图6【举一反三】2.如图,在长方体1111ABCD A B C D -中,11AA =,2AB AD ==,E ,F 分别是AB ,BC 的中点,证明:11,,,A C F E 四点共面.【反思】可以看出同一法同样可以用于证明立体几何,除了证明题之外还有一类解答题,同样是可以用同一法的思想来解答的.假设原命题为“若p 且q ,则r ",当用同一法证明时,证明其逆命题成立则原命题成立,也就是证明“若r ,则p 且q ”.当q 未知时,这就不是证明题,而是解答题.【典例3】直线m 、n 分别和平行直线a 、b 、c 都相交,交点为A 、B 、C 、D 、E 、F ,如图8,求证:直线a 、b 、c 、m 、n 共面.图8【分析】证明若干条直线共面的方法有两类:一是先确定一个平面,证明其余的直线在这个平面里;二是分别确定几个平面,然后证明这些平面重合.证明:∵a ∥b ,∴过a 、b 可以确定一个平面α.∵A ∈a ,a ⊂α,∴A ∈α,同理B ∈a .又∵A ∈m ,B ∈m ,∴m ⊂α.同理可证n ⊂α.∵b ∥c ,∴过b ,c 可以确定平面β,同理可证m ⊂β.∵平面α、β都经过相交直线b 、m ,∴平面α和平面β重合,即直线a 、b 、c 、m 、n 共面.【举一反三】3.证明两两相交而不共点的四条直线在同一平面内.已知:如图,直线1234,,,l l l l 两两相交,且不共点.求证:直线1234,,,l l l l 在同一平面内.2.利用直线的垂面唯一性证两平面重合【典例4】过球外一点作球的切线,求证:所有切点共面.证明:如图10,设球O 外一点P ,切线为,,,PA PB A B 为切点,联结,,PO AO BO ,过A 作1AO PO ⊥于1O ,过1,,A B O 三点作截面得到小圆1O .联结,AO BO ,易知Rt Rt AOP BOP ≌△△,∴PA PB =.在Rt PAO △中,190,OAP AO PO ∠=︒⊥,∴221PO PO PA PB ⋅==,图10则在Rt POB △中可断定1BO PO ⊥,∴PO ⊥平面1AO B ,且11O A O B =(全等三角形对应边上的高相等),由此可知,过点P 作球的切线的切点与点1O 的距离相等,∴点1O 是小圆的圆心.同理,球的任意切线12,,PC PC ⋅⋅⋅;12,,C C ⋅⋅⋅为切点,则平面1112,,AO C AO C ⋅⋅⋅都与直线PO 垂直,所有这些垂面都过点1O ,∴它们都应重合,由此可知,过球外一点作球的切线,所有切点共面.【反思】上例应用了如下结论:过定点作定直线的垂直平面存在且唯一.【举一反三】(2022·安徽马鞍山·马鞍山二中月考)4.四棱锥P -ABCD 中,平面PCD ⊥平面ABCD ,PD PC =,90DPC ∠= ,//AD BC ,90ABC ∠= ,1AD AB ==,2BC =,M 为PC 的中点,2PN ND = .(1)证明:A ,B ,M ,N 四点共面;(2)求二面角M -AB -C 的余弦值.3.利用平行平面的唯一性,证平面重合【典例5】正方体1111ABCD A B C D -中,,,,,,E F G H I J 是它们所在棱的中点,求证:这六个中点共面.证明:见图6,连FI ,易证EJ FI ∥,∴这两条平行线可以确定一个平面α.同理FI GH ∥,则这两条平行线又可确定一个平面β,连11,,AC AD D C ,则1,,EF AC IJ D A EF ∥∥与IJ 是平面α内的相交直线.∴平面EFIJ ∥平面1ACD ,同理,平面FGHI ∥平面1ACD .即平面,αβ都过点F ,且都平行于平面1ACD ,∴平面α与β必重合.【反思】上例利用了下列结论:过平面外一点可以作且只可以作一个与已知平面平行的平面.【举一反三】5.如图,多面体ABCGDEF 中,AB ,AC ,AD 两两垂直,平面ABC //平面,DEFG 平面BEF //平面ADGC ,AB =AD =DG =2, 1.AC EF == 判断点B ,C ,F ,G 是否共面,并说明理由.类型二 利用反证法证明点或线共面问题【典例6】若空间一个四边形邻边的夹角均为90︒,求证:这个四边形必是矩阵.证明:如图15,设四边形ABCD 中,90A B C D ∠=∠=∠=∠=︒,要证它是矩形,应先证明它是个平面图形.图15若四边形ABCD 不是平面图形,则四个线段,,,AB BC CD DA 中必有异面直线.设AB 与CD 为异面直线,而,AD BC 与这两条直线都相交且垂直,∴,AD BC 都是,AB CD 的公垂线,但异面直线的公垂线是存在且唯一的,矛盾.∴,AB CD 不可能是异面直线.同理,,AD BC 也不可能是异面直线.∴四边形ABCD 是一个平面图形.再证ABCD 为矩阵是显而易见的.【典例7】若空间四点,,,A B C D ,满足条件AC BD AB CD AD BC ⋅=⋅+⋅,求证:,,,A B C D 四点共面.证明:如图16,若,,,A B C D 四点不共面,则四点构成一个空间四边形A BCD -,将ABD △绕BD 旋转到BCD △所在平面α内,点A 移到点1A .图16在平面四边形1A BCD 中,应有111A C BD A B CD A D BC⋅≤⋅+⋅但在ACE △中1AC AE EC A C<+=(1)求平面PBC 与平面PAD 所成二面角的正弦值;(2)若E 是棱PB 的中点,对于棱出点E 的位置,并加以证明;若不存在,请说明理由.类型三 利用向量法证明点或线共面问题图20证明:如图20,设,AB a AD =【典例9】四面体ABCD 中,,,,E F G 四点共面.图23证明:如图23,联结EG ,则(12EG EB BG EB BC =+=+(1)求FH (用向量,,a b c 表示)(2)求证:点E ,F ,G ,H 四点共面.【典例10】设O 为平面ABC 共面,且PA ⊂平面ABC .31 证明:A ,B ,M ,N 四点共面;一、单选题:10.已知a 、b 、c 是空间三条不同的直线,则下列命题正确的是(E F G H四点共面A.,,,FG平面ADCB.//FG HE交于点P C.若直线,△的面积为6,则D.若ABD①点E,F,G,H在同一个平面上;②直线DE,BF,CI交于同一点;③直线BF与直线1B C所成角的余弦值为④该正方体过EH的截面的面积最大值为(1)求证:E,F,G,(2)求证:EH,FG,(2022下·辽宁抚顺16.如图,在三棱柱(1)证明:E,F,G,(2)证明:EG,FH,AA(2022下·安徽芜湖·高一校考期中)(1)求证:E ,F ,C 1,1A 四点共面;(2)求证:A 1E ,1C F ,1B B 交于一点18.如图,在正方体ABCD (1)证明:E 、C 、D 1、F (2)设1D F CE O ⋂=,证明:19.如图,ABCD 为空间四边形,点CD ,AD 上,且DH =(1)求证:E ,F ,G ,H 四点共面;(2)求证:EH ,FG 必相交且交点在直线BD 上.(2022·河南·校联考三模)20.如图,在长方体1111ABCD A B C D -中,E ,F(1)证明:E ,F ,D ,B 四点共面.(2)证明:BE ,DF ,1CC 三线共点.(2023·四川成都·校联考模拟预测)21.如图,在三棱柱ABC A -3(1)求证:B ,D ,E ,1B 四点共面;(2)求四棱锥11A BDEB -的体积.(2023·四川成都·校联考模拟预测)22.如图,在三棱柱ABC(1)求证:B ,D ,E ,1B 四点共面;(2)求二面角11A BB D --的余弦值.参考答案:因为,,,E F G H 分别是棱AB 易得11//HM B D ,11//GF B D ,所以,,,H M F G 四点共面,又111//,//,EM AB HG DC AB设正方形的的边长为a则()()1,,,0,0,0,2a B a a a D E a ⎛ ⎝,则1(,,),(,,0),22a a DB a a a GF == 设(),,n x y z = 是平面EFGH 的法向量,a a ⎧1111//,//,//A C AC A C FE FE AC ∴''∴,F 为BC 中点,E '∴为AB 中点,E '∴与E 重合,即11,,,A CF E 四点共面.3.证明见解析【分析】证明几条直线共面的依据是公理3及推论和公理1.先证某两线确定平面α,然后证其它直线也在α内.【详解】图①中,没有三条直线交于一点,因为12l l P = ,所以12,l l 确定平面α,又因1323,l l A l l C ⋂=⋂=,所以,A C α∈,所以3l α⊂,同理可得4l α⊂,所以直线1234,,,l l l l 在同一平面内;图②中,123,,l l l 三条直线交于一点,因为又因1424,l l A l l B ⋂=⋂=,所以,A B α∈,所以4l α⊂,同理3l α⊂,所以直线1234,,,l l l l 在同一平面内,综上所述,所以直线1234,,,l l l l 在同一平面内.4.(1)证明见解析120∠=︒,1PADBC=,AB AD PA==A B C D∴(0,0,0),(0,0,2),(0,1,2)(0,2,0)设面PBC的法向量为(,,)m x y z==---=(3,1,2),(0,1,0)BP BC假设在棱CD上存在点F,使得∴四点共线,记该平面为E F D P,,,PE DF⊂面α∴∈面α,,P∈∈B PEC DF,8.(1)111 242 a b c--(2)证明见解析【分析】(1)根据向量的线性运算结合空间向量基本定理运算求解线的性质,结合平行线的传递性证明【详解】(1)∵【点睛】9.证明见解析【分析】延长CD,BA交于点从而可得QM与PD的交点为点N重合,从而可得结论10.B【分析】根据已知条件判断a 、c 的位置关系,可判断AB 选项的正误;利用锥体可判断D 选项的正误.【详解】对于A 选项,若a b ⊥ ,b c ⊥,则a 与c 平行、相交或异面,对于B 选项,若a b ⊥ ,//b c ,则a c ⊥,B 选项正确;对于C 选项,若////a b c ,将a 、b 、c 视为三棱柱的三条侧棱所在直线,C 选项错误;对于D 选项,若a 、b 、c 共点,将a 、b 、c 视为三棱锥共顶点的三条棱所在直线,则【分析】根据平面的基本性质,异面直线的判定定理,逐一验证各个选项.【详解】如下图所示:根据题意,连接11,A C AC ,则11//A C AC ,所以11,,,A C C A 四点共面,所以1AC ⊂面11ACC A ,又1M A C ∈,所以M ∈面11ACC A ,又M ∈面1AB D ,所以点M 在面11ACC A 与面11AB D 的交线上面,同理可得点O 在面11ACC A 与面11AB D 的交线上面,所以A ,M ,O 三点共线,故A 选项错误,B 选项正确;由异面直线判定定理可知C 选项中1,OM DD 为异面直线,故C 选项错误;由异面直线判定定理可知D 选项中1,AM BB 为异面直线,故D 选项错误.故选:B.12.AD【分析】A 选项举出反例即可说明;C 选项根据共面不具有传递性即可判断;B 选项根据点共面的性质判定即可;D 选项根据过直线与直线外一点可确定个平面,即可判断.【详解】A 正确,可以用反证法证明,假设任意三点共线,则四个点必共面,与不共面的四点矛盾;B 从条件看出两平面有三个公共点A ,B ,C ,但是若A ,B ,C 共线,则结论不正确;C 不正确,共面不具有传递性,若直线a ,b 共面,直线a ,c 共面,则直线b ,c 可能不在一个平面内;D 正确,两两相交的直线有三个公共点,确定一个平面.所以111222 BCDS CO BD==⨯故选:ACD.【分析】对于①,由FG EH ∥即可证得点E ,F ,G ,H 共面;对于②,延长,DE CI 交于M ,由平面EDBF ⋂平面ICBF BF =,证得M BF ∈,即可证得直线DE ,BF ,CI 交于同一点;对于③,取AB 中点N ,1NA D ∠或其补角即为直线BF 与直线1B C 所成角,再由余弦定理求解即可;对于④,求出截面11A BCD 的面积即可判断.【详解】对于①,如图,连接1,FG A B ,因为点F ,G 分别为线段11A B ,1B B 的中点,则1FG A B ,又点E ,H 分别为线段11A D ,BC 的中点,则1EH A B ,则FG EH ∥,则,FG EH 共面,即点E ,F ,G ,H 在同一个平面上,①正确;对于②,连接,,EF FI EI ,易得EI CD ,则,EI CD 共面,延长,DE CI 交于M ;易得EF BD ∥,则,EF BD 共面;FI BC ,,FI BC 共面;平面EDBF ⋂平面ICBF BF =,又M ∈平面EDBF ,M ∈平面ICBF ,则M BF ∈,即直线DE ,BF ,CI 交于同一点,②正确;对于③,取AB 中点N ,连接角即为直线BF 与直线1B C 又22,A D A N DN ===对于④,连接1A B ,易得A 面;又1BC A B ⊥,12,BC A B =17.(1)证明见解析(2)证明见解析【分析】(1)连接EF ,根据E ,F 分别为AB ,BC 的中点,得到EF AC ∥,再根据三棱柱的性质证明即可;(2)由(1)得EF AC ≠且E ,F ,1A ,1C 四点共面,得到1A E 与1C F 必相交,设11A E C F P ⋂=,再证明1P BB ∈即可.【详解】(1)证明:如图,连接EF ,∵E ,F 分别为AB ,BC 的中点,∴EF AC ∥..又在三棱柱111ABC A B C 中,11AC A C ∥,∴11EF A C ∥.则E ,F ,1A ,1C 四点共面.(2)由(1)得EF AC ≠且E ,F ,1A ,1C 四点共面,则1A E 与1C F 必相交.设11A E C F P ⋂=.∵1A E ⊂平面11AA B B ,∴P ∈平面11AA B B .∵1C F ⊂平面11BB C C ,∴P ∈平面11BB C C ..又平面11AA B B ∩平面111BB C C BB =∴1P BB ∈.则1A E ,1C F ,1B B 交于一点.18.(1)证明见解析(2)证明见解析【分析】(1)利用三角形的中位线及平行四边形的性质证明1//EF CD ,从而得到四点共面;(2)根据平面的性质,证明点O ∈平面ABCD ,O ∈平面ADD 1A 1,从而A ,O ,D 三点共线.【详解】(1)证明:如图,连接EF ,1A B ,1D C .在正方体1111ABCD A B C D -中,E 、F 分别是AB 、AA 1的中点,所以 1//EF A B .又11//BC A D ,且11BC A D =,所以四边形11BCD A 是平行四边形,所以1A B 1//D C .1//EF D C ∴,所以E 、C 、D 1、F 四点共面;(2)由1D F CE O ⋂=,1O D F ∴∈,又1D F ⊂平面11ADD A ,O ∴∈平面11ADD A ,同理O ∈平面ABCD ,又平面11ADD A 平面ABCD AD =,O AD ∴∈,即A ,O ,D 三点共线.19.(1)证明见解析(2)证明:易知13HG AC=,又EF=结合(1)的结论可知,四边形EFGH是梯形,因此直线EH,FG不平行.设它们交点为P,P∈平面ABD,同理P又平面ABD⋂平面BCD BD=,20.(1)证明见解析(2)证明见解析【分析】(1)连接EF,BD,11B D,易得明;.(2)由直线BE 和DF 相交,延长BE ,DF ,设它们相交于点P ,然后再论证P ∈平面11BB C C ,P ∈平面11CDD C 即可.【详解】(1)如图,连接EF ,BD ,11B D .∵EF 是111B C D △的中位线,∴11EF B D ∥.∵1BB 与1DD 平行且相等,∴四边形11BDD B 是平行四边形,∴11BD B D ∥,∴EF BD ∥,∴E ,F ,D ,B 四点共面.(2)∵EF BD ∥,且EF BD ≠,∴直线BE 和DF 相交.延长BE ,DF ,设它们相交于点P ,∵P ∈直线BE ,直线BE ⊂平面11BB C C ,∴P ∈平面11BB C C ,∵P ∈直线DF ,直线DF ⊂平面11CDD C ,在三棱柱111ABC A B C -中,四边形则160A AC ∠=︒,又AC =又O 为AC 的中点,所以又平面11AA C C ⊥平面ABC则()0,0,0O ,()0,2,0A -,所以()3,1,0BD =- ,1BB AA = 设平面1B BD 的一个法向量为令13z =-,则11x =,1y =。
导数中证明不等式技巧——构造、切线放缩、二元变量、凹凸反转专题

导数中证明不等式技巧——构造、切线放缩、二元变量、凹凸反转专题典例1】已知函数$f(x)=1-\ln(x)e^x,g(x)=\frac{x}{1-bx}$,若曲线$y=f(x)$与曲线$y=g(x)$的一个公共点是$A(1,1)$,且在点$A$处的切线互相垂直。
求$a,b$的值,并证明:当$x\geq1$时,$f(x)+g(x)\geq\frac{2}{x}$。
典例2】已知函数$f(x)=(x+b)(e^x-a)$,在$(-1,f(-1))$处的切线方程为$(e-1)x+ey+e-1=0$。
求$a,b$的值,并证明:若$m\leq\frac{f(x)}{x^2+x}$,则$f(x)\geq mx^2+x$。
典例3】已知函数$f(x)=x\ln x+ax+1$,$a\in\mathbb{R}$。
1)当$x>0$时,若关于$x$的不等式$f(x)\geq k$恒成立,求$a$的取值范围;2)当$n\in\mathbb{N^*}$时,证明:$\frac{n^3}{n+1}<\ln2^2+\ln2+\frac{1}{n+1}<\frac{n}{n+1}$。
典例4】已知函数$f(x)=\frac{2\ln x+2}{e^x}$。
1)求函数$f(x)$的单调区间;2)证明:当$x>0$时,$f'(x)\ln(x+1)<\frac{2}{x+2}$。
典例5】已知函数$f(x)=e^x-x^2$。
1)求曲线$f(x)$在$x=1$处的切线方程;2)证明:当$x>0$时,$e^x+(2-e)x-1\geq\ln x+1$。
典例7】已知函数$f(x)=x^2+ax+b\ln x$,曲线$y=f(x)$在点$(1,f(1))$处的切线方程为$y=2x$。
1)求实数$a,b$的值;2)设$F(x)=f(x)-x^2+mx(m\in\mathbb{R})$,$x_1,x_2$$(x_1<x_2)$分别是函数$F(x)$的两个零点,求证:$F'(x)$在$(x_1,x_2)$内至少有一个零点。
中考数学 考点系统复习 第六章 圆 微专题(七) 与切线有关的常考五大模型

1 ∴CD=3,∠DAC=2∠BAC, ∴AD= AC2-CD2=4,∠DAO=90°, ∵∠ADC=90°, ∴四边形 ADEO 是矩形, ∴OE=AD=4, ∴⊙O 的半径是 4.
类型三: 与锐角三角函数结合
【类型归纳】
模型展示
常见辅助线
连接圆心与切点
若问题中涉及到直角(或构造出直角)时,可以利用锐角三角函数来
半圆与 AB,AC 相切,切点分别为 D,E.过半圆上一点 F 作半圆的切线,
BM·CN 分别交 AB,AC 于点 M,N,那么 BC2 的值为 A.18 B.14 C.12 D.1
(B )
7.★如图,AB 为⊙O 的直径, C 为⊙O 上一点, AD 和过 C 点的切线互
25 相垂直,垂足为 D.若 AD=4,AC=5,则 AB 的长为 4 .
AD⊥DC,若⊙O 的半径为 3,AD=4,则 AC=2 6.连接 BC,OC,由
常见结论 与方法
AD⊥DC 和直径所对的圆周角为直角,可得∠ACB=∠ADC=90°, ∵DC 是⊙O 的切线,∴∠DCA=∠ABC,∴△ADC∽△ACB,得出AADC=
AACB,进而求出 AC=2 6.
对应练习
6.★如图,在等腰三角形 ABC 中,O 为底边 BC 的中点,以点 O 为圆心作
OB=3,PB=2.连接 OC,由切线的性质可得 OC⊥PC,易得 PO=BO
+PB=5,再利用勾股定理,可得 PC= PO2-OC2=4.
对应练习 1.★(2022·深圳)如图,三角形 ABE 为直角三角形,∠ABE=90°,BC 为⊙O 的切线,C 为切点,CA=CD,则△ABC 和△CDE 的面积之比为( B ) A.1∶3 B.1∶2 C. 2∶2 D.( 2-1)∶1
