大连理工大学
- 1 -
《高等代数下》试卷及答案二
一、填空题（每小题4分，共32分）。
1. 判断下面所定义的变换, 哪些是线性变换, 哪些不是线性变换:
1) 在P[x] 中, ),1())((xfxf ];[)(xPxf
2) 在P[x] 中, ,1)())((xfxf ][)(xPxf.
2. 设2222:RR的线性变换，，XdcbaX)( 其中R是实数域，
求在基1000,0100,0010,000122211211EEEE下的矩阵
3．已知三级矩阵A的三个特征值为1，2，3，则EAAA21*相似于对角矩阵
4．设四级矩阵A的最小多项式为)2()1()(2m，写出A的所有可能的Jordan标准形
5．已知矩阵2121A，则A初等因子组, ，
不变因子组为 ，各阶行列式因子组为
6. 在欧氏空间4R中（内积按通常定义），向量)0,1,1,0(),1,1,0,0(之间的夹角
7．设321,,是三维欧式空间的一组标准正交基，
),22(3211k),22(3212k )22(3213k
也是一组标准正交基，
则k= 。
8．设),(f是数域P上三维线性空间V上的一个双线性函数，321,,是V的一组基，矩
- 2 -
阵012120101A是),(f在321,,下的度量矩阵，设
21321
,2
，则),(f=
二．计算
1．（6分）已知三级实对称矩阵A的三个特征值为3,2,1321，对应21,的特征向量
分别为)0,1,0(),1,0,1(21pp，求3对应的特征向量.
2．（10分）设V是数域P上的一个线性空间，321,,是它的一组基，f是V上的一个线性
函数，已知3)(,1)2(,1)(213221fff，求)(332211xxxf.
三．（12分）在nxP][中)1(n，微分变换)('))((:xfxfDD是nxP][上的线性变换
1. 求D的特征多项式；
2. 证明D在任何一组基下都不可能是对角矩阵;
3. 求D的核及值域.
四．（10分）设A是数域P上一个n级矩阵，证明A与A的转置矩阵'A相似.
五．设323121232221321666222),,(xxxxxxxxxxxxf
1．(8分) 用正交线性替换化下列二次型为标准形（要有过程）；
2．(2分) 在空间直角坐标系321XXXO中, 1),,(321xxxf表示何种曲面.
六．（10分）设V是n维欧氏空间，证明对于任意n级正定矩阵A，都存在V的一组基，使
得关于这组基的度量矩阵是A.
七．（10分）设21,是n维线性空间V上线性变换，且
v121（v
1
是V上的恒等变换），且 秩21秩n，证明：
1．)()(21VVV；
2．01221；2,1,2iii.
- 3 -
参考答案
一、填空题（每小题4分，共32分）。
1.1）是线性变换 2)不是线性变换
2. 00000000ababcdcd 3． 9001700237003 4． 1000110000100002 1000110000200002
5． 22,1 ，21,1,12， 21,1,12
6. 3 7． k= 13。8． -1
二．计算
1．解：设),,(321xxxp是3对应的特征向量，则p与21,pp皆正交，
即
13
0xx
2
0x
可得 1,0,1p
于是 33的所有特征向量为 kp，
0k
2．
解：由题意可知
122313()()1()2()1()()2ffffff 1
2
3
()2()1()0fff
所以 )()()()(332211332211fxfxfxxxxf=
12
2xx
三．解：1. 取nxP][的一组基 1，x，2x，，1nx，则有
- 4 -
212101000020(1,,)(1,,)00010000nnDxxxxxxn
，
即D在基12,,,,1nxxx下的矩阵为D=0000100002000010n，所以D的特征多项式
()nfED
.
2．由1知D只有一个特征值0（n重），唯一的一个特征子空间是一维的，维数小于n，所以D在任
何一组基下的矩阵都不是对角矩阵。
3．D的核1(0)()[](())0nDfxPxDfx 所以 ()fxp，pP 即1(0)DP，
D的值域121][),,,1())(,),(),1(()][(nnnnxPxxLxDxDDLxPD
四．
证明：由于
EA与'EA
互为转置矩阵，所以具有相同的各级行列式因子，因此具有相同的不变因
子，故A相似于A’
五．
解：由题意可知此二次型对应的矩阵为
A=233323332
A的特征多项式为
2
)5)(4(||)(AEf
，因此A的特征值5,421
对应41的特征向量为 1111'p，
对应52线性无关的特征向量为2(110)'p，3(101)'p，将其正交化、单位化后得正交
- 5 -
矩阵
111
326
111
326
12
036Q
即经正交替换X=QY，f化成标准形222123455fyyy，
当1),,(321xxxf时，其为单叶双曲面。
六．证明：设
12,n为V的一组标准正交基，关于12,n
的度量矩阵为E，又由于A正定，所
以存在可逆矩阵C，使得'ACEC，令11(,)(,)nnC，关于基1,n的度量矩阵'CECA。
七．
证明：1，
V
，则有12()()，
111()()s为1()V的基，212()()sn为2
()V
的基，可由111()()s，
212()()sn
表出，又dimVn，故为一组基，
则)()(21VVV
2．V，由于 12()()
则有11112()(())()，且又有 11121()(())(()) 所以有
1221
()()
12
()()VV=0
，从而12210，且有 211()()得211，
同理222，
大连理工823复试科目
大连理工823复试科目大连理工大学的823复试科目主要涉及到物理和化学的内容，具体包括以下几个方面：一、复试科目总体情况大连理工大学的823复试科目主要包括物理和化学两门课程。
物理部分主要涉及普通物理学、热力学、电磁学和光学等，化学部分则包括无机化学、分析化学和有机化学等。
这些科目是理工科研究生入学考试的重要内容，也是复试中考察的重点。
二、考试范围和要求1. 普通物理学：考生需要掌握物理的基本概念和规律，如力学、电磁学、光学等。
同时，考生需要具备一定的数学基础，能够运用数学知识解决物理问题。
2. 热力学：考生需要掌握热力学的基本原理和定律，如热力学第一定律和第二定律等。
同时，考生需要了解热力学在工程中的应用，如能量转换和传输等。
3. 电磁学：考生需要掌握电磁学的基本概念和规律，如电场、磁场、电磁感应等。
同时，考生需要了解电磁波的传播和辐射等。
4. 光学：考生需要掌握光的波动性和粒子性，以及光的干涉、衍射、折射等基本光学现象。
同时，考生需要了解现代光学技术如激光技术等的应用。
5. 无机化学：考生需要掌握无机化学的基本原理和反应规律，如酸碱反应、氧化还原反应、沉淀溶解等。
同时，考生需要了解无机化合物在工业生产中的应用。
6. 分析化学：考生需要掌握分析化学的基本原理和方法，如光谱分析、色谱分析等。
同时，考生需要了解分析化学在环境监测、食品检测等领域的应用。
7. 有机化学：考生需要掌握有机化学的基本概念和反应规律，如烷烃、烯烃、醇酚等。
三、考试形式和难度考试形式通常为笔试，考试时间为3小时。
题目难度中等偏难，考察内容广泛且深入。
要求考生具备扎实的基础知识和较强的解决问题能力。
四、复试准备建议考生在准备复试时，首先要夯实基础，把高中和大学期间的物理和化学知识熟练掌握。
其次，要通过习题练习提升解题能力，学会用物理和化学知识解决实际问题。
最后，要认真研读大连理工大学的复试考试大纲，按照要求进行针对性复习。
大连理工大学大学生作息时间表
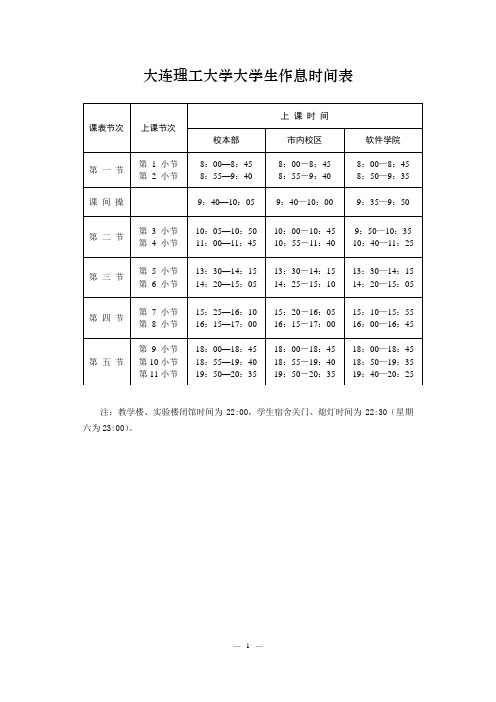
大连理工大学大学生作息时间表
注：教学楼、实验楼闭馆时间为22:00，学生宿舍关门、熄灯时间为22:30（星期六为23:00）。
所学课程考核成绩记录
大学生活纪要（一）2008年8月30日到大连理工大学报到，大学生活开始了！
大学生活纪要（二）
大学生活纪要（三）
大学生活纪要（四）大学生活纪要（五）
大学生活纪要（六）
大学生活纪要（七）
大学生活纪要（八）
环境与生命学院
创新园大厦 研究生 教育大楼
东山生活区
综合教学楼
辰男建筑 艺 术 馆
第二教学馆
公安处
化学楼
第一食堂
电气工程系
机械工程学院
材料工程学院 主楼阶梯教室 模具研究所
西便门
校医院
山上礼堂
教育书
店 综合实验楼 2号
电教馆
第一教学馆
计算中心
西门
南门
东门
图书馆
北门
工 程 力学系
综合实验楼
3
号
管理学院。
大连理工大学重点学科及特色专业介绍
大连理工大学重点学科及特色专业介绍 大连理工大学(Dalian University of Technology)，简称大工，坐落于滨城大连，是中央直管、教育部直属的副部级全国重点大学，中国著名的“四大工学院”之一，国家“211工程”、“985工程”、“卓越工程师教育培养计划”、“国家大学生创新性实验计划”和“111计划”重点建设的大学，“卓越大学联盟”、“中俄工科大学联盟”、“中欧工程教育平台”主要成员。
校园环境 学校依山傍海，办学条件优良。已形成一校、两地(大连市、盘锦市)、三区(大连凌水主校区、开发区校区、盘锦校区)的办学格局。截至2014年5月，学校总占地面积433.2万平方米，建筑面积154.8万平方米。学校图书馆藏书299.2万余册，中外文电子期刊5.8万余种。学校现有运动场馆面积21.5万平方米。同时，学校拥有国内一流的校园网络体系。（截至2014年5月）
校园无线网络成为亚洲高校中首个运用双频接入900兆的校园无线网络，是当前商用无线网络的最高速率标准。
学科建设 截至2014年5月，学校建有一级学科国家重点学科4个(涵盖15个二级学科)，二级学科国家重点学科6个，二级学科国家重点（培育）学科2个。有27个一级学科博士点，128个二级学科博士点，42个一级学科硕士点，218个二级学科硕士点，24个博士后科研流动站，还有工商管理硕士(MBA，含EMBA)、公共管理硕士(MPA)、建筑学硕士、工程硕士、金融硕士、应用统计硕士、艺术硕士、翻译硕士、会计硕士、工程管理硕士10个类别专业学位授予权以及高校教师在职攻读硕士学位授予权。
重点学科 一级学科国家重点学科(4个)：力学、水利工程、化学工程与技术 、管理科学与工程 二级学科国家重点学科(6个)：计算数学、等离子体物理、机械制造及自动化、结构工程、船舶与海洋结构物设计制造、环境工程
二级学科国家重点(培育)学科(2个)：动力机械及工程、技术经济及管理 特色专业 机械是大连理工大学的王牌学科，现设有4个本科专业及方向——机械设计制造及其自动化 (含机电外贸日语强化、英语强化)、工业设计、测控技术与仪器、物流工程，他们的大量优秀成果都已经转化成优质的产品，如全液压汽车起重机系列设计，已与国内有关企业合 作应用，每年形成上亿的产值;智能控制装置，已广泛应用于我国石化企业;制球机械和故障诊断仪已在国内形成较大影响等。
大连理工大学简介ppt模板模板
学 在 大 工 创 新 在 大 工
大连理工大学
四、创新培养 挑战自我
“创新教育”被教育部确认为学校办学特色
全国较早倡导创新教育的高校之一 被共青团中央、全国青联命名为“全国青年科技创新教育基地” 在创新教育方面先后2次获得国家级教学成果一等奖
大连理工大学
这里是读书做学问的好地方！ ——江泽民
13 大连理工大学
卓越工程师培养--全面提高工程实践能力-工程师的摇篮
免试推荐研究生制度--比例15%，全国高校自主选择 复合型人才培养--辅修专业制、双学位制—提高就业竞争力 理科拔尖人才培养--华罗庚班、张大煜化学菁英班、王大珩物理科学班 创新人才培养--4个创新实验班、9个创新实践班 国际化人才培养—3个国际班继续招生，拓展国际视野和国际竞争力
6 大连理工大学
六、国际交流 寰球视野
我校代表队参加了在美国纽约举办 的世界模拟联合国大会
我校学生赴日本金泽学院大 学文化交流与访问
我校代表团赴澳大利亚文化 研习营
我校赴瑞典皇家工学院交换学生参加 斯德哥尔摩和平游行支持北京奥运
我校代表团赴英国文化研习营
1
大连理工大学
一、知名学府 工科十强
1949年4月建校 教育部直属重点高校
大连工学院
国家首批“985工程”重点建设高校（34所）
国家首批“211工程”重点建设高校（27所）
国家首批设立研究生院的重点高校（33所） 国家卓越工程师培养计划试点学校 国家首批“大学生创新性实验计划”试点学校 国家副部级中管干部高校（31所） 胡锦涛同志来我校视察 拥有国家级2011协同创新中心（辽宁重大装备制造协同创新中心） 2014年《泰晤士报》亚洲大学百强榜(亚洲排名79，国内排名15) 综合实力位列国内工科院校十强
大连理工大学校园地图
大连理工大学校园地图
一、校园地图：
学校西部（图片来源：学校官网）
1、西部主要分布：有机械工程学院、能动学院、环境学院、化工学院。
2、主要建设有：发展用地、教学楼和体育场。
（操场也分为两个区域，西区操场和东区操场一般举办啥大型活动都在行知操场举行）
3、一共四个大门（如图：东西南北门，北门通常是不开的，平时允许学生进出的是东门和南门，西门是开学时的统一入口）学校西部有西门，从学校西门进迎面是第一教学楼，东边是体育场，南边是教学楼各个通道四通发达可以去到任意地方
学校中部（图片来源：学校官网）
1、中部主要分布：高级经理学院、经济管理学院、船舶工程学院、运城学部、创新创业学院等。
2、主要建设有：学生宿舍、综合楼、足球场、办公楼、
实验室、研究所等。
学校东部（图片来源：学校官网）
1、主要建设：学生文化中心、幼儿园、汽车驾驶学校、
学术交流公寓、室内体育场/游泳馆、校史馆、博物馆等。
大连理工人工智能专业评级
大连理工人工智能专业评级大连理工人工智能专业评级一、导言人工智能（Artificial Intelligence，简称AI）是近年来备受瞩目的学科领域，其应用范围广泛，对社会发展具有重要意义。
大连理工大学作为国内知名高校之一，在人工智能领域拥有丰富的教学和研究资源。
本文将对大连理工大学的人工智能专业进行评级，并从课程设置、教学质量、科研实力等多个方面进行综合分析。
二、课程设置1. 本科阶段大连理工大学的人工智能专业本科阶段的课程设置较为全面，涵盖了基础理论和实践技能两个方面。
主要包括数学基础、计算机科学基础、数据结构与算法、机器学习等核心课程。
还设有专门针对人工智能领域的深度学习、自然语言处理、计算机视觉等高级课程。
通过这些课程的学习，学生可以全面掌握人工智能领域的基础知识和技术。
2. 硕士研究生阶段在硕士研究生阶段，大连理工大学的人工智能专业提供了更加深入和专业化的课程。
除了继续加强对基础理论的学习外，还设置了一系列高级课程，如模式识别、数据挖掘、人工智能系统设计等。
还有一些选修课程供学生选择，以满足个性化的学术需求。
三、教学质量1. 教师队伍大连理工大学人工智能专业拥有一支优秀的教师队伍。
这些教师中既有经验丰富的教授和副教授，也有年轻有为的讲师和助教。
他们中的许多人在人工智能领域具有较高的知名度和影响力，并且积极参与国内外重要学术会议和期刊的评审工作。
2. 实践环节大连理工大学注重培养学生的实践能力，在人工智能专业中设置了多个实践环节。
在本科阶段，学生将参与小组项目开发，通过团队合作解决实际问题；在研究生阶段，学生将参与科研项目，与导师一起深入研究特定领域的问题。
这些实践环节使学生能够将所学知识应用于实际情境中，提升综合能力。
四、科研实力大连理工大学在人工智能领域具有较强的科研实力。
学校设有多个人工智能相关的研究机构和实验室，如模式识别与智能系统实验室、机器人学与人工智能实验室等。
这些机构和实验室致力于开展前沿的科学研究，并取得了一系列重要成果。
大连理工大学有哪些专业和学院及院系排名
大连理工大学有哪些专业和学院及院系排
名
经济学类
汉语言文学广播电视新闻学雕塑艺术设计英语日语新闻传播学
法学类
国际经济与贸易金融学经济学
教育学类
艺术教育
文学类
机械设计与制造
理学类
工程管理工商管理物流管理公共事业管理信息管理与信息系统人力资源管理工业工程会计学市场营销
工学类
法学
管理学类
高分子材料与工程无机非金属材料工程机械设计制造及其自动化材料成型及控制工程金属材料工程过程装备与控制工程工业设计测控技术与仪器热能与动力工程计算机科学与技术通信工程网络工程软件工程自动化建筑学电气工程及其自动化电子信息工程土木工程水利水电工程建筑环境与设备工程港口航道与海岸工程城市规划环境工程化工与制药化学工程与工艺制药工程物流工程船舶与海洋工程工程力学生物工程材料车辆工程机械土建能源动力电子科学与技术信息工程给水排水工程测绘工程安全工程交通工程生物医学工程电气信息管理科学与工程飞行器设计与工程功能材料纳米材料与技术物联网工程传感网技术能源化学工程海洋资源开发技术
制造类
水土保持与荒漠化防治
农学类
数学与应用数学信息与计算科学应用物理学应用化学光信息科学与技术电子信息科学与技术材料物理环境科学生物技术数学物理学电子信息科学化学。
大连理工转专业政策
大连理工转专业政策1. 背景介绍大连理工大学是中国的一所重点高校，拥有优质的教学资源和丰富的专业设置。
然而，由于个人兴趣、职业规划或其他原因，部分学生可能在入学后希望转换专业。
为了满足学生的需求，大连理工大学制定了转专业政策。
2. 转专业申请条件大连理工大学对转专业申请设置了一些基本条件：•学生必须已经完成至少一年的本科课程；•学生必须成绩合格，没有挂科；•学生需要通过面试和考试等环节进行评估。
3. 转专业申请流程下面是转专业申请的基本流程：3.1 提交申请材料学生需要准备以下材料并提交给相关部门：•转专业申请表；•相关成绩单和课程表；•推荐信（如果有）；•其他支持材料（如实习证明、获奖证书等）。
3.2 面试和考试根据不同专业的要求，学校会安排面试和考试环节。
面试通常是由相关专业的教师组成的小组进行，目的是了解学生的专业兴趣、动机和适应能力。
考试则是为了测试学生在相关领域的基础知识和能力。
3.3 综合评估学校会综合考虑申请材料、面试和考试成绩等因素，对每个申请进行评估。
评估结果将决定学生是否能成功转专业。
4. 转专业政策说明大连理工大学的转专业政策有以下几个要点：4.1 限制转专业次数为了保证教育质量和稳定性，学校对每个学生的转专业次数进行限制。
通常，本科生只允许转一次专业。
4.2 转专业审核转专业审核由相关部门负责，他们会仔细审查每个申请，并与原专业和目标专业的教师进行沟通。
审核结果将根据学生的表现和实际情况来决定。
4.3 转入条件不同专业对于转入条件有一定要求，例如： - 学分要求：需要满足一定数量或特定课程类型的学分； - 成绩要求：需要达到一定的平均绩点或相关课程的成绩要求； - 排名要求：需要在原专业中有一定的排名。
4.4 转出条件转出条件通常包括： - 学分要求：需要满足一定数量或特定课程类型的学分； - 成绩要求：需要达到一定的平均绩点或相关课程的成绩要求； - 排名要求：需要在原专业中有一定的排名。
大连理工大学专业历史历任校长简介
大连理工大学毕业证样本历任校长大连理工大学简介乘车路线地址：大连理工大学（英语：Dalian University of Technology，DUT），创立于1949年4月，是中华人民共和国创立的第一所正规高等院校。
坐落于美丽的北方明珠大连市的大连理工大学，作为中华人民共和国创立的第一所正规高等院校，传统理工科著名重点学府，“四大工学院”之一，是中国少有的未进行过合并的一所一流大学。
已形成以理工为主，理、工、经、管、文、法、哲等协调发展的多学科体系。
大连火车站-星海广场-理工大学约13公里换乘1次在大连火车站上车，乘坐531(大连火车站-河口)坐8站在星海广场下车在星海广场上车，乘坐406(希望广场-百合山庄)坐8站在理工大学下车。
大连火车站-盖州街-栾金东街约15公里换乘1次在大连火车站上车，乘坐31(寺儿沟-锦泉南园)坐8站在盖州街下车在盖州街上车，乘坐10(沙河口火车站-百合山庄)坐17站在栾金东街下车。
大连理工大学开发区校区开发区铁山西路31号。
大连理工大学历任校（院）长及任职年限：金同稷任大连工学院院长（1985.09至1988.01）任大连理工大学校长：（1988.01至1991.12）；林安西任大连理工大学校长（1991.12至1995.11）；程耿东任大连理工大学校长（1995.11年到2006.4）；欧进萍任大连理工大学校长：（2006.4到至今）。
大连理工大学所设院系和专业学科：学校设有研究生院，7个学部（下设29个院系）、7个独立建制的学院、教学部，3个专门学院和1所独立学院：研究生院人文与社会科学学部人文学院公共管理与法学学院马克思主义学院MPA教育中心艺术教育中心外国语学院英语语言文学系日语语言文学系俄语语言文学系西语教研室（法语、德语、西班牙语等）建筑与艺术学院建筑系城市规划系工业设计系艺术系管理与经济学部经济学院工商管理学院管理科学与工程学院中国大企业研究中心（与中国大连高级经理学院合作）全国工商管理案例研究中心数学科学学院国家性示范理科数学基地班信息与计算科学系数学与应用数学系物理与光电工程学院应用物理学（物理基础科学班）应用物理学电子科学与技术光信息科学与技术等离子体物理与三束材料改性教育部重点实验室（与材料学院共建）化工与环境生命学部化学学院化工学院制药科学与技术学院化工机械学院环境科学与技术学院生命科学与技术学院精细化工国家重点实验室工业生态与环境工程教育部重点实验室机械工程与材料能源学部机械工程学院材料科学与工程学院能源与动力学院精密与特种加工教育部重点实验室海洋能源利用与节能教育部重点实验室建设工程学部土木工程学院水利工程学院交通运输学院建设管理系国家深海工程创新研究实验中心海岸及近海工程国家重点实验室运载工程与力学学部工程力学系船舶工程学院汽车工程学院航空航天学院工业装备国家重点实验室船舶与海洋国家工程中心电子信息与电气工程学部计算机科学与工程学院电子科学与技术学院控制科学与工程学院信息科学与技术学院电气工程学院生物医学工程系大连微电子学院（与INTEL（英特尔）、大连市政府共建，学院拥有INTEL捐赠的全球高校唯一的8英寸芯片完整生产线，以及相关的超净实验室）国家示范性软件学院软件工程系网络工程系嵌入系软件系数字媒体技术系创新实验学院体育教育部国际文化交流学院国防教育学院城市学院继续教育学院附属幼儿园、初中和附属高中附属校医院大连理工大学历史变迁过程详解：1946年11月，大连工业专门学校在这里成立，简称大连工专，隶属大连市政府。
大连理工转专业政策
大连理工转专业政策一、背景介绍大连理工大学是中国一所著名的高等学府，拥有优秀的师资力量和丰富的教学资源。
在大学期间，学生可能会发现自己对原本选择的专业不感兴趣，或者发现自己的兴趣和潜力更适合其他专业。
为了满足学生个性化发展的需求，大连理工大学制定了转专业政策，允许学生在一定条件下转换专业。
二、转专业条件大连理工大学对转专业设置了一定的条件，以确保学生转专业的合理性和可行性。
具体条件如下：1.学生必须已完成入学前两学年的学习，并且成绩达到一定的要求。
通常要求学生的平均绩点不低于3.0，且专业课成绩达到相应标准。
2.学生需要通过转专业考试或面试。
转专业考试主要考察学生对目标专业的基础知识和能力，以及学习动机和发展规划。
3.目标专业需要有足够的空余名额。
如果目标专业已满员，学生将无法转专业。
4.学生需要提交转专业申请，包括个人简历、成绩单、转专业申请书等材料。
三、转专业流程大连理工大学的转专业流程相对简洁明了。
学生需要按照以下步骤进行：1.学生首先需要仔细阅读转专业政策和相关规定，了解转专业的条件和要求。
2.学生根据自己的兴趣和发展规划选择目标专业，并与目标专业的教务办公室联系，了解目标专业的具体要求和流程。
3.学生准备转专业申请材料，包括个人简历、成绩单、转专业申请书等。
申请书需要详细说明转专业的原因和动机，以及对目标专业的认识和规划。
4.学生提交转专业申请材料到原专业的教务办公室。
教务办公室将审核材料，并将学生的申请转交给目标专业的教务办公室。
5.目标专业的教务办公室将对学生进行转专业考试或面试。
考试或面试的结果将作为转专业的重要依据。
6.目标专业的教务办公室根据考试或面试结果，以及目标专业的招生情况，决定是否录取该学生为转专业生。
7.如果学生被录取为转专业生，学生需要办理相关手续，包括填写转专业意见书、缴纳转专业费用等。
8.学生完成转专业手续后，将正式成为目标专业的学生，开始学习新的专业课程。
四、注意事项在转专业过程中，学生需要注意以下事项：1.转专业是一项重要的决策，需要充分考虑自身的兴趣和发展规划。