第四章叠加定理、戴维宁定理和诺顿定理
第四章(习题答案)

§4-3 戴维宁定理和诺顿定理
(一)戴维宁定理的证明
设流过端口以外的电路中的电流为 i,则据替代定 ,则据替代定 理,外电路可以用一个电流为 i的电流源 iS替代,如图(a)所 替代,如图(a) (a)所 示;则又据 叠加定理,得其相应的分电路 (b),(c): 示;则又据叠加定理 ,得其相应的分电路(b) (c): 叠加定理,得其相应的分电路 (b),
:在线性 线性电路中,任一支路的电流或电 叠加定理 :在 线性 电路中,任一支路的电流或电 压是电路中各个独立电源(激励) 单独作用 时在 压是电路中各个独立电源(激励)单独作用 单独作用时在 该支路中产生的电流或电压的 代数和. 该支路中产生的电流或电压的代数和 代数和.
§4-1 叠加定理
也就是说,只要电路存在唯一解,线性电路中 的任一结点电压,支路电压或支路电流均可表示为 以下形式: y = H 1uS1 + H 2 uS 2 + + H m uSm + K 1 iS1 + K 2 iS 2 + + K n iSn ——表示电路中独立 其中:uSk 表示电路中独立电压源的电压 独立电压源的电压
+ Req + u RL
uS1
NS
uS2
RL
口 含一 源 端
1
戴维宁定理
- -
uoc
维 宁 等 效 电 路
1' i1
RL
isc
1'
1'
u R Geq L
-
+
诺顿定理
诺 顿 等 效 电 路
1'
§4-3 戴维宁定理和诺顿定理
对外电路而言,"含源一端口NS"可以用一条含源支路 对外电路而言," 含源一端口N 可以用一条含源支路 等效替代 戴维宁等效电路和诺顿等效电路称为一端口的等效发电机 戴维宁等效电路和诺顿等效电路称为一端口的等效发电机
电路理论_(4)

例:电路如图(a), 电路响应
i2 i2 iS 0 i2 uS 0 i2(1) i2(2)
u1 u1 iS 0 u1 uS 0 u1(1) u1(2)
电路等效为下图
i (1)
2
uS R1 R2
i(2)
2
R1iS R1 R2
u (1) 1
R1uS R1 R2
u(2) 1
R1R2iS R1 R2
18
二、 诺顿定理
诺顿定理:任何一个线性含源二端网络,对外电路来讲,可 以用一个电流源和电导的并联组合等效变换。其电流源的电 流 iS = isc 为网络端口的短路电流;电导Geq=(1/ Req )为网络 内部电源均为0时的端口的输入电导。
含源一端 口网络
戴维宁等效电路 诺顿等效电路
两种等效电路共有3个参数: uoc , isc ,Req 其关系为: uoc = isc Req 戴维宁等效电路和诺顿等效电路统称为一端口的等效发电机。
33
4-6 对偶原理
注意以下关系式:u Ri, i Gu 对于CCVS: u2 ri1, 对于VCCS: i2 gu1
对偶元素:电压与电流;电阻与电导;CCVS与VCCS;r与g
n
R Rk k 1
i u R
uk
Rk R
u
两个电路互为对偶
n
G Gk k 1
u i G
ik
Gk G
i
显然,在上式中将对偶元素互 换,则对应关系式彼此转换
+
6
例:4-2 求图示电路中的电压 u3 。
+
7
例:4-3 求图示电路中的电压 u3 。
+
8
线性电路的齐性定理:当所有激励(独立电压源和独立电流源) 都同时增大或减小K倍时,响应(电压或电流)也将同样增大或 减小。 例:4-4 求图示电路中的各支路电流。
电路分析基础第04章电路定理

Pmax
uo2c 4 Req
•最大功率匹配条件
RL Req
最大功率 匹配条件
Pmax
uo2c 4 Req
匹配:RL=Req时,P达到最大值, 称负载电阻与一端口的输入电阻匹配
扩音机为例
Ri
变
压
R=8Ω
ui
器
信号源的内阻Ri为 1kΩ, 扬声器上不可能得到最大功率。 为了使阻抗匹配,在信号源和扬声器之间连上一个变 压器。
第四章 电路定理
§4.1 叠加定理** §4.2 替代定理 §4.3 戴维宁定理** §4.4 特勒根定理 §4.5 互易定理 §4.6 对偶原理
§4.1 叠加定理
一、内容
在线性电阻电路中,任一支路电流(或支路电 压)都是电路中各个独立电源单独作用时在该 支路产生的电流(或电压)之叠加。
i i(1) i(2)+ uu(1)u(2)+
pmax
uo2c 4Req
0.2mW
注
(1) 最大功率传输定理用于一端口电路给定,
(2)
负载电阻可调的情况;
(2) 一端口等效电阻消耗的功率一般并不等于
(3) 大
端口内部消耗的功率,因此当负载获取最
(4)
功率时,电路的传输效率并不一定是50%;
(3) 计算最大功率问题结合应用戴维宁定理
(4) 或诺顿定理最方便.
4、恢复原电路
a
R0
+ Uabo
-
I b
I = U abo 9 R 0 10
例. 求U0 。
解
6
+ 9V 3
–
– 6I + a
+
I
第四章 网络定理
第四章 电路定理基本内容介绍叠加定理、替代定理、戴维宁定理和诺顿定理、对偶原理及其在线性电路分析中的应用。
重 点1.叠加定理;2.戴维宁定理和诺顿定理; 3.特勒根定理。
难 点1.各电路定理的应用条件;2.各电路定理对含受控源电路的处理。
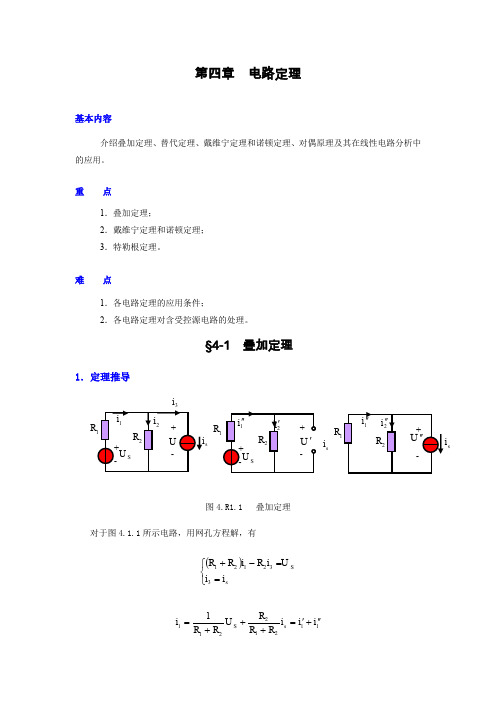
§4-1叠加定理1.定理推导图4.R1.1 叠加定理对于图4.1.1所示电路,用网孔方程解,有()⎩⎨⎧==-+sSi i U i R i R R 332121 112122111i i i R R R U R R i s S ''+'=+++=R ss iR s i22211212i i i R R R R R U i s S ''+'=+-+=U U i R R RR U R R R U s S ''+'=+++-=2121212可见,由于电阻都是线性的,故支路电流21,i i 和支路电压U 都是电流源s i和电压源sU 的一次函数。
当ss U i ,0时=总能作用,有sssU R R R U U R R i U R R i 21221221111+-='+='+='当=s U 时,s i单独作用,有sssi R R R U i R R i i R R i 21221221111+-=''+="+="而U U U i i i i i i ''+'="+'="+'=2221112.定理描述叠加定理:在线性电路中,由n 个独立电源共同作用产生的各支路电流或支路电压,等于各个独立电源分别单独作用时在相应支路中产生的电流或电压的叠加。
所谓独立电源不作用,指独立电压源短路,独立电流源开路,受控源则保留。
注意:1)叠加定理适用于非线性电路;2)叠加时,电路的连接以及电路中所有电路和受控源都不要变动。
第4章 电路的基本定理

i 1.2A
u 2(2 i) 1.6V
i i i 1.4 1.2 0.2A u u u 7.2 1.6 5.6V
【例4-4】图示N为线性含源网络。已知:当iS1=8A, iS2=12A 时,响应ux=80V;当iS1=-8A, iS2=4A时,响应ux=0V;当 iS1 =iS2 =0A时,响应ux=-40V。当iS1 =iS2 =20A时,ux为多少? 解 设网络N内所有独立源作为一组, 所产生的响应分量为ux(3), iS1和 iS2产 生的响应分量为AiS1与B iS2 。则
uk 为原值
(b)
ik 可以是任意值(电压源特点)
原电路[图(a)]的所有支路电压和电流将满足图(b)的全 部约束关系。若电路只有惟一解,则所有电压和电流保持原 值。
替代定理不适用:
⑴ 电路在替代前后,具有多解;
⑵ 被替代支路中,含有网络N中受控源的控制量, 且替代将使控制量消失。
【例4-6】图a电路中,i1=4A, i2=6A, i3=10A,u1=80V,
uS u Rin i iS
iS
u
i
uS
N
输入电阻
【例4-5】已知U=68V,求各支路电流。
A
U
I1
1
I3
1
I5
1
I7
1
U2
1
U4
1
U6
1
1
B
I2
I4
I6
I8
解 设 I8=1A,则
I 7 I 8 1A
电路第4章

B i5 R5 i4 2Ω 20Ω R6 20Ω
第4章 41
_
设
'
C
K us us
'
i5 i5 1 A , 则
' '
u BC ( R 5 R 6 ) i 5 22 V
120 33 . 02
'
3 . 63
i4
'
'
u BC R4
'
'
1 . 1 A i3 i 4 i5 2 . 1 A
-
2i
b
分析: (1)由于原电路接有负载,因此首先断开负载;
(2)由于原电路中含有受控源,只能用外加电压源法 或短路电流法。
第4章 43
解:(1) 求开路电压 1A 1 i + -
u n1 5
2
3 a 2Ω 2i
5Ω 5V
6Ω
+ uoc
- b
1 5
u n1 ( 1 2
1 5
1 2 1 2
电阻和电压源的串联与电导和电流源的并联可以进行等效变换, 它们可以相互进行等效变换。维宁定理和诺顿定理统称为等效 发电机定理。
例4.3:求下图的诺顿等效电路。 解:<1> 求短路电流isc <2> 求等效电导Geq
i
2u1
3
i sc 10
3
A
1
isc
2
u1
a uoc
实验模拟
1A
b
+ 29.13Ω 48.89V -
解: (1)求开路电压uoc (2) 求等效电阻
10Ω 20Ω 1KΩ
Chapter4电路定理
a
c
a
R1 Rab R2 i3i3 R3
R5
+ ++
uS1 uab uS2
R4RRcd6
– ––
b
b
d
例2 求图示电路的等效发电机。
解:
iSc
40 20
40 40
60 20
3
1A
Req 20 // 40 // 20
1
1 1
1
8
20 40 20
20Ω
40Ω
20Ω 3A
+
25V
20
U
-
-
用结点电压法
o
1'
uao
1 5
1 20
1 4
25 5
3
U 4
uao
16
U 2
由 I uao U
4
U 32 8I
+ 8 I +1
4A
32V
-
U
-
1'
I +1
8 U
-
1'
i
ia
a +
Req
+
uoc=Reqisc
Nu
+
-b
uoc
-
u isc -
3.定理的应用
(1)开路电压uoc和短路电流iSc的计算
戴维宁等效电路中电压源电压等于将外电路断开时的开 路电压uoc,电压源方向与所求开路电压方向有关。诺顿等效 电路中电流源电流等于将外电路短路时的短路电流iSc,电流源 方向与所求短路电流的方向有关。计算uoc、 iSc的方法视电路 形式选择前面学过的任意方法,使易于计算。
电路理论第4章-电路定理
本章主要内容
一、叠加定理
四、戴维南定理和诺顿定理 五、最大功率传输定理
第四章、电路定理
一、叠加定理
几个概念 (1)线性电阻:电阻的伏安特性曲线为线性。
R为常数,符合u=iR 。
(2)激励:独立电源又称为激励,由于它的存在, 电路中能够产生电流或电压。
(3)响应:由激励在电路中产生电流或电压称 为响应。
(3)、有源二端网络:二端网络中含有电源。
有源二端网络:
第四章、电路定理 四、戴维南定理和诺顿定理 说明有源一端口网络,其对外的最简等效电路是一
个电压源与电阻的串联.
等效
第四章、电路定理
四、戴维南定理和诺顿定理
1. 戴维宁定理
任何一个线性含源一端口网络,对外电路来说,
总可以用一个电压源和电阻的串联组合来等效置
+-+-UUoocc
66
66
bb 10V
44
+–
+ Req Uoc
–
Ia Rx b
①求开路电压
Uoc = U1 - U2 = -104/(4+6)+10 6/(4+6) = 6-4=2V
②求等效电阻Req
Req=4//6+6//4=4.8
③ Rx =1.2时,
I= Uoc /(Req + Rx) =0.333A
u(2) (6i(2) 6) (21) 8V u u(1) u(2) 9 8 17V
3A
+ - 6 i (2)
+ u(1)
6 3
1
- 6V
+
3+u(2) - +
12V -
1 2A
叠加定理、戴维南定理和诺顿定理资料
有源二端网络可 化简为一个电源
电流源 (诺顿定理)
17
1. 戴维南定理
任何一个线性含源一端口网络,对外电路来说,总可
以用一个电压源和电阻的串联组合来等效置换;此电压源
的电压等于外电路断开时端口处的开路电压E,而电阻等
于一端口的输入电阻(或等效电阻R0)。
i
i a
a R0
A
u
b
+
u
E
-
b
等效电源的电动势E 是有源二端网络的开路 电压U0,即将负载断开后 a 、b两端之间的
电压。
等效电源的内阻R0等于有源二端网络 中所 有电源均除去(理想电压源短路,理想电流 源开路)后所得到的无源二端网络 a 、b两端 之间的等效电阻。
19
例
a
10
I
+ 10
+
+
U0C
20V –
10V ––
(1) u0.45V0.210V4V (2) u0.410V0.25V5V (3) u[0.420coω s(t)0.215sin2ω( t)]V
[8coω s(t)3sin2ω( t)]V
练习1: 求电压U.
– 8 3A 6
解
12V
12V电源作用: U(1) 1234V + 2 9
+
3
U- -
3A电源作用: U(2)(6//3)36V U462 V
叠加定理、戴维南定理和诺顿定 理
学习目标
掌握叠加原理、戴维南定理和诺顿定律
五、叠加原理
叠加原理:对于线性电路,任何一条支路的电 流或某个元件两端的电压,都可以看成是由电 路中各个电源(电压源或电流源)分别作用时, 在此支路中所产生的电流或电压的代数和。
叠加定理,戴维南定理和诺顿定理
(3)电路如图所示。若已知:
(1) uS1 5V, uS2 10V (2) uS1 10V, uS2 5V
(3) uS1 20 cos tV, uS2 15sin 2 t V 试用叠加定理计算电压u 。
R
Rab
R1 R2 R1 R2
1 1.5 1 1.5
0.6
23
据图1-7(b),可以很容易求得电阻R3的电流为:
I3
E R R3
4.8 0.6 10
0.45 A
24
2、诺顿定理
2、诺顿定理: 任何一个含源线性二端网络都可以等效成
为一个理想电流源和内阻并联的电源。
25
图中等效电源的电流ΙS等于该含源二端网络 的短路电流。内阻R0则等于该二端网络中所有 电源都为零时的两个输出端点之间的等效电阻,
b+ –
解
12V
(1) 求短路电流Isc
I1 =12/2=6A
– 24V
+
应用分 流公式
I2=(24+12)/10=3.6A Is=-I1-I2=- 3.6-6=-9.6A
(2) 求等效电阻Req
a
10
R0
2
b
R0=10//2=1.67
(3) 诺顿等效电路:
a I 4
b
-9.6A 1.67
I =2.83A
I1'
R1
E1 R2 //
R3
R1 R2
R2 R3 R2 R3
R3 R1
E1
E2单独作用时((c)图)
I1
R3 R1 R3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章电路定理一、教学基本要求1、了解叠加定理的概念,适用条件,熟练应用叠加定理分析电路。
2、掌握戴维宁定理和诺顿定理的概念和应用条件,并能应用定理分析求解具体电路。
二、教学重点与难点1. 教学重点:叠加定理、戴维宁定理和诺顿定理。
2.教学难点:各电路定理应用的条件、电路定理应用中受控源的处理。
三、本章与其它章节的联系:电路定理是电路理论的重要组成部分,本章介绍的叠加定理、戴维宁定理和诺顿定理适用于所有线性电路问题的分析,对于进一步学习后续课程起着重要作用,为求解电路提供了另一类分析方法。
四、学时安排总学时:6五、教学内容§4.1 叠加定理1.叠加定理的内容叠加定理表述为:在线性电路中,任一支路的电流(或电压)都可以看成是电路中每一个独立电源单独作用于电路时,在该支路产生的电流(或电压)的代数和。
2.定理的证明图 4.1图4.1所示电路应用结点法:解得结点电位:支路电流为:以上各式表明:结点电压和各支路电流均为各独立电源的一次函数,均可看成各独立电源单独作用时,产生的响应之叠加,即表示为:式中a1,a2,a3,b1,b2,b3和c1,c2,c3是与电路结构和电路参数有关的系数。
3.应用叠加定理要注意的问题1) 叠加定理只适用于线性电路。
这是因为线性电路中的电压和电流都与激励(独立源)呈一次函数关系。
2) 当一个独立电源单独作用时,其余独立电源都等于零(理想电压源短路,理想电流源开路)。
如图4.2所示。
=三个电源共同作用is1单独作用+ +u s2单独作用us3单独作用图 4.23) 功率不能用叠加定理计算(因为功率为电压和电流的乘积,不是独立电源的一次函数)。
4) 应用叠加定理求电压和电流是代数量的叠加,要特别注意各代数量的符号。
即注意在各电源单独作用时计算的电压、电流参考方向是否一致,一致时相加,反之相减。
5) 含受控源(线性)的电路,在使用叠加定理时,受控源不要单独作用,而应把受控源作为一般元件始终保留在电路中,这是因为受控电压源的电压和受控电流源的电流受电路的结构和各元件的参数所约束。
6) 叠加的方式是任意的,可以一次使一个独立源单独作用,也可以一次使几个独立源同时作用,方式的选择取决于分析问题的方便。
4.叠加定理的应用例4-1 求图示电路的电压U.例4-1图解:应用叠加定理求解。
首先画出分电路图如下图所示当12V电压源作用时,应用分压原理有:当3A电流源作用时,应用分流公式得:则所求电压:例4-2计算图示电路的电压u 。
例4-2图解:应用叠加定理求解。
首先画出分电路图如下图所示当 3A 电流源作用时:其余电源作用时:则所求电压:本例说明:叠加方式是任意的,可以一次一个独立源单独作用,也可以一次几个独立源同时作用,取决于使分析计算简便。
例4-3计算图示电路的电压u 电流i 。
例4-3 图解:应用叠加定理求解。
首先画出分电路图如下图所示当 10V 电源作用时:解得:当5A电源作用时,由左边回路的KVL:解得:所以:注意:受控源始终保留在分电路中。
例4-4封装好的电路如图,已知下列实验数据:当时,响应,当时,响应,求:时,i = ?例4-4图解:根据叠加定理,有:代入实验数据,得:解得:因此:本例给出了研究激励和响应关系的实验方法5. 齐性原理由以上叠加定理可以得到齐性原理。
齐性原理表述为:线性电路中,所有激励(独立源)都增大(或减小)同样的倍数,则电路中响应(电压或电流)也增大(或减小)同样的倍数。
当激励只有一个时,则响应与激励成正比。
例4-5 求图示电路的电流i,已知:R L=2ΩR1=1ΩR2=1Ωu S =51V例4-5图解:采用倒推法:设i' =1A 。
则各支路电流如下图所示,此时电源电压为:,根据齐性原理:当电源电压为:时,满足关系:§4.2 替代定理1.替代定理的内容替代定理表述为:对于给定的任意一个电路,若某一支路电压为u k、电流为i k,那么这条支路就可以用一个电压等于u k的独立电压源,或者用一个电流等于i k的独立电流源,或用R=u k/i k的电阻来替代,替代后电路中全部电压和电流均保持原有值(解答唯一)。
以上表述可以用图4.3来表示。
图 4.3 替代定理2.定理的证明这里对定理给出其中一种替代的证明。
设图4.4所示电路中支路k的电压为u k,电流为i k,在支路k串入极性相反,电压值为u k的两个电压源如图4.5所示,则根据等效的思想,图4.5对外可以等效为图4.6所示的电路,即电压为u k的支路可以用电压为u k的理想电压源替代。
替代定理的正确性可作如下解释:替代前后KCL,KVL关系相同,其余支路的u、i关系不变。
k支路用理想电压源u k替代后,其余支路电压保持不变(KVL),因此其余支路电流也不变,故第k条支路i k也不变(KCL)。
同理k支路用理想电流源i k替代后,其余支路电流不变(KCL),因此其余支路电压不变,故第k条支路u k也不变(KVL)。
图 4.4 图 4.5 图 4.63.应用替代定理要注意的问题1) 从理论上讲,替代定理适用于线性电路,也适用于非线性电路。
2) 替代后电路必须有唯一解,即替代后不能形成电压源回路和电流源节点。
3) 替代后其余支路及参数不能改变。
4.替代定理的应用例4-6若要使图示电路中的电流,试求电阻R x。
例4-6 图解:因为,为避免求解复杂的方程,应用替代定理,把10V电压源和3Ω电阻串联支路用电流为I的电流源替代,电路如图(b)所示。
然后应用叠加定理,分电路图如图(c)、(d)所示。
例4-6 图(b)例4-6 图(c)例4-6 图(d)由图得:因此例4-7求图示电路中的电流I1例4-7 图(a)解:应用替代定理,图(a)简化为图(b)所示的电路,然后应用叠加定理得:例4-7 图(b)§4.3 戴维宁定理和诺顿定理1.戴维宁定理的内容戴维宁定理表述为:任何一个线性含源一端口网络,对外电路来说,总可以用一个电压源和电阻的串联组合来等效替代;此电压源的电压等于外电路断开时一端口网络端口处的开路电压u oc,而电阻等于一端口的输入电阻(或等效电阻R eq)。
以上表述可以用图4.7来表示。
图 4.7 戴维宁定理2.定理的证明这里给出戴维宁定理的一般证明。
图4.8(a)为线性有源一端口网络A与负载网络N 相连,设负载上电流为i,电压为u。
根据替代定理将负载用理想电流源i 替代,如图4.8(b)所示。
图 4.8替代后不影响A中各处的电压和电流。
由叠加定理u可以分为两部分,如图4.9所示,即:其中是A内所有独立源共同作用时在端口产生的开路电压,是仅由电流源i作用在端口产生的电压,即:,图 4.9因此上式表示的电路模型如图 4.10所示。
这就证明了戴维宁定理是正确的。
图 4.103.应用戴维宁定理要注意的问题1)含源一端口网络所接的外电路可以是任意的线性或非线性电路,外电路发生改变时,含源一端口网络的等效电路不变。
2)当含源一端口网络内部含有受控源时,控制电路与受控源必须包含在被化简的同一部分电路中。
3)开路电压u oc的计算戴维宁等效电路中电压源电压等于将外电路断开时的开路电压u oc,电压源方向与所求开路电压方向有关。
计算u oc的方法视电路形式选择前面学过的任意方法,使易于计算。
4)等效电阻的计算等效电阻为将一端口网络内部独立电源全部置零(电压源短路,电流源开路)后,所得无源一端口网络的输入电阻。
常用下列三种方法计算:5)当网络内部不含有受控源时可采用电阻串并联和△- Y 互换的方法计算等效电阻;6)外加电源法(加电压求电流或加电流求电压)。
如图 4.11 所示。
图 4.11 用外加电源法求戴维宁等效电阻则7)开路电压,短路电流法。
即求得网络A端口间的开路电压后,将端口短路求得短路电流,如图4.12所示。
则:以上方法中后两种方法更具有一般性。
4.戴维宁定理的应用例4-10 计算图示电路中R x分别为1.2Ω、5.2Ω时的电流I ;例4-10 图(a)解:断开Rx支路,如图(b)所示,将其余一端口网络化为戴维宁等效电路:例4-10 图(b)例4-10 图(c)1)求开路电压U oc2)求等效电阻R eq。
把电压源短路,电路为纯电阻电路,应用电阻串、并联公式,得:3)画出等效电路,接上待求支路如图(d)所示,例4-10 图(d)当Rx=1.2Ω时,当Rx =5.2Ω时,例4-11 计算图示电路中的电压U0;例4-11 图(a)解:应用戴维宁定理。
断开3Ω电阻支路,如图(b)所示,将其余一端口网络化为戴维宁等效电路:1)求开路电压U oc2)求等效电阻R eq方法1:外加电压源如图(c)所示,求端口电压U 和电流I0的比值。
注意此时电路中的独立电源要置零。
因为:所以方法2:求开路电压和短路电流的比值。
把电路断口短路如图(d)所示。
注意此时电路中的独立电源要保留。
对图(d)电路右边的网孔应用KVL,有:所以I =0 ,则3) 画出等效电路,如图(e)所示,解得:例4-11 图(b)例4-11 图(c)例4-11 图(d)例4-11 图(e)注意:计算含受控源电路的等效电阻是用外加电源法还是开路、短路法,要具体问题具体分析,以计算简便为好。
例4-12 求图示电路中负载R L消耗的功率。
例4-12 图(a)解:应用戴维宁定理。
断开电阻R L所在支路,如图(b)所示,将其余一端口网络化为戴维宁等效电路。
首先应用电源等效变换将图(b)变为图(c)。
例4-12 图(b)例4-12 图(c)1) 求开路电压U oc由 KVL 得:解得:,2) 求等效电阻R eq,用开路电压、短路电流法。
端口短路,电路如图(d)所示,短路电流为:因此:例4-12 图(d)3) 画出戴维宁等效电路,接上待求支路如图(e)所示,则:例4-12 图(e)例4-13 电路如图所示,已知开关S扳向1,电流表读数为2A;开关S扳向2,电压表读数为4V;求开关S扳向3后,电压U 等于多少?例4-13 图(a)解:根据戴维宁定理,由已知条件得所以等效电路如图(b)所示,例4-13 图(b)则:5.诺顿定理的内容诺顿定理表述为:任何一个含源线性一端口电路,对外电路来说,可以用一个电流源和电导 (电阻)的并联组合来等效置换;电流源的电流等于该一端口的短路电流,而电导(电阻)等于把该一端口的全部独立电源置零后的输入电导(电阻)。
以上表述可以用图4.13来表示。
图 4.13 诺顿定理诺顿等效电路可由戴维宁等效电路经电源等效变换得到。
诺顿等效电路可采用与戴维宁定理类似的方法证明。
需要注意的是:(1)当含源一端口网络A的等效电阻时,该网络只有戴维宁等效电路,而无诺顿等效电路。
(2)当含源一端口网络A的等效电阻时,该网络只有诺顿等效电路而无戴维宁等效电路。
