2017版《高考调研》大一轮复习(新课标,数学理)题组训练第四章三角函数题组24 Word版含解析
大一轮复习(新课标,数学理)题组训练第四章三角函数题组22含解析

题组层级快练(二十二)1.(2016·衡水调研卷)与图中曲线对应的函数是( )A .y =sinxB .y =sin|x|C .y =-sin|x|D .y =-|sinx|答案 C2.(2016·西安九校联考)将f(x)=cosx 图像上所有的点向右平移π6个单位,得到函数y =g(x)的图像,则g(π2)=( ) A.32B .-32 C.12 D .-12答案 C解析 由题意得g(x)=cos(x -π6),故g(π2)=cos(π2-π6)=sin π6=12.3.(2015·山东)要得到函数y =sin(4x -π3)的图像,只需将函数y =sin4x 的图像( )A .向左平移π12个单位B .向右平移π12个单位C .向左平移π3个单位D .向右平移π3个单位答案 B解析 y =sin(4x -π3)=sin4(x -π12),故要将函数y =sin4x 的图像向右平移π12个单位.故选B.4.若把函数y =f(x)的图像沿x 轴向左平移π4个单位,沿y 轴向下平移1个单位,然后再把图像上每个点的横坐标伸长到原来的2倍(纵坐标保持不变),得到函数y =sinx 的图像,则y =f(x)的解析式为( ) A .y =sin(2x -π4)+1B .y =sin(2x -π2)+1C .y =sin(12x +π4)-1D .y =sin(12x +π2)-1答案 B解析 将y =sinx 的图像上每个点的横坐标变为原来的一半(纵坐标保持不变),得到y =sin2x 的图像,再将所得图像向上平移1个单位,得到y =sin2x +1的图像,再把函数y =sin2x +1的图像向右平移π4个单位,得到y =sin2(x -π4)+1的图像,即函数f(x)的图像,所以f(x)=sin2(x -π4)+1=sin(2x -π2)+1,故选B.5.函数y =sinx -cosx 的图像可由y =sinx +cosx 的图像向右平移( ) A.3π2个单位 B .π个单位 C.π4个单位 D.π2个单位 答案 D解析 y =sinx +cosx =2sin ⎝ ⎛⎭⎪⎫x +π4,y =sinx -cosx =2sin ⎝ ⎛⎭⎪⎫x -π4=2sin ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫x -π2+π4.6.(2015·邯郸一中期末)设函数f(x)=2sin(π2x +π5).若对任意x ∈R ,都有f(x 1)≤f(x)≤f(x 2)成立,则|x 1-x 2|的最小值为( ) A .4 B .2 C .1 D.12答案 B解析 f(x)的周期T =4,|x 1-x 2|min =T 2=2. 7.(2013·湖北)将函数y =3cosx +sinx(x ∈R )的图像向左平移m(m>0)个单位长度后,所得到的图像关于y 轴对称,则m 的最小值是( ) A.π12 B.π6 C.π3 D.5π6答案 B解析 y =3cosx +sinx =2(32cosx +12sinx)=2sin(x +π3)的图像向左平移m 个单位后,得到y =2sin(x +m +π3)的图像,此图像关于y 轴对称,则x =0时,y =±2,即2sin(m +π3)=±2,所以m +π3=π2+k π,k ∈Z ,由于m>0,所以m min =π6,故选B.8.电流强度I(安)随时间t(秒)变化的函数I =Asin (ωt +φ)(A>0,ω>0,0<φ<π2)的图像如右图所示,则当t=1100秒时,电流强度是( )A .-5 AB .5 AC .5 3 AD .10 A答案 A解析 由图像知A =10,T 2=4300-1300=1100.∴ω=2πT=100π.∴T =10sin(100πt +φ).(1300,10)为五点中的第二个点,∴100π×1300+φ=π2. ∴φ=π6.∴I =10sin(100πt +π6),当t =1100秒时,I =-5 A ,故选A.9. (2016·武汉市二中)已知函数f(x)=Acos (ωx +φ)的图像如图所示,f(π2)=-23,则f(0)=( )A .-23B .-12C.23D.12答案 C解析 由图像可知所求函数的周期为23π,故ω=3,将(11π12,0)代入解析式得114π+φ=π2+2k π(k ∈Z ),所以φ=-9π4+2k π,令φ=-π4代入解析式得f(x)=Acos(3x -π4),又因为f(π2)=-Acos π4=-23,所以f(0)=Acos(-π4)=Acos π4=23,故选C. 10.将函数y =sinx 的图像向左平移φ(0≤φ<2π)个单位后,得到函数y =sin(x -π6)的图像,则φ等于( )A.π6B.5π6C.7π6D.11π6答案 D解析 平移后图像的解析式为y =sin(x +φ),依题意可得φ=2k π-π6,k ∈Z ,又0≤φ<2π,故只有选项D 正确.11.(2016·宁夏一模)函数y =⎩⎪⎨⎪⎧kx +1,-3≤x<0,2sin (ωx +φ),0≤x ≤8π3的图像如下图,则( )A .k =13,ω=12,φ=π6B .k =13,ω=12,φ=π3C .k =-13,ω=2,φ=π6D .k =-3,ω=2,φ=π3答案 A解析 由图像可知f(-3)=0⇒-3k +1=0⇒k =13.又知T 4=8π3-5π3=π⇒T =4π,故ω=12,根据五点法作图可知(8π3,-2)应为第四个点,即令12· 8π3+φ=3π2⇒φ=π6.12.(2014·四川卷改编)(1)为了得到函数y =sin(x +1)的图像,只需把函数y =sinx 的图像上所有的点向________平移________个单位长度.(2)为了得到函数y =sin(2x +1)的图像,只需把函数y =sin2x 的图像上所有的点向________平移________个单位长度.答案 (1)左,1 (2)左,1213.将函数y =sin(-2x)的图像向右平移π3个单位,所得函数图像的解析式为________.答案 y =sin(23π-2x)14.(2014·重庆文)若将函数f(x)=sin (ωx +φ)⎝⎛⎭⎫ω>0,-π2≤φ<π2图像上每一个点的横坐标缩短为原来的一半,纵坐标不变,再向右平移π6个单位长度得到y =sinx 的图像,则f ⎝⎛⎭⎫π6=________.答案22解析 将y =sinx 的图像向左平移π6个单位长度可得y =sin ⎝ ⎛⎭⎪⎫x +π6的图像,保持纵坐标不变,横坐标变为原来的2倍可得y =sin ⎝ ⎛⎭⎪⎫12x +π6的图像,故f(x)=sin ⎝ ⎛⎭⎪⎫12x +π6.所以f ⎝ ⎛⎭⎪⎫π6=sin ⎝ ⎛⎭⎪⎫12×π6+π6=sin π4=22.15.若函数y =sin2x 的图像向右平移φ(φ>0)个单位,得到的图像恰好关于直线x =π6对称,则φ的最小值是________. 答案5π12解析 y =sin2x 的图像向右平移φ(φ>0)个单位,得y =sin2(x -φ)=sin(2x -2φ).因其中一条对称轴方程为x =π6,则2·π6-2φ=k π+π2(k ∈Z ).因为φ>0,所以φ的最小值为5π12. 16. (2014·北京)函数f(x)=3sin(2x +π6)的部分图像如图所示.(1)写出f(x)的最小正周期及图中x 0,y 0的值; (2)求f(x)在区间[-π2,-π12]上的最大值和最小值.答案 (1)T =π,x 0=7π6,y 0=3 (2)最大值为0,最小值为-3解析 (1)f(x)的最小正周期为π. x 0=7π6,y 0=3.(2)因为x ∈[-π2,-π12],所以2x +π6∈[-5π6,0].于是,当2x +π6=0,即x =-π12时,f(x)取得最大值0;当2x +π6=-π2,即x =-π3时,f(x)取得最小值-3.17.(2016·江西测试)已知函数f(x)=4cosxsin(x +π6)+a 的最大值为2.(1)求实数a 的值及f(x)的最小正周期; (2)在坐标纸上作出f(x)在[0,π]上的图像. 答案 (1)a =-1,T =π (2)略解析 (1)f(x)=4cosx(sinxcos π6+cosxsin π6)+a=3sin2x +cos2x +1+a =2sin(2x +π6)+a +1,最大值为3+a =2,∴a =-1.T =2π2=π.(2)列表如下:画图如下:18.已知函数f(x)=Asin (ωx +φ)(x ∈R ,A>0,ω>0,|φ|<π2)的部分图像如图所示.(1)试确定函数f(x)的解析式; (2)若f(α2π)=13,求cos(2π3-α)的值.答案 (1)f(x)=2sin(πx +π6) (2)-1718解析 (1)由图像知,f(x)max =A =2,设函数f(x)的最小正周期为T ,则T 4=56-13=12,所以T =2,∴ω=2πT =2π2=π,故函数f(x)=2sin(πx +φ). 又∵f(13)=2sin(π3+φ)=2,∴sin(π3+φ)=1.∵|φ|<π2,即-π2<φ<π2,∴-π6<π3+φ<5π6.故π3+φ=π2,解得φ=π6,∴f(x)=2sin(πx +π6). (2)∵f(α2π)=13,即2sin(π·α2π+π6)=2sin(α2+π6)=13,∴sin(α2+π6)=16.∴cos(π3-α2)=cos[π2-(π6+α2)]=sin(π6+α2)=16.∴cos(2π3-α)=cos[2(π3-α2)]=2cos 2(π3-α2)-1=2×(16)2-1=-1718.1.(2015·湖南理)将函数f(x)=sin2x 的图像向右平移φ(0<φ<π2)个单位后得到函数g(x)的图像,若对满足||f (x 1)-g (x 2)=2的x 1,x 2,有||x 1-x 2min =π3,则φ=( ) A.5π12 B.π3 C.π4 D.π6答案 D解析 向右平移φ个单位后,得到g(x)=sin(2x -2φ).又∵|f(x 1)-g(x 2)|=2,∴不妨2x 1=π2+2k π,2x 2-2φ=-π2+2m π,∴x 1-x 2=π2-φ+(k -m)π,又∵||x 1-x 2min =π3,∴π2-φ=π3⇒φ=π6,故选D 项.2.(2016·西安八校联考)若函数y =cos (ωx +π6)(ω∈N *)图像的一个对称中心是(π6,0),则ω的最小值为( )A .1B .2C .4D .8答案 B解析 πω6+π6=k π+π2(k ∈Z ),∴ω=6k +2(k ∈Z ),∴ωmin =2,故选B.3. (2016·洛阳统考)已知函数f(x)=Asin (ωx +φ)(A>0,ω>0,|φ|<π2)的部分图像如图所示,则f(x)的解析式是( )A .f(x)=sin(3x +π3)B .f(x)=sin(2x +π3)C .f(x)=sin(x +π3)D .f(x)=sin(2x +π6)答案 D解析 由图像可知T 4=5π12-π6,∴T =π,∴ω=2πT =2,故排除A 、C ,把x =π6代入检验知,选项D 符合题意.4.(2016·武汉调研)已知函数f(x)=sin(2x -π2)(x ∈R ),下列结论错误的是( )A .函数f(x)是偶函数B .函数f(x)的最小正周期为πC .函数f(x)在区间[0,π2]上是增函数D .函数f(x)的图像关于直线x =π4对称答案 D解析 f(x)=sin(2x -π2)=-cos2x ,此函数为最小正周期为π的偶函数,所以A ,B 正确,函数图像的对称轴方程为x =k π2(k ∈Z ),显然,无论k 取任何整数,x ≠π4,所以D 错误,答案为D.5.(2013·福建文)将函数f(x)=sin(2x +θ)(-π2<θ<π2)的图像向右平移φ(φ>0)个单位长度后得到函数g(x)的图像,若f(x),g(x)的图像都经过点P(0,32),则φ的值可以是( ) A.5π3B.5π6C.π2D.π6答案 B解析 因为函数f(x)的图像过点P ,所以θ=π3,所以f(x)=sin(2x +π3).又函数f(x)的图像向右平移φ个单位长度后,得到函数g(x)=sin[2(x -φ)+π3]的图像,所以sin(π3-2φ)=32,所以φ可以为5π6,故选B.6.将函数y =sin(2x +π4)的图像上各点的纵坐标不变,横坐标伸长到原来的2倍,再向右平移π4个单位,所得到的图像解析式是( ) A .f(x)=sinx B .f(x)=cosx C .f(x)=sin4x D .f(x)=cos4x答案 A解析 y =sin(2x +π4)→y =sin(x +π4)→y =sin(x -π4+π4)=sinx.7.(2014·浙江)为了得到函数y =sin3x +cos3x 的图像,可以将函数y =2cos3x 的图像( ) A .向右平移π4个单位B .向左平移π4个单位C .向右平移π12个单位D .向左平移π12个单位答案 C解析 因为y =sin3x +cos3x =2cos ⎝ ⎛⎭⎪⎫3x -π4=2cos3⎝ ⎛⎭⎪⎫x -π12,所以将函数y =2cos3x 的图像向右平移π12个单位后,可得到y =2cos ⎝⎛⎭⎪⎫3x -π4的图像,故选C.8.(2016·重庆一中)要得到函数y =sin 12x 的图像,只需将函数y =sin(12x -π3)的图像( )A .向左平移π3个单位B .向右平移π3个单位C .向左平移2π3个单位D .向右平移2π3个单位答案 C9.(2016·临沂一中月考)如图的函数的解析式为( )A .y =2sin ⎝⎛⎭⎫2x -π8B .y =2sin ⎝⎛⎭⎫2x +π8C .y =2sin ⎝⎛⎭⎫2x +π4D .y =2sin ⎝⎛⎭⎫2x -π4答案 C解析 A =2,T =7π8-⎝ ⎛⎭⎪⎫-π8=π,ω=2,当x =-π8时,y =0.10.(2016·长沙雅礼中学)将函数y =sin2x 的图像向左平移π4个单位,再向上平移1个单位,所得图像的函数解析式是( ) A .y =cos2x B .y =2cos 2x C .y =1+sin(2x +π4)D .y =2sin 2x 答案 B解析 所得解析式是y =sin2(x +π4)+1=cos2x +1=2cos 2x.11.(2016·杭州学军中学)已知函数y =sin (ωx +φ)(ω>0,0<φ≤π2),且此函数的图像如图所示,则点P(ω,φ)的坐标是( )A .(2,π2)B .(2,π4)C .(4,π2)D .(4,π4)答案 B解析 ∵T =2(7π8-3π8)=π,∴ω=22×3π8+φ=π,∴φ=π4,∴选B.12.已知函数y =sin ωx (ω>0)在一个周期内的图像如图所示,要得到函数y =sin(12x +π12)的图像,则需将函数y =sin ωx 的图像向________平移________个单位长度.答案 左,π6解析 由图像知函数y =sin ωx 的周期为T =3π-(-π)=4π, ∴ω=2πT =12,故y =sin 12x.又y =sin(x 2+π12)=sin 12(x +π6),∴将函数y =sin 12x 的图像向左平移π6个单位长度,即可得到函数y =sin(x 2+π12)的图像.13.若函数y =Asin (ωx +φ)(A ,ω,φ为常数,A>0,ω>0)在闭区间[-π,0]上的图像如图所示,则ω=________.答案 3解析 由函数y =Asin (ωx +φ)的图像可知: T 2=(-π3)-(-23π)=π3,∴T =23π. ∵T =2πω=23π,∴ω=3.14.已知函数f(x)=Atan (ωx +φ)(ω>0,|φ|<π2),y =f(x)的部分图像如图所示,则f(π24)=________.答案3解析 由图像知T 2=38π-π8=π4,T =π2,ω=πT =2,2×π8+φ=π2+k π,φ=π4+k π,k ∈Z .又|φ|<π2,∴φ=π4.∵函数f(x)的图像过点(0,1),∴f(0)=Atan π4=A =1.∴f(x)=tan(2x +π4).∴f(π24)=tan(2×π24+π4)=tan π3= 3. 15.(2015·湖南文)已知ω>0,在函数y =2sin ωx 与y =2cos ωx 的图像的交点中,距离最短的两个交点的距离为23,则ω=________. 答案π2解析 由题意,两函数图像交点间的最短距离即相邻的两交点间的距离,设相邻的两交点坐标分别为P(x 1,y 1),Q(x 2,y 2),易知|PQ|2=(x 2-x 1)2+(y 2-y 1)2,其中|y 2-y 1|=2-(-2)=22,|x 2-x 1|为函数y =2sin ωx -2cos ωx =22sin (ωx -π4)的两个相邻零点之间的距离,恰好为函数最小正周期的一半,所以(23)2=(2π2ω)2+(22)2,ω=π2.16.(2016·石家庄二中调研)某同学用“五点法”画函数f(x)=Asin (ωx +φ)在某一个周期内的图像时,列表并填入的数据如下表:(1)求x 1,x 2,x 3(2)将函数f(x)的图像向左平移π个单位,可得到函数g(x)的图像,求函数y =f(x)·g(x)在区间(0,5π3)的最小值.答案 (1)x 1=5π3,x 2=11π3,x 3=14π3,f(x)=2sin(12x -π3)解析 (1)由2π3ω+φ=0,8π3ω+φ=π可得ω=12,φ=-π3,由12x 1-π3=π2,12x 2-π3=3π2,12x 3-π3=2π可得x 1=5π3,x 2=11π3,x 3=14π3, 又Asin(12×5π3-π3)=2,∴A =2,∴f(x)=2sin(12x -π3).(2)函数f(x)=2sin(12x -π3)的图像向左平移π个单位,得g(x)=2sin(12x -π3+π2)=2cos(x 2-π3)的图像,∴y =f(x)g(x)=2sin(x 2-π3)·2cos(x 2-π3)=2sin(x -2π3),∵x ∈(0,5π3),∴x -2π3∈(-2π3,π),∴当x -2π3=-π2,即x =π6时,y =f(x)·g(x)取得最小值-2.。
(新课标)高考数学大一轮复习第四章三角函数题组21理

cos
4π 8
-
sin
4π 8
等于
(
题组层级快练 ( 二十一 )
)
A. 0
2 B. 2
C. 1
答案 B
1
2. tan15 °+ tan15 ° = (
)
2 D.- 2
A. 2
B. 2+ 3
C. 4
43 D.
3
答案 C
1
sin15 ° cos15°
1
2
解析 方法一: tan15 °+ tan15 ° = cos15° +sin15 ° = cos15°sin15 ° =sin30 ° = 4.
π
1
又∵α∈( 2 ,π ) ,∴ cos α=- 2.
3 ∴sin α= 1-cos2α= .
2
∴sin2 α=-
3
,
cos2
α=
2cos
2α-
1=-
1 .
2
2
sin2 α ∴tan2 α= cos2α = 3.
1
2cos4x - 2cos2x + 2
6.化简:
π
π
.
2tan ( 4 - x)· sin2 ( 4 +x)
1 2sin48 °
13.若 θ∈ [0 ,π ) 且 cos θ(sin θ+ cos θ ) =1,则 θ= ________. π
答案 0 或 4
14.设 α 为第四象限的角,若
sin3 α sin α
=
13 5
,则
tan2 α= ________.
3 答案 -
4
sin3 α sin (2α+α) sin2 αcosα+ cos2αsin α 13
2017版大一轮复习题组训练第四章三角函数题组19 含解析

题组层级快练(十九)1.下列各数中与sin2 016°的值最接近的是( ) A.12 B.32C .-12D .-32答案 C解析 2 016°=5×360°+180°+36°, ∴sin2 016°=-sin36°和-sin30°接近,选C. 2.sin 2(π+α)-cos(π+α)cos(-α)+1的值为( ) A .1 B .2sin 2α C .0 D .2 答案 D3.tan(5π+α)=m ,则sin (α-3π)+cos (π-α)sin (-α)-cos (π+a )的值为( )A.m +1m -1B.m -1m +1 C .-1 D .1 答案 A解析 由tan(5π+α)=m ,∴tan α=m 原式=-sin α-cos α-sin α+cos α=sin α+cos αsin α-cos α=m +1m -1∴选A.4.1+2sin (π-3)cos (π+3)化简的结果是( ) A .sin3-cos3 B .cos3-sin3 C .±(sin3-cos3) D .以上都不对 答案 A解析 sin(π-3)=sin3,cos(π+3)=-cos3, ∴1-2sin3·cos3=(sin3-cos3)2=|sin3-cos3|. ∵π2<3<π,∴sin3>0,cos3<0. ∴原式=sin3-cos3,选A. 5.化简cos α1-sin α1+sin α+sin α1-cos α1+cos α(π<α<3π2)得( )A .sin α+cos α-2B .2-sin α-cos αC .sin α-cos αD .cos α-sin α解析 原式=cos α(1-sin α)2cos 2α+sin α(1-cos α)2sin 2α,∵π<α<32π,∴cos α<0,sin α<0.∴原式=-(1-sin α)-(1-cos α)=sin α+cos α-2. 6.记cos(-80°)=k ,那么tan100°=( ) A.1-k 2kB .-1-k 2kC.k1-k 2D .-k1-k 2答案 B解析 cos(-80°)=cos80°=k ,sin80°=1-k 2,tan80°=1-k 2k,tan100°=-tan80°=-1-k 2k.7.已知A =sin (k π+α)sin α+cos (k π+α)cos α(k ∈Z ),则A 的值构成的集合是( )A .{1,-1,2,-2}B .{-1,1}C .{2,-2}D .{1,-1,0,2,-2}答案 C解析 当k 为偶数时,A =sin αsin α+cos αcos α=2; 当k 为奇数时,A =-sin αsin α-cos αcos α=-2.8.(tanx +1tanx)cos 2x =( ) A .tanx B .sinx C .cosx D.1tanx答案 D解析 (tanx +1tanx )cos 2x =sin 2x +cos 2x sinxcosx ·cos 2x =cosx sinx =1tanx.9.若A 为△ABC 的内角,且sin2A =-35,则cos(A +π4)等于( )A.255B .-255C.55D .-55解析 cos 2(A +π4)=[22(cosA -sinA)]2=12(1-sin2A)=45.又cosA<0,sinA>0,∴cosA -sinA<0. ∴cos(A +π4)=-255.10.若3sin α+cos α=0,则1cos 2α+sin2α的值为( )A.103B.53C.23 D .-2答案 A解析 由3sin α=-cos α,得tan α=-13.1cos 2α+sin2α=cos 2α+sin 2αcos 2α+2sin αcos α=1+tan 2α1+2tan α=1+191-23=103. 11.已知tan θ=2,则sin 2θ+sin θcos θ-2cos 2θ=( ) A .-43B.54 C .-34D.45答案 D解析 sin 2θ+sin θcos θ-2cos 2θ=sin 2θ+sin θcos θ-2cos 2θsin 2θ+cos 2θ=tan 2θ+tan θ-2tan 2θ+1=4+2-24+1=45.12.(2016·山东师大附中月考)若cos(π6-α)=m(|m|≤1),则sin(23π-α)的值为( )A .-mB .-m 2C.m2 D .m答案 D解析 sin(2π3-α)=sin(π2+π6-α)=cos(π6-α)=m ,选D.13.(2016·衡水调研卷)已知A 为锐角,lg(1+cosA)=m ,lg11-cosA =n ,则lgsinA 的值为( )A .m +1nB.12(m -n) C.12(m +1n ) D.12(m -1n) 答案 B解析 lg(1+cosA)=m ,lg(1-cosA)=-n ∴lg(1-cos 2A)=m -n ∴lgsin 2A =m -n ∴lgsinA =12(m -n)选B.14.已知sin θ=55,则sin 4θ-cos 4θ的值为________. 答案 -35解析 由sin θ=55,可得cos 2θ=1-sin 2θ=45,所以sin 4θ-cos 4θ=(sin 2θ+cos 2θ)(sin 2θ-cos 2θ)=sin 2θ-cos 2θ=15-45=-35.15.化简sin 6α+cos 6α+3sin 2αcos 2α的结果是________. 答案 1解析 sin 6α+cos 6α+3sin 2αcos 2α=(sin 2α+cos 2α)(sin 4α-sin 2αcos 2α+cos 4α)+3sin 2αcos 2α=sin 4α+2sin 2αcos 2α+cos 4α=(sin 2α+cos 2α)2=1. 16.化简1-2sin40°·cos40°cos40°-1-sin 250°为________.答案 117.若tan α+1tan α=3,则sin αcos α=________,tan 2α+1tan 2α=________.答案 13,7解析 ∵tan α+1tan α=3,∴sin αcos α+cos αsin α=3.即sin 2α+cos 2αsin αcos α=3.∴sin αcos α=13.又tan 2α+1tan 2α=(tan α+1tan α)2-2tan α1tan α=9-2=7. 18.(2016·浙江嘉兴联考)已知α为钝角,sin(π4+α)=34,则sin(π4-α)=________,cos (α-π4)=________. 答案 -74,34解析 sin(π4-α)=cos[π2-(π4-α)]=cos(π4+α),∵α为钝角,∴34π<π4+α<54π.∴cos(π4+α)<0.∴cos(π4+α)=-1-(34)2=-74.cos (α-π4)=sin[π2+(α-π4)]=sin(π4+α)=34.19.已知0<α<π2,若cos α-sin α=-55,试求2sin αcos α-cos α+11-tan α的值.答案55-95解析 ∵cos α-sin α=-55,∴1-2sin αcos α=15. ∴2sin αcos α=45.∴(sin α+cos α)2=1+2sin αcos α=1+45=95.∵0<α<π2,∴sin α+cos α=35 5.与cos α-sin α=-55联立,解得 cos α=55,sin α=255.∴tan α=2. ∴2sin αcos α-cos α+11-tan α=45-55+11-2=55-95.1.若tan α=3,则sin2αcos 2α的值等于( )A .2B .3C .4D .6答案 D 解析sin2αcos 2α=2sin αcos αcos 2α=2tan α=2×3=6,故选D.2.已知cosA +sinA =-713,A 为第四象限角,则tan α等于( )A.125B.512 C .-125D .-512答案 C解析 ∵cosA +sinA =-713,①∴(cosA +sinA)2=(-713)2,∴2cosA ·sinA =-120169.∴(cosA -sinA)2=(cosA +sinA)2-4cosAsinA. ∵A 为第四象限角,∴cosA -sinA =1713.②∴联立①②,∴cosA =513,sinA =-1213.∴tanA =sinA cosA =-125,选C.3.已知sin(π4+α)=32,则sin(3π4-α)的值为________.答案32解析 sin(3π4-α)=sin[π-(π4+α)]=sin(π4+α)=32.4.若α∈(0,π2),且sin 2α+cos2α=14,则tan α的值等于________.答案3解析 由二倍角公式可得sin 2α+1-2sin 2α=14,即-sin 2α=-34,sin 2α=34.又因为α∈(0,π2),所以sin α=32,即α=π3,所以tan α=tan π3= 3. 5.已知-π2<α<0,且函数f(α)=cos(3π2+α)-sin α·1+cos α1-cos α-1.(1)化简f(α);(2)若f(α)=15,求sin α·cos α和sin α-cos α的值.答案 (1)f(α)=sin α+cos α (2)-1225,-75解析 (1)f(α)=sin α-sin α·(1+cos α)21-cos 2α-1=sin α+sin α·1+cos αsin α-1=sin α+cos α.(2)方法一:由f(α)=sin α+cos α=15,平方可得sin 2α+2sin α·cos α+cos 2α=125,即2sinα·cos α=-2425.∴sin α·cos α=-1225.∵(sin α-cos α)2=1-2sin α·cos α=4925,又-π2<α<0,∴sin α<0,cos α>0,∴sin α-cos α<0,∴sin α-cos α=-75.方法二:联立方程⎩⎪⎨⎪⎧sin α+cos α=15,sin 2α+cos 2α=1,解得⎩⎨⎧sin α=-35,cos α=45或⎩⎨⎧sin α=45,cos α=-35.∵-π2<α<0,∴⎩⎨⎧sin α=-35,cos α=45.∴sin α·cos α=-1225,sin α-cos α=-75.。
2017版高考数学(鲁、京、津专版理)一轮复习文档:第四章 三角函数、解三角形 4.4 含答案
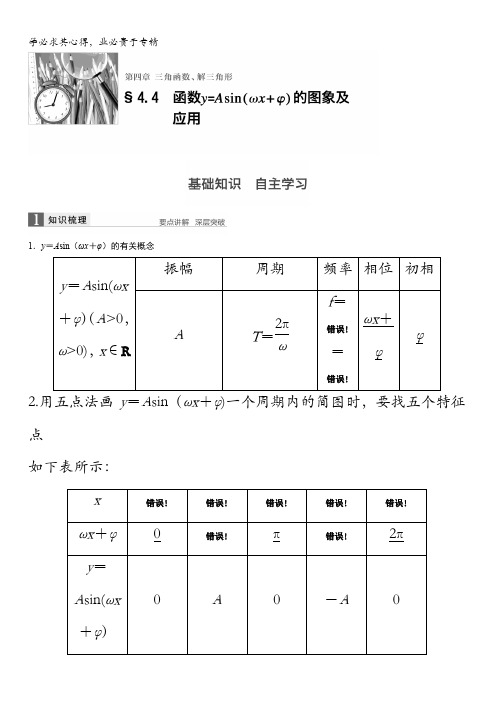
1.y=A sin(ωx+φ)的有关概念y=A sin(ωx +φ)(A>0,ω>0),x∈R 振幅周期频率相位初相A T=2πωf=错误!=错误!ωx+φφ2.用五点法画y=A sin(ωx+φ)一个周期内的简图时,要找五个特征点如下表所示:x错误!错误!错误!错误!错误!ωx+φ0错误!π错误!2πy=A sin(ωx+φ)0A0-A03。
函数y=sin x的图象经变换得到y=A sin(ωx+φ)(A〉0,ω>0)的图象的步骤如下:【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)利用图象变换作图时“先平移,后伸缩”与“先伸缩,后平移”中平移的长度一致.(×)(2)y=sin错误!的图象是由y=sin错误!的图象向右平移错误!个单位得到的.( √)(3)由图象求解析式时,振幅A的大小是由一个周期内的图象中的最高点的值与最低点的值确定的.(√)(4)函数f(x)=A sin(ωx+φ)的图象的两个相邻对称轴间的距离为一个周期.(×)(5)函数y=A cos(ωx+φ)的最小正周期为T,那么函数图象的两个相邻对称中心之间的距离为错误!.(√)1.y=2sin错误!的振幅、频率和初相分别为( )A.2,错误!,-错误! B.2,错误!,-错误!C.2,错误!,-错误!D.2,错误!,-错误!答案A2.为了得到函数y=sin(2x+1)的图象,只需把函数y=sin 2x的图象上所有的点()A.向左平行移动错误!个单位长度B.向右平行移动错误!个单位长度C.向左平行移动1个单位长度D.向右平行移动1个单位长度答案A解析y=sin 2x的图象向左平移错误!个单位长度得到函数y=sin 2(x +错误!)的图象,即函数y=sin(2x+1)的图象.3.(2015·湖南)将函数f(x)=sin 2x的图象向右平移φ错误!个单位后得到函数g(x)的图象,若对满足|f(x1)-g(x2)|=2的x1,x2,有|x1-x2|min=错误!,则φ等于()A。
(新课标)2017版高考数学大一轮复习第四章三角函数4(精)

专题层级训练
1.(2016· 泉州质检)如图所示,为了测量某湖泊两侧A,B间 的距离,李宁同学首先选定了与A,B不共线的一点C(△ABC的 角A,B,C所对的边分别记为a,b,c),然后给出了三种测量方 案:
①测量A,C,b;②测量a,b,C;③测量A,B,a,则一 定能确定A,B间的距离的所有方案的序号为( A.①② C.①③ B.②③ D.①②③ )
应用正、余弦定理解斜三角形应用题的一般步骤是: (1)分析:理解题意,分清已知与未知,画出示意图; (2)建模:根据已知条件与求解目标,把已知量与求解量尽 量集中在有关的三角形中,建立一个解斜三角形的数学模型;
(3)求解:利用正弦定理或余弦定理有序地解三角形,求得 数学模型的解; (4)检验:检验上述所求的解是否具有实际意义,从而得出 实际问题的解.
【解析】 由题意知AB=5(3+ 3) 海里, ∠DBA=90°-60°=30°,∠DAB=90°-45°= 45°,∴∠ADB=180°-(45°+30°)=105°. DB AB 在△DAB中,由正弦定理,得 = . sin∠DAB sin∠ADB AB· sin∠DAB 5(3+ 3)· sin45° ∴DB= = sin∠ADB sin105° 5(3+ 3)· sin45° 5 3( 3+1) = = sin45°cos60°+cos45°sin60° 3+ 1 2 =10 3(海里).
7.如图所示,飞机的航线和山顶在同一个铅垂面内,若飞机 的高度为海拔18 km,速度为1 000 km/h,飞行员先看到山顶的 俯角为30°,经过1 min后又看到山顶的俯角为75°,则山顶的 海拔高度为(精确到0.1 km)( )
A.11.4 km C.6.5 km
B.6.6 km D.5.6 km
2017版《高考调研》大一轮复习(新课标,数学理)题组训练选考部分 选修系列4题组75 Word版含解析

题组层级快练(七十五)1.在同一平面直角坐标系中,经过伸缩变换⎩⎪⎨⎪⎧x ′=5x ,y ′=3y 后,曲线C 变为曲线x ′2+y ′2=1,则曲线C 的方程为( ) A .25x 2+9y 2=1 B .9x 2+25y 2=1 C .25x +9y =1 D.x 225+y 29=1 答案 A2.极坐标方程ρ=cos θ化为直角坐标方程为( ) A .(x +12)2+y 2=14B .x 2+(y +12)2=14C .x 2+(y -12)2=14D .(x -12)2+y 2=14答案 D解析 由ρ=cos θ,得ρ2=ρcos θ,∴x 2+y 2=x.选D.3.设点M 的直角坐标为(-1,-3,3),则它的柱坐标为( ) A .(2,π3,3)B .(2,2π3,3)C .(2,4π3,3)D .(2,5π3,3)答案 C4.极坐标方程ρcos θ=2sin2θ表示的曲线为( ) A .一条射线和一个圆 B .两条直线 C .一条直线和一个圆 D .一个圆 答案 C5.(2016·北京海淀期末练习)下列极坐标方程表示圆的是( ) A .ρ=1 B .θ=π2C .ρsin θ=1D .ρ(sin θ+cos θ)=1 答案 A解析 ρ=1化为直角坐标方程为x 2+y 2=1,表示圆心在原点,半径为1的圆,故A 正确;θ=π2化为直角坐标方程为x =0(y ≥0),表示射线,故B 不正确;ρsin θ=1化为直角坐标方程为y =1,表示直线,故C 不正确;ρ(sin θ+cos θ)=1化为直角坐标方程为x +y =1,表示直线,故D 不正确. 6.在极坐标系中,过点(2,π2)且与极轴平行的直线方程是( )A .ρ=0B .θ=π2C .ρcos θ=2D .ρsin θ=2答案 D解析 极坐标为(2,π2)的点的直角坐标为(0,2),过该点且与极轴平行的直线的方程为y =2,其极坐标方程为ρsin θ=2,故选D.7.在极坐标系中,圆ρ=-2sin θ的圆心的极坐标是( ) A .(1,π2)B .(1,-π2)C .(1,0)D .(1,π)答案 B解析 由ρ=-2sin θ得ρ2=-2ρsin θ,化成直角坐标方程为x 2+y 2=-2y ,化成标准方程为x 2+(y +1)2=1,圆心坐标为(0,-1),其对应的极坐标为(1,-π2).8.在极坐标系中,点(2,-π3)到圆ρ=-2cos θ的圆心的距离为( ) A .2 B.4+π29C.9+π29D.7答案 D解析 在直角坐标系中,点(2,-π3)的直角坐标为(1,-3),圆ρ=-2cos θ的直角坐标方程为x 2+y 2=-2x ,即(x +1)2+y 2=1,圆心为(-1,0),所以所求距离为(1+1)2+(-3-0)2=7.故选D.9.(2016·皖北协作区联考)在极坐标系中,直线ρ(3cos θ-sin θ)=2与圆ρ=4sin θ的交点的极坐标为( ) A .(2,π6)B .(2,π3)C .(4,π6)D .(4,π3)答案 A解析 ρ(3cos θ-sin θ)=2可化为直角坐标方程3x -y =2,即y =3x -2.ρ=4sin θ可化为x 2+y 2=4y ,把y =3x -2代入x 2+y 2=4y ,得4x 2-83x +12=0,即x 2-23x +3=0,所以x =3,y =1.所以直线与圆的交点坐标为(3,1),化为极坐标为(2,π6),故选A. 10.在极坐标系中,与圆ρ=4sin θ相切的一条直线的方程是( ) A .ρsin θ=2 B .ρcos θ=2 C .ρcos θ=4 D .ρcos θ=-4答案 B解析 方法一:圆的极坐标方程ρ=4sin θ即ρ2=4ρsin θ,所以直角坐标方程为x 2+y 2-4y =0.选项A ,直线ρsin θ=2的直角坐标方程为y =2,代入圆的方程,得x 2=4,∴x =±2,不符合题意;选项B ,直线ρcos θ=2的直角坐标方程为x =2,代入圆的方程,得(y -2)2=0,∴y =2,符合题意.同理,以后选项都不符合题意. 方法二:如图,⊙C 的极坐标方程为ρ=4sin θ,CO ⊥Ox ,OA 为直径,|OA|=4,直线l 和圆相切, l 交极轴于点B(2,0),点P(ρ,θ)为l 上任意一点, 则有cos θ=|OB||OP|=2ρ,得ρcos θ=2.11.(2015·湖南)在直角坐标系xOy 中,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,若曲线C 的极坐标方程为ρ=2sin θ,则曲线C 的直角坐标方程为________. 答案 x 2+y 2-2y =0解析 两边同乘以ρ,得ρ2=2ρsin θ,即x 2+y 2=2y ,故曲线C 的直角坐标方程为x 2+y 2-2y =0.12.(2015·北京)在极坐标系中,点(2,π3)到直线ρ(cos θ+3sin θ)=6的距离为________.答案 1解析 点(2,π3)的直角坐标为(1,3),直线ρ(cos θ+3sin θ)=6的直角坐标方程为x +3y -6=0,所以点(1,3)到直线的距离d =|1+3×3-6|1+3=1.13.在极坐标系中,设曲线C 1:ρ=2sin θ与C 2:ρ=2cos θ的交点分别为A ,B ,则线段AB 的垂直平分线的极坐标方程为________. 答案 ρsin θ+ρcos θ=1(或ρsin (θ+π4)=22)解析 曲线C 1:ρ=2sin θ的直角坐标方程为x 2+y 2-2y =0,曲线C 2:ρ=2cos θ的直角坐标方程为x 2+y 2-2x =0,所以AB 的方程为-x +y =0.又易知AB 的垂直平分线斜率为-1,经过圆C 1的圆心(0,1),所以AB 的垂直平分线的方程为x +y -1=0,化为极坐标方程为ρsin θ+ρcos θ=1,或化成ρsin (θ+π4)=22. 14.在直角坐标系xOy 中,以原点O 为极点,x 轴的非负半轴为极轴建立极坐标系,已知圆C 的圆心的极坐标为(2,π4),半径r =2,点P 的极坐标为(2,π),过P 作直线l 交圆C 于A ,B 两点.(1)求圆C 的直角坐标方程; (2)求|PA|·|PB|的值.答案 (1)(x -1)2+(y -1)2=2 (2)8 解析 (1)圆C 的圆心的极坐标C(2,π4), ∴x =2cos π4=1,y =2sin π4=1,∴圆C 的直角坐标方程为(x -1)2+(y -1)2=2.(2)点P 的极坐标为(2,π),化为直角坐标为P(-2,0). 当直线l 与圆C 相切于点D 时,则|PD|2=|PC|2-r 2=(-2-1)2+(0-1)2-(2)2=8. ∴|PA|·|PB|=|PD|2=8.15.(2016·河北唐山三模)在极坐标系Ox 中,直线C 1的极坐标方程为ρsin θ=2,M 是C 1上任意一点,点P 在射线OM 上,且满足|OP|·|OM|=4,记点P 的轨迹为C 2. (1)求曲线C 2的极坐标方程;(2)求曲线C 2上的点到直线C 3:ρcos (θ+π4)=2距离的最大值.答案 (1)ρ=2sin θ(ρ≠0) (2)1+322解析 (1)设P(ρ,θ),M (ρ1,θ),依题意有 ρ1sin θ=2,ρρ1=4.消去ρ1,得曲线C 2的极坐标方程为 ρ=2sin θ(ρ≠0).(2)将C 2,C 3的极坐标方程化为直角坐标方程,得C 2:x 2+(y -1)2=1,C 3:x -y =2. C 2是以点(0,1)为圆心,以1为半径的圆,圆心到直线C 3的距离d =322,故曲线C 2上的点到直线C 3距离的最大值为1+322.16.(2014·辽宁)将圆x 2+y 2=1上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.(1)写出C 的参数方程;(2)设直线l :2x +y -2=0与C 的交点为P 1,P 2,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,求过线段P 1P 2的中点且与l 垂直的直线的极坐标方程.答案 (1)⎩⎪⎨⎪⎧x =cost ,y =2sint ,(t 为参数) (2)ρ=34sin θ-2cos θ解析 (1)设(x 1,y 1)为圆上的点,在已知变换下变为C 上点(x ,y),依题意,得⎩⎪⎨⎪⎧x =x 1,y =2y 1,由x 12+y 12=1得x 2+(y 2)2=1,即曲线C 的方程为x 2+y 24=1. 故C 的参数方程为⎩⎪⎨⎪⎧x =cost ,y =2sint ,(t 为参数)(2)由⎩⎪⎨⎪⎧x 2+y 24=1,2x +y -2=0,解得⎩⎪⎨⎪⎧x =1,y =0,或⎩⎪⎨⎪⎧x =0,y =2. 不妨设P 1(1,0),P 2(0,2),则线段P 1P 2的中点坐标为(12,1),所求直线斜率为k =12,于是所求直线方程为y -1=12(x -12),化为极坐标方程,并整理得2ρcos θ-4ρsin θ=-3,即ρ=34sin θ-2cos θ.1.(2016·广东肇庆一模)已知曲线C 的极坐标方程为ρ=2(ρ>0,0≤θ<2π),曲线C 在点(2,π4)处的切线为l ,以极点为坐标原点,以极轴为x 轴的正半轴建立直角坐标系,则l 的直角坐标方程为________. 答案 x +y -22=0解析 根据极坐标与直角坐标的转化公式可以得到曲线ρ=2⇒x 2+y 2=4,点(2,π4)⇒(2,2).因为点(2,2)在圆x 2+y 2=4上,故圆在点(2,2)处的切线方程为2x +2y =4⇒x +y -22=0,故填x +y -22=0.2.在极坐标系中,直线l 的方程为ρcos θ=5,则点(4,π3)到直线l 的距离为________.答案 3解析 在直角坐标系中,直线l 的方程为x =5.在直角坐标系中,x =4cos π3=2,y =4sin π3=23,故点(4,π3)的直角坐标为(2,23),到直线x =5的距离为5-2=3. 3.在极坐标系中,直线ρsin (θ+π4)=2被圆ρ=2截得的弦长为________. 答案 4 3解析 直线ρsin (θ+π4)=2的直角坐标方程为x +y -22=0,圆ρ=4的直角坐标方程为x 2+y 2=16.圆心的坐标是(0,0),半径是4,圆心到直线的距离d =|-22|12+12=2,所以直线ρsin (θ+π4)=2被圆ρ=4截得的弦长是242-22=4 3. 4.在极坐标系中,曲线C 1:ρ=2与曲线C 2:ρ=4sin θ(π2<θ<π)交点的极坐标是________.答案 (2,5π6)解析 由题意分析可得,曲线C 1是圆心为(0,0),半径为2的圆,曲线C 1的方程为x 2+y 2=4.对ρ=4sin θ变形得ρ2=4ρsin θ,所以曲线C 2的方程为x 2+y 2=4y.联立两个方程,解得⎩⎨⎧x =3,y =1,或⎩⎨⎧x =-3,y =1.又∵π2<θ<π,∴交点为(-3,1),转化为极坐标ρ=2,tan θ=1-3,由题意θ=5π6,所以交点的极坐标为(2,5π6).5.(2014·陕西)在极坐标系中,点(2,π6)到直线ρsin (θ-π6)=1的距离是________.答案 1解析 ρsin (θ-π6)=ρ(sin θcos π6-sin π6cos θ)=1,因为在极坐标系中,ρcos θ=x ,ρsin θ=y , 所以直线可化为x -3y +2=0. 同理点(2,π6)可化为(3,1),所以点到直线距离d =|3-3+2|3+1=1.6.(2016·唐山模拟)已知圆C :x 2+y 2=4,直线l :x +y =2.以O 为极点,x 轴的正半轴为极轴,取相同的单位长度建立极坐标系. (1)将圆C 和直线l 的方程化为极坐标方程;(2)P 是l 上的点,射线OP 交圆C 于点R ,又点Q 在OP 上且满足|OQ|·|OP|=|OR|2,当点P 在l 上移动时,求点Q 轨迹的极坐标方程.答案 (1)C :ρ=2 l :ρ(cos θ+sin θ)=2 (2)ρ=2(cos θ+sin θ)(ρ≠0)解析 (1)将x =ρcos θ,y =ρsin θ代入圆C 和直线l 的直角坐标方程得其极坐标方程为 C :ρ=2,l :ρ(cos θ+sin θ)=2.(2)设P ,Q ,R 的极坐标分别为(ρ1,θ),(ρ,θ),(ρ2,θ), 则由|OQ|·|OP|=|OR|2得ρρ1=ρ22. 又ρ2=2,ρ1=2cos θ+sin θ,所以2ρcos θ+sin θ=4,故点Q 轨迹的极坐标方程为ρ=2(cos θ+sin θ)(ρ≠0). 7.已知极坐标方程C 1:ρ=10,C 2:ρsin (θ-π3)=6.(1)化C 1,C 2的极坐标方程为直角坐标方程,并分别判断曲线形状; (2)求C 1,C 2交点间的距离.答案 (1)C 1:x 2+y 2=100,C 2:3x -y +12=0 (2)16 解析 (1)由C 1:ρ=10,得ρ2=100.∴x 2+y 2=100. 所以C 1为圆心在(0,0),半径等于10的圆. 由C 2:ρsin (θ-π3)=6,得ρ(12sin θ-32cos θ)=6.∴y -3x =12,即3x -y +12=0. 所以C 2表示直线.(2)由于圆心(0,0)到直线3x -y +12=0的距离为d =|12|(3)2+(-1)2=6<10,所以直线C 2被圆截得的弦长等于2102-62=16.8.在直角坐标系xOy 中,以O 为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为ρcos (θ-π3)=1,M ,N 分别为C 与x 轴,y 轴的交点.(1)写出C 的直角坐标方程,并求M ,N 的极坐标; (2)设MN 的中点为P ,求直线OP 的极坐标方程. 答案 (1)x +3y -2=0,M(2,0),N(233,π2)(2)θ=π6,ρ∈R解析 (1)由ρcos (θ-π3)=1,得ρ(12cos θ+32sin θ)=1. 从而C 的直角坐标方程为12x +32y =1,即x +3y =2.当θ=0时,ρ=2,所以M(2,0); 当θ=π2时,ρ=233,所以N(233,π2).(2)M 点的直角坐标为(2,0),N 点的直角坐标为(0,233).所以P 点的直角坐标为(1,33),则P 点的极坐标为(233,π6).所以直线OP 的极坐标方程为θ=π6,ρ∈(-∞,+∞).。
2017版高考数学(文)(全国)一轮复习文档:第四章 三角函数、解三角形 4.5 含答案
1.两角和与差的余弦、正弦、正切公式cos(α-β)=cos αcos β+sin αsin β(C(α-β)) cos(α+β)=cos_αcos_β-sin_αsin_β(C(α+β))sin(α-β)=sin_αcos_β-cos_αsin_β(S(α-β)) sin(α+β)=sin_αcos_β+cos_αsin_β(S(α+β)) tan(α-β)=错误!(T(α-β))tan(α+β)=错误!(T(α+β))2.二倍角公式sin 2α=2sin_αcos_α;cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α;tan 2α=2tan α1-tan2α。
3.公式的逆用、变形等(1)tan α±tanβ=tan(α±β)(1∓tan_αtan_β);(2)cos2α=错误!,sin2α=错误!;(3)1+sin 2α=(sin α+cos α)2,1-sin 2α=(sin α-cos α)2,sin α±cos α=2sin错误!.【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)存在实数α,β,使等式sin(α+β)=sin α+sin β成立.( √)(2)在锐角△ABC中,sin A sin B和cos A cos B大小不确定.(×)(3)公式tan(α+β)=错误!可以变形为tan α+tan β=tan(α+β)(1-tan αtan β),且对任意角α,β都成立.( ×)(4)存在实数α,使tan 2α=2tan α.(√)(5)两角和与差的正弦、余弦公式中的角α,β是任意的.(√)1.化简错误!等于()A.1 B.错误!C。
错误!D.2答案C解析原式=错误!=错误!=错误!=错误!。
2.若错误!=错误!,则tan 2α等于( )A.-错误! B.错误!C.-错误! D.错误!答案B解析由错误!=错误!,等式左边分子、分母同除cos α得,错误!=错误!,解得tan α=-3,则tan 2α=错误!=错误!.3.(2015·重庆)若tan α=错误!,tan(α+β)=错误!,则tan β等于() A。
2017版《高考调研》大一轮复习(新课标,数学理)题组训练选考部分 选修系列4题组74 Word版含解析
题组层级快练(七十四)1. (2016·天津和平区模拟)如图,AB 是半圆的直径,点D 是弧AC 的中点,∠ABC =50°,则∠DAB 等于( )A .55°B .60°C .65°D .70°答案 C解析 如图,连接BD ,∵AB 是半圆的直径,∴∠ADB =90°,∵点D 是AC ︵的中点,∴∠ABD =∠CBD.∵∠ABC =50°,∴∠ABD =25°.∴∠DAB =90°-25°=65°.故选C.2.如图所示,在半径为2的⊙O 中,∠AOB =90°,D 为OB 的中点,AD 的延长线交⊙O 于点E ,则线段DE 的长为( )A.55B.255C.355D.32答案 C解析 延长BO 交圆O 于点F ,由D 为OB 的中点,知DF =3,DB =1.又∠AOB =90°,所以AD = 5.由相交弦定理知AD·DE =DF·DB ,即5DE =3×1,解得DE =355.3.如图所示,E ,C 分别是∠A 两边上的点,以CE 为直径的⊙O 交∠A 的两边于D ,B ,若∠A =45°,则△AEC 与△ABD 的面积比为( )A .2∶1B .1∶2 C.2∶1 D.3∶1答案 A解析 连接BE ,易知△ABD ∽△AEC ,求△AEC 与△ABD 的面积比即求AE 2∶AB 2的值,设AB =a ,∵∠A =45°,CE 为⊙O 的直径, ∴∠CBE =∠ABE =90°. ∴BE =AB =a ,∴AE =2a. ∴AE 2∶AB 2=2a 2∶a 2.∴AE 2∶AB 2=2∶1,∴S △AEC ∶S △ABD =2∶1.4.(2014·天津)如图,△ABC 是圆的内接三角形,∠BAC 的平分线交圆于点D ,交BC 于点E ,过点B 的圆的切线与AD 的延长线交于点F.在上述条件下,给出下列四个结论:①BD 平分∠CBF ;②FB 2=FD·FA ;③AE·CE =BE·DE ;④AF·BD =AB·BF.则所有正确结论的序号是( ) A .①② B .③④ C .①②③ D .①②④答案 D解析 因为∠BAD =∠FBD ,∠DBC =∠DAC ,又AE 平分∠BAC ,所以∠BAD =∠DAC ,所以∠FBD =∠DBC ,所以BD 平分∠CBF ,结论①正确;易证△ABF ∽△BDF ,所以AB AF =BD BF ,所以AB·BF =AF·BD ,结论④正确;由AF BF =BF DF ,得BF 2=AF·DF ,结论②正确,选D.5.(2015·重庆)如图,圆O 的弦AB ,CD 相交于点E ,过点A 作圆O 的切线与DC 的延长线交于点P ,若PA =6,AE =9,PC =3,CE ∶ED =2∶1,则BE =________.答案 2解析 由切割线定理,知PA 2=PC·PD ,即62=3PD ,解得PD =12,所以CD =PD -PC =9,所以CE =6,ED =3.由相交弦定理,知AE·BE =CE·ED ,即9BE =6×3,解得BE =2. 6.(2015·湖北)如图,PA 是圆的切线,A 为切点,PBC 是圆的割线,且BC =3PB ,则AB AC =________.答案 12解析 因为PA 是圆的切线,A 为切点,PBC 是圆的割线,由切割线定理,知PA 2=PB·PC =PB(PB +BC).因为BC =3PB ,所以PA 2=4PB 2,即PA =2PB.由△PAB ∽△PCA ,所以AB AC =PB PA =12. 7.(2015·广东)如图,已知AB 是圆O 的直径,AB =4,EC 是圆O 的切线,切点为C ,BC =1.过圆心O 作BC 的平行线,分别交EC 和AC 于点D 和点P ,则OD =________.答案 8解析 由题意得OP =12BC =12,OA =2,于是PA =CP =22-(12)2=152.因为∠DCP =∠B =∠POA ,又∠DPC =∠APO ,所以△DCP ∽△AOP ,故PD PA =PCPO ,即PD=15212×152=152,所以OD =152+12=8.8.如图,PT 是圆O 的切线,PAB 是圆O 的割线,若PT =2,PA =1,∠P =60°,则圆O 的半径为________.答案3解析 连接AT ,BT.在△APT 中,∠P =60°,PT =2,PA =1,则由余弦定理得AT =3,∴∠TAP =90°,∴∠BA T =90°,∴BT 是圆O 的直径,∵PT 是圆O 的切线,PAB 是圆O 的割线,∴PT 2=PA·PB ,∴PT PB =PA PT .又∠P 为公共角,∴△PA T ∽△PTB ,∴PT PA =BTAT,得BT =23,因此圆的半径为 3.9.如图,PAB ,PCD 为圆O 的两条割线,若PA =5,AB =7,CD =11,AC =2,则BD =________.答案 6解析 因为PAB ,PCD 为圆O 的两条割线,所以PA·PB =PC·PD.因为PA =5,AB =7,CD =11,所以PB =5+7=12,PD =PC +CD =PC +11,所以5×12=PC(PC +11),PC 2+11PC -60=0,(PC +15)(PC -4)=0.因为PC 大于0,所以PC +15≠0,所以PC -4=0,PC =4.因为∠PAC =∠D(圆内接四边形的任一外角等于它的内对角),又∠P =∠P ,所以△PAC ∽△PDB ,所以BD AC =PB PC .因为AC =2,PB =12,PC =4,所以BD 2=124,所以BD =6.10.如图,圆O 的直径AB 与弦CD 交于点P ,CP =75,PD =5,AP =1,则∠DCB =________.答案 45°解析 由相交弦定理可得CP·PD =AP·PB ,∴PB =CP·PD AP =75×51=7.∴直径2R =AP +PB =1+7=8,∴半径R =4.∴OP =OA -AP =4-1=3. 连接DO ,在△ODP 中,OP 2+OD 2=32+42=52=PD 2,∴∠POD =90°. 连接BD ,由△DOB 为等腰直角三角形可得DB =2R. 由正弦定理可得DB sin ∠DCB =DBsin ∠A =2R ,∴sin ∠DCB =DB 2R =22,由图可知,∠DCB 为锐角,∴∠DCB =45°.11.如图,BD 是半圆O 的直径,A 在BD 的延长线上,AC 与半圆相切于点E ,AC ⊥BC ,若AD =23,AE =6,则EC =________.答案 3解析 如图,连接OE.由切割线定理得AE 2=AD·AB ,∴AB =6223=63,∴OE =OD =OB =12(AB -AD)=23,由于E 是切点,∴OE ⊥AC ,又AC ⊥BC ,∴OE ∥BC ,∴AE EC =AO OB ,即6EC =23+2323,EC =3.12.如图,BD 是⊙O 的直径,E 是⊙O 上的一点,直线CE 交BD 的延长线于A 点,BC ⊥AE 于C 点,且∠CBE =∠DBE.求证:AC 是⊙O 的切线. 答案 略证明 连接OE ,由OE =OB ,得∠OEB =∠OBE.∵∠CBE =∠DBE ,∴∠CBE =∠OEB. ∴OE ∥BC.又BC ⊥AE ,∴OE ⊥AC. ∴AC 是⊙O 的切线.13.(2016·内蒙古赤峰宁城月考)如图,已知AB 是⊙O 的直径,AC 是⊙O 的弦,∠BAC 的平分线AD 交⊙O 于D ,过点D 作DE ⊥AC 交AC 的延长线于点E ,OE 交AD 于点F.若AC AB =35.(1)求证:OD ∥AE ; (2)求AFFD 的值.答案 (1)略 (2)85解析 (1)证明:连接BC ,设BC 交OD 于点M. 因为OA =OD ,所以∠OAD =∠ODA.又因为∠OAD =∠DAE ,所以∠ODA =∠DAE ,所以OD ∥AE. (2)因为AC ⊥BC ,且AC ⊥DE ,所以BC ∥DE. 所以四边形CMDE 为平行四边形,所以CE =MD. 由AC AB =35,设AC =3x ,AB =5x ,则OM =32x. 又OD =52x ,所以MD =52x -32x =x ,所以AE =AC +CE =4x.因为OD ∥AE ,所以AF FD =AE OD =4x 52x =85.14.(2016·江西六校第二次联考)如图,AB是圆O的直径,C,D是圆O上两点,AC与BD 相交于点E,GC,GD是圆O的切线,点F在DG的延长线上,且DG=GF.求证:(1)D,E,C,F四点共圆;(2)GE⊥AB.答案略证明(1)如图,连接OC,OD,则OC⊥CG,OD⊥DG,设∠CAB=∠1,∠DBA=∠2,∠ACO=∠3,∠COB=2∠1,∠DOA=2∠2.所以∠DGC=180°-∠DOC=2(∠1+∠2).因为∠DGC=2∠F,所以∠F=∠1+∠2.又因为∠DEC=∠AEB=180°-(∠1+∠2),所以∠DEC+∠F=180°,所以D,E,C,F四点共圆.(2)延长GE交AB于H.因为GD=GC=GF,所以点G是经过D,E,C,F四点的圆的圆心.所以GE=GC,所以∠GCE=∠GEC.又因为∠GCE+∠3=90°,∠1=∠3,所以∠GEC+∠1=90°,所以∠AEH+∠1=90°,所以∠EHA=90°,即GE⊥AB.15.如图,四边形ABDC内接于圆,BD=CD,过C点的圆的切线与AB的延长线交于E 点.(1)求证:∠EAC=2∠DCE;(2)若BD⊥AB,BC=BE,AE=2,求AB的长.答案(1)略(2)AB=5-1解析(1)证明:因为BD=CD,所以∠BCD=∠CBD.因为CE 是圆的切线所以∠ECD =∠CBD. 所以∠ECD =∠BCD ,所以∠BCE =2∠ECD. 因为∠EAC =∠BCE ,所以∠EAC =2∠ECD. (2)因为BD ⊥AB ,所以AC ⊥CD ,AC =AB.因为BC =BE ,所以∠BEC =∠BCE =∠EAC ,所以AC =EC.由切割线定理得EC 2=AE·BE ,即AB 2=AE·(AE -AB),即AB 2+2AB -4=0,解得AB =5-1.16. (2015·陕西)如图,AB 切⊙O 于点B ,直线AO 交⊙O 于D ,E 两点,BC ⊥DE ,垂足为C.(1)证明:∠CBD =∠DBA ;(2)若AD =3DC ,BC =2,求⊙O 的直径. 答案 (1)略 (2)3解析 (1)证明:因为DE 为⊙O 的直径, 则∠BED +∠EDB =90°,又BC ⊥DE ,所以∠CBD +∠EDB =90°, 从而∠CBD =∠BED.又AB 切⊙O 于点B ,得∠DBA =∠BED , 所以∠CBD =∠DBA. (2)由(1)知BD 平分∠CBA ,则BA BC =ADCD =3,又BC =2,从而AB =3 2. 所以AC =AB 2-BC 2=4,所以AD =3.由切割线定理得AB 2=AD·AE ,即AE =AB 2AD=6,故DE =AE -AD =3,即⊙O 的直径为3.1. 如图,若AB 是⊙O 的直径,CD 是⊙O 的弦,∠ABD =58°,则∠BCD =________.答案 32°解析 根据直径所对的圆周角为直角可得∠ADB =90°,根据∠ABD =58°可得∠A = 32°,根据同弧所对的圆周角相等可得∠BCD =∠A =32°.2.如图,BC 是圆O 的一条弦,延长BC 至点E ,使得BC =2CE =2,过E 作圆O 的切线,A 为切点,∠BAC 的平分线AD 交BC 于点D ,则DE 的长为________.答案3解析 由切割线定理得AE 2=EC·EB =1×3=3,所以AE = 3.因为AD 是∠BAC 的平分线,所以∠BAD =∠CAD.因为AE 是圆O 的切线,所以∠EAC =∠ABC.因为∠ADC =∠BAD +∠ABC ,所以∠ADC =∠BAD +∠EAC =∠EAD ,所以DE =AE = 3.3.如图所示,已知AB ,BC 是⊙O 的两条弦,AO ⊥BC ,AB =3,BC =22,则⊙O 的半径等于________.答案 1.5解析 设⊙O 的半径为r ,BC 与AO 交于点D ,因为AB ,BC 是⊙O 的两条弦,AO ⊥BC ,AB =3,BC =22,所以AD =1,所以r 2=2+(r -1)2,解得r =1.5.4.如图,PA 是圆的切线,A 为切点,PBC 是圆的割线,且PB BC =12,则PABC=________.答案32解析 由题意,可设PB =x ,则BC =2x ,根据切割线定理,可得PA 2=PB·PC =3x 2,PA =3x ,所以PA BC =32.5.如图,过点P作圆O的割线PAB与切线PE,E为切点,连接AE,BE,∠APE的平分线与AE,BE分别交于点C,D,若∠AEB=30°,则∠PCE=________.答案75°解析∵PE是圆的切线,∴∠PEB=∠PAC.∵PC是∠APE是平分线,∴∠EPC=∠APC,根据三角形的外角与内角关系有∠EDC=∠PEB+∠EPC,∠ECD=∠PAC+∠APC,∴∠EDC=∠ECD,∴△EDC为等腰三角形.又∠AEB=30°,∴∠EDC=∠ECD=75°,即∠PCE=75°.6.如图,PB为△ABC外接圆O的切线,BD平分∠PBC,交圆O于D,点C,D,P共线.若AB⊥BD,PC⊥PB,PD=1,则圆O的半径是________.答案 2解析如图所示,连接AD,∵PB为圆O的切线,∴∠PBD=∠BCD=∠BAD.∵BD为∠PBC 的平分线,∴∠PBD=∠CBD,∴∠PDB=∠CBD+∠BCD=∠PBD+∠PBD=2∠PBD.又∵PC⊥PB,∴∠PBD=∠BCD=∠CBD=∠BAD=30°,∠PDB=60°.由PD=1,得BD=2PD=2.在△ABD中,∵AB⊥BD,∴AD是圆O的直径,且直径AD=2BD=4,∴圆O的半径为2.7.如图,已知⊙O的割线PAB交⊙O于A,B两点,割线PCD经过圆心,若PA=3,AB=4,PO=5,则⊙O的半径为________.答案 2解析 设圆的半径为r ,PA =3,PB =7,PC =5-r ,PD =5+r ,由割线定理PA·PB =PC·PD ,得3×7=(5+r)(5-r),解得r =2.8.已知⊙O 1和⊙O 2交于点C 和点D ,⊙O 1上的点P 处的切线交⊙O 2于A ,B 两点,交直线CD 于点E ,M 是⊙O 2上的一点,若PE =2,EA =1,∠AMB =45°,那么⊙O 2的半径为________.答案 322解析 由切线定理和割线定理可知,PE 2=EC·ED =EA·(EA +AB),将PE =2,EA =1代入,得AB =3.连接AO 2,BO 2,由∠AMB =45°可得△ABO 2为等腰直角三角形,所以⊙O 2的半径r =22AB =322. 9.如图所示,圆O 的两条弦AB 和CD 交于点E ,EF ∥CB ,EF 交AD 的延长线于点F ,FG 切圆O 于点G .(1)求证:△DEF ∽△EAF ;(2)如果FG =1,求EF 的长.答案 (1)略 (2)1解析 (1)证明:因为EF ∥BC ,所以∠DEF =∠ECB.又因为∠ECB =∠A ,所以∠DEF =∠A ,又∠DFE 为公共角,所以△DEF ∽△EAF.(2)由(1)知△DEF ∽△EAF ,所以EF AF =DF EF,即EF 2=AF·DF.又因为FG 为切线,所以FG 2=FD·FA ,所以EF =FG =1.10.如图,AB 是⊙O 的一条切线,切点为B ,直线ADE ,CFD ,CGE 都是⊙O 的割线,已知AC =AB.(1)求证:FG ∥AC ;(2)若CG =1,CD =4,求DE GF的值. 答案 (1)略 (2)4解析 (1)证明:因为AB 为切线,AE 为割线,所以AB 2=AD·AE.又因为AC =AB ,所以AD·AE =AC 2,所以AD AC =AC AE. 又因为∠EAC =∠DAC ,所以△ADC ∽△ACE ,所以∠ADC =∠ACE. 又因为∠ADC =∠EGF ,所以∠EGF =∠ACE ,所以FG ∥AC.(2)由题意可得G ,E ,D ,F 四点共圆,所以∠CGF =∠CDE ,∠CFG =∠CED.所以△CGF ∽△CDE ,所以ED GF =CD CG. 又因为CG =1,CD =4,所以DE GF=4.。
2017版《高考调研》大一轮复习(新课标,数学理)题组训练选考部分 选修系列4题组73 Word版含解析
题组层级快练(七十三)1.如图,在△ABC 中,∠AED =∠B ,DE =6,AB =10,AE =8,则BC 的长为( )A.154 B .7 C.152 D.245答案 C解析 由已知条件∠AED =∠B ,∠A 为公共角,所以△ADE ∽△ACB ,则有DE BC =AEAB ,从而BC =6×108=152.选C.2.如图,E 是▱ABCD 的边AB 延长线上的一点,且DC ∶BE =3∶2,则AD ∶BF =( )A .5∶3B .5∶2C .3∶2D .2∶1答案 B解析 由题可得△BEF ∽△CDF ,∴DC BE =DF EF =32,∴AD BF =DE EF =DF EF +1=52. 3.如图,DE ∥BC ,DF ∥AC ,AD =4 cm ,BD =8 cm ,DE =5 cm ,则线段BF 的长为( )A .5 cmB .8 cmC .9 cmD .10 cm答案 D解析 ∵DE ∥BC ,DF ∥AC , ∴四边形DECF 是平行四边形.∴FC =DE =5 cm.∵DF ∥AC ,∴BF FC =BDDA .即BF 5=84,∴BF =10 cm.4.如图,∠ACB =90°,CD ⊥AB 于点D ,以BD 为直径的圆与BC 交于点E ,则( )A .CE ·CB =AD·DB B .CE ·CB =AD·ABC .AD ·AB =CD 2 D .CE ·EB =CD 2答案 A解析 在直角三角形ABC 中,根据直角三角形射影定理可得CD 2=AD·DB ,再根据切割线定理可得CD 2=CE·CB.所以CE·CB =AD·DB.5.Rt △ABC 中,∠CAB =90°,AD ⊥BC 于D ,AB ∶AC =3∶2,则CD ∶BD =( ) A .3∶2 B .2∶3 C .9∶4 D .4∶9答案 D解析 由△ABD ∽△CBA ,得AB 2=BD·BC. 由△ADC ∽△BAC ,得AC 2=DC·BC. ∴CD·BC BD·BC =AC 2AB 2=49,即CD ∶BD =4∶9. 6.如图所示,在▱ABCD 中,BC =24,E ,F 为BD 的三等分点,则BM -DN =( )A .6B .3C .2D .4答案 A解析 ∵E ,F 为BD 的三等分点,四边形ABCD 为平行四边形,∴M 为BC 的中点.连CF 交AD 于P ,则P 为AD 的中点,由△BCF ∽△DPF 及M 为BC 中点知,N 为DP 的中点,∴BM -DN =12-6=6,故选A.7.如图所示,在矩形ABCD 中,AB =12,AD =10,将此矩形折叠使点B 落在AD 边的中点E 处,则折痕FG 的长为( )A .13 B.635 C.656 D.212答案 C解析 过A 作AH ∥FG 交DG 于H , 则四边形AFGH 为平行四边形. ∴AH =FG.∵折叠后B 点与E 点重合,折痕为FG ,∴B 与E 关于FG 对称. ∴BE ⊥FG ,∴BE ⊥AH.∴∠ABE =∠DAH ,∴Rt △ABE ∽Rt △DAH. ∴BE AB =AH AD. ∵AB =12,AD =10,AE =12AD =5,∴BE =122+52=13.∴FG =AH =BE·AD AB =656.8.如图,在△ABC 中,DE ∥BC ,EF ∥CD ,若BC =3,DE =2,DF =1,则AB 的长为________.答案 92解析AD AB =DE BC =23,DF AD =CE AC =13.∵BC =3,DE =2,DF =1,解得AB =92. 9.如图,在Rt △ABC 中,CD 为斜边AB 上的高,CD =6,且AD ∶BD =3∶2,则斜边AB 上的中线CE 的长为________.答案562解析 ∵CD 2=BD·AD ,设BD =2k ,则AD =3k , ∴36=6k 2,∴k =6,∴AB =5k =5 6. ∴CE =12AB =562.10. (2016·广东梅州联考)如图,在△ABC 中,BC =4,∠BAC =120°,AD ⊥BC ,过B 作CA 的垂线,交CA 的延长线于E ,交DA 的延长线于F ,则AF =________.答案433解析 设AE =x ,∵∠BAC =120°,∴∠EAB =60°. 又AE BE =x 3x =13, 在Rt △AEF 与Rt △BEC 中,∠F =90°-∠EAF =90°-∠DAC =∠C , ∴△AEF ∽△BEC ,∴AF BC =AE BE .∴AF =4×13=433.11.(2015·江苏)如图,在△ABC 中,AB =AC ,△ABC 的外接圆⊙O 的弦AE 交BC 于点D.求证:△ABD ∽△AEB.答案 略证明 因为AB =AC ,所以∠ABD =∠C. 又因为∠C =∠E ,所以∠ABD =∠E , 又∠BAE 为公共角,可知△ABD ∽△AEB.12.如图,在Rt △ABC 中,∠BAC =90°,AD ⊥BC 于D ,DF ⊥AC 于F ,DE ⊥AB 于E ,求证:AD 3=BC·BE·CF.答案 略证明 在Rt △ABC 中,因为AD ⊥BC , 所以AD 2=BD·DC ,且AD·BC =AB·AC.在Rt △ABD 和Rt △ADC 中, 因为DE ⊥AB ,DF ⊥AC ,由射影定理,得BD 2=BE·BA ,DC 2=CF·AC. 所以BD 2·DC 2=BE·BA·CF·AC =BE·CF·AD·BC =AD 4. 所以AD 3=BC·BE·CF.13. (2016·甘肃河西三校第一次联考)如图,△ABC 的角平分线AD 的延长线交它的外接圆于点E.(1)证明:△ABE ∽△ADC ;(2)若△ABC 的面积S =12AD ·AE ,求∠BAC 的大小.答案 (1)略 (2)90°解析 (1)证明:由已知条件,可得∠BAE =∠CAD.因为∠AEB 与∠ACB 是同弧所对的圆周角,所以∠AEB =∠ACD. 故△ABE ∽△ADC.(2)因为△ABE ∽△ADC ,所以AB AE =ADAC ,即AB·AC =AD·AE.又S =12AB ·ACsin ∠BAC ,且S =12AD ·AE ,故AB·ACsin ∠BAC =AD·AE.则sin ∠BAC =1,又∠BAC 为三角形内角,所以∠BAC =90°.14. (2016·沧州七校联考)如图,点A 为圆外一点,过点A 作圆的两条切线,切点分别为B ,C ,ADE 是圆的割线,连接CD ,BD ,BE ,CE.(1)求证:BE·CD =BD·CE ;(2)延长CD ,交AB 于点F ,若CE ∥AB ,证明:F 为线段AB 的中点. 答案 (1)略 (2)略证明 (1)如图,由题意可得∠ACD =∠AEC ,∠CAD =∠EAC , ∴△ADC ∽△ACE ,∴CD CE =ACAE.同理△ADB ∽△ABE ,BD BE =ABAE .又∵AB =AC ,∴CD CE =BDBE ,∴BE ·CD =BD·CE. (2)如图,由切割线定理,得FB 2=FD·FC. ∵CE ∥AB ,∴∠FAD =∠AEC.又∵AC 切圆于C ,∴∠ACD =∠AEC ,∴∠FAD =∠FCA ,又∠F =∠F , ∴△AFD ∽△CFA ,∴AF CF =FDAF ,即AF 2=FD·FC.∵FB 2=AF 2,即FB =FA ,∴F 为线段AB 的中点.1.如图, 在△ABC 中,AE =ED =DC ,FE ∥MD ∥BC ,FD 的延长线交BC 的延长线于点N ,且EF =1,则BN =( )A .2B .3C .4D .6答案 C解析 ∵FE ∥MD ∥BC ,AE =ED =DC , ∴EF BC =AE AC =13,EF CN =ED DC =11. ∴EF =CN ,∴EF BN =EF BC +CN =14.∴BN =4EF =4.(或由△FDE ≌△NDC ⇒EF =CN).2.如图,在直角梯形ABCD 中,上底AD =3,下底BC =33,与两底垂直的腰AB =6,在AB 上选取一点P ,使△PAD 和△PBC 相似,则这样的点P( ) A .有1个 B .有2个 C .有3个 D .不存在答案 B 解析 设AP =x.(1)若△ADP ∽△BPC ,则AD BP =APBC ,即36-x =x 33,所以x 2-6x +9=0,解得x =3. (2)若△ADP ∽△BCP ,则AD BC =APBP ,即333=x 6-x,解得x =32.∴符合条件的点P 有两个.故选B.3.如图,AC 为⊙O 的直径,BD ⊥AC 于P ,PC =2,PA =8,则CD 的长为________,cos ∠ACB =________.答案 25,55解析 由射影定理,得 CD 2=CP·CA =2×10. ∴CD =2 5.cos ∠ACB =sin ∠A =sin ∠D =CP CD =225=55.4.如图,D 、E 分别是△ABC 的边AB 、AC 上的点,DE ∥BC ,且ADDB =2,那么△ADE 与四边形DBCE 的面积比是________.答案 45解析 ∵DE ∥BC ,∴△ADE ∽△ABC , ∵AD DB =2,∴AD AB =23. 故S △ADE S △ABC =49,∴S △ADE S 四边形DBCE =45. 5.如图,等边三角形DEF 内接于△ABC ,且DE ∥BC ,已知AH ⊥BC 于点H ,BC =4,AH =3,则△DEF 的边长为________.答案 43解析 设DE =x ,AH 交DE 于点M ,显然MH 的长度与等边三角形DEF 的高相等,又DE ∥BC ,则DE BC =AM AH =AH -MH AH ,所以x4=3-32x 3=2-x 2,解得x =43.6.(2016·贵阳市高三适应性监测考试)如图,已知圆O 两弦AB 与CD 交于点E ,EF ∥AD ,EF 与CB 延长线交于点F ,FG 切圆O 于点G.(1)求证:△BEF ∽△ECF ; (2)求证:FG =EF.证明 (1)因为EF ∥AD ,所以∠FEA =∠DAB.又∠DAB =∠BCD ,所以∠FEB =∠FCD.又∠BFE=∠BFE,所以△BEF∽△ECF.(2)由(1)得EFFC=FBFE,所以EF2=FC·FB.又因为FG2=FB·FC,所以EF2=FG2.所以FG=EF.。
2017版高考数学北师大版(理)一轮复习第4章三角函数、解三角形4.6简单的三角恒等变换文档
1.公式的常见变形 (1)1+cos α=2cos 2α2;1-cos α=2sin 2α2;(2)1+sin α=(sin α2+cos α2)2;1-sin α=(sin α2-cos α2)2.(3)tan α2=sin α1+cos α=1-cos αsin α.2.辅助角公式a sin x +b cos x =a 2+b 2sin(x +φ), 其中sin φ=b a 2+b 2,cos φ=aa 2+b 2.【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”) (1)y =3sin x +4cos x 的最大值是7.( × ) (2)设α∈(π,2π),则1-cos (π+α)2=sin α2.( × ) (3)在非直角三角形中有:tan A +tan B +tan C =tan A tan B tan C .( √ ) (4)设5π2<θ<3π,且|cos θ|=15,那么sin θ2的值为155.( × )(5)公式a sin x +b cos x =a 2+b 2sin(x +φ)中φ的取值与a ,b 的值无关.( × )1.计算tan ⎝⎛⎭⎫π4+α·cos2α2cos 2⎝⎛⎭⎫π4-α的值为( )A.-2B.2C.-1D.1答案 D解析 tan ⎝⎛⎭⎫π4+α·cos2α2cos 2⎝⎛⎭⎫π4-α=sin ⎝⎛⎭⎫π4+α·cos2α2sin 2⎝⎛⎭⎫π4+αcos ⎝⎛⎭⎫π4+α =cos2α2sin ⎝⎛⎭⎫π4+αcos ⎝⎛⎭⎫π4+α=cos2αsin ⎝⎛⎭⎫π2+2α=cos2αcos2α=1,选D. 2.2sin 235°-1cos10°-3sin10°的值为( ) A.1 B.-1 C.12 D.-12答案 D解析 原式=2sin 235°-12⎝⎛⎭⎫12cos10°-32sin10°=-cos70°2sin20°=-12. 3.(教材改编)sin15°-3cos15°=________. 答案 - 2解析 sin15°-3cos15°=2sin(15°-60°) =-2sin45°=- 2.4.若f (x )=2tan x -2sin 2 x 2-1sin x 2cosx2,则f ⎝⎛⎭⎫π12的值为______. 答案 8解析 ∵f (x )=2tan x +1-2sin 2x 212sin x=2tan x +2cos xsin x=2sin x cos x =4sin2x,∴f ⎝⎛⎭⎫π12=4sinπ6=8. 5.若锐角α、β满足(1+3tan α)(1+3tan β)=4,则α+β=________. 答案 π3解析 由(1+3tan α)(1+3tan β)=4, 可得tan α+tan β1-tan αtan β=3,即tan(α+β)= 3.又α+β∈(0,π),∴α+β=π3.题型一 三角函数式的化简与求值例1 (1)化简:2cos 4x -2cos 2x +122tan ⎝⎛⎭⎫π4-x sin 2⎝⎛⎭⎫π4+x =________.(2)已知α∈⎝⎛⎭⎫0,π2,且2sin 2α-sin α·cos α-3cos 2α=0,则sin ⎝⎛⎭⎫α+π4sin2α+cos2α+1=________. 答案 (1)12cos2x (2)268解析 (1)原式=12(4cos 4x -4cos 2x +1)2×sin ⎝⎛⎭⎫π4-x cos ⎝⎛⎭⎫π4-x ·cos 2⎝⎛⎭⎫π4-x=(2cos 2x -1)24sin ⎝⎛⎭⎫π4-x cos ⎝⎛⎭⎫π4-x=cos 22x2sin ⎝⎛⎭⎫π2-2x=cos 22x 2cos2x =12cos2x . (2)∵α∈⎝⎛⎭⎫0,π2,且2sin 2α-sin α·cos α-3cos 2α=0,则(2sin α-3cos α)·(sin α+cos α)=0,∴2sin α=3cos α,又sin 2α+cos 2α=1, ∴cos α=213,sin α=313, ∴sin ⎝⎛⎭⎫α+π4sin2α+cos2α+1=22(sin α+cos α)(sin α+cos α)2+(cos 2α-sin 2α) =268. 思维升华 (1)三角函数式的化简要遵循“三看”原则,一看角,二看名,三看式子结构与特征.(2)三角函数式化简要注意观察条件中角之间的联系(和、差、倍、互余、互补等),寻找式子和三角函数公式之间的共同点.(1)cos π9·cos 2π9·cos ⎝⎛⎭⎫-23π9等于( ) A.-18B.-116C.116D.18(2)若1+cos2αsin2α=12,则tan2α等于( )A.54B.-54C.43D.-43答案 (1)A (2)D解析 (1)原式=cos π9·cos 29π·cos (-3π+49π)=-cos π9·cos 29π·cos 49π·sinπ9sin π9=-12sin 29π·cos 29π·cos 49πsinπ9=-18sin 89πsinπ9=-18.(2)1+cos2αsin2α=2cos 2α2sin αcos α=cos αsin α=12,∴tan α=2,∴tan2α=2tan α1-tan 2α=41-4=-43.题型二 三角函数的求角问题例2 (1)已知锐角α,β满足sin α=55,cos β=31010,则α+β等于( ) A.3π4 B.π4或3π4 C.π4D.2k π+π4(k ∈Z )(2)已知方程x 2+3ax +3a +1=0(a >1)的两根分别为tan α、tan β,且α、β∈⎝⎛⎭⎫-π2,π2,则α+β等于( ) A.π8 B.-3π4C.π8或-3π8D.π4或-3π4答案 (1)C (2)B 解析 (1)由sin α=55,cos β=31010且α,β为锐角, 可知cos α=255,sin β=1010,故cos(α+β)=cos αcos β-sin αsin β =255×31010-55×1010=22, 又0<α+β<π,故α+β=π4.(2)依题意有⎩⎪⎨⎪⎧tan α+tan β=-3a ,tan α·tan β=3a +1,∴tan(α+β)=tan α+tan β1-tan α·tan β=-3a1-(3a +1)=1. 又⎩⎪⎨⎪⎧tan α+tan β<0,tan α·tan β>0,∴tan α<0且tan β<0. ∴-π2<α<0且-π2<β<0,即-π<α+β<0,结合tan(α+β)=1, 得α+β=-3π4.思维升华 通过求角的某种三角函数值来求角,在选取函数时,有以下原则: (1)已知正切函数值,则选正切函数.(2)已知正弦、余弦函数值,则选正弦或余弦函数.若角的范围是⎝⎛⎭⎫0,π2,则选正弦、余弦皆可;若角的范围是(0,π),则选余弦较好;若角的范围为⎝⎛⎭⎫-π2,π2,则选正弦较好.(1)已知sin α=55,sin(α-β)=-1010,α,β均为锐角,则角β等于( ) A.5π12 B.π3 C.π4D.π6(2)在△ABC 中,tan A +tan B +3=3tan A ·tan B ,则C 等于( ) A.π3 B.2π3 C.π6D.π4答案 (1)C (2)A解析 (1)∵α、β均为锐角,∴-π2<α-β<π2.又sin(α-β)=-1010,∴cos(α-β)=31010. 又sin α=55,∴cos α=255, ∴sin β=sin [α-(α-β)] =sin αcos(α-β)-cos αsin(α-β) =55×31010-255×(-1010)=22. ∴β=π4.(2)由已知可得tan A +tan B =3(tan A ·tan B -1), ∴tan(A +B )=tan A +tan B1-tan A tan B =-3,又0<A +B <π,∴A +B =23π,∴C =π3.题型三 三角恒等变换的应用例3 已知函数f (x )=sin(x +θ)+a cos(x +2θ),其中a ∈R ,θ∈⎝⎛⎭⎫-π2,π2. (1)当a =2,θ=π4时,求f (x )在区间[0,π]上的最大值与最小值;(2)若f ⎝⎛⎭⎫π2=0,f (π)=1,求a ,θ的值. 解 (1)f (x )=sin ⎝⎛⎭⎫x +π4+2cos ⎝⎛⎭⎫x +π2 =22(sin x +cos x )-2sin x =22cos x -22sin x=sin ⎝⎛⎭⎫π4-x ,因为x ∈[0,π],从而π4-x ∈⎣⎡⎦⎤-3π4,π4, 故f (x )在[0,π]上的最大值为22,最小值为-1. (2)由⎩⎪⎨⎪⎧f ⎝⎛⎭⎫π2=0,f (π)=1.得⎩⎪⎨⎪⎧cos θ(1-2a sin θ)=0,2a sin 2θ-sin θ-a =1,由θ∈⎝⎛⎭⎫-π2,π2知cos θ≠0, 解得⎩⎪⎨⎪⎧a =-1,θ=-π6.思维升华 三角恒等变换的综合应用主要是将三角变换与三角函数的性质相结合,通过变换把函数化为y =A sin(ωx +φ)+k 的形式再研究性质,解题时注意观察角、函数名、结构等特征.(1)(2014·课标全国Ⅱ)函数f (x )=sin(x +φ)-2sin φcos x 的最大值为________.(2)函数f (x )=sin(2x -π4)-22sin 2x 的最小正周期是________.答案 (1)1 (2)π解析 (1)因为f (x )=sin(x +φ)-2sin φcos x =sin x cos φ-cos x sin φ=sin(x -φ), -1≤sin(x -φ)≤1,所以f (x )的最大值为1. (2)f (x )=22sin2x -22cos2x -2(1-cos2x ) =22sin2x +22cos2x -2=sin(2x +π4)-2, ∴T =2π2=π.8.化归思想和整体代换思想在三角函数中的应用典例 (12分)(2015·重庆)已知函数f (x )=sin ⎝⎛⎭⎫π2-x sin x -3cos 2x . (1)求f (x )的最小正周期和最大值; (2)讨论f (x )在⎣⎡⎦⎤π6,2π3上的单调性.思维点拨 (1)讨论形如y =a sin ωx +b cos ωx 型函数的性质,一律化成y =a 2+b 2sin(ωx +φ)型的函数.(2)研究y =A sin(ωx +φ)型函数的最值、单调性,可将ωx +φ视为一个整体,换元后结合y =sin x 的图像解决. 规范解答解 (1)f (x )=sin ⎝⎛⎭⎫π2-x sin x -3cos 2x =cos x sin x -32(1+cos2x )=12sin2x -32cos2x -32=sin ⎝⎛⎭⎫2x -π3-32,[4分] 因此f (x )的最小正周期为π,最大值为2-32.[6分](2)当x ∈⎣⎡⎦⎤π6,2π3时,0≤2x -π3≤π,[7分] 从而当0≤2x -π3≤π2,即π6≤x ≤5π12时,f (x )单调递增,[9分]当π2≤2x -π3≤π,即5π12≤x ≤2π3时,f (x )单调递减.[11分] 综上可知,f (x )在⎣⎡⎦⎤π6,5π12上单调递增;在⎣⎡⎦⎤5π12,2π3上单调递减.[12分] 温馨提醒 (1)讨论三角函数的性质,要先利用三角变换化成y =A sin(ωx +φ),φ的确定一定要准确.(2)将ωx +φ视为一个整体,设ωx +φ=t ,可以借助y =sin t 的图像讨论函数的单调性、最值等.[方法与技巧]1.三角函数的求值与化简要注意观察角、函数名称、式子结构之间的联系,然后进行变换.2.利用三角函数值求角要考虑角的范围.3.与三角函数的图像与性质相结合的综合问题.借助三角恒等变换将已知条件中的函数解析式整理为f (x )=A sin(ωx +φ)的形式,然后借助三角函数图像解决. [失误与防范]1.利用辅助角公式,a sin x +b cos x 转化时一定要严格对照和差公式,防止搞错辅助角.2.计算形如y =sin(ωx +φ), x ∈[a ,b ]形式的函数最值时,不要将ωx +φ的范围和x 的范围混淆.A 组 专项基础训练 (时间:40分钟)1.(2015·陕西)“sin α=cos α”是“cos2α=0”的( ) A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件答案 A解析 sin α=cos α⇒cos2α=cos 2α-sin 2α=0; cos2α=0⇔cos α=±sin α⇏sin α=cos α,故选A. 2.已知sin2α=23,则cos 2⎝⎛⎭⎫α+π4等于( ) A.16B.13C.12D.23答案 A解析 因为cos 2⎝⎛⎭⎫α+π4=1+cos2⎝⎛⎭⎫α+π42=1+cos ⎝⎛⎭⎫2α+π22=1-sin2α2,所以cos 2⎝⎛⎭⎫α+π4=1-sin2α2=1-232=16,故选A. 3.若α∈⎝⎛⎭⎫π2,π,且3cos2α=sin ⎝⎛⎭⎫π4-α,则sin2α的值为( ) A.118 B.-118C.1718D.-1718答案 D解析 cos2α=sin ⎝⎛⎭⎫π2-2α=sin ⎣⎡⎦⎤2⎝⎛⎭⎫π4-α=2sin ⎝⎛⎭⎫π4-αcos ⎝⎛⎭⎫π4-α代入原式,得6sin ⎝⎛⎭⎫π4-αcos ⎝⎛⎭⎫π4-α=sin ⎝⎛⎭⎫π4-α,∵α∈⎝⎛⎭⎫π2,π,∴cos ⎝⎛⎭⎫π4-α=16,∴sin2α=cos ⎝⎛⎭⎫π2-2α=2cos 2⎝⎛⎭⎫π4-α-1=-1718.4.若sin2α=55,sin(β-α)=1010,且α∈⎣⎡⎦⎤π4,π,β∈⎣⎡⎦⎤π,3π2,则α+β的值是() A.7π4 B.9π4 C.5π4或7π4 D.5π4或9π4答案 A解析 ∵α∈⎣⎡⎦⎤π4,π,∴2α∈⎣⎡⎦⎤π2,2π.∵sin2α=55,∴2α∈⎣⎡⎦⎤π2,π,∴α∈⎣⎡⎦⎤π4,π2,cos2α=-255.∵β∈⎣⎡⎦⎤π,3π2,∴β-α∈⎣⎡⎦⎤π2,5π4,∴cos(β-α)=-31010,∴cos(α+β)=cos [2α+(β-α)]=cos2αcos(β-α)-sin2αsin(β-α)=⎝⎛⎭⎫-255×⎝⎛⎭⎫-31010-55×1010=22.又∵α+β∈⎣⎡⎦⎤5π4,2π,∴α+β=7π4. 5.函数f (x )=sin(2x +θ)+3cos(2x +θ)⎝⎛⎭⎫|θ|<π2的图像关于点⎝⎛⎭⎫π6,0对称,则f (x )的单调递增区间为( )A.⎣⎡⎦⎤π3+k π,5π6+k π,k ∈Z B.⎣⎡⎦⎤-π6+k π,π3+k π,k ∈Z C.⎣⎡⎦⎤-7π12+k π,-π12+k π,k ∈Z D.⎣⎡⎦⎤-π12+k π,5π12+k π,k ∈Z 答案 C解析 ∵f (x )=sin(2x +θ)+3cos(2x +θ)=2sin ⎝⎛⎭⎫2x +θ+π3, 由题意知2×π6+θ+π3=k π(k ∈Z ), ∴θ=k π-23π(k ∈Z ). ∵|θ|<π2,∴θ=π3. ∴f (x )=2sin ⎝⎛⎭⎫2x +23π. 由2k π-π2≤2x +23π≤2k π+π2(k ∈Z ), 得k π-712π≤x ≤k π-π12(k ∈Z ).故选C. 6.已知tan(π4+θ)=3,则sin2θ-2cos 2θ的值为________. 答案 -45解析 ∵tan(π4+θ)=3, ∴1+tan θ1-tan θ=3,解得tan θ=12. ∵sin2θ-2cos 2θ=sin2θ-cos2θ-1=2sin θcos θsin 2θ+cos 2θ-cos 2θ-sin 2θsin 2θ+cos 2θ-1 =2tan θ1+tan 2θ-1-tan 2θ1+tan 2θ-1 =45-35-1=-45. 7.若tan α+1tan α=103,α∈(π4,π2),则sin(2α+π4)的值为________. 答案 -210解析 由tan α+1tan α=103得sin αcos α+cos αsin α=103, ∴1sin αcos α=103,∴sin2α=35. ∵α∈(π4,π2),∴2α∈(π2,π), ∴cos2α=-45. ∴sin(2α+π4)=sin2αcos π4+cos2αsin π4=22×(35-45)=-210. 8.若α、β是锐角,且sin α-sin β=-12,cos α-cos β=12,则tan(α-β)=________. 答案 -73解析 ∵sin α-sin β=-12,cos α-cos β=12, 两式平方相加得:2-2cos αcos β-2sin αsin β=12, 即2-2cos(α-β)=12,∴cos(α-β)=34. ∵α、β是锐角,且sin α-sin β=-12<0, ∴0<α<β<π2,∴-π2<α-β<0. ∴sin(α-β)=-1-cos 2(α-β)=-74.∴tan(α-β)=sin (α-β)cos (α-β)=-73. 9.已知函数f (x )=2cos x (sin x +cos x ).(1)求f ⎝⎛⎭⎫5π4的值;(2)求函数f (x )的最小正周期及单调递增区间.解 (1)f ⎝⎛⎭⎫5π4=2cos 5π4⎝⎛⎭⎫sin 5π4+cos 5π4 =-2cos π4⎝⎛⎭⎫-sin π4-cos π4=2. (2)因为f (x )=2sin x cos x +2cos 2x=sin2x +cos2x +1=2sin ⎝⎛⎭⎫2x +π4+1, 所以T =2π2=π,故函数f (x )的最小正周期为π. 由2k π-π2≤2x +π4≤2k π+π2,k ∈Z , 得k π-3π8≤x ≤k π+π8,k ∈Z . 所以f (x )的单调递增区间为⎣⎡⎦⎤k π-3π8,k π+π8,k ∈Z . 10.已知函数f (x )=sin ⎝⎛⎭⎫ωx +π6+sin ⎝⎛⎭⎫ωx -π6-2cos 2ωx 2,x ∈R (其中ω>0). (1)求函数f (x )的值域;(2)若函数f (x )的图像与直线y =-1的两个相邻交点间的距离为π2,求函数f (x )的单调递增区间. 解 (1)f (x )=32sin ωx +12cos ωx +32sin ωx -12cos ωx -(cos ωx +1) =2⎝⎛⎭⎫32sin ωx -12cos ωx -1 =2sin ⎝⎛⎭⎫ωx -π6-1. 由-1≤sin ⎝⎛⎭⎫ωx -π6≤1, 得-3≤2sin ⎝⎛⎭⎫ωx -π6-1≤1, 所以函数f (x )的值域为[-3,1].(2)由题设条件及三角函数的图像和性质可知,f (x )的周期为π,所以2πω=π,即ω=2.所以f (x )=2sin ⎝⎛⎭⎫2x -π6-1,再由2k π-π2≤2x -π6≤2k π+π2(k ∈Z ),解得k π-π6≤x ≤k π+π3(k ∈Z ).所以函数f (x )的单调递增区间为⎣⎡⎦⎤k π-π6,k π+π3(k ∈Z ).B 组 专项能力提升(时间:25分钟)11.设α∈(0,π2),β∈(0,π2),且tan α=1+sin βcos β,则( )A.3α-β=π2B.2α-β=π2C.3α+β=π2D.2α+β=π2答案 B解析 由tan α=1+sin βcos β得sin αcos α=1+sin βcos β,即sin αcos β=cos α+cos αsin β,∴sin(α-β)=cos α=sin(π2-α).∵α∈(0,π2),β∈(0,π2),∴α-β∈(-π2,π2),π2-α∈(0,π2),由sin(α-β)=sin(π2-α),得α-β=π2-α,∴2α-β=π2.12.定义运算⎪⎪⎪⎪⎪⎪a b c d =ad -bc ,若cos α=17,⎪⎪⎪⎪⎪⎪sin α sin βcos α cos β=3314,0<β<α<π2,则β等于()A.π12B.π6C.π4D.π3答案 D解析 依题意有sin αcos β-cos αsin β=sin(α-β)=3314, 又0<β<α<π2,∴0<α-β<π2, 故cos(α-β)=1-sin 2(α-β)=1314, 而cos α=17,∴sin α=437, 于是sin β=sin [α-(α-β)]=sin αcos(α-β)-cos αsin(α-β) =437×1314-17×3314=32, 故β=π3,故选D. 13.若f (x )=3sin x -4cos x 的一条对称轴方程是x =a ,则a 的取值范围可以是( )A.⎝⎛⎭⎫0,π4 B.⎝⎛⎭⎫π4,π2 C.⎝⎛⎭⎫π2,3π4D.⎝⎛⎭⎫3π4,π答案 D解析 因为f (x )=3sin x -4cos x =5sin(x -φ)⎝⎛⎭⎫其中tan φ=43且0<φ<π2,则sin(a -φ)=±1, 所以a -φ=k π+π2,k ∈Z ,即a =k π+π2+φ,k ∈Z ,而tan φ=43且0<φ<π2,所以π4<φ<π2,所以k π+3π4<a <k π+π,k ∈Z ,取k =0,此时a ∈⎝⎛⎭⎫3π4,π,故选D. 14.若sin x +cos x sin x -cos x=3,tan(x -y )=2,则tan(y -2x )=________. 答案 43解析 由sin x +cos x sin x -cos x =3,得tan x +1tan x -1=3,即tan x =2.又tan(y -x )=-tan(x -y )=-2,所以tan(y -2x )=tan (y -x )-tan x 1+tan (y -x )tan x=-2-21-4=43. 15.已知函数f (x )=2cos 2ωx -1+23cos ωx sin ωx (0<ω<1),直线x =π3是f (x )图像的一条对称轴. (1)试求ω的值;(2)已知函数y =g (x )的图像是由y =f (x )图像上各点的横坐标伸长到原来的2倍,然后再向左平移2π3个单位长度得到的,若g ⎝⎛⎭⎫2α+π3=65,α∈⎝⎛⎭⎫0,π2,求sin α的值. 解 f (x )=2cos 2ωx -1+23cos ωx sin ωx=cos2ωx +3sin2ωx=2sin ⎝⎛⎭⎫2ωx +π6. (1)由于直线x =π3是函数f (x )=2sin ⎝⎛⎭⎫2ωx +π6图像的一条对称轴, ∴sin ⎝⎛⎭⎫2π3ω+π6=±1. ∴2π3ω+π6=k π+π2(k ∈Z ), ∴ω=32k +12(k ∈Z ). 又0<ω<1,∴-13<k <13. 又∵k ∈Z ,从而k =0,∴ω=12. (2)由(1)知f (x )=2sin ⎝⎛⎭⎫x +π6, 由题意可得g (x )=2sin ⎣⎡⎦⎤12⎝⎛⎭⎫x +2π3+π6, 即g (x )=2cos 12x . ∵g ⎝⎛⎭⎫2α+π3=2cos ⎝⎛⎭⎫α+π6=65,∴cos ⎝⎛⎭⎫α+π6=35. 又α∈⎝⎛⎭⎫0,π2, ∴π6<α+π6<2π3, ∴sin ⎝⎛⎭⎫α+π6=45. ∴sin α=sin ⎣⎡⎦⎤⎝⎛⎭⎫α+π6-π6 =sin ⎝⎛⎭⎫α+π6cos π6-cos ⎝⎛⎭⎫α+π6sin π6 =45×32-35×12=43-310.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题组层级快练(二十四)1.(2016·北京西城期末)已知△ABC 中,a =1,b =2,B =45°,则A 等于( ) A .150° B .90° C .60° D .30°答案 D解析 由正弦定理,得1sinA =2sin45°,得sinA =12.又a<b ,∴A<B =45°.∴A =30°,故选D.2.(2016·安徽合肥模拟)在△ABC 中,A =60°,AB =2,且△ABC 的面积为32,则BC 的长为( ) A.32B. 3 C .2 3 D .2答案 B解析 因为S =12AB ·ACsinA =12×2×32AC =32,所以AC =1,所以BC 2=AB 2+AC 2-2AB·ACcos60°=3. 所以BC = 3.3.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知cos2A +cos2B =2cos2C ,则cosC 的最小值为( ) A.32B.22C.12 D .-12答案 C解析 由cos2A +cos2B =2cos2C ,得1-2sin 2A +1-2sin 2B =2(1-2sin 2C),即sin 2A +sin 2B =2sin 2C ,由正弦定理可得a 2+b 2=2c 2.由余弦定理可得c 2+2abcosC =2c 2,所以cosC =c 22ab =a 2+b 24ab ≥2ab 4ab =12,所以cosC 的最小值为12,故选C.4.已知△ABC 的三个内角的比是A ∶B ∶C =3∶2∶1,那么对应的三边之比a ∶b ∶c =( ) A .3∶2∶1 B.3∶2∶1 C.3∶2∶1 D .2∶3∶1答案 D解析 由题意知A =π2,B =π3,C =π6.由正弦定理知a ∶b ∶c =sinA ∶sinB ∶sinC =2∶3∶1,故选D.5.(2014·江西文)在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c.若3a =2b ,则2sin 2B -sin 2Asin 2A 的值为( ) A .-19B.13 C .1 D.72答案 D解析 由正弦定理可得2sin 2B -sin 2A sin 2A =2(sinB sinA )2-1=2(b a )2-1,因为3a =2b ,所以b a =32,所以2sin 2B -sin 2A sin 2A =2×(32)2-1=72. 6.(2016·江西七校一联)在△ABC 中,若sin(A -B)=1+2cos(B +C)sin(A +C),则△ABC 的形状一定是( ) A .等边三角形 B .不含60°的等腰三角形 C .钝角三角形 D .直角三角形 答案 D解析 sin(A -B)=1+2cos(B +C)sin(A +C)=1-2cosAsinB ,∴sinAcosB -cosAsinB =1-2cosAsinB ,∴sinAcosB +cosAsinB =1,即sin(A +B)=1,则有A +B =π2,故三角形为直角三角形.7.(2016·东北三校联考)已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且c -bc -a=sinAsinC +sinB ,则B =( )A.π6B.π4C.π3D.3π4答案 C解析 由sinA =a 2R ,sinB =b 2R ,sinC =c 2R ,代入整理得c -b c -a =ac +b ⇒c 2-b 2=ac -a 2,所以a 2+c 2-b 2=ac ,即cosB =12,所以B =π3,故答案为C.8.(2014·江西理)在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c ,若c 2=(a -b)2+6,C =π3,则△ABC 的面积是( )A .3 B.932 C.332 D .3 3答案 C解析 利用所给条件以及余弦定理整体求解ab 的值,再利用三角形面积公式求解. ∵c 2=(a -b)2+6,∴c 2=a 2+b 2-2ab +6. ① ∵C =π3,∴c 2=a 2+b 2-2abcos π3=a 2+b 2-ab.②由①②得-ab +6=0,即ab =6. ∴S △ABC =12absinC =12×6×32=332.9.(2014·新课标全国Ⅱ理)已知钝角三角形ABC 的面积是12,AB =1,BC =2,则AC =( )A .5 B. 5 C .2 D .1 答案 B解析 由题意可得12AB ·BC ·sinB =12,又AB =1,BC =2,所以sinB =22,所以B =45°或B =135°.当B =45°时,由余弦定理可得AC =AB 2+BC 2-2AB·BC·cosB =1,此时AC =AB =1,BC =2,易得A =90°,与“钝角三角形”条件矛盾,舍去.所以B =135°.由余弦定理可得AC =AB 2+BC 2-2AB·BC·cosB = 5.故选B.10.(2016·上海杨浦质量调研)设锐角△ABC 的三内角A ,B ,C 所对边的边长分别为a ,b ,c ,且a =1,B =2A ,则b 的取值范围为( ) A .(2,3) B .(1,3) C .(2,2) D .(0,2) 答案 A解析 由a sinA =b sinB =bsin2A ,得b =2cosA.π2<A +B =3A<π,从而π6<A<π3.又2A<π2, 所以A<π4,所以π6<A<π4,22<cosA<32,所以2<b< 3.11.在△ABC 中,三边长a ,b ,c 满足a 3+b 3=c 3,那么△ABC 的形状为( ) A .锐角三角形 B .钝角三角形 C .直角三角形 D .以上均有可能 答案 A解析 由题意可知c>a ,c>b ,即角C 最大,所以a 3+b 3=a·a 2+b·b 2<ca 2+cb 2,即c 3<ca 2+cb 2,所以c 2<a 2+b 2.根据余弦定理,得cosC =a 2+b 2-c 22ab >0,则0<C<π2,即三角形为锐角三角形.12.(2016·启东中学期末)在△ABC 中,若A =60°,AC =2,BC =3,则AB 等于________. 答案 1解析 ∵A =60°,AC =2,BC =3,设AB =x ,由余弦定理,得BC 2=AC 2+AB 2-2AC·ABcosA ,化简得x 2-2x +1=0,∴x =1,即AB =1.13.在△ABC 中,若AB =3,AC =1,B =30°,则△ABC 的面积为________. 答案34或32解析 如图所示,由正弦定理,得sinC =c·sinB b =32.而c>b ,∴C =60°或C =120°. ∴A =90°或A =30°. ∴S △ABC =12bcsinA =32或34.14.(2015·重庆文)设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且a =2,cosC =-14,3sinA =2sinB ,则c =________. 答案 4解析 由3sinA =2sinB 及正弦定理,得3a =2b ,所以b =32a =3.由余弦定理cosC =a 2+b 2-c 22ab,得-14=22+32-c 22×2×3,解得c =4.15.(2016·河北唐山一模)在△ABC 中,角A ,B ,C 的对边a ,b ,c 成等差数列,且A -C =90°,则cosB =________. 答案 34解析 ∵a ,b ,c 成等差数列,∴2b =a +c. ∴2sinB =sinA +sinC.∵A -C =90°,∴2sinB =sin(90°+C)+sinC. ∴2sinB =cosC +sinC.∴2sinB =2sin(C +45°). ①∵A +B +C =180°且A -C =90°,∴C =45°-B 2,代入①式中,2sinB =2sin(90°-B2).∴2sinB =2cos B2.∴4sin B 2cos B 2=2cos B 2.∴sin B 2=24.∴cosB =1-2sin 2B 2=1-14=34.16.对于△ABC ,有如下命题:①若sin2A =sin2B ,则△ABC 为等腰三角形;②若sinA =cosB ,则△ABC 为直角三角形;③若sin 2A +sin 2B +cos 2C<1,则△ABC 为钝角三角形.其中正确命题的序号是________.(把你认为所有正确的都填上) 答案 ③解析 ①sin2A =sin2B ,∴A =B ⇒△ABC 是等腰三角形,或2A +2B =π⇒A +B =π2,即△ABC 是直角三角形.故①不对.②sinA =cosB ,∴A -B =π2或A +B =π2.∴△ABC 不一定是直角三角形. ③sin 2A +sin 2B<1-cos 2C =sin 2C , ∴a 2+b 2<c 2.∴△ABC 为钝角三角形.17.(2015·新课标全国Ⅰ文)已知a ,b ,c 分别为△ABC 内角A ,B ,C 的对边,sin 2B =2sinAsinC. (1)若a =b ,求cosB ;(2)设B =90°,且a =2,求△ABC 的面积. 答案 (1)14(2)1解析 (1)由题设及正弦定理可得b 2=2ac. 又a =b ,可得b =2c ,a =2c. 由余弦定理可得cosB =a 2+c 2-b 22ac =14.(2)由(1)知b 2=2ac.因为B =90°,由勾股定理得a 2+c 2=b 2. 故a 2+c 2=2ac ,得c =a = 2.所以△ABC 的面积为1.18.(2016·湖北黄冈中学、黄石二中、鄂州高中三校联考)已知△ABC 的三内角A ,B ,C 所对的边分别是a ,b ,c ,向量m =(sinB ,1-cosB)与向量n =(2,0)的夹角θ的余弦值为12.(1)求角B 的大小;(2)若b =3,求a +c 的取值范围. 答案 (1)23π (2)(3,2]解析 (1)∵m =(sinB ,1-cosB),n =(2,0), ∴m ·n =2sinB ,|m |=sin 2B +(1-cosB )2=2-2cosB =2|sin B2|.∵0<B<π,∴0<B 2<π2.∴sin B2>0.∴|m |=2sin B2.又∵|n |=2,∴cos θ=m ·n |m |·|n |=2sinB 4sinB 2=cos B 2=12.∴B 2=π3,∴B =23π. (2)由余弦定理,得b 2=a 2+c 2-2accos 23π=a 2+c 2+ac =(a +c)2-ac ≥(a +c)2-(a +c 2)2=34(a +c)2,当且仅当a =c 时,取等号.∴(a +c)2≤4,即a +c ≤2. 又a +c>b =3,∴a +c ∈(3,2].1.(2016·衡水调研卷)在△ABC 中,AC =2,BC =1,cosC =34.(1)求AB 的值; (2)求sin(2A +C)的值. 答案 (1)2 (2)378解析 (1)由余弦定理,得 AB 2=AC 2+BC 2-2AC·BCcosC =22+12-2×2×1×34=2.∴AB = 2.(2)由cosC =34且0<C<π,得sinC =1-cos 2C =74.由正弦定理,得AB sinC =BC sinA ,解得sinA =BCsinC AB =148,所以cosA =528. 由二倍角公式,得sin2A =2sinAcosA =5716且cos2A =1-2sin 2A =916.故sin(2A +C)=sin2AcosC +cos2AsinC =378.2.(2013·新课标全国Ⅱ理)△ABC 的内角,A ,B ,C 的对边分别为a ,b ,c ,已知a =bcosC +csinB. (1)求B ;(2)若b =2,求△ABC 面积的最大值. 答案 (1)π4(2)2+1解析 (1)由已知及正弦定理,得sinA =sinBcosC +sinCsinB.①又A =π-(B +C),故sinA =sin(B +C)=sinBcosC +cosBsinC.②由①②和C ∈(0,π),得sinB =cosB. 又B ∈(0,π),所以B =π4.②△ABC 的面积S =12acsinB =24ac.由已知及余弦定理,得4=a 2+c 2-2accos π4.又a 2+c 2≥2ac ,故ac ≤42-2,当且仅当a =c 时,等号成立.因此△ABC 面积的最大值为2+1.3.如图所示,在△ABC 中,∠B =π3,AB =8,点D 在BC 边上,且CD =2,cos ∠ADC =17.(1)求sin ∠BAD ; (2)求BD ,AC 的长.答案 (1)3314(2)BD =3,AC =7解析 (1)在△ADC 中,因为cos ∠ADC =17,所以sin ∠ADC =437.所以sin ∠BAD =sin(∠ADC -∠B) =sin ∠ADCcosB -cos ∠ADCsinB =437×12-17×32=3314.(2)在△ABD 中,由正弦定理,得 BD =AB·sin ∠BADsin ∠ADB =8×3314437=3.在△ABC 中,由余弦定理,得 AC 2=AB 2+BC 2-2AB·BC·cosB =82+52-2×8×5×12=49.所以AC =7.4.(2012·安徽)设△ABC 的内角A ,B ,C 所对边的长分别为a ,b ,c ,且有2sinBcosA =sinAcosC +cosAsinC. (1)求角A 的大小;(2)若b =2,c =1,D 为BC 的中点,求AD 的长. 答案 (1)π3 (2)72解析 (1)方法一:由题设知,2sinBcosA =sin(A +C)=sinB ,因为sinB ≠0,所以cosA =12.由于0<A<π,故A =π3.方法二:由题设可知,2b ·b 2+c 2-a 22bc =a·a 2+b 2-c 22ab +c ·b 2+c 2-a 22bc ,于是b 2+c 2-a 2=bc ,所以cosA =b 2+c 2-a 22bc =12.由于0<A<π,故A =π3.(2)方法一:因为AD →2=(AB →+AC →2)2=14(AB →2+AC →2+2AB →·AC →)=14(1+4+2×1×2×cos π3)=74, 所以|AD →|=72,从而AD =72.方法二:因为a 2=b 2+c 2-2bccosA =4+1-2×2×1×12=3,所以a 2+c 2=b 2,B =π2.因为BD =32,AB =1,所以AD =1+34=72. 5.(2013·新课标全国Ⅰ理)如图所示,在△ABC 中,∠ABC =90°,AB =3,BC =1,P 为△ABC 内一点,∠BPC =90°.(1)若PB =12,求PA ;(2)若∠APB =150°,求tan ∠PBA. 答案 (1)72 (2)34解析 (1)由已知得∠PBC =60°,所以∠PBA =30°.在△PBA 中,由余弦定理,得PA 2=3+14-2×3×12cos30°=74,故PA =72.(2)设∠PBA =α,由已知得PB =sin α.在△PBA 中,由正弦定理,得3sin150°=sin αsin (30°-α).化简得3cos α=4sin α,所以tan α=34,即tan ∠PBA =34. 6.(2015·浙江文)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c.已知tan(π4+A)=2.(1)求sin2Asin2A +cos 2A的值;(2)若B =π4,a =3,求△ABC 的面积.答案 (1)25(2)9解析 (1)由tan(π4+A)=2,得tanA =13,所以sin2A sin2A +cos 2A =2tanA 2tanA +1=25. (2)由tanA =13,A ∈(0,π),得sinA =1010,cosA =31010.又由a =3,B =π4及正弦定理a sinA =bsinB ,得b =3 5.由sinC =sin(A +B)=sin(A +π4),得sinC =255. 设△ABC 的面积为S ,则S =12absinC =9.7.(2015·湖北文)设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,a =btanA. (1)证明:sinB =cosA ;(2)若sinC -sinAcosB =34,且B 为钝角,求A ,B ,C.答案 (1)略 (2)A =30°,B =120°,C =30° 解析 (1)由a =btanA 及正弦定理,得sinA cosA =a b =sinAsinB ,所以sinB =cosA.(2)因为sinC -sinAcosB =sin[180°-(A +B)]-sinAcosB =sin(A +B)-sinAcosB =sinAcosB +cosAsinB -sinAcosB =cosAsinB , 所以cosAsinB =34.由(1)sinB =cosA ,因此sin 2B =34.又B 为钝角,所以sinB =32,故B =120°. 由cosA =sinB =32知A =30°,从而C =180°-(A +B)=30°. 综上所述,A =30°,B =120°,C =30°.。
