arcsin的定义域和值域范围
反正弦函数

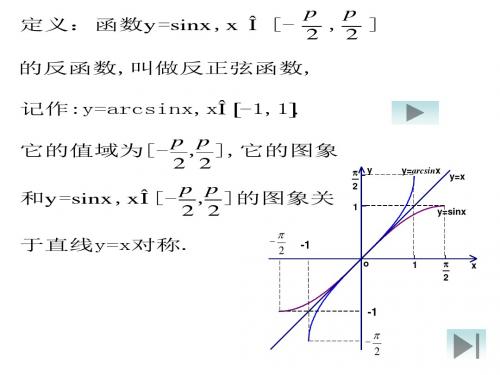
反正弦函数定义函数y=sinx,x∈[-π/2,π/2]的反函数叫做反正弦函数,记作x=arcsiny.习惯上用x表示自变量,用y表示函数,所以反正弦函数写成y=arcsinx.的形式请注意正弦函数y=sinx,x∈R因为在整个定义域上没有一一对应关系,所以不存在反函数。
反正弦函数只对这样一个函数y=sinx,x∈[-π/2,π/2]成立,这里截取的是正弦函数靠近原点的一个单调区间,叫做正弦函数的主值区间。
理解函数y=arcsinx中,y表示的是一个弧度制的角,自变量x是一个正弦值。
这点必须牢记性质根据反函数的性质,易得函数y=arcsinx的定义域[-1,1]arcsin图像值域[-π/2,π/2]是单调递增函数图像关于原点对称,是奇函数所以有arcsin(-x)=-arcsinx,注意x的取值范围:x∈[-1,1]导函数:(arcsinx)´=1/√(1-X²)反正弦恒等式sin(arcsinx)=x,x∈[-1,1](arcsinx)'=1/√(1-x^2)arcsinx=-arcsin(-x)函数图像我们知道这个结论函数f(x)的图像和它的反函数的图像关于直线y=x对称”,先画出函数y=sinx在[-π/2,π/2]上的图像,用平板玻璃或透明纸画好图像,翻转过来。
证明单调性在x,y∈[-π/2,π/2]x<y时:sinx-siny=2sin[(x-y)/2]cos[(x+y)/2]∵2sin[(x-y)/2]∈[-π,0]<>0cos[(x+y)/2]∈[-π,0]><0∴sinx-siny<0,sinx<siny.∴在-1<x<y<1时,arcsin x<arcsiny∴是增函数奇偶性∵y=sinx,y=x都是奇函数,∴y=arcsina也是奇函数应用临界角是最少的入射角使得全内反射发生。
反三角函数特殊值表

反三角函数特殊值表反三角函数是一种基本初等函数。
它是反正弦arcsinx,反余弦arccosx,反正切arctanx,反余切arccotx,反正割arcsecx,反余割arccscx这些函数的统称,各自表示其正弦、余弦、正切、余切,正割,余割为x的角。
反三角函数特殊值表反三角函数的分类1.反正弦函数正弦函数y=sinx在[-π/2,π/2]上的反函数,叫做反正弦函数。
记作arcsinx,表示一个正弦值为x的角,该角的范围在[-π/2,π/2]区间内。
定义域[-1,1],值域[-π/2,π/2]。
2.反余弦函数余弦函数y=cosx在[0,π]上的反函数,叫做反余弦函数。
记作arccosx,表示一个余弦值为x的角,该角的范围在[0,π]区间内。
定义域[-1,1],值域[0,π]。
3.反正切函数正切函数y=tanx在(-π/2,π/2)上的反函数,叫做反正切函数。
记作arctanx,表示一个正切值为x的角,该角的范围在(-π/2,π/2)区间内。
定义域R,值域(-π/2,π/2)。
4.反余切函数余切函数y=cotx在(0,π)上的反函数,叫做反余切函数。
记作arccotx,表示一个余切值为x的角,该角的范围在(0,π)区间内。
定义域R,值域(0,π)。
5.反正割函数正割函数y=secx在[0,π/2)U(π/2,π]上的反函数,叫做反正割函数。
记作arcsecx,表示一个正割值为x的角,该角的范围在[0,π/2)U(π/2,π]区间内。
定义域(-∞,-1]U[1,+∞),值域[0,π/2)U(π/2,π]。
6.反余割函数余割函数y=cscx在[-π/2,0)U(0,π/2]上的反函数,叫做反余割函数。
记作arccscx,表示一个余割值为x的角,该角的范围在[-π/2,0)U(0,π/2]区间内。
定义域(-∞,-1]U[1,+∞),值域[-π/2,0)U(0,π/2]。
arc反三角函数公式

反三角函数是一种基本初等函数。
它是反正弦arcsinx,反余弦arccosx,反正切arctanx,反余切arccotx,反正割arcsecx,反余割arccscx这些函数的统称,各自表示其反正弦、反余弦、反正切、反余切,反正割,反余割为x 的角。
反三角函数的分类反正弦函数:正弦函数y=sinx在[-π/2,π/2]上的反函数,叫做反正弦函数。
记作arcsinx,表示一个正弦值为x的角,该角的范围在[-π/2,π/2]区间内。
定义域[-1,1],值域[-π/2,π/2]。
反余弦函数:余弦函数y=cosx在[0,π]上的反函数,叫做反余弦函数。
记作arccosx,表示一个余弦值为x的角,该角的范围在[0,π]区间内。
定义域[-1,1],值域[0,π]。
反正切函数:正切函数y=tanx在(-π/2,π/2)上的反函数,叫做反正切函数。
记作arctanx,表示一个正切值为x的角,该角的范围在(-π/2,π/ 2)区间内。
定义域R,值域(-π/2,π/2)。
反余切函数:余切函数y=cotx在(0,π)上的反函数,叫做反余切函数。
记作arccotx。
表示一个余切值为x的角,该角的范围在(0,π)区间内。
定义域R,值域(0,π)。
反正割函数:正割函数y=secx在[0,π/2)U(π/2,π]上的反函数,叫做反正割函数。
记作arcsecx,表示一个正割值为x的角,该角的范围在[0,π/2)U(π/2,π]区间内。
定义域(-∞,-1]U[1,+∞),值域[0,π/2)U(π/2,π]。
反余割函数:余割函数y=cscx在[-π/2,0)U(0,π/2]上的反函数,叫做反余割函数。
记作arccscx,表示一个余割值为x的角,该角的范围在[-π/ 2,0)U(0,π/2]区间内。
定义域(-∞,-1]U[1,+∞),值域[-π/2,0)U (0,π/2]。
反三角函数的公式余角关系公式arcsin(x)+arccos(x)=π/2arctan(x)+arccot(x)=π/2arcsec(x)+arccsc(x)=π/2负数关系公式arcsin(-x)=-arcsin(x)arccos(-x)=π-arccos(x)arctan(-x)=-arctan(x)arccot(-x)=π-arccot(x)arcsec(-x)=π-arcsec(x)arcsec(-x)=-arcsec(x)倒数关系公式arcsin(1/x)=arccsc(x)arccos(1/x)=arcsec(x)arctan(1/x)=arccot(x)=π/2-arctan(x)(x>0) arccot(1/x)=arccot(x)=π/2-arccot(x)(x>0) arccot(1/x)=arctan(x)+π=3π/2-arccot(x)(x<0) arcsec(1/x)=arccos(x)arccsc(1/x)=arcsin(x)。
高中数学反三角函数公式总结

高中数学反三角函数公式总结如何学好高中数学高中数学解题方法与技巧怎样学好高中数学高中数学怎么学成绩提高快反三角函数的和差公式与对应的三角函数的和差公式没有关系y=arcsinx,定义域[-1,1],值域[-π/2,π/2]y=arccosx,定义域[-1,1],值域[0,π]y=arctanx,定义域-∞,+∞,值域-π/2,π/2y=arccotx,定义域-∞,+∞,值域0,πsinarcsinx=x,定义域[-1,1],值域[-1,1]arcsin-x=-arcsinx证明方法如下:设arcsinx=y,则siny=x,将这两个式子代入上式即可得其他几个用类似方法可得cosarccosx=x,arccos-x=π-arccosxtanarctanx=x,arctan-x=-arctanx反三角函数其他公式cosarcsinx=√(1-x^2)arcsin-x=-arcsinxarccos-x=π-arccosxarctan-x=-arctanxarccot-x=π-arccotxarcsinx+arccosx=π/2=arctanx+arccotxsinarcsinx=cosarccosx=tanarctanx=cotarccotx=x当x∈[-π/2,π/2]有arcsinsinx=xx∈[0,π],arccoscosx=xx∈-π/2,π/2,arctantanx=xx∈0,π,arccotcotx=xx>0,arctanx=π/2-arctan1/x,arccotx类似若arctanx+arctany∈-π/2,π/2,则arctanx+arctany=arctanx+y/1-xy最牛高考励志书,淘宝搜索《高考蝶变》购买!1.反函数的定义设函数y=fx的定义域是A,值域是C.我们从式子y=fx中解出x得到式子x=φy.如果对于y在C中的任何一个值,通过式子x=φy,x在A中都有唯一的值和它对应,那么式子x=φy叫函数y=fx的反函数,记作x=f-1y,习惯表示为y=f-1x.注意:函数y=fx的定义域和值域,分别是反函数y=f-1x的值域和定义域,例如:fx的定义域是[-1,+∞],值域是[0,+∞),它的反函数定义域为[0,+∞),值域是[-1,+∞。
常见函数解析式定义域值域的求法总结

常见函数解析式定义域值域的求法总结
一、常见函数解析式
1、二次函数
解析式:y=ax2+bx+c
定义域:全实数集
值域:ax2+bx+c的值
2、三角函数
解析式:y=sinx,y=cosx,y=tanx,y=cotx,y=secx,y=cscx
定义域:全实数集
值域:[-1,1]
3、反三角函数
解析式:y=arcsinx,y=arccosx,y=arctanx,y=arccotx,
y=arcsecx,y=arccscx
定义域:-[1,1],(-∞,+∞)
值域:[-π/2,π/2]
4、双曲函数
解析式:y=sinhx,y=coshx,y=tanhx,y=cothx,y=sechx,y=cschx 定义域:全实数集
值域:[-1,1]
5、对数函数
解析式:y=lgx,y=lnx
定义域:x>0
值域:(-∞,+∞)
6、指数函数
解析式:y=ex
定义域:全实数集
值域:(0,+∞)
二、定义域和值域的求法
1、函数的定义域
定义域的求法:一般取出函数的变量,求出它所在的域,如果有多个变量,一般要满足多个变量的取值范围,才能满足函数的定义域,比如:函数f(x,y)=x2+y2,则它的定义域就是x,y取得所有实数
2、函数的值域
值域的求法:一般取定义域,将变量取不同的值,将函数求出不同的值并且收集,得到函数的值域,比如:函数f(x)=x2+x+2,值域就是1,3,5,7……。
arcsinx的平方求导

arcsinx的平方求导在微积分学中,求导是一项基本且重要的技能。
求导的基本思想是通过对函数进行微小的变化来计算函数的变化率。
在本文中,我们将探讨一个特殊的函数——arcsinx的平方的求导方法。
首先,让我们回顾一下arcsinx函数的定义。
arcsinx函数是反正弦函数,其定义域为[-1,1],值域为[-π/2,π/2]。
当x的取值在[-1,1]之间时,arcsinx函数的值等于使得sinx=y的x值,其中y 为函数的自变量。
因此,我们可以将arcsinx函数表示为:y = arcsinx(x) <=> x = sin(y)现在,我们考虑arcsinx的平方函数,即:y = (arcsinx(x))^2我们的目标是求出y关于x的导数。
为了做到这一点,我们需要使用链式法则。
具体来说,我们可以将y表示为:y = f(g(x)) = g(x)^2其中,f(t) = t^2,g(x) = arcsinx(x)。
根据链式法则,y关于x的导数可以表示为:y' = f'(g(x)) * g'(x)其中,f'(t) = 2t,g'(x)是arcsinx函数的导数。
现在,我们需要计算g'(x)。
为了计算g'(x),我们可以使用反函数求导法则。
根据此法则,如果y = f(x)是一个可逆函数,那么y关于x的导数可以表示为: dy/dx = 1 / (dx/dy)因此,我们可以将g(x)表示为:g(x) = sin(y)然后,我们可以计算出:dg/dx = cos(y) * dy/dx现在,我们需要计算dy/dx。
为了做到这一点,我们可以使用导数的定义:dy/dx = lim(h->0) [(arcsinx(x+h) - arcsinx(x))/h] 根据arcsinx函数的定义,我们可以将上式表示为:dy/dx = lim(h->0) [(sin(arcsinx(x+h)) -sin(arcsinx(x)))/h]现在,我们可以使用sin函数的差公式来计算上式:sin(a+b) - sin(a) = 2cos[(a+b)/2] * sin[(b-a)/2] 应用到上式得:dy/dx = lim(h->0) [2cos(arcsinx(x+h)+arcsinx(x))/2 * sin(arcsinx(x+h)-arcsinx(x))/2h]根据arcsinx函数的定义,我们可以将cos(arcsinx(x))和sin(arcsinx(x))表示为:cos(arcsinx(x)) = sqrt(1-x^2)sin(arcsinx(x)) = x因此,我们可以将dy/dx表示为:dy/dx = lim(h->0) [2sqrt(1-(x+h)^2)*x -2sqrt(1-x^2)*(x+h)] / 2h化简得:dy/dx = lim(h->0) [sqrt(1-(x+h)^2) - sqrt(1-x^2)] / h 现在,我们可以将g'(x)表示为:g'(x) = cos(y) * dy/dx = cos(arcsinx(x)) * dy/dx =sqrt(1-x^2) * lim(h->0) [sqrt(1-(x+h)^2) - sqrt(1-x^2)] / h 化简得:g'(x) = -x / sqrt(1-x^2)现在,我们可以将y'表示为:y' = f'(g(x)) * g'(x) = 2g(x) * g'(x) = 2arcsinx(x) * (-x / sqrt(1-x^2))化简得:y' = -2x * arcsinx(x) / sqrt(1-x^2)因此,我们得到了arcsinx的平方函数关于x的导数。
反余弦函数与反正切函数
探究一
1-1
例1 求下列反三角函数的值
(1)arccos 1 2
(2)arccos( 3 ) 2
(3)arccos1
解 : (1) cos 1 , [0, ],arccos 1
3 23
23
解 : (2) cos 5 3 , 5 [0, ],arccos( 3 ) 5
1
x
2
-1
- 2
(1)反正弦函数y=arcsinx在区间[-1,1]上是增函数 (2)反正弦函数y=arcsinx在区间[-1,1]上的
图像关于原点对称,说明是奇函数
即arcsin(-x)=-arcsinx,x∈[-1,1]
(3)x
1, ymin
,x
2
1,
ymax
2
y 2
y y tan x, x ( , )
22
y
y arctan x, x R
2
0 x
2
2
0
x
2
根据定义可得:
cos(arccos x) x, x [1,1]
tan(arctan x) x, x R
反正弦函数,反余弦函数,反正切 函数都叫做反三角函数.
探究三
例2 求y cos x, x [ , 2 ]的反函数
解: y = cos x, x ? [p, 2p]
由诱导公式知 y = cos x = cos(- x)
= cos(2p - x) 又 x 蝄[p, 2p], 2p - x ? [0, p]
\ 2p - x = arccos y
\ x = 2p - arccos y
反三角函数定义域是什么 如何确定定义域

反三角函数定义域是什么如何确定定义域2021-09-15 14:16:06反三角函数是数学科目中比较重要的一个知识点,反三函数定义域是比较常考的,下面是相关的内容,大家快来复习吧!反三角函数定义域是什么如何确定定义域1反三角函数定义域1、反正弦函数y=arcsinx,表示一个正弦值为x的角,该角的范围在[-π/2,π/2]区间内。
定义域[-1,1] 。
2、反余弦函数y=arccosx,表示一个余弦值为x的角,该角的范围在[0,π]区间内。
定义域[-1,1] 。
3、反正切函数y=arctanx,表示一个正切值为x的角,该角的范围在(-π/2,π/2)区间内。
定义域R。
4、反余切函数y=arccotx,表示一个余切值为x的角,该角的范围在(0,π)区间内。
定义域R。
5、反正割函数y=arcsecx,表示一个正割值为x的角,该角的范围在[0,π/2)U(π/2,π]区间内。
定义域(-∞,-1]U[1,+∞)。
6、反余割函数y=arccscx,表示一个余割值为x的角,该角的范围在[-π/2,0)U(0,π/2]区间内。
定义域(-∞,-1]U[1,+∞)。
2什么是反三角函数反三角函数是一种基本初等函数。
它是反正弦arcsin x,反余弦arccos x,反正切arctan x,反余切arccot x,反正割arcsec x,反余割arccsc x 这些函数的统称,各自表示其反正弦、反余弦、反正切、反余切,反正割,反余割为x的角。
为了使单值的反三角函数所确定区间具有代表性,常遵循如下条件:1、为了保证函数与自变量之间的单值对应,确定的区间必须具有单调性;2、函数在这个区间最好是连续的(这里之所以说最好,是因为反正割和反余割函数是尖端的);3、为了使研究方便,常要求所选择的区间包含0到π/2的角;4、所确定的区间上的函数值域应与整函数的定义域相同。
这样确定的反三角函数就是单值的,为了与上面多值的反三角函数相区别,在记法上常将Arc中的A改记为a,例如单值的反正弦函数记为arcsin x。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
arcsin的定义域和值域范围
定义域和值域是数学中的一个基本概念,在求解函数的过程中也常常会用到。
其中,定义域指的是函数的取值范围,值域则是函数的取值范围。
下面就来讨论一下arcsin函数的定义域和值域范围。
arcsin函数,即反正弦函数,是一种常用的反三角函数,它的定义域为[-1,1],即x只能取-1到1之间的值,任何超出
这个范围的值都不在函数的定义域范围内,所以求解arcsin(x)时,x的取值范围只能是[-1,1]。
值域范围是[-π/2, π/2],即y只能取-π/2到π/2之间的值,任何超出这个范围的值都不在函数的值域范围内,所以求解arcsin(x)时,y的取值范围只能是[-π/2, π/2]。
因此,arcsin函数的定义域和值域范围分别是[-1,1]和[-π/2, π/2]。
arcsin函数在数学中有着广泛的应用,例如在求解三角函数、圆弧长度、曲线积分等问题中都会有所使用,这就要求我们必须牢记它的定义域和值域范围。
只有在函数定义域范围内的输入值才能得到函数定义域范围内的输出值,而超出定义域范围的输入值则会得到无意义的输出值,最终对正确求解函数会造成很大的影响。
总之,arcsin函数的定义域和值域范围是[-1,1]和[-π/2, π/2],在求解函数的过程中,一定要牢记这两个范围。
