曲线拟合的最小二乘法 共21页PPT资料
第3章曲线拟合的最小二乘法计算方法
最小二乘拟合,特别是多项式拟合,是最流行的数据处理 方法之一.它常用于把实验数据(离散的数据)归纳总结为经 验公式(连续的函数),以利于进一步的推演分析或应用.
1
结束
§3.2 线性拟合和二次拟合函数
1. 线性拟合
计 已知数据点为 ( xi , yi ), i 1,2,..., n
算 用直线 p( x) a bx作为近似曲线,均方误差为
计
i xi yi xi yi xi2 xi2yi xi3
xi4
0 3 5 15 9 45 27
81
算
1 5 2 10 25 50 125 625
方
2 6 1 6 36 36 216 1296
法
3 8 2 16 64 128 512 4096
课
4 10 4 40 100 400 1000 10000
件
Y ln y, A ln a Y A bx
8
i
xi
0
1
yi
Yi
15.3
2.7279
xi2
xiYi
1
2.7279
1
2
20.5
3.0204
4
6.0408
计
2
3
27.4
3.3105
9
9.9315
算
3
4
36.6
3.6000
16
14.4000
方
4
5
49.1
3.8939
25
19.4695
法
5
6
65.6
4
例1 设5组数据如下表,用一多项式对其进行拟合。
x 3 5 6 8 10
计
计算方法 第三章曲线拟合的最小二乘法20191103
§2 多项式拟合函数
例3.1 根据如下离散数据拟合曲线并估计误差
x 1 23 4 6 7 8 y 2 36 7 5 3 2
解: step1: 描点
7
*
step2: 从图形可以看出拟
6 5
*
合曲线为一条抛物线：
4
y c0 c1 x c2 x2
3 2 1
* *
* * *
step3: 根据基函数给出法
法
18
定理 法方程的解是存在且唯一的。
证： 法方程组的系数矩阵为
(0 ,0 ) (1 ,0 )
G
(0
,1
)
(1 ,1 )
(0 ,n ) (1 ,n )
(n ,0 )
(
n
,
1
)
(n ,n )
因为0( x),1( x), ...,n( x)在[a, b]上线性无关，
所以 G 0,故法方程 GC F 的解存在且唯一。
第三章 曲线拟合的最小二乘法
2
最小二乘拟合曲线
第三章 曲线拟合的最小二乘
2021/6/21
法
3
三次样条函数插值曲线
第三章 曲线拟合的最小二乘
2021/6/21
法
4
Lagrange插值曲线
第三章 曲线拟合的最小二乘
2021/6/21
法
5
一、数据拟合的最小二乘法的思想
已知离散数据： ( xi , yi ), i=0,1,2,…,m ,假设我们用函
便得到最小二乘拟合曲线
n
* ( x) a*j j ( x) j0
为了便于求解，我们再对法方程组的导出作进一步分析。
第三章 曲线拟合的最小二乘
西北工业大学 计算方法课件 第五章 曲线拟合的最小二乘法 西工大 nwpu
ϕ
r
2.70 480
2.00 670
1.61 830
1.20 1080
1.02 1260
变形为: 解:变形为: 1 = 1 − e cosϕ, 则有如下数据
r
p
p
1 y= r
0.370370 0.669131
0.50000 0.390731
0.621118
0.83333
0.980392
t = cosϕ
其矩阵形式为 Ax = b 方程组的系数矩阵和增广矩阵的秩不相等时， 当方程组的系数矩阵和增广矩阵的秩不相等时， 方程组无解，此时方程组称为矛盾方程组 矛盾方程组。 方程组无解，此时方程组称为矛盾方程组。对于 的矛盾方程组（ ），我 rankA＝n（A的秩为n）的矛盾方程组（N>n），我 们寻求其最小二乘意义下的解。 们寻求其最小二乘意义下的解。
k
(2)矩阵
∂2 f 2 ∂x1 P 0 2 ∂ f M = ∂x2∂x1 P 0 ⋮ 2 ∂ f ∂x ∂x n 1 P0
P 0
∂2 f ∂x1∂x2
P 0
∂2 f 2 ∂x2 P 0 ⋮ ∂2 f ∂xn∂x2 P
0
P 0 2 ∂ f ⋯ ∂x2∂xn P 0 ⋱ ⋮ ∂2 f ⋯ 2 ∂xn P 0 ∂2 f ⋯ ∂x1∂xn
1.最小二乘原则 1.最小二乘原则
由于矛盾方程组的精确解不存在， 由于矛盾方程组的精确解不存在，我们转而 寻求其某种意义下，即最小二乘意义下的解。 寻求其某种意义下，即最小二乘意义下的解。 n 令 δi = ∑aij xj −bi (i =1,2,⋯, N) 偏差。 称 δi 为偏差。 工程实际中的许多问题都可以归结为矛盾方程组， 工程实际中的许多问题都可以归结为矛盾方程组， 实际中需要寻求矛盾方程组的一组解， 实际中需要寻求矛盾方程组的一组解，以使得偏差的 N 尽可能地小。 绝对值之和 ∑δi 尽可能地小。为了便于分析
最小二乘法PPT课件
模型2（幂函数模型）
线性模型并未得到广泛的接受，要改进结果，能够 想到的自然首先是幂函数模型，即令L=kBa，对此式 取对数，得 到lnL=lnk+a lnB。将原始数据也取对数， 问题即转化了线性模型，可用最小二乘法求出参数。 几十年前英国和爱尔兰采用的比较举重成绩优劣 的 Austin公式：L′=L/B3/4就是用这一方法求得的。
67.5
135
146.1(5) 144.8(5) 144.7(6) 145.8(5)
75
145
145.0(6) 145.0(3) 145.0(5) 145.0(6)
42.5
162.5 151.3(1) 152.2(1) 153.5(1) 152.1(1)
体重 抓举成绩 (公斤) (公斤)
Austin( 幂函数)
经典公式
O’ Carroll
Vorobyev
52
105
138.2(7) 134.0(8) 139.7(8) 138.8(7)
56
117.5 146.3(4) 142.8(6) 145.7(4) 146.6(4)
60
125
147.8(3) 145.0(3) 146.2(3) 147.7(3)
和挺举。52 表中给出了1到09 1977年底为14止1 九个
重量级的56世界纪录。120.5
151
60
130
161.5
显然，运动67员.5 体重越大，他1能41举.5 起的重量也越1大80，但举重
成绩和运动75员体重到底是怎1样57关.5 系的，不同量1级95运动员的 成绩又如何比较优劣呢？运动成绩是包括生理条件、心理 因素等等众82多.5 相关因素共同1作70用的结果，要建20立7.精5 确的模
最小二乘法与曲线拟合(共24张PPT)
j 1
n
aNj
xj
bN
j1
2a1k
a2k
aNk
(
Ax
b)
Q
故 x1
Q
x2
Q
2
AT
(
Ax
b)
2(
AT
Ax
AT b )
xn
令
Q 0
(k 1,2,, n)
即
ATxAk x
AT b
〔*〕
因为rankA=n，故由引理2知，上式有唯一解。设
解为x1=a1, x2=a2,…, xn=an，记为点P0(a1,a2,…,an)，
或写为
其矩阵形式为
a11x1 a12x2 a1n xn b1 a21x1 a22x2 a2n xn b2
aN1x1 aN 2 x2 aNn xn bN
n
aij x j bi ( j 1,2,, N )
j 1
Ax b
当方程组的系数矩阵与增广矩阵的秩不相等时， 方程组无解，此时方程组称为矛盾方程组。对于 rankA＝n〔A的秩为n〕的矛盾方程组〔N>n〕，我 们寻求其最小二乘意义下的解。
从给定的一组试验数据出发，寻求函数的一个近似表 达式y= (x)，要求近似表达式能够反映数据的根本趋势 而又不一定过全部的点(xi,yi)，这就是曲线拟合问题，函 数的近似表达式y= (x)称为拟合曲线。本章介绍用最小 二乘法求拟合曲线。
§5.1 用最小二乘法求解矛盾方程组
一、矛盾方程组的定义
设线性方程组
3.最小二乘法解矛盾方程组
计算步骤：
〔1〕判断方程组的秩是否满足rankA=n？
〔2〕写出正那么方程组；
〔3〕求解正那么方程组，其解就是矛盾方程组 的最小二乘解。
第5章-1 曲线拟合(线性最小二乘法)讲解
求所需系数，得到方程： 29.139a+17.9b=29.7076 17.9a+11b=18.25
通过全选主元高斯消去求得：
a=0.912605
b=0.174034
所以线性拟合曲线函数为： y=0.912605x+0.174034
练习2
根据下列数据求拟合曲线函数： y=ax2+b
x 19 25 31 38 44 y 19.0 32.3 49.0 73.3 97.8
∑xi4 a + ∑xi2 b = ∑xi 2yi
∑xi2 a + n b = ∑yi
7277699a+5327b=369321.5 5327a+5b=271.4
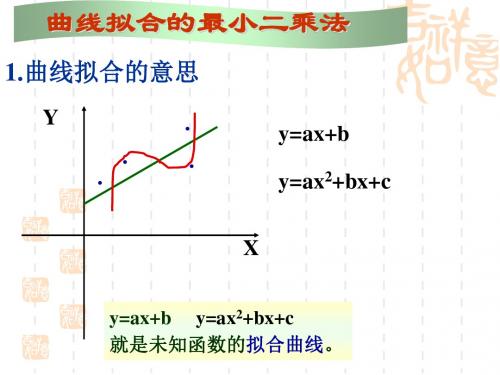
曲线拟合的最小二乘法
1.曲线拟合的意思
Y
.
.
.
.
y=ax+b y=ax2+bx+c
X
y=ax+b y=ax2+bx+c 就是未知函数的拟合曲线。
2最小二乘法原理
观测值与拟合曲线值误差的平方和为最小。
yi y0 y1 y2 y3 y4…… 观测值 y^i y^0 y^1 y^2 y^3 y^4…… 拟合曲线值
拟合曲线为： y=(-11x2-117x+56)/84
x
yHale Waihona Puke 1.61 1.641.63 1.66
1.6 1.63
1.67 1.7
1.64 1.67
1.63 1.66
1.61 1.64
1.66 1.69
1.59 1.62
曲线拟合的最小二乘法
插 值 含 义 的 图 像 表 示 :
Y
y pn (x )
插 值
X
《数值计算》课件 第四章 插值与拟合
拟合含义的图像表示:
Y
y p n (x )
曲线拟合
X
返回
《数值计算》课件 第四章 插值与拟合
Байду номын сангаас、直线拟合
假设所给数据点 ( xi , yi )( i 1, 2, , N )的分布 大致成一直线 .
yi
解之得
a 3.9374, b 7.4626 ,
因而拟合直线为 y 3.9374 7.4626 x
《数值计算》课件 第四章 插值与拟合
二、多项式拟合
问题 对于给定的一组数据 ( xi , yi )( i 1, 2, , m )求作n ( n m )次多项式 y aj x j ,
j 0 n
使总误差 j Q yi a j xi i 1 j 0
m n 2
为最小.
多 项 式 拟 合 问 题
上述拟合多项式的构造可归结为多元函数的极值问题 .
《数值计算》课件 第四章 插值与拟合
(1)最小二乘拟合多项式Pn ( x ) 的求解
利用多元函数的极值含义 （即由多元函数的极值的必要条件）可得 对
m
x
j i
yi
(j=0,1，…,n)
第四章 插值与拟合
m m m 具体化取 j=2 时所对应的等式为 : yi n m 1 x x i a0 i 0 m m i m m m i 03 i 0n 2 2 2 x m a m mx x a a x y x y 0 i 1 i n 1n i i i a1 i 2 i x xi i xi i 0 i 0 i i 0 0 i 0 i 0 i 0 i 0 这是关于系数 a 的线性方程组 a0 ， a1 ，…， m n m m x in x in 1 x i2 n 写成矩阵形式为 a n m n i 0 i 0 xi yi i 0 i 0
最小二乘法拟合曲线
最小二乘法（Least Squares Method，简称LSM）是一种常用的拟合曲线的方法。
它的基本思想是通过调整拟合曲线的参数使得拟合曲线与实际数据的误差的平方和最小。
过程如下：
1.定义拟合曲线的形式：根据要求拟合的曲线的类型和需要拟合的参数个数，定义拟合曲线的形式。
例如，如果要拟合一条一次函数，则可以使用y = ax + b的形式。
2.定义误差：设实际数据点的横纵坐标分别为（x1, y1）、（x2, y2）、…、（xn, yn），则对于每一个数据点，可以定义误差为真实数据点的纵坐标与拟合曲线的纵坐标之差的平方。
3.最小化误差的平方和：将所有数据点的误差平方和最小化，从而得到最优的拟合曲线。
4.求解参数：根据定义的拟合曲线形式和误差表达式，通过一定的数学方法求解出最优的拟合曲线的参数。
最小二乘法的优点是可以得到一条能够很好地描述实际数据的拟合曲线，并且可以很方便地求解拟合曲线的参数。
但是，最小二乘法也有一些缺点：对于存在异常值的数据，最小二乘法得到的拟合曲线可能不太准确。
在拟合曲线的形式不确定的情况下，最小二乘法可能得到不同的拟合曲线。
在拟合数据量较少的情况下，最小二乘法得到的拟合曲线可能不太稳定。
总的来说，最小二乘法是一种常用的拟合曲线方法，但是也要根据具体情况选择合适的拟合方法。
曲线拟合的最小二乘法
一、曲线拟合是什么？曲线拟合也就是求一条曲线,使数据点均在离此曲线的上方或下方不远处, 它既能反映数据的总体分布,又不至于出现局部较大的波动, 能反映被逼近函数的特性,使求得的逼近函数与已知函数从总体上来说其偏差按某种方法度量达到最小。
设函数y=f(x)在m个互异点的观测数据为求一个简单的近似函数φ(x)，使之“最好”地逼近f(x),而不必满足插值原则。
这时没必要取φ(xi) = yi, 而要使i=φ(xi)yi 总体上尽可能地小。
这种构造近似函数的方法称为曲线拟合,称函数y=φ(x)为经验公式或拟合曲线。
如下为一个曲线拟合示意图。
清楚什么是曲线拟合之后，我们还需要了解一个概念——残差。
曲线拟合不要求近似曲线严格过所有的数据点，但使求得的逼近函数与已知函数从总体上来说其偏差按某种方法度量达到总体上尽可能地小。
若令（1-1）则为残向量（残差）。
“使（1-1）尽可能地小”有不同的准则（1）残差最大值最小（2）残差绝对值和最小（绝对值的计算比较麻烦）（3）残差平方和最小（即最小二乘原则。
计算比较方便，对异常值非常敏感，并且得到的估计量具有优良特性。
）二、最小二乘法是什么？个人粗俗理解：按照最小二乘原则选取拟合曲线的方法,称为最小二乘法。
百度百科：最小二乘法（又称最小平方法）是一种数学优化技术。
它通过最小化误差的平方和寻找数据的最佳函数匹配。
利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。
最小二乘法还可用于曲线拟合。
其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
三、求解最小二乘法（包含数学推导过程）我们以最简单的线性模型来解释最小二乘法。
什么是线性模型呢？监督学习中，如果预测的变量是离散的，我们称其为分类（如决策树，支持向量机等），如果预测的变量是连续的，我们称其为回归。
回归分析中，n个自变量，且因变量和自变量之间是线性关系，则称为一/多元线性回归分析。
最小二乘法曲线拟合原理
最小二乘法曲线拟合原理最小二乘法曲线拟合原理是指用曲线来拟合已知数据点的一种优化算法，也叫“误差最小化法”，更多的称之为“最小二乘法”，简称LSM。
最小二乘法曲线拟合的应用范围很广，拟合分析复杂数据的应用越来越多。
最小二乘法曲线拟合的原理最小二乘曲线拟合的基本原理是构造一个最适合拟合给定数据点的函数，使拟合后函数拟合数据点和真实数据点之间的均方误差（SSE）最小。
均方误差是指观测值和拟合函数值之间的差的平方（SSE = SΣ(Yi - Xk)^2）。
均方误差最小，表明拟合函数就是最适合拟合数据的函数，而最小二乘法的基本思想就是求均方误差最小，即求解最优解的函数，这个函数就是最合适拟合给定数据点的曲线函数，即最小二乘法曲线拟合函数。
最小二乘法曲线拟合的应用最小二乘法曲线拟合最常见的应用是拟合曲线，以解决未知函数形式的问题。
拟合曲线可以使用曲线来估计一组数据，曲线拟合可以使得模型更准确地拟合数据，并且可以获得该曲线的未知参数。
如果数据不符合一个函数，可以使用自定义函数进行拟合，比如指数函数、sin函数、双曲线等。
最小二乘法也可以用于拟合回归模型，这是一种统计学中常用的方法，它可以用来推断大量随机变量的变化趋势，或者用来分析一个可能受其他变量影响的变量之间的关系。
最小二乘法也可以用于数值估计，比如最小二乘法用于数值拟合，用于数值拟合可以求出未知函数的参数，用于回归分析中，可以估计因变量受自变量影响的参数。
最小二乘法曲线拟合的缺点最小二乘法曲线拟合的最大缺点是其依赖性强：由于拟合的曲线函数有固定形式，因此无法拟合数据点的异常值，也无法拟合数据不具有规律性的情况；另外，最小二乘法曲线拟合也可能因过拟合导致拟合出的函数复杂度较高，从而影响精度。
总结最小二乘法曲线拟合原理指用曲线来拟合已知数据点的一种优化算法，它的基本原理是构造一个最适合拟合给定数据点的函数，使拟合后函数拟合数据点和真实数据点之间的均方误差最小。
曲线拟合--最小二乘法
曲线拟合--最小二乘法1：已知平面上四个点：（0，1）、（1，2.1）、（2，2.9）和（3，3.2），求出一条直线拟合这四个点，使得偏差平方和变为极小。
解：设直线方程为：0 1 0 01 2.1 1 2.12 2.9 4 5.83 3.2 9 9.6Sum=6 Sum=9.2 Sum=14 Sum=17.5 代入正规方程：，编程求解上方程组：>> eq1='14*A+6*B=17.5';>>eq2='6*A+4*B=9.2';>> [A,B]=solve(eq1,eq2,'A,B');>> disp(A)0.74>> disp(B)1.19所以直线方程为：2：已知数据如下表所示1 2 4 610 5 2 1试求（1）用抛物线拟合这些数据使得偏差平方和最小；（2）用型如的函数来拟合这些数据使得偏差平方和最小。
（3）比较这两种拟合结果。
解：（1）设抛物线方程为：1 10 1 1 1 10 102 5 4 8 16 10 20 4 2 16 64 256 8 326 1 36 216 1296 6 36 Sum=13 Sum=18 Sum=57 Sum=289 Sum=1569 Sum=34 Sum=98代入正规方程：得到系数A，B，C的方程组：编程求解上方程组：>>eq1='1569*A+289*B+57*C=98';>>eq2='289*A+57*B+13*C=34';>>eq3='57*A+13*B+4*C=18';>> [A,B,C]=solve(eq1,eq2,eq3,'A,B,C');>> disp(A); disp(B); disp(C)102/199-1048/1992848/199>> A=102/199; disp(A) 0.5126>> B=-1048/199; disp(B) -5.2663>> C=2848/199; disp(C) 14.3116所以得到抛物线的方程为：（2）设函数1 10 1 1 102 5 1/2 1/4 5/24 2 1/4 1/16 1/26 1 1/6 1/36 1/6Sum=13 Sum=18 Sum=23/12 Sum=193/144 Sum=79/6 得到系数A，B的方程组：编程求解上方程组：>> eq1='4*A+23*B/12=18';>>eq2='23*A/12+193*B/144=79/6';>> [A,B]=solve(eq1,eq2,'A,B');>> disp(A); disp(B)-160/243872/81>> A=-160/243; disp(A)-0.6584>> B=827/81; disp(B)10.2099所以得到的函数为：（3）比较（1）和（2）两种方法拟合的方程：编程画出抛物线的图像为：>> x=-2:0.1:12;>> y=0.5126*x.^2-5.2663*x+14.3116;plot(x,y);grid on（a）再编程画出的图像为：>> x=-2:0.1:12;>> y=-0.6584+10.2099*(x.^(-1));>> plot(x,y);grid on>> x=-1:0.01:1;>> y=-0.6584+10.2099*(x.^(-1));plot(x,y);grid on(b)比较两图像可知，图像（b）在点（0，0）处不连续。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
这种构造近似函数 的方法称为曲线拟合，P差(x”)
称为拟合函数
“使 i =P (xi) yi 尽可能地小”有不同的准
则
常见做法：
较复杂，
使 m 1im a|P x(xi)yi |最小
m
使 | P(xi ) yi | 最小 i1
m
使 | P(xi ) yi |2最小 i1
k 0
m
n
记： I(0,1, , n) [yi k k(xi)]2
i0
k0
则最小二乘问题，即求极小值问题 (1) 的解 * ( x ) ，也就是求
多元二次函数 I(0,1, ,n) 的极小值点 (0*,1*, ,n*) ，
使得： I (0 * ,1 * ,,n * ) 0 , m 1 ,i n , n R I (0 ,1 ,,n ) ( 2 )
{k (x)}kn0
在点列 {
x
i
}
m i
0
处的值向量组
{
k
}
n k
0
线性无关，则最小二乘问题存在唯一
n
解 *(x) k*k (x) ，其中 (0*,1*, ,n*)T为正规方程的解. k0
注: (1) 最小二乘问题的解与所选基函数无关。即对于n +1维连
续函数空间
第3章 曲线拟合的最小二乘法
1 拟合曲线
给出一组离散点，确定一个函数逼近原函数，插值是这样 的一种手段。在实际中，数据不可避免的会有误差，插值函数 会将这些误差也包括在内。
因此，我们需要一种新的逼近原函数的手段： ①不要求过所有的点（可以消除误差影响）； ②尽可能表现数据的趋势，靠近这些点。
第3章 曲线拟合的最小二乘法
(4)
序{列x i }
m i
0
确定，与离散点的函数{值y
(1 )
则称 * ( x ) 为离散数据 {xi , yi}im0 在子空间 中的最小二乘
拟合。
对于选定的基函数 {k (x)}kn0 ，定义中的拟合曲线即拟合模
n
型 (x)
kk (x) ，是待定参数
{
k
}n k0
的线性函数，故
k0
称之为线性最小二乘问题。
n
由于 (xi) kk(xi), i0,1 ,2, ,m
k0
即： (( 0 0,, 1 0)) (0,n)
(( 1 1,, 1 0)) (1,n)
(( n n,, 1 0)) 1 0((y y,, 1 0)) (n,n)n (y,n)
G
d
方程 G d 称之为正规方程 ( 或法方程 ) 。
即： n k mk (x i)l(x i) m y i l(x i) , l 0 ,1 , ,n ( 3 )
k 0 i 0
i 0
记 m +1 维向量:
y k ([y 0 k ,( y x 1 0 ,),,k y (m x ) 1 T ), , k(x m )]T, k 0 ,1 ,2 , ,n
称为均方误差。由于计算其最小值的方法容易实现而被广 泛采用。按均方误差达到极小构造拟合曲线的方法称为最 小二乘法。
1 线性拟合和最小二乘拟合
对于已知的 m +1 对离散数据
{xi
,
yi
}m i0
，记
a0 m ii n m {xi}, bm 0 ia x m {xi}
在连续函数空间C [a , b]中选定n +1个线性无关的基函数
问题：极值问题 (2) 的解是否存在，是否唯一，即最小二乘问 题 (1) 的解是否存在唯一？如果存在唯一，如何求之？
正规(法)方程和解的存在唯一性
由于 I(0,1, ,n) 是关于待定参数 0,1, ,n 的二次多
项式函数，所以 (2) 式有解的必要条件为：
I (0 , 1 , l ,n ) 2 i m 0 [ y i k n 0kk ( x i) ]l( x i) 0 ,l 0 ,1 , ,n
形式化描述
仍然是已知 x1 … xm ; y1 … ym, 求一个简单易算的近 似函数 P (x) 来拟合这些数据。
但是 ① m 很大；
② yi 本身是测量值，不准确，即 yi f (xi)
这时没必要取 P (xi) = yi , 而要使 i=P (xi) yi 总体上
尽可能地小。
称为“残
{k (x)}kn0 ，并记由它们生成的子空间为：
span{ 0(x),1(x), ,n(x)}
n
{ (x)|(x) kk(x), 0,1, ,n R } k0 n
若有 *(x) k*k(x) 使得 k0
m
m
i 0 [y i* (x i)]2 m (x i ) n i 0 [y i(x i)]2
其中
k
为函数
k
(x)
在点列
{
x
i
}
m i
0
处取值的向量，由向量
内积的定义，可得：
(k,l)m im0k(xi)l(xi), k,l 0,1, ,n (y,l)i0 yil(xi), l 0,1, ,n
故方程 (3) 可写成:
n
k(k,l)(y,l), l0,1, ,n
的任何基
{k (x)}kn0
，只要它们在点列
{
x
i
}
m i
0
处的值向量组
{
k
}
n k
0
线性无关，就可以用相应的正规方程求
解，从而得到相同的拟合曲线。(2)在离散点列{xi
,
yi
}m i0
中，对自变量序列
{
x
i
}
m i
0
没有特别
要求，既不需要有序，也可以重复。
(3) Gram矩阵G由子空间 的基函数 {k (x)}kn0 和自变量
由此可见，最小二乘问题存在唯一解的必要条件就是正规方程 的系数矩阵 G 非奇异。显然G 为对称矩阵，称为Gram 矩阵.
定理1：Gram 矩阵
G 非奇异的充要条件是向量组
{
k
}
n k
0
线
性无关。
定理2：对于已知的
m
+1
对离散数据
{xi
,
yi
}m i0
，选定
n
+1维连
续函数空间
，如果它有一组基