2015最小二乘法与曲线拟合
最小二乘曲线拟合excel
最小二乘曲线拟合excel在Excel中使用最小二乘法进行曲线拟合最小二乘法是数据分析中常用的一种方法，用于计算一个数学模型与试验数据之间的误差最小的拟合曲线。
在Excel中，我们可以使用最小二乘法进行曲线拟合，以获得一个最符合数据的曲线。
1. 数据导入首先，我们需要将拟合曲线所需的数据导入Excel中。
将独立变量和对应的因变量数据分别放在两列中。
示例数据如下所示：独立变量(X) 因变量(Y)1 3.52 6.83 8.94 12.55 16.76 19.22. 绘制散点图为了更直观地观察数据之间的关系，我们可以在Excel中绘制出散点图。
选中数据范围，然后点击“插入”选项卡中的“散点图”图标，选择所需的散点图类型即可。
3. 添加趋势线接下来，我们需要给散点图添加趋势线。
在Excel中，趋势线可以帮助我们更好地观察数据拟合的情况。
右击散点图上的任意一组数据点，选择“添加趋势线”选项。
在弹出的对话框中，选择“多项式”作为趋势线类型，并输入所需的阶数。
4. 计算拟合方程在添加趋势线之后，Excel会自动计算出拟合方程的系数，并在图表中显示。
我们可以通过以下步骤获取拟合方程：右击趋势线，选择“添加标签”，勾选“显示方程式”。
拟合方程将显示在图表中。
例如，一个二次多项式拟合的方程可能如下所示：y = ax^2 + bx + c。
其中a、b、c分别为二次、一次和常数项的系数。
5. 检验拟合效果拟合曲线的好坏可以通过判断拟合曲线与原始数据的偏离程度来评估。
在Excel中，我们可以通过计算决定系数（R²）来进行评估。
右击趋势线，选择“添加标签”，勾选“显示R²值”。
决定系数的范围从0到1，越接近1表示拟合效果越好。
6. 绘制拟合曲线我们也可以在Excel中绘制出拟合曲线，以便更直观地展示拟合效果。
选择刚才绘制的散点图，右击任意数据点，选择“选择数据”。
在弹出的对话框中，选择原始数据列和拟合曲线所对应的数据列，然后点击“确定”。
第三章 最小二乘法与曲线拟合
实例：考察某种纤维的强度与其拉伸倍数的关系,下表 是实际测定的24个纤维样品的强度与相应的拉伸倍数 是记录:
编 号 拉伸倍数 1 1.9 2 2 3 2.1 4 2.5 5 2.7 6 2.7 7 3.5 8 3.5 9 4 10 4 11 4.5 12 4.6
xi
强 度 1.4 1.3 1.8 2.5 2.8 2.5 3 2.7 4 3.5 4.2 3.5
n n 即 aij aik x j aik bi j 1 i 1 i 1 m
2
(k 1, 2,, m)
——（2）
称（2）为（1）的正规方程组（法方程组）。 （2）的解即为（1）的解，称此方法为最小二乘法。
例：利用最小二乘法求矛盾方程组： 2x +4y =11 3 x 5 y 3 x 2 y 6 4 x 2 y 14
曲线拟合问题：
要求近似曲线严格通过所给定的点——插值法 作近似曲线，考虑初值误差——最小二乘法
一、最小二乘原则：
1. 偏差：一般的，对给定的一组数据，不能要求 y = f(x)严格通过所有数据点( xi，yi )。若拟合曲线 为y ( x)，称 i ( xi ) yi为偏差(i =1,2, n)。
2 （3） 使偏差平方和最小，即 i 2 ( xi ) yi］ ［ 最小。 i 1 i 1 m m
※常用第三种方法，称为最小二乘原则。
二、矛盾方程组：
1、 a11 x1 a12 x2 a1m xm b1
a x a x a x b 21 1 22 2 2m m 2 ——（1） an1 x1 an 2 x2 anm xm bn
最小二乘法与曲线拟合(共24张PPT)
j 1
n
aNj
xj
bN
j1
2a1k
a2k
aNk
(
Ax
b)
Q
故 x1
Q
x2
Q
2
AT
(
Ax
b)
2(
AT
Ax
AT b )
xn
令
Q 0
(k 1,2,, n)
即
ATxAk x
AT b
〔*〕
因为rankA=n，故由引理2知，上式有唯一解。设
解为x1=a1, x2=a2,…, xn=an，记为点P0(a1,a2,…,an)，
或写为
其矩阵形式为
a11x1 a12x2 a1n xn b1 a21x1 a22x2 a2n xn b2
aN1x1 aN 2 x2 aNn xn bN
n
aij x j bi ( j 1,2,, N )
j 1
Ax b
当方程组的系数矩阵与增广矩阵的秩不相等时， 方程组无解，此时方程组称为矛盾方程组。对于 rankA＝n〔A的秩为n〕的矛盾方程组〔N>n〕，我 们寻求其最小二乘意义下的解。
从给定的一组试验数据出发，寻求函数的一个近似表 达式y= (x)，要求近似表达式能够反映数据的根本趋势 而又不一定过全部的点(xi,yi)，这就是曲线拟合问题，函 数的近似表达式y= (x)称为拟合曲线。本章介绍用最小 二乘法求拟合曲线。
§5.1 用最小二乘法求解矛盾方程组
一、矛盾方程组的定义
设线性方程组
3.最小二乘法解矛盾方程组
计算步骤：
〔1〕判断方程组的秩是否满足rankA=n？
〔2〕写出正那么方程组；
〔3〕求解正那么方程组，其解就是矛盾方程组 的最小二乘解。
最小二乘法曲线拟合原理
最小二乘法曲线拟合原理最小二乘法曲线拟合是一个重要的数值分析方法，它是通过最小二乘法对样本点与直线或曲线之间的关系进行拟合和分析，从而估算出一个函数的一组参数。
最小二乘法曲线拟合是一种经典的数值分析方法，可以用来拟合函数和曲线，估算出参数，预测数据，分析函数，优化模型，甚至可以分析复杂多变量函数。
最小二乘法曲线拟合的核心方法是使用最小二乘法把拟合的曲线拟合到观察到的数据，通过求解方程的最小二乘法，把一系列的观察数据点拟合为最小二乘法曲线，计算出拟合曲线的最佳系数，满足拟合效果的最佳拟合曲线。
最小二乘法曲线拟合的核心目标是通过计算拟合曲线的最小均方误差(SSE)、平均均方误差(MSE)、最大均方误差(MAXE)等方法，使拟合曲线与观察数据点之间的差距最小，从而求解出最佳拟合曲线系数。
最小二乘法曲线拟合具有很强的解析性，可以用数学计算方法快速求解，可以满足各种不同应用场景的需求，因而被广泛应用于科学研究、工程设计、市场分析等领域。
最小二乘法曲线拟合最常见的应用场景有：根据观察数据拟合和估计函数的参数；分析函数的性质；优化模型的能力；预测数据等等。
当应用最小二乘法拟合函数时，首先需要把观察数据用直线或曲线拟合，然后使用极小化残差平方和的方法，来求解参数，这是一个典型的最优化问题，利用一般最优化算法来求解，如梯度下降算法、牛顿法等。
此外，在应用最小二乘法曲线拟合的过程中，还可以考虑几种情况，比如样本数据受到误差的影响，具有某种偏差性；偏差是否服从正态分布；样本数据的分布是否同分布；拟合曲线的拟合是否收敛，参数计算是否准确等等。
总之，最小二乘法曲线拟合是一种重要的数值分析方法，可以用来拟合函数和曲线、估算参数、预测数据、优化模型等。
在应用最小二乘法曲线拟合时，需要考虑一些影响因素，比如样本数据受到误差的影响、偏差是否服从正态分布等，因此，它是一种有效的数值分析方法。
第5章-1 曲线拟合(线性最小二乘法)讲解
求所需系数，得到方程： 29.139a+17.9b=29.7076 17.9a+11b=18.25
通过全选主元高斯消去求得：
a=0.912605
b=0.174034
所以线性拟合曲线函数为： y=0.912605x+0.174034
练习2
根据下列数据求拟合曲线函数： y=ax2+b
x 19 25 31 38 44 y 19.0 32.3 49.0 73.3 97.8
∑xi4 a + ∑xi2 b = ∑xi 2yi
∑xi2 a + n b = ∑yi
7277699a+5327b=369321.5 5327a+5b=271.4
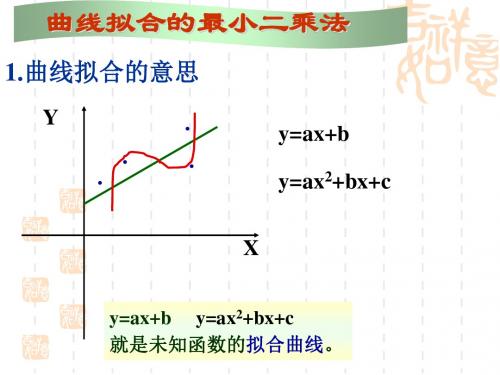
曲线拟合的最小二乘法
1.曲线拟合的意思
Y
.
.
.
.
y=ax+b y=ax2+bx+c
X
y=ax+b y=ax2+bx+c 就是未知函数的拟合曲线。
2最小二乘法原理
观测值与拟合曲线值误差的平方和为最小。
yi y0 y1 y2 y3 y4…… 观测值 y^i y^0 y^1 y^2 y^3 y^4…… 拟合曲线值
拟合曲线为： y=(-11x2-117x+56)/84
x
yHale Waihona Puke 1.61 1.641.63 1.66
1.6 1.63
1.67 1.7
1.64 1.67
1.63 1.66
1.61 1.64
1.66 1.69
1.59 1.62
最小二乘法拟合原理
最小二乘拟合在物理实验中经常要观测两个有函数关系的物理量。
根据两个量的许多组观测数据来确定它们的函数曲线，这就是实验数据处理中的曲线拟合问题。
这类问题通常有两种情况：一种是两个观测量x 与y 之间的函数形式已知，但一些参数未知，需要确定未知参数的最佳估计值；另一种是x 与y 之间的函数形式还不知道，需要找出它们之间的经验公式。
后一种情况常假设x 与y 之间的关系是一个待定的多项式，多项式系数就是待定的未知参数，从而可采用类似于前一种情况的处理方法。
一、最小二乘法原理在两个观测量中，往往总有一个量精度比另一个高得多，为简单起见把精度较高的观测量看作没有误差，并把这个观测量选作x ，而把所有的误差只认为是y 的误差。
设x 和y 的函数关系由理论公式y ＝f （x ；c 1，c 2，……c m ） （0-0-1）给出，其中c 1，c 2，……c m 是m 个要通过实验确定的参数。
对于每组观测数据（x i ，y i ）i ＝1，2，……，N 。
都对应于xy 平面上一个点。
若不存在测量误差，则这些数据点都准确落在理论曲线上。
只要选取m 组测量值代入式（0-0-1），便得到方程组y i ＝f （x ；c 1，c 2，……c m ） （0-0-2）式中i ＝1，2，……，m.求m 个方程的联立解即得m 个参数的数值。
显然N<m 时，参数不能确定。
在N>m 的情况下，式（0-0-2）成为矛盾方程组，不能直接用解方程的方法求得m 个参数值，只能用曲线拟合的方法来处理。
设测量中不存在着系统误差，或者说已经修正，则y 的观测值y i 围绕着期望值 <f （x ；c 1，c 2，……c m ）> 摆动，其分布为正态分布，则y i 的概率密度为()()[]⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧--=22212,......,,;exp 21i mi i i i c c c x f y y p σσπ,式中i σ是分布的标准误差。
曲线最小二乘法拟合
最小二乘法拟合曲线算法1、概述给定数据点P(x i ,y i )，其中i=1,2,…,n 。
求近似曲线y= φ(x)。
并且使得近似曲线与y=f(x)的偏差最小。
近似曲线在点pi 处的偏差δi = φ(x i )-y ，i=1,2,...,n 。
按偏差平方和最小的原则选取拟合曲线，这种方法为最小二乘法，偏差平方和公式为：min σ2 = (φ(x i −y i ))2ni =1n i =12、推导过程1）设拟合多项式为：y = a 0+ a 1x +⋯+a k x k2）各点到这条曲线的距离之和，即偏差平方如下:R 2= [y i −(a 0+ a 1x +⋯+a k x k )]2ni =13）多项式系数为学习对象，为了求得符合条件的系数值，对上面等式的a i 分别求导，得：−2 y i − a 0+ a 1x +⋯+a k x k =0ni=1−2 y i − a 0+ a 1x +⋯+a k x k x =0ni=1……−2 y i − a 0+ a 1x +⋯+a k x k x k =0ni=14）将等式移项化简，得：a 0+ a 1x +⋯+a k x k = y i ni =1n i =1a 0+ a 1x +⋯+a k x k x = y i x ni =1n i =1……a 0+ a 1x +⋯+a k x k x k = y i x k ni =1n i =15）依上式得矩阵为：x i0 ni=1⋯x i kni=1⋮⋱⋮x i k ni=1⋯x i2kni=1a0⋮a k=y i x i0ni=1⋮y i x i kni=1上边等式左边为1+K阶对称矩阵，解此矩阵方程即可得到曲线系数a k6）对于AX=B，A为对称矩阵，对称矩阵可以分解为一个下三角矩阵、一个上三角矩阵（下三角矩阵的转置）和一个对角线矩阵相乘。
即A=LDL T所以AX=LDL T X=B，令DL T X=Y -> LY=B，其中L为下三角矩阵，且已知，可求出Y。
【最新精选】标准曲线的最小二乘法拟合和相关系数
【最新精选】标准曲线的最小二乘法拟合和相关系数标准曲线的最小二乘法拟合与相关系数尹情胜标准曲线的最小二乘法拟合和相关系数(合肥工业大学控释药物研究室尹情胜)1 目的用最小二乘法拟合一组变量(，，i,1-n)之间的线性方程(y,ax+b)，表示两变量间的函数关系;(开创者:德国数学家高斯)一组数据(，，i,1-n)中，两变量之间的相关性用相关系数(R)来表示。
(开创者:英国统计学家卡尔?皮尔逊)2 最小二乘法原理用最小二乘法拟合线性方程时，其目标是使拟合值()与实测值()差值的平方和(Q)最小。
式(1) 3 拟合方程的计算公式与推导当Q最小时，;得到式(2)、式(3):式(2)式(3)由式(3)和式(4)，得出式(4)和式(5):式(4)式(5) E-mail:595771829@ 1 / 15标准曲线的最小二乘法拟合与相关系数尹情胜式(4)乘以n，式(5)乘以，两式相减并整理得斜率a:斜率 (k,xy,xx，n*积和-和积)式(6)截距b的计算公式为公式(5)，也即:截距 b,(y-x),n，差平均差)式(7)E-mail:595771829@ 2 / 15标准曲线的最小二乘法拟合与相关系数尹情胜 4 相关系数的意义与计算公式相关系数(相关系数的平方称为判定系数)是用以反映变量之间相关关系密切程度的统计指标。
相关系数(也称积差相关系数)是按积差方法计算，同样以两变量与各自平均值的离差为基础，通过两个离差相乘来反映两变量之间相关程度;着重研究线性的单相关系数。
相关系数r取值在-1到1之间。
r = 0时，称x,y不相关; | r | = 1时，称x,y完xyxyxy全相关，此时，x,y之间具有线性函数关系; | r | < 1时，X的变动引起Y的部分变动，xyr的绝对值越大，x的变动引起y的变动就越大， |r | > 0.8时称为高度相关，当0.5< | xyxyr|<0.8时称为显著相关，当 0.3<| r |<0.5时，成为低度相关，当 | r | < 0.3时，称为xyxyxy无相关。
利用最小二乘法求解拟合曲线
实验三 函数逼近一、实验目标1. 掌握数据多项式拟合的最小二乘法。
2. 会求函数的插值三角多项式。
二、实验问题（1）由实验得到下列数据jx 0.00.10.20.30.50.81.0jy 1.00.410.500.610.912.022.46试对这组数据进行曲线拟合。
（2）求函数在区间上的插值三角多项式。
()2cos f x x x =[,]ππ-三、实验要求1. 利用最小二乘法求问题（1）所给数据的3次、4次拟合多项式，画出拟合曲线。
2. 求函数在区间上的16次插值三角多项式，并画出插值多项()2cos f x x x =[,]ππ-式的图形，与的图形比较。
()f x 3.对函数，在区间上的取若干点，将函数值作为数据进行适()2cos f x x x =[,]ππ-当次数的最小二乘多项式拟合，并计算误差，与上题中的16次插值三角多项式的结果进行比较。
《数值分析》实验报告【实验课题】利用最小二乘法求上述问题所给数据的2次，3次、4次拟合多项式，画出拟合曲线【实验目标】（1）加深对用最小二乘法求拟合多项式的理解（2）学会编写最小二乘法的数值计算的程序；【理论概述与算法描述】在函数的最佳平方逼近中,如果只在一组离散点集()[,]f x C a b ∈()f x 上给出，这就是科学实验中经常见到的实验数据{,0,1,,}i x i m =⋅⋅⋅的曲线拟合，这里，要求一个函数{(,),0,1,,}i i x y i m =⋅⋅⋅(),0,1,,i i y f x i m ==⋅⋅⋅与所给数据拟合，若记误差*()y S x ={(,),0,1,,}i i x y i m =⋅⋅⋅,,设是上*()(0,1,,)ii i S x y i m δ=-=⋅⋅⋅()01,,,Tm δδδδ=⋅⋅⋅01(),(),,()n x x x ϕϕϕ⋅⋅⋅[,]C a b 的线性无关函数族，在中找一个函数，使误差平01{(),(),,()}n span x x x ϕϕϕϕ=⋅⋅⋅*()S x 方和|2222*2()0|||[()][()]min mmmii i i i S x i i i S x y S x y ϕδδ∈=====-=-∑∑∑这里0011|()()()()()n n S x a x a x a x n m ϕϕϕ=++⋅⋅⋅+<这就是一般的最小二乘逼近，用几何语言说，就称为曲线拟合的最小二乘法。
最小二乘法拟合原理
最小二乘法拟合原理最小二乘法（Least Squares Method）是一种常用的线性回归分析方法，用于拟合数据点到一个理论模型的直线或曲线的原理。
它的目标是通过最小化实际数据点与拟合曲线之间的垂直距离（也称为残差）的平方和来找到最佳的拟合曲线。
假设我们有一个包含n个数据点的数据集，其中每个数据点的坐标可以表示为（xi，yi）。
我们希望找到一个模型y=f(x,θ)，其中x是自变量，θ是模型的参数，使得对于每个数据点，模型预测的y值与实际的观测值之间的差异最小化。
yi = yi_true + ei以线性回归为例，模型可以表示为y=θ0+θ1x，其中θ0和θ1是要估计的参数。
我们的目标是找到最佳的θ0和θ1，使得所有数据点的残差平方和最小。
残差可以定义为：ei = yi - (θ0 + θ1xi)为了最小化残差平方和，我们需要对残差平方和进行求导，并令导数等于零。
这样一来，我们就能得到使得残差平方和最小的参数估计值。
对于线性回归而言，最小二乘法的公式可以写为：θ1 = (sum(xi - x_mean)(yi - y_mean))/(sum(xi - x_mean)^2)θ0 = y_mea n - θ1x_mean其中，x_mean和y_mean分别是自变量和因变量的均值。
需要注意的是，最小二乘法只是一种估计参数的方法，它没有办法告诉我们模型是否真实有效。
为了评估拟合效果，我们还需要使用一些指标，如决定系数（coefficient of determination），来评估拟合曲线与数据之间的拟合程度。
总结起来，最小二乘法是一种通过最小化实际数据点与拟合曲线之间的垂直距离的平方和来找到最佳的拟合曲线的方法。
它的原理建立在数据具有随机误差，且服从独立同分布的正态分布的假设上。
通过最小二乘法，我们可以估计出模型的参数，以及评估拟合程度，从而对数据进行分析、预测与优化。
最小二乘法的曲线拟合问题
量看作没有误差，并把这个观测量选作 x，而把所有的误差只认为是 y 的误差。设 x 和 y 的
函数关系由理论公式
y＝f（x；c1，c2，……cm）
（3-3-1）
给出，其中 c1，c2，……cm 是 m 个要通过实验确定的参数。对于每组观测数据（xi，yi）
i＝1，2，……，N。都对应于 xy 平面上一个点。若不存在测量误差，则这些数据点都准确
曲线拟合（5）
最小二乘法的曲线拟合问题 ——曲线拟合（5）
目录
1 绪论………………………..……………………………….………………………….1 1.1 课题研究的背景和方法………………………………………………………………1
2 曲线拟合……………………………….…………………………………...1 2.1 曲线拟合………………………………………………………...…………………….1 2.2 常用函数………………………………………………………...…………………….1
根据式（3-3-8）的要求，应有
a 0 i N 1 y i a 0 a 1 x i 2 a a ˆ 2 i N 1 y i a ˆ 0 a ˆ 1 x i 0 , a 1 i N 1 y i a 0 a 1 x i 2 a a ˆ 2 i N 1 y i a ˆ 0 a ˆ 1 x i 0 .
在 X 上满足 Haar 条件，此时(3.1.5)的解存在唯
从而得到最小二乘拟合曲线
可以证明对
，有
(3.1.6)
曲线拟合（5）
故(3.1.6)得到的 均方误差为
即为所求的最小二乘解.它的平方误差为 (3.1.7)
在最小二乘逼近中，若取
，则
，表示为
(3.1.8)
python曲线拟合的最小二乘法
Python曲线拟合的最小二乘法引言在实际应用中，我们经常需要通过已知数据去拟合一条曲线，以便更好地理解数据的趋势和规律。
曲线拟合是一种常用的数据分析方法，而最小二乘法则是其中最常见和重要的一种技术手段。
本文将介绍如何使用Python进行曲线拟合，并着重讨论最小二乘法的应用和原理。
1. 什么是最小二乘法？最小二乘法是一种数学优化方法，用于确定一组数据和一个数学关系式之间的最优拟合曲线。
具体来说，对于给定的一组数据点，最小二乘法的目标是找到一个数学模型，使得该模型计算出的值与实际观测值之间的残差平方和最小。
2. 最小二乘法的原理考虑一个简单的情况，假设我们有一组数据点(x1, y1), (x2, y2), … , (xn, yn)，我们想要用一条直线y = ax + b来拟合这些数据。
最小二乘法的目标是找到最优的参数a和b，使得拟合后的直线与数据点之间的残差平方和最小。
为了求解最优参数，可以通过最小化残差平方和的方式来进行。
具体来说，可以定义一个损失函数，即残差平方和的平均值，如下所示：J(a, b) = (1/n) * Σ(yi - (axi + b))^2其中，n表示数据点的个数，xi和yi分别表示第i个数据点的横坐标和纵坐标。
通过最小化这个损失函数，可以得到最优的参数a和b。
对于更复杂的情况，比如需要拟合高阶曲线，最小二乘法的原理类似，只是拟合模型不同。
还可以通过增加更多的参数来适应更复杂的曲线形状。
3. 使用Python进行最小二乘法曲线拟合在Python中，使用最小二乘法进行曲线拟合非常方便，可以使用scipy库的optimize模块中的curve_fit函数来实现。
我们需要导入必要的库：import numpy as npfrom scipy.optimize import curve_fitimport matplotlib.pyplot as plt我们可以定义拟合的数学模型。
以拟合一条指数函数为例，定义一个指数函数的模型：def func(x, a, b, c):return a * np.exp(-b * x) + c接下来，我们可以生成一组测试数据：x = np.linspace(0, 4, 50)y = func(x, 2.5, 1.3, 0.5)使用curve_fit函数进行曲线拟合：params, params_covariance = curve_fit(func, x, y)我们可以绘制原始数据和拟合曲线的图像：plt.plot(x, y, 'bo', label='Original Data')plt.plot(x, func(x, params[0], params[1], params[2]), 'r-', label='Fitted Curv e')plt.legend()plt.show()4. 个人观点和总结最小二乘法在数据分析和曲线拟合中被广泛应用，其原理简单而有效。
最小二乘法曲线拟合实验报告
竭诚为您提供优质文档/双击可除最小二乘法曲线拟合实验报告篇一：实验3曲线拟合的最小二乘法实验三曲线拟合的最小二乘法1、实验目的：在科学研究与工程技术中，常常需要从一组测量数据出发，寻找变量的函数关系的近似表达式，使得逼近函数从总体上与已知函数的偏差按某种方法度量能达到最小而又不一定过全部的点。
这是工程中引入最小二曲线拟合法的出发点。
充分掌握：1．最小二乘法的基本原理；2．用多项式作最小二乘曲线拟合原理的基础上，通过编程实现一组实验数据的最小二乘拟合曲线。
2、实验要求:1)认真分析题目的条件和要求，复习相关的理论知识，选择适当的解决方案和算法；2)编写上机实验程序，作好上机前的准备工作；3)上机调试程序，并试算各种方案，记录计算的结果（包括必要的中间结果）；4)分析和解释计算结果；5)按照要求书写实验报告；3、实验内容：1)给定数据如下：x：0.15，0.4，0.6，1.01，1.5，2.2，2.4，2.7，2.9，3.5，3.8，4.4，4.6，5.1，6.6，7.6；y：4.4964，5.1284，5.6931，6.2884，7.0989，7.5507，7.5106，8.0756，7.8708，8.2403，8.5303，8.7394，8.9981，9.1450，9.5070，9.9115；试作出幂函数拟合数据。
2)已知一组数据：x：0，0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9，1y：-0.447，1.978，3.28，6.16，7.08，7.34，7.66，9.56，9.48，9.30，11.2；试用最小二乘法求多项式函数，使与此组数据相拟合。
4、题目：曲线拟合的最小二乘法5、原理：从整体上考虑近似函数同所给数据点(i=0,1,…,m)误差(i=0,1,…,m)的大小，常用的方法有以下三种：一是误差(i=0,1,…,m)绝对值的最大值，即误差向量的∞—范数；二是误差绝对值的和，即误差向量r的1—范数；三是误差平方和的算术平方根，即误差向量r的2—范数；前两种方法简单、自然，但不便于微分运算，后一种方法相当于考虑2—范数的平方，因此在曲线拟常采用误差平方和来度量误差(i=0，1，…，m)的整体大小.。
最小二乘法拟合曲线公式
最小二乘法拟合曲线公式
最小二乘法是一种常用的数学方法，可以用来拟合一条曲线，使得曲线上的点与实际观测值的误差最小化。
最小二乘法拟合曲线的公式为：
y = a + bx
其中，y 是因变量，x 是自变量，a 和 b 是拟合曲线的系数。
最小二乘法通过最小化误差平方和来确定 a 和 b 的值，即：
b = (n∑xy - ∑x∑y) / (n∑x^2 - (∑x)^2)
a = (∑y - b∑x) / n
其中，n 是数据点的个数，∑表示求和符号，x 和 y 分别表示自变量和因变量的值。
拟合曲线的误差可以通过计算残差平方和来评估，即：
SSR = ∑(y - )^2
其中，y 是实际观测值，是拟合曲线的预测值。
最小二乘法拟合曲线的优点在于可以用简单的数学公式表示，易于理解和应用。
- 1 -。
最小二乘法 拟合曲线
使用最小二乘法拟合直线数据
最小二乘法是一种拟合曲线或直线的常用方法。
它通过最小化误差的平方和来找到最佳拟合参数。
假设我们有一组点(x, y)，我们希望找到一条曲线y = f(x) 来拟合这些点。
最小二乘法的基本思想是：找到一条曲线，使得所有点到这条曲线的垂直距离的平方和最小。
最小二乘法通常用于线性回归和非线性回归。
在非线性回归中，我们通常需要使用一些优化算法来找到最佳参数。
下面是一个简单的Python 代码示例，演示如何使用最小二乘法拟合一条直线：
import numpy as np
import matplotlib.pyplot as plt
# 生成一组随机数据
x = np.random.rand(50)
y = 2 * x + 1 + np.random.randn(50) * 0.1
# 使用最小二乘法拟合直线
p, _, _, _ = np.polyfit(x, y, 1, method='leastsq')
# 绘制原始数据和拟合直线
plt.scatter(x, y, color='blue')
plt.plot(x, p[0] * x + p[1], color='red')
plt.show()
在这个例子中，我们首先生成了一组随机数据(x, y)。
然后，我们使用np.polyfit函数来拟合一条直线。
最后，我们将原始数据和拟合直线绘制在同一张图上。
第五章 最小二乘法和曲线拟合
i 1 n
1 1 y f ( xi , C ) 2 exp{ [ i ]} 2 i 2 i 1 (5.1.7)
1 n [ yi f ( xi , C )]2 exp{ } n2 2 (2 ) 1... n 2 i 1 i
最大似然法要求上式取极值，即要求指数项中
残差平方和表为
R i2 V TV
上一内容
下一内容 回主目录 返回 总目录 动画演示
2013-7-29 13
正则方程可表为
F T FC F T Y
其中
n T F F x i
(5.2.5)
xi T FY 2 xi
xi x y i i
上一内容
下一内容 回主目录 返回
(5.2.3)
总目录
动画演示
2013-7-29
11
另一形式为
简记几个表达式
1 1 x xi , y yi , L2 ( xi x ) 2 , L2y ( yi y ) 2 x n n L ( x x )( y y ) x y 1 x y i i i i i i xy n
合值 由最小二乘法的准则知
R i [ yi f ( xi ; C )]2
i 1 2 i i i 1 n n
(5.1.5)
取最小值。 由极值条件有
0 ck f ( xi ; C ) 2i [ yi f ( xi ; C )] c , k 1, 2,..., m i i i k
返回 总目录 动画演示
2013-7-29 10
上一内容
下一内容
回主目录
整理得
利用最小二乘法求解拟合曲线
实验三 函数逼近一、 实验目标1. 掌握数据多项式拟合的最小二乘法。
2. 会求函数的插值三角多项式。
二、实验问题（2）求函数()2cos f x x x =在区间[,]ππ-上的插值三角多项式。
三、 实验要求1. 利用最小二乘法求问题（1）所给数据的3次、4次拟合多项式，画出拟合曲线。
2. 求函数()2cos f x x x =在区间[,]ππ-上的16次插值三角多项式，并画出插值多项式的图形，与()f x 的图形比较。
3. 对函数()2cos f x x x =，在区间[,]ππ-上的取若干点，将函数值作为数据进行适当次数的最小二乘多项式拟合，并计算误差，与上题中的16次插值三角多项式的结果进行比较。
《数值分析》实验报告【实验课题】 利用最小二乘法求上述问题所给数据的2次，3次、4次拟合多项式，画出拟合曲线 【实验目标】（1）加深对用最小二乘法求拟合多项式的理解 （2）学会编写最小二乘法的数值计算的程序；【理论概述与算法描述】在函数的最佳平方逼近中()[,]f x C a b ∈ ,如果()f x 只在一组离散点集{,0,1,,}i x i m =⋅⋅⋅上给出，这就是科学实验中经常见到的实验数据{(,),0,1,,}i i x y i m =⋅⋅⋅的曲线拟合，这里(),0,1,,i i y f x i m ==⋅⋅⋅，要求一个函数*()y S x =与所给数据{(,),0,1,,i i x y i m =⋅⋅⋅拟合，若记误差*()(0,1,,)i i i S x y i m δ=-=⋅⋅⋅,()01,,,Tm δδδδ=⋅⋅⋅,设01(),(),,()n x x x ϕϕϕ⋅⋅⋅是[,]C a b 上的线性无关函数族，在01{(),(),,()}n span x x x ϕϕϕϕ=⋅⋅⋅中找一个函数*()S x ，使误差平方和|2222*2()0|||[()][()]min mmmii i i i S x i i i S x y S x y ϕδδ∈=====-=-∑∑∑这里0011|()()()()()n n S x a x a x a x n m ϕϕϕ=++⋅⋅⋅+<这就是一般的最小二乘逼近，用几何语言说，就称为曲线拟合的最小二乘法。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解： 由题目可知：
a0 a 2 2 a0 4 a 2 9 a0 9a2 16 a0 16a2 30 a0 25a2 52
1 1 1 4 A 1 9 1 16 1 25
由
AT Ax AT b 可得
Q 0, k 0,1,2,, m a k
得
j k ( y a x ) x i j i i 0, i 1 j 0
n
m
k 0,1,, m
即有
m a0n a1 xi am xi yi 2 m 1 a x a x a x xi yi 0 i 1 i m i a0 xim a1 xim1 am xi2 m xim yi
x i1.36
i
1
16.844 18.475 20.963
用最小二乘法求以上数据的拟合函数
解:把表中所给数据画在坐标纸上,将会看到数据 点的分布可以用一条直线来近似地描述,
设所求的拟合直线为
y( x) a0 a1 x
则正规方程组为
4 4 4a0 a1 xi yi i 1 i 1 4 4 4 2 a x a x 0 i 1 i xi y i i 1 i 1 i 1
5 55 a0 109 55 979 1962 a 2
a0 0.641177 , a2 2.040107
2
y 0.641177 2.040107 x
（3）可化为线性拟合的非线性拟合 例 设某实验数据如下: 1 2 3 4 5 6
（提示：将拉伸倍数作为x, 强度作为y, 在座标纸上标出各点，可以发现什么?）
9 8 7 6 5 4 3 2 1 0 0 2 4 6 8 10 12
从上图中可以看出强度与拉伸倍数大致成线形关系， 可用一条直线来表示两者之间的关系。
解：设
则：
y=a+bx
a 1.9 b 1.4 a 2.0b 1.3 a 9.5b 8.1 a 10.0 8.1
y( x) a0 a1 x
F (a0 , a1 ) (a0 a1 xi yi ) 2 为最小，
i 1
m
其中每组数据与拟合曲线的偏差为
y( xi ) yi a0 a1 xi yi
i 1,2,, m
根据最小二乘原理，应取 a0 和 a1使 F (a0 , a1 ) 有 极小值， 故 a0 和 a1应满足下列条件：
这是关于系数
aj
的线性方程组
正则方程组
也可利用矛盾方程组来做来自 a0 a1 x1 a x y1 a0 a1 x2 a x y2 m a0 a1 xn am xn yn
m m 1 m m 2
利用
A Ax A b
其中
xi 7.32
i 1
4
x
i 1
4 i 1 i
4
2 i
13.8434
i
y
i 1
4
i
70.376
x y
132.12985
将以上数据代入上式正规方程组,得 4a0 7.32a1 70.376 7.32a0 13.8434a1 132.12985
1 1 1 A 1 1 1 0 0 .2 0 .4 0 .6 0 .8 1 .0
1.000 0 1.221 0.04 1.492 0.16 b 1.882 0.36 2.226 0.64 2.718 1
, 解得 a0 3.9374 a1 7.4626
即得拟合直线 y 3.9374 7.4626 x
（2）多项式拟合
有时所给数据点的分布并不一定近似地呈一条
直线,这时仍用直线拟合显然是不合适的 ,可用多项
式拟合。 对于给定的一组数据， xi , yi , i 1,2,, n 寻求次数不超过m (m<<n ) 的多项式，
代人 y( x) a0 a1 x 即得拟合曲线。
求解该方程组，解得 a0与a1
例：某种合成纤维的强度与其拉伸倍数有直接关 系，下表是实际测定的24个纤维样品的强度与 相应拉伸倍数的记录。试确定这种关系。
编号 1 2 3 4 5 6 7 8 9 10 11 12 拉伸倍数 1.9 2.0 2.1 2.5 2.7 2.7 3.5 3.5 4.0 4.0 4.5 4.6 强度 kg/mm2 1.4 1.3 1.8 2.5 2.8 2.5 3.0 2.7 4.0 3.5 4.2 3.5 编号 13 14 15 16 17 18 19 20 21 22 23 24 拉伸倍数 5.0 5.2 6.0 6.3 6.5 7.1 8.0 8.0 8.9 9.0 9.5 10.0 强度 kg/mm2 5.5 5.0 5.5 6.4 6.0 5.3 6.5 7.0 8.5 8.0 8.1 8.1
2
由法方程组（5.46）, n=6, 经计算得
2 x 15 , x 55 , x 225 , x 797 , y 14 , x y 30 , x i i i i i yi 122 i 1 i 1 i 1 i 1 i 1 i 1 i 1 6 6
y 1.006321428 0.862589295x 0.842410704x2
2 y a a x 例：试用最小二乘法求形如 0 2 的多项 式，使之与下列数据拟合。
xi
yi
1 2
2 9
3 16
4 30
5 52
2 9 b 16 30 52
T T
m a0n a1 xi am xi yi 即有 2 m 1 a x a x a x xi yi 0 i 1 i m i a0 xim a1 xim1 am xi2 m xim yi
由
AT Ax AT b 可得
3 2.2 a0 10.479 6 3 2 .2 1.8 a1 6.433 2.2 1.8 1.5664 a2 5.08612
0 1.006321428,1 0.862589295,2 0.842410704
留着一切测试误差。
希望从给定的数据(xi,yi)出发,构造一个近似函数 ( x) ,不要求函数 完全通过所有的数据点，只要求所得 ( x) 的近似曲线能反映数据的基本趋势， 如图1所示。 y 图1 曲线拟合示意图
o
x
曲线拟合函数 ( x) 不要求严格地通过所有数据点 也就是说拟合函数 ( x) 在xi处的偏差(亦称残差）
由 AT Ax AT b
计算出它的正规方程得
24a 127.5b 113.1 127.5a 829.61b 731.60
解得： a=0.15 , b=0.859 直线方程为：y=0.15+0.859x
例
设有某实验数据如下： 2 1.37 3 1.95 4 2.28
yi 14.094
T
e 的1-范数
e
1
为了便于计算、分析与应用，通常要求 e 的2-范数
e
2
2 i i 0
n
1 2
即
2 n ( xi ) f ( x i ) i 0
1 2
e
2 2
2 i ( xi ) f ( x i ) i 0 i 0
例1 设函数y=f(x)的离散数据如下表所示
0 1 0.2 1.221
i
2 0.4 1.492
3 0.6 1.822
4 0.8 2.226
5 1 2.718
yi
xi
0 1.000
试用二次多项式拟和上述数据 解：设
y a0 a1x a2 x2
则
a0 0a1 0a2 1.000 a0 0.2a1 0.04a2 1.221 a0 0.4a1 0.16a2 1.492 a0 0.6a1 0.36a2 1.822 a0 0.8a1 0.64a2 2.226 a0 a1 a2 2.718
i
xi yi
0 0.5 1 1.5 2
2.5
2.0 1.0 0.9 0.6 0.4 0.3
用最小二乘法求拟合曲线
xi 0 1 2 3 4 5 yi 5 2 1 1 2 3 用最小二乘法求一个多项式拟合这组数据
解：将已给数据点描在坐标系中，可以看出这些点 接近一条抛物线，因此设所求的多项式为
i
例 设某实验数据如下： 1 2 3 4 5 6
y a0 a1 x a2 x
6 6 2 i 6 3 i 6 4 i 6
i ( xi ) f ( xi ) (i 0,1,, n)
不都严格地等于零。即为矛盾方程组。
但是,为了使近似曲线能尽量反映所给数据点的 变化趋势,要求 i 按某种度量标准最小。若记向量 即要求向量 e 或∞-范数 e
e 0 , 1 ,, n 的某种范数 e 最小,如
n
n
2
为最小。这种要求误差（偏差）平方和最小的 拟合称为曲线拟合的最小二乘法。
实质仍然是求矛盾方程组的最小二乘解。
（1）直线拟合 设已知数据点 xi , yi , i 1,2,, m , 分布大致为一条直线。 作拟合直线
该直线不是通过所有的数据点 x , y , i i 而是使偏差平方和