计算机图形学实验报告2 - DDA画线
DDA算法 中点画线算法 Bresenham算法

实验1直接绘制实验(提示:#表示Project的编号,##表示Project题目)学号姓名上交时间1.问题描述如何利用OpenGL实现直线光栅化的DDA算法、中点画线算法和Bresenham算法2.算法描述DDA算法:据直线公式y = kx + b来推导出来的,其关键之处在于如何设定单位步进,即一个方向的步进为单位步进,另一个方向的步进必然是小于1。
中点划线法:在画直线段的过程中,当前像素点为(xp ,yp ),下一个像素点有两种可选择点P1(xp +1,yp )或P2(xp +1,yp +1)。
若M=(xp +1,yp +0.5)为P1与P2之中点,Q 为P理想直线与x=xp +1垂线的交点。
当M在Q的下方,则P2应为下一个像素点;M在Q的上方,应取P1为下一个像素点。
Bresenham算法:过各行、各列像素中心构造一组虚拟网格线,按直线从起点到终点的顺序计算直线各垂直网格线的交点,然后确定该列像素中与此交点最近的像素。
实验结果成功运行三个算法,并且能转换出通用Bresenham算法。
3.分析与评论(分析每个算法的运行时间,对你的本实验的工作进行评论,同时也可以对老师提出建议。
)附录: Source Code(in C)#include <GL/glut.h> //需要正确安装GLUT,安装方法如预备知识中所述void myDisplay(void){glClearColor(0.0, 0.0, 0.0, 0.0);glClear(GL_COLOR_BUFFER_BIT);glColor3f (1.0f, 1.0f, 1.0f);glRectf(-0.5f, -0.5f, 0.5f, 0.5f);glBegin (GL_TRIANGLES);glColor3f (1.0f, 0.0f, 0.0f); glVertex2f (0.0f, 1.0f);glColor3f (0.0f, 1.0f, 0.0f); glVertex2f (0.8f, -0.5f);glColor3f (0.0f, 0.0f, 1.0f); glVertex2f (-0.8f, -0.5f);glEnd ();glColor3f(1,0,0);glBegin(GL_LINE_LOOP);glVertex2f (0.0f, 0.5f);glVertex2f (0.4f, -0.25f);glVertex2f (-0.4f, -0.25f);glEnd ();glPointSize(3);glBegin (GL_POINTS);glColor3f (1.0f, 0.0f, 0.0f); glVertex2f (-0.4f, -0.4f);glColor3f (0.0f, 1.0f, 0.0f); glVertex2f (0.0f, 0.0f);glColor3f (0.0f, 0.0f, 1.0f); glVertex2f (0.4f, 0.4f);glEnd ();glFlush();}int main(intargc, char *argv[]){glutInit(&argc, argv);glutInitDisplayMode(GLUT_RGB | GLUT_SINGLE);glutInitWindowPosition(100, 100);glutInitWindowSize(400, 400);glutCreateWindow("Hello World!");glutDisplayFunc(&myDisplay);glutMainLoop();return 0;}通用算法:int Sign(int n){if(n>0) return 1;if(n==0) return 0;if(n<0) return -1;}void Bresenham(int x0,int y0,int x1,int y1,void (*setPixel)(intx,int y)){ int x,y,dx,dy,s1,s2,temp=0,interchange;x=x0; y=y0;dx=abs(x1-x0); dy=abs(y1-y0);s1=Sign(x1-x0); s2=Sign(y1-y0);if(dy>dx){temp=dx; dx=dy; dy=temp;interchange=1;}elseinterchange=0;int e=2*dy-dx;for(inti=1;i<=dx;++i){setPixel(x,y);while(e>0){if(interchange==1)x=x+s1;elsey=y+s2;e=e-2*dx;}if(interchange==1)y=y+s2;elsex=x+s1;e=e+2*dy;}}(以上是实验报告的最小要求,以后可以会根据各个Project的不同情况增加内容。
《计算机图形学》实验指导书

计算机图形学实验指导书袁科计算机技术实验中心目录实验一实现DDA、中点画线算法和Bresenham画线算法 (24)实验二实现Bezier曲线 (25)实验三实现B样条曲线 (26)实验四实现多边形填充的边界标志算法 (27)实验五实现裁剪多边形的Cohen-Sutherland算法 (28)实验六二维图形的基本几何变换 (30)实验七画图软件的编制 (31)实验一实现DDA、中点画线算法和Bresenham画线算法【实验目的】1、掌握直线的多种生成算法;2、掌握二维图形显示原理。
【实验环境】VC++6.0/ BC【实验性质及学时】验证性实验,2学时,必做实验【实验内容】利用任意的一个实验环境,编制源程序,分别实现直线的三种生成算法,即数字微分法(DDA)、中点画线法以及Bresenham画线算法。
【实验原理】1、数字微分法(Digital Differential Analyzer,DDA)算法思想:基于直线的微分方程来生成直线。
ε=1/max(|△x|,|△y|)max(|△x|,|△y|)=|△x|,即|k|≤1 的情况:max(|△x|,|△y|)=|△y|,此时|k|≥1:2、中点画线法算法思想:每次在最大位移方向上走一步,另一方向是否走步取决于误差项的判断。
3、Bresenham画线算法算法思想:其基本思想同中点算法一样,即每次在最大位移方向上走一步,而另一个方向是否走步取决于误差项的判断。
【实验要求】1.上交源程序;2.上交实验报告,实验报告内容如下:(1) 实验名称(2) 实验目的(3) 算法实现的设计方法及程序流程图(4) 程序结果分析【分析与思考】(1) 上述所阐述的三个算法,其基本算法只能适用于直线的斜率(|K|<=1) 的情形,如何将上述算法进行推广,使其能够处理任意斜率的直线?(2) 计算机显示屏幕的坐标圆心在哪里,与我们平时的习惯有什么差异,如何协调二者?实验二 实现Bezier 曲线【实验目的】1、掌握Bezier 曲线的定义;2、能编程实现N 次Bezier 曲线的绘制与显示。
计算机图形学 直线段生成绘制的实现算法

实验二直线段生成绘制的实现算法班级 08信计学号60姓名杨平萍分数一、实验目的和要求:1、掌握光栅图形显示基本原理2、熟悉直线的DDA算法、Bresenham算法绘制直线3、上机操作实现DDA算法、Bresenham算法。
二、实验内容:1、了解DDA算法、Bresenham算法的原理2、编程实现DDA算法、Bresenham算法绘制直线段3、分析对比二算法三、程序执行和运行结果DDA算法的实现#include"stdio.h"#include"graphics.h"void DDALine(int x1,int y1, int x2,int y2){double dx, dy,e,x,y;int i;dx=x2-x1;dy=y2-y1;e=(fabs(dx)>fabs(dy))? fabs(dx):fabs(dy);dx/=e;dy/=e;x=x1;y=y1;for(i=1;i<=e;i++){putpixel((int)(x+0.5),(int)(y+0.5),YELLOW);x+=dx;y+=dy;}}void main(){int driver=VGA;int mode=VGAHI;initgraph(&driver,&mode,"");DDALine(100,150,250,300 );getch();closegraph();}运行结果:Bresenham算法的实现:#include<stdio.h>#include<graphics.h>void Bresenhamline(int x1,int y1,int x2,int y2){int x,y,dx,dy,p;x=x1;y=y1;dx=x2-x1;dy=y2-y1;p=2*dy-dx;for(;x<=x2;x++){putpixel(x,y,RED);if(p>=0){y++;p+=2*(dy-dx);}else{p+=2*dy;}}}main(){int driver=VGA;int mode=VGAHI;initgraph(&driver,&mode,"");Bresenhamline(50,150,200,250);getch();closegraph();}运行结果:3、对比Bresenham算法、DDA算法、中点算法三种算法的像素逼近效果和程序执行速度三两种算法的像素逼近效果和程序执行速度。
计算机图形学报告

学院 班级 学号 姓名
学院名称
专业班级
学号
学生姓名
实验日期
成绩
课程名称
计算机图形学
实验名称
实验一维基本图形生成的算法实现
、实验目的:
1.通过实验,进一步理解和掌握DDA和中点算法,Bresenham算法;
2.掌握DDA和中点算法,Bresenham算法算法生成直线段的基本过程;掌握中点算法
void getcode(int x,int y,int d[4]);/*定义获得端点的代码函数*/
int aa=1;
getcode(x1,y1,a);
getcode(x2,y2,b);
/*1:裁剪循环开始*/
while(aa!=O) {
if((a[0]+a[1]+a[2]+a[3]==0)&&(b[0]+b[1]+b[2]+b[3]==0))/*第一种情况线段完全可见
*/
aa=O;
return;
else if((a[0]&&b[0])+(a[1]&&b[1])+(a[2]&&b[2])+(a[3]&&b[3])!=0) /*线段完全不可见*/
setcolor(0);
setwritemode(0); /*设置画线的输出模式为覆盖方式*/
line(x1,y1,x2,y2); /*进行裁剪也就是进行覆盖*/
aa=0;
return;
/*2
else
if(a[0]+a[1]+a[2]+a[3]==0)/*寻找不可见点*/
使用DDA和Bresenham绘制直线

1ɺ 凡使用 LineTo()函数、Polyline()函数绘制直线的,本次实验没有成绩。 2ɺ 如对 Visual C++的编译环境不熟悉,请课下提前参考 Visual C++的相关书籍和 MSDN。
int i; float dx,dy,length,x,y;
if (fabs(x1-x0)>=fabs(y1-ylse length=fabs(y1-y0);
dx=(x1-x0)/length; dy=(y1-y0)/length; i=1; x=x0; y=y0; while(i<=length) {
Bresenham 算法是 DDA 算法画线算法的一种改进算法。本质上它也是采取了步进的思 想。不过它比 DDA 算法作了优化,避免了步进时浮点数运算,同时为选取符合直线方程的 点提供了一个好思路。首先通过直线的斜率确定了在 x 方向进行单位步进还是 y 方向进行单 位步进:当斜率 k 的绝对值|k|<1 时,在 x 方向进行单位步进;当斜率 k 的绝对值|k|>1 时, 在 y 方向进行单位步进。
图3
图4 4ɺ 在函数体 void DDALine(int x0, int y0, int x1, int y1, COLORREF color)中,实现 DDA
算法。具体代码参考教材 P30~P31。需要注意的是,调用 Setpixel 函数之前需要得 到设备上下文,即在函数体中加入如下代码:
CDC *pDC = this->GetDC(); 然后,用 pDC->SetPixel(int (x + 0.5), int (y + 0.5), color); 代替原来程序中的 SetPixel(int (x + 0.5), int (y + 0.5), color);即可。 以后使用 Bresenham 绘制直线的算法中调用 SetPixel 函数的情况按同样的方 法处理。 5ɺ 同 步 骤 3 类 似 , 在 CGView.cpp 文 件 中 ( 类 CCGView 中 ), 添 加 函 数 void Bresenham_Line(int x0, int y0, int x1, int y1, COLORREF color)。实现代码参考教材 P33 的 Bresenham 画线算法程序。参考步骤 4,注意对函数 Setpixel 的调用。
河南工业大学-图形学实验二
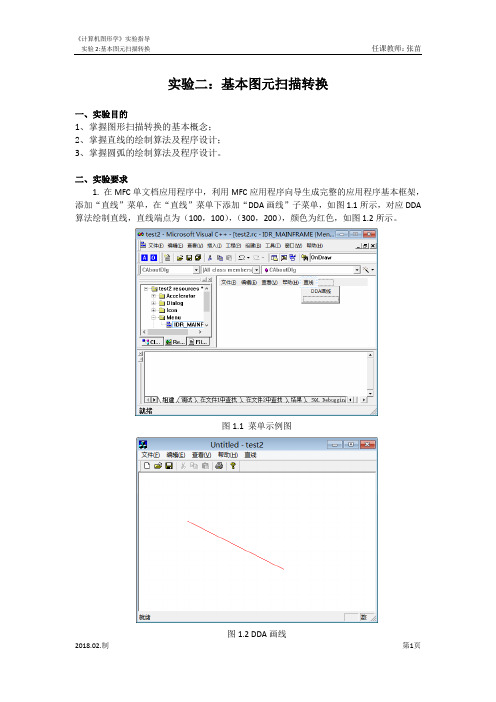
实验二:基本图元扫描转换一、实验目的1、掌握图形扫描转换的基本概念;2、掌握直线的绘制算法及程序设计;3、掌握圆弧的绘制算法及程序设计。
二、实验要求1. 在MFC单文档应用程序中,利用MFC应用程序向导生成完整的应用程序基本框架,添加“直线”菜单,在“直线”菜单下添加“DDA画线”子菜单,如图1.1所示,对应DDA 算法绘制直线,直线端点为(100,100),(300,200),颜色为红色,如图1.2所示。
图1.1 菜单示例图图1.2 DDA画线2. 在上题基础上,在“直线”菜单下再添加一个“中点画线”子菜单,如图2.1所示,利用中点画线算法画线,实现鼠标按下抬起绘制直线段的功能,颜色为黑色,如图2.2所示。
图2.1菜单示例图图2.1绘制矩形制作动画图3. 在上题基础上,添加“圆形”菜单,如图3.1所示,利用Bresenham算法编程实现圆的扫描转换,绘制半径为200的黑色圆,如图3.2所示。
图3.1菜单示例图图3.2 Bresenham画圆三、实验内容○1“直线”菜单,“DDA画线”子菜单,“中点画线”子菜单的构建○2DDA画线void CMainFrame::OnDda(){// 获得设备指针CDC *pDC=GetDC();// 定义直线两端点和直线颜色(红色)int x0=100,y0=100,x1=300,y1=200,c=RGB(255,0,0);float x,y,i;float dx,dy,k;dx=(float)(x1-x0);dy=(float)(y1-y0);k=dy/dx;y=y0; x=x0;if(abs(k)<1){ for(;x<=x1;x++){pDC->SetPixel(x,int(y+0.5),c);y=y+k;}}if(abs(k)>=1){for(;y<=y1;y++){pDC->SetPixel(int(x+0.5),y,c);x=x+1/k;}}ReleaseDC(pDC); //释放设备指针}○3中点画线0≤k≤1时中点画线算法的算法步骤为:1.输入直线的两端点P0(x0,y0)和p1(x1,y1)。
计算机图形学上机报告
计算机图形学上机报告计算机图形学上机实验报告计算机科学与技术学院班级:学号:姓名:指导教师:完成⽇期:实验⼀:基本图元绘制⼀. 实验⽬的1. 了解如何利⽤OpenGL库绘制图形2. 理解glut程序框架3. 理解窗⼝到视区的变换4. 理解OpenGL实现动画的原理⼆. 实验内容1. 实现中点Bresenham算法画直线2. 实现改进Bresenham算法画直线3. 实现圆的绘制三. 实验结果1.DDA算法画直线2. 中点Bresenham算法画直线3. 改进Bresenham算法画直线4. Bresenham算法画圆四. 源程序#include#include#include "stdio.h"int m_PointNumber = 0; //动画时绘制点的数⽬int m_DrawMode = 4; //绘制模式 1 DDA算法画直线// 2 中点Bresenham算法画直线// 5 四分法绘制椭圆//绘制坐标线void DrawCordinateLine(void){int i = 0 ;//坐标线为⿊⾊glColor3f(0.0f, 0.0f ,0.0f);glBegin(GL_LINES);for (i=10;i<=250;i=i+10){glVertex2f((float)(i), 0.0f);glVertex2f((float)(i), 250.0f);glVertex2f(0.0f, (float)(i));glVertex2f(250.0f, (float)(i));}glEnd();}//绘制⼀个点,这⾥⽤⼀个正⽅形表⽰⼀个点。
void putpixel(GLsizei x, GLsizei y){glRectf(10*x,10*y,10*x+10,10*y+10);}void DDACreateLine(GLsizei x0, GLsizei y0, GLsizei x1, GLsizei y1, GLsizei num) {//设置颜⾊glColor3f(1.0f,0.0f,0.0f);//对画线动画进⾏控制if(num == 1)printf("DDA画线算法:各点坐标\n");else if(num==0)return;//画线算法的实现GLsizei dx,dy,epsl,k;GLfloat x,y,xIncre,yIncre;x = x0;y = y0;if(abs(dx) > abs(dy)) epsl = abs(dx);else epsl = abs(dy);xIncre = (float)dx / epsl ;yIncre = (float)dy / epsl ;for(k = 0; k<=epsl; k++){putpixel((int)(x+0.5), (int)(y+0.5));if (k>=num-1) {printf("x=%f,y=%f,取整后x=%d,y=%d\n", x, y, (int)(x+0.5),(int)(y+0.5));break;}x += xIncre;y += yIncre;if(x >= 25 || y >= 25) break;}}void BresenhamLine(GLsizei x0, GLsizei y0, GLsizei x1, GLsizei y1, GLsizei num) {glColor3f(1.0f,0.0f,0.0f);if(num == 1)printf("中点Bresenham算法画直线:各点坐标及判别式的值\n");else if(num==0)return;//画线算法的实现GLsizei dx,dy,d,UpIncre,DownIncre,x,y,xend=0;if(x0>x1){x=x1;x1=x0;x0=x;y=y1;y1=y0;y0=y;}x=x0;y=y0;dx=x1-x0;dy=y1-y0;d=dx-2*dy;putpixel(x,y);if (x>=num-1) {break;}x++;if(d<0){y++;d+=UpIncre;}else d+=DownIncre;if(x >= 50 || y >= 50) break;}}void Bresenham2Line(GLsizei x0, GLsizei y0, GLsizei x1, GLsizei y1, GLsizei num) { glColor3f(1.0f,0.0f,0.0f);if(num == 1)printf("改进的Bresenham算法画直线:各点坐标及判别式的值\n");else if(num==0)return;//画线算法的实现GLsizei x,y,dx,dy,e;dx=x1-x0;dy=y1-y0;e=-dx;x=x0;y=y0;while (x<=x1){putpixel(x,y);if (x>=num-1) {break;}x++;e=e+2*dy;if(e>0){y++;if(x >= 50 || y >= 50) break;}}void BresenhamCircle(GLsizei x, GLsizei y, GLsizei r, GLsizei num) {glColor3f(1.0f,0.0f,0.0f);if(num == 1)printf("Bresenham算法画圆:各点坐标及判别式的值\n");x=0,y=r;GLsizei d=1-r;while (xputpixel(x,y);if (x>=num) {break;}putpixel(y,x);if (x>=num) {break;}putpixel(-y,x);if (x>=num) {break;}putpixel(-x,y);if (x>=num) {break;}putpixel(-x,-y);if (x>=num) {break;}putpixel(-y,-x);if (x>=num) {putpixel(y,-x);if (x>=num) {break;}putpixel(x,-y);if(d<0)d+=2*x+3;else{d+=2*(x-y)+5;y--;}x++;}}//初始化窗⼝void Initial(void){// 设置窗⼝颜⾊为蓝⾊glClearColor(1.0f, 1.0f, 1.0f, 1.0f);}// 窗⼝⼤⼩改变时调⽤的登记函数void ChangeSize(GLsizei w, GLsizei h){if(h == 0) h = 1;// 设置视区尺⼨glViewport(0, 0, w, h);// 重置坐标系统glMatrixMode(GL_PROJECTION); glLoadIdentity();// 建⽴修剪空间的范围if (w <= h)glOrtho (0.0f, 250.0f, 0.0f, 250.0f*h/w, 1.0, -1.0); elseglOrtho (0.0f, 250.0f*w/h, 0.0f, 250.0f, 1.0, -1.0); }void ReDraw(void){//⽤当前背景⾊填充窗⼝glClear(GL_COLOR_BUFFER_BIT);//画出坐标线DrawCordinateLine();switch(m_DrawMode){case 1:DDACreateLine(0,0,20,15,m_PointNumber); break;case 2:BresenhamLine(0,0,20,15,m_PointNumber); break;case 3:Bresenham2Line(1,1,8,6,m_PointNumber); break;case 4:BresenhamCircle(5,5,18,m_PointNumber); break;default:break;}glFlush();}//设置时间回调函数void TimerFunc(int value){if(m_PointNumber == 0)value = 1;m_PointNumber = value; glutPostRedisplay();glutTimerFunc(500, TimerFunc, value+1); }void Keyboard(unsigned char key, int x, int y){if (key == '1') m_DrawMode = 1;if (key == '2') m_DrawMode = 2;if (key == '3') m_DrawMode = 3;if (key == '4') m_DrawMode = 4;m_PointNumber = 0;glutPostRedisplay();}//void main(void)int main(int argc, char* argv[]){glutInit(&argc, argv);//初始化GLUT库OpenGL窗⼝的显⽰模式glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB); glutInitWindowSize(800,600); glutInitWindowPosition(100,100); glutCreateWindow("基本图元绘制程序"); glutDisplayFunc(ReDraw);glutReshapeFunc(ChangeSize); glutKeyboardFunc(Keyboard);//键盘响应回调函数glutTimerFunc(500, TimerFunc, 1);// 窗⼝初始化Initial();glutMainLoop(); //启动主GLUT事件处理循环return 0;}实验⼆:⽇地⽉模型⼀. 实验⽬的1. 理解OpenGL中的变换过程2. 理解透视投影与平⾏投影的不同3. 了解深度测试⼆. 实验内容1. 通过变换调整观察的位置与⽅向三. 实验结果太阳、地球和⽉亮的运动模型图1.图2.图3.四. 源程序#include#include#include#includevoid Initial(){glEnable(GL_DEPTH_TEST); // 启⽤深度测试glFrontFace(GL_CCW); // 指定逆时针绕法表⽰多边形正⾯glClearColor(1.0f, 1.0f, 1.0f, 1.0f ); //背景为⽩⾊}void ChangeSize(int w, int h){if(h == 0) h = 1;// 设置视区尺⼨glViewport(0, 0, w, h);glMatrixMode(GL_PROJECTION);glLoadIdentity();// 设置修剪空间GLfloat fAspect;fAspect = (float)w/(float)h;gluPerspective(45.0, fAspect, 1.0, 500.0);/*if (w <= h)glOrtho (-nRange, nRange, nRange*h/w, -nRange*h/w, -nRange*2.0f, nRange*2.0f);elseglOrtho (-nRange*w/h, nRange*w/h, nRange, -nRange, -nRange*2.0f, nRange*2.0f); */glLoadIdentity();}void RenderScene(void){// 绕原⼦核旋转的⾓度static float fElect1 = 0.0f;static float f2=0.0f;glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); // 重置模型视图矩阵glMatrixMode(GL_MODELVIEW);glLoadIdentity();//将图形沿z轴负向移动glTranslatef(0.0f, 0.0f, -250.0f);// 绘制红⾊的原⼦核glColor3f(1.0f, 0.0f, 0.0f);glutSolidSphere(50.0f, 15, 15);// 当前绘制颜⾊变为黄⾊glColor3f(0.0f, 0.0f, 0.0f);//绘制第⼀个电⼦//保存当前的模型视图矩阵glRotatef(fElect1, 0.0f, 1.0f, 0.0f);//绕y轴旋转⼀定的⾓度glTranslatef(80.0f, 0.0f, 0.0f);//平移⼀段距离glutSolidSphere(12.0f, 15, 15);//画出电⼦// 恢复矩阵// 第⼆个电⼦glPushMatrix();glRotatef(45.0f, 0.0f, 0.0f, 1.0f);glRotatef(f2, 0.0f, 1.0f, 0.0f);glTranslatef(-20.0f, 0.0f, 0.0f);glutSolidSphere(6.0f, 15, 15);glPopMatrix();/* // 第三个电⼦glPushMatrix();glRotatef(-45.0f,0.0f, 0.0f, 1.0f);glTranslatef(0.0f, 0.0f, 60.0f);glutSolidSphere(6.0f, 15, 15);glPopMatrix();*/// 增加旋转步长fElect1 += 10.0f;f2=fElect1*6;if(fElect1 > 360.0f){fElect1 = 10.0f;}glutSwapBuffers();}void TimerFunc(int value){glutPostRedisplay();glutTimerFunc(100, TimerFunc, 1);}int main(int argc, char* argv[]){glutInit(&argc, argv);glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB | GLUT_DEPTH); glutCreateWindow("⽇地⽉模型");glutReshapeFunc(ChangeSize);glutDisplayFunc(RenderScene);glutTimerFunc(500, TimerFunc, 1);Initial();glutMainLoop();return 0;}。
计算机图形学基础教程实验报告
湖北民族学院信息工程学院实验报告(数字媒体技术专业用)班级:姓名:谌敦斌学号:031241318实验成绩:实验时间:2013年10 月14 日9、10 节实验地点:数媒实验室课程名称:计算机图形学基础教程实验类型:设计型实验题目:直线与圆的绘制一、实验目的通过本次实验,熟练掌握DDA、中点、Bresenham直线绘制方法和中点、Bresenham圆的画法,能够在vc环境下独立完成实验内容,逐渐熟悉opengl的语法特点,提高程序基本绘图的能力。
二、实验环境(软件、硬件及条件)Microsoft vc++6.0 多媒体计算机三、实验内容1.从DDA、中点、Bresenham画线法中任选一种,完成直线的绘制。
2.从中点、Bresenham画圆法中任选一种,完成圆的绘制。
四、实验方法与步骤打开vc++6.0,新建一个工程,再在工程里面建一个.cpp文件,编辑程序,编译连接后执行即可。
程序如下bresenham画线法:#include<graphics.h>#include<conio.h>int bresenham(int x0,int y0,int x1,int y1,int color) {int x,y,dx,dy,e,i;dx=x1-x0;dy=y1-y0;e=-dx;y=y0;for(x=x0;x<=x1;x++){putpixel(x,y,color);e+=2*dy;if(e>=0){ y++;e-=2*dx;}}return 0;}int main(){initgraph(640,480);bresenham(0,0,500,200,255);while(!kbhit()){}closegraph();return 0;}Bresenham画圆法:#include<graphics.h>#include<conio.h>int circlepoints(int x,int y,int color){putpixel(255+x,255+y,color);putpixel(255+y,255+x,color);putpixel(255-x,255+y,color);。
计算机图形学直线段生成绘制的实现算法
计算机图形学直线段⽣成绘制的实现算法实验⼆直线段⽣成绘制的实现算法班级 10信计专接本学号 20100504008 姓名吴晓楠分数⼀、实验⽬的和要求:1.了解计算机图形学的原理、⽅法和应⽤。
2.熟悉直线的⽣成算法,掌握直线的绘制3.实现C语⾔编写图形程序。
学会了解VC++的基本应⽤同时了解TC图形环境配置,学习简单的图形画法,并⽐较画法的优劣,尝试在计算机实现,得到图形,验证⽐较图形。
⼆、实验内容:1、掌握直线段的⽣成算法,并⽤C/WIN-TC/VC++实现算法,包括中点法⽣成直线,微分数值法⽣成直线段等。
2、编程实现DDA算法、Bresenham算法、中点画线法绘制直线段三、实验结果分析1、⽣成直线的DDA算法算法思想:⼀个坐标轴上以单位间隔增量,决定另⼀个坐标轴上最靠近线段路径的对应整数值。
假定x2﹣x1的绝对值⼤于y2﹣y1的绝对值,取x为⼀个象素单位长,即x 每次递增⼀个象素,然后利⽤下式计算相应的y值:yk+1﹦yk﹢△y﹦yk﹢m·△x 对于|m|>1的线段,可通过计算由Y⽅向的增量△y引起的改变来⽣成直线:xk+1﹦xk﹢△x﹦xk﹢m·△y⽣成直线的DDA算法思想是源⽤初中直线的⽅程得出来的,⽽⽣成直线的中点算法是通过将DDA算法的⽅程式改为隐函数形式,然后通过与中点的⽐较确定该取的像素,绘制图线。
/* DDA */#includevoid linedda(int x0,int y0,int x1,int y1,int color){int x,dy,dx,y;float m;dx=x1-x0;dy=y1-y0;m=dy/dx;y=y0;for(x=x0;x<=x1;x++){putpixel(x,(int)(y+0.5),color);y+=m;}}main(){int a,b,c,d,e;int graphdriver=DETECT;int graphmode=0;initgraph(&graphdriver,&graphmode,""); cleardevice();a=0;b=100;c=200;d=300;e=200;linedda(a,b,c,d,e);getch();closegraph();}运⾏结果:VC++环境:#include#include// 四舍五⼊int Round(float x){return (int)(x < 0 ? x - 0.5 : x + 0.5); }// 使⽤ DDA 算法画任意斜率的直线(包括起始点,不包括终⽌点)void Line_DDA(int x1, int y1, int x2, int y2, int color){float x, y; // 当前坐标点float cx, cy; // x、y ⽅向上的增量int steps = abs(x2 - x1) > abs(y2 - y1) ? abs(x2 - x1) : abs(y2 - y1); x = (float)x1;y = (float)y1;cx = (float)(x2 - x1) / steps;cy = (float)(y2 - y1) / steps;for(int i = 0; i < steps; i++){putpixel(Round(x), Round(y), color); // 在坐标 (x, y) 处画⼀个 color 颜⾊的点x += cx;y += cy;}}// 主函数void main(){initgraph(640, 480);// 测试画线Line_DDA(100, 100, 100, 478, RED);// 按任意键退出getch();}2、Bresenham直线算法是⽤来描绘由两点所决定的直线的算法,它会算出⼀条线段在 n 维光栅上最接近的点。
计算机图形学实验二
计算机图形学实验指导书信息科学技术学院二○一三年十一月计算机图形学实验报告实验名称直线、圆弧及曲线的生成算法评分实验日期2013 年11 月 6 日指导教师姓名专业班级11地信学号2011083027一、实验目的1、几种直线生成算法的比较,特别掌握用Bresenham直线生成算法。
2、掌握用像素点法直接生成其它曲线的方法。
二、实验要求1、用不同的生成算法在屏幕上绘制出直线的图形,对不同的算法可设置不同的线形或颜色表示区别。
2、用Bresenham生成算法在屏幕上绘制出圆弧的图形,用动画的方式表演图形的生成。
三、关键算法及实现原理1、有关直线生成算法有:DDA(数值微分)直线算法、逐点比较法、直线Bresenham 生成算法。
直线Bresenham生成算法思想如下(第一象限,且斜率k<1的情况图2-1 a 中的1a):1)画点(x1,y1),dx=x2-x1,dy=y2-y1,计算误差初值P1=2dy-dx,i=1;2)求直线下一点位置x i+1=x i+1 如果P i>0,则y i+1=y i+1,否则y i+1=y i;3)画点(x i+1,y i+1);4)求下一个误差P i+1点,如果P i>0,则P i+1=P i+2dy-2dx,否则P i+1=P i+2dy;5)i=i+1,如果i<dx+1则转步骤2,否则结束操作。
Bresenham生成算法的优点如下;1)不必计算直线的斜率,因此不做除法。
2)不用浮点数,只用整数。
3)只做整数加减运算和乘2运算,而乘2运算可以用移位操作实现。
Bresenham算法的速度很快,并适于用硬件实现。
对于图2-1 a中的2a,只需将x i+1=x i+1改为x i+1=x i-1。
对于图2-1 a中的1b,斜率k>1的情况,可交换变量x和y,y每次长1个单位。
对P i进行判断,x i+1=x i或x i+1=x i+1。
2、有关圆弧生成算法有:逐点比较法、DDA(数值微分)直线算法、圆的Bresenham生成算法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
班 级 R数学111
大连交通大学
姓 名
实 验 报 告
同 组 人 无
课程名称: 计算机图形学 成 绩
实验名称: DDA画线 _ 指导老师 任洪海
实验目的:
函数画线
实验要求:
掌握DDA画线算法
实验仪器:
软件:VC++6.0,windows XP
硬件:计算机
实验步骤、内容:
一、新建MFC工程
1.开始所有程序Microsoft Visual C++ 6.0Microsoft Visual C++ 6.0
2.文件-->新建-->工程,工程名称填[项目名],左边的类型选择MFC AppWizard [exe],点击确定
3.在“您要创建的应用程序类型是:”,选择“单文档”,点击完成,点击确定。
二、添加菜单
1.左侧视图栏中有三个视图:ClassView、ResourceView、FileView,点击中间的 ResourceView
2.展开[项目名]resources,展开Menu,双击IDR_MAINFRAME
3.在右侧窗口中双击菜单栏中的虚线框,在弹出的菜单项目属性中的标明文本框中填入“画线”,点击关闭
4.在“画线”菜单下,会出现子菜单项的虚线框,双击它。
5.在弹出的窗口中填入ID框填:ID_DDA;标明填:函数DDA画线。点击关闭(注:ID框必须全英文,其
他不限)
三、创建、编辑函数
1.点击VC++菜单栏中的:查看建立类向导
2.在弹出的MFC ClassWized窗口中,Class name选择C[项目名]view
3.Object IDs选择ID_DDA,Messages选择COMMAND
4.点击Add Function,点击OK,点击Edit Code,进入编辑函数的界面([项目名]View.cpp)
void C[项目名]View::OnDda()
{
// TODO: Add your command handler code here
}
在大括号内填入以下代码
CDC *pDC=GetDC();
int k;
double x1=50,y1=50,x2=200,y2=350;
double x,y,deltx,delty,length;
if(fabs(x2-x1)>fabs(y2-y1))
length=fabs(x2-x1);
else
length=fabs(y2-y1);
deltx=(x2-x1)/length;
delty=(y2-y1)/length;
x=x1;y=y1;k=1;
while(k<=length){
pDC->SetPixel((int)x,(int)y,RGB(255,0,0));
x+=deltx; y+=delty; k++;
}
Sleep(1);
ReleaseDC(pDC);
四、将#include
五、运行结果
直接点击感叹号运行,然后点击刚建立的菜单画线
在界面上可以看到从(2,3)到(6,9)一条黑色的直线
实验心得:
写完代码直接运行报错:error C2065: 'fabs' : undeclared identifier,结果发现#include
上 ,加上之后正常了
2014年11月10日
教师评语:
年 月 日
