结构力学崔恩第习题解答
结构力学课后习题答案

习题7-1 试确定图示结构的位移法基本未知量数目,并绘出基本结构。
(a) (b) (c)EIEI EI 2EI2EI1个角位移 3个角位移,1个线位移 4个角位移,3个线位移(d) (e) (f)EI 1=∞EAEIEI 1=∞3个角位移,1个线位移 2个线位移 3个角位移,2个线位移(g) (h) (i)k一个角位移,一个线位移一个角位移,一个线位移三个角位移,一个线位移7-2 试回答:位移法基本未知量选取的原则是什么?为何将这些基本未知位移称为关键位移?是否可以将静定部分的结点位移也选作位移法未知量?7-3 试说出位移法方程的物理意义,并说明位移法中是如何运用变形协调条件的。
7-4 试回答:若考虑刚架杆件的轴向变形,位移法基本未知量的数目有无变化?如何变化?7-5 试用位移法计算图示结构,并绘出其内力图。
(a)lACD i iiq解:(1)确定基本未知量和基本结构有一个角位移未知量,基本结构见图。
11r 11Z 3i 4i2i ii1M 图1pR 213ql216qlp M 图(2)位移法典型方程11110p r Z R (3)确定系数并解方程iql Z ql iZ ql R i r p24031831,821212111(4)画M 图2724ql 2524qlM 图218ql 216ql (b)4m ADB 10kNEI 2EI2.5kN/m EI解:(1)确定基本未知量1个角位移未知量,各弯矩图如下11r 11Z 1M 图32EI EI12EI 590p M 图(2)位移法典型方程11110pr Z R (3)确定系数并解方程1115,352pr EI R 153502EIZ 114Z EI(4)画M 图()KNm M 图2640147(c) F P解:(1)确定基本未知量一个线位移未知量,各种M 图如下11r 1M 图11Z 27EI 227EI 27EI 1243EI2243EI1243EI p M 图pF 1pR (2)位移法典型方程11110pr Z R (3)确定系数并解方程1114,243p pr EI R F 140243p EIZ F 12434Z EI(4)画M 图94pF 94pF 92p F M 图(d)解:(1)确定基本未知量一个线位移未知量,各种M 图如下11Z2/25EA a4/25EA a11r 1M 图25EA11r 1M 图2/25EA a 2/25EA a 简化图1p R pF pF 45a35a15a pM(2)位移法典型方程11110pr Z R (3)确定系数并解方程11126/,55p p r EA a R F 126055pEA Z F a13a Z EA(4)画M 图a 2a a 2aaEAEAABCDEFF PF PEI 1=∞图M 0.6p F ap F a1.2p F 0.6pF (e)解:(1)确定基本未知量两个线位移未知量,各种M 图如下图11Z 11r 21r 112121424EA r lEA r l1M 2EA lEA l图21Z 12r 22r 22214EA r l2M 2EA lEA lllEAABCDEAEAF P图120p p pR F R p M 1pR pF 0(2)位移法典型方程1111221211222200p pr Z r Z R r Z r Z R (3)确定系数并解方程1112212212221,44214,0pp p EA EA r r r l lEA r lR F R 代入,解得121222121212ppl Z F EA lZ F EA(4)画M 图图M 122212pF 2212pF 1212pF 7-6 试用位移法计算图示结构,并绘出M 图。
结构力学习题课后答案(高等教育版)

习 题8-1 试说出单元刚度矩阵的物理意义及其性质与特点。
8-2 试说出空间桁架和刚架单元刚度矩阵的阶数。
8-3 试分别采用后处理法和先处理法列出图示梁的结构刚度矩阵。
(a)解:(a )用后处理法计算 (1)结构标识(2)建立结点位移向量,结点力向量[]T44332211 θνθνθνθν=∆[]Ty M F M F M F M F F 4y43y32y211 =θ(3)计算单元刚度矩阵⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡=2222322211211462661261226466126122EI 21 l l -l l l -l -l l -l l l l - l k k k k k ①①①①①⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡=222233332232223 33 6 3632336 362EI 21 l l - l l l - l -l l -l l l -l l k k k k k ②②②②②lll⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡=222234443343323 33 6 3632336 362EI 2 1 l l - l l l - l -l l -l l l -l l k k k k k ③③③③③(4)总刚度矩阵⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡++=222222222234443343333322322222112112 3300003 6 3 6 000 03403003601236000 0 3632600 363186120000 26460 0 0 06126122EI 0 0 00 0 0 4 3 2 1 4 3 2 1 l l -l l l - l - - l l -l l l l - l - - l l -l l -l l l l - -l -- l l -l l l l - l k k k k k k k k k k k k k ③③③③②②②②①①①①θ (5)建立结构刚度矩阵支座位移边界条件[][]00004311 θ θ θν=将总刚度矩阵中对应上述边界位移行列删除,得刚度结构矩阵。
结构力学课后习题答案
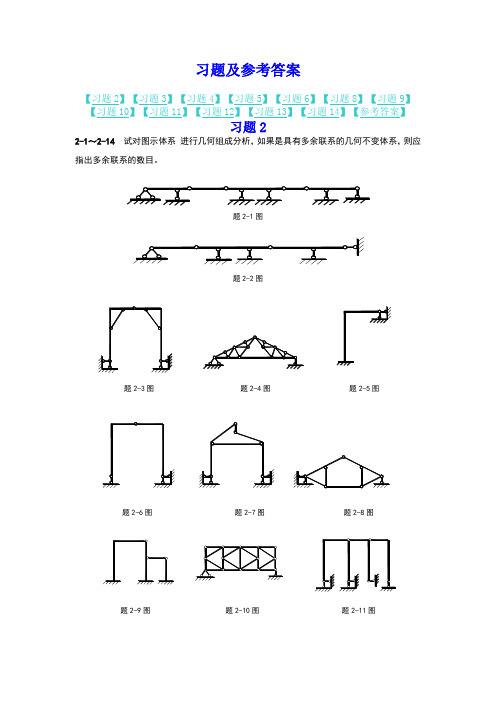
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN10kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)8kN /m20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6检查下列刚架的M图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1图示抛物线三铰拱轴线方程xxllfy)(42-=,试求D截面的内力。
题5-1图5-2带拉杆拱,拱轴线方程xxllfy)(42-=,求截面K的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
(a)题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(a)P题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。
结构力学课后习题答案

结构⼒学课后习题答案附录B 部分习题答案2 平⾯体系的⼏何组成分析2-1 (1)× (2)× (3)√ (4)× (5)× (6)×。
2-2 (1)⽆多余约束⼏何不变体系;(2)⽆多余约束⼏何不变体系;(3)6个;(4)9个;(5)⼏何不变体系,0个;(6)⼏何不变体系,2个。
2-3 ⼏何不变,有1个多余约束。
2-4 ⼏何不变,⽆多余约束。
2-5 ⼏何可变。
2-6 ⼏何瞬变。
2-7 ⼏何可变。
2-8 ⼏何不变,⽆多余约束。
2-9⼏何瞬变。
2-10⼏何不变,⽆多余约束。
2-11⼏何不变,有2个多余约束。
2-12⼏何不变,⽆多余约束。
2-13⼏何不变,⽆多余约束。
2-14⼏何不变,⽆多余约束。
5-15⼏何不变,⽆多余约束。
2-16⼏何不变,⽆多余约束。
2-17⼏何不变,有1个多余约束。
2-18⼏何不变,⽆多余约束。
2-19⼏何瞬变。
2-20⼏何不变,⽆多余约束。
2-21⼏何不变,⽆多余约束。
2-22⼏何不变,有2个多余约束。
2-23⼏何不变,有12个多余约束。
2-24⼏何不变,有2个多余约束。
2-25⼏何不变,⽆多余约束。
2-26⼏何瞬变。
3 静定梁和静定刚架3-1 (1) √;(2) ×;(3) ×;(4) √;(5) ×;(6) √;(7) √;(8) √。
3-2 (1) 2,下;(2) CDE ,CDE ,CDEF ;(3) 15,上,45,上;(4) 53,-67,105,下; (5) 16,右,128,右;(6) 27,下,93,左。
3-3 (a) 298AC M ql =-,Q 32AC F ql =;(b) M C = 50kN·m ,F Q C = 25kN ,M D = 35kN·m ,F Q D = -35kN ;(c) M CA = 8kN·m ,M CB = 18kN·m ,M B = -4kN·m ,F Q BC = -20kN ,F Q BD = 13kN ; (d) M A = 2F P a ,M C = F P a ,M B = -F P a ,F Q A = -F P ,F Q B 左 = -2F P ,F Q C 左 = -F P 。
结构力学课后习题答案[1]
![结构力学课后习题答案[1]](https://img.taocdn.com/s3/m/8c0493dc80eb6294dd886c23.png)
)e( 移位线个 1�移位角个 3 移位角个 1
)d(
)c(
。构结本基出绘并�目数量知未本基法移位的构结示图定确试 1-7
)b(
) a(
题
习
33 -7
下如图矩弯各�量知未移位角个 1 m4 m4
量知未本基定确�1� �解 C IE
m4
D Nk01
IE
B
IE2 m/Nk5.2
A )b(
图M
42 lq 2 5
图矩弯终最画�4� 得解�入代
61.53
IE
3
0 � p 2 R , 0 3 � p 1R 6 � 2 2r IE � 1 2r � 2 1r , I E 2 � 1 1r
程方解并数系定确�3�
p2
11
1
0�
R � 2 Z 2 2r � 1 Z 1 2r R � 2 Z 2 1r � 1 Z 11r
N K 0 3 � � p 2 R , N K 0 3 � p 1R 4 � � 2 2r 0 � 1 2r � 2 1r , i1 1 � 1 1r
p2
得解�入代
i3
程方解并数系定确�3�
0�
R � 2 Z 2 2r � 1 Z 1 2r R � 2 Z 2 1r � 1 Z 11r
程方型典法移位�2�
程方型典法移位�2�
0�
p1
图p M
03 � p 1R � 0 � p 1R
03
04 -7
m2
m2 数常=IE F
B E
m2
m2
D
A
m2
Nk03
C )c(
90.92 55.43
图M
81.8 19.02 54.57 02
结构力学第2章习题及参考答案

结构力学第2章习题及参考答案word文档,精心编排整理,均可修改你的满意,我的安心2第2章 习 题字体如需要请自己调整2-1 试判断图示桁架中的零杆。
2-1(a )解 静定结构受局部平衡力作用,平衡力作用区域以外的构件均不受力。
所有零杆如图(a-1)所示。
2-1 (b)解 从A 点开始,可以依次判断AB 杆、BC 杆、CD 杆均为无结点荷载作用的结点单杆,都是零杆。
同理,从H 点开始,也可以依次判断HI 杆、IF 杆、FD 杆为零杆。
最后,DE 杆也变成了无结点荷载作用的结点D 的单杆,也是零杆。
所有零杆如图(b-1)所示。
(a-(a)(b)(b-32-1(c)解 该结构在竖向荷载下,水平反力为零。
因此,本题属对称结构承受对称荷载的情况。
AC 、FG 、EB 和ML 均为无结点荷载作用的结点单杆,都是零杆。
在NCP 三角形中,O 结点为“K ”结点,所以F N OG =-F N OH (a )同理,G 、H 结点也为“K ”结点,故F N OG =-F N GH (b ) F N HG =-F N OH (c )由式(a )、(b )和(c )得(c-1)FN OG=F N GH=F N OH=0同理,可判断在TRE三角形中FN SK=F N KL=F N SL=0D结点也是“K”结点,且处于对称荷载作用下的对称轴上,故ID、JD杆都是零杆。
所有零杆如图(c-1)所示。
2-2试用结点法求图示桁架中的各杆轴力。
2-2(a)(a-33 3(a-33 345解 (1)判断零杆①二杆结点的情况。
N 、V 结点为无结点荷载作用的二杆结点,故NA 、NO 杆件和VI 、VU 杆件都是零杆;接着,O 、U 结点又变成无结点荷载作用的二杆结点,故OP 、OJ 、UT 、UM 杆件也是零杆。
②结点单杆的情况。
BJ 、DK 、QK 、RE 、HM 、SL 、LF 杆件均为无结点荷载作用的结点单杆,都是零杆;接着,JC 、CK 、GM 、LG 杆件又变成了无结点荷载作用的结点单杆,也都是零杆。
结构力学-崔恩第-复习要点

结构力学(崔恩第)复习要点第1章绪论3.支座与结点——约束(位移)——约束(反)力第2章平面体系的几何组成分析13~15.几何不变体系与几何可变体系、约束(联系)虚铰17.组成规则:刚片—联系—条件—结论(二元体、)19.瞬变体系;22.几何特性——静力特性——静定与超静定结构习题:2-1、5、9、10、14第3章静定梁和刚架31.单跨梁(截面法、微分关系、叠加法作弯矩图、作剪力图)【例3-1】38.静定多跨梁(几何组成:基本部分与附属部分、受力分析:内力特点、求解次序)42.静定平面刚架(基本类型、支反力、截面法求内力——绘制M、Q、N图、校核)习题:3-1a、b、3、7、8a、b第四章静定拱58.拱特点59.三铰拱数解法(支反力、M、Q、N——截面法)(公式—竖向荷载)64.三铰拱的合理拱轴线(荷载、三铰位置确定——内力特点)习题:4-2第五章静定平面桁架76.计算简图(组成特点、几何组成分类)78.结点法(求解次序与步骤、三角分解、零杆判断、力沿作用线移动到适当位置分解、平面汇交力系,对任一点之矩=0、对称性利用)82.截面法(力矩法、投影法、)联合应用87.组合结构(梁式杆、链杆、求解步骤)96.静定结构特性(基本特性、非荷载因素影响等)习题:5-1b、3a、f第6章结构位移计算104.位移107.虚功原理——两个状态(平衡、变形协调)113、一般公式:单位荷载法(广义位移—广义力)114.荷载作用下的位移计算(公式——梁和刚架、桁架)118.图乘法(公式、条件、常用简单图形面积与形心位置、应用)124.温度作用(公式):变形——弯曲方向125.支座移动(公式):刚性位移126.互等定理(功的互等定理、位移互等定理)习题:6-8、10、12第7章力法134.超静定结构的基本特征——静力特征、几何特征135.确定超静定次数137.力法中的三个基本概念141.力法的典型方程——物理意义:主系数、副系数——性质142.力法计算步骤155.温度变化和支座移动等因素影响—原因—力法计算133.荷载作用下超静定结构内力分布与各杆刚度的相对值有关160.对称性的利用——对称结构:对称荷载;反称荷载——内力172.超静定结构位移的计算——利用基本体系(静定结构)求原结构的位移174.校核——平衡、位移条件247.超静定结构特性第10章影响线253.概念——定义254.静力法(简支、悬臂、外伸梁)257.机动法作影响线(虚位移原理、虚位移图——步骤)多跨静定梁的影响线261.间接荷载作用(直接荷载作用——节间连直线)262.桁架影响线266.三铰拱影响线267.影响线应用——利用影响线求量值(集中荷载、分布荷载)268.最不利荷载位置(定义、最大/小值,简单情况、行列荷载—临界位置,三角形影响线)277.绝对最大弯矩(定义、行列移动集中荷载计算公式-a的+、-)278.简支梁包络图(定义、绘制方法*)279.超静定结构的影响线(机动法——虚位移图)281.连续梁的均布活载最不利位置——内力包络图习题:10-2、10、15、17。
结构力学 第三章 作业参考答案

即可作出全部的弯矩图。
9
华南农业大学 水利与土木工程学院(College of water conservancy and Civil Engineering, SCAU)
3—16 试作出图示刚架的 M 图。
20kN 50kN m D 3m E 10kN/m C FC A FA 4m B FB 4m 2m F
(1)
=> FB = 20 kN 首先可得: M DC = 10 × 2 = 40 kNim
D M DB =120 M DC =40 M DA =160
M DB = 30 × 4 = 120 kNim
在 D 结点弯矩平衡: => M DA
M DB + M DC − M DA = 0 = 160 kNim
结构力学 第三章 习题 参考答案
结构力学 第三章习题 参考答案
2005 级 TANG Gui-he(整理)
3—1 试作出图示单跨梁的 M 图和 Fs 图。
40kN
20kN/m
A 2m FAy 4m 4m FB
B 2m
40kN m 80kN m A 20kN m M(kN m) 40kN m B 10kN m
3—19 试作图示刚架的 M 图。
20kN
24 16
C
24
16
B FAx A FBy FAy
FBx
1m
2m
2m
2m
M图(kN m)
(1) (2) (3)
解:对整体:
∑M ∑F
y
A
=0
FBy × 4 + FBx ×1 = 20 × 2 FAy + FBy = 20 FAx − FBx = 0 FBx × 2 − FBy × 2 = 0
