岩体本构关系与强度理论
岩石的强度理论及破坏判据[详细]
![岩石的强度理论及破坏判据[详细]](https://img.taocdn.com/s3/m/b87c145d5ef7ba0d4b733ba7.png)
分析，库仑准则的有效取值范围由图 6-8给出，并可
用方程表示为：
σ3 σ1=σ3
1
f
2
1
f
3
f
2
1
f
2c
P β
3 1
1
1 2
c
1
1 2
c
0
σc / 2
σc
σ1
-σt
A
S
图7-8 σ1－σ3坐标系中的库仑准则的完整强度曲线
在此库仑准则条件下，岩石可能发生以下四种方式的破坏。
(1)当 0 11 11 22时cc，33岩石t属t单轴拉伸破裂； (2)当 1122cc11 c时c，t岩t石3 属3 0双0轴 拉伸破裂；
四、 格里菲斯强度理论
格里菲斯（Griffith ，1920年）认为:脆性材料断 裂的起因是分布在材料中的微小裂纹尖端有拉应力 集中（这种裂纹称之为Griffith裂纹）。
格里菲斯原理认为:当作用力的势能始终保持不 变时，裂纹扩展准则可写为：
(Wd Wc ) 0 C
式中：C为裂纹长度参数；Wd为裂纹表面的表面能； We为储存在裂纹周围的弹性应变能。
1
τ3
2
2α
式中：为t 岩石的单轴抗拉强度σ；0 σ3 t
n 为待定系数。
σ σ
σ
c
利用图 7-10中的关系，有：
σ 3
1 2
(1 3)
1 2
(1
3)
ctg 2
sin 2
1.双向压7缩应4力2圆，2.双向拉压应力圆，
3..双向拉伸应力圆 图7-10 二次抛物型强度包络线
其中：
n( t )
d ctg2
n
d
04岩石的本构关系和强度准则1
15
4.2 应变及应变状态分析
微分单元体的变形
16
4.2 应变及应变状态分析
微分单元体的变形
正应变与位移分量之间的关系
显然微分线段伸长，则正应变ε x,ε y,ε z 大于零；反之则小于零。
17
4.2 应变及应变状态分析
微分单元体的变形
剪应变与位移分量之间的关系
xy
19
4.3 岩石的应力应变关系
求解岩石力学问题是从岩石的单元微分体出发，研究微分 体的力的平衡关系(平衡方程)、位移与应变的关系(几何方程) 以及应力与应变的关系(物理方程或本构方程)，得到相应的基 本方程，然后结合岩石的边界条件，联立、积分求解这些方程， 从而求得整个岩石内部的应力场和位移场。 平衡方程和几何方程与岩石材料的性质无关，只有本构关 系反映岩石材料的性质。所谓岩石本构关系是指岩石的应力或 应力速率与其应变或应变速率的关系。在只考虑静力问题情况 下，本构关系就是指应力与应变，或者应力增量与应变增量之 间的关系。
11 12 13 11 12 13 22 23 12 22 23 21 31 32 33 13 23 33
7
4.1 应力及应力状态分析
二、一点应力状态的张量表达
20
4.3 岩石的应力应变关系
岩石在弹性阶段的本构关系称为岩石弹性本构关系，岩 石在塑性阶段的本构关系称为岩石塑性本构关系。岩石弹性
本构关系和塑性本构关系通称为弹塑性本构关系。弹性本构 关系按是否为线性又分为线弹性本构关系与非线弹性本构关 系。弹塑性本构关系按物质是否为各向同性又分为各向同性 本构关系和非各向同性本构关系。 如果外界条件不变，岩石的应力或应变随时间而变化， 则称岩石具有流变性。岩石产生流变时的本构关系称为岩石 的流变本构关系。
岩石的强度理论与本构关系
岩石的强度理论与本构关系朱浮声(东北大学土木系,沈阳110006)朱浮声,1948年6月生于黑龙江齐齐哈尔11976年毕业于东北大学,1983年获中国矿业大学工学硕士学位,1991年获东北大学博士学位11988年曾在美国南伊利诺大学作访问学者,1993年在瑞典皇家工学院任客座教授1现任东北大学土木工程系教授,辽宁省力学学会理事1主要研究方向为计算岩土力学和岩土加固技术1在国内外学术刊物上发表论文50余篇,出版5锚喷加固设计方法6等学术专著2部,译著1部1摘要本文简要介绍了岩石强度理论和本构关系的发展和现状,讨论了它们不同的特点与适用条件1关键词岩石,岩体,强度理论,本构关系1前言随着电子计算机的飞速发展和计算技术的逐步完善,对岩石强度理论和本构关系提出了更高要求,以便更真实描述岩石和岩体力学特征,求解复杂的工程岩石力学问题1由于岩石材料力学性质的某些相似性和其它历史原因,岩石强度理论和本构关系的早期研究曾大量引用了土力学成果,并提出了一些适用于岩土介质的强度理论和本构关系1随着岩石力学的发展,人们认识到,岩石和岩体的物理力学性质不仅有别于其它非摩擦工程材料,而且,与土或混凝土等摩擦材料也存在较明显差异1例如,岩石破坏包括脆性、延性及由脆性向延性转化等复杂类型;岩体的力学特性受控于岩块和不连续面的力学特性;岩石工程的稳定性通常受主要不连续面控制等1因此,近年来又提出了适用于岩石、不连续面和岩体的强度理论或本构方程式1本文旨在介绍这些理论研究的最新进展,并对已有岩土强度理论和本构关系的适用条件和局限性加以简要评价1限于篇幅,本文仅涉及与时间无关的各向同性和等向强化模型12岩土共用的强度理论和本构关系211弹性均质、各向同性或横观各向同性模型曾被广泛用于描述岩土力学特征,特别是峰值强度前的应力-应变关系,并得到了大量解析解和实用近似解1考虑到应力-应变曲线的明显非线性特性,曾将非线性弹性理论与计算机技术相结合,提出了一批数值算法,并在60~70年代的岩土力学分析中不断被引用1例如,以曲线各点的割线模量取代弹性常数,构成了各种超弹性模型[1],或以增量形式描述非线性弹性应力-应变关系,形成了亚弹性模型[2]等1但是,由于这些模型只考虑到岩土材料的弹性特征,并且,随着模型阶次增高,待定常数的数目往往过多,因而,限制了它们的广泛应用1212 理想塑性强度理论在计算岩土力学中,广泛采用了莫尔-库伦强度准则(Mohr -Coulomb)和德鲁克-普拉格准则(Drucker -Prager)1莫尔-库伦准则可以表述为R 1-B R 3=C (1)式中,B 和C 一般是常数1在主应力空间,式(1)表示一个以静水应力轴为中心轴,具有不规则六角形截面的角锥体表面(图1)1这个准则由于较好地表征了岩土介质在压缩条件下的某些弹塑性力学特征,因而得到了较广泛的应用1但是,由于忽略了中间主应力对破坏的作用,存在明显的缺陷1另外,由于屈服面在三维应力空间中存在/角隅0,给数值计算带来了诸多困难1为了解决上述问题,曾对莫尔-库伦准则进行修正,将米赛斯准则(M ises)加上一个静水应力因子,形成了著名的德鲁克-普拉格准则,不仅考虑到三个主应力对破坏的影响,并且消除了屈服面存在的角隅1这个准则可表述为A J 1+J 2=C (2)式中,J 1和J 2是主应力不变量,A 和C 是正常数1图1 莫尔-库伦准则和德鲁克-普拉格准则屈服面在主应力空间,式(2)是一个以静水应力轴为中心轴的圆锥体(图1)1它虽然克服了莫尔-库伦准则的上述缺点,但在破坏状态下,该准则给出了较大的材料体积膨胀,这与岩土介质的试验结果明显不符1我国学者俞茂由正交八面单元体的三个主应力出发,提出了双剪强度理论和适用于岩土体的广义双剪强度理论(包括屈服准则)[3],并得到了双剪统一强度理论[4]R 1-A 1+b (b R 2+R 3)=R t ,R 2F R 1+A R 31+A11+b (R 1+b R 2)-A R 3=R t ,R 2E R 1+A R 31+A (3)式中,A 和b 是常数,R t 是材料单轴抗拉强度1在主应力空间,式(3)表示一个以静水应力轴为中心轴,具有不等边十二边形截面的锥体表面1可以证明,广义双剪理论和莫尔-库伦准则在P 平面上的屈服曲线分别是各种岩土屈服准则的上限和下限1213应变硬化(软化)一般地,岩土体应力状态满足屈服准则时,将出现屈服应力随变形增大而不断增高(硬化)或降低(软化)现象1对于前者,屈服面在主应力空间是连续扩大的;对于后者,则表现为屈服面的不断收缩1当满足破坏条件时,将形成屈服面与破坏面(残余破坏面)相互重合,而屈服面与破坏面始终相一致的情况仅发生在完全塑性材料中1因此,为了建立岩土介质完整的本构关系,必须同时考虑屈服准则、流动法则和软(硬)化定律等三方面1其中,对材料硬(软)化特图2帽盖模型屈服面性的研究多借助于控制该材料硬化特性的屈服面,称之为硬化帽盖(图2)1根据不同的岩土介质和试验,提出了不同形状的帽盖[5],其一般表达式为f1(J1,J c2,k1)=0(4)式中,J c2为应力偏量第二不变量,k1为硬化参数1除了屈服帽盖,岩土帽盖模型还包括一个固定屈服面,例如,通常以初始德鲁克-普拉格破坏面与米赛斯屈服面光滑相接表示1一般地,固定屈服面取为强度理论限定的破坏面f2(J1,J c2)=0(5) 3岩石和岩体强度理论与本构关系如前所述,在一定条件下,可以使用相同强度理论分析岩土力学问题1但在一般情况下,岩石的破坏面具有如下特征:(1)在主应力空间,破坏曲面在原点附近的顶角是张开的;(2)岩石破坏包络线,即破坏面在伦杜列克面(Rendulic)上的子午线不是直线,而是曲线;(3)岩石有抗拉强度1通常,前述岩土体的屈服和强度准则都可以满足条件(1)和(3),为了满足条件(2),需要进行必要修正1311岩土强度理论的修正为了使强度理论满足上述条件(2),从而应用于岩石力学问题分析中,早期的工作多采用对破坏曲线近似逼近方法,例如,以双曲线或抛物线取代莫尔-库伦准则中的直线等1更一般的方法是直接采用莫尔强度理论,并通过对P平面上多边形屈服曲线角点的光滑化得到各种角隅模型[6]1典型范例是关于岩石的吉姆-拉德破坏准则(Kim-Lade)1拉德曾提出如下土体两参数破坏准则[7](J21/J3-27)(J1/P a)m=G1(6)式中,P a是该应力状态下大气压力,m和G1是常数,其中,破坏面在原点附近的张角随G1变化,而子午线曲率随m值变化(图3)1在主应力空间,拉德准则是一个以静水应力轴为中心轴,具有带圆角三角形截面的子弹头形曲面,该曲面顶点位于原点1图3拉德破坏准则破坏面[7]为了得到适用于岩石的强度准则,吉姆和拉德对式(6)进行了修正,即考虑岩石凝聚力和抗拉强度的作用,在式(6)的法向主应力分量叠加一个常应力项aP aR x=R x+aP aR y=R y+aP a(7)R z=R z+aP a研究式中,a是一个无因次常数,aP a的值反映了岩石的抗拉强度1不难看到,这个三参数强度准则较好地反映了岩石破坏面的上述3个特征,同时,原作者通过87组不同岩石的试验数据对模型进行了多次验证1312岩石的脆性破坏准则岩石三轴试验结果表明,在侧限压力较低时,岩石试件的破坏应力随变形增大而不断降低,在很小或完全未出现永久变形的情况下发生突然的脆性破坏1随着侧限压力增大,通常出现由脆性向延性破坏的转变,这种现象可以由塑性变形机制来解释(岩石破裂流动与颗粒滑移等)1岩石脆性破坏准则研究仍处于发展阶段1其中,格里菲斯理论(Griffith)是一个基于理想脆性假定的二维准则,由此理论预测的脆性材料单轴抗压与抗拉强度R c和R t的关系式R c=-8R t1由于岩石裂纹随围压增高将出现闭合,此时应考虑闭合裂纹表面间摩擦作用,因此,提出了关于岩石修正的格里菲斯理论[8]S=2R t+R n tg<(8)式中,S和R n为裂纹面上切应力与法应力,<为内摩擦角1显然,这种修正是将低应力条件下的格里菲斯理论转化为高应力条件下的莫尔理论1M urrell考虑到中间主应力的作用,提出了一个三维脆性破坏准则,这个准则预测R c/P a=12 |R t/P a|1在主应力空间,这个准则表示为一个以静水压力轴为中心轴的椭球面与一个处于拉应力区的四棱锥面相切得到的曲面(图4)1需要指出,这个准则虽计及中间主应力影响,并具有弯曲的子午线,但它的基本出发点却是基于单轴抗拉强度判据1图4M urrell三维脆性破坏准则破坏面[9]313岩石破坏的经验准则由于岩石和岩体力学特征的复杂性,针对不同岩石和荷载条件提出了大量实用经验准则1其中,霍克-布朗准则是应用最广的1这个准则依据格里菲斯和修正格里菲斯理论的基本概念,采用/试凑法0得到了分别适用于岩石和岩体的经验准则[10]R1=R3+m R c R3+S R c2(9)式中,m和S是表征岩石或岩体性质及其破坏范围的常数1在主应力空间,这是一个以静水应力轴为中心轴、具有6条抛物线围成的6边形截面的锥体表面(图5)1这个准则给出R c=-(7~25)R t,这与大量试验结果接近,因而,得到较广泛应用1图5霍克-布朗经验破坏准则破坏面4节理和节理岩体天然岩体由节理和岩块组合而成1对于起控制作用的节理,通常采用/节理单元0来模拟1早期的节理单元是一个非线性弹性模型,给出了节理面两侧力-位移的增量表达式1为了考虑节理延性和切向-法向作用的相互影响,普遍采用了遵循莫尔-库伦准则的弹塑性节理模型1但是,如果采用关联流动法则,这个模型将产生一个无法消除的剪胀率1因此,罗伯茨等(Roberts)建议用非关联流动法则,相应塑性势函数Q为Q=|R s|-R n tg W(10)式中,R s和R n是节理切向和法向应力,W是节理剪胀角,可由试验确定1由于试验水平和理论的限制,节理面的理论模型尚不成熟,在应用中最可靠、最广泛的是巴登(Barton)提出的经验准则[11]F=|R s|-R n tg<(JRC lg(JCS/R n)+<r)=0(11)式中,JR C是节理面粗糙度系数,JCS是节理面抗压强度,<和<r分别是节理面摩擦角和残余摩擦角1这些参数都可以由简单原位试验得到1国际岩石力学学会制订了规范用于获取和解释这些参数,从而,推动了这一准则的普遍应用1对于受多组节理切割的岩体,由于很难同时模拟这几组节理,通常需找到节理岩体的本构关系1目前,此项研究仍处于开始阶段,应予充分重视1对于等距排列的平行节理(未充填),若节理连续分布且尺寸远小于岩体或结构物尺寸,提出了/节理岩体层状模型0(Multilaminate model)[12]1这实质上是一种等效材料模型,在最终形成的弹塑性或粘弹塑性本构关系中,以不同力学模型分别描述各层岩石和节理面的力学特征,并同时考虑它们对岩体力学的影响,得到节理岩体总的粘塑性应变速率ÛE VP=C i3F i45Q i5R+E nJ=1C J3F J45Q J5R J5R J5R(12)式中,F i和F J分别是第i层岩石和第J层节理的屈服(破坏)函数,Q i和Q J为相应塑性势,R J 表示J组节理面上法向和切向应力,C i和C k是相应粘性参数1式(12)中等号右端第一项与岩石特性有关,第二项则涉及n个节理面的力学特征1如果不考虑岩体的流变特性,采用关联流动法则,可以给出弹塑性节理岩体的类似表达式15结束语(1)非线性弹性模型曾在岩土力学中应用1由于高次模型待定常数过多,且为区分加、卸载情况需给出复杂应力状态下加载条件,限制了它们的使用范围,在岩石力学中应用较少,并主要用于比例加载条件下1(2)莫尔-库伦准则和德鲁克-普拉格准则在岩土力学分析中得到广泛应用1前者的缺点是忽略了中间主应力的作用,并且,在三维主应力空间存在屈服面角隅,给计算带来了困难1后者虽然克服了上述问题,但在破坏状态下给出较大体积膨胀,这与岩土试验结果严重不符1广义双剪强度理论及其角隅模型展示了广阔应用前景,但需大量试验与工程验证1各种帽盖模型考虑到岩土介质的应变硬(软)化,计及剪胀或剪缩,但公式推导中加入种种补充假定,模型的可靠性需进一步验证1(3)岩石、岩体和土体的强度理论和本构关系相似又相区别1吉姆-拉德的三参数岩石破坏准则经过87组岩样检验1有较高可信度1各种岩石脆性破坏准则都源于单向抗拉强度判据,它们的可靠性有待检验1岩石和岩体经验破坏准则在应用中占重要地位,其中,霍克-布朗准则适用于R1>314R3条件下延性岩石(体),在无控制作用节理存在的岩体工程分析中得到普遍应用1(4)在主要节理面的模拟中采用了莫尔-库伦准则和关联/非关联流动法则1已提出的8参数节理模型可用于研究节理加载-卸载-再加载过程[12],但最可靠、应用最广的仍是巴登经验准则1对无控制性不连续面的节理岩体提出了等效模型和相应本构关系1节理岩体的强度理论和本构关系研究仍处于初始阶段,是目前主要研究方向之一1参考文献1Fung Y C1Foundations of Solid M echanics1Prentice-Hall,19652T ruesdell C1Hypoelas ticity1J Ration M ech A nal,1955,4:83~1333俞茂等1双剪应力强度理论及其推广1中国科学A辑,1985,28(11)4俞茂1统一强度理论及其应用1强度理论研究新进展1西安:西安交通大学出版社,1993133~445S chofield A N,Worth C P1Critical S tate Soil M echanics1M cGraw-Hill Book Company,19686Zienkiew icz O C,Pande G N1Som e useful forms of isotropic yield surfaces for soil and rock mechanics1Finite Elements in Geome-chanics1Gudehus G(eds)1John Wiley&Sons,19777Kim M K,Lade P V1M odelling rock strength in three-dimensions1Int J Roc k M ec h M in S ci&Geomech,1984,21:21~338M cCli ntok F A,Walsh J B1Fri ction on Griffith cracks under pressure1Proc4th US Nat Congr Appl M ech,196211015~10219M urrel l S A F1A cri terion for bri ttle fracture of rocks and concrete under triaxial stress and the effect of pore pres sure on the creter-i on1Proc5th US S ym p Rock M ech,Pergamon Press,19631563~57710Hoek E,Brown E T1岩石地下工程1连志升等译,北京:冶金工业出版社,198611Barton N R,Choubey V1The shear strength of rock joints in theory and practice1Rock M ech,1977,10:1~5412Pande G N,Beer G,Williams J R1Numerical M ethods in Rock M echanics1W i ley,199013Pande G N1A constitutive model of rock joints1Proc Int Symp Fund Rock Joints1Center Pub11985(1996年5月31日收到第1稿,1996年8月12日收到修改稿)(上接第7页)29Levy D,Powell K,van Leer B1An i m plementati on of a grid-i ndependent upwind scheme for the Euler equati ons1AIAA89-1931-CP 30Rumsey C L,van Leer B,Roe P L1A grid-independent approximate Riemann solver w ith applications to the Euler and Navier-Stokes equations1J Comput Physics,1993,105(2):306~32331Roe P L1Discrete models for the numerical analysis of time-dependent multidimensional gas dynamics1J Comp ut Phys,1986,63: 458~47632Roe P L1Discontinuous sol utions to hyperbolic system s under operator splitting1Nu merical M ethods f or Par tial Diff erential Equa-tions,1991,7:277~29733Lacor C,Hirsch Ch1Genuinely upw ind algorithms for th e multidimensionalEuler equations1AIA A J,1992,30(1):56~6334Parpia I H,M ichalek D J1Grid-independent upw ind sch eme for multidimensi onal flow1AIA A J,1993,31(4)135Hartwich P M1Comparison of coordinate-i n variant and coordinate-aligned u pw ind for the Euler equations1A IAA J,1994,32(9): 1791~179936van Leer B1Advancing the accuracy and efficiency of explicit Euler solvers1AIAA90-001237Zhang X D,Trepanier J-Y,Reggio M,et al1Grid i nfluence on upw ind schemes for Euler and Navier-Stokes equations1A IAA J, 1996,34(4):717~72738Abarbanel S,Duth P,Gottlieb D1Splitting methods for low M ach number Euler and Navier-Stokes equations1Comp uters&Fluids, 1989,17(1):1~12(1996年11月29日收到第1稿,1997年3月30日收到修改稿)。
岩石的本构关系和强度(公式)
246
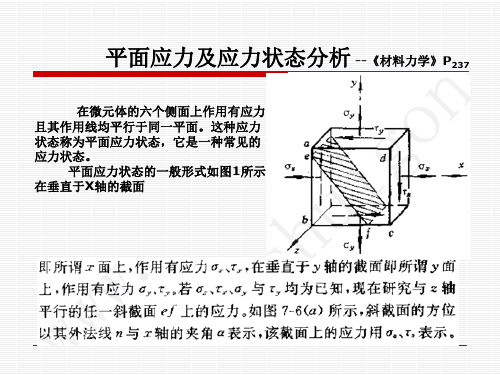
平面应力及应力状态分析
极限莫尔圆公式：
几何图形推导
对于A点：莫尔圆半径
R
1 3
2
在△ABO1中：
A A B R cos
O1 B R sin
B 1 R O1 B 1 1 3
2 R sin 1
平面应力及应力状态分析
平面应力及应力状态分析
平面应力及应力状态分析
根据几何关系/三角相似关系：
OC BO1 sin AC AO1
AO c ctg 1 3 BO1 2
C A O
B
1 3 c ctg
2
AO1 AO OO1
面法线的平衡方程为：
237
N 0
即：
dA ( x dAcos ) sin ( x dAcos ) cos ( y dAsin ) cos - ( y dAsin ) sin 0
T 0 沿斜面切向的平衡方程为：
由此得出
即：
dA ( x dAcos ) cos ( x dAcos ) sin ( y dAsin ) sin ( y dAsin ) cos 0
2
1 sin 2 1 sin 2
1 tg 1 tg 2 2 1 3 1 tg 1 tg 2 2
2
0 0 1 3 tg 45 2C tg 45 2 2
x y
sin 2 x cos 2
平面应力及应力状态分析 --《材料力学》P
237
岩石的本构关系和强度(公式)
平面应力及应力状态分析
计算岩石的抗压强度
ctΒιβλιοθήκη 1 sin o 2C cos c 2C 2Ctg 45 1 sin 2 1 sin
抗拉强度
2C cos Rt 1 sin
内聚力
C
C
t c
2
2
1 sin 2 1 sin 2
1 tg 1 tg 2 2 1 3 1 tg 1 tg 2 2
2
0 0 1 3 tg 45 2C tg 45 2 2
1 3
2
1 3
2
sin
1 1 1 1 n 1 3 1 3 sin 1 3 1 3 cos 2 2 2 2 2 1 1 f 1 3 cos 1 3 sin 2 2 2
极值应力与主应力
237
平面应力及应力状态分析 --《材料力学》P
极值应力与主应力
237
平面应力及应力状态分析 --《材料力学》P
极值应力与主应力
237
平面应力及应力状态分析 --《材料力学》P
极值应力与主应力
237
平面应力及应力状态分析 --《材料力学》P
极值应力与主应力
237
平面应力及应力状态分析 --《材料力学》P
O1
1 3 / 2 sin 1 3 / 2 c ctg
平面应力及应力状态分析
莫尔-库伦破坏准则：
1
3 / 2 sin 3 / 2 c ctg
岩石力学名词解释
一.岩石的物理力学性质1.岩体：位于一定地质环境中，在各种宏观地质界面（断层、节理、破碎带等）分割下形成的有一定结构的地质体。
由结构面与结构体组成的地质体。
2.岩石：是经过地质作用而天然形成的一种或多种矿物的集合体。
具有一定结构构造的矿物（含结晶和非结晶的）集合体。
3.岩（体）石力学：是力学的一个分支学科，是研究岩（体）石在各种力场作用下变形与破坏规律的理论及其实际应用的一门基础学科。
4.结构面：指在地质历史发展过程中，岩体内形成的具有一定的延伸方向和长度，厚度相对较小的宏观地质界面或带。
5.岩石质量指标（RQD）：指大于10cm的岩芯累计长度与钻孔进尺长度之比的百分数。
6.空隙指数：指在0.1MPa压力条件下，干燥岩石吸入水的重量与岩石干重量的比值。
7.软化性：软化性是指岩石浸水饱和后强度降低的性质。
8.软化系数：指岩石试件的饱和抗压强度与干燥状态下的抗压强度的比值。
9.膨胀性：是指岩石浸水后体积增大的性质。
10.单轴抗压强度：是指岩石试件在单轴压力下达到破坏的极限值。
，11.抗拉强度：是指岩石试件在单向拉伸条件下试件达到破坏的极限值。
12.抗剪强度：指岩石抵抗剪切破坏的能力。
13.形状效应：在岩石试验中，由于岩石试件形状的不同，得到的岩石强度指标也就有所差异。
这种由于形状的不同而影响其强度的现象称为“形状效应”。
14.尺寸效应：岩石试件的尺寸愈大，则强度愈低，反之愈高，这一现象称为“尺寸效应”。
引起结构面尺寸效应的基本因素：结构面的强度与峰值剪胀角。
15.延性度：指岩石在达到破坏前的全应变或永久应变。
16.流变性：指在外界条件不变时，岩石应变或应力随时间而变化的性质。
17.蠕变：指在应力不变的情况下，岩石的变形随时间不断增长的现象。
18.应力松弛：是指当应变不变时，岩石的应力随时间增加而不断减小的现象。
19.弹性后效：是指在加荷或卸荷条件下，弹性应变滞后于应力的现象。
20.峰值强度：若岩石应力—应变曲线上出现峰值，峰值最高点的应力称为峰值强度。
岩石力学第四章 岩石本构关系与强度理论
yx
14
下面推导平面应力问题的平衡微分方程，对单元体列平
衡方程：
Fx 0 :
(
x
x x
dx ) dy
1
x
dy
1
(
yx
yx y
dy )
dx
1
o
x
yx
y
P A xy X x B C y
D
x
x
x
dx
Y
xy
xy x
dx
y
yx y
y
yx y
dy
dy
yx dx 1 X dx dy 1 0
无外力作用。
y
x
注意：平面应力问题z =0，但 z 0 ，这与平面应变
问题相反。
11
2、平面应变问题 很长的柱体，在柱面上承受平行于柱面并且不沿长度变
化的面力，同时体力也平行于柱面并且不沿长度变化。
εz = 0 τzx = 0 τzy = 0
如：水坝、受内压的圆柱管道和长水平巷道等。
y
x
P
x
图 2－2
是坐标的已知函数。
23
2、应力边界条件
当物体的边界上给定面力时，则物体边界上的应力应满 足与面力相平衡的力的平衡条件。
l(x)s m(yx)s X
m(y)s
l(xy)s
Y
其中 X 和 Y 为面力分量，( x )s、( y )s 、( xy ) s 、( yx )s 为边界上的应 力分量。
当边界面垂直于 x轴时，应力边界条件简化为：
变分量与应力分量之间的
关系如下：
x
1 E
x
y
z
y
1 E
y
第7章岩体本构关系与强度理论
σ σc
σ
利用图7-10中的关系，有：
σ3
1 2
(1 3)
1 2
(1
3)
ctg 2
sin 2
1.双向压7 缩应4力2圆，2.双向拉压应力圆，
3..双向拉伸应力圆 图7-10 二次抛物型强度包络线
其中：
n( t )
1 3 2
sin 2
(
1 3 )2 2
2
(
1
3
)
2
规定：
1、σ1为最大主应力 、σ2 为中间主应力、 σ3 为最小主应力 ；
2、压应力为正，拉应力为负，剪应力以逆时 针为正。位移与应变的规定也一样。
二、 岩石弹性本构关系 1．平面弹性本构关系
据广义虎克定理有：
成E/（1- μ 2） ，μ换成μ/（1- μ）。
2. 空间问题弹性本构方程
x
1 E
x
( y
z )
y
1 E
y
( z
x )
z
1 E
z
( x
y )
yz
2(1 E
) yz , zx
1
1 f f2
2
f
f
)
σ1
1 tan2 c
1 3tg 2 (45 / 2) 2ctg(45 / 2)
σc
arc( tan2 θ)
第四章-岩石本构关系与强度理论
0
0t + 0
设初始条件 t=0
=
0
K1
+0=
0
K1
0 =
0
K1
4.4 岩石流变理论
4.4.2 流变模型理论
组合模型——马克斯威尔(Maxwell)体
蠕变方程:
=
1
2
0t +
0 =
0
K1
0
K1
蠕变曲线
0
o
等速蠕变，且不稳定
t
(a)蠕变曲线
4.4 岩石流变理论
是弹性变形后的一个阶段，材料进入塑性的特征是当荷
载卸载以后存在不可恢复的永久变形。
（1）屈服条件：材料最先达到塑性状态的应力条件。
（2）加-卸载准则（塑性发展或退化）：材料进入塑性状态
以后继续塑性变形或回到弹性状态的准则。
（3）本构方程：材料在塑性阶段的应力应变关系或应力增
量与应变增量间的关系。
1
=
+
K1
2
= 0e
−
K1
2
0
t
o
t
(b)松弛曲线
4.4 岩石流变理论
4.4.2 流变模型理论
组合模型——马克斯威尔(Maxwell)体
瞬变应变量
描述岩石的特点
具有瞬变性
有不稳定的蠕变
有松弛
有残余（永久）变形
0 =
无弹性后效
0
0
K1
o
0
=
1
+ t
——岩石的蠕变特性对于岩石工程稳定意义重大，重点
第7次课 7.3强度理论
I1 ii 1 2 3 x y z
为应力第一不变量；
J2
1 1 2 2 2 si si 1 2 2 3 3 1 2 6
为应力偏量第二不变量；
2 sin 3 (3 sin )
利用这些式子可判断岩石试件是否破坏。
2、双曲线型 砂岩、灰岩、花岗岩等坚硬、较坚硬岩石的强度包 络线近似于双曲线（图 7-11 ) ，其表达式为：
τ
t tan 2 1 t t
2 2
式中，φ1为包络线渐近线的倾角，
渐
近
线
包
络
线
1 c tan 1 3 2 t
限状态时，滑动平面上的剪应力达到一个取决于正
应力与材料性质的最大值”，并可用下列函数关系表示： f
上式在 坐标系中为一条对称于 轴的曲线，它可 通过试验方法求得，即由对应于各种应力状态（单轴拉伸、单 轴压缩及三轴压缩）下的破坏莫尔应力圆包络线，即各破坏莫 尔圆的外公切线（图7-9) ，称为莫尔强度包络线给定。
一、 库仑强度准则
岩石的破坏：剪切破坏。 认为岩石的剪切强度等于岩石本身的粘结力和剪切面上由法 向力产生的摩擦阻力。平面应力中的剪切强度准则（图）为：
| | c tan
σ1 σ σ3 θ
或
| | tan c
（7-27）
L
σ3
Φ c
D
A
σ1 图7-6
O
σ3
B
四、Griffith强度准则的三维推广 （Murrell强度准则）
Murrell将Griffith强度准则从二维推广到三维，得到强度准则
第七章 岩体本构关系与强度理论
14
最易扩展的裂纹端部附近的最大切向拉应力
第 七 章 岩 石 的 破 坏 判 据
( 1 3 ) 2 b m 4( 1 3 )
用单轴拉伸破坏时的抗拉强度来表示临界值
( 1 3 ) 2 8 t 1 3
1 3 1 2( 1 3 )
σb：椭圆周边切向应力； m=b/a，a为椭圆长半轴，b为椭圆短半轴； α：椭圆偏心角。
11
假定： （1）岩体内裂纹形状是一个很扁平的椭圆； （2）岩石性质的局部变化忽略不计； （3）岩体内裂纹与裂纹之间相互不发生影响； （4）椭圆形裂纹周围的应力系统作为平面问题处理。
裂纹尖端附近，α→0，故sinα→α，cosα→1
12
2、强度准则 （1）以σy 、τxy表示的强度准则
第 七 章 岩 石 的 破 坏 判 据
当单向拉伸破坏时，τxy=0，σy=σt，代入得
b m t t 2 t
或
2 1/ 2 2 t y ( t2 xy )
4 t ( t y )
d b 0 d
sin 2 0
( 1 3 )
2 1 2 3 2 1
12 32
2 3
0
1 2
0
2 cos 2 2 2
1 3 cos2 2(1 3 )
β称为破裂发生角
二、莫尔判据
第 七 章 岩 石 的 f ( ) 破 坏 判 •判断岩石中一点是否会发生剪切破坏时，可在莫尔包络 据 线上，叠加上反映实际研究点应力状态的莫尔应力圆， 如果应力圆与包络线相切或相割，则研究点将产生破坏； 如果应力圆位于包络线下方，则不会产生破坏。 5
33岩石力学及工程岩石本构关系及强度理论
主要包括本构方程、蠕变方程和松弛方程。
1.经验方程法 根据岩石蠕变试验结果，由数理统计学的回 归拟合方法建立的方程。通常形式为： t 0 1 t 2 t 3 t 2.微分方程法 将岩石介质理想化，归纳成各种模型，模型 可用理想化的具有基本性能（弹性、塑性和 粘性）的元件组合而成。通过这些元件不同 形式的串联和并联得到一些典型的流变模型 体。
1.平衡微分方程
x yx fx 0 x y xy y f 0 y x y
2018/9/18 3
2.几何方程
u x x v y y v u xy x y
2018/9/18
16
三、粘性元件（牛顿体N） 1.定义 牛顿流体是一种理想粘性体，即应力与应变速率成 正比，用符号N表示 。 2.力学模型
图3-4 牛顿流体力学模型及其动态
2018/9/18 17
3.本构方程
d 或 dt
1
将（5-13）式积分，得：
t C
2018/9/18
19
3.4.4 组合流变模型
三种基本元件进行组合时应力、应变的计算规则： 1.串联组合体中各元件的应力相等；应变等于各元件应 变之和。 2.并联组合体中各元件的应变相等；应力等于各元件应 力之和。
5.4.4.1 圣维南体（St.V:H-C）
一、力学模型
图3-5 圣维南体力学模型
2018/9/18 20
2018/9/18 27
三、蠕变方程 0 后，保持 如果在 t 0 时，施加一个不变的应力 恒定，根据本构方程可得： 0 k
0 解上述微分方程，代入初始条件，可得蠕变方程：
二讲、本构关系和强度理论
2）
单轴抗压强度的影响因素
（1）承压板给予单轴抗压强度的影响(摩擦力和刚度)
（2）试件尺寸和形状对单轴抗压强度的影响
方形试件的四个边角会产生明显的应力集中现象。试 件的强度通常随其尺寸的增大而减小。高径比在2～3时， 岩石的单轴抗压强度值趋于稳定。 （3） 加载速率对单轴抗压强度的影响
岩石的单轴抗压强度通常随加载速率的提高而增大。 （4）环境对岩石单轴抗压强度的影响 含水量的影响（软化系数）、温度的影响。
图 1-24 根据岩石强度曲线判断岩石破坏状态示意图
图 1-25 斜直线强度曲线
4) 格里菲斯强度理论 1） 格里菲斯强度理论的基本思想 （1） 在脆性材料内部随机地分布着扁平的（用橢圆）裂 纹，在外力作用下，微裂纹尖端附近的应力很大时，裂 纹开始扩展。 （2） 理论分析：裂纹将沿着与最大拉应力成直角的方向 扩展。在单轴压缩的情况下，裂纹最终向最大主应力的 方向过渡，类似于单轴压缩的情况下的劈裂现象。 （3） 当作用在裂纹尖端附近的有效应力达到形成新裂纹 所需能量时，裂纹开始扩展，其表达式为：
1) 位移边界гd，即全部边界上的位移是已知的；
2) 面力边界гt，即全部边界上的面力是已知的；
3) 混合边界，即部分边界（位移边界гd）上的位移 是已知的；而其余边界（面力边界гt）上的面力 是已知的。
边界条件是求解弹性力学问题的重要条件，在位移 边界条件中，所研究物体的边界上的位移分量已知，设 u,v为物体的边界位移。
1e
E
t t1
4 岩石的强度理论 1） 平面问题的简化 平面应力问题，主要特征为：σz＝0 εz≠0。
平面应变问题，主要特征为：σz≠0 εz＝0。
二维的应力状态
第7张 岩体本构关系与强度理论
（2）塑性状态的加-卸载准则
塑性加载：对材料施加应力增量后，材料从 一种塑性状态变化到另一种塑性状态，且有新的 塑性变形出现； 中性变载：对材料施加应力增量后，材料从一 种塑性状态变化到另一种塑性状态，但没有新的 塑性变形出现； 塑性卸载：对材料施加应力增量后，材料从塑 性状态退回到弹性状态。
（3）本构方程
典型岩石蠕变方程：幂函数方程、指数方程、幂指数对数混合方程
2. 理论模型模拟法
将介质理想化，归纳成各种模型，模型可用理想化的具有基本性能（包括 弹性、塑性和粘性）的元件组合而成。
岩石的长期强度:由于流变作用，岩石强度随外载
作用时间的延长而降低，通常把作用时间 度（最低值）称为长期强度。 的强 t
（1）屈服条件：塑性状态的应力条件。
（2）加-卸载准则：材料进入塑性状态后继续塑性变形 或回到弹性状态的准则，通式写成：
式中： 垂直于 轴的平面上平行于 轴的应力 j i ij
( ij , Ha ) 0
(i x, y, z;， j x, y, z) a 1,。 2 为某一函数关系， H 为与加载历史有关的参数， a
0 -σ t
σ3
σ σ 1=
3
P β
σ c/ 2 A σc σ1
值，而是无限增长直到破坏，这种蠕变称为不稳定蠕变。这是 典型的蠕变曲线，根据应变速率不同，其蠕变过程可分为三个 阶段，即减速蠕变阶段或初始蠕变阶段、等速蠕变阶段及加速 蠕变阶段。
在一系列的岩石流变试验基础上建立反映岩石流变性质 的流变方程，通常有二种方法：
1．经验法
岩石蠕变经验方程：
ε ε 2( t) ε 1( t)
砂岩 0.65
白垩 0.62
粘质页岩 0.50
岩石力学第四章岩石本构关系与强度理论PPT课件
介绍了岩石本构关系的定义、分类和特点 ，以及不同类型本构关系的适用范围和局 限性。
介绍了岩石强度理论的定义、分类和特点 ，以及不同类型强度理论的适用范围和局 限性。
岩石本构关系与强度理论的实验 研究
介绍了实验研究在岩石本构关系与强度理 论中的重要性，以及实验研究的方法和步 骤。
岩石本构关系与强度理论的应用 实例
岩石力学第四章：岩石本构关系与 强度理论
目录
• 引言 • 岩石本构关系 • 岩石强度理论 • 岩石破坏准则 • 本章总结与展望
01 引言
课程背景
01
岩石力学是一门研究岩石材料在 各种力场作用下的行为和性能的 科学。
02
本章重点介绍岩石的本构关系和 强度理论，为后续章节的学习奠 定基础。
本章目标
探索新的应用领域
将岩石本构关系与强度理论应用到更广泛的领域，如环境工程、地质 工程和地震工程等，为解决实际问题提供更多帮助。
结合数值计算方法
将岩石本构关系与强度理论结合数值计算方法，实现更加高效、精确 的数值模拟和分析，为工程设计和优化提供更多支持。
THANKS FOR WATCHING
感谢您的观看
3
该准则适用于分析简单应力状态下的岩石破坏， 但在复杂应力状态下需要考虑其他因素。
应变能密度准则
应变能密度准则是基于岩石在受力过 程中储存的应变能密度来描述其应力 状态。
当应变能密度达到一定阈值时，岩石 会发生破坏。该准则适用于分析岩石 在复杂应力状态下的破坏机制。
莫尔-库仑强度理论
01
莫尔-库仑强度理论是岩石力学中最常用的强度理论之一。
弹性本构关系
描述
弹性本构关系描述了岩石在受力后立即发生的弹性变形阶段的应力应变关系。
岩石力学岩体的本构关系与强度理论
eij
si0j
(c 2G
3ip ) 2i0
si0jc
(1
2G
3ip ) 2c i0
eij
sij(21G
3ip ) 2i
令
3G ip ，有 3ip
i
2i
2G
所以： eij
1 2G
sij
这就是Hencky 本构方程，它 包括了弹性变形与塑性变形
eij
eiej
eipj
1 2G
sij
⑶ 应变偏量与应力偏量成比例
（2）非稳定蠕变：岩石承受的恒定荷载较大，当岩石应力超过 某一临界值时，变形随时间增加而增大，其变形速率逐渐增大，最 终导致岩体整体失稳破坏。
（3）岩石的长期强度：岩石的蠕变形式取决于岩石应力大小， 当应力小于某一临界值时，岩石产生稳定蠕变；当应力大于该值时， 岩石产生非稳定蠕变。则将该临界应力称为岩石的长期强度。
可见，σ、ε与时间t无关。
2、粘性介质及粘性元件（牛顿体）
d dt
tc
加载瞬间，无变形 即当t=0时,σ=σ0,ε=0,则 c=0
σ2
ωσ σ1
σ3
e2
ωdε e1
e3
3、Levy-Mises本构方程 因为ε0=0，所以eij=εij，εij=ε0δij+eij
⑴应变偏量的增量与应力偏量的关系
由假定⑴，并参照Page57和Page21
de1p s
de2p s
de3p s
1
2
3
d ip cos d
2 3
i
cos
d ip cos(d
⑴Lode试验 Lode参数代表Mohr圆心的相对位置
=2
岩体本构关系与强度理论
( m ) 2 2 4 m t (3)
（3）式是满足强度判据的极限莫尔应力圆的表达式
（3）式对
m 求导得
2( m ) 4 t m 2 t (4)
把（4）式带入（3）得
(2 t ) 4( 2 t ) t (5)
2
2( c 2 t )
2
c2
( c t ) ( 1 3 2 t ) 4( c 2 t ) 2
( 1 3 )
Kf 3 cos 3 sin
2
C
破坏判据小结
一、库仑--纳维尔判据
C tg 1
2C 3 ( 1 f
2
f)
1 f 2 f
适用条件：低应力或坚硬、较坚硬的岩石的剪切破坏.
二、莫尔判据
1. 斜直线型：同库仑--纳维尔判据 2. 二次抛物线型：
t
=８，
2. 适用脆性岩石拉破坏。
修正的格里菲斯判据（考虑摩擦效应f,C）
2 t f 1 3
1 f 2 f 1 f 2 f 4 t 1 f 2 f 3 1 f 2 f 1 f 2 f c
四、八面体强度判据八面体：空间坐标中每个卦限取一等斜面，八个等斜面构成的 多面体 判据认为：岩石破坏是八面体上的剪应力（τ 8）=临界值引起。 八面体应力
3 t
( 1 3 ) 2 8 t 1 3
Griffth准则图解
Grriffith强度准则评价：
优点： ①岩石抗压强度为抗拉强度的8倍，反映了岩石的真实情况； ②证明了岩石在任何应力状态下都是由于拉伸引起破坏；
③指出微裂隙延展方向最终与最大主应力方向一致。
岩石力学-岩石本构关系与强度理论
岩石的本构关系分类: 弹性本构关系（线性、非线性） 塑性本构关系 弹塑性本构关系（各向同性、非各向同性）
岩石破坏形式:1.断裂破坏 2.流动破坏（塑性变形活着流动现象)
在弹性体内的任意一点P，沿x轴和y轴的方向取两个微小在度
的线段PA＝dx和PB=dy，受力后，P，A，B三点移动到P′，
A′，B ′,现以u，v表示P点在x方向和y方向的位移分量，则A
点在x方向的位移分量为u＋
，u dx
x
线段PA的正应变是:
B点在y方向的位移为
，因此，线段PB的正应变是：
在分析PA，PB两线段之间直角的改变，也就是剪应变
xy
即剪应变 γxy ；
综合以上正应变、剪应变求解公式，可得平面问题中的几何方程；
当物体的位移分量完全确定时，应变分量就可以完全确定。 应变分量完全确定时，位移分量却不能完全确定。物体的位移 不但与物体的变形有关，还与物体的刚体运动有关。 平衡方程和几何方程与材料的性质无关；只有本构关系反映材
料的性质。 岩石本构关系：是指岩石的应力或应力速率与其应变或应变速 率的关系。 若只考虑静力问题，则本构关系是指应力与应变，或者应力增 量与应变增量之间的关系。
这两个微分方程中包含着三个未知函数 σx σy τyx=τxy， 是一个超静定问题。还必须考虑变形和位移才能求解。
4.1.2几何方程
物体在外力作用下将产生形状和尺寸的改变， 这种改变使物体内各点的位置发生了变化，即 各点都有位移。现在推导应变（单位长度的变 形）分量和位移之间的关系，也就是平面问题 的几何方程。
剪应变
一部分是x方向的线段PA向y方向的线段PB的转角 a yx 。
a 另一部分是y方向的线段PB向x方向的线段PA的转角
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Rockmass Mechanics
第七章 岩体本构关系与强度理论
概述 岩石的本构关系 岩石强度理论 岩体变形及本构关系 岩体破坏机制及破坏判据
概述
－－岩体的力学性质表现为弹性、塑性和粘性或三者之间的组合，如
粘弹性、弹粘性、弹塑性、弹塑粘性等。
如何求解岩体的基本力学问题呢？
3
(12c)1
1 3c
3(12)t
那么最大正应变强度判据可写成：
f C tg
1 1 3 c
当岩石应力条件满足以上判据时，岩石发生张破裂。取其中最小的
比较。 该强度理论适用于无围压和低围压及脆性岩石。
0
0
2. （二次）抛物线型 岩性较坚硬至较弱的岩石，
如泥灰岩、泥岩、砂岩、泥页 岩、页岩等岩石的强度包络线 近似于二次抛物线。
3．双曲线型 岩性坚硬、较坚硬的岩石，
如砂岩、灰岩、花岗岩等，其强 度包络线近似于双曲线。
二次抛物线型莫尔强度包络线 双曲线型莫尔强度包络线
0
说明：莫尔－库仑判据（强度理论）实质上是一种剪应力强度判据（理 论），既适用于塑性岩石，又适用于脆性岩石的剪切破坏，应用很广。
那么，岩石承受低于瞬时强度的荷载作用，是否会破坏？
只要收到长期荷载作用下，由于流变作用，岩石完全可能发生破坏。 而且岩石强度随外荷载作用时间的延长而降低，通常将时间t→∞的强度 （最低值）称为岩石的长期强度。
对大多数岩石，长期强度/瞬时强度（S∞/S0）一般为0.4～0.8，软的 和中等坚固岩石为0.4～0.6，坚固岩石为0.7～0.8。
2.莫尔－库仑强度理论
（Coulomb-Mohr Strength theory）
十 八 世 纪 末 ， 库 仑 （ Coulomb ） 提 出 了 最 大 剪 应 力 理 论 ， 后 来 纳 维 尔
（Navier）在此基t) g
岩石流变理论
流变性质就是指材料的应力-应变关系与时间因素有关的性质，材料变 形过程中具有时间效应的现象称为流变现象。包括蠕变、松弛和弹性后效。
不稳定蠕变
稳定蠕变
在一系列岩石流变试验基础上建立反映岩石流变性质的流变方程，通 常有两种方法：
（1）经验（方程）法
根据岩石蠕变试验结果，由数理统计学的回归拟合方法建立经验方 程。其通式一般为：
当材料中的点可能滑动面上的τ超过该面上的剪切强度时，该点就产生剪切 破坏，而剪切强度又是法向应力σ的函数：
τ=f (σ)
通过试验方法（单轴拉伸、压缩及三轴压缩），可以确定破坏时的莫尔应力 圆的包络线（强度曲线）。
为了便于计算，他提出了包络线的型式：（斜）直线型、抛物线型、双曲线 型等。
1．斜直线型（与Coulomb-Navier基本一致）
31312 0
t
E
当σ3－μ（σ1+σ2）＜0时，ε3＜0即张应变。那么，
E 强度判据写成：
［σ3－μ（σ1+σ2）］=－Eε0
图4.25 岩石张破裂图
0
极限张应变值ε0的确定：
①单向拉伸破坏瞬间的极限应变：0 σt—岩石抗拉强度
1极Ec
②单轴压缩条件下的极限应变，即： 3(12)t
岩石名称 粘土 石灰岩 盐岩
砂岩
S∞/S0
0.74 0.73
0.70
0.65
白垩 粘质页岩
0.62
0.50
0
岩石的强度理论
最大正应变（强度）理论 莫尔－库仑（Mohr-Coulomb）强度理论 Griffith强度理论－修正的Griffith强度理论 八面体强度理论
－米赛斯（Mises）强度判据 －德鲁克—普拉格（Drucker-Prager）判据
岩体微元→建立力学平衡方程、几何方程（位移和应变关系）和 物理方程或本构方程→引入边界条件→应力场和位移场。
－－岩体本构关系是指岩体在外力作用下，应力或应力速率与其应 变或应变速率的关系。对于静力题，本构关系是指应力与应变，或 者应力增量与应变增量之间的关系。
岩体本构关系
区分
岩石本构关系
弹性本构关系-弹性阶段
坏判据的理论。
岩石的本构关系
岩石力学中的符号规定
①力和位移分量的正方向与坐标轴的正方向一致； ②压缩的正应力和应变取为正，拉伸的正应力和应变为负。
岩石弹性本构关系
平面弹性本构关系
岩石塑性本构关系--自阅！
应力应变不存在一一对应关系，只能建立应力增量和应变增量间的 关系。包括三组方程：屈服条件、加卸载准则和本构方程
典型的岩石蠕变方程有：幂函数方程、指数方程、幂指数对数混合方程等。
（2）理论模型模拟法-（蠕变模型法或流变模型理论法、微分方程法）
把岩石材料抽象成一系列简单的元件（如弹簧、阻尼器等）及其组合 模型来模拟岩石的蠕变特性，建立其本构方程。
一般情况下，当荷载达到岩石瞬时强度（通常是岩石单轴抗压强度） 时，岩石发生破坏。
岩
石 本
线性和非线性弹性本构关系
弹塑性本构关系-与时间无关
构
关
塑性本构关系-塑性阶段
系
流变本构关系-与时间有关
－－岩石强度是指岩石抵抗破坏的能力。破坏是指岩石材料的应力 超过了它的极限或者变形超过了它的允许范围，但教材主要指应力 超过了它的极限。
－－岩石强度理论是指研究岩石在各种应力状态下的强度准则或破
0
1. 最大正应变（理论）强度判据 （Maximum Positive Strain Criterion）
物体发生张性破裂的原因是由最大延伸应变ε达到一定极限应变ε0。
其强度条件（判据）：
张应变控制下的张破裂力学模型如图4.25所示，岩石张破裂是侧向应
变ε3 ≥ε0 所致。
由广义虎克定理（Generalized Hooke’s Law）：
破坏判据可写成：
/2 sin
f 1 f 2
13 13
sin 令f=tgφ
1
2C3( 1
1 f 2 f2f
f
)
()/2Cctg2C Coulomb-Navier判据
13
13
库仑-纳维尔理论强度包络线
0
1900年，莫尔在库仑判据的基础上，提出了Mohr理论，认为：