新乡学院期末考试试题标准或参考答案及评分标准
2022年新乡学院生物技术专业《微生物学》期末试卷B(有答案)
2022年新乡学院生物技术专业《微生物学》期末试卷B(有答案）一、填空题1、在细菌中，存在着4种不同的糖被形式，即______、______、______和______。
2、病毒粒的对称体制有______、______和______。
3、在EMP途径中，有一个三碳中间代谢物______在酶的催化下形成______，其间产生本途径中第一个ATP，它是通过______磷酸化而实现的。
4、营养物质进入细胞的主要影响因素是______、______和______。
5、蕈菌从其______、______、______、______和______等方面来考察，证明它是典型的微生物，其大型子实体相当于其他真菌的______。
6、微生物是一切______生物的总称，其特点是______、______和______。
7、现代发酵罐除罐体外，还要有一系列必要的附属装置，包括______、______、______、______、______和______等。
8、微生物寄生于其他微生物的例子如______、______；微生物寄生于植物的例子如______；微生物寄生于动物的例子如______。
9、通常情况下，菌种可保藏在______℃和______℃的低温下。
10、周围免疫器官包括______、______和______。
二、判断题11、质粒与染色体DNA一样，失去质粒，细菌细胞就会死亡。
（）12、微生物营养就是微生物获得和利用营养物质的过程。
（）13、在光能自养型生物中，凡属原核生物者必不产氧。
（）14、病毒的早期蛋白多为参与病毒基因组复制，调节病毒基因组表达以及改变或抑制宿主分子合成的非结构蛋白。
（）15、Mucor和Rhizopus所形成的孢囊孢子无鞭毛，不能游动，通常为圆形。
（）16、支原体是没有细胞壁的革兰氏阴性细菌，故在《系统手册》中归属于缺壁型门中。
（）17、稀释平板测数时，放线菌计数的标准是选择每皿中菌落数在30～300个之间的稀释度进行计数。
2022年新乡学院生物技术专业《微生物学》期末试卷A(有答案)
2022年新乡学院生物技术专业《微生物学》期末试卷A(有答案）一、填空题1、在革兰氏阳性细菌细胞壁的肽聚糖成分中，肽包括______和______ 两种，聚糖则包括______和______两种糖。
2、温和噬菌体能以______整合在寄主细胞的染色体上，形成______细胞，该细胞具有______、______、______、______、______等几个特征（填三个特征即可）。
3、根据受氢体性质不同，可把生物氧化分为______、______和______ 三种类型。
4、在配制异养微生物培养基时，常用的生长因子来源是______、______、______或______等。
5、丝状真菌的无隔菌丝是由______细胞组成，有隔菌丝是由______细胞组成。
6、第一个用自制显微镜观察到微生物的学者是______，被称为微生物学研究的先驱者，而法国学者______和德国学者______则是微生物生理学和病原菌学研究的开创者。
7、消毒和灭菌的区别是______。
8、在工业防霉剂的筛选中，经常要用8种霉菌作为模式试验菌种，如______、______、______和______等。
9、筛选营养缺陷型的四个环节是______、______、______和______。
10、目前对抗体形成机制具有影响力的学说称为______，它是由______（国）的学者______提出的。
二、判断题11、古生菌是一类细胞壁上不含肽聚糖的原核生物。
（）12、在微生物遗传实验中所用到的基本培养基就其成分而言，应归属于天然培养基中。
（）13、EMP途径主要存在于厌氧生活的细菌中。
（）14、在病毒分离时，经盲传3代仍无感染症状出现，便可认定没有病毒存在。
（）15、一个酵母菌细胞上，只可能有一个蒂痕，但芽痕则可以有多个。
（）16、菌株的概念与克隆的概念相差甚远。
（）17、使用手提灭菌锅灭菌后，为了尽快排除锅内蒸汽，可直接打开排气阀排气。
化工原理下册期末考试试卷及答案
新乡学院 2011―2012学年度第一学期《化工原理》期末试卷B 卷课程归属部门：化学与化工学院 试卷适用范围：09化学工程与工艺1.萃取操作是依据： ，以达到分离 混合物的目的。
2.吸收操作是依据： ，以达到分离 混合物的目的。
3.物料的干燥速率曲线包括：恒速干燥阶段和 阶段，恒速干燥阶段，物料表面温度等于 ，主要干燥的水份为 。
4.在一定条件下，当某气体与所接触液体达到相平衡状态时，若将系统温度降低，系统将进行_________过程。
5．某精馏塔，进料状态参数q 等于0.8时，则进料为 ____ _，进料为含苯0.4的苯-甲苯溶液，则进料状态方程为： 。
6.板式塔的负荷性能图中包括_____线，最左边的线为： 。
7.溶解度曲线将三角形相图分为两个区域，曲线内为 ，曲线外为 ，萃取操作只能在 进行。
8.在1atm 下，不饱和湿空气的温度为295K ，相对湿度为60%，当加热到373K 时，该空气下列状态参数将如何变化？湿度H ，相对湿度φ ，湿球温度t w ， 露点t d ，焓I 。
（升高，降低，不变，不确定） 9.塔顶冷凝器的作用： ，塔底再沸器的作用： 。
10.吸收速率方程中，K Y 是以 为推动力的 吸收系数，其单位是 。
11.增加吸收剂用量，操作线的斜率 ，吸收推动力 。
12.某两组份混合物的平均相对挥发度0.2=α，在全回流下，从塔顶往下数对第1,+n n层塔板取样测得n n y x 则,3.0= = ，1+n y = ，1+n x = 。
1. 恒摩尔流假定主要前提是分子汽化潜热相近，它只适用于理想物系。
2.离开精馏塔任意一块理论板的液相泡点温度都小于气相的露点温度。
3.若精馏段操作线方程为y=0.75x+0.3，这绝不可能。
4.若吸收塔的操作液汽比小于最小液气比，吸收塔将不能操作。
5.在稳定操作中的吸收塔内，任意截面上传质速率N A 都相等。
6.萃取操作时，如果选择性系数等于1或无穷大时，就无法用萃取分离。
河南省师范大学附属中学新乡学院附中联考2022-2023学年九年级上学期期末数学试题及解析
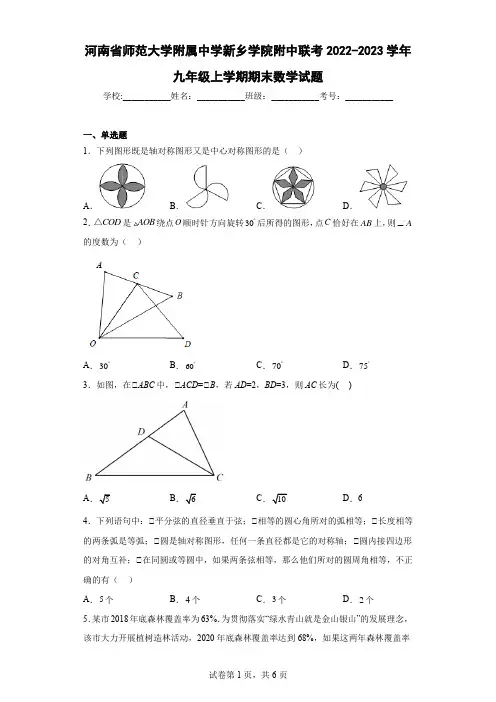
河南省师范大学附属中学新乡学院附中联考2022-2023学年九年级上学期期末数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．下列图形既是轴对称图形又是中心对称图形的是（ ）A ．B ．C ．D ． 2．COD △是AOB 绕点O 顺时针方向旋转30︒后所得的图形，点C 恰好在AB 上，则A ∠的度数为（ ）A ．30︒B ．60︒C ．70︒D ．75︒3．如图，在△ABC 中，△ACD =△B ，若AD =2，BD =3，则AC 长为( )A B C D ．64．下列语句中：△平分弦的直径垂直于弦；△相等的圆心角所对的弧相等；△长度相等的两条弧是等弧；△圆是轴对称图形，任何一条直径都是它的对称轴；△圆内接四边形的对角互补；△在同圆或等圆中，如果两条弦相等，那么他们所对的圆周角相等，不正确的有（ ）A ．5个B ．4个C ．3个D ．2个5．某市2018年底森林覆盖率为63%．为贯彻落实“绿水青山就是金山银山”的发展理念，该市大力开展植树造林活动，2020年底森林覆盖率达到68%，如果这两年森林覆盖率的年平均增长率为x ，那么，符合题意的方程是（ ）A ．()0.6310.68x +=B ．()20.6310.68x += C ．()0.63120.68x +=D ．()20.63120.68x += 6．下列说法正确的是（ ）A ．若你在上一个路口遇到绿灯，则在下一路口必遇到红灯B ．某篮球运动员2次罚球，投中一个，则可断定他罚球命中的概率一定为50%C ．若某种彩票中奖的概率是1%，则买100张该种彩票一定会中奖D ．“明天我市会下雨”是随机事件7．如图，菱形ABCD 的顶点B ，C ，D 均在△A 上，点E 在弧BD 上，则△BED 的度数为（ ）A ．90°B ．120°C ．135°D ．150°8．如图，在平面直角坐标系中，菱形ABCD 的边AD y ⊥轴，垂足为E ，顶点A 在第二象限，顶点B 在y 轴正半轴上，反比例函数(0k y k x=≠,0)x >的图象同时经过顶点C D 、．若点C 的横坐标为5，2BE DE =，则k 的值为（ ）A ．403B ．52C ．54D ．2039．如图所示是抛物线()20y ax bx c a =++≠的部分图象，其顶点坐标为()1,n ，且与x轴的一个交点在点()3,0和()4,0之间，则下列结论：其中正确的结论个数是（ ）△0a b c -+>；△30a c +>；△()24b a c n =-；△一元二次方程21ax bx c n ++=+没有实数根．A ．1个B ．2个C ．3个D ．4个10．如图，已知点A 、B 在反比例函数y k x=（k ＞0，x ＞0）的图象上，点P 沿C →A →B →O 的路线（图中“→”所示路线）匀速运动，过点P 作PM ⊥x 轴于点M ，设点P 的运动时间为t ，△POM 的面积为S ，则S 关于t 的函数图象大致为（ ）A ．B ．C ．D ．二、填空题11．已知扇形的圆心角为150°，弧长为20πcm ，则扇形的面积 _______cm 2．12．若关于x 的方程（k ﹣1）x 2+2kx +k ＝0有两个不相等的实数根，则实数k 的取值范围是 _____．13．如图，已知△ABC和△A'B'C是以点C为位似中心的位似图形，且△ABC和△A'B'C 的周长之比为1：2，点C的坐标为（﹣1，0），若点B的对应点B'的横坐标为5，则点B的横坐标为_____．14．如图，△ABC的顶点A，B分别在x轴，y轴上，∠ABC＝90°，OA＝OB＝1，BC＝ABC绕点O顺时针旋转，每次旋转90°，则第2021次旋转结束时，点C 的坐标为_____．15．如图，在平面直角坐标系中，点P，A的坐标分别为（1，0），（2，4），点B是y 轴上一动点，过点A作AC⊥AB交x轴于点C，点M为线段BC的中点，则PM的最小值为_____．三、解答题16．解方程：（1）x2﹣6x﹣4＝0；（2）3x（x+1）＝3x+3．17．已知：△ABC在坐标平面内，三个顶点的坐标分别为A（0，3），B（3，4），C（2，2）．（正方形网格中，每个小正方形的边长是1个单位长度）（1）画出△ABC向下平移4个单位，再向左平移1个单位得到的△A1B1C1，并直接写出C1点的坐标；（2）画出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2，并直接写出C2点的坐标；（3）请求出（2）中△ABC旋转过程中所扫过的面积为．18．一只不透明的袋子中装有2个白球和1个红球，这些球除颜色外都相同，搅匀后从中任意摸出1个球（不放回），再从余下的2个球中任意摸出1个球．（1）用树状图或列表等方法列出所有可能出现的结果；（2）求两次摸到的球的颜色不同的概率．19．如图，在△ABC中，AB＝AC，以AB为直径的△O交BC于D，交AC于E，连接OE，过点D作DF△AC于F．（1）求证：DF与△O相切；（2）填空：△若△CDF 的面积为3，则△CDE 的面积为 ．△当△CDF 的度数为 时，OE ∥BC ，此时四边形ODCE 的形状是： ．20．小红经营的网店以销售文具为主，其中一款笔记本进价为10元/本，拟采取线上和线下两种方式进行销售．调查发现，线下的月销量y （单位：本）与线下售价x （单位：元/本，1216x ≤≤，且x 为整数）满足一次函数的关系，部分数据如下表：（1）求y 与x 的函数关系式；（2）若线上售价始终比线下每本便宜1元，且线上的月销量固定为40件．试问：当x 为多少时，线上和线下月利润总和达到最大？并求出此时的最大利润．21．如图，在直角梯形OABC 中，BC △AO ，△AOC ＝90°，点A ，B 的坐标分别为（5，0），（2，6），点D 为AB 上一点，且BD ＝2AD ，双曲线y ＝k x （k ＞0）经过点D ，交BC 于点E ．（1）求双曲线的解析式；（2）求四边形ODBE 的面积．参考答案：1．A【分析】根据中心对称图形与轴对称图形的概念进行判断即可．【详解】解：A ．既是中心对称图形，也是轴对称图形，故此选项符合题意；B ．不是中心对称图形，也不是轴对称图形，故此选项不合题意；C ．不是中心对称图形，是轴对称图形，故此选项不合题意；D ．是中心对称图形，不是轴对称图形，故此选项不合题意；故选：A ．【点睛】本题考查的是中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后与自身重合．2．D【分析】根据旋转的性质可得30AOC ∠=︒，OA OC =，利用等边对等角以及三角形内角和定理即可求解．【详解】解：△COD △是AOB 绕点O 顺时针方向旋转30︒后所得的图形，△30AOC ∠=︒，OA OC =， △180752AOC A ︒-∠∠==︒， 故选：D ．【点睛】本题考查旋转的性质，掌握旋转的性质是解题的关键．3．C【分析】根据相似三角形的对应边成比例得出AC ：AB ＝AD ：AC ，即AC 2＝AB •AD ，将数值代入计算即可求出AC 的长．【详解】解：在△ADC 和△ACB 中，△△ACD ＝△B ，△A ＝△A ，△△ADC △△ACB （两角对应相等，两三角形相似）；△AC ：AB ＝AD ：AC ，△AC 2＝AB •AD ．△AD ＝2，AB ＝AD +BD ＝2+3＝5，△AC 2＝5×2＝10，△AC =．故选C ．【点睛】本题考查了相似三角形的判定与性质，用到的知识点为：△如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似（简叙为两角对应相等，两三角形相似）；△相似三角形的对应边成比例．4．A【分析】根据垂径定理、圆周角定理、圆内接四边形的性质、圆心角，弧，弦之间的关系，等弧的定义等知识进行判断即可．【详解】解：△平分弦（不是直径）的直径垂直于弦，△错误；△同圆或者等圆中相等的圆心角所对的弧相等，△错误；△必须是完全重合的两条弧是等弧，△错误；△圆是轴对称图形，任何一条直径所在直线都是它的对称轴，△错误；△圆内接四边形的对角互补，正确；△在同圆或等圆中，如果两条弦相等，那么他们所对的圆周角相等或互补，△错误； 故选：A ．【点睛】本题考查垂径定理、圆周角定理、圆内接四边形的性质、圆心角，弧，弦之间的关系，等弧的定义等知识，解题的关键是了解圆的有关定义及性质．5．B【分析】设年平均增长率为x ，根据2020年底森林覆盖率＝2018年底森林覆盖率乘()21x +，据此即可列方程求解．【详解】解：设年平均增长率为x ，由题意得：()20.6310.68x +=， 故选：B ．【点睛】此题主要考查了一元二次方程的应用，关键是根据题意找到等式两边的平衡条件，列出方程即可．6．D【分析】根据概率的定义进行判断即可.【详解】A 若你在上一个路口遇到绿灯，则在下一路口不一定遇到红灯，故本选项错误；B. 某篮球运动员2次罚球，投中一个，这是一个随机事件，不能断定他罚球命中的概率一定为50%，故本选项错误；C. 若某种彩票中奖的概率是1%，则买100张该种彩票不一定会中奖，故本选项错误；D. “明天我市会下雨”是随机事件，故本选项正确；故选D【点睛】本题考查了概率的定义，注意区分必然事件、可能事件、随机事件的区别.7．B【分析】连接AC ，根据菱形的性质得到△ABC 、△ACD 是等边三角形，求出△BCD =120°，再根据圆周角定理即可求解．【详解】如图，连接AC△AC =AB =AD△四边形ABCD 是菱形△AB =BC =AD =CD =AC△△ABC 、△ACD 是等边三角形△△ACB =△ACD =60°△△BCD =120°△优弧BD BD =△△BED =△BCD =120°故选B ．【点睛】此题主要考查圆内角度求解，解题的关键是熟知菱形的性质及圆周角定理．8．A【分析】由题意易得5,AB BC CD AD AD//BC ====，则设DE =x ，BE =2x ，然后可由勾股定理得()225425x x -+=，求解x ，进而可得点5,5k C ⎛⎫ ⎪⎝⎭，则2,45k D ⎛⎫+ ⎪⎝⎭，最后根据反比例函数的性质可求解．【详解】解：△四边形ABCD 是菱形，△,AB BC CD AD AD//BC ===，△AD y ⊥轴，△90DEB AEB ∠=∠=︒，△90DEB CBO ∠=∠=︒，△点C 的横坐标为5，△点5,5k C ⎛⎫ ⎪⎝⎭，5AB BC CD AD ====， △2BE DE =，△设DE =x ，BE =2x ，则5AE x =-，△在Rt △AEB 中，由勾股定理得：()225425x x -+=，解得：122,0x x ==（舍去），△2,4DE BE ==， △点2,45k D ⎛⎫+ ⎪⎝⎭， △245k k ⎛⎫⨯+= ⎪⎝⎭， 解得：403k =； 故选A ．【点睛】本题主要考查菱形的性质及反比例函数与几何的综合，熟练掌握菱形的性质及反比例函数与几何的综合是解题的关键．9．D【分析】根据图象开口向下，对称轴为直线1x =可得抛物线与x 轴另一交点坐标在(1,0)-，(2,0)-之间，从而判断△．由对称轴为直线1x =可得b 与a 的关系，将2b a =-代入函数解析式根据图象可判断△由2ax bx c n ++=有两个相等实数根可得△24()0b a c n =--=，从而判断△．由函数最大值为y n =可判断△． 【详解】解：抛物线顶点坐标为(1,)n ，∴抛物线对称轴为直线1x =，图象与x 轴的一个交点在(3,0)，(4,0)之间，∴图象与x 轴另一交点在(1,0)-，(2,0)-之间，1x ∴=-时，0y >，即0a b c -+>，故△正确，符合题意． 抛物线对称轴为直线12b x a=-=， 2b a ∴=-，22y ax ax c ∴=-+，1x ∴=-时，30y a c =+>，故△正确，符合题意．抛物线顶点坐标为(1,)n ，2ax bx c n ∴++=有两个相等实数根，∴△24()0b a c n =--=，24()b a c n ∴=-，故△正确，符合题意．2y ax bx c =++的最大函数值为y n =，21ax bx c n ∴++=+没有实数根，故△正确，符合题意．故选：D ．【点睛】本题考查二次函数的性质，解题关键是掌握二次函数与方程及不等式的关系．10．D【分析】分别求当点P 在C →A 路线上运动时；当A →B 路线上运动时；当点P 在B →O 路线上运动时，S 关于t 的函数的解析式，即可求解．【详解】解：当点P 在C →A 路线上运动时，设点P 运动速度为a ， △1122S OM PM OA at =⋅=⋅ ， △a 、OA 为常数，△S 是关于t 的一次函数，图象为自左向右上升的线段；当A →B 路线上运动时，122k S OM PM =⋅=，保持不变，△本段图象为平行于x 轴的线段；当点P 在B →O 路线上运动时，随着t 的增大，点P 从点B 运动至点O ，OM 的长在减小，△OPM 的高PM 也随之减小到0， 即12S OM PM =⋅的图象为开口向下的抛物线的一部分． 故选：D【点睛】本题主要考查了动点问题的函数图象，明确题意，得到每一段的函数解析式是解题的关键．11．240π【分析】先求解扇形所在圆的半径，再利用扇形的面积公式求解扇形的面积即可. 【详解】解： 扇形的圆心角为150°，弧长为20π， 15020,180r24,r215024240.360S故答案为：240π【点睛】本题考查的是扇形的弧长，扇形的面积，掌握“利用扇形的公式求解扇形的面积”是解题的关键.12．0k > 且1k ≠【分析】利用一元二次方程根的判别式，即可求解．【详解】解：△关于x 的方程（k ﹣1）x 2+2kx +k ＝0有两个不相等的实数根，∴()()22410k k k -->且10k -≠ ，解得：0k > 且1k ≠ ．故答案为：0k > 且1k ≠【点睛】本题考查了一元二次方程的定义，一元二次方程根的判别式，熟练掌握二次函数()20y ax bx c a =++≠ ，当240b ac ∆=-> 时，方程有两个不相等的实数根；当240b ac ∆=-= 时，方程有两个相等的实数根；当24<0b ac ∆=- 时，方程没有实数根是解题的关键．13．-4【分析】过点B 作BD △x 轴于点D ，过点B ′作B ′H △x 于点H ，则BD △B ′H ，可得△BCD △△B ′CH ，从而CD BC CH B C ='，再由相似三角形的周长之比等于相似比，可得12BC B C ='，继而得到12CD CH =，即可求解．【详解】解：如图，过点B 作BD △x 轴于点D ，过点B ′作B ′H △x 于点H ，则BD △B ′H ，△△DBC =△HB′C ，△BDC =△B′HC ，△△BCD △△B ′CH ， △CD BC CH B C='， △△ABC 和△A ′B ′C ′的周长之比为1△2， △12BC B C ='， △12CD CH =， △点C 的坐标为（－1，0），点B 的对应点B ′的横坐标为5，△OC ＝1，OH ＝5，△CH ＝6， △12CD CH =＝3， △OD ＝OC +CD =1+3=4，△点B 的横坐标为－4．故答案为:4-【点睛】本题主要考查了位似图形，相似三角形的判定和性质，熟练掌握位似图形，相似三角形的判定和性质定理是解题的关键．14．()3,2-【分析】过点C 作CD y ⊥ 轴于点D ，根据 OA ＝OB ＝1，∠AOB =90°，可得△ABO =45°，从而得到∠CBD =45°，进而得到BD =CD =2，，可得到点()2,3C ，再由将△ABC 绕点O 顺时针旋转，第一次旋转90°后，点()3,2C -，将△ABC 绕点O 顺时针旋转，第二次旋转90°后，点()2,3C --，将△ABC 绕点O 顺时针旋转，第三次旋转90°后，点()3,2C -，将△ABC 绕点O 顺时针旋转，第四次旋转90°后，点()2,3C ，由此发现，△ABC 绕点O 顺时针旋转四次一个循环，即可求解．【详解】解：如图，过点C 作CD y ⊥ 轴于点D ，△OA ＝OB ＝1，∠AOB =90°，△△ABO =45°，△∠ABC ＝90°，∴∠CBD =45°，∴∠BCD =45°，∴BD =CD ，∵BC ＝∴(2222BD CD BC +== ，∴BD =CD =2，∴OD =OB +BD =3，∴点()2,3C ，将△ABC 绕点O 顺时针旋转，第一次旋转90°后，点()3,2C -，将△ABC 绕点O 顺时针旋转，第二次旋转90°后，点()2,3C --，将△ABC 绕点O 顺时针旋转，第三次旋转90°后，点()3,2C -，将△ABC 绕点O 顺时针旋转，第四次旋转90°后，点()2,3C ，由此发现，△ABC 绕点O 顺时针旋转四次一个循环，∵20214551÷= ，∴第2021次旋转结束时，点C 的坐标为()3,2-．故答案为：()3,2-【点睛】本题主要考查了勾股定理，坐标与图形，图形的旋转，明确题意，准确得到规律是解题的关键．15【分析】连接AM ，OM ，根据直角三角形斜边中线等于斜边一半可得：AM OM =，则点M在线段AO 的垂直平分线上，作线段AO 的垂直平分线交x 轴，y 轴于点E ，D 则当PM DE⊥时，PM 最小，再利用相似三角形的判定和性质，结合勾股定理解答即可．【详解】如图：过点A 作AF y ⊥于点F ，连接AM ，OM90BAC BOC ∠=∠=︒，M 为BC 中点，∴AM OM =∴点M 在线段AO 的垂直平分线上作线段AO 的垂直平分线交y 轴，x 轴于点D ，E ，当PM DE ⊥，PM 最小连接AD ，则AD OD = A （2，4）2AF ∴=，4OF =设OD AD t ==，则4FD t =-，222FD AF AD +=()22242t t ∴-+=52t ∴= 52OD ∴=90FOA AOE ∠+∠=︒，90AOE OED ∠+∠=︒FOA OED ∴∠=∠90AFO DOE ∠=∠=︒FAO ODE ∴△∽△AF OF OD OE∴=，即AF OE OD OF =， 5OE ∴= P （1，0）4PE ∴=在Rt AFO △中OA =当PM DE ⊥时， PM 最小90PME AFO ∴∠=∠=︒PME AFO △∽△PM PE AF OA∴=2PM ∴=PM ∴=【点睛】本题考查了线段垂直平分线的判定和性质，直角三角形的性质，相似三角形的判定和性质，点到直线的距离，勾股定理等知识，能够综合熟练运用这些性质和判定是解题关键．16．（1）x 1，x 2=（2）x 1=-1，x 2=1【分析】（1）根据配方法即可求解；（2）根据因式分解法即可求解．【详解】（1）x 2﹣6x ﹣4＝0x 2﹣6x +9＝13（x -3）2＝13x-△x1，x2=（2）3x（x+1）＝3x+33x（x+1）-3（x+1）=03（x+1）（x-1）=0△x+1=0或x-1=0△x1=-1，x2=1．【点睛】此题主要考查解一元二次方程，解题的关键是熟知配方法与因式分解法的运用．17．（1）见解析，C1（1，-2）；（2）见解析，C2（-1，1）；（3）52π+52【分析】（1）将A、B、C分别向下平移4个单位，再向左平移1个单位，顺次连接即可得出△A1B1C1，即可得出写出C1点的坐标；（2）根据旋转的性质，找到各点的对应点，顺次连接可得出△A2B2C2，即可写出C2点的坐标；（3）根据扇形和三角形的面积公式即可得到结论．【详解】解：（1）△A1B1C1如图1所示，C1（1，-2）；（2）△A2B2C2如图2所示，C2（-1，1）；（3）△AB =AC BC△AC 2+BC 2=AB 2，△△ABC 是等腰直角三角形，扇形AOB 2△S △ABC =1252， △△ABC 旋转过程中所扫过的面积=2AOB S +扇形 S △ABC=290?360π⨯+52=52π+52． 故答案为：52π+52． 【点睛】本题考查了旋转作图及平移作图的知识，解答此类题目的关键是就是寻找对应点，要求掌握旋转三要素、平移的特点．18．（1）详见解析；（2）23．【分析】（1）首先根据题意画出树状图，然后由树状图求得所有等可能的结果；（2）由（1）中树状图可求得两次摸到的球的颜色不同的情况有4种，再利用概率公式求解即可求得答案．【详解】解：（1）如图：，所有可能的结果为（白1，白2）、（白1，红）、（白2，白1）、（白2，红）、（红，白1）、（红，白2）；（2）共有6种情况，两次摸到的球的颜色不同的情况有4种，概率为42 63 ．19．（1）见解析（2）△6△30；菱形【分析】（1）由等腰三角形的性质得△ABC＝△C，由OB＝OD，得△ABC＝△ODB，则△ODB ＝△C，得出OD∥AC，再由DF△AC，得出OD△DF，即可得出结论；（2）△由圆周角定理和平角性质得△ABC＋△AED＝180°，△DEC＋△AED＝180°，推出△ABC ＝△DEC，△C＝△DEC，得出DE＝DC，由等腰三角形的性质得CE＝2CF，则S△CDE＝2S△CDF，即可得出结果；△利用平行线的性质证明OE是△ABC的中位线，得出BC＝2OE＝AB＝AC，则△ABC为等边三角形，得△C＝60°，证明△CDE为等边三角形，得出△CDE＝60°，由等腰三角形的性质得△CDF＝12△CDE＝30°，由OE∥CD，OD∥CE，得四边形ODCE为平行四边形，再由OD＝OE，得出平行四边形ODCE为菱形．【详解】解：（1）证明：△AB＝AC，△△ABC＝△C，连接OD，△OB＝OD，△△ABC＝△ODB，△△ODB＝△C，△OD∥AC，△DF△AC，△OD△DF，△DF与△O相切；（2）解：△△△ABC＋△AED＝180°，△DEC＋△AED＝180°，△△ABC＝△DEC，△△ABC＝△C，△△C＝△DEC，△DE＝DC，△DF△AC，△CE＝2CF，△S△CDE＝2S△CDF＝2×3＝6，故答案为：6；△△OE∥BC△AO AE OB EC△O点是AB中点△E点是AC中点△OE是△ABC的中位线，△BC＝2OE＝AB＝AC，△△ABC为等边三角形，△△C＝60°，△DE＝DC，△△CDE为等边三角形，△△CDE＝60°，△DF△AC，△△CDF＝12△CDE＝12×60°＝30°，△OE∥CD，OD∥CE，△四边形ODCE为平行四边形，△OD ＝OE ，△平行四边形ODCE 为菱形，故答案为：30；菱形．【点睛】本题是圆综合题，主要考查了圆周角定理、切线的判定、平行线的性质与性质、三角形中位线定理、等腰三角形的判定与性质、等边三角形的判定与性质、平行四边形的判定、菱形的判定、三角形面积计算等知识；熟练掌握切线的判定和等腰三角形的判定与性质、等边三角形的判定与性质是解题的关键．20．（1）10240y x =-+；（2）当16x =元/件时，线上和线下月利润总和达到最大，此时的最大利润为680元．【分析】（1）根据线下的月销量y （单位：本）与线下售价x （满足一次函数的关系，将表格中任意两对数值代入一次函数，计算求解即可．（2）先算线下利润=线下月销售量y×每本笔记本利润（x -10），再算线上利润=线上的月销量固定为40件×每本笔记本利润(110)x --，可求线上和线下月利润总和为w 元，其结果可表示成以x 为自变量的二次函数，运用求二次函数最大值的方法运算求解．【详解】解：（1）△y 与x 满足一次函数的关系，△设y kx b =+，将12,120x y ==；13,110x y ==代入得：1201211013k b k b =+⎧⎨=+⎩， 解得：10240k b =-⎧⎨=⎩， △y 与x 的函数关系式为：10240y x =-+；（2）设线上和线下月利润总和为w 元，则(10)40(110)w y x x =-+--，(10240)(10)40440x x x =-+-+-，2103802840x x =-+-，210(19)770x =--+ ，△100a =-<，抛物线开口向下，抛物线的对称轴为直线19x =，△当1216x ≤≤，且x 为整数，在对称轴左侧，W 随x 的增大而增大，△当16x =元/件时，线上和线下月利润总和达到最大，此时的最大利润为-10×9+770=680元．【点睛】本题考查一次函数、二次函数在销售中求最大值，找出题中的数量关系，掌握二次函数求最值的方法是解题关键．21．（1）y=8x；（2）12 【详解】（1）作BM △x 轴于M ，作BN △x 轴于N ，利用点A ，B 的坐标得到BC =OM =5，BM =OC =6，AM =3，再证明△ADN △△ABM ，利用相似比可计算出DN =2，AN =1，则ON =OA ﹣AN =4，得到D 点坐标为（4，2），然后把D 点坐标代入y=k x 中求出k 的值，即可得到反比例函数解析式；（2）根据反比例函数k 的几何意义和OCE OAD ODBE OABC S S SS =--四边形梯形进行计算．解：（1）作BM △x 轴于M ，作DN △x 轴于N ，如图，△点A ，B 的坐标分别为（5，0），（2，6），△263BC OM BM OC AM =====，，，△DN BM ∥， ADNABM ∴ ， △DN BM =AN AM =AD AB ， 即6DN =3AN =13， 21DN AN ∴==，，△4ON OA AN ==﹣，△D 点坐标为()4,2，把D （4，2）代入y=k x得 248k =⨯=，△反比例函数解析式为y=8x；（2）OCE OAD ODBE OABC S S S S =--四边形梯形=1 2×（2+5）×6﹣12×|8|﹣12×5×2=12．【点睛】本题考查了反比例函数图像上点的坐标特征、反比例函数k的几何意义，相似三角形的判定和性质，割补法求面积；理解反比例函数图像的特征，会运用相似比计算线段的长度是解题的关键．。
2012-2013下12制药工程有机A卷答案
CH2CH3 OH
C6H5CH3 则 C 为： H Br CH3 (R)
C6H5CH3 Br H CH3 (S)
A B C D
I2
B. 麦芽糖
蓝色 D A B C
斐林试剂
C. 蔗糖
D. 淀粉
不反应 C A B
水解
能水解 B A
2、
解答：
CHO ，
COCH3 ，
CH CH2 ，
C CH
有银镜
加入Ag+(NH3)2
CHO C CH
有白色沉淀
COCH3 有亮黄色沉淀 CH CH2 无现象
无现象 和
COCH3
加入I2/NaOH
后括号内，每小题 2 分，共 30 分）
1A 6B 11D
2A 7C 12D
3D 8C 13A
4D 9A 14B
5D 10B 15C
三、完成反应方程式（每题 2 分，共 20 分）
本题主要考查学生对基本理论掌握程度和分析问题的能力。 评分标准： 1.写出主要产物就行，每小题给 2 分；全错或不答给 0 分。 2.部分正确可根据对错程度，依据答案评分点给分。 参考答案：
。在较高温度或光照射下，烷基苯与卤
素作用，芳烃的侧链卤化。
CH3 光照下 不足量的Br2 CH2CH3 A CH2CH3 B
+
CH2Br
CH3
CHBrCH3 C
CH2Br 水解
CH2OH 氧化 CH2CH3
COOH
CH3 水解 CHCH3 Br C
CH3
COOH 氧化 COOH
CH2CH3 B
COOH
1、
2、
3、
4、
5、
新乡学院考古期末考试试题
新乡学院考古期末考试试题### 新乡学院考古期末考试试题一、选择题（每题2分，共20分）1. 中国最早的文字记载是：A. 甲骨文B. 金文C. 小篆D. 隶书2. 考古学中，地层学的基本法则是：A. 地层越深，年代越新B. 地层越浅，年代越新C. 地层越深，年代越旧D. 地层越浅，年代越旧3. 以下哪项不是考古学研究的主要方法：A. 地层分析B. 碳-14测年C. 遥感技术D. 化学分析4. 洛阳铲是用于：A. 挖掘文物B. 探测地层C. 清洗文物D. 修复文物5. 以下哪个遗址不属于新石器时代：A. 半坡遗址B. 龙山文化遗址C. 仰韶文化遗址D. 殷墟二、填空题（每空1分，共10分）1. 考古学是一门研究______和______的学科，它通过分析古代人类遗留下来的物质文化来了解古代社会。
2. 考古学中的“三重证据法”指的是______、______和______。
3. 我国著名的考古学家裴文中，他主持发掘的______遗址，为研究新石器时代晚期文化提供了重要资料。
4. 考古发掘中，常用的文物保护方法包括______、______和______。
三、简答题（每题10分，共30分）1. 简述考古学与历史学的区别和联系。
2. 描述考古学中常用的碳-14测年法的基本原理。
3. 阐述考古学在文化遗产保护中的作用。
四、论述题（共40分）考古学是一门综合性学科，它在研究古代人类社会方面发挥着重要作用。
请结合你本学期所学知识，论述考古学在现代科学研究中的地位和作用，并举例说明考古学如何帮助我们更好地理解古代文明。
答案提示：1. 考古学与历史学的区别在于考古学更侧重于通过物质遗存来研究历史，而历史学则侧重于文献记载。
两者的联系在于它们都致力于对过去的研究和解释。
2. 碳-14测年法是一种放射性同位素测年技术，它通过测量样本中的碳-14含量来确定其年代。
3. 考古学在文化遗产保护中的作用包括：为文化遗产的保护和修复提供科学依据，通过考古发掘揭示文化遗产的历史价值和艺术价值，以及通过教育和宣传提高公众对文化遗产保护的意识。
新乡学院期末考试试题
新乡学院期末考试试题### 新乡学院期末考试试题#### 一、选择题（每题2分，共20分）1. 以下哪项不是新乡学院的校训？A. 厚德B. 博学C. 求实D. 创新2. 新乡学院的成立时间是：A. 1949年B. 1950年C. 1951年D. 1952年3. 新乡学院的校徽中包含以下哪个元素？A. 书籍B. 火炬C. 地球D. 飞鸟4. 新乡学院的图书馆藏书量大约为：A. 50万册B. 100万册C. 150万册D. 200万册5. 新乡学院的校歌名称是：A. 《新乡学院校歌》B. 《新乡学院之歌》C. 《青春新乡》D. 《新乡学院进行曲》...（此处省略其他选择题）#### 二、填空题（每空1分，共10分）1. 新乡学院位于_______省_______市。
2. 新乡学院的校训是“厚德、_______、求实、_______”。
3. 新乡学院的校徽设计中，_______象征着知识与智慧。
4. 新乡学院的校园占地面积约为_______公顷。
5. 新乡学院的校庆日是每年的_______月_______日。
...（此处省略其他填空题）#### 三、简答题（每题10分，共20分）1. 简述新乡学院的发展历程。
2. 描述新乡学院的校园文化特色。
#### 四、论述题（每题15分，共30分）1. 论述新乡学院在培养学生创新能力方面所采取的措施。
2. 分析新乡学院如何结合地方特色，推动学科建设和专业发展。
#### 五、案例分析题（共20分）请根据以下案例，分析新乡学院在促进学生全面发展方面所采取的策略，并提出你的建议。
案例背景：新乡学院近年来加大了对学生综合素质培养的投入，通过举办各类学术讲座、文化节、体育竞赛等活动，鼓励学生积极参与，拓宽视野，提升能力。
#### 六、作文题（共30分）题目：我与新乡学院的故事要求：结合自身经历，写一篇不少于800字的记叙文，描述你在新乡学院的学习生活以及所获得的成长和感悟。
新乡期末考试题目及答案
新乡期末考试题目及答案一、选择题（每题2分，共20分）1. 请从下列选项中选择正确的一项：a) 地球是平的b) 地球是圆的c) 地球是三角形的d) 地球是多边形的答案：b2. 以下哪个不是中国的传统节日？a) 春节b) 清明节c) 圣诞节d) 中秋节答案：c3. 以下哪个是化学元素的符号？a) Aub) Agc) AuAgd) AuAgCu答案：b4. 以下哪个是数学中的基本运算符号？a) ∑b) ∫c) ∞d) √答案：d5. 以下哪个是计算机编程语言？a) Javab) C++c) Pythond) All of the above答案：d6. 以下哪个是文学作品的作者？a) 《红楼梦》- 曹雪芹b) 《西游记》- 吴承恩c) 《水浒传》- 施耐庵d) All of the above答案：d7. 以下哪个是物理学中的基本概念？a) 力b) 质量c) 速度d) All of the above答案：d8. 以下哪个是生物学中的基本单位？a) 细胞b) 组织c) 器官d) 系统答案：a9. 以下哪个是历史事件？a) 法国大革命b) 美国独立战争c) 中国抗日战争d) All of the above答案：d10. 以下哪个是地理学中的概念？a) 大气层b) 地壳c) 洋流d) All of the above答案：d二、填空题（每空2分，共20分）11. 地球的自转周期是________。
答案：24小时12. 中国的首都是________。
答案：北京13. 化学元素周期表中，氢的原子序数是________。
答案：114. 勾股定理的公式是 a² + b² = c²，其中c是________。
答案：斜边15. 计算机编程中，if语句用于实现________。
答案：条件判断16. 《红楼梦》的作者是________。
答案：曹雪芹17. 物理学中，牛顿第二定律的公式是 F = m × a，其中a表示________。
新乡市期末考试试题及答案
新乡市期末考试试题及答案一、选择题（每题2分，共20分）1. 请选出下列单词的正确拼写：A. seperateB. separateC. seprateD. seporate答案：B2. 下列哪个选项是“化学”的英文表达？A. PhysicsB. ChemistryC. BiologyD. Geology答案：B3. 根据题目所给的数学公式，下列哪个选项是正确的？A. \( a + b = b + a \) （加法交换律）B. \( a \times b = b \times a \) （乘法交换律）C. \( a \times (b + c) = a \times b + a \times c \) （乘法分配律）D. 以上都是答案：D4. 以下哪个历史事件标志着中国近代史的开端？A. 鸦片战争B. 辛亥革命C. 五四运动D. 新文化运动答案：A5. 根据题目所给的物理定律，下列哪个选项是正确的？A. 牛顿第一定律B. 牛顿第二定律C. 牛顿第三定律D. 以上都是答案：D6. 根据题目所给的生物分类，下列哪个选项是错误的？A. 动物界B. 植物界C. 微生物界D. 元素界答案：D7. 以下哪个选项是“可持续发展”的英文表达？A. Sustainable DevelopmentB. Continuous DevelopmentC. Infinite DevelopmentD. Endless Development答案：A8. 根据题目所给的地理知识，下列哪个选项是正确的？A. 地球上最大的陆地是亚洲B. 地球上最大的海洋是太平洋C. 地球上最高的山峰是珠穆朗玛峰D. 以上都是答案：B9. 以下哪个选项是“环境保护”的英文表达？A. Environmental ProtectionB. Environmental PollutionC. Environmental DestructionD. Environmental Degradation答案：A10. 下列哪个选项是“信息技术”的英文表达？A. Information TechnologyB. Communication TechnologyC. Computer TechnologyD. Network Technology答案：A二、填空题（每空1分，共10分）11. 请填写下列成语的后半部分：一言既出，______。
河南省新乡市2022-2023学年高一下学期期末测试数学试题(解析版)
河南省新乡市2022-2023学年高一下学期期末测试数学试题注意事项：1．答题前，考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.2．回答选择题时，选出每小题〖答 案〗后，用铅笔把答题卡上对应题目的〖答 案〗标号涂黑.如需改动，用橡皮擦干净后，再选涂其他〖答 案〗标号.回答非选择题时，将〖答 案〗写在答题卡上.写在本试卷上无效.3．考试结束后，将本试卷和答题卡一并交回.4．本试卷主要考试内容：人教A 版必修第一册至第二册.一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1. 已知集合{}30A x x =-<，(){}ln 4B x y x ==-，则AB =（ ）A.()3,4 B.(),3-∞-C.()0,3D.(),3-∞〖答 案〗D〖解 析〗因为{}{}303A x x x x =-<=<， 又(){}{}{}ln 4404B x y x x x x x ==-=->=<， 所以(),3A B =-∞.故选：D 2. 复数4i1iz +=+在复平面内对应的点在（ ） A. 第一象限 B. 第二象限C. 第三象限D. 第四象限〖答 案〗D〖解 析〗因为()()()()24i 1i 4i 44i i i 53i 1i 1i 1i 222z +-+-+-====-++-， 所以复数4i1i z +=+在复平面内对应点为53,22⎛⎫- ⎪⎝⎭，位于第四象限. 故选：D 3. 若0x 是方程02.56log xx =+的解，则0x ∈（ ）A.()0,1B.()1,2C.()2,3D.()3,4〖答 案〗C 〖解 析〗设()()02.560log f x x x x =-->，函数2y x 在()0,∞+上单调递增，函数0.5log y x =在()0,∞+上单调递减，所以函数()f x ()0,∞+上单调递增，又()150f =-<，()210f =-<，()0.533log 30f =->，()0.544log 40f =->， 所以()()230f f ⋅<，根据零点存在性定理，函数()f x 在()2,3上存在一个零点，即()02,3x ∈.故选：C.4. 若平面上的三个力1F ，2F ，3F 作用于一点，且处于平衡状态．已知11N F =，32N F =，1F 与3F 的夹角为60︒，则2F 的大小为（ ）A. 1NB.C.D. 3N〖答 案〗C〖解 析〗根据三力平衡得1320F F F ++=，即132F F F +=-， 两边同时平方得222113322F F F F F +⋅+=， 即222113322cos 60F F F F F +⋅︒+=，即222211212272F +⨯⨯⨯+==，解得27F =.故选：C.5. 甲、乙两名射击运动员各射击6次的成绩如下：若甲射击成绩的中位数等于乙射击成绩的平均数，则b =（ ） A. 7 B. 8C. 9D. 10〖答 案〗A〖解 析〗对于甲的成绩，因为有3个8，且还有1个7，无论a 为何值，甲射击成绩的中位数一定是8， 所以()110779886b +++++=，解得7b =. 故选：A6. 已知()1cos 3αβ-=，1cos cos 4αβ=，则()cos αβ+=（ ） A. 16-B.16C. 1112-D.1112〖答 案〗B〖解 析〗由()1cos 3αβ-=，可得1cos cos sin sin 3αβαβ+=，因为1cos cos 4αβ=，可得1sin sin 12αβ=，又因为()111cos cos cos sin sin 4126αβαβαβ+=-=-=. 故选：B.7. “2log 2a <”是“对任意()1,x ∈-+∞，()2440x a x a +-+->恒成立”的（ ）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件〖答 案〗A〖解 析〗由2log 2a <，即22log log 4a <，所以04a <<， 由()1,x ∈-+∞，()2440x a x a +-+->恒成立，即()2441x x a x ++>+在()1,-+∞上恒成立，所以()()2211211x a x x x +<=+++++，又()112241x x +++≥=+，当且仅当111x x +=+，即0x =时取等号， 所以4a <，因为()0,4真包含于(),4-∞，所以“2log 2a <”是“对任意()1,x ∈-+∞，()2440x a x a +-+->恒成立”的充分不必要条件. 故选：A8. 已知在正四棱台1111ABCD A B C D -中，1133AB A B ==，若异面直线1AA 与BC 所成角1111ABCD A B C D -的体积为（ ）A.B.133C.D.263〖答 案〗D〖解 析〗如图在正四棱台1111ABCD A B C D -中，//BC AD ， 所以1A AD ∠为异面直线1AA 与BC 所成角，又1133AB A B ==，所以3AD =，111A D =，且11312cos 6A AD AA -∠==，所以1AA =， 连接11A C 、AC ，过点1A 作1A E AC ⊥交AC 于点E ，过点1C 作1C F AC ⊥交AC 于点F ，则AC ==11AC ==，所以112AC AC AE CF -===12A E ==，即正四棱台1111ABCD A B C D -的高2h =，所以棱台的体积((221126312333V S S h '=++=+⨯=.故选：D二、选择题：本题共4小题，每个小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9. 已知复数1z 在复平面内对应的点为()13,4Z -，复数2z 在复平面内对应的点为2Z ，且21z =，则（ ）A. 212524i z =-B. 15z =C. 复数1z 在复平面内对应的点在第一象限D. 12Z Z 的最小值为4 〖答 案〗BCD〖解 析〗由题意得，134i z =-，所以()222134i 924i 16i 724i z =-=-+=--，故A 错误；而15z ==，故B 正确；因为134i z =+，故复数1z 在复平面内对应的点为()3,4，在第一象限，故C 正确； 因为21z =，所以点2Z 在以原点O 为圆心，1为半径的圆上， 而12Z Z 表示点1Z ，2Z 之间的距离， 所以121min1514Z Z OZ =-=-=，故D 正确.故选：BCD.10. 已知,,a b c 分别是ABC 三个内角,,A B C 的对边，则下列选项正确的是（ ） A. 若ABC 为锐角三角形，则0AB BC ⋅> B. 若6b =，10c =，30B =︒，则ABC 有两解 C.ABC 内切圆的半径tan BA BC Br a b c⋅⋅=++D. 若AB BC ⊥，则2AB AC AC ⋅= 〖答 案〗BC〖解 析〗对于A ：因为()cos π0AB BC AB BC B ⋅=⋅->，所以()cos π0B ->，则cos 0B <，即B 为钝角，所以ABC 为钝角三角形，故A 错误； 对于B ：因为6b =，10c =，30B =︒，由正弦定理sin sin b c B C =，即610sin 30sin C=︒， 所以51sin sin 3062C =>︒=，所以C 有两个解，所以ABC 有两解，故B 正确； 对于C ：()11sin 22ABC S a b c r ac B =++=△， 又cos cos B B a A BC C B BA B c ⋅⋅==，所以cos BBA B ac C⋅=，所以111sin tan 22cos 2B BA rBCBA aBC b c BB ， 所以tan Bra b cBA BC ，故C 正确；对于D ：因为cos A AB AC AB AC ⋅=⋅，又AB BC ⊥，所以cos AB A AC=，所以2cos AB AC AB AC AB AC A CB AB A A =⋅⋅==⋅⋅，故D 错误；故选：BC11. 甲、乙两位同学从,,,A B C D 这4种课外读物中各自选读2种，设事件G =“甲、乙两人所选的课外读物恰有1种相同”，事件M=“甲、乙两人所选的课外读物完全不同”，事件N =“甲、乙两人均未选择A 课外读物”，则（ ） A. G 与M 互斥 B. ()13P G =C. M 与N 互斥D. G 与N 相互独立〖答 案〗ACD〖解 析〗因为“甲、乙两人所选的课外读物恰有1种相同”与“甲、乙两人所选的课外读物完全不同”不能同时发生，所以G 与M 互斥，A 正确.()1114322244C C C 2C C 3P G ==，B 不正确.“甲、乙两人所选的课外读物完全不同”与“甲、乙两人均未选择A 课外读物”不能同时发生，所以M 与N 互斥，C 正确.()22332244C C 1C C 4P N ==， ()11322244C C 1C C 6P GN ==，因为()()()P GN P G P N =，所以G 与N相互独立，D 正确. 故选：ACD.12. 如图，在长方体1111ABCD A B C D -中，12AB AA ==，4BC =，E 为CD 的中点，M 是1A C 上一点，N 是平面1AED 上一点，则（ ）A. 长方体1111ABCD A B C D -的外接球的表面积为24πB. 1A C AE ⊥C. 1AC ∥平面1AEDD. MN的最小值为21〖答 案〗ACD〖解 析〗由长方体1111ABCD A B C D -中，12AB AA ==，4BC =， 设长方体1111ABCD A B C D -的外接球的半径为R=，则2R =R =所以长方体的外接球的表面积为24π24πS R ==，所以A 正确； 在长方体1111ABCD A B C D -中，可得1AA ⊥平面ABCD ， 因为AE ⊂平面ABCD ，所以1AA AE ⊥ 假设1A C AE ⊥，且111AA A C A =，11,AA AC ⊂平面1AA C ，所以⊥AE 平面1AA C ， 又因为AC ⊂平面1AA C ，所以AE AC ⊥，因为在矩形ABCD 中，AE 与AC 不垂直，所以假设不成立，所以1A C 与AE 不垂直，所以B 错误；连接1A D 交1AD 于点F ，连接EF ，因为E 为CD 的中点，所以1//EF A C ， 又因为1AC ⊄平面1AED ，且EF ⊂平面1AED ，所以1//AC 平面1AED ，所以C 正确； 因为1//AC 平面1AED ，且点M 在1A C 上的一动点， 所以M 点到平面1AED 的距离等于A 点到平面1AED 的距离，设距离为d ， 因为长方体1111ABCD A B C D -中，12AB AA ==，4BC =，可得11AD D E AE ==所以12cos 5AD E ∠=，所以1sin 5D AE ∠=，所以112AED S=⨯=又由1111A AED E AA D V V --=，可得111421332h =⨯⨯⨯⨯，所以21h =，即MN 的最小值为21，所以D 正确. 故选：ACD.三、填空题：本题共4小题，每小题5分，共20分．把〖答 案〗填在答题卡中的横线上． 13. 某学校有3名男生和2名女生报名学科竞赛，计划从这5名同学中随机选择2人代表学校去参加比赛，则这2人性别相同的概率为________． 〖答 案〗25〖解 析〗3名男生记为ABC ，2名女生记为ab ，从中随机选2人有AB ，AC ，Aa ，Ab , BC ，Ba ，Bb ，Ca ，Cb ，ab 共10种选法，则选出性别相同的有AB ，AC ， BC ，ab ，4种取法， 所以取出的2个球都是白球的概率为42105P ==， 故〖答 案〗为：2514. 已知()()2N,ln e 1n xn f x x x ⎡⎤∈=+-⎣⎦为奇函数，则n 的值可以为________．（写出一个满足条件的即可）〖答 案〗1（〖答 案〗不唯一） 〖解 析〗因为2e 10x +>恒成立， 当0n =时，函数()f x 的定义域为()(),00,∞-+∞，当N n *∈时，函数()f x 的定义域为R ，所以对于N n ∈，函数()f x 的定义域关于原点对称， 而()()()()()()()()222222e 1ln e 1ln ln e 1ln e ln e 1e x n n n n xx x x x f x x x x x x x x x -⎡⎤⎡⎤+⎣⎦⎣⎦⎛⎫+⎡⎤-=-++=-+=-+-⎭=-+- ⎪⎣⎦⎝，当n 为正奇数时，()()()()2ln e 1n xf x x x f x -=-+⎤=-⎣⎦-⎡，函数为奇函数， 当n 为0或正偶数时，()()()2ln e 1n xf x x x x f -=+⎤=⎣⎦-⎡，函数为偶函数，不符合题意.综上所述，当n 为正奇数时，函数()f x 为奇函数， 所以n 的值可以为1（〖答 案〗不唯一）. 故〖答 案〗为：1（〖答 案〗不唯一）.15. 已知函数()sin 10y x ωω=->在[]0,π上有且仅有2个零点，则ω的取值范围为________．〖答 案〗59,22⎡⎫⎪⎢⎣⎭〖解 析〗函数sin 1y x ω=-在[]0,π上有且仅有2个零点， 由sin 10x ω-=，可得sin 1x ω=， 由[]0,πx ∈，0ω>，得[]0,πx ωω∈，所以5π9ππ22ω≤<，即5922ω≤<， 所以ω的取值范围为59,22⎡⎫⎪⎢⎣⎭.故〖答 案〗为：59,22⎡⎫⎪⎢⎣⎭.16. 开封铁塔是宋都开封具有代表性的文物，是文物价值最高、份量最重的宝物之一．1961年，它被国务院定为中国首批国家重点保护文物之一．如图，为测量开封铁塔的高度，选择C 和一个楼房DE 的楼顶E 为测量观测点，已知,,A CD 在水平地面上，开封铁塔AB 和楼房DE 都垂直于地面．已知15m DE =，45ACD ∠=︒，60ADC ∠=︒，在C 点处测得E 点的仰角为15︒，在E 点处测得B 点的仰角为45︒，则开封铁塔AB 的高度为________m ．〖答 案〗30+〖解 析〗过点E 作EF AB ⊥，交AB 于点F ， 易知BFE △为等腰直角三角形，所以BF EF AD ==， 在Rt ECD △中，因为15ECD ∠=︒，所以15tan15tan15ED CD ==︒︒，ACD 中，由正弦定理得sin 45sin 75AD CD=︒︒，即1515sin 45cos15cos15tan15sin15AD CD ===︒︒︒︒︒，而()sin15sin 4530sin 45cos30cos 45sin 304︒=︒-︒=︒︒-︒︒=，所以)151514AD==，则)1511530AB BF AF AD ED+=+=+=+=.故〖答案〗为：30+四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17. 已知复数z的虚部为2-，且()2i2iz+为纯虚数．（1）求z；（2）若复数z是关于x的方程()20,x mx n m n++=∈R的一个根，求,m n的值．解：（1）设2iz a=-，Ra∈，则()()()22i2i2i i2iz a+=-+()()()()22i i224i i2i224ia a a a a=--=-++-=-++，又()2i2iz+为纯虚数，所以22040aa-=⎧⎨+≠⎩，解得1a=，所以12z i=-.（2）因为复数12z i=-是关于x的方程()20,x mx n m n++=∈R的一个根，所以12iz=+也是关于x的方程()20,x mx n m n++=∈R的一个根，所以()()12i12i12i12imn-++=-⎧⎨-⋅+=⎩，解得25mn=-⎧⎨=⎩.18. 某中学为研究本校高三学生在市联考中数学成绩，随机抽取了100位同学的数学成绩作为样本，得到以[)[)[)[)[)[]80,90,90,100,100,110,110,120,120,130,130,140分组的样本频率分布直方图，如图所示．（1）求直方图中a 的值；（2）请估计本次联考该校数学成绩的平均数；（同一组中的数据用该组区间的中点值作代表） （3）请估计本次联考该校数学成绩的40%分位数．解：（1）由频率分布直方图可得()0.0060.0120.040.0260.006101a +++++⨯=， 解得0.01a =.（2）本次联考该校数学成绩的平均数为：()850.006950.0121050.041150.0261250.011350.00610109⨯+⨯+⨯+⨯+⨯+⨯⨯=.（3）成绩在[)80,90的频率为0.006100.06⨯=，[)90,100的频率为0.012100.12⨯=， [)100,110的频率为0.04100.4⨯=，因为0.060.120.180.4+=<，0.060.120.40.580.4++=>，所以第40%分位数在[)100,110之间，设为m ，则()0.060.121000.040.4m ++-⨯=， 解得105.5m =，所以本次联考该校数学成绩的40%分位数为105.5. 19. 已知函数()22xxf x -=-．（1）求不等式()22xf x >-的解集； （2）若不等式()()1222xf x mf x -+>对()0,x ∈+∞恒成立，求实数m 的取值范围．解：（1）令()()222222x x x xg x f x -=+-=-+-， 则不等式()22xf x >-即为()0g x >， 因为22xy =-，2x y =在定义域R 上单调递增，2x y -=在定义域R 上单调递减，所以()g x 在定义域R 上单调递增，又()111222021g -=-+-=，所以1x >时()0g x >， 即不等式()22xf x >-的解集为()1,+∞.（2）由()()1222xf x mf x -+>对()0,x ∈+∞恒成立，可得()222222xx x x m --+>-对()0,x ∈+∞恒成立，令22x x t -=-，因为()0,x ∈+∞，所以()0,t ∈+∞，()2222222222x x x xt --+-=+=+，所以222t m t t t+<=+，又2t t +≥=，当且仅当2t t =，即t =时取等号，所以m <m的取值范围为(,-∞.20. 在ABC 中，角,,A B C所对的边分别为,,sin cos a b c B b b A -=． （1）求A ；（2）若ABC 为锐角三角形，且2b c +=，求a 的取值范围． 解：（1sin cos sin sin sin cos B b b A A B B B A -=⇒-=， 因为()0,πB ∈，所以sin 0B ≠，π1sin sin sin cos 1cos sin()62A B B B A A A A -=⇒-=⇒-=， 因为()0,πA ∈，所以ππ5π,666A ⎛⎫-∈- ⎪⎝⎭， 因此有πππ663A A -=⇒=； （2）由正弦定理得sin sin sin a b c A B C ===，所以,b B c C==，所以2π3b c B C B B ⎛⎫+==- ⎪⎝⎭3πsin cos2sin2226B B a B⎛⎫⎛⎫=+=+=⎪ ⎪⎪⎝⎭⎭，所以1πsin6aB=⎛⎫+⎪⎝⎭，因为ABC为锐角三角形，可得π22ππ32BB⎧<<⎪⎪⎨⎪<-<⎪⎩，解得ππ62B<<，所以ππ2π363B<+<πsin16B⎛⎫<+≤⎪⎝⎭，所以11πsin6B≤<⎛⎫+⎪⎝⎭，所以a∈21. 某项考试按科目A、科目B依次进行，只有当科目A成绩合格时，才可继续参加科目B 的考试．已知每个科目只允许有一次补考机会，两个科目成绩均合格方可获得证书．现某人参加这项考试，科目A每次考试成绩合格的概率均为34，科目B每次考试成绩合格的概率均为12．假设各次考试成绩合格与否均互不影响．（1）求他在科目B考试第一次合格的概率；（2）在这项考试过程中，假设他不放弃所有的考试机会，求他可获得证书的概率．解：（1）科目A考试合格的概率为3131544416+⨯=，则他在科目B考试第一次合格的概率为1511516232⨯=.（2）他考试的次数为2且获得证书的概率为1313428P=⨯=，他考试的次数为3且获得证书的概率为2311131942244232P=⨯⨯+⨯⨯=，他考试的次数为4且获得证书的概率为313113442264P=⨯⨯⨯=，所以他可获得证书的概率为393458326464++=. 22. 如图，在四棱锥M ABCD -中，AD BC ∥，AC CD ⊥，2BC AD =，△MAD 为等边三角形，平面MAD ⊥平面ABCD ，点N 在棱MD 上，直线//MB 平面ACN ．（1）证明：2MN ND =．（2）设二面角M AC D --的平面角为α，直线CN 与平面ABCD 所成的角为θ，若tan α的取值范围是⎡⎣，求tan θ的取值范围．（1）证明：连接BD 交AC 于O ，连接ON ．因为//AD BC ，2BC AD =，所以根据相似的性质可得2BO BCOD AD==． 因为直线//MB 平面ACN ，MB ⊂平面MBD ，平面ACN 平面MBD ON =，所以//MB ON ，则2MN BOND OD==，所以2MN ND =． （2）解：取AD 的中点E ，AC 的中点F ，连接ME ，EF ，MF ． 因为△MAD 为等边三角形，所以不妨设6MA AD MD ===，则ME =ME AD ⊥．因为平面MAD ⊥平面ABCD ，平面MAD ⋂平面ABCD AD =，ME ⊂平面AMD , 所以ME ⊥平面ABCD ，,EF AC ⊂平面ABCD,所以ME EF ⊥，ME AC ⊥． 又因为E ，F 分别为AD ，AC 的中点，所以//EF CD ，而AC CD ⊥，所以AC EF ⊥，又ME EFE ⋂=，,ME EF ⊂平面MEF ,则AC ⊥平面MEF ，MF ⊂平面MEF 得AC MF ⊥， 所以∠MFE 是二面角M AC D --的平面角，即MFE α∠=． 设EF m =，则tan ME EF α⎡==⎣，得m ⎡∈⎣． 过N 作//NH ME 交AD 于H ，连接CH ，由于ME ⊥平面ABCD ，所以NH ⊥平面ABCD ， 则∠NCH 为直线CN 与平面ABCD 所成的角，即NCH θ∠=．13NH ME ==113DH ED ==，2CD m =．因为cos 3CD m ADC AD ∠==，所以CH ==，则tan NH HCθ===．因为m ⎡∈⎣，所以tan 11θ=⎣⎦． 故tan θ的取值范围为⎣⎦．。
新乡学院《物理化学》试卷参考答案及评分标准
新乡学院《物理化学》试卷参考答案及评分标准一、选择题（请将正确答案的标号填在规定的表格内，每小题2分，共30分）本题主要考查学生对基本理论的掌握程度和辨别问题的能力。
评分标准：本题属单项选择，每小题选择正确给2分，选错、多选或不选给0分。
参考答案： 题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 答案 DCDBDBCDDBBCDAC二、填空题（本题共16个空，每空1分，共16分）本题主要考查学生对基本理论掌握程度和分析问题的能力。
评分标准：1．所填答案与标准答案相同，每空给1分；填错或不填给0分。
2．所填答案是同一问题（概念、术语）的不同描述方法，视为正确的，给1分。
参考答案：1、①38.3J ·K -1； 0； 11.49KJ ； 0 ；2、0.180kg ·mol -1 ；3、封闭系统；隔离系统；纯物质的完美晶体；4、溶质不挥发、溶质与溶剂不形成固溶体；5、低；6、①△H ； ②△U 、△H 、△S 、△A 、△G ； ③△G ； ④△U7、简单低共熔混合物相图；少1个；三、证明题 （本题共2个小题，每小题5分，共10分）本题主要考查学生对基本问题的分析和逻辑推理能力。
评分标准：所写答案与标准答案相同，每小题给5分。
思路清晰，推理正确，视情况给分 。
参考答案：1、 在T-S 图等压线上，曲线的斜率为p S T)(∂∂，（1分） 由基本公式：dH =TdS+VdP 则：p T H )(∂∂ = Cp =T ·p TS)(∂∂ （3分） ∴ p S T )(∂∂=CpT即为T-S 图等压线上，曲线的斜率，当T 相同时，斜率相等 （1分）2、U = H －PV ∴d U = dH －d(PV)（2分）∴ p V U )(∂∂ = p V H )(∂∂－P = p V T p T H )()(∂∂∂∂－P =Cp p V T )(∂∂－P 错误！未找到引用源。
新乡期末考试题目及答案
新乡期末考试题目及答案一、选择题（每题2分，共20分）1. 下列哪个选项是新乡市的著名景点？A. 泰山B. 华山C. 红旗渠D. 嵩山答案：C2. 新乡市位于哪个省份？A. 山东省B. 河南省C. 河北省D. 江苏省答案：B3. 新乡市的市花是什么？A. 牡丹B. 荷花C. 菊花D. 月季答案：D4. 新乡市的市树是什么？A. 松树B. 柳树C. 银杏D. 梧桐5. 新乡市的总面积是多少平方公里？A. 8000平方公里B. 8500平方公里C. 9000平方公里D. 9500平方公里答案：B6. 新乡市的人口数量是多少？A. 500万B. 600万C. 700万D. 800万答案：C7. 新乡市的气候类型是什么？A. 温带季风气候B. 亚热带季风气候C. 热带季风气候D. 寒带气候答案：A8. 新乡市的行政区划包括哪些？A. 红旗区、卫滨区、牧野区B. 红旗区、卫滨区、凤泉区C. 红旗区、牧野区、凤泉区D. 红旗区、卫滨区、牧野区、凤泉区答案：D9. 新乡市的著名历史人物是谁？B. 李白C. 杜甫D. 曹操答案：A10. 新乡市的著名特产是什么？A. 信阳毛尖B. 洛阳牡丹C. 新乡牛肉D. 开封灌汤包答案：C二、填空题（每题2分，共20分）1. 新乡市的市花是________，市树是________。
答案：月季、银杏2. 新乡市位于河南省的________部。
答案：北部3. 新乡市的气候类型属于________。
答案：温带季风气候4. 新乡市的总面积约为________平方公里。
答案：85005. 新乡市的人口数量约为________万。
答案：7006. 新乡市的著名历史人物岳飞是________朝的民族英雄。
答案：南宋7. 新乡市的著名景点红旗渠位于________区。
答案：林州市8. 新乡市的市树银杏在________区有大量种植。
答案：凤泉区9. 新乡市的著名特产新乡牛肉以其________而闻名。
新乡学院 2012―2013学年度第2学期
新乡学院 2012―2013学年度第2学期《电子技术》期末试卷A 卷课程归属部门：机电工程学院 试卷适用范围：2011材料本科 考试形式：闭卷 考试时间：110分钟1 两种载流子，当温度升高时，半导体的导电性能显著增强。
2、_____反相___。
（同相、反相）3、将2013个“14、由NPN 输出电压出现顶部被削平5、在共射、共集和共基三种基本放大电路组态中，输入电阻最大的是_共集________组态。
OTL 和负反馈，为了得到稳定的电流应引入 （串联、并联、电压、电流）10、三变量的逻辑函数有___8___个最小项，任意两个不同的最小项的逻辑乘积为__ __0__，一、填空题（每空1分，共20分）院系:________ 班级:__________ 姓名:______________ 学号:_____________…….……………………….密…………………封…………………线…………………………全部最小项之逻辑和为。
1112、优先编码器74LS148输入为0I72、1Y 、0Y 。
当使能输入0S =，1560I I I ===时，输出210Y Y Y1、某正常放大工作电路中的三极管三极M 、P 、N 的直流电位分别为-1.3、-6V 、-2V ，由此可知该三极管为 型管，由 材料制造，且M 、P 、N 分别为极、 极和 极。
（ A ）A 、PNP 硅 E ，C ，B B 、PNP 锗C ，E ，B C 、NPN 硅 E ，B ，CD 、PNP 硅 C ，E ，B2、在基本共射放大电路中，若更换晶体管使β值由50变为100,则电路的放大倍数（ C ）。
A 、约为原来的1/2倍 B 、约为原来的2倍 C 、基本不变 D 、无法确定3、七段显示译码器的输出Ya ～Yg=0010010驱动共阳极七段发光管可显示( B )。
A 、1 B 、2 C 、3 D 、44、可以放大电流，但不能放大电压的是（ B ）组态放大电路。
新乡期末精选检测题(Word版 含答案)
新乡期末精选检测题（Word 版 含答案）一、第一章 运动的描述易错题培优（难）1．如图所示，物体沿曲线轨迹的箭头方向运动，AB 、ABC 、ABCD 、ABCDE 四段曲线轨迹运动所用的时间分别是：1s 、2s 、3s 、4s ，下列说法正确的是（ ）A ．物体在AB 段的平均速度为1m/sB ．物体在ABC 5m/s C ．AB 段的平均速度比ABC 段的平均速度更能反映物体处于A 点时的瞬时速度D ．物体在B 点的速度等于AC 段的平均速度【答案】ABC【解析】【分析】【详解】A ．由图可知物体在AB 段的位移为1m ，则物体在AB 段的平均速度1m/s 1m/s 1x v t === 选项A 正确； B ．物体在ABC 段的位移大小为 2212m 5m x =+=所以物体在ABC 段的平均速度5m/s 2x v t == 选项B 正确；C ．根据公式x v t=可知，当物体位移无限小、时间无限短时，物体的平均速度可以代替某点的瞬时速度，位移越小平均速度越能代表某点的瞬时速度，则AB 段的平均速度比ABC 段的平均速度更能反映物体处于A 点时的瞬时速度，选项C 正确；D ．根据题给条件，无法得知物体的B 点的运动速度，可能很大，也可能很小，所以不能得出物体在B 点的速度等于AC 段的平均速度，选项D 错误。
故选ABC 。
2．节能减排可体现在我们日常生活中．假设公交车通过城市十字路口时允许的最大速度为10m/s，一辆公交车在距离十字路口50m的车站停留，乘客上下完后，司机看到红灯显示还有10s，为了节能减排．减少停车，降低能耗，公交车司机启动公交车，要使公交车尽快通过十字路口且不违章，则公交车启动后的运动图象可能是（）A．B．C．D．【答案】ABD【解析】【分析】【详解】因速度图像与坐标轴围成的面积等于物体的位移，由速度图像可知，A、B、D三个图像与坐标轴围成的面积均大于50m，且速度不超过10m/s；C图像中公交车的位移可能恰好等于50m，且速度小于10m/s,故公交车启动后的运动图像可能是ABD。
概率论与数理统计期末试卷5
新乡学院期末考试试卷概率论与数理统计考试范围 第1至7章命题人院系 数学与信息科学 考试形式闭卷课程类别必修 学 期专业一、选择题（本题共_5__小题,每小题 3 分，共 15 分) (从下列备选答案中选择正确答案)1．设A ，B 为任意两个事件，0)(,>⊂B P B A ，则下式成立的为（ ） （A ）B)|()(A P A P < （B ）B)|()(A P A P ≤ （C ）B)|()(A P A P > （D ）B)|()(A P A P ≥ 2. 下列函数为随机变量的密度函数的为：( )(A) ⎩⎨⎧∈=其他,0],0[,cos )(πx x x f (B) ⎪⎩⎪⎨⎧<=其他,02,21)(x x f(C) ⎪⎩⎪⎨⎧<≥=--0,00,21)(222)(x x e x f x σμπσ (D) ⎩⎨⎧<≥=-0,00,)(x x e x f x3．设随机变量)4,(~2μN X ，)5,(~2μN Y ，}{41-≤=μX P P ，}{52+≥=μY P P ，则（ ）（A ） 对任意的实数21,P P =μ， （B ）对任意的实数21,P P <μ， （C ）只对实数μ的个别值，有21P P =， （D ）对任意的实数21,P P >μ4．如果随机变量Y X ,满足)()(Y X D Y X D -=+，则必有（ ） （A ）独立与Y X （B ）不相关与Y X （C ）0=DY （D ）0=DX5．设随机变量X 的概率密度函数为()x f ，且)()(x f x f -=，又)(x F 为分布函数，则对任意实数a ，有（ ） (A) (),1)(0dx x f a F a⎰-=- (B) (),21)(0dx x f a F a ⎰-=- (C) )()(a F a F =-， (D) ()1)(2-=-a F a F ， 二、填空题（本题共 5 小题，每小题 3 分，共 15 分） 1.事件A 在4次独立实验中至少成功一次的概率为8180，则事件A 在一次实验中成功的概率为 。
新乡工程学院期末考试卷
新乡工程学院期末考试卷考试科目：[科目名称]考试时间：120分钟总分：100分一、选择题（每题2分，共20分）1. 计算机科学中，以下哪个是数据结构的基本概念？A. 算法B. 数据C. 程序D. 编译器2. 在经济学中，需求曲线通常：A. 向右上方倾斜B. 向右下方倾斜C. 向左上方倾斜D. 向左下方倾斜3. 以下哪个不是牛顿运动定律？A. 惯性定律B. 动量守恒定律C. 作用力与反作用力定律D. 加速度定律4. 化学中，原子量单位是：A. 摩尔B. 克C. 原子质量单位（amu）D. 千克5. 以下哪个是生物多样性的组成部分？A. 遗传多样性B. 物种多样性C. 生态系统多样性D. 以上都是二、填空题（每空1分，共15分）1. 计算机程序设计语言中，______是一种面向对象的编程语言。
2. 经济学中的边际成本是指每增加一单位产品所增加的______。
3. 牛顿第一定律又称为______定律。
4. 化学中，元素周期表的元素按照______和______递增排列。
5. 生物学中，细胞的遗传信息存储在______中。
三、简答题（每题10分，共30分）1. 描述计算机操作系统的基本功能。
2. 解释经济学中的供求法则。
3. 简述牛顿的三大运动定律。
四、计算题（每题15分，共30分）1. 假设一个物体在自由落体运动中，从静止开始下落，忽略空气阻力，给定初始高度为50米。
请计算物体落地所需的时间。
2. 假设一个企业生产某种商品，固定成本为10000元，每单位产品变动成本为50元，商品的市场价格为150元。
计算该企业在生产100单位产品时的总成本和利润。
五、论述题（15分）请论述生物多样性对生态系统的重要性，并举例说明。
[注：以上内容为示例，实际考试题目应根据具体课程内容和教学大纲来设计。
]。
河南省新乡市2023-2024学年高二下学期7月期末测试物理试题(含答案)
新乡市2023-2024学年高二下学期7月期末测试物理本试卷满分100分，考试用时75分钟。
注意事项：1．答题前，考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动，用橡皮擦干净后，再选涂其他答案标号。
回答非选择题时，将答案写在答题卡上。
写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
4．本试卷主要考试内容：高考全部内容。
一、单项选择题：本题共7小题，每小题4分，共28分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．如图所示，AB为一段完全固定且不变形的钢丝，一杂技演员手握长杆正在“走钢丝”，演员从A端缓慢走到B端的过程中，先“下坡”后“上坡”，下列说法正确的是（）A．演员“下坡”过程中受到的静摩擦力逐渐增大B．演员“下坡”过程中钢丝对他的作用力逐渐增大C．演员“上坡”过程中对钢丝的压力逐渐减小D．演员“上坡”过程中所受的静摩擦力方向沿“坡”向下2．物理学家康普顿在研究石墨对X射线的散射时，发现在散射的X射线中，部分波长发生改变，这个现象称为康普顿效应，我国物理学家吴有训进一步证实了该效应的普遍性。
如图所示，一个光子和一个静止的电子相互碰撞后，电子向某一个方向运动，光子沿另一个方向散射出去，下列说法正确的是（）A．散射光子的速度变小B．散射光子的速度可能变大C．散射光子的频率变小D．散射光子的波长变短3．如图所示，将一篮球从地面上方的B点斜向上抛出，刚好垂直击中篮板上的A点。
若抛射点水平向右移动一小段距离，仍使抛出的篮球垂直击中A点，不计空气阻力，则下列方法可行的是（）A ．增大抛射速度的大小，同时增大抛射角B ．增大抛射速度的大小，同时减小抛射角C ．减小抛射速度的大小，同时增大抛射角D ．减小抛射速度的大小，同时减小抛射角4．钳形电流表是电机运行和维修工作中最常用的测量仪表之一，其主要由一只电流表和电流互感器组成，工作原理与变压器相同。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
新乡学院期末考试试题标准或参考答案及评分
标准
Document number：BGCG-0857-BTDO-0089-2022
新乡学院20 -20 学年第学期期末考试
《》试题标准或参考答案及评分标准（A/B卷）
适用范围：
一、名词解释（本题共4个小题，每小题4分，共16分）
本题主要考查学生对基本概念的掌握程度；
评分标准：每小题给出正确答案给4分，如果和本答案不一致，只要描述正确，给4分，部分正确可根据对错程度分别给1分或2分或3分，答案错误或不答给0分。
参考答案：
1．软件危机是指在计算机软件的开发和维护过程中所遇到的一系列问题。
2．模块耦合是对一个软件结构内不同模块之间互连程度的度量。
3．软件维护就是在软件交付使用之后，为了改正错误或满足新的需要而修改软件的过程。
4．软件重用是指同一事物不做修改或稍加改动就在不同环境中多次重复使用。
二、选择题（本题共10个小题，每个小题中只有一个正确答案，请将正确答案的标号填在题后括号内，每小题1分，共10分）
本题主要考查学生对基本理论的掌握程度和和辨别问题的能力。
评分标准：本题属单项选择，每小题选择正确给1分，选错、多选或不选给0分。
参考答案：
1.C
2.C
3.B
4.C
5.C
6.B
7.B
8.C
9.C 10.A
三、填空题（本题共10个空，每空2分，共20分）
本题主要考查学生对基本理论掌握程度和分析问题的能力。
评分标准：
1．所填答案与标准答案相同，每空给2分；填错或不填给0分。
2．所填答案是同一问题（概念、术语）的不同描述方法，视为正确，给2分。
参考答案：
1.编码阶段
2.方法工具过程（顺序无关）
3.功能性能（顺序无关）
4．模块独立性顺序内聚
5.E-N+2（或P+1）
6.人力资源
四、判断题（本题共10个小题，每小题1分，共10分）
本题主要考查学生对基本问题的分析能力。
评分标准：
所填答案与标准答案相同，每小题给1分；选错或不选给0分。
参考答案：
1.×
2.√
3.×
4.√
5.√
6.×
7.√
8.√
9.√10.√
五．简答题（本题共4个小题，每小题6分，共24分）
本题主要考查学生对基本问题的理解和掌握程度。
评分标准：
1.所答要点完整，每小题给6分；全错或不答给0分。
2.部分正确可根据对错程度，依据答案评分点给分。
试题：1、简述“双百方针”提出后，在文学创作方面出现的三个突破。
参考答案：
⑴、敢于大胆正视人民内部矛盾，揭露生活中的矛盾冲突，突破了“无冲
突”论的禁锢。
（2分）
⑵、发挥讽刺的积极作用，突破了人民内部不适用讽刺这一文学手段的囿见。
（2分）
⑶、创作题材不断扩大，突破了回避描写爱情或爱情不能作为作品题材的条条框框。
（2分）
试题：2、简述老舍《茶馆》的主题和结构。
参考答案：
主题：埋葬旧时代，暗示光明的到来。
（2分）
结构：《茶馆》采取三个横断面连缀式结构，每一幕内部也以许多小小的戏剧冲突连缀。
剧本以“人物带动故事”，“主要人物由壮到老，贯串全剧”，“次要人物父子相承”，“无关紧要的人物招之即来、挥之即去”。
同时，人物的故事、命运又暗示着时代的发展，从而使得剧本紧针密线，形散神凝，以貌似平淡散乱的人物、情节织出一幅“清明上河图”式的从清末到民国末年的民间众生相。
（4分）
试题： 3、简要的评价民间叙事长诗《阿诗玛》被改变这一文学现象。
参考答案：
（1）《阿诗玛》的改编象征着民族文学的统一，也使之进入了汉语文化圈，并取得了一定的地位。
（2分）
（2）但这种地位是边缘化的，在进入汉语文化圈的同时，付出了巨大的代价：为了迎合共名的话语形态，不可避免地失去了许多民间文学的优秀内容。
（2分）
（3）单纯的主流话语无法完全霸占民间文化，民间文化已成为一种文化积淀，主导着民间文学在主流话语霸权压一下，仍具有永远的生命力。
（2分）
试题：4、研究者认为，《文革十年》，中国当代文学基本是一片空白，你是否同意这种观点，并说明你的理由。
参考答案：
（1）不正确。
（2分）
（2）“潜在伤痕”的存在使得知识分子的文化传统以“破碎”的方式隐遁于民间。
（2分）
（3）潜在文学具有独特的审美价值和文学价值，比如小说《波动》，朦胧诗等。
（2分）
六．论述题（本题共2个小题，每小题10分，共20分）
本题主要考查学生分析问题、解决问题的能力，对问题进行剖析和综述的能力。
评分标准：
1.所答要点完整，每小题给6分；全错或不答给0分。
2.部分正确可根据对错程度，依据答案评分点给分。
试题： 1、结合具体作品，谈谈你对“伤痕文学”的评价，你认为“伤痕文学”的得与失对当下文学有何启示意义。
参考答案：
（1）对伤痕文学的评价：有独特的价值也有局限性。
（2分）
（2）意义：深刻的评判了几十年的文化和政治，敢于正视历史，是“五四”现实战斗精神高扬的标志。
（2分）
（3）局限性：“伤痕文学”从某一角度讲，同样是与“政治”紧密联系的，走的是文革文学的老路，具体表现为：
a其出现是为了迎合改革派对凡是派的斗争需要。
（1分）
b《班主任》的成功恰恰说明了“伤痕文学”迎合当时政治的需要。
（1分）
c“伤痕文学”的核心概念、思维方式甚至表现形式都与“十七年文学”有着内在的联系。
（1分）
（4）启示意义：
应尊重文学自身的客观规律，还给文学独立的生存空间。
（3分）
试题：2、结合50-70年代文学具体作品，试论述当代文学观念中战争文化心理的特征，并根据你的理解谈谈战争文化心理的存在对中国当代文学的影响。
参考答案：
特征：（1）明确的目的性和功利性，文学宣传的职能性与真实性的冲突。
（2分）
（2）二分法思维习惯被滥用，文学创作出现雷同模式。
（1分）
（3）英雄主义和乐观主义基调的确立。
（2分）
对当代文学的影响：
（1）社会主义悲剧被取消。
（2分）
（2）个体价值被取消。
（1分）
（3）政治因素成为评价文学的主要标准。
（2分）。