常用对数表
高一上册数学对数知识点

高一上册数学对数知识点对数是数学中一种重要的运算形式,能够将指数运算转化为对数运算,从而简化计算过程。
它在解决指数方程、评估指数函数的值以及处理复杂的数学问题方面起着重要作用。
在高中数学课程中,学习对数是必不可少的一部分。
下面我将为大家介绍高一上册数学中的几个重要的对数知识点。
一、对数的定义与性质1. 对数的定义:对于正数a(a≠1)和正数x,如果满足a^x=b (b>0),那么称x为以a为底b的对数,记作logₐb=x。
其中,a 被称为对数的底数,b被称为真数。
2. 对数的性质:(1)logₐ1=0,任何数的以自身为底的对数等于1。
(2)logₐa=1,任何数以其自身为底的对数等于1。
(3)logₐ(a*b)=logₐa+logₐb,任何两个正数的乘积的对数等于它们的对数之和。
(4)logₐ(a/b)=logₐa-logₐb,任何两个正数的商的对数等于它们的对数之差。
(5)logₐ(a^p)=p*logₐa,任何数的幂的对数等于指数与幂的底数的对数乘积。
二、常用对数与自然对数1. 常用对数:以10为底的对数称为常用对数,常用对数的记作logb,其中b表示真数。
常用对数的底数为10,即log₁₀b。
2. 自然对数:以自然常数e(约等于2.71828)为底的对数称为自然对数,自然对数的记作lnx,其中x表示真数。
三、对数运算的应用1. 对数方程:对数方程是指以对数形式表示的方程。
通过对数的性质,可以将一些指数方程转化为对数方程,从而更方便地解决问题。
2. 指数函数:指数函数是以指数形式表示的函数,具有形如f(x)=a^x的表达式,其中a为底数。
对数函数则是指数函数的逆运算,可以通过对数函数求解指数函数的值。
3. 对数尺度:对数尺度在测量和表达某些现象时往往更加合适。
例如在地震的震级表中,每增加一个单位的震级,地震的能量就增加10倍。
四、常用对数的换底公式1. 换底公式:对于任意正数a、b以及正整数n,换底公式为logₐb=logₐn * lognb。
对数与对数运算

(2).(log4 3 log8 3)(log3 2 log9 2)
3) log4 3 log9 2 log1 4 32
2
例2 20世纪30年代,里克特制订了一种表明地震 能量大小的尺度,就是使用测震仪衡量地震能量 的等级,地震能量越大,测震仪记录的地震曲线 的振幅就越. 这就是我们常说的里氏震级M,其 计算公式为M=lgA-lgA0. 其中A是被测地震的 最大振幅,A0是“标准地震”的振幅(使用标准 振幅是为了修正测震仪距实际震中的距离造成的 偏差).
温故知新
对数的运算性质
如果 a > 0,a 1,M > 0, N > 0 有:
loga MN loga M loga N
loga
M N
loga M
loga
N
loga M n n loga M (n R)
语言表达: 两个正数的积的对数等于这两个正数的对数和
两个正数的商的对数等于这两个正数的对数差
(1)假设在一次地震中,一个距离震中100千米的测震仪 记录的地震最大振幅是20,此时标准地震的振幅是 0.001,计算这次地震的震级(精确到0.1);
(2)5级地震给人的震感已比较明显,计算是。7.6级地 震的最大振幅上是5级地震的最大振幅多少倍?(精确 到1);
例题解析
例3 生物机体内碳14的“半衰期”为 5730年,湖南长沙马王堆汉墓女尸出 土时碳14的残余量约占原始含量的 76.7%,试推算马王堆古墓的年代.
2.2.1对数与对数的运算性质(3)
温故知新
1、对数的定义: 如果ax=N(a>0,a≠1)那么数x叫做以a为底 N的对数。 记作: x=logaN , 其中a叫做对数的底数,N叫做真数,x=logaN 叫做对数式.
常用对数表

常用对数表
常用对数表是数学家必不可少的一部工具,它收集了常用的对数值,供数学家使用来更方便地解决一些算法问题。
本文将首先介绍常用对数表,然后详细介绍它的使用方法,最后说明它如何在实际应用中发挥作用。
一、什么是常用对数表
常用对数表,又称为对数索引表,是一种收集和发布常用的对数的索引书,它由多个表格组成,每个表格上都有一组数字组成的矩阵,这些矩阵都是由数学家计算出来的,它们收集的数字是基于特定的数学原理,是可以用来计算各种对数值的参考。
二、常用对数表的使用
常用对数表可以用来计算一个数字的对数。
当某一特定数字被置于表格中某一行某一列时,这个数字的对数就可以从表格中获得。
另外,还可以通过将另一个数字乘以10的n次方,然后在表格中获得另一个数字的对数,并将结果加和或者减去部分后得出结果。
当使用常用对数表时,可以为数学家节省计算时间,节省做题的功夫。
三、常用对数表在实际应用中的作用
常用对数表的应用非常普遍,它可以用在很多数学家的研究中。
通过使用常用对数表,可以轻松快速地解决一些复杂的数学问题,比如求出复杂的多项式的对数,比较数学公式的有效性等等。
此外,它还可以用于科学研究,比如量子力学研究、天文学研究等。
综上所述,常用对数表是数学家不可或缺的帮手,它能够大大提
升数学家的计算效率,节省大量的计算时间,同时也可以用在科学研究中。
因此,常用对数表在实际应用中的作用也是非常重要的。
log常用对数表

log常用对数表常用对数表是一种常见的数学工具,用于将指数形式的数值转换为对数形式。
在科学、工程和商业领域中,常用对数表被广泛应用于各种计算和测量中,例如声学、光学、电磁学、化学和经济学等。
常用对数表通常包括自然对数表和常用对数表两种。
自然对数表以e(约等于2.71828)为底,常用对数表则以10 为底。
下面是常用对数表的一些基本信息和应用示例。
1. 基本信息常用对数表通常以10 的幂次方为间隔进行排列,例如10^0、10^1、10^2、10^3 等。
每个数值对应一个对数值,即以10 为底数的指数形式。
例如,在常用对数表中,10^2 对应的对数值是2,表示100 的以10 为底的对数值是2。
2. 应用示例常用对数表在各种领域中有广泛的应用。
例如:声学中,声音的频率和声压级之间的关系可以用对数来表示,因此常用对数表在声学测量中非常有用。
光学中,光的强度和曝光时间之间的关系也可以用对数来表示,因此常用对数表在摄影和电影制作中有重要的应用。
电磁学中,无线电波的功率和频率之间的关系可以用对数来表示,因此常用对数表在无线电通信中有广泛的应用。
化学中,pH 值是一种常见的对数测量单位,因此常用对数表在化学实验中有重要的应用。
经济学中,货币的汇率和通货膨胀率之间的关系可以用对数来表示,因此常用对数表在经济学研究中也有广泛的应用。
除了在各个专业领域中的应用,常用对数表还有一些有趣的数学性质和实际应用。
1. 对数的换底公式对数的换底公式是指可以用任意正实数作为底数来表达对数值。
换底公式为log_b(a) = log_c(a) / log_c(b),其中a、b、c 均为正实数,且b 和c 均不为1。
这个公式表明,如果我们知道以任意正实数为底的对数值,就可以求出以其他正实数为底的对数值。
2. 对数的运算性质对数具有一些重要的运算性质,例如对数的乘积法则、商数法则和幂次法则等。
这些法则可以帮助我们方便地进行对数计算,简化复杂的问题。
对数估算方法--杨岸杰

对数值比较大小的估算方法和原理一、建议记住下列常用数据()lg .,lg .,()ln ..,ln .≈≈≈≈≈120301030477122069310703110lg lg .,lg lg .,lg lg lg .lg lg .,lg lg .=≈=-≈=+≈=≈=≈10以内其它的一些常用对数,可以换算得到:422060205120699062307781,8320903092309542lg lg lg .+≈≈68此外,708451,很少用到2--浙江杨岸杰二、观察下表log .=..%log ...%log .=..%log .=0.8333.%log ...%log ...%≈+≈≈-≈-≈-≈≈-≈≈-345678对数值分数值相对误差2206309066675673330795207500536444086140800071355508982723666092080857168877709358087506508log .=..%log ...%log .=..%log .=..%log ...%log ...%≈-≈≈+≈+≈+≈≈+≈≈+234567对数值分数值相对误差331585015000536244126191333356635511610125007674661113312000779577108601166774368810686114296957n ≥发现有以下规律:当2时()1相同的单调性和极限;()=n n ≥22时偏小;3时偏大;log ()n n n n++⇒11处理()log n nn n +⇒+1处理1()%3相对误差先增后减,不超过8.()1相同的单调性和极限;()=n n ≥22时偏大;3时偏小;()%3相对误差先减后增,不超过8.三、原因分析ln()()log ()ln x x f x x x x+=+=>11,0()x h x x +=1两个函数的图像n ≥可以看到2时,两者非常接近 感兴趣的同学可以通过计算,分析具体原因。
对数函数知识点总结
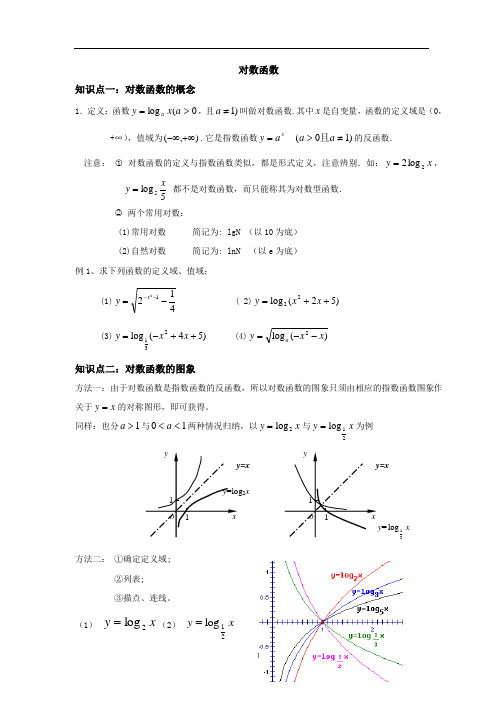
对数函数知识点一:对数函数的概念1.定义:函数0(log >=a x y a ,且)1≠a 叫做对数函数.其中x 是自变量,函数的定义域是(0,+∞),值域为),(+∞-∞.它是指数函数xa y = )10(≠>a a 且的反函数.注意: ○1 对数函数的定义与指数函数类似,都是形式定义,注意辨别.如:x y 2log 2=,5log 5xy = 都不是对数函数,而只能称其为对数型函数. ○2 两个常用对数: (1)常用对数 简记为: lgN (以10为底) (2)自然对数 简记为: lnN (以e 为底)例1、求下列函数的定义域、值域:(1)41212-=--xy ( 2))52(log 22++=x x y (3))54(log 231++-=x x y (4))(log 2x x y a --=知识点二:对数函数的图象方法一:由于对数函数是指数函数的反函数,所以对数函数的图象只须由相应的指数函数图象作关于x y =的对称图形,即可获得。
同样:也分1>a 与10<<a 两种情况归纳,以x y 2log =与x y 21log =为例方法二: ①确定定义域; ②列表; ③描点、连线。
(1)x y 2log =(2) x y 21log =y=x o 11 yxy =log 2x o 11 yxy=xy =x 21log(3)x y 3log =(4) x y 31log =思考:函数x y 2log =与y =3log x 与y对函数的相同性质和不同性质. 相同性质: 不同性质:例2、作出下列对数函数的图象:知识点三:对数函数的性质由对数函数的图象,观察得出对数函数的性质.思考:底数a 是如何影响函数x y a log =的.(学生独立思考,师生共同总结)规律:在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大. 例3、比较下列各组数中两个值的大小:⑴ 5.8log ,4.3log 22; ⑵7.2log ,8.1log 3.03.0; ⑶)1,0(9.5log ,1.5log ≠>a a a a . 变式训练:(1)若3log 3log n m <,求n m 和的关系。
高中数学拓展知识-对数表

对数表的历史对数表的应用领域是极其广阔的,但对数表的编制也经历了一个漫长的过程。
早在公元前200年,古希腊数学家阿基米德(Archimedes )就注意到表2-2中两数列之间的关系:100 101 102 103 104 105 106 107 01234567…可以用下面数列中两数的加、减关系来替代上面数列中两数的乘、除关系,这样就把繁复的乘、除运算转化成简单的加、减运算。
在1544年,德国数学家施蒂费尔(Stifel ,1487-1567)在《整数的算术》中又重新发现了这个性质。
不过,Archimedes 和Stifel 的先驱性工作,成了Napier 发明对数的“巨人肩膀”。
在1594年,Napier 发明了对数,在1614年出版的《奇妙的对数定律说明书》中公布了他编制的间隔为1′的7位正弦对数表。
要编制对数表,先要解决选择底数的问题。
我们已经学过换底公式abb c c a log log log, 所以,只要选择合适的底数使对数表编制方便就可以了。
如果以a =10为底数,则有表2-2表2-3b a log0.0000 0.00010.00020.0003⋯⋯ b1.0000⋯⋯显然,这种对数表的真数多是无理数,使用起来很不方便。
如果以a =1010000为底数,则有b a log0.0000 0.0001 0.0002 0.0003 ⋯⋯ b1.0000101102103⋯⋯显然,这种对数表的真数间隔很大,使用起来也不方便。
如果以a =1.000110000为底数,则有b a log0.0000 0.0001 0.0002 0.0003 ⋯⋯ b1.00001.0001001.0002001.000300⋯⋯显然,这种对数表的真数间隔已经小多了。
实际上,要使间隔更小,可以取底数1(1+)na n=,其中n>10000。
Napier 编制第一张对数表时选1000000)0000001.1(=a 。
对数恒等式

对数恒等式说明:本文提到的所有公式的证明都是不作要求的,写出来是为了提供参考。
其中含*的公式是重点,要求熟记以及灵活应用,其它的作为阅读材料。
定义:对数源出于指数log xa a N x N=⇔=,0a >且1a ≠,0N >常用对数:10lg log N N =;自然对数:ln log e N N =, 2.718281828459e = 一.基本关系式 .(基础)把指数式代入对数式消去N ,得到 *(F1)log x a a x =,0a >且1a ≠,x ∈R说明:x a a x xa a x a =−−−−−→−−−−−−→−log 为底做对数运算以为底作指数运算以特别地,对应0x =和1x =的情况,有 *(F1.1)log 10a =,0a >且1a ≠ *(F1.2)log 1a a =,0a >且1a ≠ 把对数式代入指数式消去x ,得到 (F2)真数还原:logaNa N=,0a >且1a ≠,0N >说明:log log aNa a a N N aN −−−−−−→−−−−−−→=以为底做对数运算以为底做指数运算应用举例: 例1:求值(E1)321log 256;(E2)3log 227;(E3)9log 227。
解:(E1)()558855322218log log 2log 22565--===-(E2)()()33333log 2log23log 2log 2332733328=====(E3)为了底数变为相同,先分析27与9的关系,()33322227339===,所以()999log 2333log 2log 222227992⎛⎫==== ⎪⎝⎭注:需要使用的指数恒等式:()()srr rs sr s a a a a ===,0a ≥。
做这一类题的关键在于关注底数是否相同,底数不同的想办法化成同底数,然后应用公式。
自己动手:(Q1)7log 49;(Q2)12log 8;(Q3)127log243;(Q4)2log 52;(Q5)32log533-。
