第六章利率期限结构
第6章-利率期限结构理论01
§6.2 收益率曲线的构建原理 证券提供的现金流总是离散的，理论上只能得到收益率曲线上有限个点。为了得到整条收益率曲线，主要有直 接法和间接法两种构建方式。 1．直接法 直接法：利用息票债券市场价格推导出隐含零息债券价格的方法。 假设条件：为了讨论问题方便，假定n个到期收益率恰可由n种零息债券的价格解出。
（6.2） 假设F是可逆的，即假设各种债券的支付之间不存在线性相关关系，（6.2）式可写为： 说明：推导出来的价格并不是真实的零息债券的市场价值，而是与市场价格保持一致的隐含的零息债券价格。
收益率曲线的构建：将所得的隐含的零息债券价格代入
1
yt,ti [B(t,ti )] ti t 1 即得t时刻发行的期限为 ti t 的零息债券的到期收益率 yt, ti 。
套期保值策略资产负债匹配的最重要策略是套期保值策略其基本思想是假定资产和负债受相同风险因素的影响如果能求出资产和负债与因素间的函数关系通过调整所持有资产的头寸可做到当风险因素变化时资产与负债的变化量大小相等但方向相反从而资产与负债构成的组合不受风险因素的影响
第二篇 利率期限结构与随机利率模型 第6章 利率期限结构理论
A．87.6 B．99.99 C．102.4 D．101.35 E．132.2 【答案】B 【解析】由零息票收益率曲线推导下一年的远期利率：
1
f1,1
1.082 1.07
1.0901
解得：f1,1 9.01% 。
利用下一年的期望利率9.01%，计算债券的预计价格，得：
p=109/1.0901=99.99（美元）
图6-2为通过计算得到的收益率绘得收益率曲线的散点图。其中横坐标为债券的到期时间，单位为年；纵坐标 为相应零息债券的到期收益率。
利率期限结构是什么
利率期限结构是什么利率期限结构是指不同期限的借贷利率之间的差异关系。
它是金融市场的一种重要现象，对经济和金融市场的运行具有重要影响。
本文将详细介绍利率期限结构的概念、形成原因以及其在金融市场中的意义。
一、利率期限结构的概念利率期限结构是一种描述不同借贷期限下利率水平和利率之间关系的工具。
在金融市场中，借款人通常可以选择不同期限的借贷方式，而不同期限的借贷利率通常是不同的。
利率期限结构的形成是由市场供求关系、风险偏好以及宏观经济环境等多种因素综合影响的结果。
二、利率期限结构的形成原因1.市场供求关系：供求关系是影响利率期限结构的重要因素之一。
当市场中借款需求大于借款供给时，长期借款的利率往往比短期借款的利率更高，从而形成正斜率的利率期限结构；相反，当借款供给大于需求时，长期借款的利率可能低于短期借款利率，形成负斜率的利率期限结构。
2.风险偏好：借款人对于风险的偏好也会影响利率期限结构。
一般来说，借款期限越长，风险越高，借款人要求的利率也越高。
因此，利率期限结构通常呈现出逐渐上升的形态。
3.宏观经济环境：宏观经济变量对利率期限结构的形成也有一定的影响。
例如，经济增长预期、通货膨胀预期、货币政策等因素都可能对利率期限结构产生影响。
三、利率期限结构的意义1.预测经济走势：利率期限结构可以作为一种预测经济走势的工具。
根据利率期限结构的形态，我们可以得出市场对未来经济走势的预期。
如果利率期限结构呈现出正斜率形态，说明市场预期未来经济将好转；反之，如果利率期限结构呈现负斜率或平坦的形态，说明市场对经济未来不太乐观。
2.引导市场定价：利率期限结构对市场定价也具有指导意义。
借款人和投资者可以根据利率期限结构来确定借贷和投资的最佳期限，从而在市场中获取更优的收益。
3.评估金融风险：利率期限结构的变动可以反映金融市场的风险环境。
例如，当利率期限结构出现倒挂，即长期利率低于短期利率时，可能预示着经济衰退和金融风险上升。
利率期限结构ppt课件
例题
• 策略一 投资于一个两年期债券
1（ 1i2t）2 1
1
• 策略二 连续投资于两个一年期债券
i i 1 (1 )(1 e ) 1
t
t 1
1
套利之下，策略一和策略二的收益率趋于相等
(1i2t)2
(1
it
)(1
ie ) t 1
结论
• 简化
e
i i t
t1
i2t
2
• 一般的
•
e ...... e
市场分割假说对三个事实的解释
• 无法解释第一个事实和第二个事实，因为它将不同期限的债券市场看成完全分割的市场。
• 市场分割假说可以解释第三个事实，即典型的收益率曲线总是向上倾斜的。因为在现实经济 中，人们更偏好期限更短，风险较小的债券，而债券发行者一般倾向于发行长期债券以满足 经济发展之需，使得短期债券价格较高，利率较低，长期债券价格较低，利率较高，因此收 益率曲线向上倾斜。
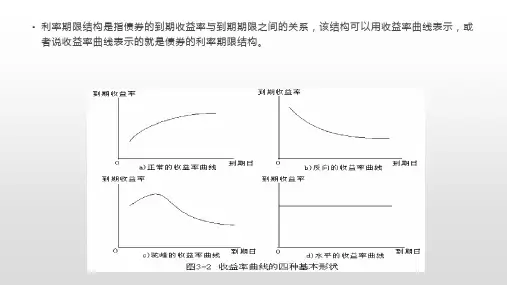
• 利率期限结构是指债券的到期收益率与到期期限之间的关系，该结构可以用收益率曲线表示，或 者说收益率曲线表示的就是债券的利率期限结构。
三个事实
1 不同期限债券利率随时间一起波动 短期利率低，收益率曲线向上倾斜，反之则反
2
收益率曲线几乎都是向上倾斜的，表明长期利率往往高于短期利率
3
纯粹预期假说 分割市场假说 流动性升水假说
• 即典型的收益率曲线总是向上倾斜的。因为投资者偏好短期债券，故随着债券期限延长，期限补偿亦相应 增加，即便未来短期利率预期平均值保持不变，长期利率也将高于短期利率，从而使得收益率曲线总是向 上倾斜。
i i i t t1
t ( n 1)
int
n
对收益率曲线形状的解释
货币金融学第六章 利率风险结构和利率期限结构
第六章利率风险结构和利率期限结构一、利率风险结构相同到期期限的债券的利率水平不同三个影响因素：1. 违约风险在到期期限相同的情况下，有违约风险的债券与无违约风险债券之间的利差被称为（信用/ 违约）风险溢价。
当一个公司遭受重大损失时，会导致违约的可能性增大，企业债券的违约风险提高，预期回报率下降。
此时，该企业债券的需求量下降，价格下降，均衡利率（承诺收益率）上升。
同时，无违约风险的国债的相对预期回报率上升，需求量增大，价格上升，均衡利率（承诺收益率）下降。
这会产生两种债券之间的利差，即企业债券的风险溢价。
而普通公司的债券的违约风险或多或少会高于国债的违约风险，所以公司债券的风险溢价总为正，且风险溢价随违约风险的上升而增加。
2. 流动性企业债券的流动性低于国债无风险债券的流动性，导致企业债券需求量低于国债需求量，进而导致企业债券价格低，均衡利率（承诺收益率）高。
这个利差被称为流动性风险溢价。
3. 所得税债券利息适用的所得税税率越低，相对的预期回报率就越高，需求量就越大，价格越高，均衡利率（承诺收益率）越低。
而所得税税率高的债券，产生的利差被称为税收风险溢价。
二、利率的期限结构利率的期限结构指的是：具有相同风险、流动性和税收特征的债券，由于距离到期日的时间不同，利率也会有所差别。
将期限不同但风险、流动性和税收政策相同的债券的收益率连成一条曲线，得到收益率曲线。
收益率曲线有三种形状——向上倾斜、平坦和翻转三种，分别反映长期利率高于短期利率、长期利率与短期利率持平、长期利率低于短期利率三种预期。
利率期限结构有三个经验事实：到期收益率不同的债券的利率随时间一起波动；收益率曲线大部分时间是向上倾斜的（长期利率高于短期利率）；如果短期利率较低，收益率曲线很可能向上倾斜，而短期利率较高，则收益率曲线很可能向下倾斜。
三个解释利率期限结构的理论：预期理论、分割市场理论、流动性溢价理论/ 期限优先理论1. 预期理论假设：对于到期期限不同的债券没有特别的偏好，不同到期期限的债券之间完全可代替，此时选择持有债券的标准是债券的预期回报率高低。
利率的期限结构投资学财经大学
(五)短期利率和收益率曲线斜率
当下一年度短期利率 r2 大于今年得短期利 率r1时, 收益率曲线 向上倾斜。
暗示收益率预计会 上升。
当下一年得短期利率 r2 小于今年得短期利 率r1时, 收益率曲线 会下降。
暗示收益率预计会 下降。
图 15、3 短期利率和即期利率
(六)根据观察到得收益率解出 未来短期利率
(1 y2 )2 (1 r1)[1 E(r2 )]
也就是5%,利率期限结构呈现水平。 如果下一年得期望短期收益率E(r2) 就是6%,
则两年期即期利率y2将就是5、5%,利率期限 结构呈现向上。而下一年得期望短期收益率 E(r2) 如果就是4%,则两年期即期利率y2将就 是4、5%,利率期限结构呈现向下。
例15、1 附息债券得估值
使用表15、1得折现率,计算3年期, 票面利率为 10% 得附息债券(假设面值为$1000)得价值:
价值
$100 1.05
$100 1.062
$1100 1.073
价值 = $1082、17 ,又有:
1082.17
$100 1.0688
$100 1.06882
$1100 1.06883
利率的期限结构投资学财经大学
一、利率期限结构概述
利率期限结构就是不同期限债券贴现现金流得 利率结构。
通常情况下,期限短得现金流用较低得利率贴 现,即要求较低得收益率;期限长得现金流用较 高得利率贴现,即要求较高得收益率。
收益率曲线显示了收益率和期限之间得关系, 所以收益率曲线就是利率期限结构得图形表现。
收益率曲线有四种类型:
从收益率曲线四种类型中可以看到,不同期限债 券得收益率不相同。
收益率曲线在固定收益证券领域有重要得作用。
6.利率期限结构分析
利率期限结构
Shape of the yield curve
humped yield curve is the yield curve that yields increasing with maturity for a range of maturities and then the yield curve becoming inverted.
The more common practice is to use the spread between the 30-year and 2-year yield.
10
利率期限结构
Yield Curve Shifts
A shift in the yield curve refers to the relative change in the yield for each Treasury maturity.
Think about: ▪ What does a flattening of the yield curve mean? Under what circumstance a flattening of the yield curve will happen?
9
利率期限结构
the steepness or slope of the yield curve
The spread between these yields for long-term Treasury yields and short-term Treasury yields is referred to as the steepness or slope of the yield curve.
A parallel shift nonparallel shift
第6章 利率的风险结构和期限结构
(6-1)
例1：如果一年的即期利率为7%,两年的 即期利率为12%,则第二年的远期利率是 多少？
解：（1+12%）2=（1+7%）（1+f2） 则第二年的远期利率f2=17%
二、期限结构和收益率曲线的含义
对于风险、流动性和税收待遇相同的债 券，到期收益率随到期日的不同而不同，两 者之间的关系称为利率的期限结构。将利率 的期限结构用图形来描述，就是收益率曲线 （yield curve）。 在实际当中，收益率曲线是通过对国债 国债 的市场价格与收益的观察来建立的。这一方 面是因为国债通常被认为没有违约风险，另 一方面也因为国债市场是流动性最好的债券 市场。 收益率曲线是一种时点图 时点图。 时点图
由此可以得到
(1 + y2 ) 2 f2 = −1 1 + r1 (1 + y3 ) 3 f3 = −1 2 (1 + y2 ) (1 + y4 ) 4 f4 = −1 3 …… (1 + y3 )
一般地，第n年的远期利率就定义为：
(1 + yn ) n fn = −1 n −1 (1 + yn −1 )
主要有以下三种理论解释这些现象。
一、预期理论 预期理论
该理论认为，远期利率等于市场整体对未来 短期利率的预期。 例3：如果当前的3年期和2年期零息票债券的 到期收益率分别为y3=10%和y2=9%，则根据式 （6-1），意味着市场在当前将第3年的短期利率 确定为远期利率f3 =1.13/1.092-1=12%。 即意味着市场预期第3年的短期利率r3为12%， 即f3=r3。
96.15 =
100 1 + r1
100 92.19 = (1 + y2 ) 2
货币金融学 第6章 利率的风险与期限结构
表 6-1 穆 迪 、 标 准 普 尔和惠誉的债券评级
5-7
• 流动性 • 具有流动性的资产是指在需要的时候能够按照较低
的成本迅速变现的资产。 • 在其他条件相同的情况下，流动性越高的证券，利
率将越低；相反，流动性越低的证券，利率将越高 。
5-8
• 所得税因素 • 证券持有人真正关心的是税后的实际利率，所以，
• 如图6-6b所示，平缓上升的收益率曲线 表明预期未来短期利率上升和下跌的幅 度都不大；
• 如图6-6c所示，平坦的收益率曲线表明 预期未来短期利率将小幅下降。
• 最后，翻转的收益率曲线，即图6-6d， 表明预期未来短期利率将急剧下降。
图6-6 基于流动性溢价理论的收 益率曲线和市场对于未来的短期 利率的预期结果
本章小结
1. 具有相同到期期限的债券利率出现差异有三个原因：违约风险、流 动性以及所得税因素。债券违约风险越大，其相对于其他债券的利 率就越高；债券的流动性越强，其利率就越低；具有免税特征的债 券利率低于不具备这一特征的债券利率。由于这些因素形成的具有 相同期限债券利率之间关系，被称为利率的风险结构。
的原因。 –如果一种债券所支付的利息享有税收优惠（比如免缴联邦
所得税的市政债券），那么它的利率就会较低。
5-11
6.2 利率的期限结构
• 利率的期限结构指利率与期限之间的变化关系，研究的是风 险因素相同、而期限不同的利率差异是由哪些因素决定的。
• 收益率曲线：具有相同的风险、流动性和税收特征而期限不 同的债券收益率连成的曲线。可以分为： –向上倾斜的 –平坦的 –向下倾斜的
均值加上随债券供求状况的变动而变动的流动性溢价。
• 假设：具有不同到期期限的债券之间可以相互替代，但不是 完全相互替代。由于短期债券的利率风险相对较小，因此投
第6章 利率结构理论
依此类推，可得：n年期债券的利率，等于期限内当前短期利率和
预期短期利率的平均值。
=
+ + + ⋯ + +(−)
简单运用与计算，请见相关教材中的举例。
9
★课堂拓展：一般性公式推导（阅读&自学）
假定投资者在进行投资选择时，考虑两种债券投资方式，一种是
用于购买1年期的债券；
方案B：也可以现在就购买2年到期的债券。
设在期初时，1年期债券的年利率为Rt ，2年期债券的年利率为
R2t，预计一年后1年期债券年利率为+1
。容易求得：
方案A投资的预期回报率为： 1 + 1 + +1
−1
方案B投资的预期回报率为： 1 + 2
费莱德里奇·A·卢兹（1940）进一步发展。这一理论认为：长期债
券的利率等于长期债券到期期限内短期债券利率的预期平均值。
关键假设：
投资者依据预期回报率选择债券，对不同期限债券无偏好差异，
不同期限的债券具有完全替代性。
持有和买卖债券没有交易成本，投资者可以无成本地进行债券
替代。
投资者能对未来利率形成准确预期并依据预期作出投资选择。
的风险结构和期限结构。
利率结构理论的应用——比如银行贷款定价中有一种方法是
“基准利率加点定价模型”。
2
2.利率的风险结构
利率的风险结构考察的是期限相同而风险因素不同的各种信用工
具利率之间的关系。
利率的风险结构，主要是由信用工具的违约风险，流动性以及税
收等因素决定的。
违约风险：证券的违约风险越大，为弥补证券持有人所承担的
第6章利率的风险结构和期限结构
第6章 利率的风险结构和期限结构[本章内容]债券种类繁多，其利率也千差万别。
本章通过考察各种利率之间的相互关系，从而对利率作一完整的理解。
第一，考察债券期限相同但是利率各不相同的原因。
尽管奉贤、流动性及所得税规定在风险结构决定中都发挥着某种作用，但是我们仍旧把这些利率间的相互关系，统称为利率的风险结构。
第二，债券的期限也影响其利率，不同期限债券利率之间的关系称作利率的期限结构。
第三，考察利率之间相互波动的来源和原因，并讨论用于解释这些波动的各种理论。
6.1 利率的风险结构[对期限相同的债券而言，利率变化呈以下重要特点：在任一给定年份，不同种类债券的利率各不相同，利率之间的差幅随时间变动而变动。
那么，影响期限相同债券的利率差异的原因有哪些呢？] 一、违约风险债券发行人有可能违约，即不能支付利息或在债券到期时不能清偿债券面值，这是债券所具有的风险，它会影响债券的利率。
（一）无违约风险债券与风险升水 1．无违约风险债券美国国债几乎没有什么违约风险，这类债券称为无违约风险债券。
2．风险升水有违约风险债券与无违约风险债券利率的差额，称为风险升水。
即人们为持有某种风险债券必须获得额外的利息。
（二）违约风险对债券利率水平影响的分析 1．模型观察无违约风险债券（财政债券）和长期公司债券的市场供求图。
假定公司债券最初没有违约的可能，故它能象美国国债那样都属于无违约风险债券。
因此，两种债券具有相同的属性（相同的风险和期限）、相等的初始均衡价格和均衡利率（PPTC11=和i iT C11=，而且公司债券的风险升水（i i TC 11-）为零）。
2．分析（1）现在假设公司由于遭受惨重的损失从而违约的可能性增加，则公司债券的违约风险将增大，其预期回报率将降低，公司债券的回报率将更加不确定，图7-2（a ）中公司债券的需求曲线从DC1向左移动到DC 2。
（2）相对于公司债券来说，无违约风险的国债预期回报率较高，相对风险较小。
利率期限结构
利率期限结构利率期限结构是指同一借款主体在不同期限借款时所面临的不同利率水平和利率变化情况。
研究利率期限结构对理解金融市场和货币政策等具有重要意义。
一、利率期限结构的概念利率期限结构是利率和借贷期限之间的关系。
其基本原理是资金成本和市场供求关系上的交互作用，表示了市场对不同期限借款的需求和供应关系及其对借款利率的影响。
在短期内，利率期限结构一般呈现上行趋势。
这是因为短期资金需求呈现急需的状况，供求不平衡，导致利率上涨。
而在长期内，利率期限结构一般呈现平稳或下降趋势。
这是因为长期资金成本相对较低，资金需求量相对较小，导致利率基本稳定或下降。
二、利率期限结构的形状类型利率期限结构的形状主要包括以下三种类型：1. 上凸型利率期限结构：在上凸型利率期限结构中，长期借款利率高于短期借款利率。
这种形状出现的时候，一般反映了市场对未来通货膨胀率和利率相对乐观的预期。
2. 倒挂型利率期限结构：在倒挂型利率期限结构中，短期借款利率高于长期借款利率。
这种形状出现的时候，一般反映了市场对未来经济前景和通货膨胀率相对悲观的预期。
3. 平坦型利率期限结构：在平坦型利率期限结构中，不同期限的借款利率基本相同。
这种形状出现的时候，一般反映了市场对未来通货膨胀率和利率相对中性的预期。
三、利率期限结构的决定因素影响利率期限结构的因素主要包括以下三个方面：1. 货币市场供求关系：货币市场供求关系决定短期利率水平。
2. 预期通货膨胀率：这是决定长期利率水平的根本因素。
市场对未来通货膨胀率的不确定性也会影响长期利率结构的形态和变化。
3. 长短期利率之间的互动关系：长短期利率之间的互动关系也是决定利率期限结构形态和变化的重要因素。
四、利率期限结构对金融市场的影响利率期限结构的形态和变化对金融市场和货币政策等具有深远的影响，主要体现在以下几个方面：1. 对股票市场的影响：当利率期限结构呈现上凸型，即长期利率高于短期利率时，大多数上市公司的借款成本比较高，导致企业利润减少，从而对股票市场产生负面影响。
第6章利率的风险和期限结构
为了新建存款保险基金， FIRREA 大幅度提高了存款机构的保险费，它还恢复了 1982年《存款机构法案》所放松的一些管制措施，他要求储蓄机构将其资产的至少70%用 于抵押贷款和其他与住宅相关的工具，并且将他们的不动产贷款限制在其资本的4倍以内。储 贷协会不再被允许购置垃圾债券，而且已持有的垃圾债券必须在 1994年前变现。核心资本 比率从3%提高到8%，而且条款规定储蓄机构也要遵守与商业银行相同的风险资本要求。 陷入危机的储蓄机构不再被允许吸收代理存款，利用合计手法来作弊的渠道亦被堵截，加紧 了对储货协会证券投资的限制。最后，立法机构被授权命令储货协会放弃某些冒险的经营。 (参见[美]劳斯德B· 托马斯《货币· 银行与金融市场》，中译本，机械工业出版社，1999年) 附：案例2-2，查尔斯凯亭和林肯储货协会丑闻与案例2-3，80年代中后期至90年代初俄亥俄· 玛丽兰和罗德岛三个州的银行恐谎案例。
在80年代初，储蓄机构还被授权发行期限为两年半的浮息存款证，发行这一工具是为 了使其能够同期限为两年半的财政债券进行竞争。这些法规的调整，使储贷协会解决了资金 来源不足的困难，但并没有解决他们的根本问题，即储贷协会的资产主要是固定利率的抵押 贷款，而且大部分是过去几年发放的，而且还要持续多年，根据合同，储贷协会不能提高已 发放固定利率抵押贷款的利率。这样储贷协会要将其抵押贷款的平均收益率提高一个百分点 也需要多年时间。 因为老抵押贷款利率不能提高，抵押贷款平均收益率提高要完全靠提高新的抵押贷款 利率。而由于新的购房者对抵押贷款利率十分敏感，当抵押贷款利率提高时，他们延迟购买 住宅，这一现象又使储贷协会无法通过对新抵押贷款制定较高利率来迅速提高他们的平均收 益率。而且联帮法规要求储贷协会将其绝大部分资金投放于住房固定利率抵押贷款上，而不 能用于其它投资。所以，到70年代末以后，储贷协会全部抵押贷款的平均收益低于新的抵押 贷款利率，储贷协会的全部资产收益率低于资金成本， 1981 年差额为 -0.8% ，该行业 1981年亏损60亿美元，1982年亏损50亿美元，储贷协会的问题越来越严重。
米什金-货币金融学 第六章 利率的风险和期限结构
二、利率风险结构：所得税因素
• 市政债券利率低于国库券利率的图示分析。
二、利率风险结构：小结
• 利率风险结构取决于违约风险、流动性、所得税 三个因素。 • 一种债券的利率水平与债券的违约风险正相关， 与债券的流动性负相关，一种债券在税收安排上 越有利，其利率水平越低。 • 问题：1993年，美国总统克林顿将所得税最高一 级税率从31%提高到40%，2001年，布什政府计 划在未来10年内将最高一级所得税税率从39%降 低到35%。这对国库券和市政债券的利率会产生 什么影响？
2(i2t ) it i
e t 1
it i i2t 2
e t 1
三、利率期限结构：预期假说
• 上式表明：两期债券的利率必定等于两个 一期债券利率的平均值。 • 如果债券的期限扩展到n期，那么n期债券 的利率等于在n期债券的期限内预计出现的 所有一期债券利率的平均值。
int
货币金融学
Economics OF Money ,Banking AND Financial Markets
2nd edition, Mishkin
ch6 利率的风险和期限结构
• • • • 本讲内容概要： 一、序言 二、利率风险结构 三、利率期限结构
一、利率的风险和期限结构：序言
• 本章核心问题：讲述各种利率之间的关系，是 具体买入/卖出哪种债券的决策依据。 • 利率风险结构的内涵：期限相同的债券由于风 险、流动性和税收安排不同往往具有不同的利 率水平。 • 利率期限结构的内涵：即使风险、流动性和税 收安排相同，期限不同的债券往往具有不同的 利率水平。 • 本章我们将考察各种利率之间相互波动的来源 和原因，并考察解释这些波动的各种理论。
二、利率风险结构：违约风险
利率期限结构课件
市场供求关系是影响利率期限结构的重要因素， 长期债券相对于短期债券风险更大，因此需要更 高的收益率来吸引投资者。
02 经济预期
经济预期也是影响利率期限结构的重要因素，如 果预期未来经济形势好，长期债券收益率会相对 较高。
03 通货膨胀
通货膨胀对利率期限结构的影响主要体现在预期 通货膨胀率上，如果预期通货膨胀率上升，长期 债券收益率也会相应上升。
金融衍生品定价
期权定价
利率期限结构提供了隐含波动率等参 数，用于期权定价模型，如布莱克-舒 尔斯模型。通过这些模型可以计算期 权的理论价值。
利率期货定价
利率期限结构用于确定期货合约的理 论价格。期货合约的未来现金流可以 通过利率期限结构折现到当前价值， 从而计算出期货合约的理论价值。
06
未来研究方向
3
股票市场与货币政策的关系
货币政策通过利率传导机制影响股票市场，央行 可以通过调整利率来调节股票市场的资金供求关 系。
利率期限结构与货币政策
01
货币政策目标与利率期限结构
央行通过货币政策操作影响利率期限结构，以实现经济增长、物价稳定
等政策目标。
02
利率传导机制
央行通过调整短期利率，影响长期利率，进而影响实体经济，这是货币
02
利率期限结构的理论模型
预期理论
总结词
预期理论认为长期债券的利率等于未来短期利率的预期平均值。
详细描述
预期理论认为，投资者会根据对未来短期利率的预期来决定是否购买长期债券。因此，长期债 券的利率应该等于未来短期利率的预期平均值。如果未来短期利率的预期值上升，长期债券的 利率也会相应上升。
市场分割理论
偏好理论认为，投资者对不同期限的债券有不同的风险偏好。对于风险厌恶程度较高的投资者来说，他们更倾向 于购买短期债券；而对于风险偏好较高的投资者来说，他们更倾向于购买长期债券。因此，长期债券的利率与未 来短期利率的关系取决于投资者的风险偏好。
利率期限结构模型
根据状态变量集中随机变量的个数，可以将利率期限结构模型区分为单因素和两(多)因素模型两大类。
一般单因素模型
对 取不同的形式，得到了不同的模型。其一般形式如下：
模型
布伦南和施瓦茨(Brennen&Schwartz,1979)
●
●
●
1
瓦西塞克(Vasicek,1977)
静态模型
动态模型
样条函数模型
节约型模型
指数样条法（Vasicek&Fong，1982）
均衡模型
套利模型
Vasicek模型（Vasicek，1977）
CIR模型（Cox、Ingersoll&Ross，1985）
Ho-Lee模型（Ho&Lee，1986）
Hull-White模型（Hull&White，1990）
而将参数 的估计过程定义为：
多项式样条法
多项式样条函数假设折现因子是到期期限s的多项式分段连续函数 。 在运用此函数时，仔细选择多项式的阶数是至关重要的。阶数的多少决定了利率曲线的平滑程度和拟合程度，同时也影响到待估参数的数量。本书将多项式样条函数的阶数定为3。这是因为，当多项式样条函数为二阶时， 的二阶导数 是离散的；当阶数过高（四阶或五阶）时，验证三阶或四阶导数是否连续的难度将增大，待估参数的数量也将增大。
利率期限结构模型
利率期限结构模型简介
利率期限结构相间t的价格，即在未来时间T支付单位1的债券在时间t的价格。
起息日为时间t，剩余到期期限为 年的零息票债券利率。有：
起息日为时间t，剩余到期期限为 年的连续复合利率。有：
其中
通过求解偏微分方程或鞅方法，可以推导出在时间T到期的贴现债券在时间t的价格为：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第六章 利率期限结构
一、利率期限结构 利率期限结构----是指某一时点上，不同期限债券的
收益率与到期期限之间的关系。
广义利率期限结构：指任何种类债券的收益率与其到 期期限的关系。
狭义利率期限结构：指任国债的即期利率与其到期期 限的关系。
第六章 利率期限结构
预期理论认为只有预期是影响利率期限结构的唯一因 素，又称为无偏预期利率，纯预期理论。
第六章 利率期限结构
两个2年期债券策略
2年投资期
1年投资期 1年投资期
预期利率表明长期债券是短期债券的理想替代物， 长期债券与短期债券取得相同收益率。
(1 s2)2 (1 s1)[1 E(s1,2)]
第六章 利率期限结构
收益率曲线的类型 上升型----表明短期债券收益率小于中期债券收益率，
中期券收益率小于长期债券收益率。 下降型----与上面相反 扁平型----短、中、长各期债券收益率大体相当。 驼峰型----表明短期和长期债券收益率较低，而中期
债券收益率较高。
2012-05-15
201 -05-15
第六章 利率期限结构
利率水平,如5.7%。
第六章 利率期限结构
S S’
6%
5.7%
D D’
1年期借贷市场
第六章 利率期限结构
长短期借贷市场的利率调整过程 2年期借贷市场资金供求关系 价格（利率）便宜，导致资金需求增加，资金供给减
少， 需求曲线右移，供给曲线左移，产生高于6.2%的新的
利率水平，如6.35%。
（需求减少）； 贷款者放弃2年期贷款（供给减少），转向1年期贷款
（供给增加）； 2年期利率将会上升，1年期利率将会下降，市场重回
均衡。
第六章 利率期限结构
长短期借贷市场的利率调整过程 1年期借贷市场资金供求关系 价格（利率）昂贵，导致资金需求减少，资金供给增
加， 需求曲线左移，供给曲线右移，产生低于6%的新的
第六章 利率期限结构
收益率曲线的类型 按照债券信用品质划分： 国债收益率曲线 金融债券收益率曲线 公司债券收益率曲线 中央银行票据收益率曲线
第六章 利率期限结构
收益率曲线的类型 按照债券息票划分： 平价收益率曲线 零息收益率曲线
收益率曲线查询
/icbweb/index.htm?lx=yc
第六章 利率期限结构
问题的提出: 在无违约风险债券的定价中，现金流是稳定的，其定
价核心是确定合适的贴现率。 在以往的债券定价中，假定各期的到期收益率是不变
的。 实际中，到期收益率是随着到期时间的变化而变化，
如何给债券定价？ ----利率期限结构
第六章 利率期限结构
本章内容提要： 什么是利率期限结构? 利率期限结构理论：预期理论、流动性偏好理论、市
第六章 利率期限结构
交易所固定利率国债收益率曲线 2012-05-15
第六章 利率期限结构
银行间固定利率国债收益率曲线 2012-05-15
第六章 利率期限结构
收益率曲线的类型 上升型（正常型） 下降型（倒置型） 扁平型 驼峰型
第六章 利率期限结构
1）
2）
3）
4）
第六章 利率期限结构
国银 债行
收间
益固
率定
曲利
线率
银 债行 收间 ０ 益固 率定 曲利 线率
国
第六章 利率期限结构
收益率曲线的移动 平行移动 斜向移动 正蝶式移动 负蝶式移动
第六章 利率期限结构
1）平行移动 3）正蝶式移动
2）斜向移动 4）负蝶式移动
第六章 利率期限结构
收益率曲线的移动 平行移动----所有期限利率变化同样幅度。 斜向移动----收益率曲线变得更陡峭或更平缓。 正蝶式移动----长期和短期债券收益率上升，中期债
券收益率下降（图3包括了平移）。 负蝶式移动----长期和短期债券收益率下降，中期债
券收益率上升（图4包括了平么会有不同的形状?由什么因素决定？ 根据收益率曲线的不同形状,如何预期未来利率的水平？
----利率期限结构理论
第六章 利率期限结构
第六章 利率期限结构
S
S’ 6.35%
6.2%
D D’
2年期借贷市场
第六章 利率期限结构
长短期借贷市场的利率调整过程 由于(1+6.35%)2=(1+5.7%)X(1+7%),市场达到新
的均衡。
第六章 利率期限结构
二、利率期限结构理论 预期理论 流动性偏好理论 市场分割理论
第六章 利率期限结构
预期理论：认为利率期限结构完全取决于市场对未来 利率的预期。
在市场均衡条件下，远期利率代表了市场未来时期即 期利率的预期，即
ft1,t E(st1,t )
远期利率是市场未来即期利率的无偏估计。
第六章 利率期限结构
例：假定1年期利率为6%，市场预期1年后利率为7%， 那么，2年期的即期利率为
[(1+6%)(1+7%)]1/2-1=6.5% 若2年期市场利率低于该水平，如6.2%，即 [(1+6%)(1+7%)]1/2-1>6.2%
此时，2年期借款利率便宜，1年期借款利率昂贵；
第六章 利率期限结构
2年期借款利率便宜，1年期借款利率昂贵； 借贷者转向2年期借款（需求增加），放弃1年期借款
即期利率----是指当前时点上零息债券的到期收益率。
注意：即期利率并不是一个能够直接观察到的市场变 量，而是一个基于现金流折现法，通过对市场数据进 行分析而得到的利率。
第六章 利率期限结构
附息国债到期后，投资者得到本息的一次性支付，这 种一次性所得收益与本金的比率就是即期利率。
零息国债到期后，投资者按票面价值获得一次性的支 付，这种与折价购买的差额相对于购买价格的比率就 是即期利率。
第六章 利率期限结构
利率期限结构 利率期限结构----是指零息国债的到期收益率与其到
期期限的关系。
第六章 利率期限结构
收益率曲线 收益率曲线----指某个时点上特定种类债券的到期收
益率与其剩余期限之间对应关系的图形描述.
收益率曲线即为利率期限结构的几何表示。
第六章 利率期限结构
中国固定利率国债收益率曲线 2012-05-15