小学奥数知识点趣味学习---之数一数

【K12学习】一年级数学上册《数一数》知识点

一年级数学上册《数一数》知识点数一数概念数数，就是按照一定的顺序，从1开始数数，数到最后一个物体对应的那个数，也就是说最后数到几，就是这种物体的总个数。

举例说明★--------1个星星★★--------2个星星★★★--------3个星星★★★★--------4个星星★★★★★--------5个星星★★★★★★--------6个星星★★★★★★★--------7个星星★★★★★★★★--------8个星星★★★★★★★★★--------9个星星★★★★★★★★★★--------10个星星上面的星星都数对了吗？是不是觉得这样有些枯燥呢？那么，大家还记得一首叫做《数鸭子》的儿歌吗？接下来我们就通过这首儿歌来再来学习一下数数吧~数鸭子门前大桥下，游过一群鸭快来快来数一数，二四六七八。

门前大桥下，游过一群鸭快来快来数一数，二四六七八。

嘎嘎嘎嘎真呀真多呀数不清到底多少鸭数不清到底多少鸭赶鸭老爷爷，胡子白花花唱呀唱着家乡戏，还会说笑话小孩小孩快快上学校别考个鸭蛋抱回家门前大桥下，游过一群鸭快来快来数一数，二四六七八。

这首儿歌是不是生动形象的为各位小朋友表现出数数的诀窍呢？那就一块来数一数上图中有几只鸭子吧。

图中是不是有1只大鸭子和7只小鸭子呢？你数对了吗？数数的技巧大家要有顺序的数数，不能跳跃的去数，从上往下或者是从左往右，有顺序数一个划一个，这样就不会数错。

会用画画的方式以不同形状的图形来表示物体的个数，通过不同的图形来辨别每个图形的个数。

动动脑筋做习题数一数下面每个图形都有几个。

■■▲▲▲▲●●●●●●●●●★数一数有几个五角星，几个三角形，几个正方形。

■■■■▲■■▲■■▲▲▲★★▲▲▲★★★▲▲★★★★五角星个，三角形个，正方形个数一数自己铅笔盒里几只铅笔，几个橡皮。

___________________________________________参考答案数一数下面每个图形都有几个。

(完整word版)一年级奥数【数一数】

第04讲数一数前两节课我们认识了许多几何图形，这节课我们在前面的基础上学习几何图形的计数问题。

通过本节课的学习，培养我们的空间想象能力，并且掌握图形计数的一些数学方法：分类法，归纳法等。

具体我们应该掌握以下问题：一、基本图形的识别二、点的计数问题三、线段的计数问题四、角的计数问题五、三角形的计数问题六、四边形的计数问题七、探索题目一、基本图形的识别例1 请观察下列图形，数一数，图中有几种图形，分别为什么图形？各有几个？解：上图中共有三种图形：三角形、矩形和圆，其中有6个三角形，4个长方形，4个圆。

例2 请观察下图中有几种角，并数一数它们分别有几个？解：上图中有三种角：锐角，直角和钝角，其中有3个锐角，2个直角，4个钝角。

[分析]这种类型的题目主要考察我们对于前两节课所学基本几何图形的识别问题。

而对于这几种图形的计数问题是比较简单的。

所以，能够熟练的识别几何图形是解决这类问题的关键。

二、点的计数问题例3 数一数，下图中共有多少点？解：1+3+6+9+12=31答：上题中共有31个点。

三、线段的计数问题例4 数一数，下图中共有几条线段？解：3+2+1=6答：上图中共有6条线段。

解：5+4+3+2+1=15答：上图中共有15条线段。

同学们，通过这两道题，我们能发现什么规律，考虑一下。

[分析]通过上面的两道例题，我们仔细分析，发现对于线段的计数问题是由规律可循的，即：如果图中有4个点，则线段的个数有：3+2+1；如果图中有6个点，则线段的个数有：5+4+3+2+1；。

那么，如果图中有10个点，那么线段的个数有多少个呢？所以，对于这类问题，我们主要是先找到点的个数，然后按照规律计算出线段的个数。

四、角的计数问题例6 数一数，下图中有几个锐角？解：3+2+1=6答：上图中共有6个锐角。

想一想：同学们，你们仔细看一下，仔细想一想，这道题有没有规律，这个规律和第三类问题的线段的计数问题的规律有相似之处吗？五、三角形的计数问题答：共有3+1个三角形。

小学趣味数学(简单奥数)

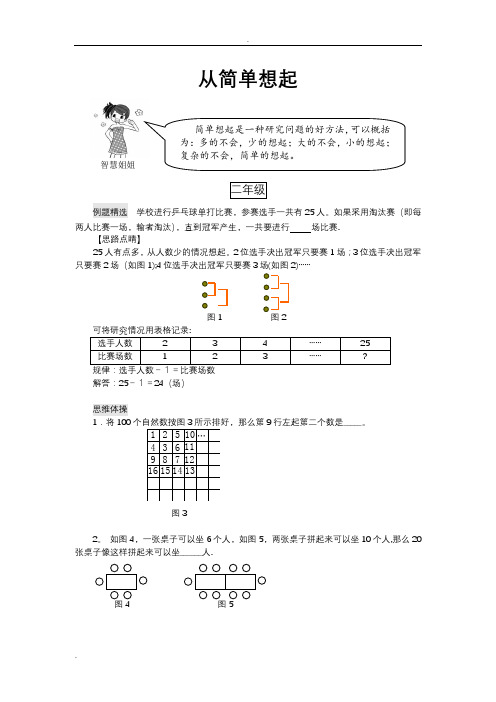
51061171214132143981615从简单想起二年级例题精选学校进行乒乓球单打比赛，参赛选手一共有25人。

如果采用淘汰赛（即每两人比赛一场，输者淘汰），直到冠军产生，一共要进行场比赛.【思路点睛】25人有点多，从人数少的情况想起。

2位选手决出冠军只要赛1场；3位选手决出冠军只要赛2场（如图1);4位选手决出冠军只要赛3场(如图2)……图1 选手人数 2 3 4 …… 25 比赛场数123……?规律：选手人数－１＝比赛场数解答：25－１＝24（场）思维体操1．将100个自然数按图3所示排好，那么第9行左起第二个数是_____。

图32。

如图4，一张桌子可以坐6个人，如图5，两张桌子拼起来可以坐10个人,那么20张桌子像这样拼起来可以坐______人.简单想起是一种研究问题的好方法，可以概括为：多的不会，少的想起；大的不会，小的想起；复杂的不会，简单的想起。

智慧姐姐 …3．100个6相乘，积的个位数字是______。

例题精选线段AB 上共有12个端点，那么这条线段上一共有__ __条不同的线段。

【思路点睛】12个端点太多了,从2个端点开始想起。

AB 上共有2个点，有线段：1条AB 上共有3个点，有线段：1＋2＝3（条) AB 上共有4个点,有线段：1＋2＋3＝6（条）AB 上共有5个点，有线段:1＋2＋3＋4＝10（条） ……AB 上共有12个点,有线段：1＋2＋3＋4＋…＋9＋10＋11＝66（条）思维体操1.如图6，圆周上有10个点,过这些点最多可以画__ __条线段。

图62．100个3相乘，积的个位数字是______。

3．在一张纸上，画10条直线,最多可以有______个交点。

例题精选一个楼梯共有8个台阶，规定上楼时每次只能跨上一个或跨上两个台阶.从地面到最上层共有______种不同的跨法。

【思路点睛】8个台阶太多了，从少的想起。

只有一个台阶，那只有一种跨法，如图7；有两个台阶，则有两种跨法，如图8；有三个台阶，如果第一次跨两个台阶，还剩下一个台阶,跨法同图7，如果第一次跨一个台阶,还剩下两个台阶，跨法同图8，1＋2＝3(种)；有四个台阶，如果第一次跨两个台阶,还剩下两个台阶，跨法同图8；如果第一次跨一个台阶，还剩下三个台阶，跨法同图9， 2＋3＝5（种)；……图710个310个3 10个9 10个910个9规律：从第三个台阶起，所登台阶的跨法数等于前两个所登台阶跨法数的和。

小学奥数模块教程1 数的认识

第一讲数的认识第一部分知识点梳理1.自然数、整数、负数。

（1）自然数：用来表示物体个数的0，1，2，，3……叫自然数。

任何非“0”的自然数都是若干个“1”组成，所以“1”是自然数的基本单位。

1也是最小的一位数。

“0”是最小的自然数。

（2）正数、负数：数的定义：像—1，—2，—3，…这样的数叫做负数。

“—”叫做负号，读作：负。

正数的定义：学过的1,2,3，…这样的数叫做正数。

正数的前面可以加“+”，一般情况下省略不写。

（3）负数、0、正数间的关系：正数>0>负数，0既不是正数也不是负数。

（3）整数：整数包括自然数和负整数，或者说整数由正整数、零、负整数组成。

（4）整数的读写：先分级（从右到左每四位数为一级），再从高位到低位一级一级地读写读法：从高位到地位，一级一级地读，每级末尾的0都不读出来，其它数位连续几个0的都只读一个零。

写法：从高位到地位，一级一级地写，哪个数位上一个单位也没有，就在那个数位上写0。

（5）整数的大小比较：数位不同时，数位多的数就大。

数位相同时，左起第一位上的数大那个数就大，如果左起第一位数相同就比较左起第二位上的数，以此类推比较出数的大小。

（6）数位顺序表：把按照数位的顺序从右到左排列的表，叫数位顺序表。

（注意区别：数级、数位、计数单位）（7）多位数的改写：如果改写的是整万或整亿的数，就把原数末尾划去4个0或8个0，同时加上“万”或“亿”字。

如果改写的多位数不是整万或整亿的数，就在万位或亿位的右下角点上小数点，去掉小数点末尾的0，再在小数的后面加上“万”或“亿”字。

（8）准确数和近似数、省略：数据与实际完全符合的，叫准确数。

数据只是与实际大体符合或者说接近实际的数，叫近似数。

先用四舍五入法省略万位或亿位后面的数，再在这个数的后面加写“万”或“亿”字。

因为得出的数是近似数，所以要用“≈”连接。

2.数的整除（1）整除的意义：整数a除以整数b(b≠0)，除得的商正好是整数，就说a能被b整除。

小学四年级上册《数一数》知识点归纳-最新教育文档

小学四年级上册《数一数》知识点归纳
人口普查（亿以内数的读法、写法）
【知识点】：
亿以内数的读数方法。

含有个级、万级和亿级的数，必须先读亿级，再读万级，最后读个级。

（即从高位读起）亿级或万级的数都按个级读数的方法，在后面要加上亿或万。

在级末尾的零不读，在级中间的零必须读。

中间不管有几个零，只读一个零。

亿以内数的写数方法。

从高位写起，按照数位的顺序写，中间或末尾哪一位上一个也没有，就在那一位上写0。

比较数大小的方法。

多位数比较大小，如果位数不同，那么位数多的这个数就大，位数少的这个数就小。

如果位数相同，从左起第一位开始比起，哪个数字大，哪个数就大。

如果左起第一位上的数相同，就开始比第二位直到比出大小为止。

国土面积（多位数的改写）
【知识点】：
改写以万或亿为单位的数的方法。

以万为单位，就要把末尾的四个0去掉，再添上万字；以亿为单位，就要把末尾八个0去掉，再添上亿字。

改写的意义。

为了读数、写数方便。

森林面积（求近似数）
【知识点】：
精确数与近似数的特点。

精确数一般都以一为单位，近似数都是省略尾数，以万或亿为单位。

用四舍五入法保留近似数的方法。

根据题中要求，看到所要保留位数的下一位，如果这一位满5，则向前一位进一；如果不够5则舍去。

而不管尾数的后几位是多少。

如精确到万位，只看千位，精确到亿位，只看到千万位。

最后一定要写出单位名称。

小学三年级奥数趣味学习——速算与巧算(加减法中的巧算)

小学三年级奥数趣味学习——速算与巧算（加减法中的巧算）一、加法中的巧算1.什么叫“补数”？两个数相加，若能恰好凑成整十、整百、整千、整万…，就把其中的一个数叫做另一个数的“补数”。

如：1+9=10，3+7=10，2+8=10，4+6=10，5+5=10。

又如：11+89=100，33＋67=100，22+78=100，44+56=100，55+45=100，在上面算式中，1叫9的“补数”；89叫11的“补数”，11也叫89的“补数”.也就是说两个数互为“补数”。

对于一个较大的数，如何能很快地算出它的“补数”来呢？一般来说，可以这样“凑”数：从最高位凑起，使各位数字相加得9，到最后个位数字相加得10。

如：87655→12345，46802→53198，87362→12638，…下面讲利用“补数”巧算加法，通常称为“凑整法”。

2.互补数先加。

例1 巧算下面各题：①36+87+64②99+136＋101③ 1361＋972＋639＋28解：①式=（36＋64）＋87=100＋87=187②式=（99＋101）＋136=200+136=336③式=（1361＋639）＋（972＋28）=2000+1000=30003.拆出补数来先加。

例2 ①188＋873 ②548＋996 ③9898＋203解：①式=（188+12）+（873-12）（熟练之后，此步可略）＝200+861=1061②式=（548-4）＋（996＋4）=544+1000=1544③式=（9898＋102）＋（203-102）=10000+101=101014.竖式运算中互补数先加。

如：减法中的巧算1、把几个互为“补数”的减数先加起来，再从被减数中减去。

例1：① 300-73-27② 1000-90-80-20-10解：①式= 300-（73＋27）＝300-100=200②式=1000-（90＋80＋20＋10）＝1000-200＝8002.先减去那些与被减数有相同尾数的减数。

小学奥数知识点趣味学习——奥数知识点汇总

小学奥数知识点趣味学习——奥数知识点汇总1、年龄问题的三大特征①两个人的年龄差是不变的；②两个人的年龄是同时增加或者同时减少的；③两个人的年龄的倍数是发生变化的；2、植树问题总结:基本类型：在直线或者不封闭的曲线上植树，两端都植树在直线或者不封闭的曲线上植树，两端都不植树在直线或者不封闭的曲线上植树，只有一端植树。

3、鸡兔同笼问题基本概念：鸡兔同笼问题又称为置换问题、假设问题，就是把假设错的那部分置换出来；基本思路：①设，即假设某种现象存在（甲和乙一样或者乙和甲一样）：②假设后，发生了和题目条件不同的差，找出这个差是多少；③每个事物造成的差是固定的，从而找出出现这个差的原因；④再根据这两个差作适当的调整，消去出现的差。

基本公式：①把所有鸡假设成兔子：鸡数＝（兔脚数×总头数－总脚数）÷（兔脚数－鸡脚数）②把所有兔子假设成鸡：兔数＝（总脚数一鸡脚数×总头数）÷（兔脚数一鸡脚数）关键问题：找出总量的差与单位量的差。

4、盈亏问题盈亏问题基本概念：一定量的对象，按照某种标准分组，产生一种结果：按照另一种标准分组，又产生一种结果，由于分组的标准不同，造成结果的差异，由它们的关系求对象分组的组数或对象的总量．基本思路：先将两种分配方案进行比较，分析由于标准的差异造成结果的变化，根据这个关系求出参加分配的总份数，然后根据题意求出对象的总量．基本题型：①一次有余数，另一次不足；基本公式：总份数＝（余数＋不足数）÷两次每份数的差②当两次都有余数；基本公式：总份数＝（较大余数一较小余数）÷两次每份数的差③当两次都不足；基本公式：总份数＝（较大不足数一较小不足数）÷两次每份数的差基本特点：对象总量和总的组数是不变的。

关键问题：确定对象总量和总的组数。

5、牛吃草问题牛吃草问题基本思路：假设每头牛吃草的速度为“1”份，根据两次不同的吃法，求出其中的总草量的差；再找出造成这种差异的原因，即可确定草的生长速度和总草量。

小学奥数知识点趣味学习-奥数知识点汇总

小学奥数知识点趣味学习-奥数知识点汇总1、年龄问题的三大特征①两个人的年龄差是不变的；②两个人的年龄是同时增加或者同时减少的；③两个人的年龄的倍数是发生变化的；2、植树问题总结:基本类型：在直线或者不封闭的曲线上植树，两端都植树在直线或者不封闭的曲线上植树，两端都不植树在直线或者不封闭的曲线上植树，只有一端植树。