数字图像处理冈萨雷斯第三版第四章
数字图像处理课件(冈萨雷斯)N04

Original Bacteria image
after thresholding
Which pixels belong to the same object (region labeling)?
How large is each object (region counting)?
Pixel Operations no. 4
Digital Image Pຫໍສະໝຸດ ocessing(信息学院 陈辉)
Pixel Operations no. 3
Arithmetic Operations
Arithmetic Operations of two pixels: Addition: p+q; Subtraction p –q; Multiplication p×q; Division p÷q. (used for averaging to reduce noise, remove static scene, correct shading,etc.)
Digital Image Processing(信息学院 陈辉)
Pixel Operations no. 7
Region counting algorithm
Measures the size of each region Initialize counter(label)=0 for all label Loop through all pixels f(x,y), left to right, top to bottom • If f(x,y)=0, do nothing. • If f(x,y)=1, increment counter(label(x,y))
Region labeling algorithm (4-neighborhood)
冈萨雷斯数字图像处理第3版第4章习题4.164.43备课讲稿

4.16 证明连续和离散二维傅里叶变换都是平移和旋转不变的。
首先列出平移和旋转性质:002(//)00(,)(,)j u x M v y N f x y e F u u v v π+⇔-- (4.6-3) 002(//)00(,)(,)j x r M y v N f x x y y F u v e π-+--⇔ (4.6-4)旋转性质:cos ,sin ,cos ,sin x r y r u v θθωϕωϕ====00(,)(,)f r F θθωϕϕ+⇔+ (4.6-5) 证明:由式(4.5-15)得:由式(4.5-16)得:依次类推证明其它项。
4.17 由习题4.3可以推出1(,)u v δ⇔和(,)1t z δ⇔。
使用前一个性质和表4.3中的平移性质证明连续函数00(,)cos(22)f t z A u t v z ππ=+的傅里叶变换是0000(,)[(,)(,)]2AF u v u u v v u u v v δδ=+++-- 证明:000000002()2()002()2()2()2()2()2()2((,)(,)cos(22)[]222j ut vz j ut vz j u t v z j u t v z j ut vz j u t v z j u t v z j ut vz j u F u v f t z e dtdzA u t v z e dtdzA e e e dtdzA A e e dtdz e e πππππππππππ∞∞-+-∞-∞∞∞-+-∞-∞∞∞+-+-+-∞-∞∞∞+-+-+--∞-∞==+=+=+⎰⎰⎰⎰⎰⎰⎰⎰)00000000(,)(,)22[(,)(,)]2t vz dtdz A Au u v v u u v v Au u v v u u v v δδδδ∞∞+-∞-∞=--+++=--+++⎰⎰ 4.18 证明离散函数(,)1f x y =的DFT 是1,0{1}(,)0,u v u v δ==⎧ℑ==⎨⎩其它证明:离散傅里叶变换112(//)00(,)(,)M N j ux M vy N x y F u v f x y e π---+===∑∑112(//)00112(//)00{1}M N j ux M vy N x y M N j ux M vy N x y e e ππ---+==---+==ℑ==∑∑∑∑如果0u v ==,{1}1ℑ=,否则:1100{1}{cos[2(//)]sin[2(//)]}M N x y ux M vy N j ux M vy N ππ--==ℑ=+-+∑∑考虑实部,1100{1}cos[2(//)]M N x y ux M vy N π--==ℑ=+∑∑,cos[2(//)]ux M vy N π+的值介于[-1, 1],可以想象,1100{1}cos[2(//)]0M N x y ux M vy N π--==ℑ=+=∑∑,虚部相同,所以1,0{1}(,)0,u v u v δ==⎧ℑ==⎨⎩其它4.19 证明离散函数00cos(22)u x v y ππ+的DFT 是00001(,)[(,)(,)]2F u v u Mu v Nv u Mu v Nv δδ=+++--证明:000000112(//)00112(//)0000112()2()2(//)00112()2(//)00(,)(,)cos(22)1[]21{2M N j ux M vy N x y M N j ux M vy N x y M N j u x v y j u x v y j ux M vy N x y M N j u x v y j ux M vy N x y F u v f x y e u x v y e e e e e e πππππππππ---+==---+==--+-+-+==--+-+====+=+=∑∑∑∑∑∑∑∑000000112()2(//)0011112(//)2(//)2(//)2(//)00000000}1{}21[(,)(,)]2M N j u x v y j ux M vy N x y M N M N j Mu x M Nv y N j Mu x M Nv y N j ux M vy N j ux M vy N x y x y e e e e e e u Mu v Nv u Mu v Nv ππππππδδ---+-+==----+-+-+-+====+=+=+++--∑∑∑∑∑∑4.20 下列问题与表4.1中的性质有关。
数字图像处理课件(冈萨雷斯第三版)_图文

图像数据文件主要是用光栅形式,即图像是一些图像点 的集合,比较适合变化复杂的图像。它的主要缺点是缺少 对象和像素点之间的联系,且在伸缩图像的过程中图像会 改变。例如,常见的图象文件类型有bmp,jpg等等。图象 处理的程序必须考虑图象文件的格式,否则无法正确地打 开和保存图象文件。
pgm格式
美国的许多大学用pgm格式,避免使用压缩文件格式,对 初学者来说是很方便的。下面是一幅该格式的图象。
补充:图象和视觉基础
2.1 概论和综述 2.2 人眼与亮度视觉 2.3 颜色视觉 2.4 光度学和成象模型 2.5 成象变换 2.6 采样和量化 2.7 象素间联系 2.8 算术和逻辑运算 2.9 坐标变换
第2章 图象和视觉基础
2.1 概论和综述
该基础包括视觉基础、成像基础和图像基础三部分 :
0x36 0x34 0x30 0x20 0x34
0x38 0x30 0x0A 表示640(SP)480(LF);
0x32 0x35 0x35 0x0A ………………………………… 表示255(LF) ………………………………… 0x27 0x27 …
表示23, 23,…(像素灰度值)
这幅图象文件的解码:
下面是一个Matlab程序
% 打开蝴蝶图象,进行Fourier变换 h=imread('butterfly.jpg'); % open an image figure; imshow(h); % 因为图像的格式uint8不能做加减法, % 所以需要把格式uint8变成格式double h=double(h); [m,n,p]=size(h); hf=fftshift(fft2(h)); % 2D Fourier变换, 得到2D复数值图像 hfa=log(abs(hf)); % 模的图像,用log来调整灰度的对比度 % 求出模的灰度最大值,从而把其灰度的值域变为[0,255] m=max(max(max(hfa))); hfa=hfa*255/m; figure; imshow(uint8(hfa)); Imwrite(uint8(hfa),’butterfly_fft.jpg’,’jpg’);
数字图像处理(冈萨雷斯)-4_fourier变换和频域介绍(dip3e)经典案例幻灯片PPT

F (u,v)
F *(u, v)
f ( x ,y ) ☆ h ( x ,y ) i f f t c o n j F ( u , v ) H ( u , v )
h(x,y):CD 周期延拓
PAC1
h:
PQ
QBD1
DFT
H (u,v)
F*(u,v)H(u,v)
IDFT
R(x,y):PQ
✓ 使用这组基函数的线性组合得到任意函数f,每个基函数的系 数就是f与该基函数的内积
图像变换的目的
✓ 使图像处理问题简化; ✓ 有利于图像特征提取; ✓ 有助于从概念上增强对图像信息的理解;
图像变换通常是一种二维正交变换。
一般要求: 1. 正交变换必须是可逆的; 2. 正变换和反变换的算法不能太复杂; 3. 正交变换的特点是在变换域中图像能量将集中分布在低频率 成分上,边缘、线状信息反映在高频率成分上,有利于图像处理
4.11 二维DFT的实现
沿着f(x,y)的一行所进 行的傅里叶变换。
F (u ,v ) F ( u , v ) (4 .6 1 9 )
复习:当两个复数实部相等,虚部互为相 反数时,这两个复数叫做互为共轭复数.
4.6
二维离散傅里叶变换的性质
其他性质:
✓尺度变换〔缩放〕及线性性
a f( x ,y ) a F ( u ,v ) f( a x ,b y ) 1 F ( u a ,v b ) |a b |
域表述困难的增强任务,在频率域中变得非常普通
✓ 滤波在频率域更为直观,它可以解释空间域滤波的某些性质
✓ 给出一个问题,寻找某个滤波器解决该问题,频率域处理对 于试验、迅速而全面地控制滤波器参数是一个理想工具
✓ 一旦找到一个特殊应用的滤波器,通常在空间域用硬件实现
数字图像处理第三版( Rafael C.Gonzalez著)第4章答案
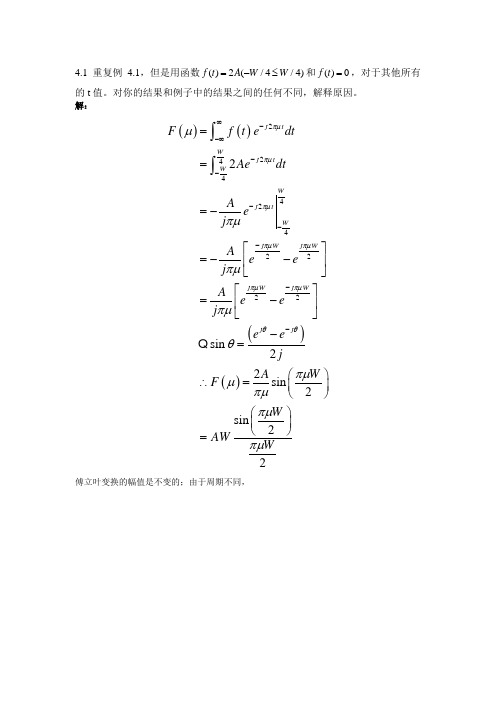
4.1 重复例4.1,但是用函数()2(/4/4)f t A W W =-≤和()0f t =,对于其他所有的t 值。
对你的结果和例子中的结果之间的任何不同,解释原因。
解:()()()()224442422222sin 22sin 2sin 22j tWj tW Wj tW j Wj W j W j Wj j F f t e dtA edtA ej A ee j A e ej ee jAW F W A WWπμπμπμπμπμπμπμθθμπμπμπμθπμμπμπμπμ∞--∞-------===-⎡⎤=--⎢⎥⎣⎦⎡⎤=-⎢⎥⎣⎦-=⎛⎫∴=⎪⎝⎭⎛⎫ ⎪⎝⎭=⎰⎰傅立叶变换的幅值是不变的;由于周期不同,4.2 证明式(4.4-2)()()()()()()~~2222j tj tn j tn j n Ttn n F f t edtf t t n T edt f t t n T edt f eπμπμπμπμμδδ∞--∞∞∞--∞=-∞∞∞--∞=-∞∞-∆=-∞==-∆=-∆=⎰∑⎰∑⎰∑中的()~F μ在两个方向上是无限周期的,周期为1/T ∆证明:(1) 要证明两个方向上是无限周期1/T ∆,只需证明根据如下式子:可得:其中上式第三行,由于k, n 是整数,且和的极限是关于原点对称。
(2) 同样的需要证明根据如下式子:()()()()()()~~2222j tj tn j tn j n Ttn n F f t edtf t t n T edt f t t n T edt f eπμπμπμπμμδδ∞--∞∞∞--∞=-∞∞∞--∞=-∞∞-∆=-∞==-∆=-∆=⎰∑⎰∑⎰∑可得:其中第三行由于k, n 都为整数,所以21j kneπ-=。
4.3 可以证明(Brancewell[2000])1()1()t t δδ⇔⇔和。
使用前一个性质和表4.3中的平移性质,证明连续函数()cos(2)f t nt π=的傅立叶变换是()()()()1/2F n n μδμδμ=++-⎡⎤⎣⎦,其中是一个实数。
冈萨雷斯数字图像处理4讲解

一、背景知识
频域滤波,就是对图像做傅里叶变换后进行的处理 频域滤波在图像增强、图像复原、图像数据压缩等
过程中都起着重要作用 频域滤波包括低通滤波、高通滤波和高频强调滤波
一、二维离散傅里叶变换
令f(x,y)表示一幅大小为MXN的图像,其中 x=0,1,2, …,M-1, y=0, 1, 2, …, N-1
二、 Matlab中的二维DFT
显示频谱: FC = fftshift(F) imshow(abs(FC), [])
对数变换可以拓展显示范围 S2 = log(1 + abs(FC)) imshow(S2, [])
二、 Matlab中的二维DFT
傅里叶逆变换: f=ifft2(F)
图像处理中,逆变换结果一般只取实部: f = real(ifft2(F))
三、频域滤波
P = 2^nextpow2(2*m); PQ = [P, P]; elseif nargin == 3 m = max([AB CD]); P = 2^nextpow2(2*m); PQ = [P, P]; else error('Wrong number of inputs.') end
f (x, y)
1
M 1 N 1
F (u, v)e j 2 (ux / M vy/ N )
MN u0 v0
其中x=0,1,2, …,M-1和y=0, 1, 2, …, N-1 F(u,v)在这里称为傅里叶系数 Matlab中F(1,1)=F(0,0)
一、二维离散傅里叶变换
在原点处的频率值F(0,0)称为直流分量 傅里叶变换的频谱定义为
M 1 N 1
F(u, v)
f (x, y)e j2 (ux/ M vy/ N )
冈萨雷斯数字图像处理4
五、低通频域滤波器
理想低通滤波器(ILP)具有传递函数:
1 H (u, v) 0
若D(u, v) D0 若D(u, v) D0
n阶巴特沃兹低通滤波器(BLPF),截止频率
为D0
H
(u,
v)
1ຫໍສະໝຸດ [1 D(u, v)
/
D0
]2n
高斯低通滤波器(GLPF)的传递函数为:
H (u, v) eD2 (u,v)/ 2D02
五、在频率域直接生成滤波器
其中函数meshgrid用来生成网格数组,语 法:
[C, R] = meshgrid(c,r);
c和r是输入的行向量,C和R是输出的矩阵 C和R的维数为length(c)*length(r) 其中C的行是c的副本,R的列是r的副本 如c=[0,1]; r=[0, 1, 2]; 则C=[0 1 R=[0 0
M 1 N 1
F(u, v)
f (x, y)e j2 (ux/ M vy/ N )
x0 y0
其中u=0,1,2, …,M-1和v=0, 1, 2, …, N-1
频域系统是由F(u,v)所构成的坐标系统,其中u和 v是频率变量
利用欧拉公式可以手工计算傅里叶变换
一、二维离散傅里叶变换
自定义函数paddedsize()用来计算P、Q的最小偶 数值,以满足快速傅里叶变换FFT的计算需要
三、频域滤波
为避免折叠误差的干扰,在做频域滤波前要对输入 的图像和滤波器进行扩充补零的操作
设f(x,y)的大小为AXB, h(x,y)的大小为CXD, 则扩充后的函数大小为PXQ,其中: P>=A+C-1 Q>=B+D-1
冈萨雷斯_数字图像处理第3版第4章习题
首先列出平移和旋转性质:002(//)00(,)(,)j u x M v y N f x y e F u u v v π+⇔-- 002(//)00(,)(,)j x r M y v N f x x y y F u v e π-+--⇔旋转性质:cos ,sin ,cos ,sin x r y r u v θθωϕωϕ====00(,)(,)f r F θθωϕϕ+⇔+ 证明:由式得: 由式得:依次类推证明其它项。
由习题可以推出1(,)u v δ⇔和(,)1t z δ⇔。
使用前一个性质和表中的平移性质证明连续函数00(,)cos(22)f t z A u t v z ππ=+的傅里叶变换是0000(,)[(,)(,)]2AF u v u u v v u u v v δδ=+++-- 证明:000000002()2()002()2()2()2()2()2()2((,)(,)cos(22)[]222j ut vz j ut vz j u t v z j u t v z j ut vz j u t v z j u t v z j ut vz j u F u v f t z e dtdzA u t v z e dtdzA e e e dtdz A A e e dtdz e e πππππππππππ∞∞-+-∞-∞∞∞-+-∞-∞∞∞+-+-+-∞-∞∞∞+-+-+--∞-∞==+=+=+⎰⎰⎰⎰⎰⎰⎰⎰)00000000(,)(,)22[(,)(,)]2t vz dtdzA Au u v v u u v v Au u v v u u v v δδδδ∞∞+-∞-∞=--+++=--+++⎰⎰ 证明离散函数(,)1f x y =的DFT 是1,0{1}(,)0,u v u v δ==⎧ℑ==⎨⎩其它证明:离散傅里叶变换112(//)00(,)(,)M N j ux M vy N x y F u v f x y e π---+===∑∑112(//)00112(//)00{1}M N j ux M vy N x y M N j ux M vy N x y e e ππ---+==---+==ℑ==∑∑∑∑如果0u v ==,{1}1ℑ=,否则:1100{1}{cos[2(//)]sin[2(//)]}M N x y ux M vy N j ux M vy N ππ--==ℑ=+-+∑∑考虑实部,1100{1}cos[2(//)]M N x y ux M vy N π--==ℑ=+∑∑,cos[2(//)]ux M vy N π+的值介于[-1, 1],可以想象,1100{1}cos[2(//)]0M N x y ux M vy N π--==ℑ=+=∑∑,虚部相同,所以1,0{1}(,)0,u v u v δ==⎧ℑ==⎨⎩其它证明离散函数00cos(22)u x v y ππ+的DFT 是00001(,)[(,)(,)]2F u v u Mu v Nv u Mu v Nv δδ=+++--证明:000000112(//)00112(//)0000112()2()2(//)00112()2(//)00(,)(,)cos(22)1[]21{2M N j ux M vy N x y M N j ux M vy N x y M N j u x v y j u x v y j ux M vy N x y M N j u x v y j ux M vy N x y F u v f x y e u x v y e e e e e e πππππππππ---+==---+==--+-+-+==--+-+====+=+=∑∑∑∑∑∑∑∑000000112()2(//)0011112(//)2(//)2(//)2(//)00000000}1{}21[(,)(,)]2M N j u x v y j ux M vy N x y M N M N j Mu x M Nv y N j Mu x M Nv y N j ux M vy N j ux M vy N x y x y e e e e e e u Mu v Nv u Mu v Nv ππππππδδ---+-+==----+-+-+-+====+=+=+++--∑∑∑∑∑∑ 下列问题与表中的性质有关。
数字图像处理第四章部分答案(全手打来自文库)
6,7→7
8
求变换后的匹配直方图
p(j)
0.14 0.22 0.25 0.33 0.06
4.5
解:已知通过图像平均法可以将噪声均方差降低到原来的 1/ m ,m 为用于平均的图像个数,
所以 g=1/10 n= 1/ m n
所以 M=100,T=3.33 秒
4.8 解:对提示表达式进行傅里叶变换得
4.2
解:1、[0,15]=3/2[0,10]; 2、[15,25]=15+[10,20]-10; 3、[25,30]=25+1/2([20,30]-20);
4.4
直方图均衡化
步
计算方法或公式
骤
1 列出图像灰度级(i 或 j)
2 计算原始直方图:p(i)=ni∕n
计算结果
0
1
2
3
4
5
6
7
0.14 0.22 0.25 0.17 0.10 0.06 0.03 0.03
4
计算原始累积直方图 pi 0.14 0.36 0.61 0.78 0.88 0.94 0.97 1.00
5
计算规定累积直方图 pj 0
0
0
0.19 0.44 0.65 0.89 1.00
6
按照 pi→ pj 找到对应的 3
4
5
6
6
6
7
7
i和j
7
确定变换关系 i→j
0→3 1→4 2→5 3,4,5→6
0.14
(j)=nj∕n
直方图规定化
0.22 0.25 0.17 0.10 0.12步 Nhomakorabea 计算方式
计算结果
1
列出图像灰度级 i,j 0
数字图像处理第三版中文答案解析冈萨雷斯
数字图像处理第三版中文答案解析引言《数字图像处理》是一本经典的图像处理教材,目前已经出版了第三版。
本文是对该书答案解析的总结,将分析和解释书中的问题和答案。
目录•第一章:绪论•第二章:数字图像基础•第三章:灰度变换•第四章:空间滤波•第五章:频域滤波•第六章:图像复原•第七章:几何校正•第八章:彩色图像处理•第九章:小波与多分辨率处理第一章:绪论本章主要介绍了数字图像处理的概念和基本步骤。
答案解析中包括对一些基本概念和术语的解释,以及相关的数学公式和图像处理方法的应用。
第二章:数字图像基础本章介绍了数字图像的表示和存储方法,以及图像的采样和量化过程。
答案解析中详细解释了图像的像素值和灰度级之间的关系,以及采样频率和量化步长对图像质量的影响。
第三章:灰度变换本章讲述了图像的灰度变换方法,包括线性和非线性变换。
答案解析中对不同灰度变换函数的作用和效果进行了解释,并给出了一些实例和应用。
第四章:空间滤波本章介绍了图像的空间滤波方法,包括平滑和锐化滤波。
答案解析中解释了不同滤波器的原理和效果,并给出了滤波器设计的步骤和实例。
第五章:频域滤波本章讲述了图像的频域滤波方法,包括傅里叶变换和滤波器设计。
答案解析中详细解释了傅里叶变换的原理和应用,以及频域滤波器的设计方法和实例。
第六章:图像复原本章介绍了图像的复原方法,包括退化模型和复原滤波。
答案解析中详细解释了退化模型的建立和复原滤波器的设计方法,以及如何根据退化模型进行图像复原的实例。
第七章:几何校正本章讲述了图像的几何校正方法,包括图像的旋转、缩放和平移等操作。
答案解析中给出了不同几何变换的矩阵表示和变换规则,以及几何校正的应用实例。
第八章:彩色图像处理本章介绍了彩色图像的表示和处理方法,包括RGB和HSV 等颜色模型的转换和处理。
答案解析中详细解释了不同颜色模型的表示和转换方法,以及彩色图像处理的实例和应用。
第九章:小波与多分辨率处理本章讲述了小波和多分辨率处理的方法和应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目的:尽可能模糊细节,而保留大的可识别特征
4.9、频率域锐化
图像的边缘、细节主要位于高频部分,而图像的模糊是由于高 频成分比较弱产生的。频率域锐化就是为了消除模糊,突出边 缘。因此采用高通滤波器让高频成分通过,使低频成分削弱, 再经逆傅立叶变换得到边缘锐化的图像 频率域锐化滤波器主要有: 理想高通滤波器 布特沃思高通滤波器 高斯高通滤波器 频率域的拉普拉斯算子 钝化模板、高频提升滤波和高频加强滤波
H (u) Ae
u2 /2 2
(4.7 5)
(4.7 6)
对应空间域高斯低通滤波器为 h( x)
2 Ae
2 2 2 x2
频率域高斯高通滤波器函数
H (u) Ae
2 u2 /21
Be
2 u2 /2 2
(4.7 7) A
B ,
2
1
对应空间域高斯高通滤波器为
(4.8 2)
理想低通滤波器
说明:在半径为D0的圆内,所有频率没有衰减地通过滤 波器,而在此半径的圆之外的所有频率完全被衰减掉
理想低通滤波器
总图像功率值PT 其中:
PT P ( u, v ) (4.8 3)
u 0 v 0
2 2 2
P 1 Q 1
P ( u, v ) F ( u, v ) R ( u, v ) I ( u, v )
第 4章
频率域滤波基础
4.7.1、频率域的其他特性:
F ( u, v )
M 1 N 1 x 0 y 0
f ( x , y )e
i 2 (
ux vy ) M N
①变化最慢的频率成分(u=v=0)对应一幅图像的平均灰度级
F (0 , 0 )
M 1 N 1 x 0 y 0
2n
(4.9 3)
1
2n
1 D( u, v ) / D0 1
2n
1 D0 / D( u, v )
二阶巴特沃思高通滤波示例:
D0=30 D0=60 D0=160
结论:BHPF的结果比IHPF的结果平滑得多
4.9.3、高斯高通滤波器
原始图
D0=10的ILPF滤波 损失能量为8%
D0=30的ILPF滤波 损失能量为5.4%
D0=60的ILPF滤波 损失能量为3.6%
D0=160的ILPF滤波 损失能量为2%
D0=460的ILPF滤波 损失能量为0.5%
理想低通滤波器举例——具有振铃现象
a ) 半径为10的 频域ILPF
b ) 半径为10空 域ILPF
f ( m , n)h( x m , y n )
(4.6 23)
对比空间域滤波:在 M× N的图像f上,用m×n的滤波器进行线 a b 性滤波 g ( x, y ) w( s, t ) f ( x s, y t ) ( 3.4 1)
s a t b
图4.36
4.7.4 、 空间域滤波和频域滤波之间的对应关系
大小为M×N的两个函数f(x,y)和h(x,y)的频率域滤波表示为: H (u, v ) F (u, v ) 由卷积定理,该运算对应的空间域运算为:
f ( x , y )★ h( x , y )
M 1 N 1 m 0 n 0
h( x ) 2 1 Ae
2 2 2 2 1 x
2 2 Be
2 2 2 2 2 x
(4.7 8)
频域高斯低通滤 波器
频域高斯高通滤 波器
空域高斯低通滤波器及模板
空域高斯高通滤波器及模板
图4.37
例4.15
f ( x, y ) : 600 600
F (u, v ) : 600 600
图4.38
h33 ( x, y)
H (u, v ) : 602 602
g( x, y) 1 H (u, v)F (u, v) h33 ( x, y)☆ f602602 ( x, y)
H 33 (u, v )
图4.39
空域线性滤 波的结果
4.8.1、理想低通滤波器
截断傅里叶变换中的所有处于指定距离D0之外的高频成分
结论:图a和b的振铃问题十分明显
4.9.2 、巴特沃思高通滤波器
n阶巴特沃思高通滤波器(BHPF)定义如下
1 H BHPF ( u, v ) 2n 1 [ D0 D( u, v )]
H hp ( u, v ) 1 H lp ( u, v ) 1 D( u, v ) / D0 1 D ( u , v ) / D 0
IDFT
前处x , y)
思想:通过滤波器函数以某种方式来修改图像变换, 然后通过取结果的反变换来获得处理后的输出图像
4.7.2、频率域滤波基础: DFT
F (u , v) 滤波器 H (u , v)
IDFT
H (u , v) F (u , v) 后处理
前处理
f (x , y)
1 D( u, v ) D0 H ILPF ( u, v ) 0 D( u, v ) D0
频率域的中心在 离如下
P Q ( , ) 2 2
, D0 0 (4.8 1)
,从点(u,v)到中心(原点)的距
1 2
P 2 Q 2 D( u, v ) ( u ) ( v ) 2 2
几种高通滤波器图示:
IHPF
BHPF
GHPF
几种高通滤波器空域图示:
IHPF BHPF GHPF
4.9.1、理想高通滤波器(IHPF)
截断傅里叶变换中所有处于指定距离D0之内的低频成分
0 D( u, v ) D0 H IHPF ( u, v ) 1 D( u, v ) D0
从幅度谱中我们可以看出明亮线和原始图像中对应的轮廓
线是垂直的。如果原始图像中有圆形区域那么幅度谱中也
呈圆形分布。
傅里叶频谱显示了±450的强边缘,在垂直轴偏左的部分有垂 直成分(对应两个氧化物突起)。
频率域滤波的基本步骤 DFT
F (u , v) 滤波器 H (u , v) H (u , v) F (u , v)
低通滤波器:
使低频通过,高频衰减的滤波器
被低通滤波的图像比原始图像少了尖锐的细节部分
而突出了平滑过渡部分
高通滤波器:
使高频通过,低频衰减的滤波器
被高通滤波的图像比原始图像少了灰度级的平滑 过渡而突出了边缘等细节部分
陷波滤波结果
高通滤波结果
高通滤波改进结果
陷波滤波器将原 点设置为0,平 均灰度为0,负 灰度置为0。
该高通滤波器原 点为0,因此几乎 没有平滑的灰度 级细节,且图像 较暗。
在高通滤波器中 加入常量,以使 F(0,0)不被完全 消除。(防止直 流项消除,保持 色调)
错误的填充图像会导致错误的结果
4.7.3、频率域的滤波步骤:
1、对要滤波的图像 f M N ( x, y) 进行填充得到 f PQ ( x, y) ,典 型地:P=2M,Q=2N x y ( 1) 2、填充图像,用 乘以输入图像进行中心变换
原点在频率域的中心,半径为D0的圆包含
其中
100 u
%的功率
P ( u, v ) / PT (4.8 4) v
理想低通滤波器举例
①87%以上的功率(能量)集中在半径小于10的圆周内;
②随滤波器半径的增加,越来越少的功率被滤出掉,使模糊 减弱;
理想低通滤波器举例
fP Q ( x , y) ( 1) x y F (u
x y F ( u , v ) f ( x , y )( 1) 3、变换到频域 P Q
P Q ,v ) 2 2
P Q H ( u , v ) ( 4、生成一个实的、中心对称的滤波器 PQ ,中心在 2 , 2 )
1 2
(4.8 2)
4.8.2、布特沃思低通滤波器
它的特性是连续性衰减,而不象理想滤波器那样陡峭变化,
即明显的不连续性。因此采用该滤波器滤波在抑制噪声的 同时,图像边缘的模糊程度大大减小,没有振铃效应产生
布特沃斯低通滤波器举例
原始图
D0=10的BLPF滤波
D0=30的BLPF滤波
D0=60的BLPF滤波
, D0 0 (4.9 2)
频率域的中心在 ( P , Q ) ,从点(u,v)到中心(原点)的 2 2 距离如下
P 2 Q 2 D( u, v ) ( u ) ( v ) 2 2
1 2
(4.8 2)
理想高通滤波示例:
D0=30 D0=60 D0=160
频域滤波: G(u, v) F (u, v) H (u, v)
5、变换到空间域: gPQ ( x, y)
1
6、取实部: real g P Q ( x , y ) x y g ( x , y ) real g ( x , y ) ( 1) 7、取消输入图像的乘数: p P Q 8、提取M N 区域: gM N ( x , y ) gPQ ( x , y )的对应部分
c ) 图像b)的水平 扫描线灰度变化
4.8.2 、布特沃思低通滤波器
n阶布特沃思低通滤波器(BLPF)定义如下
1 H BLPF ( u, v ) 1 [ D( u, v ) D0 ]2 n
(4.5 8)
D0为截至频率距原点的距离,D(u,v)是点(u,v)距原点的距离。
P 2 Q 2 D( u, v ) ( u ) ( v ) 2 2
D0=160的BLPF滤波
D0=460的BLPF滤波
布特沃斯低通滤波器举例——振铃现象
