冈萨雷斯数字图像处理第三版第四章(精校版)
数字图像处理课件(冈萨雷斯第三版)精简
• 为什么需要数字图象(digital image )？ 普通图象包含的信息量巨大，需要使用计算机对图象进行 处理。因此，需要把普通图象转变成计算机能处理的数字 图象。现在的数码相机可以直接地把视觉图象变成数字图 象。数字图象类似于光栅图形，由有限行和有限列组成。 每个基本单元叫做一个象素(pixel)。三维图象的象素又叫 做体素(voxel)。通常的二维数字图像是一个矩型，可以用 一个二维数组 I(x,y) 来表示，其中 x,y是二维空间中的某坐 标系的坐标，I(x,y)表示图像在该点处的灰度值等性质。彩 色可以是红绿蓝三个单色的一定灰度值的合成。一般来说， 这些坐标和灰度值是实数，不仅依赖于坐标系的选取，而 且依赖于灰度值的度量单位。但是，数字计算机只可能表 示有限字长的有限个数字。所以必须把灰度值离散化。简 单地说，数字图象等同于一个整数值的有限矩阵。数字图 像是数字图像处理和分析的对象。
1.2 图象处理和分析
1.2.1 图象处理和分析系统 图像处理和分析系统包括如下模块：图像采集模块、图像 显示模块、图像存储模块、图像通讯模块和图像处理和分 析模块。 1.2.2 模块 • 图象采集模块 CCD • 图象显示模块 CRT，LCD • 图象存储模块 内存、帧缓存、硬盘 • 图象通讯模块 LAN、WAN • 图象处理和分析模块
注意： 视觉：指光对感官的刺激和视觉系统的感觉。 视知觉：指如何通过视觉形成关于外部世界的表象。
2.2 人眼与亮度视觉
2.2.1 人眼成象
人的眼球是一个复杂的视觉器官。眼球的前部有晶状体， 相当于照相机的镜头。眼球内侧的后部有视网膜。视网膜 表面分布着两种感光细胞：锥细胞和柱细胞。眼内有六、 七百万的锥细胞，它们对明亮的光和颜色很敏感。人眼借 助于锥细胞来区分细节，因为每个锥细胞都连到神经末梢。 锥细胞的视觉称为适亮视觉。眼内有75万到150万柱细胞。 它们分布面大，且几个柱细胞连到一个神经末稍。分辨率 低，主要提供整体视觉印象。虽然它们对颜色不敏感，但 是对弱光较敏感。柱细胞的视觉称为适暗视觉。 视网膜的中心是中央凹，面积约1.51.5mm2，锥细胞 的密度达到150000个/mm2,是眼内最敏感的区域。
冈萨雷斯数字图像处理第3版第4章习题4.164.43备课讲稿
4.16 证明连续和离散二维傅里叶变换都是平移和旋转不变的。
首先列出平移和旋转性质：002(//)00(,)(,)j u x M v y N f x y e F u u v v π+⇔-- (4.6-3) 002(//)00(,)(,)j x r M y v N f x x y y F u v e π-+--⇔ (4.6-4)旋转性质：cos ,sin ,cos ,sin x r y r u v θθωϕωϕ====00(,)(,)f r F θθωϕϕ+⇔+ (4.6-5) 证明：由式(4.5-15)得：由式(4.5-16)得：依次类推证明其它项。
4.17 由习题4.3可以推出1(,)u v δ⇔和(,)1t z δ⇔。
使用前一个性质和表4.3中的平移性质证明连续函数00(,)cos(22)f t z A u t v z ππ=+的傅里叶变换是0000(,)[(,)(,)]2AF u v u u v v u u v v δδ=+++-- 证明：000000002()2()002()2()2()2()2()2()2((,)(,)cos(22)[]222j ut vz j ut vz j u t v z j u t v z j ut vz j u t v z j u t v z j ut vz j u F u v f t z e dtdzA u t v z e dtdzA e e e dtdzA A e e dtdz e e πππππππππππ∞∞-+-∞-∞∞∞-+-∞-∞∞∞+-+-+-∞-∞∞∞+-+-+--∞-∞==+=+=+⎰⎰⎰⎰⎰⎰⎰⎰)00000000(,)(,)22[(,)(,)]2t vz dtdz A Au u v v u u v v Au u v v u u v v δδδδ∞∞+-∞-∞=--+++=--+++⎰⎰ 4.18 证明离散函数(,)1f x y =的DFT 是1,0{1}(,)0,u v u v δ==⎧ℑ==⎨⎩其它证明：离散傅里叶变换112(//)00(,)(,)M N j ux M vy N x y F u v f x y e π---+===∑∑112(//)00112(//)00{1}M N j ux M vy N x y M N j ux M vy N x y e e ππ---+==---+==ℑ==∑∑∑∑如果0u v ==，{1}1ℑ=，否则：1100{1}{cos[2(//)]sin[2(//)]}M N x y ux M vy N j ux M vy N ππ--==ℑ=+-+∑∑考虑实部，1100{1}cos[2(//)]M N x y ux M vy N π--==ℑ=+∑∑，cos[2(//)]ux M vy N π+的值介于[-1, 1]，可以想象，1100{1}cos[2(//)]0M N x y ux M vy N π--==ℑ=+=∑∑，虚部相同，所以1,0{1}(,)0,u v u v δ==⎧ℑ==⎨⎩其它4.19 证明离散函数00cos(22)u x v y ππ+的DFT 是00001(,)[(,)(,)]2F u v u Mu v Nv u Mu v Nv δδ=+++--证明：000000112(//)00112(//)0000112()2()2(//)00112()2(//)00(,)(,)cos(22)1[]21{2M N j ux M vy N x y M N j ux M vy N x y M N j u x v y j u x v y j ux M vy N x y M N j u x v y j ux M vy N x y F u v f x y e u x v y e e e e e e πππππππππ---+==---+==--+-+-+==--+-+====+=+=∑∑∑∑∑∑∑∑000000112()2(//)0011112(//)2(//)2(//)2(//)00000000}1{}21[(,)(,)]2M N j u x v y j ux M vy N x y M N M N j Mu x M Nv y N j Mu x M Nv y N j ux M vy N j ux M vy N x y x y e e e e e e u Mu v Nv u Mu v Nv ππππππδδ---+-+==----+-+-+-+====+=+=+++--∑∑∑∑∑∑4.20 下列问题与表4.1中的性质有关。
数字图像处理第三版第四章
Digital Image Processing, 3rd ed.
Gonzalez & Woods
Chapter 4
Filtering in the Frequency Domain
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
Chapter 4
Filtering in the Frequency Domain
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
Chapter 4
Filtering in the Frequency Domain
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
Chapter 4
Filtering in the Frequency Domain
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
Chapter 4
Filtering in the Frequency Domain
© 1992–2008 R. C. Gonzalez & R. E. Woods
大学遥感数字图像处理教案
大学遥感数字图像处理教案大学遥感数字图像处理教案课程名称：遥感数字图像处理课时数：48学时课程设计：王老师教材：1. 《数字图像处理》(第3版) - 冈萨雷斯 / 伍兹2. 《数字遥感图像处理》 - Mather / Koch教学目标：1. 熟悉遥感数字图像处理的基本原理和流程，了解数字图像的基本概念和处理方法。
2. 掌握数字图像处理软件的使用，学习图像增强、分割、融合等处理方法。
3. 熟悉常用的遥感数据格式，能够读取、转换遥感数据。
4. 运用遥感数字图像处理技术，对不同类型的遥感数据进行处理，获得有用的信息。
教学内容：第一章数字图像基础知识1.1 数字图像的定义和特点1.2 图像采集和表示方法1.3 图像处理的基本概念和分类1.4 图像文件格式第二章数字图像增强2.1 空间域增强方法2.2 频域增强方法2.3 灰度变换2.4 直方图处理第三章数字图像分割3.1 基本概念和流程3.2 阈值分割3.3 区域分割3.4 模型分割第四章数字图像融合4.1 基本概念和流程4.2 像元级融合4.3 特征级融合4.4 决策级融合第五章遥感数据格式5.1 常用遥感数据格式5.2 遥感数据的读取和转换方法第六章遥感数字图像处理实例6.1 单波段图像处理实例6.2 多波段图像处理实例6.3 地物分类实例6.4 遥感图像融合实例教学方法：1. 讲授理论知识，辅以实例分析，使学生能够理解和掌握处理方法。
2. 实验操作，让学生在软件中进行图像处理和数据读取等相关操作，以加深理解和掌握处理技能。
3. 课堂讨论，通过分析学生操作的结果，针对处理方法中的问题进行讨论，促进学生思考和交流。
评估方法：1. 实验报告：学生根据作业布置的题目进行实验操作，提交一份实验报告。
2. 课堂讨论：对学生在课堂中的问题解答和参与情况进行评估。
3. 期末考试：对学生整个学期的知识掌握水平进行综合评估。
教学建议：1. 建议学生提前学习相关的数字图像处理和遥感知识，提高学习效果。
数字图像处理第三版( Rafael C.Gonzalez著)第4章答案
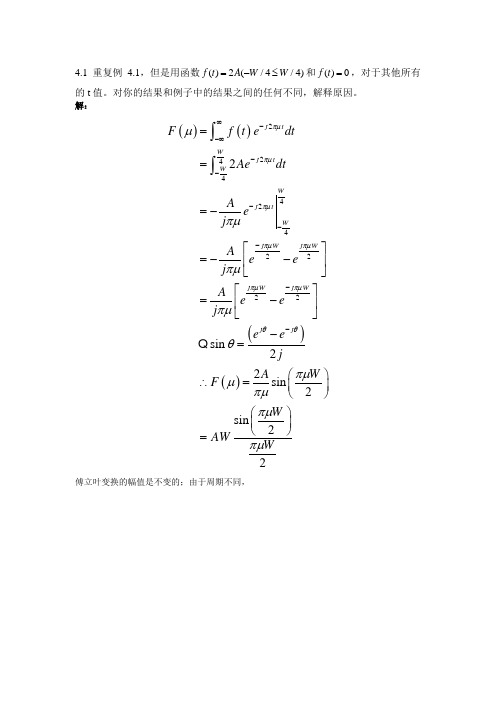
4.1 重复例4.1，但是用函数()2(/4/4)f t A W W =-≤和()0f t =，对于其他所有的t 值。
对你的结果和例子中的结果之间的任何不同，解释原因。
解：()()()()224442422222sin 22sin 2sin 22j tWj tW Wj tW j Wj W j W j Wj j F f t e dtA edtA ej A ee j A e ej ee jAW F W A WWπμπμπμπμπμπμπμθθμπμπμπμθπμμπμπμπμ∞--∞-------===-⎡⎤=--⎢⎥⎣⎦⎡⎤=-⎢⎥⎣⎦-=⎛⎫∴=⎪⎝⎭⎛⎫ ⎪⎝⎭=⎰⎰傅立叶变换的幅值是不变的；由于周期不同，4.2 证明式（4.4-2）()()()()()()~~2222j tj tn j tn j n Ttn n F f t edtf t t n T edt f t t n T edt f eπμπμπμπμμδδ∞--∞∞∞--∞=-∞∞∞--∞=-∞∞-∆=-∞==-∆=-∆=⎰∑⎰∑⎰∑中的()~F μ在两个方向上是无限周期的，周期为1/T ∆证明：(1) 要证明两个方向上是无限周期1/T ∆，只需证明根据如下式子：可得：其中上式第三行，由于k, n 是整数，且和的极限是关于原点对称。
(2) 同样的需要证明根据如下式子：()()()()()()~~2222j tj tn j tn j n Ttn n F f t edtf t t n T edt f t t n T edt f eπμπμπμπμμδδ∞--∞∞∞--∞=-∞∞∞--∞=-∞∞-∆=-∞==-∆=-∆=⎰∑⎰∑⎰∑可得：其中第三行由于k, n 都为整数，所以21j kneπ-=。
4.3 可以证明（Brancewell[2000]）1()1()t t δδ⇔⇔和。
使用前一个性质和表4.3中的平移性质，证明连续函数()cos(2)f t nt π=的傅立叶变换是()()()()1/2F n n μδμδμ=++-⎡⎤⎣⎦，其中是一个实数。
冈萨雷斯数字图像处理4讲解
一、背景知识
频域滤波，就是对图像做傅里叶变换后进行的处理 频域滤波在图像增强、图像复原、图像数据压缩等
过程中都起着重要作用 频域滤波包括低通滤波、高通滤波和高频强调滤波
一、二维离散傅里叶变换
令f(x,y)表示一幅大小为MXN的图像，其中 x=0,1,2, …,M-1, y=0, 1, 2, …, N-1
二、 Matlab中的二维DFT
显示频谱: FC = fftshift(F) imshow(abs(FC), [])
对数变换可以拓展显示范围 S2 = log(1 + abs(FC)) imshow(S2, [])
二、 Matlab中的二维DFT
傅里叶逆变换： f=ifft2(F)
图像处理中，逆变换结果一般只取实部: f = real(ifft2(F))
三、频域滤波
P = 2^nextpow2(2*m); PQ = [P, P]; elseif nargin == 3 m = max([AB CD]); P = 2^nextpow2(2*m); PQ = [P, P]; else error('Wrong number of inputs.') end
f (x, y)
1
M 1 N 1
F (u, v)e j 2 (ux / M vy/ N )
MN u0 v0
其中x=0,1,2, …,M-1和y=0, 1, 2, …, N-1 F(u,v)在这里称为傅里叶系数 Matlab中F(1,1)=F(0,0)
一、二维离散傅里叶变换
在原点处的频率值F(0,0)称为直流分量 傅里叶变换的频谱定义为
M 1 N 1
F(u, v)
f (x, y)e j2 (ux/ M vy/ N )
数字图像处理(冈萨雷斯)-4 频域平滑及锐化滤波
频域图像增强
——图像的频域分析 频率域滤波
频率域平滑（低通）滤波器
频率域锐化（高通）滤波器
4.8 频率域平滑滤波
第4章 频率域滤波
• 图像的平滑除了在空间域中进行外，也可以在频率域中进
行。由于噪声主要集中在高频部分，为去除噪声改善图像 质量，滤波器采用低通滤波器 H 可达到平滑图像的目的
2 2 2 2
H (u, v) 4 (u v ) (4.9 5)
2 2 2
原点从(0,0)移到(P/2,Q/2),所以，滤波函数平移为
H (u, v) 4 2 (u P 2) 2 (v Q 2) 2 4 2 D 2 (u, v) (4.9 6)
(u P 2)2 (v Q 2) 2 F (u, v) f ( x, y) 4
2 2
从原始图像中减去拉普拉斯算子部分，形成
g(x,y)的增强图像
g ( x, y ) f ( x, y ) f ( x, y ) (4.9 8)
4.8 频率域平滑滤波
理想低通滤波器 总图像功率值PT
P 1 Q 1 u 0 v 0
PT P ( u, v ) (4.8 3)
2
其中:
P (u, v ) F (u, v ) R2 (u, v ) I 2 (u, v )
原点在频率域的中心，半径为D0的圆包含%的功率
圆环具有半径5,15,30,80和230个像素
图像功率为92.0%,94.6%,96.4%,98.0%和99.5%
4.8
频率域平滑滤波
理想低通滤波器举例4.16——具有振铃现象
原图
冈萨雷斯数字图像处理4
五、低通频域滤波器
理想低通滤波器(ILP)具有传递函数：
1 H (u, v) 0
若D(u, v) D0 若D(u, v) D0
n阶巴特沃兹低通滤波器(BLPF)，截止频率
为D0
H
(u,
v)
1ຫໍສະໝຸດ [1 D(u, v)
/
D0
]2n
高斯低通滤波器(GLPF)的传递函数为：
H (u, v) eD2 (u,v)/ 2D02
五、在频率域直接生成滤波器
其中函数meshgrid用来生成网格数组，语 法：
[C, R] = meshgrid(c,r);
c和r是输入的行向量，C和R是输出的矩阵 C和R的维数为length(c)*length(r) 其中C的行是c的副本，R的列是r的副本 如c=[0,1]; r=[0, 1, 2]; 则C=[0 1 R=[0 0
M 1 N 1
F(u, v)
f (x, y)e j2 (ux/ M vy/ N )
x0 y0
其中u=0,1,2, …,M-1和v=0, 1, 2, …, N-1
频域系统是由F(u,v)所构成的坐标系统，其中u和 v是频率变量
利用欧拉公式可以手工计算傅里叶变换
一、二维离散傅里叶变换
自定义函数paddedsize()用来计算P、Q的最小偶 数值，以满足快速傅里叶变换FFT的计算需要
三、频域滤波
为避免折叠误差的干扰，在做频域滤波前要对输入 的图像和滤波器进行扩充补零的操作
设f(x,y)的大小为AXB， h(x,y)的大小为CXD， 则扩充后的函数大小为PXQ，其中： P>=A+C-1 Q>=B+D-1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
D0=80的高斯低通滤波器 修复字符
D0=80
GLPF
用于机器识别系统识别断裂字符的预处理
人脸图像处理
原图像 D0=100的GLPF滤波, 细纹减少 D0=80的GLPF滤波， 细纹减少
卫星、航拍图像处理
佛罗里达亮 墨西哥湾暗
奥基乔 比湖 D0=30的GLPF滤波图 D0=10的GLPF滤波图
例4.15
图4.38
h33 ( x, y)
H (u, v ) : 602 602
g( x, y) 1 H (u, v)F (u, v) h33 ( x, y)☆ f602602 ( x, y)
H 33 (u, v )
图4.39
空域线性滤波 的结果
4.8.1
理想低通滤波器
截断傅里叶变换中的所有处于指定距离D0之外的高频成分
1 D( u, v ) D0 H ILPF ( u, v ) 0 D( u, v ) D0
频率域的中心在 离如下
P Q ( , ) 2 2
, D0 0 (4.8 1)
，从点(u,v)到中心（原点）的距
P 2 Q 2 D( u, v ) ( u ) ( v ) 2 2
fP Q ( x , y) ( 1) x y F (u P Q ,v ) 2 2
3、变换到频域
x y F ( u, v ) f ( x , y )( 1) P Q
P Q H ( u , v ) ( 4、生成一个实的、中心对称的滤波器 PQ ，中心在 , ) 2 2
对应空间域高斯高通滤波器为
h( x ) 2 1 Ae
2 2 2 2 1 x
2 2 Be
2 2 2 2 2 x
(4.7 8)
图4.37
频域高斯低通滤波器 频域高斯高通滤波器
空域高斯低通滤波器及模板
空域高斯高通滤波器及模板
f ( x, y ) : 600 600
F (u, v ) : 600 600
低通滤波器：
使低频通过，高频衰减的滤波器
被低通滤波的图像比原始图像少了尖锐的细节部分
而突出了平滑过渡部分
高通滤波器：
使高频通过，低频衰减的滤波器
被高通滤波的图像比原始图像少了灰度级的平滑 过渡而突出了边缘等细节部分
陷波滤波结果
高通滤波结果
高通滤波改进结果
陷波滤波器将原点 设置为0，平均灰 度为0，负灰度置 为0。
1 2
(4.8 2)
4.8.2 布特沃思低通滤波器
它的特性是连续性衰减，而不象理想滤波器那样陡峭变化，
即明显的不连续性。因此采用该滤波器滤波在抑制噪声的 同时，图像边缘的模糊程度大大减小，没有振铃效应产生
布特沃斯低通滤波器举例
原始图
D0=10的BLPF滤波
D0=30的BLPF滤波
D0=60的BLPF滤波
频率域的中心在 距离如下
P Q ( , ) 2 2
, D0 0 (4.9 2)
，从点(u,v)到中心（原点）的
1 2
P 2 Q 2 D( u, v ) ( u ) ( v ) 2 2
(4.8 2)
理想高通滤波示例：
D0=30 D0=60 D0=160
s a t b
(4.6-23)和(3.4-1)本质上是相似的；相差之处只在于：常数、负号及求和的 上、下限； 在实践中，我们宁愿使用(3.4-1)和较小的滤波器模板来实现滤波处理； 滤波在频率域中更为直观，可以在频率域指定滤波器，做反变换，然后在空 间域使用结果滤波器作为在空间域构建小滤波器模板的指导；
该高通滤波器原点为 0，因此几乎没有平 滑的灰度级细节，且 图像较暗。
在高通滤波器中加 入常量，以使F(0,0) 不被完全消除。 （防止直流项消除， 保持色调）
错误的填充图像会导致错误的结果
4.7.3 频率域的滤波步骤：
1、对要滤波的图像 f M N ( x, y) 进行填充得到 f PQ ( x, y) ，典 型地：P=2M,Q=2N x y ( 1) 2、填充图像，用 乘以输入图像进行中心变换
目的：尽可能模糊细节，而保留大的可识别特征
4.9
频率域锐化
图像的边缘、细节主要位于高频部分，而图像的模糊是由于高 频成分比较弱产生的。频率域锐化就是为了消除模糊，突出边 缘。因此采用高通滤波器让高频成分通过，使低频成分削弱， 再经逆傅立叶变换得到边缘锐化的图像
频率域锐化滤波器主要有： 理想高通滤波器
H LP (u, v ) FPQ (u, v ) ( 1) x y real g PQ ( x , y ) gM N ( x, y)
图4.36
4.7.4 空间域滤波和频域滤波之间的对应关系
大小为M×N的两个函数f(x,y)和h(x,y)的频率域滤波表示为： H (u, v ) F (u, v ) 由卷积定理，该运算对应的空间域运算为：
原点在频率域的中心，半径为D0的圆包含%的功率
其中
100 u P ( u, v ) / PT (4.8 4) v
理想低通滤波器举例
①87%以上的功率(能量)集中在半径小于10的圆周内;
②随滤波器半径的增加,越来越少的功率被滤出掉,使模糊 减弱;
理想低通滤波器举例
c ) 图像b）的水平 扫描线灰度变化
4.8.2 布特沃思低通滤波器
n阶布特沃思低通滤波器(BLPF)定义如下
1 H BLPF ( u, v ) 1 [ D( u, v ) D0 ]2 n
(4.5 8)
D0为截至频率距原点的距离，D(u,v)是点(u,v)距原点的距离。
P 2 Q 2 D( u, v ) ( u ) ( v ) 2 2
F (u, v)H(u, v)
8、提取M N 区域: gM N ( x , y ) gPQ ( x , y )的对应部分
f M N ( x, y )
f PQ ( x, y )
(1)x y f PQ ( x, y)
FP Q ( u, v )
H LP (u, v ) : P Q
频率域高斯低通滤波器函数
H (u) Ae
u2 /2 2
(4.7 5)
(4.7 6)
对应空间域高斯低通滤波器为 h( x)
2 Ae
2 2 2 x2
频率域高斯高通滤波器函数
H (u) Ae
2 u2 /21
Be
2 u2 /2 2
(4.7 7)
A B , 1 2
频域滤波:
G(u, v) F (u, v) H (u, v)
1
5、变换到空间域: gPQ ( x, y)
6、取实部:
x y g ( x , y ) real g ( x , y ) ( 1) P Q 7、取消输入图像的乘数: p
real g P Q ( x , y )
从幅度谱中我们可以看出明亮线和原始图像中对应的轮廓
线是垂直的。如果原始图像中有圆形区域那么幅度谱中也
呈圆形分布。
傅里叶频谱显示了±450的强边缘，在垂直轴偏左的 部分有垂直成分（对应两个氧化物突起）。
频率域滤波的基本步骤 DFT
F (u , v) 滤波器 H (u , v) H (u , v) F (u , v)
布特沃思高通滤波器 高斯高通滤波器 频率域的拉普拉斯算子
钝化模板、高频提升滤波和高频加强滤波
几种高通滤波器图示：
IHPF
BHPF
GHPF
几种高通滤波器空域图示：
IHPF BHPF GHPF
4.9.1
理想高通滤波器（IHPF）
截断傅里叶变换中所有处于指定距离D0之内的低频成分
0 D( u, v ) D0 H IHPF ( u, v ) 1 D( u, v ) D0
g (x , y)
g ( x , y)
1
H (u, v)F (u, v)
陷波滤波器（带阻滤波）
M N 0 ( u, v ) ( , ) H ( u, v ) 2 2 其它 1
设臵F(0,0)=0(结果图像的平均值为零)，而保留其 它傅里叶变换的频率成分不变 由于图像平均值为0而产生整体平均灰度级的降低， 因此几乎没有平滑的灰度级细节
f ( x , y )★ h( x , y )
M 1 N 1 m 0 n 0
f ( m , n)h( x m , y n)
(4.6 23)
对比空间域滤波：在M×N的图像f上，用m×n的滤波器进行线 a b 性滤波 g ( x, y ) w( s, t ) f ( x s, y t ) ( 3.4 1)
原始图
D0=10的ILPF滤波 损失能量为8%
D0=30的ILPF滤波 损失能量为5.4%
D0=60的ILPF滤波 损失能量为3.6%
D0=160的ILPF滤波 损失能量为2%
D0=460的ILPF滤波 损失能量为0.5%
理想低通滤波器举例——具有振铃现象
a ) 半径为10的频 域ILPF
b ) 半径为10空域 ILPF
二维高斯低通滤波器(GLPF)定义如下
H ( u, v ) e
(4.8 7)
当D(u,v)=D0时，滤波器下降到它最大值的0.607处
高斯低通滤波器举例
原始图
D0=10的GLPF滤波
D0=30的GLPF滤波
D0=60的GLPF滤波
D0=160的GLPF滤波
D0=460的GLPF滤波
字符识别举例
1 2