高等数学试题4

合集下载

专升本高数一模拟题4

x 0 mx
x 0 mx
2、解析：因为 f ( x) 在 x0 处连续，所以 lim f ( x) 必定存在，且等于 f ( x0 ) ；连续不一定可导。 x x0
3、解析： y
2 x u=-x , y' y=2 u
(2 x) ' =(-x)' (2u )'=-2 x
d
4、解析： A ：
b
b
f ( x)dx 0； C： f ( x) dx
xdxdy
D
1
1 y2
dy xdx
0
0
1 ( y 1 y 3 ) |10 1
23
3
解答 2：利用极坐标系计算
1 2
x | 1 2 1 y 2
0
0
dy
11 (1
y2 )dy
20
区域 D 可以表示为： 0 r 1、 0
，所以：
2
xdxdy
D
1
dr
2 r 2 cos d
0
0
1 (r 2 sin
0
) |02 dr
f ( x) 的
A ： ex +x
B： ex +x+ C
2z
8．设 z y sin x ，则：
等于
xy
A ： cosx
B： y cos x
C： ex
D： ex +C
C： cos x
D ： ycos x
9．方程 y 3y 2 y xe2 x 的待定特解应取
A ： Axe2x
B ： ( Ax B) e2x
解答：设 A
1
f ( x) dx ，则： f ( x)

大学高等数学上下考试题库(及答案)

高数试题1（上）及答案一．选择题（将答案代号填入括号内，每题3分，共30分）.1．下列各组函数中，是相同的函数的是（）.（A ）()()2ln 2ln f x x g x x == 和（B ）()||f x x = 和 ()g x =（C ）()f x x = 和 ()2g x =（D ）()||x f x x=和 ()g x =1 2．函数()00x f x a x ≠=⎨⎪=⎩ 在0x =处连续，则a =（）.（A ）0 （B ）14（C ）1 （D ）23．曲线ln y x x =的平行于直线10x y -+=的切线方程为（）.（A ）1y x =- （B ）(1)y x =-+ （C ）()()ln 11y x x =-- （D ）y x = 4．设函数()||f x x =，则函数在点0x =处（）.（A ）连续且可导（B ）连续且可微（C ）连续不可导（D ）不连续不可微5．点0x =是函数4y x =的（）.（A ）驻点但非极值点（B ）拐点（C ）驻点且是拐点（D ）驻点且是极值点6．曲线1||y x =的渐近线情况是（）. （A ）只有水平渐近线（B ）只有垂直渐近线（C ）既有水平渐近线又有垂直渐近线（D ）既无水平渐近线又无垂直渐近线 7．211f dx x x⎛⎫' ⎪⎝⎭⎰的结果是（）. （A ）1f C x ⎛⎫-+ ⎪⎝⎭（B ）1f C x ⎛⎫--+ ⎪⎝⎭（C ）1f C x ⎛⎫+ ⎪⎝⎭（D ）1f C x ⎛⎫-+ ⎪⎝⎭8．x x dxe e -+⎰的结果是（）.（A ）arctan xe C + （B ）arctan xeC -+ （C ）x x e e C --+ （D ）ln()x x e e C -++9．下列定积分为零的是（）.（A ）424arctan 1x dx x ππ-+⎰ （B ）44arcsin x x dx ππ-⎰ （C ）112x xe e dx --+⎰ （D ）()121sin x x x dx -+⎰ 10．设()f x 为连续函数，则()12f x dx '⎰等于（）.（A ）()()20f f - （B ）()()11102f f -⎡⎤⎣⎦（C ）()()1202f f -⎡⎤⎣⎦（D ）()()10f f -二．填空题（每题4分，共20分）1．设函数()2100x e x f x x a x -⎧-≠⎪=⎨⎪=⎩在0x =处连续，则a =.2．已知曲线()y f x =在2x =处的切线的倾斜角为56π，则()2f '=.3．21xy x =-的垂直渐近线有条. 4．()21ln dxx x =+⎰.5．()422sin cos xx x dx ππ-+=⎰.三．计算（每小题5分，共30分） 1．求极限①21lim xx x x →∞+⎛⎫⎪⎝⎭ ②()20sin 1lim x x x x x e →-- 2．求曲线()ln y x y =+所确定的隐函数的导数x y '. 3．求不定积分 ①()()13dx x x ++⎰②()0a > ③x xe dx -⎰四．应用题（每题10分，共20分） 1．作出函数323y x x =-的图像.2．求曲线22y x =和直线4y x =-所围图形的面积.《高数》试卷1参考答案一．选择题1．B 2．B 3．A 4．C 5．D 6．C 7．D 8．A 9．A 10．C 二．填空题1．2-2．33-３．２４．arctan ln x c+５．２三．计算题１①2e②162.11xyx y'=+-3. ①11ln||23xCx+++②22ln||x a x C-++③()1xe x C--++四．应用题１．略２．18S=《高数》试卷2（上）一.选择题(将答案代号填入括号内,每题3分,共30分) 1.下列各组函数中,是相同函数的是( ).(A) ()f x x =和()g x = (B) ()211x f x x -=-和1y x =+(C) ()f x x =和()22(sin cos )g x x x x =+ (D) ()2ln f x x =和()2ln g x x =2.设函数()()2sin 21112111x x x f x x x x -⎧<⎪-⎪⎪==⎨⎪->⎪⎪⎩，则()1lim x f x →=（）. (A) 0 (B) 1 (C) 2 (D) 不存在3.设函数()y f x =在点0x 处可导，且()f x '>0, 曲线则()y f x =在点()()00,x f x 处的切线的倾斜角为{ }. (A) 0 (B)2π(C) 锐角 (D) 钝角 4.曲线ln y x =上某点的切线平行于直线23y x =-,则该点坐标是( ). (A) 12,ln2⎛⎫⎪⎝⎭(B) 12,ln 2⎛⎫- ⎪⎝⎭ (C)1,ln 22⎛⎫⎪⎝⎭ (D) 1,ln 22⎛⎫- ⎪⎝⎭5.函数2xy x e-=及图象在()1,2内是( ).(A)单调减少且是凸的 (B)单调增加且是凸的 (C)单调减少且是凹的 (D)单调增加且是凹的6.以下结论正确的是( ).(A) 若0x 为函数()y f x =的驻点,则0x 必为函数()y f x =的极值点. (B) 函数()y f x =导数不存在的点,一定不是函数()y f x =的极值点. (C) 若函数()y f x =在0x 处取得极值,且()0f x '存在,则必有()0f x '=0. (D) 若函数()y f x =在0x 处连续,则()0f x '一定存在. 7.设函数()y f x =的一个原函数为12xx e ,则()f x =( ).(A) ()121xx e - (B) 12x x e - (C) ()121x x e + (D) 12xxe 8.若()()f x dx F x c =+⎰,则()sin cos xf x dx =⎰( ).(A) ()sin F x c + (B) ()sin F x c -+ (C) ()cos F x c + (D) ()cos F x c -+ 9.设()F x 为连续函数,则12x f dx ⎛⎫' ⎪⎝⎭⎰=( ). (A) ()()10f f - (B)()()210f f -⎡⎤⎣⎦ (C) ()()220f f -⎡⎤⎣⎦ (D) ()1202f f ⎡⎤⎛⎫- ⎪⎢⎥⎝⎭⎣⎦10.定积分badx ⎰()a b <在几何上的表示( ).(A) 线段长b a - (B) 线段长a b - (C) 矩形面积()1a b -⨯ (D) 矩形面积()1b a -⨯ 二.填空题(每题4分,共20分)1.设 ()()2ln 101cos 0x x f x xa x ⎧-⎪≠=⎨-⎪=⎩, 在0x =连续,则a =________.2.设2sin y x =, 则dy =_________________sin d x . 3.函数211xy x =+-的水平和垂直渐近线共有_______条. 4.不定积分ln x xdx =⎰______________________.5. 定积分2121sin 11x x dx x -+=+⎰___________. 三.计算题(每小题5分,共30分)1.求下列极限:①()10lim 12xx x →+ ②arctan 2lim 1x x xπ→+∞-2.求由方程1yy xe =-所确定的隐函数的导数x y '. 3.求下列不定积分:①3tan sec x xdx ⎰②)0a > ③2x x e dx ⎰ 四.应用题(每题10分,共20分) 1.作出函数313y x x =-的图象.(要求列出表格)2.计算由两条抛物线：22,y x y x ==所围成的图形的面积.《高数》试卷2参考答案一.选择题：CDCDB CADDD二填空题：1.－2 2.2sin x 3.3 4.2211ln 24x x x c -+ 5.2π 三.计算题：1. ①2e ②1 2.2yx e y y '=- 3.①3sec 3xc + ②()22ln x a x c +++ ③()222x x x e c -++四.应用题：1.略 2.13S =《高数》试卷3（上）一、填空题(每小题3分, 共24分)1. 函数219y x=-的定义域为________________________.2.设函数()sin 4,0,0xx f x x a x ⎧≠⎪=⎨⎪=⎩, 则当a =_________时, ()f x 在0x =处连续.3. 函数221()32x f x x x -=-+的无穷型间断点为________________.4. 设()f x 可导, ()xy f e =, 则____________.y '=5. 221lim _________________.25x x x x →∞+=+- 6. 321421sin 1x xdx x x -+-⎰=______________. 7. 20_______________________.x t d e dt dx -=⎰ 8. 30y y y '''+-=是_______阶微分方程.二、求下列极限(每小题5分, 共15分)1. 01lim sin xx e x →-; 2. 233lim 9x x x →--; 3. 1lim 1.2xx x -→∞⎛⎫+ ⎪⎝⎭三、求下列导数或微分(每小题5分, 共15分)1. 2xy x =+, 求(0)y '. 2. cos x y e =, 求dy . 3. 设x y xy e +=, 求dydx .四、求下列积分 (每小题5分, 共15分)1. 12sin x dx x ⎛⎫+ ⎪⎝⎭⎰. 2.ln(1)x x dx +⎰.3.120xedx ⎰五、(8分)求曲线1cos x t y t=⎧⎨=-⎩在2t π=处的切线与法线方程.六、(8分)求由曲线21,y x =+ 直线0,0y x ==和1x =所围成的平面图形的面积, 以及此图形绕y 轴旋转所得旋转体的体积. 七、(8分)求微分方程6130y y y '''++=的通解.八、(7分)求微分方程x yy e x'+=满足初始条件()10y =的特解. 《高数》试卷3参考答案一．1．3x< 2.4a = 3.2x = 4.'()x x e f e5.126.07.22x xe -8.二阶二.1.原式=0lim 1x xx→= 2.311lim36x x →=+ 3.原式=112221lim[(1)]2x x e x--→∞+= 三.1.221','(0)(2)2y y x ==+2.cos sin x dy xe dx =-3.两边对x 求写：'(1')x y y xy e y +==+'x y x y e y xy yy x e x xy++--⇒==-- 四.1.原式=lim 2cos x x C -+2.原式=2221lim(1)()lim(1)[lim(1)]22x x x d x x d x x +=+-+⎰⎰=22111lim(1)lim(1)(1)221221x x x x dx x x dx x x+-=+--+++⎰⎰=221lim(1)[lim(1)]222x x x x x C +--+++3.原式=1221200111(2)(1)222x x e d x e e ==-⎰五.sin 1,122dy dy tt t y dx dx ππ=====且切线：1,1022y x y x ππ-=---+=即法线：1(),1022y x y x ππ-=--+--=即六.12210013(1)()22S x dx x x =+=+=⎰11224205210(1)(21)228()5315V x dx x x dxx x x ππππ=+=++=++=⎰⎰七.特征方程:2312613032(cos 2sin 2)xr r r iy e C x C x -++=⇒=-±=+八.11()dxdxxx x y ee edx C -⎰⎰=+⎰1[(1)]x x e C x=-+ 由10,0y x C ==⇒=1xx y e x-∴=《高数》试卷4（上）一、选择题（每小题3分） 1、函数 2)1ln(++-=x x y 的定义域是（）.A []1,2-B [)1,2-C (]1,2-D ()1,2- 2、极限xx e ∞→lim 的值是（）.A 、 ∞+B 、 0C 、∞-D 、不存在 3、=--→211)1sin(limx x x （）.A 、1B 、 0C 、 21-D 、21 4、曲线 23-+=x x y 在点)0,1(处的切线方程是（） A 、 )1(2-=x y B 、)1(4-=x y C 、14-=x y D 、)1(3-=x y 5、下列各微分式正确的是（）.A 、)(2x d xdx = B 、)2(sin 2cos x d xdx = C 、)5(x d dx --= D 、22)()(dx x d = 6、设⎰+=C xdx x f 2cos 2)( ，则 =)(x f （）.A 、2sinxB 、 2sin x -C 、 C x +2sinD 、2sin 2x -7、⎰=+dx xx ln 2（）.A 、C x x++-22ln 212 B 、 C x ++2)ln 2(21C 、 C x ++ln 2lnD 、 C x x++-2ln 18、曲线2x y = ，1=x ，0=y 所围成的图形绕y 轴旋转所得旋转体体积=V （）. A 、⎰14dx x π B 、⎰1ydy πC 、⎰-1)1(dy y π D 、⎰-104)1(dx x π9、⎰=+101dx e e xx（）. A 、21lne + B 、22ln e + C 、31ln e + D 、221ln e + 10、微分方程 xe y y y 22=+'+'' 的一个特解为（）.A 、x e y 273=* B 、x e y 73=* C 、x xe y 272=* D 、x e y 272=*二、填空题（每小题4分）1、设函数xxe y =，则 =''y ； 2、如果322sin 3lim 0=→x mx x , 则 =m .3、=⎰-113cos xdx x ；4、微分方程 044=+'+''y y y 的通解是 .5、函数x x x f 2)(+= 在区间 []4,0 上的最大值是，最小值是；三、计算题（每小题5分） 1、求极限 x x x x --+→11lim 0； 2、求x x y sin ln cot 212+= 的导数；3、求函数 1133+-=x x y 的微分； 4、求不定积分⎰++11x dx ；5、求定积分⎰eedx x 1ln ； 6、解方程21xy xdx dy -=；四、应用题（每小题10分）1、求抛物线2x y = 与 22x y -=所围成的平面图形的面积.2、利用导数作出函数323x x y -= 的图象.参考答案一、1、C ； 2、D ； 3、C ； 4、B ； 5、C ； 6、B ； 7、B ； 8、A ； 9、A ； 10、D ；二、1、xe x )2(+； 2、94 ； 3、0 ； 4、xe x C C y 221)(-+= ； 5、8，0三、1、 1； 2、x 3cot - ； 3、dx x x 232)1(6+ ；4、C x x +++-+)11ln(212；5、)12(2e- ； 6、C x y =-+2212 ；四、1、38； 2、图略《高数》试卷5（上）一、选择题（每小题3分） 1、函数)1lg(12+++=x x y 的定义域是（）.A 、()()+∞--,01,2B 、 ()),0(0,1+∞-C 、),0()0,1(+∞-D 、),1(+∞- 2、下列各式中，极限存在的是（）.A 、 x x cos lim 0→ B 、x x arctan lim ∞→ C 、x x sin lim ∞→ D 、xx 2lim +∞→3、=+∞→xx xx )1(lim （）. A 、e B 、2e C 、1 D 、e1 4、曲线x x y ln =的平行于直线01=+-y x 的切线方程是（）. A 、 x y = B 、)1)(1(ln --=x x y C 、 1-=x y D 、)1(+-=x y 5、已知x x y 3sin = ，则=dy （）.A 、dx x x )3sin 33cos (+-B 、dx x x x )3cos 33(sin +C 、dx x x )3sin 3(cos +D 、dx x x x )3cos 3(sin + 6、下列等式成立的是（）.A 、⎰++=-C x dx x 111ααα B 、⎰+=C x a dx a xx ln C 、⎰+=C x xdx sin cos D 、⎰++=C xxdx 211tan 7、计算⎰xdx x e x cos sin sin 的结果中正确的是（）.A 、C ex+sin B 、C x e x +cos sinC 、C x ex+sin sin D 、C x e x +-)1(sin sin8、曲线2x y = ，1=x ，0=y 所围成的图形绕x 轴旋转所得旋转体体积=V （）. A 、⎰14dx x π B 、⎰1ydy πC 、⎰-1)1(dy y π D 、⎰-104)1(dx x π9、设 a ﹥0，则=-⎰dx x a a22（）.A 、2a B 、22a πC 、241a 0 D 、241a π 10、方程（）是一阶线性微分方程.A 、0ln2=+'xyy x B 、0=+'y e y x C 、0sin )1(2=-'+y y y x D 、0)6(2=-+'dy x y dx y x二、填空题（每小题4分）1、设⎩⎨⎧+≤+=0,0,1)( x b ax x e x f x ，则有=-→)(lim 0x f x ，=+→)(lim 0x f x ；2、设 xxe y = ，则 =''y ；3、函数)1ln()(2x x f +=在区间[]2,1-的最大值是，最小值是；4、=⎰-113cos xdx x；5、微分方程 023=+'-''y y y 的通解是 .三、计算题（每小题5分） 1、求极限 )2311(lim 21-+--→x x x x ；2、求 x x y arccos 12-= 的导数；3、求函数21xx y -=的微分；4、求不定积分⎰+dx xxln 21 ；5、求定积分 ⎰eedx x 1ln ；6、求方程y xy y x =+'2满足初始条件4)21(=y 的特解.四、应用题（每小题10分）1、求由曲线 22x y -= 和直线 0=+y x 所围成的平面图形的面积.2、利用导数作出函数 49623-+-=x x x y 的图象.参考答案（B 卷）一、1、B ； 2、A ； 3、D ； 4、C ； 5、B ； 6、C ； 7、D ； 8、A ； 9、D ； 10、B.二、1、 2 ，b ； 2、xe x )2(+ ； 3、 5ln ，0 ； 4、0 ； 5、xxeC e C 221+.三、1、31 ； 2、1arccos 12---x x x ； 3、dx xx 221)1(1-- ； 4、C x ++ln 22 ； 5、)12(2e- ； 6、x e x y 122-= ；四、1、 29； 2、图略《高等数学》试卷1（下）一.选择题（3分⨯10）1.点1M ()1,3,2到点()4,7,22M 的距离=21M M （）.A.3B.4C.5D.62.向量j i b k j i a+=++-=2,2，则有（）.A.a ∥bB.a ⊥bC.3,π=b aD.4,π=b a3.函数1122222-++--=y x y x y 的定义域是（）.A.(){}21,22≤+≤y x y x B.(){}21,22<+<y x y xC.(){}21,22≤+<y xy x D (){}21,22<+≤y x y x4.两个向量a 与b垂直的充要条件是（）.A.0=⋅b aB.0 =⨯b aC.0 =-b aD.0 =+b a5.函数xy y x z 333-+=的极小值是（）. A.2 B.2- C.1 D.1- 6.设y x z sin =，则⎪⎭⎫ ⎝⎛∂∂4,1πyz＝（）.A.22B.22-C.2D.2-7.若p 级数∑∞=11n p n 收敛，则（）. A.p 1< B.1≤p C.1>p D.1≥p8.幂级数∑∞=1n nnx 的收敛域为（）.A.[]1,1- B ()1,1- C.[)1,1- D.(]1,1-9.幂级数nn x ∑∞=⎪⎭⎫⎝⎛02在收敛域内的和函数是（）.A.x -11 B.x -22 C.x -12 D.x-21 10.微分方程0ln =-'y y y x 的通解为（）. A.xce y = B.xe y = C.xcxe y = D.cxe y = 二.填空题（4分⨯5）1.一平面过点()3,0,0A 且垂直于直线AB ，其中点()1,1,2-B ，则此平面方程为______________________.2.函数()xy z sin =的全微分是______________________________.3.设13323+--=xy xy y x z ，则=∂∂∂yx z 2_____________________________.4.x+21的麦克劳林级数是___________________________. 5.微分方程044=+'+''y y y 的通解为_________________________________. 三.计算题（5分⨯6）1.设v e z usin =，而y x v xy u +==,，求.,yz x z ∂∂∂∂ 2.已知隐函数()y x z z ,=由方程05242222=-+-+-z x z y x 确定，求.,yz x z ∂∂∂∂ 3.计算σd y x D⎰⎰+22sin ，其中22224:ππ≤+≤y x D . 4.如图，求两个半径相等的直交圆柱面所围成的立体的体积（R 为半径）.5.求微分方程xe y y 23=-'在00==x y条件下的特解.四.应用题（10分⨯2）1.要用铁板做一个体积为23m 的有盖长方体水箱，问长、宽、高各取怎样的尺寸时，才能使用料最省？2..曲线()x f y =上任何一点的切线斜率等于自原点到该切点的连线斜率的2倍，且曲线过点⎪⎭⎫⎝⎛31,1，求此曲线方程 .《高数》试卷2（下）一.选择题（3分⨯10）1.点()1,3,41M ，()2,1,72M 的距离=21M M （）. A.12 B.13 C.14 D.152.设两平面方程分别为0122=++-z y x 和05=++-y x ，则两平面的夹角为（）. A.6π B.4π C.3π D.2π 3.函数()22arcsin yx z +=的定义域为（）.A.(){}10,22≤+≤y x y x B.(){}10,22<+<y x y xC.()⎭⎬⎫⎩⎨⎧≤+≤20,22πy x y x D.()⎭⎬⎫⎩⎨⎧<+<20,22πy x y x 4.点()1,2,1--P 到平面0522=--+z y x 的距离为（）. A.3 B.4 C.5 D.6 5.函数22232y x xy z --=的极大值为（）. A.0 B.1 C.1- D.216.设223y xy x z ++=，则()=∂∂2,1xz （）.A.6B.7C.8D.9 7.若几何级数∑∞=0n nar是收敛的，则（）.A.1≤rB. 1≥rC.1<rD.1≤r8.幂级数()nn xn ∑∞=+01的收敛域为（）.A.[]1,1-B.[)1,1-C.(]1,1-D. ()1,1- 9.级数∑∞=14sin n n na是（）. A.条件收敛 B.绝对收敛 C.发散 D.不能确定 10.微分方程0ln =-'y y y x 的通解为（）. A.cxe y = B.xce y = C.xe y = D.xcxe y = 二.填空题（4分⨯5）1.直线l 过点()1,2,2-A 且与直线⎪⎩⎪⎨⎧-==+=t z t y t x 213平行，则直线l 的方程为__________________________.2.函数xye z =的全微分为___________________________. 3.曲面2242y x z -=在点()4,1,2处的切平面方程为_____________________________________. 4.211x+的麦克劳林级数是______________________. 5.微分方程03=-ydx xdy 在11==x y 条件下的特解为______________________________.三.计算题（5分⨯6）1.设k j b k j i a32,2+=-+=，求.b a ⨯2.设22uv v u z -=，而y x v y x u sin ,cos ==，求.,y z x z ∂∂∂∂ 3.已知隐函数()y x z z ,=由233=+xyz x 确定，求.,yz x z ∂∂∂∂ 4.如图，求球面22224a z y x =++与圆柱面ax y x 222=+（0>a ）所围的几何体的体积.5.求微分方程023=+'+''y y y 的通解. 四.应用题（10分⨯2） 1.试用二重积分计算由x y x y 2,==和4=x 所围图形的面积.2.如图，以初速度0v 将质点铅直上抛，不计阻力，求质点的运动规律().t x x =（提示：g dt x d -=22.当0=t 时，有0x x =，0v dtdx=）《高等数学》试卷3（下）一、选择题（本题共10小题，每题3分，共30分） 1、二阶行列式 2 -3 的值为（）4 5A 、10B 、20C 、24D 、222、设a=i+2j-k,b=2j+3k ，则a 与b 的向量积为（） A 、i-j+2k B 、8i-j+2k C 、8i-3j+2k D 、8i-3i+k3、点P （-1、-2、1）到平面x+2y-2z-5=0的距离为（） A 、2 B 、3 C 、4 D 、54、函数z=xsiny 在点（1，4π）处的两个偏导数分别为（） A 、,22 ,22 B 、,2222- C 、22- 22- D 、22- ,22 5、设x 2+y 2+z 2=2Rx ，则yzx z ∂∂∂∂,分别为（） A 、z y z R x --, B 、z y z R x ---, C 、zyz R x ,-- D 、zyz R x ,- 6、设圆心在原点，半径为R ，面密度为22y x +=μ的薄板的质量为（）（面积A=2R π）A 、R 2AB 、2R 2AC 、3R 2AD 、A R 2217、级数∑∞=-1)1(n nnn x 的收敛半径为（）A 、2B 、21C 、1D 、3 8、cosx 的麦克劳林级数为（）A 、∑∞=-0)1(n n)!2(2n x n B 、∑∞=-1)1(n n )!2(2n x n C 、∑∞=-0)1(n n )!2(2n x n D 、∑∞=-0)1(n n)!12(12--n x n9、微分方程(y``)4+(y`)5+y`+2=0的阶数是（） A 、一阶 B 、二阶 C 、三阶 D 、四阶 10、微分方程y``+3y`+2y=0的特征根为（） A 、-2，-1 B 、2，1 C 、-2，1 D 、1，-2 二、填空题（本题共5小题，每题4分，共20分） 1、直线L 1：x=y=z 与直线L 2：的夹角为z y x =-+=-1321___________。

大一下学期高等数学期末试题及答案__数套

高等数学（下）试卷一一、填空题（每空3分，共15分）（1）函数z =的定义域为（2）已知函数arctanyz x =，则z x ∂=∂（3）交换积分次序，2220(,)y y dy f x y dx⎰⎰＝（4）已知L 是连接(0,1),(1,0)两点的直线段，则()L x y ds +=⎰（5）已知微分方程230y y y '''+-=，则其通解为二、选择题（每空3分，共15分）（1）设直线L 为321021030x y z x y z +++=⎧⎨--+=⎩，平面π为4220x y z -+-=，则（）A. L 平行于πB. L 在π上C. L 垂直于πD. L 与π斜交（2）设是由方程xyz =(1,0,1)-处的dz =（）A.dx dy +B.dxD.dx （3）已知Ω是由曲面222425()z x y =+及平面5z =所围成的闭区域，将22()x y dv Ω+⎰⎰⎰在柱面坐标系下化成三次积分为（） A.22530d r dr dzπθ⎰⎰⎰ B.24530d r dr dzπθ⎰⎰⎰ C.2253502rd r dr dzπθ⎰⎰⎰ D.2252d r dr dzπθ⎰⎰⎰（4）已知幂级数12nnn n x ∞=∑，则其收敛半径（）A. 2B. 1C. 12D. （5）微分方程3232x y y y x e '''-+=-的特解y *的形式为y *=（）A.B.()x ax b xe +C.()xax b ce ++D.()xax b cxe ++三、计算题（每题8分，共48分）1、求过直线1L :123101x y z ---==-且平行于直线2L ：21211x y z +-==的平面方程 2、已知22(,)z f xy x y =，求zx ∂∂， z y ∂∂3、设22{(,)4}D x y x y =+≤，利用极坐标求2Dx dxdy ⎰⎰4、求函数22(,)(2)x f x y e x y y =++的极值5、计算曲线积分2(23sin )()y L xy x dx x e dy ++-⎰，其中L 为摆线sin 1cos x t t y t =-⎧⎨=-⎩从点(0,0)O 到(,2)A π的一段弧6、求微分方程 x xy y xe '+=满足 11x y ==的特解四.解答题（共22分）1、利用高斯公式计算22xzdydz yzdzdx z dxdy ∑+-⎰⎰，其中∑由圆锥面z =与上半球面z =所围成的立体表面的外侧 (10)'2、（1）判别级数111(1)3n n n n ∞--=-∑的敛散性，若收敛，判别是绝对收敛还是条件收敛；（6'）（2）在(1,1)x ∈-求幂级数1nn nx∞=∑的和函数（6'）高等数学（下）试卷二一．填空题（每空3分，共15分）（1）函数z =的定义域为；（2）已知函数xyz e =，则在(2,1)处的全微分dz = ；（3）交换积分次序，ln 1(,)e x dx f x y dy⎰⎰＝；（4）已知L 是抛物线2y x =上点(0,0)O 与点(1,1)B 之间的一段弧，则=⎰；（5）已知微分方程20y y y '''-+=，则其通解为 . 二．选择题（每空3分，共15分）（1）设直线L 为300x y z x y z ++=⎧⎨--=⎩，平面π为10x y z --+=，则L 与π的夹角为（）；A. 0B. 2πC. 3πD. 4π（2）设(,)z f x y =是由方程333z xyz a -=确定，则z x ∂=∂（）； A. 2yz xy z - B. 2yz z xy - C. 2xz xy z - D. 2xy z xy -（3）微分方程256x y y y xe '''-+=的特解y *的形式为y *=（）；A.2()x ax b e +B.2()x ax b xe +C.2()x ax b ce ++D.2()xax b cxe ++ （4）已知Ω是由球面2222x y z a ++=所围成的闭区域, 将dvΩ⎰⎰⎰在球面坐标系下化成三次积分为（）； A222sin ad d r drππθϕϕ⎰⎰⎰ B.220ad d rdrππθϕ⎰⎰⎰C.20ad d rdrππθϕ⎰⎰⎰ D.220sin a d d r drππθϕϕ⎰⎰⎰（5）已知幂级数1212nnn n x ∞=-∑，则其收敛半径（）.2 B.1 C. 12 D.三．计算题（每题8分，共48分）5、求过(0,2,4)A 且与两平面1:21x z π+=和2:32y z π-=平行的直线方程 .6、已知(sin cos ,)x yz f x y e +=，求zx ∂∂， z y ∂∂ . 7、设22{(,)1,0}D x y x y y x =+≤≤≤，利用极坐标计算arctanDydxdy x ⎰⎰ .8、求函数22(,)56106f x y x y x y =+-++的极值. 9、利用格林公式计算(sin 2)(cos 2)x x Le y y dx e y dy -+-⎰，其中L 为沿上半圆周222(),0x a y a y -+=≥、从(2,0)A a 到(0,0)O 的弧段. 6、求微分方程 32(1)1y y x x '-=++的通解.四．解答题（共22分）1、（1）（6'）判别级数11(1)2sin3n n n n π∞-=-∑的敛散性，若收敛，判别是绝对收敛还是条件收敛；（2）（4'）在区间(1,1)-内求幂级数1nn x n ∞=∑的和函数 .2、(12)'利用高斯公式计算2xdydz ydzdx zdxdy∑++⎰⎰，∑为抛物面22z x y =+(01)z ≤≤的下侧高等数学（下）模拟试卷三一．填空题（每空3分，共15分）1、函数arcsin(3)y x =-的定义域为 .2、22(2)lim 332n n n n →∞++-= .3、已知2ln(1)y x =+，在1x =处的微分dy = . 4、定积分1200621(sin )x x x dx -+=⎰.5、求由方程57230y y x x +--=所确定的隐函数的导数dydx =.二．选择题（每空3分，共15分）1、2x =是函数22132x y x x -=-+的间断点（A ）可去（B ）跳跃（C ）无穷（D ）振荡2、积分10⎰= .(A) ∞ (B)-∞(C) 0 (D) 13、函数1xy e x =-+在(,0]-∞内的单调性是。

高数期中练习题

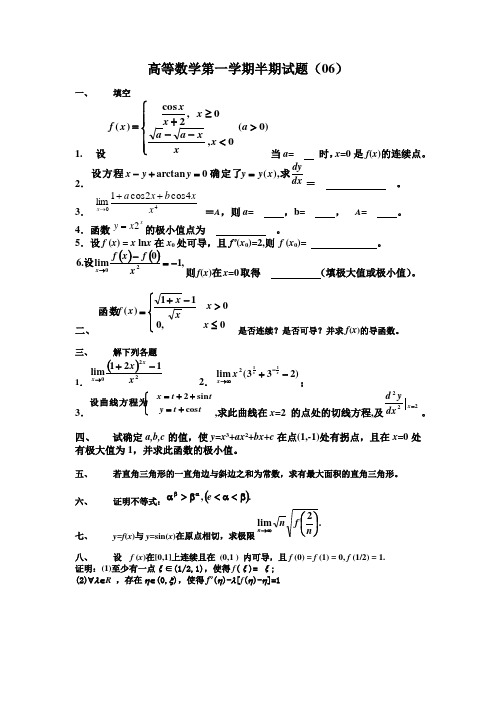
一、填空1. 设当a= 时，x =0是f (x )的连续点。

2．＝。

3．＝A ，则a= ，b = ， A = 。

4．函数的极小值点为。

5．设f (x ) = x ln x 在x 0处可导，且f’(x 0)=2,则 f (x 0)= 。

则f (x )在x =0取得（填极大值或极小值）。

二、是否连续？是否可导？并求f (x )的导函数。

三、解下列各题1．2．；3．,求此曲线在x =2 的点处的切线方程,及。

四、试确定a,b,c 的值，使y =x 3+ax 2+bx +c 在点(1,-1)处有拐点，且在x =0处有极大值为1，并求此函数的极小值。

五、若直角三角形的一直角边与斜边之和为常数，求有最大面积的直角三角形。

六、证明不等式：七、 y =f (x )与y =sin(x )在原点相切，求极限八、设 f (x )在[0,1]上连续且在 (0,1 ) 内可导，且f (0) = f (1) = 0, f (1/2) = 1. 证明：(1)至少有一点ξ∈(1/2,1)，使得f (ξ)= ξ; (2)∀λ∈R ，存在η∈(0,ξ)，使得f’(η)-λ[f (η)-η]=1)0(0,0,2cos )(>⎪⎪⎩⎪⎪⎨⎧<--≥+=a x x x a a x x xx f dx dyx y y y y x 求确定了设方程),(0arctan ==+-404cos 2cos 1limx xb x a x ++→xx y 2=()(),10lim .620-=-→x f x f x 设⎪⎩⎪⎨⎧≤>-+=0,0011)(x x xx x f 函数()220121limx x xx -+→)233(lim 112-+-∞→xx x x ⎩⎨⎧+=++=tt y tt x cos sin 2设曲线方程为222=x dxy d ().,β<α<β>ααβe .2lim ⎪⎭⎫⎝⎛∞→n f n n一、填空1. 设当a= 时，x =0是f (x )的连续点。

高等数学同济版下册期末考四套试题及答案

高等数学同济版（下册）期末考试试卷（一）一、填空题（每小题3分，共计24分)1、=的定义域为D= .2、二重积分的符号为。

3、由曲线及直线，所围图形的面积用二重积分表示为，其值为.4、设曲线L的参数方程表示为则弧长元素。

5、设曲面∑为介于及间的部分的外侧，则 .6、微分方程的通解为 .7、方程的通解为。

8、级数的和为。

二、选择题（每小题2分，共计16分)1、二元函数在处可微的充分条件是（）（A）在处连续；（B），在的某邻域内存在；(C）当时,是无穷小;（D)。

2、设其中具有二阶连续导数，则等于（）（A）; （B）；(C）; （D)0 。

3、设：则三重积分等于（）（A)4；（B）；（C）;（D）。

4、球面与柱面所围成的立体体积V=（）（A）；（B);(C)；（D）。

5、设有界闭区域D由分段光滑曲线L所围成，L取正向，函数在D上具有一阶连续偏导数，则（A）; （B）；（C）；（D）。

6、下列说法中错误的是（）（A）方程是三阶微分方程；（B）方程是一阶微分方程;（C）方程是全微分方程；（D）方程是伯努利方程。

7、已知曲线经过原点,且在原点处的切线与直线平行，而满足微分方程，则曲线的方程为（）（A）；（B)；(C)；(D)。

8、设, 则( ）（A）收敛; （B）发散；（C）不一定；（D）绝对收敛。

三、求解下列问题（共计15分）1、（7分）设均为连续可微函数.，求.2、(8分）设，求。

四、求解下列问题（共计15分)。

1、计算。

（7分）2、计算,其中是由所围成的空间闭区域（8分)五、(13分）计算，其中L是面上的任一条无重点且分段光滑不经过原点的封闭曲线的逆时针方向.六、(9分）设对任意满足方程，且存在,求。

七、（8分）求级数的收敛区间.高等数学同济版（下册）期末考试试卷（二）1、设，则。

2、。

3、设，交换积分次序后，。

4、设为可微函数，且则。

5、设L为取正向的圆周,则曲线积分。

6、设，则。

7、通解为的微分方程是。

高等数学基础(19秋)形考作业4

高等数学基础（19秋）形考作业4
1、
A 1,2
B 1,-1
C
D
我的得分：10分
我的答案：C
2、
我的得分：10分
我的答案：C
3、
A
B
C
D
我的得分：10分我的答案：D
4、
A ∞
B -∞
C 0
D
我的得分：10分我的答案：D
5、
A
B
C
D
我的得分：10分
我的答案：A
6、下列命题正确的是（）
A 驻点一定是极值点
B 极值点一定是驻点
C 可导的极值点一定是驻点
D 不可导点一定不是极值点我的得分：10分
我的答案：C
7
A
B
C
D
我的得分：10分
我的答案：B
8、
A 与Δx 是等价的无穷小
B 与Δx 是同阶的无穷小
C 比Δx 低阶的无穷小
D 比Δx 高阶的无穷小
我的得分：10分
我的答案：C
9、
A 高阶无穷小
B 同阶无穷小，但不等价
C 低阶无穷小
D 等价无穷小
我的得分：10分我的答案：A
10、
A 1
B 2
C 3
D 4
我的得分：10分我的答案：C。

自考公共课考试：2022 高等数学(一)真题及答案(4)

自考公共课考试：2022 高等数学（一）真题及答案(4)共68道题1、极限=（单选题）A. 0B. 1C. eD. +∞试题答案：B2、函数y=x5+1在定义域内：（单选题）A. 单调增加B. 单调减少C. 不增不减D. 有增有减试题答案：A3、极限=（单选题）A. 0B. 1C. eD. +∞试题答案：B4、下列无穷限反常积分收敛的是:（单选题）A.B.C.D.试题答案：A5、方程x²+x-6=0的根是：（单选题）A. x=-2, x=3B. x=2, x=-3C. x=2, x=3D. x=-2, x=-3试题答案：B6、（单选题）A. AB. BC. CD. D试题答案：C7、设函数f(x)在区间[a,b]上可导，且f＇(x)<0,>0,则在[a,b]上: （单选题）A. f(x)>0B. f(x)<0C. f(x)=0D. f(x)的值有正有负试题答案：A8、若f＇(x)=x1/2，则f(x)=（单选题）A. 2/3x2/3+CB. 3/2x2/3+CC. 2/3x3/2+CD. 3/2x3/2+C试题答案：C9、已知x=0是函数y=asinx＋1/3sin3x的驻点，则常数a= （单选题）A. -2B. -1C. 0D. 1试题答案：B10、不定积分∫(x2cosx)＇dx= （单选题）A. 2xcosx-x2sinx+C B. 2xcosx-x2sinx C. x2cosx+C D. x2cosx 试题答案：C11、曲线y=xe x+1在点(0,1)处的切线方程为（单选题）A. y=1B. y=xC. y=x+1D. y=x-1试题答案：C12、函数y=2x2 -4x +1的单调增加区间是: （单选题）A. (-∞,-1]B. (-∞,1]C. [-1,+∞)D. [1,+∞)试题答案：D13、若f＇(x)=x1/2，则f(x)=（单选题）A. 2/3x2/3+CB. 3/2x2/3+CC. 2/3x3/2+CD. 3/2x3/2+C试题答案：C14、微分方程sinxdx+cosydy=0的通解为：（单选题）A. cosy+sinx=CB. cosy-sinx=CC. siny+cosx=CD. siny-cosx=C试题答案：D15、微分方程2ydy-dx=0的通解为：（单选题）A.B.C. y²=-x+CD. y²=x+C试题答案：D16、不定积分∫(x2cosx)＇dx= （单选题）A. 2xcosx-x2sinx+C B. 2xcosx-x2sinx C. x2cosx+C D. x2cosx 试题答案：C17、某产品的成本函数C(Q)=20+2Q+1/2Q²，则Q=298时的边际成本为: （单选题）A. 100B. 200C. 300D. 400试题答案：C18、设函数f(x)在区间[a,b]上连续，则下列等式正确的是:（单选题）A.B.C.D.试题答案：A19、设函数f(x)=x2，g(x)=tanx，则当x→0时，（单选题）A. f(x)是比g(x)高阶的无穷小量B. f(x)是比g(x)低阶的无穷小量C. f(x)是比g(x)是同阶无穷小量，但不是等价无穷小量D. f(x)是比g(x)是等价无穷小量试题答案：A20、设∫f(x)dx=sin2x+C,则f(0)= （单选题）A. 2B. 1/2C. -1/2D. -2试题答案：A21、函数的定义域是：（单选题）A. (-∞,-1]B. [1,+∞)C. [-1,1]D. (-∞,-1]U[1,+∞)试题答案：D22、若曲线y=x-e x在点(x0,y0)处的切线斜率为0,则切点(x0,y0)是：（单选题）A. (1,1-e)B. (-1,-1-e-1) C. (0,1)D. (0,-1)试题答案：D23、（单选题）A. AB. BC. CD. D试题答案：A24、若极限，则常数k=（单选题）A. 1B. 2C. 3D. 4试题答案：B25、曲线y=xe x+1在点(0,1)处的切线方程为（单选题）A. y=1B. y=xC. y=x+1D. y=x-1试题答案：C26、当x→0时，下列变量中与tan(x2)等价的无穷小量是：（单选题）A. xB. 2xC. x2D. 2x2 试题答案：C27、微分方程sinxdx+cosydy=0的通解为：（单选题）A. cosy+sinx=CB. cosy-sinx=CC. siny+cosx=CD. siny-cosx=C试题答案：D28、设∫f(x)dx=sin2x+C,则f(0)= （单选题）A. 2B. 1/2C. -1/2D. -2试题答案：A29、某产品的成本函数C(Q)=20+2Q+1/2Q²，则Q=298时的边际成本为: （单选题）A. 100B. 200C. 300D. 400试题答案：C30、（单选题）A. AB. BC. CD. D试题答案：A31、微分方程2ydy-dx=0的通解为：（单选题）A.B.C. y²=-x+CD. y²=x+C试题答案：D32、下列函数中为奇函数的是：（单选题）A. (1+x²)/(1-x²)B. sin(x²)C. (ex-e-x)/2D. |x|试题答案：C33、下列各式中正确的是：（单选题）A.B.C.D.试题答案：D34、函数y=2x+1的反函数是：（单选题）A. y=x/2+1/2B. y=x/2-1/2C. y=x/2+1D. y=x/2-1试题答案：B35、设函数f(x,y)=y1nx+x2,则¶f/¶x|(2,-2)= （单选题）A. 0B. 1C. 2D. 3试题答案：D36、设函数z=ln(x+y2), 则全微分dz= （单选题）A. 1/(x+y2) (dx+2ydy)B. 1/(x+y2) (2dx+dy)C. 1/(x+y2) (2xdx+dy)D. 1/(x+y2) (dx+2dy)试题答案：A37、设函数z=sin(2x+3y)，则全微分dz|(0,0)= （单选题）A. dx+dyB. 2dx+2dyC. 3dx+2dyD. 2dx+3dy试题答案：D38、（单选题）A. AB. BC. CD. D试题答案：B39、当x→0时，下列变量中与tan(x2)等价的无穷小量是：（单选题）A. xB. 2xC. x2D. 2x2 试题答案：C40、若极限，则常数k=（单选题）A. 1B. 2C. 3D. 4试题答案：B41、函数y=(x-2)/(x2-3x+2)的间断点是: （单选题）A. x=1,x=-2B. x=-1,x=2C. x=-1,x=-2D. x=1,x=2试题答案：D42、函数的定义域是：（单选题）A. (-∞,-1]B. [1,+∞)C. [-1,1]D. (-∞,-1]U[1,+∞)试题答案：D43、函数y=x5+1在定义域内：（单选题）A. 单调增加B. 单调减少C. 不增不减D. 有增有减试题答案：A44、（单选题）A. AB. BC. CD. D试题答案：B45、设函数z=ln(x+y2), 则全微分dz= （单选题）A. 1/(x+y2) (dx+2ydy)B. 1/(x+y2) (2dx+dy)C. 1/(x+y2) (2xdx+dy)D. 1/(x+y2) (dx+2dy)试题答案：A46、函数y=2x2 -4x +1的单调增加区间是: （单选题）A. (-∞,-1]B. (-∞,1]C. [-1,+∞)D. [1,+∞)试题答案：D47、函数y=(x-2)/(x2-3x+2)的间断点是: （单选题）A. x=1,x=-2B. x=-1,x=2C. x=-1,x=-2D. x=1,x=2试题答案：D48、（单选题）A. AB. BC. CD. D49、设函数f(x)=x2，g(x)=tanx，则当x→0时，（单选题）A. f(x)是比g(x)高阶的无穷小量B. f(x)是比g(x)低阶的无穷小量C. f(x)是比g(x)是同阶无穷小量，但不是等价无穷小量D. f(x)是比g(x)是等价无穷小量试题答案：A50、设函数f(x,y)=y1nx+x2,则¶f/¶x|(2,-2)= （单选题）A. 0B. 1C. 2D. 3试题答案：D51、若曲线y=x-e x在点(x0,y0)处的切线斜率为0,则切点(x0,y0)是：（单选题）A. (1,1-e)B. (-1,-1-e-1) C. (0,1)D. (0,-1)试题答案：D52、方程x²+x-6=0的根是：（单选题）A. x=-2, x=3B. x=2, x=-3C. x=2, x=3D. x=-2, x=-353、（单选题）A. AB. BC. CD. D试题答案：C54、（单选题）A. cos(ax²+b)B. cos(at²+b)C. sin(ax²+b)D. sin(at²+b)试题答案：C55、下列函数中在点x=0处导数不存在的是：（单选题）A. y=sinxB. y=tanxC. y=x1/3D. y=2x试题答案：C56、下列各式中正确的是：（单选题）A.B.C.D.试题答案：D57、已知x=0是函数y=asinx＋1/3sin3x的驻点，则常数a= （单选题）A. -2B. -1C. 0D. 1试题答案：B58、（单选题）A. AB. BC. CD. D试题答案：D59、下列函数中为奇函数的是：（单选题）A. (1+x²)/(1-x²)B. sin(x²)C. (ex-e-x)/2D. |x|试题答案：C60、函数y=2x+1的反函数是：（单选题）A. y=x/2+1/2B. y=x/2-1/2C. y=x/2+1D. y=x/2-1试题答案：B61、设函数f(x)在区间[a,b]上可导，且f＇(x)<0,>0,则在[a,b]上: （单选题）A. f(x)>0B. f(x)<0C. f(x)=0D. f(x)的值有正有负试题答案：A62、设函数y=x2+e2x,则二阶导数y"=2+2e2x（单选题）A. 2+2e2xB. 2+4e2xC. 2x+2e2xD. 2x+4e2x试题答案：B63、下列无穷限反常积分收敛的是:（单选题）A.B.C.试题答案：A64、设函数y=x2+e2x,则二阶导数y"=2+2e2x（单选题）A. 2+2e2xB. 2+4e2xC. 2x+2e2xD. 2x+4e2x试题答案：B65、（单选题）A. cos(ax²+b)B. cos(at²+b)C. sin(ax²+b)D. sin(at²+b)试题答案：C66、设函数z=sin(2x+3y)，则全微分dz|(0,0)= （单选题）A. dx+dyB. 2dx+2dyC. 3dx+2dyD. 2dx+3dy试题答案：D67、设函数f(x)在区间[a,b]上连续，则下列等式正确的是: （单选题）B.C.D.试题答案：A68、下列函数中在点x=0处导数不存在的是：（单选题）A. y=sinxB. y=tanxC. y=x1/3D. y=2x试题答案：C。

高等数学习题答案4

四、导数的应用1. 验证函数()ln sin f x x = 在[π5π,66]上满足罗尔定理的条件，并求出相应的ξ，使()0f ξ'=.解：()lnsin f x x =在⎥⎦⎤⎢⎣⎡65,6ππ上连续，在⎪⎭⎫⎝⎛65,6ππ上可导，且 2ln 656-=⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛ππf f ，显然满足罗尔定理的三个条件. ()x x x f sin cos '=，若令()0'=ξf ，则有2πξ=. 2. 下列函数在指定区间上是否满足罗尔定理的三个条件?有没有满足定理结论中的ξ[]2(1)()1,1,1x f x =--e解：()1)1(1-==-e f f ，且连续、可导，满足罗尔定理中的三个条件. ()22'x xe x f =，若令()0'=ξf ，则有0=ξ.[](2)(),0,21f x x =-解：函数在1=x 点的导数不存在，故不满足罗尔定理的条件.[]sin ,0π(3)()0,π1,0x x f x x <≤⎧=⎨=⎩解：函数在0=x 点不连续，故不满足罗尔定理的条件.3. 不用求出函数()(1)(2)(3)f x x x x =---的导数，说明方程()0f x '=有几个实根，并指出它们所在的区间.解：0)2()1(==f f ，根据罗尔定理知：存在)2,1(1∈ξ，使得0)('1=ξf ;同理0)3()2(==f f ，根据罗尔定理知：存在)3,2(2∈ξ，使得0)('2=ξf ; 又由于)('x f 是二次方程，最多只有两个不相等的实根，故0)('=x f 的两个实根分别为)2,1(1∈ξ，)3,2(2∈ξ.4. 验证拉格朗日中值定理对函数3()2f x x x =+在区间[0,1]上的正确性. 解：割线的斜率301)0()1(=--=f f k ，23)('2+=x x f ，若令()3'=ξf ，则有33=ξ. 5. 已知函数()f x 在[,]a b 上连续，在(,)a b 内可导，且0)()(==b f a f ,试证：在(,)a b 内至少存在一点ξ，使得()()0,(,)f f a b ξξξ'+=∈证明：构造函数)()(x f e x F x=，显然)(x F 在[,]a b 上连续，在(,)a b 内可导，且0)()(==b F a F ，根据罗尔定理：在(,)a b 内至少存在一点ξ，使得0)('=ξF ，进而得到()()0,(,)f f a b ξξξ'+=∈. 6. 若方程10110n n n a x a x a x --+++=有一个正根0x ,证明方程 12011(1)0n n n a nx a n x a ---+-++=必有一个小于0x 的正根.解：令x a x a x a x f n n n 1110)(--+++= ，方程10110n n n a x a x a x --+++=有正根0x ，即0)(0=x f ，同时0)0(=f ，得到)0()(0f x f =，根据罗尔定理，存在),0(0x ∈ξ，使得0)('=ξf ，即12011(1)0n n n a nx a n x a ---+-++=必有一个小于0x 的正根.7. 设()()()f a f c f b ==,且a c b <<,()f x ''在[],a b 上存在，证明在(),a b 内至少存在一点ξ，使()0f ξ''=解：)()(c f a f =，根据罗尔定理：存在),(1c a ∈ξ，使得0)('1=ξf ;)()(c f b f =，根据罗尔定理：存在),(2b c ∈ξ，使得0)('2=ξf ;由)("x f 在],[b a 上存在，得到)('x f 在],[b a 上连续且可导，又0)(')('21==ξξf f ，根据罗尔定理知：存在),(21ξξξ∈，使得0)("=ξf . 8. 利用洛必达法则求下列极限. (1) sin3limtan5x xx π→53-= (2) 0e 1lim (e 1)x x x x x →---21=(3) lim m m n n x a x a x a →--nm a nm -=(4)0lim sin ln x x x +→ 0= (5) 0e 1lim()e 1x x x x →--23=(6) 1lim(1sin )xx x →+e =(7) 2lim (arctan )πx x x →+∞π2-=e(8)2120lim e x x x → +∞→(9) lim )x x →+∞31=(10) 1101lim (1)e xxx x →⎡⎤+⎢⎥⎣⎦21-=e921lim1x x mx nx →++-=5,求常数m ,n解：由5212lim 1lim121=+=+=-++→→m mx x n mx x x x ，得到3=m ; 由01lim 21=++=++→n m n mx x x ，得到4-=n .10．设f (x )具有二阶连续导数，且f (0)=0,试证g (x )= (),0'(0),0f x x x f x ⎧≠⎪⎨⎪=⎩解：当0≠x 时，2)()(')('x x f x x f x g -=，显然)('x g 连续; 当0=x 时，)0("212)0(')('lim )0(')(lim )0('00f x f x f x f x x f g x x 导数定义洛必达法则=-=-=→→;)0("212)("lim 2)(')(')("lim )()('lim )('lim 00200f x f x x f x f x x f xx f x x f x g x x x x ==-+=-=→→→→ )('x g 在0=x 点的函数值和极限值相等，故在0=x 点也连续;综上得到)(x g 可导，且导函数连续.11．求下面函数的单调区间与极值(1)32()26187f x x x x =---解：单调增区间为)1,(--∞，),3(+∞; 单调减区间为)3,1(-;(2)()ln f x x x=-解：单调增区间为),1(+∞; 单调减区间为)1,0(;12. 试证方程x x =sin 只有一个根.解：构造函数x x x f -=sin )(，显然)(x f 连续.0212>+-=⎪⎭⎫⎝⎛-ππf ，0212<-=⎪⎭⎫⎝⎛ππf因此022<⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛-ππf f ，根据零点定理：存在⎪⎭⎫⎝⎛-∈2,2ππξ，使得0)(=ξf . 又01cos )('≤-=x x f ，)('x f 只在一些孤立点上的值为0，因此)(x f 严格单调递减，只能存在唯一的一个根.13. 已知()([0,))f x C ∈+∞，若f (0) = 0, f ′(x )在[0,)+∞内存在且单调增加，证明()f x x在[0,)+∞内也单调增加.解：令xx f x F )()(=，则 22)]0()([)(')()(')('xf x f x x f x x f x x f x F --=-= x f x f xx f x x f )(')(')(')('2ξξ-=-=柯西中值定理，其中()x ,0∈ξ 由于函数)('x f 在],0[+∞单调递增，故0)('>x F ，即)(x F 单调增加. 14.证明下列不等式(1) 1+12x x ＞0；解：构造函数x xx f +-+=121)(0,012121)('>>+-=x xx f ，即函数)(x f 单调增加，且0)0(=f ，则 0,0)(>>x x f 时恒成立，即证.(2) x -22x ＜ln (1+x )＜x , x ＞解：构造函数)1ln()(x x x f +-=构造函数⎪⎪⎭⎫⎝⎛--+=2)1ln()(2x x x x g15. 试问a 为何值时，1()sin sin 33f x a x x =+在3x π=处取得极值?是极大值还是极小值?并求出此极值.解：x x a x f 3cos cos )('+=，令03'=⎪⎭⎫⎝⎛πf ，则2=a ; 033"<-=⎪⎭⎫⎝⎛πf ，该点是极大点. 16.讨论下列函数的凸性，并求曲线的拐点： (1)23y x x =- 解：062"=-=x y ，31=x 当⎪⎭⎫ ⎝⎛∞-∈31,x 时，0">y ，函数下凸;当⎪⎭⎫ ⎝⎛+∞∈,31x 时，0"<y ，函数上凸;拐点为⎪⎭⎫⎝⎛272,31.(2) 2ln(1)y x =+ 解： (3) =e xy x解：17.利用函数的凸性证明下列不等式：(1) e e 2x y+＞2e x y+， x ≠y解：构造函数x e x f =)(，0)(">=xe xf ，得到函数)(x f 下凸;根据下凸的定义有：2)()(2y f x f y x f +<⎪⎭⎫⎝⎛+，即22yx y x e e e+<+.(2) x ln x +y ln y ＞(x +y )ln 2x y +,x ＞0,y ＞0,x ≠y解：构造函数x x x f ln )(=18．当a ，b 为何值时，点(1，3)为曲线y =a 3x +b 2x 的拐点．解：23-=a ，29=b复习题四一、填空1．设2)(x x f =，则在x x x ∆+,之间满足拉格朗日中值定理结论的=ξ2xx ∆+. 2．设函数)(x g 在],[b a 上连续，),(b a 内可导，则至少存在一点),(b a ∈ξ，使=-)()(a g b g e e))((')(a b g e g -ξξ 成立．3．)0,0()(≥>=-x n e x x f xn的单增区间是),0(n ，单减区间是),(+∞n . 4．若点)34,1(为曲线b x ax y +-=23为拐点，则 a =31，=b 32． 5．曲线11+-=x x y 的水平渐近线为1=y ，铅垂渐近线为1-=x ．二、选择1．函数)(x f y =具有下列特征：,0)0(',1)0(==f f 当0≠x 时，0)('>x f⎩⎨⎧>><<=0,00,0)(''x x x f ，则其图形为 B（A ）（B ）（C ）（D ）2．设)(x f 在],[b a 上连续，)()(b f a f =，且)(x f 不恒为常数，则在),(b a 内 A（A ）必有最大值或最小值（B ）既有极大值又有极小值（C ）既有最大值又有最小值（D ）至少存在一点ξ，使0)('=ξf三．求极限.)1ln()21(lim2210x x e xx ++-→ 解：洛必达法则得到极限为1. 四．证明：当20π<<x 时，有x x x 3sin 2tan >+成立．解：x x x x f 3sin 2tan )(-+=，3cos 2sec )('2-+=x x x f20,0cos cos 1sin 2sin 2tan sec 2)("332π<<>-=-=x xx x x x x x f ，故有)('x f 单调递增，0)0('=f ，得到0)('>x f ，函数)(x f 单调递增且0)0(=f ，得到0)(>x f ，即证. 五. 设,],,[)(b d c a b a C x f <<<∈且证明],,[b a ∈∃ξ 使).()()()(d f c f f βαξβα+=+解：设函数)(x f 在],[b a 上的最小值和最大值分别为)(min x f 和)(max x f ，不妨设)()(d f c f ≤，则有)(max )()()(min x f d f c f x f ≤≤≤，)(m in )()()()()(x f c f c f c f d f c f ≥=+++≥+++βαββααβαββαα)(m ax )()()()()(x f d f d f d f d f c f ≤=+++≤+++βαββααβαββαα根据介值定理，],[b a ∈∃ξ，使得)()()(d f c f f βαββααξ+++=.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

模拟四
一填空题（24分）
（1）设f(x)=⎩
⎨⎧-++3)1(2arctan 92sin x b x ae x x
，00≥<x x 在x=0处可导，则a=_________,b=__________。

（2） ∞→n lim ⎰+1
021x x n
dx=___________________。

（3）方程xy ’’+y ’=4x 的通解为y=______________。

（4）设f(x)为连续函数，且x 2+y 2+z 2=⎰-+y
x dt t y x f )(，则)(y
z x z z ∂∂+∂∂＝________________。

（5）设n 阶方阵A 、B 相似，A 2＝2E ，则行列式|AB+A －B －E|＝__________________。

（6）线性方程组⎪⎩
⎪⎨⎧=++=-+=++,0,02,022z y x z y x z y x λλλλ的系数矩阵为A ，若存在一个三阶方阵B ≠0，使得AB ＝0，
则λ＝_________。

二．选择题（32）
（7）设f(x)=⎰-x
dt x t 02)arctan(，g(x)=⎰+x dt t t t sin 032)cos 3(，
当x 0→ 时，f(x)是 g(x)的 A 高阶无穷小 B 低阶无穷小 C 等价无穷小 D 同阶而非等价无穷小
（8）下列结论正确的是：
A 若)(x u ϕ=在x 0处可导，而y=f(u)在u 0=)0x （ϕ处不可导，则复合函数y=f[)(x ϕ] 在x 0处一定不可导。

B 若)(x u ϕ=在x 0处不可导，而y=f(u)在u 0=)0x （ϕ处可导，则复合函数y=f[)(x ϕ] 在x 0处一定不可导。

C 若)(x u ϕ=在x 0处可导，而y=f(u)在u 0=)0x （ϕ处可导，则复合函数y=f[)(x ϕ] 在x 0处一定可导。

D 若)(x u ϕ=在x 0处不可导，而y=f(u)在u 0=)0x （ϕ处不可导，则复合函数y=f[)(x ϕ] 在x 0处一定不可导。

（9）设f(x)是以T 为周期的可微函数，则在下列函数中以T 为周期的函数是：
A ⎰x
dt t f 0)( B ⎰x dt t f 02)( C ⎰x dt t f 02')]([ D ⎰x dt t f t f 0')()(
（10）设函数f(x)在x=x 0的某邻域内连续，在x=x 0 处可导，则函数f(x)|f(x)|在x=x 0处
A 可导，且导数为2)()(0'0x f x f
B 可导，且导数为2|)(|)(0'0x f x f
C 可导，且导数为2)(|)(|0'0x f x f
D 可导，且导数为2|)()(|0'0x f x f
(11) 设y(x)是二阶常系数微分方程y ’’+py ’+qy=sin2x+2e x 满足初始条件y(0)=y ’(0)=0的特解，则当x 0→时，函数
2))(1ln(x
x y +的极限 A 不存在 B 等于0 C 等于1 D 不能确定
（12）设函数f(x)有n 阶导数，且有2n 个极值点（n 为正整数），则方程f (n)(x)=0至少有
A n-1个实根
B n 个实根
C n+1 个实根
D n+2个实根
（13）
⎰⎰⎰⎰≤+-=11010222),(4),(y x x dy y x f dx dxdy y x f ，在下列哪种情况下成立：
A f(-x,y)=-f(x,y)
B f(-x,y)=f(x,y)
C f(-x,-y)=f(x,y)
D f(-x,y)=f(x,y)且f(x,-y)=f(x,y)
(14) 设A 为m ×n 矩阵，且r(A)＝m<n 。

则下列命题中不正确的是：
A A T x=0只有零解
B A T Ax=0有无穷多解
C b x A b T =∀,有唯一解
D b Ax b =∀,有无穷多解
三、解答题：
（15）设函数y ＝y （x ）由方程组⎩⎨⎧=+-++=0
1sin 3232y t e t t x y 所确定，试求022|=t dx y d 。

（16）（10分）已知当x 0→时，x －(a+be 2x )sinx 是x 的5阶无穷小，求常数a 和b 的值。

（17）（12分）在盛满水的圆锥形容器中放入一个铁球，使铁球与容器的壁相切。

已知该容器的上底半径为R=33，
高为h=9，问：当铁球的半径r 多大时，溢出的水最多？
（18） (10分)设函数)(x f 在[0,1]上可导，且)0(f =0，0<)('x f <1，证明：21
0])([⎰dx x f >⎰1
03)(dx x f 。

（19） (12分) 有一在原点处与x 轴相切并在第一象限的光滑曲线，P(x,y)为曲线上的任一点。

设曲线在原点与P 点之
间的弧长为S 1，曲线在P 点处的切线在P 点与切线跟y 轴的交点之间的长度为S 2，且
2
123S S +=x x )1(2+，求该曲线的方程。

（20） (10分)设)(u f 有连续的二阶导数且)sin (y e f z x
=满足方程z e y z x z x 22222=∂∂+∂∂，求)(u f 。

（21） (12分)
（1）设)()()('h x hf x f h x f θ++=+,(10<<θ),)("x f 连续，且)("x f 0≠，求0
lim →h θ。

（2）设)(!)()()()('
h x f n h x hf x f h x f n n
θ++++=+ ，10<<θ，)()1(x f n +存在，且)()1(x f n +0≠，求0
lim →h θ。

(22) (9分)设n 阶方阵A 的列向量为),,2,1(n i i =α。

n 阶方阵B 的列向量为21αα+，32αα+, ,n n αα+-1，1αα+n ，试问：当r(A)=n 时，方程组Bx=0是否有非零解？证明你的结论。

(23)(9分)设A 、B 为两个n 阶矩阵，已知：（1）A 有n 个互异的特征向量。

（2）A 的特征向量也是B 的特征向量。

求证：AB ＝BA 。