实验2
实验二实验报告

C语言程序设计报告二数据类型,运算符和简单的输入输出计算机学院软件工程2班王莹0411402011,实验目的(1)掌握C语言数据类型,了解字符型数据和整型数据的内在关系。
(2)掌握对各种数值型数据的正确输入方法。
(3)学会使用C语言的有关算数运算符,移机包含这些运算符的表达式,特别是自加(++)和自减(--)运算符的使用。
(4)学会编写和运行简单的应用程序。
(5)进一步熟悉C程序的编辑、编译、连接和运行的过程。
2,实验内容和步骤(1)输入并运行教材第3章第4题给出的程序。
○1运行以上程序,分析为什么会输出这些信息。
因为第6行是将c1,c2按%c的格式输出,97是字符a的AS CⅡ代码,98是字符b的AS CⅡ代码。
第7行是将c1,c2按5d的格式输出,所以输出两个十进制整数。
○2如果将程序第4,5行改为c1=197;c2=198;运行时会输出由于Visual C++6.0字符型数据是作为signed char类型处理,它存字符的有效范围为0~127,超出此范围的处理方法,不痛的系统得到的结果不痛,因而用“%d”格式输出,结果是不可预期的。
用“%d”格式输出时,输出c1=-59,c2=-58.这是按补码形式输出的,内存字节中第1位为1时,作为负数。
59和197之和等于256,58与198之和也等于256.○3如果将程序第3行改为int c1,c2;运行时会输出因为97和98在int类型的有效范围。
(2)输入第3章第5题得程序。
即:用下面的scanf函数输入数据,使a=3,b=7,x=8.5,y=71.82,c1=’A’,c2=’a’。
运行时分别按一下方式输入数据,观察输出结果,分析原因。
1,a=3,b=7,x=8.5,y=71.82,A,a↙2,a=3 b=7 x=8.5 y=71.82 A a↙3,a=3 b=7 8.5 71.82 A a↙4,a=3 b=7 8.5 71.82Aa↙5,3 7 8.5 71.82Aa↙6,a=3 b=7↙8.571.82↙A↙a↙7,a=3 b=7↙8.571.82↙Aa↙8,a=3 b=7↙8.671.82Aa↙12345678(3)输入以下程序○1编译和运行程序,注意i,j,m,n各变量的值。
实验二实验报告

注:表格空间不够可自行加页.
2.300
(3)保持Rc不变,放大器接入负载RL,在改变RL数值情况下测量并计算,结果填表2.3。
表2.3负载对电压增益的影响
给定参数
实测
实测计算
估算
RL
Vin(mV)
Vout(V)
Au
Au
100K
5.0
11.5m
2.3
2.26
2.2K
5.0
10.9m
2.18
2.0
5.1K
5.0
3.39m
0.678
答:1)静态工作点受所选三极管以及R1,R2,RC,RE,滑动变阻器的影响,除滑动变阻器外值都确定,所以主要受滑动变阻器的影响,调节滑动变阻器使得Ve处在1.9~2.2之间,使得电路处在静态工作点,起放大电路作用。
(2)电压放大倍数与所选三极管和输出电阻(R4,R5,R6)有关。输出电阻越大,电压放大倍数越大。输出电阻越小,电压放大倍数越小,对输出波形影响较小。
三、实验内容
1、实验电路图
2、实验原理
分压式共射极放大电路,其电压增益为:
若发射极Re加入旁路电容,电压增益变为:
3、实验步骤
1.基本电路
按所给电路图进行连接
2.静态分析
设定电路各元件参数,调整滑动变阻器RV2使电路处于放大工作状态(VE=1.9-2.2V左右),通过测量并计算填表2.1。
记录电路各阻值大小:RV2= 30k;R1= 33k;R2= 24k;RE= 2.2k;RC= 5.1k;电源V= +12V。
实验二实验报告

实验二实验报告1. 引言实验二旨在探究某一特定现象或者现象之间的关系,并且通过实验数据和分析来验证或者推论相关理论。
本实验主要目的是研究X现象,并且分析X现象与Y之间的关系。
通过实验结果的观察和数据的统计分析,我们可以深入了解该现象的特点和规律。
2. 实验设计2.1 实验装置本次实验采用了XXXX装置来模拟实验环境,并利用XX测量设备来获取相关数据。
2.2 实验步骤1) 步骤一:准备实验装置,按照实验要求设置相关参数。
2) 步骤二:开启实验装置,记录初始数据。
3) 步骤三:对实验环境进行一定的处理或者改变,观察现象,记录数据。
4) 步骤四:重复步骤三,采集足够的数据。
5) 步骤五:整理数据并进行分析。
3. 实验结果与数据分析通过实验数据的统计和分析,我们得出以下结论:在实验过程中,我们观察到X现象的特征是......通过记录的数据我们可以发现......3.2 结果二对于不同的实验环境参数,我们发现X现象与Y之间存在一定的关联性......通过数据分析,我们可以得出......3.3 结果三进一步的实验数据表明......这与我们之前的推测相符,同时也与X 理论一致......4. 讨论与分析通过实验结果与数据分析,我们可以得出以下结论:4.1 讨论一实验结果验证了X理论,并且揭示了X现象的某些特征......这对于进一步研究和应用X现象具有重要的意义......4.2 讨论二实验中发现的X与Y之间的关联性,给我们提供了一定的启示和思考......进一步探究X与Y之间的机制可以推动相关领域的发展......5. 结论通过实验二的设计与结果分析,我们得出以下结论:实验结果表明X现象在特定条件下具有一定规律性和可重复性,验证了X理论的正确性。
5.2 结论二实验进一步揭示了X与Y之间的关联性,为相关领域的研究和应用提供了参考。
6. 总结本次实验通过设计与实施,详细研究了X现象,并探究了X与Y 之间的关系。
大学计算机实验二实验报告

3) 添加应用程序桌面图标。点击开始,在菜单中点击“所有应用”,找到需要添加的应用, 直接按住该应用并拖到桌面空白处即可
4) 删除桌面图标。在需要删除的桌面图标上单击鼠标右键,在弹出的菜单中选择删除即可
二. 文件管理 1.隐藏文件或文件夹及显示隐藏的文件或文件夹。 1)对着需要隐藏的文件单击右键,在弹出的快捷窗口中单击“属性”。 2)在“常规”选项下找到“属性”单击“隐藏”点击“确定”,选择“将更改应用于此文件夹 、子文件夹和文件”后,点击“确定”即可。
1) 打开“开始”菜单,输入“控制面板”命令打开控制面板,在控制面板内选择“日期和时
间”弹出的对话框内选择“日期和时间选项卡”,更改日期、时间、时区后点击确定即可达 到更改日期、时间、时区的目的。
2) 也可在控制面板内选择“Internet 时间选项卡”,在弹出的对话框内勾选与“Internet 时间服 务器”同步,并且在服务器的下拉列表框中选择第一个选项,点击确定即可
实验过程及内容: 一. 基础操作 1. 设置桌面背景 1) 在桌面的没有桌面图标的区域单击鼠标右键,并在出现的快捷菜单中单点击“个性化”。
2) 单击“背景”。打开“背景”后,可以看见个性化设置背景。
3) 在下方的“最近使用的图像”中任意单击一张图片即可将桌面背景设置为此图片。
注:也可在第三步中点击“浏览照片”并选择自己喜欢的图片做为桌面背景。 2. 调整计算机系统的日期和时间
3. 设置桌面图标 1) 添加文件或文件夹图标。鼠标右键点击需要添加快捷方式的文件,选择“显示更多选项”, 在弹出的菜单中选择“发送到”,在弹出的新菜单中点击“桌面快捷方式”即可。 2) 添加系统图标。在设置中找到“个性化”选修卡,点击“主题”选项,点击“桌面图标设 置”在弹出的对话框内勾选需要的桌面图标点击确定即可完成设置。
实验2参考结果

实验2参考结果1.数据集BWGHT :(1) 做婴儿出生体重和母亲吸烟习惯之间的简单回归为:2ˆ119.08470.561508 (142.24) ( 4.03)0.0242 16.2 656bwghtcigs t R F n =-⋅=-===从结果可以看出,母亲怀孕期间平均每天多吸一颗烟,婴儿出生的体重平均会降低0.56盎司。
(2) 当cigs =0时,婴儿的预测出生体重为119.08盎司,当cigs=20(每天一包)时,婴儿的预测出生体重为107.8545盎司。
可见母亲每天吸一包烟对婴儿出生体重的影响是比较明显的。
(3) 使用所有样本中前一半的观测值进行估计,与前面的结果比较如下:2ˆ119.08470.561508 (0.84) (0.14)0.0242 16.2 656bwght cigs se R F n =-⋅==== 2ˆ119.08470.561508 (1.11) (0.19)0.03 10.11 328bwghtcigs se R F n =-⋅==== 使用前一半数据回归结果显示标准误均高于使用全部观测值得到的结果,这说明随着样本容量的增多,回归的标准误差会降低,这也说明了参数满足一致性和渐进正态分布的性质。
(4) 除了吸烟之外,高收入通常会使母亲得到更好的产前照顾和更好的营养,表达这一点的方程是012min bwght cigs fa c u βββ=+++,考虑2β的符号最可能为正。
(5) 一方面,高的收入会提高食物的消费水平,这样cigs 和faminc 可能存在正的相关关系;而而另一方面,高收入家庭中的母亲一般会具有较高的受教育水平,即应该具有较高的素质,她们会更加了解自己吸烟会危害到孩子的健康,这样可能会控制自己吸烟的数量,因此cigs 和faminc 可能存在负相关关系。
从数据集中样本数据来看,两者的相关系数约为-0.173,因此可以认为两者呈现了一种负相关。
(6) 估计含有cigs 和faminc 作为解释变量的模型,得到:2ˆ115.97840.50220.0996min (73.64) ( 3.55) (2.33)0.03 10.86 656bwghtcigs fa c t R F n =-⋅+⋅=-=== 当加入变量faminc 之后,吸烟对因变量的影响有所降低,但并不是十分明显。
实验2-1-答案
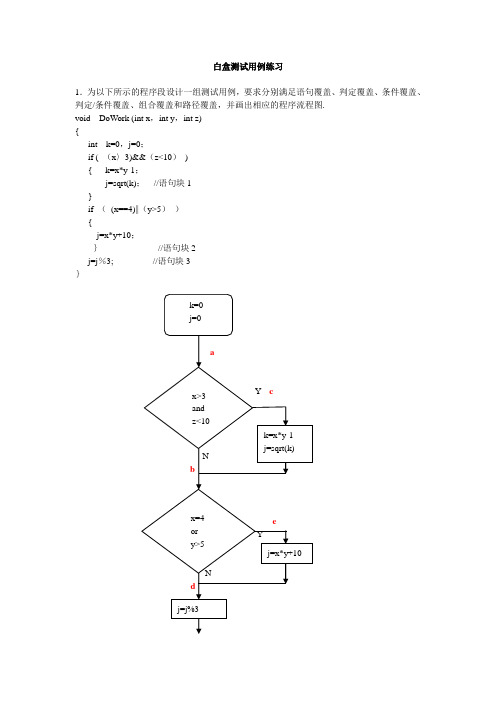
白盒测试用例练习
1.为以下所示的程序段设计一组测试用例,要求分别满足语句覆盖、判定覆盖、条件覆盖、判定/条件覆盖、组合覆盖和路径覆盖,并画出相应的程序流程图.
void DoWork (int x,int y,int z)
{
int k=0,j=0;
if ( (x〉3)&&(z<10))
{ k=x*y-1;
j=sqrt(k);//语句块1
}
if ((x==4)||(y>5))
{
j=x*y+10;
}//语句块2
j=j%3; //语句块3
}
由这个流程图可以看出,该程序模块有4条不同的路径:
P1:(a-c—e)P2:(a-c-d)
P3:(a—b-e)P4:(a—b—d)
将里面的判定条件和过程记录如下:
判定条件M={x〉3 and z<10}
判定条件N={x=4 or y〉5}
1、语句覆盖
2、判定覆盖
也可以让测试用例测试路径P2和P3.相应的两组输入数据如下:
3、条件覆盖
对于M:x>3取真时T1,取假时F1;
z〈10取真时T2,取假时F2;
对于N:x=4取真时T3,取假时F3;
y>5取真时T4,取假时F4。
条件:x〉3,z〈10,x=4,y>5
条件:x〈=3,z>=10,x!=4,y〈=5
5、组合覆盖
条件组合
1)x>3,z〈10 2)x>3,z〉=10
3) x〈=3,z<10 4)x〈=3,z〉=10
5)x=4,y〉5 6)x=4,y<=5
6。
实验二 实验报告表(1)
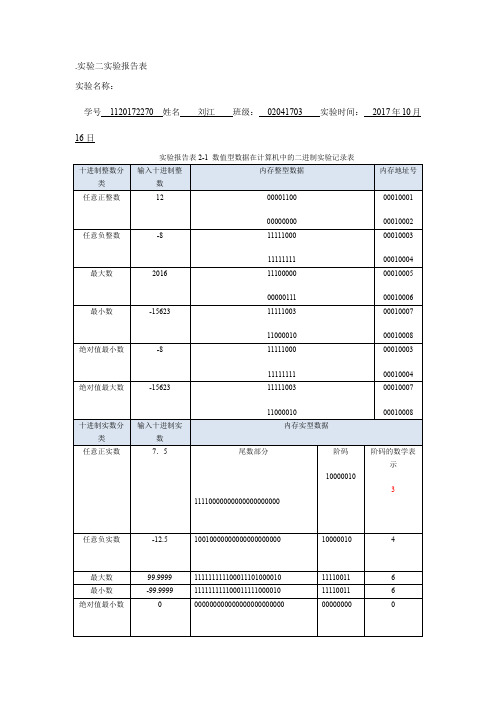
.实验二实验报告表
实验名称:
学号1120172270 姓名刘江班级:02041703 实验时间:2017年10月16日
实验报告表2-1 数值型数据在计算机中的二进制实验记录表
说明:本实验对计算机内存数据的存放拟定为:①整数用两个字节存储,并负数只考虑原码;②实数用4个字节存储,其中阶码部分占一个字节。
实验报告表2-2 其他进制数据与二进制转化实验记录表
实验报告表2-3 数据的原码、补码和反码表示实验记录表
实验报告表2-4 二进制算术运算实验记录表
实验报告表2-5溢出实验记录表
实验报告表2-6浮点数的小数点浮动实验记录表
实验报考表2-7 表示浮点数的二进制串中阶码位数改变实验记录表。
实验2实验报告

实验2实验报告在我们探索知识的道路上,实验就像是一个个神秘的冒险,每一次都充满了未知和惊喜。
今天,我要和大家分享的就是实验 2 的奇妙之旅。
这次实验的主题是关于具体实验主题。
为了能顺利完成这个实验,我们可是做了充分的准备。
老师提前给我们讲解了实验的原理和步骤,让我们心里有了个底。
实验开始啦!我紧张又兴奋地摆弄着实验器材,就像一个即将出征的战士在检查自己的武器装备。
我小心翼翼地拿起实验器材名称,眼睛紧紧盯着它,生怕一个不小心就出了差错。
旁边的小伙伴也都全神贯注,教室里安静得只能听到我们紧张的呼吸声。
按照预定的步骤,我先进行了第一步操作。
这一步看起来简单,可真做起来还真不容易。
我得控制好操作的关键因素,稍微有一点偏差,可能就会影响整个实验结果。
我深吸一口气,告诉自己要稳住。
经过几次尝试,终于成功地完成了这一步,心里不禁小小地欢呼了一下。
接下来的步骤越来越复杂,我感觉自己的大脑在飞速运转。
在进行关键步骤名称的时候,我遇到了一个大难题。
怎么都达不到预期的效果,我急得满头大汗。
这时,我想起老师说过的话:“遇到问题不要慌,要冷静思考。
”于是,我停下手中的动作,重新审视了一遍实验步骤,仔细观察了其他同学的操作,终于发现了自己的错误。
原来是我在错误的具体方面上出了岔子。
找到问题所在后,我迅速调整,终于顺利地度过了这个难关。
在整个实验过程中,我和小伙伴们互相帮助,互相鼓励。
当有人遇到困难时,大家都会停下自己的工作,一起出谋划策。
这种团队合作的氛围让我感到特别温暖,也让我明白了在学习的道路上,我们不是一个人在战斗。
经过一番努力,实验终于接近尾声。
当看到最终的实验结果时,那种成就感简直无法用言语来形容。
我们的努力没有白费,实验成功啦!通过这次实验,我不仅学到了知识,还锻炼了自己的动手能力和解决问题的能力。
更重要的是,我明白了做任何事情都要有耐心、细心,遇到困难不能轻易放弃。
这就是我的实验 2 之旅,充满了挑战和收获。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实 验 报 告课程 线性系统理论基础 实验日期 2015年5月 8 日 专业班级 自动化1201 姓名 杨志傲 学号 120610113同组人 实验名称MA TLAB 控制工具箱的应用及线性系统的运动分析评分批阅教师签字一、 实验目的加深理解能观测性、能控性、稳定性、最小实现等观念。
掌握如何使用MATLAB 进行以下分析和实现。
1、 系统的能观测性、能控性分析; 2、 系统的稳定性分析; 3、 系统的最小实现。
二、 实验内容1、 能控性、能观测性及系统实现1) 了解以下命令的功能;自选对象模型,进行运算,并写出结果。
gram, ctrb, obsv, lyap, ctrbf, obsvf, minreal ; 2) 已知连续系统的传递函数模型,182710)(23++++=s s s as s G ,当a 分别取-1,0,1时,判别系统的能控性与能观测性;3) 已知系统矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=2101013333.06667.10666.6A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=110B ,[]201=C ,判别系统的能控性与能观测性;4) 求系统1827101)(23++++=s s s s s G 的最小实现。
2、 稳定性1) 代数法稳定性判据已知单位反馈系统的开环传递函数为:)20)(1()2(100)(+++=s s s s s G ,试对系统闭环判别其稳定性2) 根轨迹法判断系统稳定性已知一个单位负反馈系统开环传递函数为)22)(6)(5()3()(2+++++=s s s s s s k s G ,试在系统的闭环根轨迹图上选择一点,求出该点的增益及其系统的闭环极点位置,并判断在该点系统闭环的稳定性。
3) Bode 图法判断系统稳定性已知两个单位负反馈系统的开环传递函数分别为ss s s G s s s s G 457.2)(,457.2)(232231-+=++=4) 用Bode 图法判断系统闭环的稳定性。
判断下列系统是否状态渐近稳定、是否BIBO 稳定。
[]x y u x x 0525,100050250100010-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=三、 实验环境Matlab6.x四、 实验原理(或程序框图)及步骤1、 能控性、能观测性及系统实现1) 系统状态能控性定义的核心是:对于线性连续定常系统(1-1),若存在一个分段连续的输入函数u(t),在有限的时间(t 1-t 0)内,能把任一给定的初态x(t 0)转移至预期的终端x(t 1),则称此状态是能控的。
若系统所有的状态都是能控的,则称该系统是状态完全能控的。
状态能控性判别式为:[]n B A AB BRank RankQ n c ==-1 当n 等于状态空间维数时则系统完全能控。
系统状态能观测性的定义:对于线性连续定常系统(2-1),如果对t0时刻存在ta ,t0<ta<∞,根据[t0,ta]上的y(t)的测量值,能够唯一地确定系统在t0时刻的任意初始状态x0,则称系统在t0时刻是状态完全能观测的,或简称系统在[t0,ta]区间上能观测。
状态能观测性判别式为:[]n CA CA CRank RankQ Tn o ==-1当n 等于状态空间维数时则系统完全能观。
2) 了解命令功能Wc = GRAM(SYS,'c')返回能控(能观)形判别矩阵;Qc=ctrb(a,b)Qc=ctrb(a,b)//生成能控(能观)判别矩阵;X=lyap(A,Q)//李雅普耨夫A'*X+X*A=-Q ;[ABAR,BBAR,CBAR,T,K] = CTRBF(A,B,C)// [ABAR,BBAR,CBAR,T,K] = OBSVF(A,B,C)//能控分解和能观分解;MSYS = MINREAL(SYS)//系统的最小实现。
3) 已知连续系统的传递函数模型,182710)(23++++=s s s as s G ,当a 分别取-1,0,1时,判别系统的能控性与能观测性。
输入系统传函,将其转换为状态空间,用gram 或者ctrl 、obsv 函数生成系统的等效判别矩阵,并求其秩如果满秩则系统能控(或能观)4) 已知系统矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=2101013333.06667.10666.6A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=110B ,[]201=C ,判别系统的能控性与能观测性;用gram 或者ctrl 、obsv 函数生成系统的等效判别矩阵,并求其秩如果满秩则系统能控(或能观) 5) 求系统1827101)(23++++=s s s s s G 的最小实现。
输入系统传递函数,将其转换为状态空间,用minreal 函数来返回一个最小系统。
代数法稳定性判据 2、 稳定性1) 已知单位反馈系统的开环传递函数对系统闭环判别其稳定性。
输入系统开环传递函数,当反馈为单位反馈时可求出闭环传函,用pzmap 函数得到所有的零极点,若极点的实部全都为零则系统是稳定的。
2) 根轨迹法判断系统稳定性用rlocus (sys )函数画出系统的根轨迹,确定一个K 值其所有的特征根也就确定了,这些特征根的实部如果都小于0,则系统是稳定的。
3) Bode 图法判断系统稳定性用bode (sys )函数画出bode 图,当系统的穿越频率所对的相角若果大于-180°则系统稳定。
4) 判断系统是否状态渐近稳定、是否BIBO 稳定。
系统渐进稳定时随着时间趋于无穷则状态会无限接近于同一个稳定状态,与初始状态和输入都没有关系。
判断条件是系统的系统的所有特征根均为负责系统渐进稳定。
BIBO 稳定是指对一个系统给一个有界的输入,他的输出也是有界的。
系统是否为最小系统,若不是先化为最小系统,然后求其特征根如果均为负系统BIBO稳定。
五、程序源代码1、能控性、能观测性及系统实现1)了解以下命令的功能[A B C D]=tf2ss([2 5 1],[1 2 3]) ctrb(A,B)ans =1 -20 1obsv(A,C)ans =1 -5-7 -3P=lyap(A,eye(size(A)))P =1.0000 -0.5000-0.5000 0.6667[Abar,Bbar,Cbar,T,k]=ctrbf(A,B,C) Abar =0 1-3 -2Bbar =1Cbar =-5 1T =0 11 0k =1 1[Abar,Bbar,Cbar,T,k]=obsvf(A,B,C) Abar =-2.3077 2.5385-1.4615 0.3077Bbar = 0.9806 0.1961 Cbar =-0.0000 5.0990 T =0.9806 0.1961 0.1961 -0.9806 k =1 1minreal(H) ans =2 s^2 + 5 s + 1 --------------- s^2 + 2 s + 32) 已知连续系统的传递函数模型,182710)(23++++=s s s as s G ,当a 分别取-1,0,1时,判别系统的能控性与能观测性; num=[0 0 1 0];den=[1 10 27 18];[A,B,C,D]=tf2ss(num,den); Qc=ctrb(A,B); rank(Qc)Qo=obsv(A,C); rank(Qo)3) 已知系统矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=2101013333.06667.10666.6A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=110B ,[]201=C ,判别系统的能控性与能观测性;A=[6.666 -10.6667 -0.3333;1 0 1;0 1 2];B=[0 1 1]';C=[1 0 2];Qc=ctrb(A,B); rank(Qc)Qo=obsv(A,C); rank(Qo)4) 求系统1827101)(23++++=s s s s s G 的最小实现。
num=[0 0 1 1];den=[1 10 27 18];[a,b,c,d]=tf2ss(num,den); sys=ss(a,b,c,d) Sys=minreal(sys) 2、 稳定性1) 代数法稳定性判据已知单位反馈系统的开环传递函数为:)20)(1()2(100)(+++=s s s s s G ,试对系统闭环判别其稳定性k=100;z=[-2];p=[0,-1,-20]; [num,den]=zp2tf(z,p,k); P=num+den; roots(P)2) 根轨迹法判断系统稳定性已知一个单位负反馈系统开环传递函数为)22)(6)(5()3()(2+++++=s s s s s s k s G ,试在系统的闭环根轨迹图上选择一点,求出该点的增益及其系统的闭环极点位置,并判断在该点系统闭环的稳定性。
num=[1 3];den1=conv([1 0],[1 5]);den2=conv([1 6],[1 2 2]); den=conv(den1,den2); W=tf(num,den); rlocus(W)3) Bode 图法判断系统稳定性已知两个单位负反馈系统的开环传递函数分别为s s s s G s s s s G 457.2)(,457.2)(232231-+=++=num=[0 0 0 2.7];den=[1 5 4 0];>> G1=tf(num,den)>> num=[0 0 0 2.7];den=[1 5 -4 0]; >> G2=tf(num,den) >> bode(G1) >> grid on >> bode(G2) >> grid on4) 判断下列系统是否状态渐近稳定、是否BIBO 稳定。
[]x y u x x 0525,100050250100010-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=a=[0 1 0;0 0 1;250 0 -5];b=[0;0;10];c=[-25 5 0];d=0;[num,den]=ss2tf(a,b,c,d,1) roots(den)六、 实验数据、结果分析1、 能控性、能观测性及系统实现1) 了解以下命令的功能;自选对象模型,进行运算,并写出结果。
结果在源程序部分已给出。
已知连续系统的传递函数模型,182710)(23++++=s s s as s G ,当a 分别取-1,0,1时,判别系统的能控性与能观测性; 当a=-1时Qc=3 Qo=3 故系统完全能控完全能观; a=0时Qc=3 Qo=3故系统完全能控完全能观; a=1时Qc=3 Qo=2 故系统完全能控不完全能观。
2) 已知系统矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=2101013333.06667.10666.6A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=110B ,[]201=C ,判别系统的能控性与能观测性;Qc=3 Qo=3 故系统完全能控完全能观。
