初中数学三角形稳定性公式证明知识点整理
数学人教版八年级上册三角形的稳定性.3三角形的稳定性
11.1.3 三角形的稳定性
1.理解三角形具有稳定性. 2.会运用三角形具有稳定性和四边形具有不稳定性 解释一些实际问题.
重点：三角形具有稳定性. 难点：三角形Leabharlann 有稳定性和四边形具有不稳定性的 应用.
阅读课本P6-7页内容，了解本节主要内容.
稳定 不稳定
稳定
不稳定性
请同学们思考，上面两幅图为什么要采用三角形的 结构？
探究：三角形的稳定性
1.将三根木条用钉子钉成一个三角形木架，然后扭 动它，它的形状会改变吗？
探究：三角形的稳定性
2.将四根木条用钉子钉成一个四边形木架，然后扭 动它，它的形状会改变吗？
探究：三角形的稳定性
3.如图，在四边形木架上再钉一根木条，将它的 一对顶点连接起来，然后再扭动它，这时木架的形状 还会改变吗？为什么？由此你能得出什么结论？
解析： ①斜钉一根木条变成三角形,利用三角形的稳定性； ②折叠点没有锁定是一个四边形，因为四边形具有不稳定性， 锁定折叠点就变成三角形，因为三角形具有稳定性. 解：①三角形具有稳定性； ②四边形具有不稳定性，三角形的稳定性.
A
C
A
A
解：如图所示：
本课时学习了三角形具有稳定性，四边形具有 不稳定性.
推荐课后完成 “课后练案”内容.
利用三角形 具有稳定性
①，④，⑥
三角形具 有稳定性 不稳定性
C
B
例：①在日常生活中，学生凳子有两条腿左右摇 晃，要克服摇晃可采用斜钉一根木条的方法，这是利用 了三角形具有稳定性 ________________；②折叠床，在折叠时是利用了 四边形具有不稳定性 展开时，利用锁扣锁住折叠点， ___________________. 三角形的稳定性 此时又利用了_______________.
三角形的稳定性知识点讲解
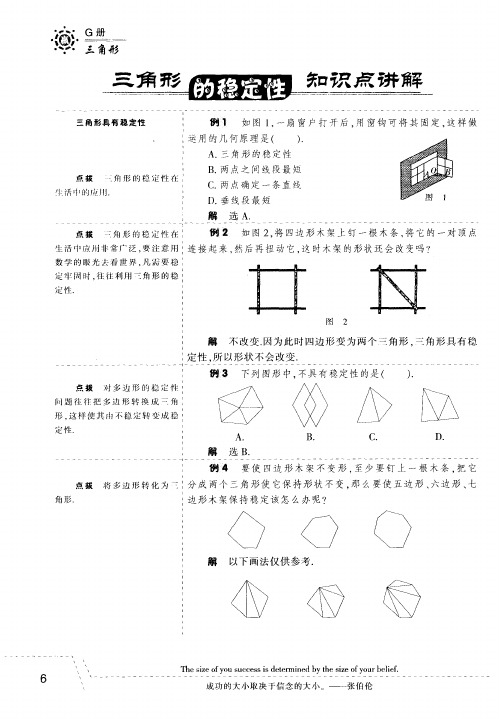
６
成 功 的 大小 取 决 于信 念 的大 小 。— — 张伯 伦
：
ｉ
— —
解
— — —— 一 一 —— — —
不 改变． 因为此 时 四边 形变 为两 个 ＿ 二角形 ， 角形 具有 稳
一 — — 一 … 一 —— — — 一 一 — — —— 一 一 一 — — — — 一 一 —— 一 … ～ —— — — —— 一 — — — — 一 … — — 一 两个 三 角形使 它保 持 形状 不 变 ， 么要使 五边 形 、 那 六边 形 、 七
！ 边形 木架保 持稳定该 怎么办呢？
解 以下 面法仅供 参考 ．
Ｔ ｅｓｚ ｆ ｏ Ｕ Ｃ Ｓ ｅ ｅｍｉ ｅ ｙｔ ｅｓｚ ｆ ｏ ｒ ｅｉｆ ｈ ｉ ｏ ｕＳ Ｃ Ｅ Ｓ ｓｄ ｔ ｒ ｎ ｄｂ ｉｅｏ ｕ ｌ ｅ ｙ ｉ ｈ ｙ ｂ ｅ
‘ 。 。 。
生 ， 府 角 的 定 在 Ｃ两 确 一 直 活， 川 形 稳 性 ．点 定 条 线 １ 。 孑 的 ．
Ｄ． 线 段 最 短 垂
解
点 拔 角 彤 的 稳 定 性 在
选 Ａ ．
例 ２ 如 图 ２ 将 四边 形 木架 上钉 一根木 条 ， 它的 一对顶 点 ， 将
生 活 巾 应 川 非 常 广 泛 ， 注 意 用 连 接 起 来 ， 后 再 扭 动 它 ， 时 木 架 的 形 状 还 会 改 变 吗 ？ 要 然 这 数 学 的 眼 光 太看 世 界 ， 需 要 稳 凡 定 牢 同 时 ， 往 利 用 ＿ 角 形 的 稳 往 三 定性．
图 ２
Ｇ 册
‘
・ ・ 三 角形 Ｖ
三 角 形
三角形具有稳定性 ：
知识 点 讲解
初中数学《三角形的高、中线和角平分线及三角形的稳定性》知识全解
《三角形的高、中线和角平分线，三角形的稳定性》知识全解 课标要求掌握三角形的高、角平分线、中线的概念，会做三角形的三线，知道三角形的三线的表示方法，理解三角形的稳定性。
知识结构（1）三角形的主要线段的定义：①三角形的角平分线：三角形的一个角的平分线和这个角的对边相交，这个角的顶点和交点之间的线段叫做三角形的角平分线．②三角形的中线：在三角形中，连结一个顶点和它的对边中点的线段叫做三角形的中线． ③三角形的高：从三角形一个顶点向它的对边画垂线，顶点和垂足间的线段叫做三角形的高线，简称三角形的高．（2）三角形的主要线段的表示法：三角形的角平分线的表示法：如上图根据具体情况使用以下任意一种方式表示：①AD 是∆ABC 的角平分线；②AD 平分∠BAC ，交BC 于D ；③如果AD 是∆ABC 的角平分线，那么∠BAD =∠DAC =21∠BAC ． 三角形的中线表示法：如上图根据具体情况使用以下任意一种方式表示：①AE 是∆ABC 的中线；②AE 是∆ABC 中BC 边上的中线；③如果AE 是∆ABC 的中线，那么BE =EC =21BC ． 三角线的高的表示法：如下图，据具体情况，使用以下任意一种方式表示：①AM 是∆ABC 的高；②AM 是∆ABC 中BC 边上的高；③如果AM是∆ABC中BC边上高，那么AM⊥BC，垂足是E；④如果AM是∆ABC中BC边上的高，那么∠AMB=∠AMC=90︒．（3）三角形的稳定性三角形具有稳定性，四边形没有稳定性．内容解析本节课主要有：动手画三角形的高，在了解三角形的高的基础上学习三角形的中线、角平分线，归纳三角形的三条重要线段的概念，掌握其画法．这是以后学习各种特殊三角形的基础，也是研究其他图形的基础知识．从生活中体验三角形的稳定性．重点难点本节课的重点是：三角形的高、中线与角平分线的概念,会用工具准确画出三角形的高、中线与角平分线．难点是钝角三角形的高的画法．教法导引引导学生动手画图，从作图中总结发现概念，从而使学生掌握三角形的高、中线与角平分线的画法．联系生活实际，了解三角形的稳定性在生产、生活中的实际应用．学法建议经过动手画图，积极参与交流，增强学生克服困难和战胜困难的自信心．通过观察和实地操作得到三角形具有稳定性，四边形没有稳定性，联系稳定性与没有稳定性在生产、生活中的广泛应用．。
初中数学三角形稳定性公式证明知识点整理
初中数学三角形稳定性公式证明知识点整理初中数学三角形稳定性公式证明知识点整理我们在学习三角形的知识中，老师经常会提到的一句话就是：三角形具有稳定性。
稳定性证明任取三角形两条边，则两条边的非公共端点被第三条边连接。
∵第三条边不可伸缩或弯折，∴两端点距离固定，∴这两条边的夹角固定;∵这两条边是任取的，∴三角形三个角都固定，进而将三角形固定，∴三角形有稳定性。
任取n边形(n≥4)两条相邻边，则两条边的非公共端点被不止一条边连接∴两端点距离不固定，∴这两边夹角不固定，∴n边形(n≥4)每个角都不固定，所以n边形(n≥4)没有稳定性。
如果不看上面的证明过程，我们就没有办法清晰的理解三角形稳定性的所有定理。
正方形定理公式正方形的特征：①正方形的四边相等；②正方形的四个角都是直角；③正方形的两条对角线相等，且互相垂直平分，每一条对角线平分一组对角；正方形的判定：①有一个角是直角的菱形是正方形；②有一组邻边相等的矩形是正方形。
希望上面对正方形定理公式知识的讲解学习，同学们都能很好的掌握，相信同学们会取得很好的成绩的哦。
平行四边形平行四边形的性质：①平行四边形的对边相等；②平行四边形的对角相等；③平行四边形的对角线互相平分；平行四边形的判定：①两组对角分别相等的四边形是平行四边形；②两组对边分别相等的四边形是平行四边形；③对角线互相平分的四边形是平行四边形；④一组对边平行且相等的四边形是平行四边形。
上面对数学中平行四边形定理公式知识的讲解学习，同学们都能很好的掌握了吧，相信同学们会从中学习的更好的哦。
直角三角形的`性质：①直角三角形的两个锐角互为余角；②直角三角形斜边上的中线等于斜边的一半；③直角三角形的两直角边的平方和等于斜边的平方（勾股定理）；④直角三角形中30度角所对的直角边等于斜边的一半；直角三角形的判定：①有两个角互余的三角形是直角三角形；②如果三角形的三边长a、b 、c有下面关系a^2+b^2=c^2，那么这个三角形是直角三角形（勾股定理的逆定理）。
《三角形的稳定性》课件
满足稳定性的条件
边长
三角形的边长不得为负数。
夹角
每个内角都应小于180度。
段角
每条边的长应该小于剩余两边的长度之和，即 a+b>c，b+c>a，a+c>b。
高度
三角形高应该穿过底边，并且垂直于底边。
三角形稳定性的判断
1 实例分析
根据三角形的形状和大小，进行直观判断三角形的稳定性。
2 公式计算
利用三角形的边长和角度，运用数学公式进行计算。
应用场景的拓展
2
将稳定性相关研究应用到更广泛的领域。
3
现有结论的深入研究
对已知的三角形稳定性结论加以深挖和 探究。
参考文献
1. 《稳定性理论》 作者：张三 出版社：人民出版社 出版时间：2010年 2. 《三角形结构稳定性计算》 作者：李四 出版社：机械工业出版社 出版时间：之一。了解三角形稳定性是我们理解这个形状 的一个重要方面。在本课件中，我们将深入探讨各种因素对三角形稳定性的 影响，并介绍三角形稳定性的应用案例。
什么是三角形的稳定性？
1 定义
当三角形的各边和角满足一定条件时，才能保持形状不变，这种形状的稳定性叫做三角 形的稳定性。
2 重要性
理解三角形稳定性可帮助我们设计更稳定的结构和设备，避免安全事故的发生。
影响三角形稳定性的因素
边长
边长越大，稳定性越 差，因为形状更容易 变形。
夹角
夹角越小，稳定性越 差，因为形状越容易 倒塌。
段角
如果任意两条边的长 度之和大于第三条边 的长度，三角形就是 稳定的。
高度
如果高度越高，三角 形越不稳定，越容易 倾倒。
3 判断表格
利用表格可以快速准确地判断三角形的稳定性。
初中三角形知识点总结
初中三角形知识点总结初中三角形知识点总结「篇一」1.知识概念1.三角形：由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
2.三边关系：三角形任意两边的和大于第三边，任意两边的差小于第三边。
3.高：从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足间的线段叫做三角形的高。
4.中线：在三角形中，连接一个顶点和它的对边中点的线段叫做三角形的中线。
5.角平分线：三角形的一个内角的平分线与这个角的对边相交，这个角的顶点和交点之间的线段叫做三角形的角平分线。
6.三角形的稳定性：三角形的形状是固定的，三角形的这个性质叫三角形的稳定性。
6.多边形：在平面内，由一些线段首尾顺次相接组成的图形叫做多边形。
7.多边形的内角：多边形相邻两边组成的角叫做它的内角。
8.多边形的外角：多边形的一边与它的邻边的延长线组成的角叫做多边形的外角。
9.多边形的对角线：连接多边形不相邻的两个顶点的线段，叫做多边形的对角线。
10.正多边形：在平面内，各个角都相等，各条边都相等的多边形叫做正多边形。
11.平面镶嵌：用一些不重叠摆放的多边形把平面的一部分完全覆盖，叫做用多边形覆盖平面。
12.公式与性质三角形的内角和：三角形的内角和为180°三角形外角的性质：性质1：三角形的一个外角等于和它不相邻的两个内角的和。
性质2：三角形的一个外角大于任何一个和它不相邻的内角。
多边形内角和公式：n边形的内角和等于(n-2)·180°多边形的外角和：多边形的内角和为360°。
多边形对角线的条数：(1)从n边形的一个顶点出发可以引(n-3)条对角线，把多边形分词(n-2)个三角形。
(2)n边形共有条对角线。
初中三角形知识点总结「篇二」初中三角形数学知识点总结三角形的一个外角大于任何一个和它不相邻的内角。
接下来为大家整合的是上海初中数学三角形知识点总结。
三角形知识点三角形两边的和大于第三边推论三角形两边的差小于第三边三角形内角和定理三角形三个内角的和等于180°推论1 直角三角形的两个锐角互余推论2 三角形的一个外角等于和它不相邻的两个内角的和推论3 三角形的一个外角大于任何一个和它不相邻的内角中考知识点总结：三角形的一个外角等于和它不相邻的两个内角的和。
人教版八年级数学上册第十一章 11.1.3 三角形的稳定性
图1
图2
知识点1 了解三角形的稳定性
我们来探究下面的问题. （1）如图，将三根木条用钉子钉成一个三 角形木架，然后扭动它，它的形状会改变吗？
（2）如图，将四根木条用钉子钉成一个四 边形木架，然后扭动它，它的形状会改变吗？
（3）如图，在四边形木架上再钉一根木条， 将它的一对不相邻的顶点连接起来，然后再扭动 它，这时木架的形状还会改变吗？
(1)请完成下表： 多边形木架的边数 至少钉木条的根数
4 5 6… 1 2 3…
n n－3
(2)要使12边形木架不变形，至少要钉____9____根木条； (3)有一个多边形木架，至少要钉18根木条，才能使它不
变形，则这个多边形的边数是____2_1___．
11.1 与三角形有关的线段
11.1.3 三角形的稳定性
R·八年级上册
新课导入
• 盖房子时，在窗框未安装好之前， 木工师傅常常先在窗框上斜钉一 根木条（如右图），为什么这样 做呢？
• 学习目标： 1．知道三角形具有稳定性，四边形没有稳定性. 2．体验稳定性与不稳定性在生产、生活中的广 泛应用.
推进新课 工程建筑中经常采用三角形的结构，如屋 顶钢架（图1），其中的道理是什么？盖房子时， 在窗框安装好之前，木工师傅常常先在窗框上斜 钉一根木条（图2），为什么要这样做呢？
8．根据所了解的平面图形的特性说明下列设计中的数学 原理．
(1)用两个钉子把木条固定在墙上； 解：两点确定一条直线．
(2)有一个不稳当的凳子，一名同学找来两根木条钉成如图 ①所示的样子； 三角形的稳定性．
(3)如图②，用三个边长相同的四边形做成的挂衣架． 解：四边形的不稳定性．
9．如图，我们知道要使四边形木架不变形，至少要钉一 根木条，要使五边形木架不变形，至少要钉几根木条？ 要使六边形木架不变形，至少要钉几根木条？要使n 边形木架不变形，又至少要钉多少根木条？
初数数学公式认识三角恒等式公式
初数数学公式认识三角恒等式公式数学是一门基础学科，而数学中的公式则是解决问题、推导论证的重要工具。
在初等数学中，三角学是一个重要的分支，而三角恒等式的认识和运用更是其中的关键。
本文将介绍一些常见的三角恒等式公式，并对其进行详细说明。
一、基础概念回顾在介绍具体的三角恒等式公式前，首先回顾一下基础的三角概念。
在直角三角形中，我们定义了三个基本比值：正弦、余弦和正切。
对于一个给定的角度，我们可以通过三角函数来表示这些比值。
例如，对于一个角度θ，正弦记为sinθ，余弦记为cosθ，正切记为tanθ。
这些函数可以用来计算角度的各种属性，如边长比值、角度之间的关系等。
二、三角恒等式公式1. 余弦平方加正弦平方等于1cos²θ + sin²θ = 1这是三角学中最基本的三角恒等式之一。
它表明对于任意一个角度θ，余弦的平方加上正弦的平方等于1。
这个恒等式相当于用三角函数表示了直角三角形中两个不同方向的边长比值之和。
2. 一角的余切等于该角的正弦除以余弦tanθ = sinθ / cosθ这个恒等式描述了正切函数与正弦、余弦函数之间的关系。
它说明了在一个给定角度θ下，正切的值可以通过该角度的正弦值除以余弦值来计算。
3. 一角的正切等于该角的正弦除以余弦的倒数tanθ = sinθ / (1 / cosθ) = sinθ · cosθ这个恒等式是由上一个恒等式推导而来。
它将余切的分母用余弦的倒数表示，并进行相乘简化。
这个恒等式在实际计算中经常被使用，能够在简化求解过程中发挥重要作用。
4. 正弦加余弦等于1sinθ + cosθ = 1这个恒等式是三角恒等式中的另一个基本公式，它表明对于一个给定的角度θ，正弦值加上余弦值等于1。
这个恒等式在某些情况下可以简化计算过程，提高计算效率。
5. 三角函数的互相倒数关系tanθ = 1 / cotθcotθ = 1 / tanθ这些恒等式描述了正切函数和余切函数之间的倒数关系。
三角形稳定性
三角形稳定性一、引言三角形稳定性是几何学中的一个基本概念，它指的是一个三角形在受力作用下保持形状不变的性质。
这一性质在工程结构设计、物理学、建筑学等领域具有重要意义。
本文将从几何学的角度，探讨三角形稳定性的原理及其在实际应用中的价值。
二、三角形稳定性的原理1.三角形的内角和根据欧几里得几何学的原理，一个三角形的内角和等于180度。
这意味着在平面内，任意三个非共线的点可以构成一个三角形，且这个三角形的内角和是固定的。
内角和的固定性为三角形稳定性提供了理论基础。
2.边长关系三角形的三条边长之间存在一定的关系。
根据三角形两边之和大于第三边的原理，任意两边之和必须大于第三边，否则无法构成一个三角形。
这一关系确保了三角形在受力时，各边之间能够相互支撑，从而保持稳定。
3.三角形的重心三角形的重心是三条中线的交点，它位于三角形内部且具有特殊的几何性质。
重心将每条中线分为两段，其中一段是另一段的两倍。
重心在三角形稳定性中起着关键作用，它使得三角形在受力时能够均匀分布压力，保持稳定。
4.三角形的内心三角形的内心是三条角平分线的交点，它位于三角形内部且具有特殊的几何性质。
内心将每条角平分线分为两段，其中一段是另一段的两倍。
内心在三角形稳定性中起着关键作用，它使得三角形在受力时能够保持角度不变，从而保持稳定。
三、三角形稳定性的应用1.工程结构设计在工程结构设计中，三角形稳定性原理被广泛应用于各种建筑和桥梁的设计。
例如，在桥梁设计中，三角形结构可以有效地承受弯曲和剪切力，保证桥梁的稳定性。
在建筑设计中，三角形框架结构可以提供更好的支撑和稳定性，提高建筑物的抗震性能。
2.物理学在物理学中，三角形稳定性原理被应用于各种力学问题的研究。
例如，在力学中，三角形结构可以用于分析力的合成和分解，从而解决复杂的力学问题。
在材料力学中，三角形稳定性原理可以用于分析材料的受力状态，预测材料的破坏和失效。
3.建筑学在建筑学中，三角形稳定性原理被应用于各种建筑结构的设计和分析。
三角形定理公式大全
三角形定理公式大全三角形是几何学中的重要图形之一，其性质和定理公式被广泛应用于数学、物理、工程等领域。
本文将为大家整理总结三角形的定理公式大全，帮助大家更好地理解和应用三角形的相关知识。
1. 三角形的基本性质：- 三角形的内角和定理：任意一个三角形的三个内角和等于180度，即∠A+∠B+∠C=180°。
- 三角形的外角和定理：三角形的一个外角等于其对角的两个内角之和，即∠A+∠B=∠D，∠A+∠C=∠E，∠B+∠C=∠F。
2. 三角形的重要定理：- 三角形的角平分线定理：三角形内角的角平分线所分角的两个角的比等于所对两边的比，即∠BAD/∠CAD=BD/DC。
- 三角形的中线定理：三角形的中线平分一条边，且平分线段的长度等于被平分边两边的和的一半，即AM=MB=1/2AB。
- 三角形的高定理：三角形的高等于底边与顶点的距离的乘积的一半，即h=BC*sinA=AC*sinB=AB*sinC。
3. 三角形的角的关系定理：- 三角形的角对边关系定理：角的对边之比等于角的正弦值之比，即a/sinA=b/sinB=c/sinC。
- 三角形的角的余角关系定理：角的余角的三角函数之比等于角的三角函数的倒数，即sin(90°-A)=cosA，cos(90°-A)=sinA。
4. 三角形的边的关系定理：- 三角形的角的角平分线定理：三角形的角的角平分线的比等于角的正切值的比，即BD/DC=tan(A/2)=tan(B/2)=tan(C/2)。
- 三角形的角的角的角平分线的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角。
初中数学三角形定理公式大全
初中数学三角形定理公式大全三角形是初中数学中的重要内容之一，其中包含了许多定理和公式。
下面是数学三角形定理公式的详细介绍：一、定理：1.角平分线定理：在任意三角形ABC中，如果BD是∠B的角平分线，则有AB/BC=AD/CD。
2.中位线定理：在任意三角形ABC中，如果DE是AB的中位线，则有DE∥BC，并且DE=1/2BC。
3.高线定理：在任意三角形ABC中，如果AD是AB的高线，则有∠ADB=90°。
4.外角定理：在任意三角形ABC中，如果∠A是外角，则有∠A=∠B+∠C。
5.等腰三角形的内角定理：在等腰三角形ABC中，如果AB=AC，则有∠B=∠C。
6.等腰三角形的底角定理：在等腰三角形ABC中，如果AB=AC，则有∠A=180°-2∠B。
7.等腰三角形的高定理：在等腰三角形ABC中，如果AB=AC，AM是BC的中线，则有BM∥AC，BM=1/2AC。
8.三角形内角和定理：在任意三角形ABC中，有∠A+∠B+∠C=180°。
二、公式：1.周长和面积公式：三角形的周长L等于三边长之和，即L=AB+BC+AC；三角形的面积S等于底边与底边上的高的乘积的一半，即S=1/2×AC×h。
2.直角三角形的斜边长度公式：在直角三角形ABC中，如果∠A=90°，则有AB²=AC²+BC²。
3.海伦公式（三角形面积公式）：在任意三角形ABC中，设s为半周长，即s=(AB+BC+CA)/2，则S=√[s(s-AB)(s-BC)(s-CA)]。
4.正弦定理：在任意三角形ABC中，有sinA/AB=sinB/BC=sinC/CA。
5.余弦定理：在任意三角形ABC中，有cosA=(BC²+CA²-AB²)/(2×BC×CA)；cosB=(CA²+AB²-BC²)/(2×CA×AB)；cosC=(AB²+BC²-CA²)/(2×AB×BC)。
三角形的稳定性初中数学原创课件
的最大长度和最短长度各是多少?
解:如图(1)当A、B、C、D依次在同一直线上时，橡
皮筋最长为1+2+5=8 (cm) ;
如图(2)当A、B、C在同一直线上，且CD与AC重
教学目标
1.了解三角形的稳定性. 2.了解三角形的稳定性和四边形的不稳定性的应用. 3.准确地在生活中使用三角形的稳定性.
新知导入
工程建筑中经常采用三角形的结构，如屋顶钢架，其中的道理是什么？盖房子时，在 窗框未安装好之前，木工师傅常常先在窗框上斜钉一根木条. 为什么要这样做呢？
新知讲解
如图所示，将三根木条用钉子钉成一个三角形木架，然 后扭动它，它的形状会改变吗？
.
课堂练习
【知识技能类作业】选做题：
5.四边形的木架只要钉上一根木条就能使其不变形.那么， 要使五边形木架不变形，至少要再钉上__2___根木条; 要使六边形木架不变形，至少要再钉上__3___根木条; 要使n边形木架不变形，至少要再钉上（_n__-_3_）_根木条.
课 堂 练 习 【综合拓展类作析
三角形的稳定性是人教版八年级上册第十一章三角形的一小节内容，这部分内容 是学生在小学已经接触过“三角形两边之和大于第三边”，在初中学习了三角形 中线、高线、角平分线等概念，会按照边长的关系和角的大小对三角形进行分类 之后的一部分内容。这部分内容在实际生活中应用广泛，但对于学生而言只能通 过实验操作去验证其稳定性，没有办法证明，所以这部分内容更多的是了解三角 形的稳定性，能举出其在实际生活中的应用，解释生活中的一些应用了三角形稳 定性及四边形不稳定性的现象。另外通过此部分的学习也让学生体会到数学源于 生活，生活中蕴含着丰富多彩的数学内容。
三角形的稳定性课件
三角形具有稳定性， 四边形具有不稳定性
三角形的性质---三角形的稳定性
用三根木棒钉一个三角形，你会发现再也无法改 变这个三角形的形状和大小，也就是说，如果一 个三角形的三条边固定了，那么三角形的形状和 大小就完全确定了.在数学上把三角形的这个性质 叫做三角形的稳定性.
三角形的稳定性在生活中有广泛的应用 ，你 能举出一些例子吗？
三角形的稳定性
生活小常识
探索与思考
(1)将三根不条用钉子钉成一个三角形木架,然后 扭动它,它的形状会改变吗?
(2)将四根不条用钉子钉成一个四边形木架,然后 扭动它,它的形状会改变吗?
(3)在四边形木架上再钉一根木条,将它的一对顶 点连接起来,然后再扭动它,它的形状会改变吗?
结论
三角形木架的形状不会改变,而四边形木架的形状 会改变.
三角形的稳定性的应用
四边形不具有稳定性，人们往往通过改造， 将其变成三角形从而增强其稳定性
三角形的稳定性的应用
三角形的稳定性的应用
三角形的稳定性的应用
三角形的稳定性的应用
房屋的人字架
三角形的稳定性的应用
照相机的三脚架
三角形的稳定性的应用 固定树的两根支撑
四边形的不稳定性有广泛的应用
用来制作防盗门、防盗窗等
练 习 1下列图形中哪些具有稳定性 具有稳定性 不具有稳定性 不具有稳定性
具有稳定性 不具有稳定性
具有稳定性
练习2
下列关于三角形稳定性和四边形不稳定性的说法
正确的是( C )
A、稳定性总是有益的，而不稳定性总是有害的 B、稳定性有利用价值，而不稳定性没有利用价值 C、稳定性和不稳定性均有利用价值
三角形的稳定性
指结构在受到外力作用时，能够保持其原有形状和承载能力，不发生破坏或失稳 的性质。
三角形与结构稳定性的关系
三角形是结构稳定性中最基本的形状之一。在建筑结构、桥梁结构、机械结构等 领域中，经常利用三角形的稳定性来增强结构的整体稳定性。例如，在建筑中， 采用三角形桁架结构可以有效地提高建筑的抗震性能。
智能化设计与优化
借助计算机技术和人工智能技术，未来三角形稳定性的设计将更加智能化。通过模拟分析、优化算法等手段，可以自 动设计出具有最优稳定性的三角形结构。
跨学科融合与创新
三角形稳定性作为数学、物理等多个学科的交叉点，未来将进一步促进不同学科之间的融合与创新。例 如，结合生物学、化学等领域的知识和技术，可以探索出具有自适应、自修复等特性的新型三角形结构 。
一个内角的平分线与另外两个 不相邻的外角的平分线的交点 ，是三角形的旁切圆的圆心。
三角形稳定性原理
02
稳定性定义及表现
稳定性定义
三角形的稳定性是指其形状和大小在受到外力作用时不易发 生改变的性质。
表现
在受到外力作用时，三角形的三个内角之和始终保持为180 度，且三条边长之间的比例关系保持不变。
结构稳定性与三角形关系
三角形分类
按边可分为不等边三角形、等腰 三角形和等边三角形；按角可分 为锐角三角形、直角三角形和钝 角三角形。
三角形内角和定理
三角形内角和定理
三角形的三个内角之和等于180°。
证明方法
可通过平行线的性质、平角定义或三角形外角定理等方法进行证明。
三角形外角定理
三角形外角定理
三角形的一个外角等于与它不相邻的 两个内角之和。
三角形稳定性的物理应用
三角形稳定性在物理学中有广泛应用，如建筑结构、桥梁设计、机械零件等领域。在这些 应用中，三角形结构能够有效地分散和承受外力，提高整体的稳定性和承载能力。
三角形的稳定性
02
三角形稳定性原理
几何形状对稳定性影响
三角形的基本几何特征
三角形由三条直线相交连接而成，具 有三个内角和三个顶点，是一种基本 的几何形状。
稳定性与形状的关系
在几何学中，三角形被认为是一种稳定 的形状，因为其三个顶点相互支撑，使 得整个结构在受到外力作用时不易发生 形变。
结构力学角度分析
结构力学的应用
三角函数关系
在直角三角形中，正弦、余弦、正切 等三角函数值与三角形的边长和角度 有密切关系。
勾股定理
边长与角度的相互影响
在非直角三角形中，三角形的边长和 角度之间也存在相互影响的关系，可 以通过正弦定理、余弦定理等公式进 行求解。
在直角三角形中，直角边的平方和等 于斜边的平方，即a²+b²=c²（其中c 为斜边，a、b为直角边）。
植物枝干形态
很多植物的枝干也呈现出三角形的形态，如松树、柏树等，这种结构使得植物更加 稳固，能够抵御风雨的侵袭。
地质地貌中三角形稳定性体现
山脉形态
在地质构造中，山脉往往呈现出三角 形的形态，这种结构使得山脉更加稳 定，不易发生大规模的地质灾害。
河流三角洲
河流在入海口处往往会形成三角洲， 这是由于河流携带的泥沙在入海口处 沉积而形成的三角形地貌，这种地貌 也具有较好的稳定性。
立柱支撑
在建筑立柱的支撑结构中，三角形 支撑可以有效分散立柱承受的压力， 提高整体结构的稳定性。
墙体加固
在建筑墙体中，三角形钢筋骨架或 支撑结构可以增强墙体的承载能力 和抗震性能。
桥梁设计中的三角形元素
拱桥结构
拱桥的主拱圈通常采用三角形截 面，这种结构可以有效提高桥梁 的承载能力和稳定性，同时降低
01
最新整理初中数学三角形证明方法
最新整理初中数学三角形证明方法初中数学中，三角形证明是一个重要的主题。
通过证明三角形的性质和定理，可以帮助学生理解和掌握三角形的特点和计算方法。
下面是一个最新的整理，介绍了一些常用的三角形证明方法。
一、三角形的边长关系证明：1.三角形两边之和大于第三边：假设三角形的三边为a、b、c，我们可以使用反证法来证明。
假设a+b<c，那么我们可以取一个较小的正数ε，使得a+b+ε=c。
由于a+b<c，所以ε>0。
然后我们通过构造一个以a和b为邻边的三角形，可以得到这个三角形的周长必定大于c，与已知条件矛盾。
2.三角形两边之差小于第三边：同样使用反证法，假设a-b>c，我们取一个较小的正数ε，使得a-b-ε=c。
然后我们可以构造一个以a和b为邻边的三角形，通过三角不等式可以得出这个三角形的周长必定小于c，与已知条件矛盾。
二、三角形的角关系证明：1.三角形内角之和为180度：通过平行线、同位角、转角等方法可以证明三角形内角之和为180度。
以三角形ABC为例，假设通过点A作直线DE与BC平行相交于D，通过点B作直线AF与AC平行相交于F。
那么三角形BDE与三角形ABC有相对应的内角是对等的，因此∠BDE=∠BA C。
同理，∠ADF=∠ABC。
所以，∠BDE+∠ADF=∠BAC+∠ABC=180度。
即，三角形ABC内角之和为180度。
2.三角形的角平分线相交于一个点：以三角形ABC为例，假设DE是∠BAC的角平分线，FG是∠ABC的角平分线。
那么我们需要证明DE与FG相交于一点。
首先证明∠ADE=∠AFG，即∠BAC的角平分线DE与∠ABC的角平分线FG相交角相等。
因为∠BDE=∠ADF（已证明∠BDE+∠ADF=180度），根据同位角性质可得∠ADE=∠AFG。
同理，我们可以证明∠AED=∠AGF，所以DE与FG相交于一点。
三、三角形的边平分线关系证明：1.三角形的角平分线相交于一个点：以三角形ABC为例，假设D是BC的角平分线，那么我们需要证明BE和CF两个边平分线在同一点上。
「口袋数学」数学八年级上册：三角形稳定性的知识要点与例题解析
「口袋数学」数学八年级上册：三角形稳定性的知识要点与例题解析三角形的稳定性当三角形的三条边长确定时，三角形的形状、大小完全被确定，这个性质叫做三角形的稳定性.要点诠释：（1）三角形的形状固定是指三角形的三个内角不会改变，大小固定指三条边长不改变．（2）三角形的稳定性在生产和生活中很有用．例如，房屋的人字梁具有三角形的结构，它就坚固而稳定；在栅栏门上斜着钉一条(或两条)木板，构成一个三角形，就可以使栅栏门不变形．大桥钢架、输电线支架都采用三角形结构，也是这个道理．（3）四边形没有稳定性，也就是说，四边形的四条边长确定后，不能确定它的形状，它的各个角的大小可以改变．四边形的不稳定性也有广泛应用，如活动挂架，伸缩尺．有时我们又要克服四边形的不稳定性，如在门框未安好之前，先在门框上斜着钉一根木板，使它不变形．经典题型3. 如图所示，木工师傅在做完门框后，为防止变形常常像图中那样钉上两条斜拉的木板条(即AB、CD)，这样做的数学道理是什么?【答案与解析】解：三角形的稳定性．【总结升华】本题是三角形的稳定性在生活中的具体应用．实际生活中，将多边形转化为三角形都是为了利用三角形的稳定性．4、（2014秋·兰州期末）如图，点D为码头，A，B两个灯塔与码头的距离相等，DA，DB为海岸线．一轮船离开码头，计划沿∠ADB 的角平分线航行，在航行途中C点处，测得轮船与灯塔A和灯塔B的距离相等．试问：轮船航行是否偏离指定航线？请说明理由．【思路点拨】只要证明轮船与D点的连线平分∠ADB就说明轮船没有偏离航线，也就是证明∠ADC=∠BDC.要证明角相等，常常通过把角放到两个三角形中，利用题目条件证明这两个三角形全等，从而得出对应角相等．【答案与解析】解：此时轮船没有偏离航线．理由：由题意知：DA=DB，AC=BC，在△ADC和△BDC中，，∴△ADC≌△BDC（SSS），∴∠ADC=∠BDC，即DC为∠ADB的角平分线，∴此时轮船没有偏离航线．【总结升华】本题考查了全等三角形的应用，解答本题的关键是：根据条件设计三角形全等，巧妙地借助两个三角形全等，寻找对应角相等．要学会把实际问题转化为数学问题来解决．举一反三：【变式】工人师傅经常利用角尺平分一个任意角，如图所示，∠AOB是一个任意角，在边OA，边OB上分别取OD＝OE，移动角尺，使角尺两边相同的刻度分别与D、E重合，这时过角尺顶点P的射线OP就是∠AOB的平分线，你能先说明△OPE与△OPD全等，再说明OP平分∠AOB吗？【答案】证明：在△OPE与△OPD中∵∴ △OPE≌△OPD （SSS）∴ ∠EOP＝∠DOP(全等三角形对应角相等) ∴ OP平分∠AOB.。
三角形公式定理大全
三角形公式定理大全《三角形公式定理大全》嘿，小伙伴们！今天咱们就来好好唠唠三角形的那些公式定理。
这三角形啊，就像一个神秘的小世界，里面藏着好多有趣的知识呢！先说说三角形的内角和定理吧。
三角形的内角和是180度，这就像一个固定的小规则。
不管是那种又高又瘦的锐角三角形，还是有一个角是直角的直角三角形，或者是有一个角很“胖”的钝角三角形，它们三个角加起来的度数就像被施了魔法一样，总是180度。
我就想啊，这多神奇啊！就好比咱们去买东西，不管是买糖果、铅笔还是小本子，它们的总价加起来就是咱们要付的钱，这是一个确定的事儿。
那要是有人问我，三角形内角和要是不等于180度会怎样？我肯定会大声说：“那可不行，那就像太阳从西边出来了，整个三角形的世界都要乱套啦！”再说说等腰三角形吧。
等腰三角形就像一个对称的小怪物。
它的两条腰是相等的呢。
等腰三角形有一个特别有趣的定理，就是等腰三角形的两个底角相等。
我有一次和同学一起做数学题，遇到一个等腰三角形，我那同学就特别迷糊，不知道两个底角相等这个事儿。
我就跟他说：“你看啊，等腰三角形就像一个长着两条一样长胳膊的小人儿，那这两条胳膊下面对应的角肯定也是一样的呀。
”我同学听了之后，一下子就明白了。
这等腰三角形的这个定理在解决好多数学问题的时候可有用了。
比如说，知道了等腰三角形的顶角的度数，就能很容易算出底角的度数啦。
等边三角形就更有趣啦！等边三角形就像是等腰三角形的超级加强版。
它三条边都相等，而且三个角也都相等，每个角都是60度呢。
这就像一个完美的小三角精灵，各个方面都那么匀称。
我在想，如果三角形都像等边三角形这么规规矩矩的，那数学世界里的三角形部分是不是就简单多啦？可是啊，那样就没有那么多有趣的挑战了。
我记得有一次老师出了一道很难的关于等边三角形的题目，要我们求它的面积。
我一开始可头疼了，但是后来我想到了等边三角形的高和边的关系，就像找到了一把解开谜题的小钥匙，一下子就把答案算出来了。
三角形稳定性的名词解释
三角形稳定性的名词解释三角形是一种由三个线段所围成的多边形。
在我们的日常生活和几何学中，我们经常会遇到三角形。
然而，不同类型的三角形在稳定性方面表现不同。
本文将通过解释三角形的稳定性来探讨三角形在不同条件下的行为和特性。
稳定性是物体在受到外力作用时保持平衡或保持形状的能力。
对于三角形来说，稳定性是指当三边之间的关系受到扰动时，三角形是否能够保持原有的形状和结构。
下面将详细解释三角形稳定性的概念。
1. 三角形边长的稳定性三角形的边长是指连接三个顶点的线段的长度。
当一个三角形的三个边长相等时，我们称之为等边三角形。
等边三角形是一种非常稳定的形状，因为它的三条边相等，任何一个边受到的压力都会平均分散到其他两个边上，保持了三角形的形状和结构。
然而，当边长不相等时，三角形的稳定性会受到影响。
较长的边往往承受更大的压力，从而将三角形拉扯成不规则的形状。
2. 三角形角度的稳定性三角形的角度是指由相邻边所夹的角度。
一个理想的三角形应该有三个内角之和等于180度的性质。
然而，当三角形的角度发生变化时，稳定性也会受到影响。
当某个角度变得非常小或非常大时，三角形的边会被扭曲或拉伸，使得三角形失去稳定性。
例如，当一个角度接近零度时，三边会趋向于共线，形成一条直线，而不再是一个三角形。
3. 三角形顶点的稳定性三角形的顶点是三边的交点。
当顶点发生移动时，三角形的形状和结构会发生变化。
在某些情况下，三角形可能会变形成其他形状，例如四边形或更大的多边形。
这种情况下，三角形失去了原有的稳定性。
然而，在某些特殊的情况下，如顶点移动到三角形的重心处，三角形的稳定性可以得到增强。
总之，三角形的稳定性取决于其边长、角度和顶点的变化。
等边三角形是最稳定的三角形形状，因为其边长相等，角度相等，顶点稳定。
而不规则三角形在边长、角度或顶点发生变化时，稳定性会受到影响。
了解三角形的稳定性对于设计和工程领域的计算和应用非常重要。
有了对三角形稳定性的清晰理解，我们可以更好地评估和分析三角形结构在受到外力作用时的行为，并做出相应的设计和调整。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
初中数学三角形稳定性公式证明知识点
整理
我们在学习三角形的知识中，老师经常会提到的一句话就是：三角形具有稳定性。
任取三角形两条边，则两条边的非公共端点被第三条边连接。
∵第三条边不可伸缩或弯折，
∴两端点距离固定，
∴这两条边的夹角固定;
∵这两条边是任取的，
∴三角形三个角都固定，进而将三角形固定，
∴三角形有稳定性。
任取n边形(n≥4)两条相邻边，则两条边的非公共端点被不止一条边连接
∴两端点距离不固定，
∴这两边夹角不固定，
∴n边形(n≥4)每个角都不固定，所以n边形(n≥4)没有稳定性。
如果不看上面的证明过程，我们就没有办法清晰的理解三角形稳定性的所有定理。
①正方形的四边相等；
②正方形的四个角都是直角；
③正方形的两条对角线相等，且互相垂直平分，每一条对角线平分一组对角；
①有一个角是直角的菱形是正方形；
②有一组邻边相等的矩形是正方形。
希望上面对正方形定理公式知识的讲解学习，同学们都能很好的掌握，相信同学们会取得很好的成绩的哦。
①平行四边形的对边相等；
②平行四边形的对角相等；
③平行四边形的对角线互相平分；
①两组对角分别相等的四边形是平行四边形；
②两组对边分别相等的四边形是平行四边形；
③对角线互相平分的四边形是平行四边形；
④一组对边平行且相等的四边形是平行四边形。
上面对数学中平行四边形定理公式知识的讲解学习，同学们都能很好的掌握了吧，相信同学们会从中学习的更好的哦。
①直角三角形的两个锐角互为余角；
②直角三角形斜边上的中线等于斜边的一半；
③直角三角形的两直角边的平方和等于斜边的平方；
④直角三角形中30度
角所对的直角边等于斜边的一半；
①有两个角互余的三角形是直角三角形；
②如果三角形的三边长a、b 、c有下面关系a^2+b^2=c^2
，那么这个三角形是直角三角形。
以上对数学直角三角形定理公式的内容讲解学习，同学们都能很好的掌握了吧，希望同学们都能考试成功。
①等腰三角形的两个底角相等；
②等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合
上面对等腰三角形的性质定理公式的内容讲解学习，同学们都能很好的掌握了吧，希望同学们在考试中取得很好的成绩。
三角形的三边关系定理及推论：三角形的两边之和大于第三边，两边之差小于第三边；
三角形的内角和定理：三角形的三个内角的和等于180度；
三角形的外角和定理：三角形的一个外角等于和它不相邻的两个的和；
三角形的外角和定理推理：三角形的一个外角大于任何一个和它不相邻的内角；
三角形的三条角平分线交于一点；
三角形的三边的垂直平分线交于一点；
三角形中位线定理：三角形两边中点的连线平行于第三边，并且等于第三边的一半；。