第三章 声波的基本性质综述
《医用物理学》 声波的基本性质

同一声压下,Z愈大,介质质元获得的振动速度愈小; 反之则反。
三、声强(intensity of sound)
定义:声波平均能流密度的大小 即声波的强度
I 1 u 2 A2 pm2 pe2 pe2
2
2u u Z
4.1 声波的基本性质
四、声的反射和折射
声强反射系数( rI ):反射波与入射波强度之比. 声强透射系数( I ):透射波与入射波强度之比
4.1 声波的基本性质
p
uA
cos t
y u u
2
声压幅值 pm uA
Vm A
有效声压
pe
pm 2
uA
2
uVm
2
4.1 声波的基本性质
二、声阻抗(acoustic impedance)
Z
p
pm uA u 单位:瑞利 m A
Pa s m1
声阻, 仅由介质的性质决定
i (incidence); i(reflect) r (transmission)
垂直入射时:
rI
Ii Ii
Z Z
2 2
Z1 Z1
2
Ii Ii
Z1
I
Ir Ii
4Z1Z 2 Z1 Z2 2
Z2
Ir
4.1 声波的基本性质
2
rI
Ii Ii
Z Z
2 2
Z1 Z1
I
Ir Ii
4Z1Z 2 Z1 Z 2 2
4.1 声波的基本性质
机械波
次声波:< 20Hz 声 波:20-20000Hz (sound wave) 超声波:> 20000Hz
4.1 声波的基本性质
一、声压(sound pressure)
声波的基本性质

纵波
横波(SV)
横波(SH)
表面波--沿无限大固体介质自由表面传播的波。
制导波--在有限空间传播的波。(兰姆波、 斯通利波)
波动方程。
2 p x2
1 c02
2 p t 2
C0 为声波传播速度。
声波在介质中的传播速度指声场能量单位时 间的传播距离。
其大小与介质声学性质、介质体密度及声波 类型有关。与声场强度无关。
声波在介质中传播时,致使介质质点产生 振动,质点振动速度不同于声波传播速度。 质点振动速度与介质、声场强度、声波类型 有关。
单位:帕(N/㎡)。1帕=1 N/㎡
1标准大气压(bar)=1.01325105 Pa (帕)
同理,由声扰动造成的密度的变化量也是位 置和时间的函数。
' 0 '(x, y, z,t) 0、-声扰动前、后的介质密度; ' 密度变化量。
声场--存在声压的空间。 有效声压--一周期内瞬时声压的均方根值。
d
)s
P为压强。
讨论:1、理想气体 C 的表达式。
理想气体的绝热方程
PV const.
对于一定质量的理想气体,有
P
const.
由此得:c2 P
P为理想气体的压强。 C 为声波在流体中的传播速度。
2、一般流体
c2
( dp
d
)s
dp
(
d
)
s
m V const.
Vd dV 0
d
声波的基础特性与应用

声波的基础特性与应用声波是一种机械波,是由物质的震动传播而产生的波动现象。
声波在空气、水、固体等介质中传播,是人类日常生活中不可或缺的一部分。
本文将介绍声波的基础特性以及其在各个领域中的应用。
### 声波的基础特性声波是一种纵波,其传播方向与振动方向一致。
声波的传播速度取决于介质的性质,一般在空气中的传播速度约为343米/秒。
声波的频率决定了声音的音调,频率越高,音调越高。
而声波的振幅则决定了声音的大小,振幅越大,声音越响亮。
声波的传播遵循波动方程,可以用以下公式表示:$$v = f \times \lambda$$其中,$v$表示声波的传播速度,$f$表示声波的频率,$\lambda$表示声波的波长。
声波的波长与频率成反比关系,频率越高,波长越短。
### 声波在医学领域的应用在医学领域,声波被广泛应用于超声波检查和超声波治疗。
超声波检查利用声波在人体组织中的传播特性,通过探头发射声波并接收回波来获取人体内部器官的影像,用于诊断疾病。
超声波治疗则利用声波的机械作用,对人体组织进行治疗,如碎石治疗、肿瘤消融等。
### 声波在通信领域的应用在通信领域,声波被应用于声纹识别技术。
声纹识别是一种生物特征识别技术,通过分析个体的声音特征来进行身份识别。
声波在此过程中起到传输和识别信息的作用,具有较高的安全性和准确性。
### 声波在工业领域的应用在工业领域,声波被应用于无损检测技术。
超声波无损检测是利用声波在材料中传播的特性,通过检测声波的传播时间和回波强度来判断材料内部是否存在缺陷,如裂纹、气孔等。
这种技术可以帮助工程师及时发现材料缺陷,确保产品质量。
### 声波在生活中的应用除了以上领域,声波在生活中还有许多其他应用。
例如,声波在音响系统中的应用,使人们能够享受高品质的音乐和影视体验;声波在声纳系统中的应用,用于水下通信和探测;声波在声波清洗中的应用,可以去除物体表面的污垢等。
总的来说,声波作为一种重要的机械波,在各个领域都有着广泛的应用。
声波的基本特性与声速

声波的基本特性与声速声波是由物体振动产生的机械波,可以在气体、液体和固体中传播。
声波在我们日常生活中起着重要作用,它具有一些基本特性,并且传播速度也是一个重要参数。
一、声波的基本特性声波具有以下几个基本特性:1. 频率:声波振动的频率决定了声音的音调,单位为赫兹(Hz)。
频率越高,音调越高;频率越低,音调越低。
人类可以听到的频率范围约为20 Hz到20,000 Hz。
2. 波长:声波的波长表示声波一个完整振动的空间长度,通常用λ表示,单位为米(m)。
声波的波长与频率成反比关系,即频率越高,波长越短;频率越低,波长越长。
3. 振幅:声波振动的振幅表示了声音的强度或音量,通常用声压表示,单位为帕斯卡(Pa)。
振幅越大,声音越响亮;振幅越小,声音越轻柔。
4. 声速:声速是声波在介质中传播的速度,通常用v表示,单位为米每秒(m/s)。
声速与介质的性质有关,例如在空气中的声速约为343 m/s,而在水中的声速约为1500 m/s。
二、声速的影响因素声速的大小受以下几个因素的影响:1. 温度:声速与温度呈正相关关系,温度越高,声速越大。
这是因为在高温下,分子的热运动加剧,导致声波传播的速度增加。
2. 介质的类型:不同的介质具有不同的声速。
一般而言,固体的声速最高,液体次之,气体最低。
这是因为固体分子之间的相互作用力较大,导致声波传播速度较快。
3. 介质的密度和弹性系数:介质的密度越大,声速越小;弹性系数越大,声速越大。
这是因为密度和弹性系数反映了介质中分子的紧密程度和分子之间相互作用的强度。
4. 湿度:湿度对声速的影响较小,一般可以忽略。
但在特定情况下,比如高湿度和高温下的空气中,湿度的增加会略微降低声速。
三、应用与意义声波的基本特性和声速在许多领域都有广泛的应用与意义。
1. 声音传播:声波的传播使我们能够听到声音。
声波在空气中的传播使得我们能够进行语言交流,而声波在固体和液体中的传播也被用于水中通讯、超声波成像等领域。
声波的基本性质及传播规律

f1 T 2
ω—角频率
2011年4月25日9时58分
4
2.1 声波的产生及描述方法
2.1.2 描述声波的基本物理量
波 形 图
波长λ :声波两个相邻同相位质点(两相邻密部或两个 相邻疏部)之间的距离叫做波长,或者说声源每振动 一次,声波的传播距离。单位:m。
声速c:声波在弹性媒质中的传播速度,单位:m/s。
播方向上单位面积的平均声能量。单位:W/m2 。
I
W S
wc0
式(2-17)
式2-15带入
I
pe2
0 c02
c0
pe2
0 c0
ue
pe 0c0
pe ue
0 c0ue2
声强是矢量,它的指向就是声传播的方向。 声压和声强都可以用来表示声音的大小。
2011年4月25日9时58分
12
2.1 声波的产生及描述方法
10lg
p12
p22 ... p02
pn2
10lg
n
100.1Lpi
i 1
式(2-23)
2011年4月25日9时58分
18
2.2 声波的叠加
上面的公式可以看出:某受声点在声源1和声源2的单 独影响下的声压级都是50dB ,则两个声源共同影响 的声压级不是100dB。
例1:某车间有5台机器,在车间中央点产生的声压级 分别为100dB、98dB、92dB、80dB、78dB,求车间 中央点的总声压级。
2.1.2 描述声波的基本物理量—声能量、声能密度
平面声波总能量
E平面
V0
pA2
0 c02
cos2 (t
kx)
式(2-13)
平面声场中任何位置上动能与位能的变化是同相位的;
声波的基本性质及其传播规律

而媒质中声波传播速度为c,则: t’= x/c代入上式则有 p(x,t)=P0cos[ω (t-x/c)]为方便起见,定义(圆)波数为 k=ω/c =2π/λ其物理意义是长为2πm的距离上所含的波长λ的数目,于是p(x,t)又可以写成: p(x,t)=P0cos (ωt- kx ) (2-7) 上式表示沿x方向传播的平面波。又因声波只含有单频ω,没有其他频率成分,所以叫简谐平面声波, P0为声压的幅值, (ωt- kx )为其相位,它描述在不同地点x 和各个时刻t声波运动状况。
第28页/共108页
设两声源频率相同,到声场中某点s的距离分别为x1和x2,则两列波在s点的瞬时声压分别为 p1=P01cos(ωt-kx1)=P01cos(ωt-φ1) p2=P02cos(ωt-kx2)=P02cos(ωt-φ2)式中 P01、P02--第一列波和第二列波的声压幅值; φ1、 φ2-- , ,是第一列波和第二列波的初相位。
第14页/共108页
图2.5 声场中媒质单元体受力图
第15页/共108页
由于该力的作用使体积元ΔV产生加速度,在我们所讨论的一般声音的情况下,由牛顿第二定律得 式中ρ为媒质的密度, 为加速度。 又由于 ΔV =SΔx 所以写成微分形式为或写成积分形式
第1页/共108页
第2页/共108页
2.1.2 描述声波的基本物理量声压:通常用p来表示压强的起伏量,即与静态压强的差p=(P-P0),称为声压。Pa,1Pa=1N/m2波长:在同一时刻,从某一个最稠密(或最稀疏)的地点到相邻的另一个最稠密(或最稀疏)的地点之间的距离称为声波的波长,λ(m)周期:振动重复1次的最短时间间隔称为周期。T(s)频率:周期的倒数即单位时间内的振动次数,称为频率,f, 赫兹(Hz),1Hz=1s-1声速:振动状态在媒质中的传播速度称为声速,c(m/s)。实际计算常取340m/s。
声波的性质
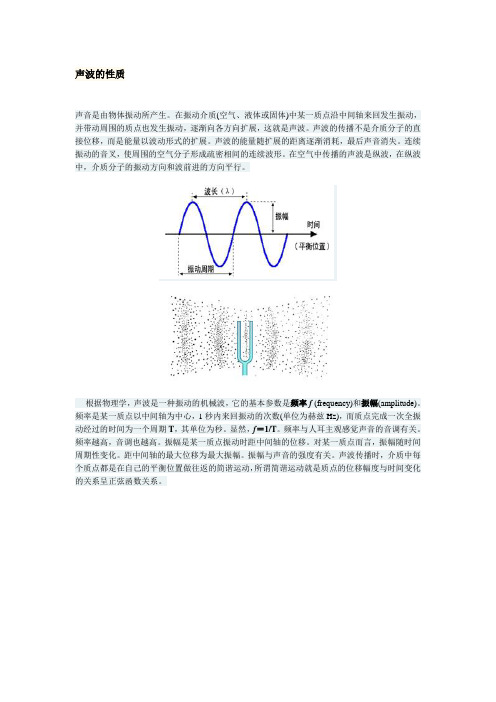
声波的性质
声音是由物体振动所产生。
在振动介质(空气、液体或固体)中某一质点沿中间轴来回发生振动,并带动周围的质点也发生振动,逐渐向各方向扩展,这就是声波。
声波的传播不是介质分子的直接位移,而是能量以波动形式的扩展。
声波的能量随扩展的距离逐渐消耗,最后声音消失。
连续振动的音叉,使周围的空气分子形成疏密相间的连续波形。
在空气中传播的声波是纵波,在纵波中,介质分子的振动方向和波前进的方向平行。
根据物理学,声波是一种振动的机械波,它的基本参数是频率f (frequency)和振幅(amplitude)。
频率是某一质点以中间轴为中心,1秒内来回振动的次数(单位为赫兹Hz),而质点完成一次全振动经过的时间为一个周期 T,其单位为秒。
显然,f=1/T。
频率与人耳主观感觉声音的音调有关。
频率越高,音调也越高。
振幅是某一质点振动时距中间轴的位移。
对某一质点而言,振幅随时间周期性变化。
距中间轴的最大位移为最大振幅。
振幅与声音的强度有关。
声波传播时,介质中每个质点都是在自己的平衡位置做往返的简谐运动,所谓简谐运动就是质点的位移幅度与时间变化的关系呈正弦函数关系。
人耳能感觉到的声波频率范围在20~20000Hz ,称为音频波。
在这个频率范围以外的振动波,就其物理特性而言与声波相似,但在人类不引起声音感觉。
声速亦称音速,是声波通过介质传播的速度,它和介质的性质与状态(如温度)等因素有关。
在空气中声速为334.8m/s(22℃时),水中声速为1440m/s ,在钢铁中声速为5000m/s 。
声学基础了解声波的性质

声学基础了解声波的性质声波是一种机械波,是由物质的振动引起的,通过介质传播的波动现象。
声波在空气、水、固体等介质中传播,是我们日常生活中常见的一种波动形式。
了解声波的性质对于深入研究声学领域具有重要意义。
本文将从声波的定义、特点、传播方式以及应用领域等方面进行探讨,帮助读者更好地理解声波的基本知识。
### 声波的定义声波是一种机械波,是由声源振动引起的,通过介质传播的波动现象。
声源振动使介质中的分子或原子发生周期性的位移,从而形成波动。
声波是一种纵波,其传播方向与振动方向一致,具有一定的频率、波长和振幅。
### 声波的特点1. **机械波特性**:声波是一种机械波,需要介质传播,无法在真空中传播。
在空气、水、固体等介质中传播时,声波会引起介质分子或原子的振动,从而传播能量。
2. **纵波特性**:声波是一种纵波,其传播方向与振动方向一致。
介质中的分子或原子沿着声波传播方向作周期性的压缩和稀疏运动。
3. **频率和波长**:声波的频率决定了声音的音调高低,频率越高,音调越高。
波长与频率成反比关系,频率越高,波长越短。
4. **振幅**:声波的振幅决定了声音的大小,振幅越大,声音越响亮。
振幅与声音的音量成正比关系。
### 声波的传播方式声波在介质中传播时,会引起介质中分子或原子的振动,从而传播能量。
声波的传播方式取决于介质的性质,一般可分为气体中的声波、液体中的声波和固体中的声波。
1. **气体中的声波**:在气体中传播时,声波会引起气体分子的振动。
声波在气体中传播速度较慢,约为343米/秒(在20摄氏度下),传播距离较远。
2. **液体中的声波**:在液体中传播时,声波会引起液体分子的振动。
声波在液体中传播速度较快,约为1500米/秒,传播距离较短。
3. **固体中的声波**:在固体中传播时,声波会引起固体中原子或分子的振动。
声波在固体中传播速度最快,取决于固体的材质和密度。
### 声波的应用领域声波作为一种重要的波动形式,在生活和科学研究中有着广泛的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
交变的压强差即为声压,符号为p,
声学基础
第三章 声波的基本概念和性质
① 声压
瞬时声压 instantaneous sound pressure
某点的瞬时声压等于在该点的瞬时总压力减去静压力. 在一定时间间隔中最大的瞬时声压称为峰值声压。
有效声压 effective sound pressure
S 4S 9S
r
r
r
声学基础
第三章 声波的基本概念和性质
④ 声压级与声强级
人们主观听觉机构对声压大小的感受不是与声压 或声强成线性关系,而是与其对数成近似线性关 系。因此通常选用对数量来表示声学量
声学基础
第三章 声波的基本概念和性质
第三章
声波的基本概念和性质
声学基础
第三章 声波的基本概念和性质
主要内容
声波的基本概念 声音的传播速度及有关现象 声波的反射与折射定理 声波的绕射和其他波动现象 运动声源的多普勒效应 声级 电-力-声类比
声学基础
第三章 声波的基本概念和性质
dv p dt x
v x t
dP c 2 d
c2 1
s
Ks
绝热体积弹性系数
绝热体积压缩系数
假设条件:媒质为理想流体;没有声扰动时媒质的初速度为零,且是均匀的; 声波传播是绝热过程;传播的是小振幅声波
声学基础
第三章 声波的基本概念和性质
音叉振动时,周围的空气分子受到扰动,形成疏密波。
声学基础
第三章 声波的基本概念和性质
① 声压
p0:没有声波时,空气处于平衡状态时的静压强, 一般等于大气压强。 P1:有声波时的压强。空气会产生稠密和稀疏相间 的变化,稠密层的压强大于静压强,稀疏层的 压强小于静压强。
pP 1 P 0
单位为牛顿/米2(N/m2)或帕(Pa)或微巴(μ bar) 声压p一般是空间和时间的函数,即p=p(x,y,z,t)
Байду номын сангаас / S
声学基础
第三章 声波的基本概念和性质
③ 声功率与声强
对于平面波,在无反射的自由声场中,由于声波在传播过程 中,波阵面的大小相同,因此,声强与离声源的距离无关。 即平面波的声强保持不变。
S S S S
对于球面波,波阵面随传播距离的增加而扩大,在离声源距离r处,
其波阵面为以r为半径的球面,面积 S=4 r 2 ,则该处的声强为 W / 4 r 2
声波的基本概念
敲打音叉之后,音叉产生振动,振动中的音叉会 来回推撞周围的空气,使得空气的压力时高时低, 而使得空气分子产生密部和疏部的变化。
声学基础
第三章 声波的基本概念和性质
然后音叉向内 缩,密部继续 往外传送,但 音叉外侧形成 疏部
声波的基本概念
向外振动的音 叉,使相邻的 空气形成密部
接着音叉向内 到平衡位置, 密部继续往外 传送
声学基础
第三章 声波的基本概念和性质
② 声波波动方程
声场的特征可以通过媒质中的声压p,质点 速度v,密度的变化量ρ ’来表征。 根据声波过程的物理性质,建立声压随空 间位置的变化和随时间的变化两者之间的 联系——声波波动方程
声学基础
第三章 声波的基本概念和性质
② 声波波动方程
为了使问题简化,必须对媒质及声波过程作出假设: 弹性媒质 连续媒质 理想流体 传播过程绝热 小振幅声波
声音的强弱只与瞬时声压的某种时间平均值有关,这种声 压的平均值称为有效声压 对简谐波有
1 T 2 p dt 从能量上考虑 pe 0 T
声学基础
第三章 声波的基本概念和性质
① 声压
声压和大气压相比是很小的,例如20Pa的声压差不多是 人耳听觉的最高极限。声压再高将使人耳疼痛难受,这一 极限称为痛阈。 如果声压很低人耳便听不见了。具有正常听力的人耳所能 听到的最低声压为2*10-5Pa,这个最低极限称为可听阈。
10 0.1
0.02
9
10 8 10
10
9
5
声学基础
第三章 声波的基本概念和性质
③ 声功率与声强
声强 sound intensity ,sound energy flux density
声强是衡量声波在传播过程中声音强弱的物理量。声场中 某一点的声强即在单位时间内,在垂直于声波传播方向的 单位面积上所通过的声能,符号为I,单位为瓦/米2 (W/m2)。
声学基础
第三章 声波的基本概念和性质
② 声波波动方程
运动方程
F1 ( P0 p ) S F2 ( P0 p dp ) S p F F1 F2 S dx x dv p Sdx S dx dt x dv p dt x
声学基础
第三章 声波的基本概念和性质
② 声波波动方程
小振幅声波一维波动方程 简化的方程: 1)运动方程:
v p 0 t x v 0 x t
2 0
2)连续性方程:
3)物态方程: p c
声学基础
第三章 声波的基本概念和性质
② 声波波动方程
均匀的理想流体媒质中小振幅声波的 波动方程(线性声波方程):
p 1 p 2 2 2 x c0 t
2 2
三维波动方程:
1 p p 2 2 c0 t
2 2
声学基础
第三章 声波的基本概念和性质
③ 声功率与声强
声功率 sound power
是表示声源单位时间内向外发射的声能 用W表示,单位为瓦
一些典型声源的声功率 声源名称 强力火箭 汽车 钢琴 声功率/W 声源名称 对话 小电钟 轻声耳语 声功率/W
② 声波波动方程
连续性方程
(媒质中单位时间内流入体积元的质量与流出该体积元的质 量之差应等于该体积元内质量的增加或减少)
( v) x S ( v) x dx S [( v) x ( v) x Sdx Sdx x t ( v) x t ( v) x dx]S x
声学基础
第三章 声波的基本概念和性质
② 声波波动方程
物态方程
P=P(ρ )
dP ( dP )s d d
dp c2 d
声学基础
第三章 声波的基本概念和性质
② 声波波动方程
理想流体媒质中的三个 基本方程
运动方程 (p 与v的关系) 连续性方程 ( ' 与v的关系) 物态方程 (p与 '的关系)
