2018-2019学年度第二学期九年级数学试卷
2018—2019学年度第二学期部分学校九年级三月联合测试数学试题含答案
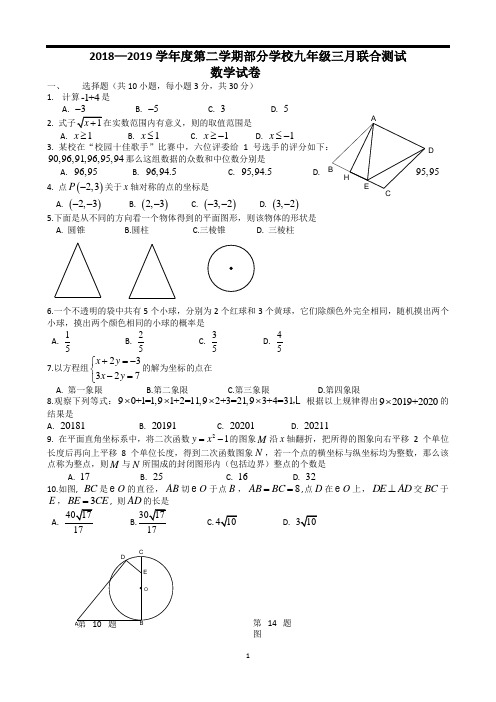
数学试卷一、 选择题（共10小题，每小题3分，共30分） 1. 计算-1+4是A.B. 5-C. 3D. 52.A. 1x ≥B. 1x ≤C. 1x ≥-D. 1x ≤-3. 某校在“校园十佳歌手”比赛中，六位评委给1号选手的评分如下：90,96,91,96,95,94那么这组数据的众数和中位数分别是A. 96,95B. 96,94.5C. 95,94.5D. 95,954. 点()2,3P -关于x 轴对称的点的坐标是A. ()2,3--B. ()2,3-C. ()3,2--D. ()3,2- 5.下面是从不同的方向看一个物体得到的平面图形，则该物体的形状是 A. 圆锥 B.圆柱 C.三棱锥 D. 三棱柱6.一个不透明的袋中共有5个小球，分别为2个红球和3个黄球，它们除颜色外完全相同，随机摸出两个小球，摸出两个颜色相同的小球的概率是A.15 B. 25 C. 35 D. 457.以方程组23327x y x y +=-⎧⎨-=⎩的解为坐标的点在A. 第一象限B.第二象限C.第三象限D.第四象限8.观察下列等式：90+1=1,91+2=11,92+3=21,93+4=31⨯⨯⨯⨯，根据以上规律得出92019+2020⨯的结果是A. 20181B. 20191C. 20201D. 202119. 在平面直角坐标系中，将二次函数21y x =-的图象M 沿x 轴翻折，把所得的图象向右平移2个单位长度后再向上平移8个单位长度，得到二次函数图象N ，若一个点的横坐标与纵坐标均为整数，那么该点称为整点，则M 与N 所围成的封闭图形内（包括边界）整点的个数是 A. 17 B. 25 C. 16 D. 3210.如图, BC 是O 的直径，AB 切O 于点B ，8AB BC ==,点D 在O 上，DE AD ⊥交BC 于E ，3BE CE =, 则AD 的长是 A.17 B.17C. D.第14题图 HEDCB A11的结果是12．从一副洗匀的普通扑克牌（共54张）中随机抽取一张，则抽出黑桃的概率是13.计算22244x x x+--= 14.如图，把菱形ABCD 沿AB 折叠，B 落在BC 上的点E 处，若040BAE ∠=，则EDC ∠的大小是15. 如图直线y x =向右平移m 个单位后得直线l ，l 与函数()30y x x=相交于点A ，与x 轴相交于点B ，则22OA OB -=16.如图，00015,37.5,75,ABC ACB DAC ∠=∠=∠=2DC =,则BD 的长为三、解答题（共8小题，共72分）17（8分）计算()232522x x xx x ⋅+-÷18（8分）如图，,BGH DHG A C ∠=∠∠=∠,求证：E F ∠=∠19（8分）学校为了了解该校学生对“军运会”的熟悉程度，在全校范围内随机抽查了部分学生进行调查统计，并将调查统计的结果分为,,A B C 三类，A 表示“非常熟悉”， B 表示“比较熟悉”， C 表示“不熟悉”，得到如下统计图，请根据图中提供的信息，解答下列问题：⑴本次随机调查的人数是 人；⑵扇形图中C 类所对应的圆心角的度数为 度；⑶若该校共有1500人，请你估计该校B 类学生的人数。
2018-2019学年度下学期九年级月考数学试卷
邵樊片九年级月考数学试卷2019. 03（本试卷满分150分，考试时间120分）请将本卷所有答案写在答题卡上．．．．．．．．．．．．．．一、选择题（本大题共有8小题，每小题3分，共24分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡．．．．上）．．．相应位置1.如果把收入100元记作+100元，那么支出80元记作（）A．﹣80元B．+100元C．+80元D．+20元2．若分式有意义，则a的取值范围是（）A．a＝0B．a＝﹣2C．a≠2D．a≠03．如图是某几何体的三视图，则这个几何体是（）A．棱B．圆柱C．棱锥D．圆锥第3题图第7题图第8题图4．在创建平安校园活动中，九年级一班举行了一次“安全知识竞赛”活动，第一小组6名同学的成绩（单位：分）分别是：87，91，93，87，97，96，下列关于这组数据说法正确的是（）A．中位数是90B．众数是87C．平均数是90D．极差是95．下列事件属于必然事件的是（）A．经过有交通信号的路口，遇到红灯B．任意买一张电影票，座位号是双号C．向空中抛一枚硬币，不向地面掉落D．三角形中，任意两边之和大于第三边6．已知一次函数y＝﹣x+m和y＝2x+n的图象都经过A（﹣4，0），且与y轴分别交于B、C两点，则△ABC的面积为（）A．48B．36C．24D．187.如图，一大桥有一段抛物线型的拱粱，小王骑自行车从O 匀速沿直线到拱粱一端A ，再匀速通过拱粱部分的桥面AC ，小王从O 到A 用了4秒，当小王骑自行车行驶10秒时和20秒时拱粱的高度相同，则小王骑自行车通过拱粱部分的桥面AC 共需 秒．A 、 22B 、 24C 、 26D 、288.如图，点M （-3，4），点P 从O 点出发，沿射线OM 方向1个单位/秒匀速运动，运动的过程中以P 为对称中心，O 为一个顶点作正方形OABC ，当正方形面积为128时，点A 坐标（ ）A. 365(,)26B. 856(,)55C.D. 二、填空题（本大题共有10小题，每小题3分，共30分．不需写出解答过程，请把答案直接填写在答题卡相应位置．．．．．．．上） 9.PM 2.5是指大气中直径小于或等于0.000 002 5m 的颗粒物，将0.000 002 5用科学记数法表示为 ．10、分解因式：2a 2﹣8ab +8b 2＝ ． 11、从平行四边形、菱形、正五边形、圆、角中随机抽取一个图形，抽到既是中心对称图形又是轴对称图形的概率是 ．12、一组“数值转换机”按下面的程序计算，如果输入的数是36，则输出的结果为106，要使输出的结果为127，则输入的最小正整数是 ．13、 关于x 、y 的二元一次方程组的解满足不等式x ﹣y ＞4，则m 的取值范围是 ．14.如图，半圆的半径OC ＝2，线段BC 与CD 是半圆的两条弦，BC ＝CD ，延长CD 交直径BA 的延长线于点E ，若AE ＝2，则弦BD 的长为 ．第14题图 第17题图 第18题图15、已知关于x 的分式方程﹣2＝有一个正数解，则k 的取值范围为 ．=-+与O相交，则b的取值范围16．以坐标原点O为圆心，作半径为3的圆，若直线y x b是．17、以矩形ABCD两条对角线的交点O为坐标原点，以平行于两边的方向为坐标轴，（x＞0）经过建立如图所示的平面直角坐标系，BE⊥AC，垂足为E．若双曲线y=3x点D，则OB•BE的值为．18、如图，已知AB=6，P为线段AB上的一个动点，分别以AP，PB为边在AB的同侧作菱形APCD 和菱形PBFE，点P，C，E在一条直线上，∠DAP=60°．M，N分别是对角线AC，BE的中点．当点P在线段AB上移动时，点M，N之间的距离最短为．三、解答题（本大题共有10小题，共96分．请在答题卡指定区域．．．．．．．内作答，解答时应写出必要的文字说明、证明过程或演算步骤）19．（本题满分8分）计算或化简：（1）2﹣1+（2018﹣π）0﹣sin30°（2）（a+1）2﹣a（a+1）﹣1．20.（本题满分8分）已知关于x的一元二次方程：x2﹣2x﹣k﹣2＝0有两个不相等的实数根．（1）求k的取值范围；（2）给k取一个负整数值，解这个方程．21．(本题满分8分) 某校在一次社会实践活动中，组织学生参观了虎园、烈士陵园、博物馆和植物园，为了解本次社会实践活动的效果，学校随机抽取了部分学生，对“最喜欢的景点”进行了问卷调查，并根据统计结果绘制了如下不完整的统计图．其中最喜欢烈士陵园的学生人数与最喜欢博物馆的学生人数之比为2：1，请结合统计图解答下列问题：（1）本次活动抽查了名学生；（2）请补全条形统计图；（3）在扇形统计图中，最喜欢植物园的学生人数所对应扇形的圆心角是度；（4）该校此次参加社会实践活动的学生有720人，请求出最喜欢烈士陵园的人数约有多少人？22.（本题满分8分）动画片《小猪佩奇》风靡全球，受到孩子们的喜爱，现有4张（小猪佩奇）角色卡片，分别是A佩奇，B乔治，C佩奇妈妈，D佩奇爸爸（四张卡片除字母和内容外，其余完全相同）姐弟两人做游戏，他们将这四张卡片混在一起，背面朝上放好．（1）姐姐从中随机抽取一张卡片，恰好抽到A佩奇的概率为．（2）若两人分别随机抽取一张卡片（不放回），请用列表或画树状图的方法求出恰好姐姐抽到A佩奇，弟弟抽到B乔治的概率．23.（本题满分10分）受益于国家支持新能源汽车发展和“一带一路”发展战略等多重利好因素，我市某汽车零部件生产企业的利润逐年提高，据统计，2014年利润为2亿元，2016年利润为2.88亿元．（1）求该企业从2014年到2016年利润的年平均增长率；（2）若2017年保持前两年利润的年平均增长率不变，该企业2017年的利润能否超过3.4亿元？24.（本题满分10分）如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别与BC、AC交于点D、E，过点D作DF⊥AC于点F．（1）求证：DF是⊙O的切线；（2）若⊙O的半径为3，∠CDF＝15°，求阴影部分的面积．25、（本题满分10分）如图，已知正方形ABCD，点M是边BA延长线上的动点（不与点A重合），且AM＜AB，△CBE由△DAM平移得到．若过点E作EH⊥AC，H为垂足.①求证：△DHK是等腰直角三角形；②若∠DHC＝60°时，求证：DM＝2BE．26.（本题满分10分）小军经销某品牌食品，他销售的该食品进价为40 元/盒，售价为60 元/盒，每月可卖出300 盒，经市场调研发现，售价在60 元/盒的基础上每涨1 元，每月要少卖10 盒，为获更大利润，现将售价提高x (x＞0) 元，设月销售量为y ( y＞0) 件.（1）写出销售量y 与x 的函数关系式，并写出自变量x 的取值范围；（2）求当售价定为多少元/盒时，才能使月销售利润最大？最大月利润是多少？（3）为了使月销售利润不少于6090 元，提价后售价a 应在什么范围？（直接写出答案）27.（本题满分12分）阅读理解：我们知道，四边形具有不稳定性，容易变形．如图1，一个矩形发生变形后成为一个平行四边形．设这个平行四边形相邻两个内角中较小的一个内角为α，我们把的值叫做这个平行四边形的变形度．（1）若矩形发生变形后的平行四边形有一个内角是150°，则这个平行四边形的变形度是；猜想证明：（2）若矩形的面积为S1，其变形后的平行四边形面积为S2，试猜想S1，S2，之间的数量关系，并说明理由；拓展探究：（3）如图2，在矩形ABCD中，E是AD边上的一点，且AB2＝AE•AD，这个矩形发生变形后为平行四边形A1B1C1D1，E1为E的对应点，连接B1E1，B1D1，若矩形ABCD m＞0），平行四边形A1B1C1D1（m＞0），试求∠A1E1B1+∠A1D1B1的度数．28.（本题满分12分）如图①，二次函数y＝x2+bx+c的图象与x轴交于A（3，0），B（﹣1，0）两点，与y轴交于点C，在x轴上有一个动点D（m，0），其中0＜m＜3．（1）求抛物线的解析式；（2）过点D作x轴的垂线交直线AC于点E，交抛物线于点F，过点F作FG⊥AC于点G，设△ADE的周长为C1，△EFG的周长为C2，若＝，求m的值．（3）如图②，动点P，Q同时从A点出发，都以每秒1个单位长度的速度分别沿AB，AC 边运动，其中一点到达端点时，另一点也随之停止运动，当P，Q运动到t秒时，△APQ沿PQ所在的直线翻折，点A恰好落在抛物线上H点处，请直接判定此时四边形APHQ的形状，并求出点H坐标．命题人:昭关中学沙峰审核人:昭关中学许吕松。
招远市2018-2019学年第二学期期末考试初三数学试题及答案
2018—2019学年度第二学期第二学段测试初三数学试题说明：1.考试时间120分钟，满分120分。
2.考试过程允许学生进行剪、拼、折叠等实验。
一、选择题（本大题共12个小题，每小题3分，满分36分）1.下列方程中是关于x的一元二次方程的是①2x2-x=15，②x2+2xy-3=0，③x2-=4，④3x2=0，⑤x2-+5=0A.①②B.①②④⑤C.①④⑤D.①③④2.如图，在△ABC中，点D，E分别在AB，AC上，若，DE=3，则BC的值为（）A.6B.8C.9D.103.一元二次方程x2-8x-1=0配方后可变形为（）A.（x+4）2=17B.（x+4）2=15C.（x-4）2=17D.（x-4）2=154.下列说法错误的是（）A.两个等边三角形一定相似B.两个等腰三角形一定相似C.两个等腰直角三角形一定相似D.两个全等三角形一定相似5.若关于x的一元二次方程kx2-2x+1=0有实数根，则k的取值范围是（）A.k<1B.k≤lC.k<l且k≠0D.k≤1且k≠06.如图，在△ABC中，点D、E、F分别是边AB、AC、BC的中点，要判定四边形DBFE是菱形，下列所添加条件不正确的是（）A.AB=ACB.AB=BCC.BE平分∠ABCD.EF=CF7.若a+c=b，那么方程ax2+bx+c=0（a≠0）必有一根是（）A.1B.-1C.±1D.08.如图，以某点为位似中心，将△OAB进行位似变换得到△DFE，若△OAB 与△DFE的相似比为k，则位似中心的坐标与k的值分别为（）A.（2，2），2B.（0，0），2C.（2，2），D.（0，0），9.某校初三66班学生毕业时，每个同学都要给其他同学写一份毕业留言作为纪念，全班学生共写了1640份留言，如果全班有x名学生，根据题意，列出方程为（）A.=1640B.=1640C.x（x+1）=1640D.x（x-1）=164010.如图，正方形ABCD中，M为BC上一点，ME⊥AM，ME交AD的延长线于点E.若AB=12，BM=5，则DE的长为（）A.18B.C.D.11.已知2是关于x的方程x2-2mx+3m=0的一个根，并且这个方程的两个根恰好是等腰△ABC的两条边长，则△ABC的周长为（）A.10B.14C.10或14D.8或1012.将正方形ABCD与等腰直角三角形EFG如图摆放，若点M、N刚好是AD的三等分点，下列结论正确的是（）①△AMH≌△NME ②=③GH⊥EF ④S△EMN:S△EFG=1：16A.①②③④B.①②③C.①③④D.①②④二、填空题（本大题共6个小题，每小题3分，满分l8分）13.若，则= .14.如图，△ABC是等边三角形，被一矩形所截，AB被截成三等分，EH∥BC，则图中阴影部分的面积是△ABC的面积的.15.某种童鞋原价为100元，由于店面转让要清仓，经过连续两次降价处理，现以64元销售，已知两次降价的百分率相同，则每次降价的百分率为.16.如图，四边形ABCD是边长为4的正方形，点E为边BC上的点，以DE为边向外作矩形DEFG，使FG过点A，若DE=5，那么DG的长为.17.已知m，n是方程2x2-4x-1=0的两个实数根，则2m2-3m+n+mn的值为.18.如图，菱形ABCD的边长为6，∠BAD=120°，点E是AB的中点，点F是AC 上的一动点，则EF+BF的最小值是.三、解答题（第19、20题各8分，第21、22题各9分，第23、24题各10分，第25题12分）19.用适当的方法解下列方程：（1）x（2-x）=x2-2（2）（x-1）（x-3）=8.20.关于x的方程（2m+l）x2+4mx+2m-3=0有两个不相等的实数根.（1）求m的取值范围；（2）是否存在实数m，使方程的两个实数根的倒数之和等于-1？若存在，求出m的值；若不存在，说明理由.21.在如图的方格中，△0AB的顶点坐标分别为0（0，0）、A（-2，-1）、B （-1，-3），△O1A1B1，与△OAB是关于点P为位似中心的位似图形。
2018-2019学年度第二学期九年级数学试卷
密封线学校：班级：姓名：考号：2018-2019学年度第二学期学业水平模拟考试九年级数学试卷（满分：120分考试时间：120分钟）真情提示：亲爱的同学，欢迎你参加本次考试，祝你答题成功！本试题分第Ⅰ卷和第Ⅱ卷两部分，共有24道题．第Ⅰ卷1—8题为选择题，共24分；第Ⅱ卷9—14题为填空题，15题为作图题，16—24题为解答题，共96分．要求所有题目均在答题卡上作答，在本卷上作答无效．第Ⅰ卷一、选择题（本题满分24分，共有8道小题，每小题3分）下列每小题都给出标号为A、B、C、D的四个结论，其中只有一个是正确的．每小题选对得分；不选、选错或选出的标号超过一个的不得分．1.如图，数轴上有A，B，C，D这4个点，其中表示互为相反数的点是( ).A.点A与点DB.点A与点CC.点B与点DD.点B与点C2.下列图形中，既是轴对称图形又是中心对称图形的是( ).A B C D3.青岛“最美地铁线”、连接崂山和即墨的地铁11号线全长约58 km，数据58 km用科学记数法可表示为( )m．A.0.58×105B.58×104C.5.8×104D.5.8×1054.计算（2a3b2）2÷ab2的结果为( ).A.2a2B.2a5b2C.4a5b2D.4a4b25.如图，△ABC的顶点坐标分别为A(4，6)，B(5，2)，C(2，1)，如果将△ABC绕点C按逆时针方向旋转90°，得到△A′B′C，那么点A，B的对应点A′，B′的坐标分别是( ).A.（﹣3，3），（﹣2，4）B.（﹣3，3），（1，4）C.（3，﹣3），（﹣2，4）D.（3，﹣3），（1，4）6.如图，若AB是⊙O的直径，CD是⊙O的弦，∠ABD=50º，则∠BCD的度数为( ).A.40ºB.45ºC.55ºD.75º7.已知反比例函数kyx=的图象如图所示，则二次函数2224y kx x k=-+的图象大致为( ).8.我们知道,一元二次方程x2= -1没有实数根,即不存在一个实数的平方等于-1.若我们规定一个新数i,使其满足i2= -1(即x2= -1方程有一个根为i),并且进一步规定：一切实数可以与新数进行四则运算,且原有的运算法则仍然成立，于是有i1=i，i2= -1，i3=i2·i=(-1)·i=-i，i4=(i2)2=(-1)2=1，从而对任意正整数n，我们可得到i4n+1=i4n·i=(i4)n·i，同理可得i4n+2=-1，i4n+3=-i，i4n=1，那么i+i2+i3+i4+…+i2018+i2019的值为().A.0B.-1C.iD.1座号密封线 第Ⅱ卷二、填空题（本题满分18分，共有6道小题，每小题3分） 9.化简：()282--= .10.甲、乙两位同学参加学校运动会铅球项目选拔赛，各投掷6次，记录成绩，计算平均数和方差的结果为10.5x =甲，10.5x =乙，20.61s =甲，20.50s =乙，则成绩较稳定的是 （填“甲”或“乙”）.11.已知一元二次方程01582=+-x x 的两个解恰好分别是等腰△ABC 的底边长和腰长，则△ABC 的周长为 .12.某内陆城市为了落实国家“一带一路”战略，促进经济发展，增强对外贸易的竞争力，把距离港口420 km 的普通公路升级成了同等长度的高速公路，结果汽车行驶的平均速度比原来提高了50%，行驶时间缩短了 2 h ．求汽车原来的平均速度.设汽车原来的平均速度为x km/h ，则可列方程为____________________.13.如图，C 为半圆内一点，O 为圆心，直径AB 的长为2 cm ，∠BOC ＝60°，∠BCO ＝90°，将△BOC 绕圆心O 逆时针旋转至△B ′OC ′位置，点C ′在OA 上，则边BC 扫过区域（图中阴影部分）的面积为 cm 2．B'C'COAEPBACD第13题图 第14题图14.如图，在Rt △ABC 中，∠ACB =90°，AC =2，BC =4，点D 在边AB 上，以CD 为折痕将△CBD 折叠，得到△CPD ，CP 与边AB 交于点E .若△DEP 为直角三角形，则BD 的长是 .三、作图题（本题满分4分，用圆规、直尺作图，不写作法，但要保留作图痕迹） 15.已知：如图，四边形ABCD ．求作：点P ，使PC ∥AB ，且点P 到点A 和点B 的距离相等．BCD结论：四、解答题（本题满分74分，共有9道小题） 16.（本小题满分8分，每题4分）（1）化简：221122121a a a a a a --⎛⎫+÷- ⎪-+⎝⎭. （2）解不等式组：17.（本小题满分6分）在学校开展的数学活动课上,小明和小刚制作了一个正三棱锥(质量均匀，四个面完全相同),并在各个面上分别标记数字1，2，3，4，游戏规则如下：每人投掷三棱锥一次,并记录底面的数字,如果底面数字的和为奇数，那么小明赢；如果底面数字的和为偶数,那么小刚赢. （1）请用列表或画树状图的方法表示上述游戏中的所有可能结果.（2）请分别求出小明和小刚能赢的概率,并判断此游戏对双方是否公平.18.（本小题满分6分）为了丰富校园文化，某校决定举行学生趣味运动会，将比赛项目确定为袋鼠跳、夹球跑、跳大绳、绑腿跑和拔河赛5项，为了解学生对这5项运动的喜欢情况，随机调查了该校部分学生最喜欢的一种项目（每名学生必选且只能选择5项中的一种），并将调查结果绘制成如图所示的不完整的统计图表：()21,321 4.x x x x <+⎧⎪⎨--≤⎪⎩密封线 学校： 班级： 姓名： 考号：根据图表中提供的信息解答下列问题：（1）求a ，b 的值.（2）请将条形统计图补充完整.（3）根据调查结果，请你估计该校2500名学生中有多少名学生最喜欢绑腿跑．19.（本小题满分6分）共享单车为人们的生活带来了极大的便利.如图，一辆单车放在水平的地面上，车把头下方A 处与坐垫下方B 处在平行于地面的水平线上，A ，B 之间的距离为49 cm ，现测得AC ，BC 与AB 的夹角分别为45°，68°.若点C 到地面的距离CD 为28 cm ，坐垫中轴E 处与点B 的距离BE 为5 cm ，求点E 到地面的距离.（结果保留一位小数，参考数据：sin68°≈0.93，cos68°≈0.37，tan68°≈2.50.）20.（本小题满分8分）如图，在平面直角坐标系xOy 中，一次函数y 1=ax ＋b （a ，b 为常数，且a ≠0）与反比例函数2my x=（m 为常数，且m ≠0）的图象交于点A (－4，2)，B (2，n )．（1）求反比例函数和一次函数的解析式. （2）连接OA ，OB ，求△AOB 的面积.（3）直接写出当0＜y 1＜y 2时，自变量x 的取值范围．21.（本小题满分8分）如图，在△ABC 中，AD 是BC 边上的中线，E 是AD 的中点，过点A 作BC 的平行线，交BE 的延长线于点F ，连接CF ．（1）求证：AF=DC ．（2）△ABC 满足什么条件时，四边形ADCF 是矩形？证明你的结论． EDCBF22.（本小题满分10分）某文具厂商设计了一款成本为18元的文具盒，投放市场进行试销，经过调查，得到每月销售量 y (万件)与销售单价x (元)之间的部分数据如下：销售单价x (元) … 20 25 30 35 … 每月销售量y (万件)…60504030…（1）求每月销售量y (万件)与销售单价x (元)之间的函数关系式． （2）求每月的利润z (万元)与销售单价x (元)之间的函数关系式．（3）根据相关部门规定，这种文具盒的销售利润率不能高于50%，而且该文具厂制造这种文具盒每月的制造成本不能超过900万元．那么，当销售单价定为多少元时，厂商每月能获得最大利润？最大利润是多少？（利润=售价-制造成本）密封线23.（本小题满分10分）【问题提出】|a-1|+|a-2|+|a-3|+…+|a-2019|的最小值是多少？【阅读理解】为了解决这个问题，我们先从最简单的情况入手.|a|的几何意义是a这个数在数轴上对应的点到原点的距离，那么|a-1|可以看作a这个数在数轴上对应的点到1的距离；|a-1|+|a-2|就可以看作a这个数在数轴上对应的点到1和2两个点的距离之和.下面我们结合数轴研究|a-1|+|a-2|的最小值.我们先看a表示的点可能的3种情况，如图所示：图①图②图③（1）如图①，a在1的左边，从图中很明显可以看出a到1和2的距离之和大于1.（2）如图②，a在1，2之间(包括在1，2上)，可以看出a到1和2的距离之和等于1.（3）如图③，a在2的右边，从图中很明显可以看出a到1和2的距离之和大于1.因此，我们可以得出结论：当a在1，2之间(包括在1，2上)时，|a-1|+|a-2|有最小值1.【问题解决】（1）|a-2|+|a-5|的几何意义是 .请你结合数轴探究：|a-2|+|a-5|的最小值是 .（2）|a-1|+|a-2|+|a-3|的几何意义是 .请你结合数轴探究：|a-1|+|a-2|+|a-3|的最小值是，并在图④的数轴上描出得到最小值时a所在的位置，由此可以得出a为 .图④（3）求出|a-1|+|a-2|+|a-3|+|a-4|+|a-5|的最小值.（4）求出|a-1|+|a-2|+|a-3|+…+|a-2019|的最小值.【拓展应用】请在图⑤的数轴上表示出a，使它到2，5的距离之和小于4，并直接写出a的范围.图⑤24.（本小题满分12分）如图，四边形ABCD为矩形，AB=4 cm，AD=3 cm，动点M，N分别从点D，B同时出发，都以1 cm/s的速度运动，点M沿DA向终点A运动，点N沿BC向终点C运动.过点N作NP⊥BC，交AC于点P，连接MP.已知动点运动了t s (0<t<3) .（1）当t为多少时，PM∥AB？（2）若四边形CDMP的面积为S，试求S与t的函数关系式.（3）在运动过程中，是否存在某一时刻t使四边形CDMP的面积与四边形ABCD的面积比为3:8？若存在，请求出t的值；若不存在，请说明理由.（4）在点M，N运动过程中，△MPA能否成为一个等腰三角形？若能，求出所有可能的t值；若不能，试说明理由．PNCAM。
2018-2019学年第二学期期中九年级数学试卷(含答案)
ABCD第4题图第6题图天水市藉口中学2018—2019学年度九年级期中考试卷数学试题A 卷（满分100分）一、选择题（共10小题，每小题4分，共40分） 1（）A ．BC D ．2 2．函数9-=x y 中自变量x 的取值范围是（ ）A ．x > 0B ．x ≥0C ．x >9D ．x ≥93．甲、乙、丙、丁四名同学在一次投掷实心球训练中，在相同条件下各投掷10次，他们成绩的平均数与方差s 2如下表：方差若要选一名成绩好且发挥稳定的同学参加比赛，则应该选择 （ ）A ．甲B ．乙C ．丙D ．丁4．将一直角三角板与两边平行的纸条如图放置．若∠1=60°，则∠2的度数为 （ ）A ．60°B ．50°C ．45°D ．30°5．已知1-=x 是一元二次方程012=++mx x 的一个根，那么m 的值是（ ）A ．0B ．1C ．2D ．－26．如图，AB 、CD 是⊙O 的两条弦，连接AD 、BC ．若60AD ∠=︒B ，则CD ∠B 的度数为（ ） A ．40︒ B ．50︒ C ．60︒ D ．70︒7．如图，每个大正方形均由边长为1的小正方形组成，则下列图中的三角形与△ABC 相似的是 （ ）81a =-，则a 的取值范围是（ ）A ．a ＞1B ．a ＜1C ．a ≥1D ．a ≤19．如图，在Rt △ABC 中，∠C=900，BC=4，AC=3，CD ⊥AB 于D ，设∠ACD=α，则cos α的值为 （ ）A ．53 B ．54 C ．34 D ．3410．已知二次函数y=ax 2+bx+c(a≠0)的图象如图所示，给出以下结论：① a+b+c<0；② a-b+c<0；③b+2a<0；④ abc>0 ． 其中所有正确结论的序号是 （ ）A ．③④BC ．②③ D第9题图 第13题图 第18题图二、填空题（共8小题，每小题4分，共32分）11．在网络上搜索“奔跑吧，兄弟”，能搜索到与之相关的结果为35 800 000个，将35 800 000用科学记数法表示为______ ． 12．分解因式：x 2-9=______．13．如图，一飞镖游戏板,其中每个小正方形的大小相等,则随意投掷一个飞镖，击中黑色区域的概率是14．已知方程 221211x x x x +-=+，设21x y x +=，则用换元法得到的方程为 ； 15．方程1352(5)(2)x x ax x x x +++=----有增根x=2，则a=16．如图，圆锥的底面半径为1，母线长为3，则这个圆锥的侧面积是 ．（结果保留π） 17．若a 2-3a +1=0，则221a a+= 18．如图，二次函数342+-=x x y 的图象交x 轴于A ．B 两点，交y 轴于点C ，则△ABC 的面积等于。
2018~2019学年九年级数学试卷及答案(word版)
2018~2019学年九年级数学试卷及答案(精选真题试卷+答案，值得下载打印练习)一、选择题（共10小题，每小题3分，共30分）1．武汉某天的最高气温是7℃，最低气温是－3℃，那么当天最高温与最低温的差是（）℃A．4 B．10 C．－10 D．－41有意义，则x的取值范围是（）2．要使分式2xA．x＞2 B．x＜2 C．x≠2D．x＝23．下列运算正确的是（）A．5a2＋3a2＝8a4 B．a3·a4＝a12 C．a＋2b＝2ab D．a3·a2＝a54．已知不透明的袋中只装有黑白两种球，这些球除颜色外都相同，其中白球有30个，黑球有n 个．随机地从袋中摸出一个球，记录下颜色后，放回袋子中并摇匀，经过如此大量重复试验，发现摸出的黑球的频率稳定在0.4附近，则n的值约为（）A．20 B．30 C．40 D．505．计算(x＋1)(x＋2)的结果为（）A．x2＋2 B．x2＋3x＋2 C．x2＋3x＋3 D．x2＋2x＋26．点A(－3，2)关于x轴对称的点的坐标为（）A．(3，－2) B．(3，2) C．(－3，－2) D．(2，－3)7．如图使用五个相同的立方体搭成的几何体，其左视图是（）8．若干名同学的年龄如下表所示，这些同学的平均年龄是14岁，则这些同学年龄的众数和中位数分别是（ ）A ．14、14B ．15、14.5C ．14、13.5D ．15、159．童威用火车棍按下列方式摆图形，第1个图形用了4根火柴棍，第2个图形用了10根火柴根，第3个图形用了18根火柴棍．依照此规律，若第n 个图形用了88根火柴棍，则n 的值为（ ）A ．6B ．7C ．8D ．910．如图，⊙O 为△ABC 的外接圆，AB ＝AC ，E 是AB 的中点，连接OE ，OE ＝25，BC ＝8，则⊙O 的半径为（ ） A ．3B ．827 C ．625 D ．5二、填空题（本大题共6个小题，每小题3分，共18分） 11．计算4的结果为___________ 12．计算111+++a aa 的结果为___________ 13．甲口袋装有2个相同的小球，球上分别写着字母A 、B ；乙口袋中装有3个相同的小球，球上分别写着字母C 、D 、E ．童威从两个口袋中各随机取出一个小球，球上的字母恰好一个为元音字母另一个为辅音字母的概率是___________（A 和E 是元音字母，B 、C 和D 是辅音字母） 14．如图，AB ∥CD ，点E 在BC 上，CD ＝CE ．若∠ABC ＝32°，则∠BED 的度数是_________15．如图，△ABC 中，∠BAC ＝60°，∠BAC 的平分线交BC 于D ．若AB ＝8，AC ＝6，则AD 的长是___________16．设[x ]表示不超过x 的最大整数，如[2.1]＝2，[3]＝3，[0.3]＝0，[－2.5]＝－3，那么方程[x ]＝－x 2＋4x ＋1的解是___________ 三、解答题（共8题，共72分） 17．（本题8分）解方程组：⎩⎨⎧=--=13432y x x y18．（本题8分）如图，点C 、F 、E 、B 在一条直线上，∠CFD ＝∠BEA ， CE ＝BF ，DF ＝AE ，写出CD 与AB 之间的数量和位置关系，并证明你的结论19．（本题8分）A 、B 、C 三名同学竞选学生会主席，他们的笔试和口试成绩（单位：分）分别用两种方式进行了统计，如下表和图1(1) 请将表格和图1中的空缺部分补充完整(2) 竞选的下一个环节是由本系的300名学生对三位候选人投票，三位候选人的得票情况如图2（每名学生都恰好推荐1名候选人），候选人每得一票计1分，请直接写出每位候选人在本环节的得分(3) 每位候选人的最后成绩为笔试得分的40%、口试得分的40%、投票得分的20%的总和．若最后成绩最高者胜出，请通过计算判断胜出者是谁？20．（本题8分）五一假期某学校计划组织385名师生租车游学，已知出租公司有42座和60座客车，每辆42座比每辆60座客车租金便宜140元，租3辆42座和2辆60座客车租金共计1880元(1) 求两种车租金每辆各多少元？(2) 若学校同时租用这两种客车8辆（可以坐不满），总租金不超过3200元，有几种租车方案？请选择最节省的租车方案21．（本题8分）已知如图，在Rt△ABC中，∠C＝90°，⊙O与△ABC的三边分别相切于点D、E、F(1) 如图1，连接AO、BO，求∠AOB的度数1，求tan∠ABD的值(2) 如图2，连BD，若tan∠DBC＝422．（本题10分）已知：如图，反比例函数xy 6=的图象在第一象限的分支上有两点A 、B ，其中点A 的横坐标为a ，点B 的横坐标为b ，且b ＝a ＋4．A 、C 两点关于原点O 对称，B 、D 两点关于原点O 对称(1) 四边形ABCD 的形状为___________，点C 、D 的坐标分别为________、________（用含a 的式子表示）(2) 若(1)中的四边形ABCD 的面积为48，试求a 的值(3) 若a ＝2，试在第三象限的双曲线上确定一点P ，使得P AB 的面积最小，请直接写出点P 的坐标23．（本题10分）已知：△ABC 中，点D 在边AC 上，且AB 2＝AD ·AC (1) 求证：∠ABD ＝∠C(2) 在边BC 上截取BE ＝BD ，ED 、BA 的延长线交于点F ，求证：FEFDAB FA =(3) 在(2)的条件下，若AD ＝4，CD ＝5，cos ∠BAC ＝31，试直接写出△FBE 的面积24．（本题12分）如图，抛物线y ＝ax 2＋bx －2a 与x 轴交于点A 和点B (1，0)，与y 轴交于点C (0，41) (1) 求抛物线的解析式(2) 若点D (2，n )是抛物线上的一点，在y 轴左侧的抛物线上存在点T ，使△TAD 的面积等于△TBD 的面积，求出所有满足条件的点T 的坐标(3) 直线y ＝kx －k ＋2，与抛物线交于两点P 、Q ，其中点P 在第一象限，点Q 在第二象限，P A 交y 轴于点M ，QA 交y 轴于点N ，连接BM 、BN ，试判断BMN 的形状并证明你的结论数学答案一． 选择题BCDAB CAACC二． 填空题2， 1， 12， 106，22三． 解答题17．解方程组⎩⎨⎧=--=13432y x x y解：把方程（1）代入方程（2）得x=4，……………………3分 把x=4代入方程（1）得y=5，……………………6分故方程组的解为45x y =⎧⎨=⎩……………………8分18．CD=AB ，CD∥AB……………………2分证明：∵ CE ＝BF ，∴CF=BE……………………3分在△ABE 和△DCF 中，DF AE CFD BEACF BE∠∠=⎧⎪⎨⎪⎩＝＝……………………5分 ∴△ABE≌△DCF……………………6分∠C ＝∠B ，CD=AB ，……………………7分∴CD∥AB ……………………8分19．（1）90，90……………………2分（2）A 105 B 120 C 75……………………5分（3）选手A：85×40%+90×40%+105×20%=91（分）选手B：95×40%+80×40%+120×20%=94（分）选手C：90×40%+85×40%+75×20%=85（分）故选手B当选……………………8分（每个选手正确得分各1分）20．（1）设60座客车租金为m元，则3（m-140）+2m=1880……………………2分解得m=460，m-140=320……………………3分答：42座客车租金为320元，60座客车租金为460元……………………4分（2）设42座客车租x辆，总租金为W元W=320x+460（8-x）= -140x+3680又4260(8)38532046083200xx xx+-+-≤≥⎧⎨⎩（）……………………5分解得3535718x≤≤，……………………6分又x为整数，故x=4或5，故共有两种租车方案。
2018-2019学年第二学期第二次模拟测试九年级数学试卷
2018-2019学年第二学期第二次模拟测试九年级数学试卷（满分 150分，考试时间 120分钟）2019.5友情提醒：本卷中的所有题目均在答题卷上作答，在本卷中作答无效。
一、选择题（本大题共有8小题，每小题3分，共24分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡．．．相应位置．．．．上） 1．下列各数中比1-小的数是A ．0 B.|1-| C ． 13- D. 2．下列计算中，正确的是A 2=±B ．a a ≥C ．D ． 211-=3．下列选项中不是中心对称图形的是A ．等边三角形B ．正方形C ． 正六边形D ． 圆 4．下面图形中哪一个可能是某正方体小纸盒展开后的图形A ．B ．C ．D ．5．和三角形三个顶点相连后，一定能把三角形分成面积相等的三部分的是该三角形的 A ．内心 B ．外心 C ．重心 D ．垂心6．已知113x y-=，则代数式232x xy y x xy y +---的值为 A ．72-B ．112-C ．92D ．347．某次数学测试统计成绩，老师发现某题题目有错误，造成该题没有同学答对，于是决定在试卷总分不变的情况下，该题不算分 ，重新统计成绩前后统计量没有发生变化的是 A ．平均数 B ．众数 C ．中位数D ．方差8．关于x 的二次函数()23y x h =-+，当13x ≤≤时，函数有最小值4，则h 的值为A ．0或2B ．2或4C ．0或4D ．0或2或4二、填空题（本大题共有10小题，每小题3分，共30分．不需写出解答过程，请把答案直接填写在答题卡相应位置．．．．．．．上） 9.单项式33a b 的次数是 ▲ ．10．分解因式：22x y xy y -+= ▲ ．11.2019年扬州国际半程马拉松比赛报名人数再创新高，全球网上报名人数达45900人，用科学记数法表示该数为 ▲ ．12. 如图，要测量小河两岸相对的两点P ，A 的距离，可以在小河边取PA 的垂线PB 上的一点C ，测得PC=100米，∠PCA=30°，则小河宽PA 是 ▲ ．（结果保留根号）（12题图） （13题图） （15题图） 13. 三角形在正方形网格中的位置如图所示，则sin ∠C 的值是 ▲ .14. 在平面直角坐标系中，把过原点，平分第一、三象限的直线向右平移3个单位后，其函数解析式为 ▲ .15．如图,四边形ABCD 为菱形,点D,C 落在以B 为圆心的弧EF 上,则∠A 的度数为 ▲ .16．用一个圆心角为240°半径为6的扇形做一个圆锥的侧面，则这个圆锥底面半径为 ▲ ． 17．如图，函数ky x=在第一象限内的图像上的 点 A 、B 、C 的横坐标别为 1、2、3， 若BC 则该k 的值为 ▲ ． 18. 记S n =a 1+a 2+…+a n ，令T n =12nS S S n++⋯+，称T n 为a 1，a 2，…，a n 这列数的“理想数”.已知a 1，a 2，…，a 500的“理想数”为2 004，那么19，a 1，a 2，…，a 500的“理想数”为 ▲ ．三、解答题（本大题共有10小题，共96分．请在答题卡指定区域．．．．．．．内作答，解答时应写出必要的文字说明、证明过程或演算步骤） 19．(本题满分8分)（1）计算：1113tan 302-⎛⎫-+ ⎪⎝⎭°；（2）解不等式：22152x x +--≤ 20．(本题满分8分)先化简再在22a -<< 的范围内选取一个你喜欢的整数a 代入求出化简后分式的值2222211a a a a a a a +++÷-+ ；21.（本题满分8分）我校九年级数学兴趣小组的同学调查了若干名同学对“初中学生不穿校服上学”现象的看法，统计整理并制作了如下的条形与扇形统计图（图1）。
包河区2018-2019学年第二学期九年级教学质量检测数学试卷
包河区2018/2019学年第二学期九年级教学质量检测（一）数学试卷一、选择题（本大题共10小题，每小题4分，满分40分） 1、以下4个数：0、1.0-、1-、2-，最小的是（ ）A 、0B 、-0.1C 、-1D 、-22、下列式子中，计算结果是8a （ ）A 、62a a + B 、210a a -C 、62a a •D 、32)(a3、2018年移动支付调查报告发布数据，当前我国手机支付用户数量已达5.7亿，其中5.7亿用科学计数法表示为（ ）A 、 4107.5⨯ B 、8107.5⨯C 、91057.0⨯D 、7107.5⨯4、将一个机器零件按如图方式摆放，则它的左视图为（ ）5、如图，DF 是BDC ∠的平分线，AB ∥CD,ABD ∠=︒118,则1∠的度数为（ ） A 、︒31 B 、 ︒26 C 、︒36 D 、︒406、某旅游景区去年第二季度游客数量比第一季度下降20%，第三、四季度游客数量持续增长，第四季度游客数量比第一季度增长15.2%，这第三、四季度的平均增长率为x ，下列方程正确的是（ ）A 、 ()()%2.1511%2012+=+-x B 、%2.151)21%)(201(+=+-xC 、%)2.151%)(201(21+-=+xD 、%2.15%20)1(2+=+x7、如图，若反比例函数)0(<=x x k y 的图像经过点⎪⎭⎫⎝⎛-4,21，点A 为图像上任意一点，点B 在x 轴负半轴上，连接AO 、 AB ，当AB=OA 时，三角形AOB 的面积为（ ） A 、1 B 、2 C 、4 D 、无法确定 8、为落实垃圾分类，环卫部门将某住宅小区的垃圾箱设计为A ，B ，C 三类广宇家附近恰好有A ，B ，C 三类垃圾箱各一个，广宇姐姐将家中的垃圾对应分成A ，B 两包，如果广宇将两包垃圾随机投放到其中的两个垃圾箱中，能实现对应投放的概率是 （ ） A 、31 B 、 92 C 、91 D 、61９.如图，在四边形ABCD 中，︒=∠=∠90B A ，︒=∠60C ，8==CD BC ，将四边形ABCD 折叠，使点C 与点A 重合，折痕为EF ，则BE 的长为（ ） A.１ B.２ Ｃ.3 Ｄ.23１0.已知ABC ∆中，︒=∠135BAC ，22==AC AB ，P 为边AC 上一动点，BC PQ //交AB 于点Q ，设x PC =，PCQ ∆的面积为y ，则y 与x 的函数关系图象是（ ）二、填空题（本大题共4小题，每小题5分，满分20分） 11.64的立方根是 。
2018-2019第二学期九年级数学参考答案及评分标准
∴ OF OD , DF OD „„„„„„„„„1 分 AC AD FC AO
∵BD=1，OB=2 ,AB 是⊙O 的直径，
第1页共4页
C E
F
2
3
1
A
O
B
D
∴AO=OB=OF=2,OD=BD+OB=3, ∵∠OFD =∠C=90°
第2页共4页
A' P
A F
B'
E
2
1
B
D
C
（2）PA⊥PC，理由如下： 在 B’C 上截取 C’E=EC，则 C’C=2EC，连接 PC’ ∵△ABC 是正三角形，将∠ACB 绕点 C 顺时针旋转 α 角度（0°<α<60°）得∠A’CB’，
∴∠ACB=∠A’CB’=60°„„„„„1 分
由（1）得△ACP∽△EDC
∵乙种书柜的数量不大于甲种书柜数量的 2 倍 ∴60-a≤2 a ∴a≥20„„„„„„„„1 分 设购买两种书柜所花费为 w 元 w=360a+300（60-a） =18000+60 a„„„„„„„„2 分 ∵k=60＞0 ∴w 随着 a 的增大而增大
∴当 a=20 时，w 有最小值=18000+60 20=19200 元„„„„„„„3 分
∴60-a=40 答：学校购买 20 个甲种书柜，40 个乙种书柜所花费费用最少，最少为 19200 元。„„„„„4 分
22.（1）证明：∵正△ABC 中，点 D 为 BC 边的中点 ∴AB=BC=AC,BC=2DC ∴AC=2DC„„„„„1 分 ∵将∠ACB 绕点 C 顺时针旋转 α 角度（0°<α<60°）得∠A’CB’， ∴∠1=∠2,即∠ACP=∠DCE ∵∠PAC=∠EDC ∴△ACP∽△EDC„„„„„2 分 ∴ AP AC PC ∴AP=2ED„„„„„3 分 ED DC EC
2018——2019 学年度第二学期九年级第一次诊断考试数学试题
26.（12 分）如图 1，抛物线 y=﹣x2+bx+c 经过 A（-1，0），B（4，0）两点，与 y 轴相交于 点 C，连结 BC，点 P 为抛物线上一动点，过点 P 作 x 轴的垂线 l，交直线 BC 于点 G，交 x 轴于点 E． ⑴求抛物线的表达式； ⑵当 P 在位于 y 轴右边的抛物线上运动时，过点 C 作 CF⊥直线 l，F 为垂足，当点 P 运动 到何处时，以 P，C，F 为顶点的三角形与△OBC 相似？并求出此时点 P 的坐标； ⑶如图 2，当点 P 在位于直线 BC 上方的抛物线上运动时，连结 PC，PB，请问△PBC 的面 积 S 能否取得最大值？若能，请求出最大面积 S，并求出此时点 P 的坐标，若不能，请说 明理由．
密封线内不要答题
22.（8 分）某电视台的一档娱乐性节目中，在游戏 PK 环节，为了随机分选游戏双方的组员， 主持人设计了以下游戏：用不透明的白布包住三根颜色长短相同的细绳 AA1、BB1、CC1， 只露出它们的头和尾（如图所示），由甲、乙两位嘉宾分别从白布两端各选一根细绳，并 拉出，若两人选中同一根细绳，则两人同队，否则互为反方队员． ⑴甲嘉宾从中任意选择一根细绳拉出，求他恰好抽出细绳 AA1 的概率； ⑵请用画树状图法或列表法，求甲、乙两位嘉宾能分为同队的概率．
Hale Waihona Puke A. 1 cm 6B. 1 cm 3
C. 1 cm 2
D.1cm
10.二次函数 y = ax 2 + bx + c(a ≠ 0)的图象如图，下列结论正确（ ）
① abc > 0 ② 4ac − b 2 < 0 ③ 3b + 2c < 0 ④a-b+c>0
A.1 个
2018-2019学年第二学期九年级数学下册期中考试卷及答案有详细解析
2018-2019学年第二学期九年级数学下册期中考试卷一、单选题1、如图，已知顶点为（﹣3，﹣6）的抛物线y=ax 2+bx+c 经过点（﹣1，﹣4），则下列结论中错误的是（ ）A ．b 2＞4ac B ．ax 2+bx+c ≥﹣6C ．若点（﹣2，m ），（﹣5，n ）在抛物线上，则m ＞nD ．关于x 的一元二次方程ax 2+bx+c=﹣4的两根为﹣5和﹣12、﹣3的相反数是（ ）A ．3B ．﹣3C ．D ．3、如图，直线AB ∥CD ，直线EF 与AB ，CD 分别交于点E ，F ，EC ⊥EF ，垂足为E ，若∠1=60°，则∠2的度数为（ ）A ．15°B ．30°C ．45°D ．60°（第3题图） （第5题图） （第6题图） 4、若a ﹣b+c=0，则关于x 的一元二次方程ax 2+bx+c=0必有一根为（ ）A ．0B ．1C ．﹣1D ．25、如图，△ABC 中，已知AB=8，∠C=90°，∠A=30°，DE 是中位线，则DE 的长为（ ） A ．4 B ．3 C ．D ．26、如图，△ABO 的面积为3，且AO=AB ，双曲线y=经过点A ，则k 的值为（ ）A ．B ．3C ．6D ．9二、填空题7、因式分解3x 2﹣3y 2=_____。
8、几个棱长为1的正方体组成的几何体的三视图如图所示，则这个几何体的体积是_____。
（第8题图） （第9题图）9、如图，某数学兴趣小组将边长为5的正方形铁丝框ABCD 变形为以A 为圆心，AB 为半径的扇形（忽略铁丝的粗细），则所得的扇形ABD 的面积为_____。
10、在函数y=中，自变量x 的取值范围是_____。
11、小明用S 2=[（x 1﹣3）2+（x 2﹣3）2+…+（x 10﹣3）2]计算一组数据的方差，那么x 1+x 2+x 3+…+x 10=_____。
2018-2019学年第二学期九年级新课结束考试数学试卷
常州外国语学校2018-2019学年第二学期九年级新课结束考试数学试卷一．选择题（共8小题）1．下列运算正确的是()A ．2(1)1a a a +=+B ．235()a a=C ．2334a a a +=D ．523a a a ÷=2．若分式||11x x -+的值为零，则x 的值是()A ．1B ．1-C ．1±D ．23．李老师为了了解学生暑期在家的阅读情况，随机调查了20名学生某一天的阅读小时数，具体情况统计如下：阅读时间（小时）2 2.53 3.54学生人数（名)12863则关于这20名学生阅读小时数的说法正确的是()A ．众数是8B ．中位数是3C ．平均数是3D ．方差是0.344．如图，在ABC ∆中，D 、E 分别是AB 、BC 上的点，且//DE AC ，若:1:4BDE CDE S S ∆∆=，则:(BDE ACD S S ∆∆=)A ．1:16B ．1:18C ．1:20D ．1:245．已知ABC ∆内任意一点(,)P a b 经过平移后对应点1(,)P c d ，已知(3,2)A -在经过此次平移后对应点1(4,3)A -，则a b c d --+的值为()A ．12B ．12-C ．2D ．2-6．如图，已知AOBC 的顶点(0,0)O ，(1,2)A -，点B 在x 轴正半轴上按以下步骤作图：①以点O 为圆心，适当长度为半径作弧，分别交边OA ，OB 于点D ，E ；②分别以点D ，E 为圆心，大于12DE 的长为半径作弧，两弧在AOB ∠内交于点F ；③作射线OF ，交边AC 于点G ，则点G 的坐标为()A ．(51-，2)B ．(5，2)C ．(35-，2)D ．(52-，2)7．二次函数228y x x m =-+满足以下条件：当21x -<<-时，它的图象位于x 轴的下方；当67x <<时，它的图象位于x 轴的上方，则m 的值为()A ．8B ．10-C ．42-D ．24-8．如图，在Rt ABC ∆中，90C ∠=︒，6AC =，8BC =，点F 在边AC 上，并且2CF =，点E 为边BC 上的动点，将CEF ∆沿直线EF 翻折，点C 落在点P 处，则点P 到边AB 距离的最小值是()A ．1.5B ．1.2C ．2.4D ．以上都不对二．填空题（共10小题）99x -有意义时，实数x 的取值范围是．10．今年1至4月份，某沿海地区苹果出口至“一带一路”沿线国家约11000000千克，数据11000000可以用科学记数法表示为．11．在实数范围内分解因式：328x x -=．12．若一个圆锥的底面圆的周长是4cm π，母线长是6cm ，则该圆锥的侧面展开图的圆心角的度数是度．13．如果一个正多边形的一个外角是60︒，那么这个正多边形的边数是．14．如果关于x 的一元二次方程240x x m +-=没有实数根，那么m 的取值范围是．15．如图，⊙O 是△ABC 的外接圆，AD 是⊙O 的直径，若⊙O 的半径为6，sin B ，则线段AC 的长是．16．如图，在Rt ABC ∆中，90A ∠=︒，AB AC =，1BC =+，点M ，N 分别是边BC ，AB 上的动点，沿MN 所在的直线折叠B ∠，使点B 的对应点B '始终落在边AC 上，若△MB C '为直角三角形，则BM 的长为．17．如图，点A 为直线y x =-上一点，过A 作OA 的垂线交双曲线(0)k y x x=<于点B ，若2212OA AB -=，则k 的值为．18．如图O 的半径为2，AB 为直径．过AO 的中点C 作CD AB ⊥交O 于点D ，DE 为O 的直径，点P 为O 上动点，则2PC PE +的最小值是．三．解答题（共10小题）19．计算：20181|1-+20．（1）化简：212(1)11x x x --÷--．（2）解不等式21．为积极响应市委政府“加快建设美丽江城”的号召，我市某街道决定从备选的五种树中选购一种进行栽种．为了更好地了解社情民意，工作人员在街道辖区范围内随机抽取了部分居民，进行“我最喜欢的一种树”的调查活动（每人限选其中一种树），并将调查结果整理后，绘制成如图两个不完整的统计图：请根据所给信息解答以下问题：（1）这次参与调查的居民人数为（2）请将条形统计图补充完整，扇形统计图中“枫树”所在扇形的圆心角度数为（3）已知该街道辖区内现有居民8万人，请你估计这8万人中最喜欢玉兰树的有多少人？22．如图，有3张背面相同的纸牌A ，B ，C ，其正面分别画有三个不同的几何图形．（1）求摸出一张纸片恰好是画有圆的概率；（2）将这3张纸牌背面朝上洗匀后摸出一张，放回洗匀后再摸出一张．求摸出两张牌面图形都是中心对称图形的纸牌的概率．（用树状图或列表法求解，纸牌可用A，B，C表示）23．如图，矩形ABCD中，8BC=，过对角线BD中点O的直线分别交AB，CDAB=，6边于点E，F．（1）求证：四边形BEDF是平行四边形；（2）当四边形BEDF是菱形时，求EF的长．24．如图，旗杆及升旗台的剖面和教学楼的剖面在同一平面上，旗杆与地面垂直，在教学楼底部E 点处测得旗杆顶端的仰角58AED ∠=︒，升旗台底部到教学楼底部的距离7DE =米，升旗台坡面CD 的坡度1:0.75i =，坡长2CD =米，若旗杆底部到坡面CD 的水平距离1BC =米，求旗杆AB 的高度约（参考数据：sin 580.85︒≈，cos580.53︒≈，tan 58 1.6)︒≈25．某企业接到一批产品的生产任务，按要求必须在15天内完成．已知每件产品的售价为65元，工人甲第x 天生产的产品数量为y 件，y 与x 满足如下关系：8(05)510(515)x x y x x ⎧=⎨+<⎩ （1）工人甲第几天生产的产品数量为80件？（2）设第x 天(015)x 生产的产品成本为P 元/件，P 与x 的函数图象如图，工人甲第x 天创造的利润为W 元．①求P 与x 的函数关系式；②求W 与x的函数关系式，并求出第几天时，利润最大，最大利润是多少？26．有一边是另一边的倍的三角形叫做智慧三角形，这两边中较长边称为智慧边，这两边的夹角叫做智慧角．（1）在Rt ABC ∆中，90ACB ∠=︒，若A ∠为智慧角，则B ∠的度数为；（2）如图①，在ABC ∆中，45A ∠=︒，30B ∠=︒，求证：ABC ∆是智慧三角形；（3）如图②，ABC ∆是智慧三角形，BC 为智慧边，B ∠为智慧角，(3,0)A ，点B ，C在函数(0)ky x x =>的图象上，点C 在点B 的上方，且点B 的纵坐标为．当ABC ∆是直角三角形时，求k 的值．27．如图，在平面直角坐标系中，一次函数2y ax bx c =++的图象经过点(6,0)A -，(4,0)B ，点(0,8)C -，直线443y =--与x 、y 轴交于点D 、E ．（1）求这个二次函数的解析式；（2）若过P 为ODE ∆的内心，连接EP 、DP 分别交x 、y 轴于点I 、N ；①求点N 的坐标；②若在x 轴上有一点H ，满足2HEB DEO ∠=∠，求点H 的坐标；（3）若G 为x 轴下方抛物线上一点，过G 作y 轴的平行线交直线DE 于点K ，点F 是点K 关于直线GE 的对称点，当点F 落在y 轴时，直接写出点G 的坐标．28．如图，ABC ∆和ADE ∆是有公共顶点的等腰直角三角形，90BAC DAE ∠=∠=︒，点P 为射线BD 、CE 的交点．（1）判断线段BD 与CE 的关系，并证明你的结论；（2）若8AB =，4AD =，把ADE ∆绕点A 旋转，①当90EAC ∠=︒时，求PB 的长；②求旋转过程中线段PB 长的最大值；（3）拓展延伸：已知⊙O 的半径为，A 为圆上一定点，P 为圆上一动点，以AP 为边作等腰Rt △APG ，P 点在圆上运动一周的过程中，求OG 的最大值．。
2018~2019学年第二学期九年级数学下册综合测试卷及答案解析
2018~2019学年第二学期九年级数学下册综合测试卷及答案一、选择题1、反比例函数，当时，随的增大而增大，则的值是（ ）A ．B ．小于的实数C ．D ．2、王华晚上由路灯下的处走到处时，测得影子的长为，继续往前走到达处时，测得影子的长为，他的身高是，那么路灯的高度（ ）A ．B ．C ．D ．3、如图，小明为测量学校旗杆的高度，在操场上选了一点，测得点到旗杆底端的水平距离为米，度，则旗杆的高度为（ ）A ．米B ．米C ．米 D ．米4、在下图中，反比例函数的图象大致是（ ）A ．B ．C ．D ．5、下列各组条件中，一定能推得与相似的是（ ）A ．且B ．且C ．且D ．且6、如图，某水库堤坝横截面迎水坡的坡度是，堤坝高为，则迎水坡面的长度是（ ）A ．B ．C ．D ．7、如图，，，且把三角形分成面积为，，三部分，则（ ）A ．B ．C ．D ．无法确定（第6题图） （第7题图） （第8题图） （第10题图） 8、如图，从山顶望地面、两点，测得它们的俯角分别为和，已知米，点在上，则山高（ ） A ．米 B ．米 C ．米 D ．米9、在反比例函数图象的每一分支上，都随的增大而减小，则的取值范围是（ ） A ．B ．C ．D ．10、如图，轮船在处观测灯塔位于北偏西方向上，轮船从处以每小时海里的速度沿南偏西方向匀速航行，小时后到达码头处，此时，观测灯塔位于北偏西方向上，则灯塔与码头的距离是（ ） A ．海里 B ．海里 C ．海里 D ．海里二、填空题11、在某一时刻，测得一根高为2m 的竹竿的影长为1m ，同时测得一栋建筑物的影长为12m ，那么这栋建筑物的高度为 m 。
12、若点在反比例函数的图象上，则代数式的值为________。
13、如图，，，已知，，则图中线段的长________，________，________。
14、墙壁处有一盏灯（如图），小明站在处测得他的影长与身长相等都为，小明向墙壁走到处发现影子刚好落在点，则灯泡与地面的距离________。
2018-2019学年度第二学期期中质量检测九年级数学试卷
九年级数学试卷第1页（共6页）2018/2019学年度第二学期期中质量检测九年级数学试卷注意事项：1．本试卷考试时间为120分钟，试卷满分150分．考试形式闭卷．2．本试卷中所有试题必须作答在答题卡上规定的位置，否则不给分．3．答题前，务必将自己的学校、班级、姓名、准考证号填写在答题卡上相应位置．一、选择题（本大题共有8小题，每小题3分，共24分．在每小题所给出的四个选项中，只有一项是符合题目要求的，请将正确选项的字母代号填写在答题卡相应位置上）1．－3的倒数是……………………………………………………………………………………（▲）A ．3B ．－3C ．13D ．－132．下列全国各地地铁标志图中，既是轴对称图形又是中心对称图形的是……………………（▲）A ．B ．C ．D ．3．如图是由4个大小相同的小立方体搭成的几何体，它的俯视图是…………………………（▲）A．B ．C ．D．4．“厉行勤俭节约，反对铺张浪费”势在必行，最新统计数据显示，中国每年浪费食物总量折合粮食大约是210000000人一年的口粮．将210000000用科学记数法表示为……………（▲）A ．2.1×109B ．0.21×109C ．2.1×108D ．21×1075．下列事件中，是必然事件的是…………………………………………………………………（▲）A ．任意画一个三角形，其内角和是180°B ．经过有交通信号灯的路口，遇到红灯C ．掷一次骰子，向上一面的点数是6D．射击运动员射击一次，命中靶心（第6题）（第8题）6．如图，将一块直角三角板DEF 放置在锐角三角形ABC 上，使得该三角板的两条直角边DE 、DF 恰好分别经过点B 、C ，若∠A ＝50°，则∠ABD ＋∠ACD 的值为…………………………（▲）A ．60°B ．50°C ．40°D ．30°7．关于x 的一元二次方程x 2＋2x ＋3m ＝0有两个不相等的实数根，则m 的取值范围是………（▲）A ．m ＜13B ．m ≤13C ．m ＞－12D ．m ≤12学校班级考号姓名………………………………………………密………………………………………封……………………………线……………………………………8．如图1，在Rt△ABC中，∠ACB＝90°，点P以每秒1cm的速度从点A出发，沿折线AC－CB 运动，到点B停止．过点P作PD⊥AB，垂足为D，PD的长y（cm）与点P的运动时间x（秒）的函数图像如图2所示．当点P运动5秒时，PD的长是……………………………………（▲）A．1.5cm B．1.2cm C．1.8cm D．2cm二、填空题（本大题共有8小题，每小题3分，共24分．不需写出解答过程，请将答案直接写在答题卡相应位置上）9．8的立方根是▲．10．要使分式21－x有意义，则x应满足的条件是▲．11．某校在“爱护地球，绿化祖国”的创建活动中，组织了100名学生开展植树造林活动，其植树情况整理如下表：植树棵树（单位：棵）456810人数（人）302225158则这100名学生所植树棵树的中位数为▲．12．如图，四边形ABCD为一长条形纸带，AB∥CD，将纸带ABCD沿EF折叠，A、D两点分别与A′、D′对应，若∠1＝2∠2，则∠AEF的度数为▲°．（第12题）（第13题）（第14题）13．如图，O是坐标原点，菱形OABC的顶点A的坐标为(3，4)，顶点C在x轴的正半轴上，则∠AOC的角平分线所在直线的函数关系式为▲．14．如图，将半径为2，圆心角为90°的扇形BAC绕点A逆时针旋转60°，点B、C的对应点分别为D、E，点D在⌒AC上，则阴影部分的面积为▲．15．在平面直角坐标系中，对于点P(x，y)和Q(x，y′)，给出如下定义：如果当x≥0时，y′＝y；当x＜0时，y′＝－y，那么称点Q为点P的“关联点”．例如：点(－5，6)的“关联点”为(－5，－6)．若点N(t，t－1)在反比例函数y＝2x的图像上，且点N是点M的“关联点”，则点M的坐标为▲．16．如图，已知在Rt△ABC中，AB＝AC＝32，在△ABC内作第1个内接正方形DEFG；然后取GF的中点P，连接PD、PE，在△PDE内作第2个内接正方形HIKJ；再取线段KJ的中点Q，在△QHI内作第3个内接正方形…，依次进行下去，则第2019个内接正方形的边长为▲．三、解答题（本大题共有11小题，共102分．请在答题卡指定区域内作答，解答时应写出文字说明、推理过程或演算步骤）17.（本题满分6分）计算：(3－π)0＋2tan60°＋|－2|－12．（第16题）九年级数学试卷第2页（共6页）九年级数学试卷第3页（共6页）18．（本题满分6分）先化简，再求值：(1－1x －1)÷x －2x 2－1，其中x ＝2019．19．（本题满分8分）＜x 3①x ＋2)②，并在数轴上表示其解集．20．（本题满分8分）某中学开展了“手机伴我健康行”主题活动，他们随机抽取部分学生进行“使用手机的目的”和“每周使用手机的时间”的问卷调查，并绘制成如图①，②的统计图，已知“查资料”的人数是40人．请你根据以上信息解答下列问题：（1）在扇形统计图中，“玩游戏”对应的圆心角度数是▲度；（2）补全条形统计图；（3）该校共有学生1200人，估计每周使用手机时间在2小时以上（不含2小时）的人数．21．（本题满分8分）某超市在周年店庆期间开展优惠活动，凡购物者可以通过转动转盘的方式享受折扣优惠，本次活动共有两种方式，方式一：转动转盘甲，指针指向A区域时，所购买物品享受9折优惠，指针指向其它区域无优惠；方式二：同时转动转盘甲和转盘乙，若两个转盘的指针指向每个区域的字母相同，所购买物品享受8折优惠，其它情况无优惠．在每个转盘中，指针指向每个区城的可能性相同（若指针指向分界线，则重新转动转盘）（1）若顾客选择方式一，则享受9折优惠的概率为▲；（2）若顾客选择方式二，请用树状图或列表法列出所有可能，并求顾客享受8折优惠的概率．如图，在平行四边形ABCD中，过点D作DE⊥AB于E，点F在边CD上，DF＝BE，连接AF、BF．（1）求证：四边形BFDE是矩形；的面积．（2）若CF＝3，BE＝5，AF平分∠DAB，求平行四边形ABCD已知AB是⊙O的直径，弦CD与AB相交，∠BCD＝25°．（1）如图1，求∠ABD的大小；（2）如图2，过点D作⊙O的切线，与AB的延长线交于点P，若DP∥AC，求∠OCD的度数．九年级数学试卷第4页（共6页）九年级数学试卷第5页（共6页）24．（本题满分10分）如图，为了将货物装入大型的集装箱卡车，需要利用传送带AB 将货物从地面传送到高1.8米（即BD ＝1.8米）的操作平台BC 上．已知传送带AB 与地面所成斜坡的坡角∠BAD ＝37°．（1）求传送带AB 的长度；（2）因实际需要，现在操作平台和传送带进行改造，如图中虚线所示，操作平台加高0.2米（即BF ＝0.2米），传送带与地面所成斜坡的坡度i ＝1︰2．求改造后传送带EF 的长度．（精确到0.1米）（参考数值：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，2≈1.41，5≈2.24）25．（本题满分10分）牧民巴特尔在生产和销售某种奶食品时，采取客户先网上订购，然后由巴特尔付费选择甲或乙快递公司送货上门的销售方式．已知甲快递公司运送2千克，乙快递公司运送3千克共需运费42元；甲快递公司运送5千克，乙快递公司运送4千克共需运费70元．（1）求甲、乙两个快递公司每千克的运费各是多少元？（2）假设巴特尔生产的奶食品当日可以全部出售，且选择运费低的快递公司运送，若该产品每千克的生产成本y 1元（不含快递运费），销售价y 2元与生产量x 千克之间的函数关系式为：y 12x ＋58(0＜x ＜8)x ≥8)，y 2＝－6x ＋120（0＜x ＜13），则巴特尔每天生产量为多少千克时获得利润最大？最大利润为多少元？26．（本题满分12分）（1）问题发现如图1，在△ABC 和△ADE 中，AB ＝AC ，AD ＝AE ，∠BAC ＝∠DAE ＝50°，连接BD ，CE 交于点F ．填空：①BD CE的值为▲；②∠BFC 的度数为▲．（图1）（图2）（备用图）（2）类比探究如图2，在矩形ABCD和△DEF中，AD＝3AB，∠EDF＝90°，∠DEF＝60°，连接AF交CE的延长线于点P．求AFCE的值及∠APC的度数，并说明理由；（3）拓展延伸在（2）的条件下，将△DEF绕点D在平面内旋转，AF，CE所在直线交于点P，若DF ＝3，AB＝7，求出当点P与点E重合时AF的长．27．（本题满分14分）在平面直角坐标系中，已知抛物线的顶点为A(－1，4)，且经过点B(－2，3)，与x轴分别交于C、D两点（点C在点D的左侧）．（1）求该抛物线对应的函数表达式；（2）如图1，点M是抛物线上的一个动点，且在直线OB的上方，过点M作x轴的平行线与直线OB交于点N，连接OM．①求MN的最大值；②当△OMN为直角三角形时，直接写出点M的坐标；（3）如图2，过点A的直线交x轴于点E，且AE∥y轴，点P是抛物线上A、D之间的一个动点，直线PC、PD与AE分别交于F、G两点．当点P运动时，EF＋EG的和是否为定值？若是，试求出该定值；若不是，请说明理由．（图1）（图2）九年级数学试卷第6页（共6页）。
2018-2019学年度第二学期九年级结课质量调查数学学科试卷含答案
.温馨提示：本试卷分为第Ⅰ卷（选择题）、第Ⅱ卷（非选择题）两部分．第Ⅰ卷为第1页至第3页，第Ⅱ卷为第4页至第8页．试卷满分120分．考试时间100分钟． 祝你考试顺利!第Ⅰ卷注意事项：1．每题选出答案后，用2B 铅笔把“答题卡”上对应题目的答案标号的信息点涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号的信息点． 2．本卷共12题，共36分．一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的） 1．cos30°的值等于（A ）12（B）2 （C（D ）12．如图是由 5 个大小相同的正方体组成的几何体，则该几何体的主视图是3．反比例函数2y x =的图象在（A ）第一、二象限 （B ）第一、三象限 （C ）第二、三象限 （D ）第二、四象限4．如图，△ABC 中，5AB =，3BC =，4AC =，以点C 为圆心的圆与AB 相切，则⊙C 的半径为 （A ）2.3（B ）2.4 （C ）2.5（D ）2.65．今年某市计划扩大城区绿地面积，现有一块长方形绿地，它的短边长为60m ，若将短 边增大到与长边相等（长边不变），使扩大后的绿地的形状是正方形，则扩大后的绿 地面积比原来增加1600㎡，设扩大后的正方形绿地边长为x m ，下面所列方程正确的 是（A ）(60)1600x x -= （B ）(60)1600x x += （C ）60(60)1600x += （D ）60(60)1600x -=6．从一个棱长为3的大正方体挖去一个棱长为1的小正方体，得到的几何体如图所示， 则该几何体的左视图是7．边长相等的正三角形和正六边形的面积之比为（A ）1∶3 （B ）2∶3 （C ）1∶6 （D ）18．有两把不同的锁和三把钥匙，其中两把钥匙恰好分别能打开这两把锁，第三把钥匙不 能打开这两把锁，任意取出一把钥匙去开任意的一把锁，一次打开锁的概率是 （A ）12 （B ）13 （C ）29 （D ）16（A ） （B ） （C ） （D ）主视方向（A ） （B ） （C ） （D ）.x32AC9．已知函数1y x=的图象如图所示，当x ≥－1时，y 的取值范围是 （A ）y ≤－1或y ＞0 （B ）y ＞0（C ）y ≤－1或y ≥0 （D ）－1≤y ＜010．如图，I 是△ABC 的内心，AI 的延长线和△ABC 的外接圆相交于点D ，连接BI ，BD ，DC ．下列说法中错误的是（A ）线段DB 绕点D 顺时针旋转一定能与线段DC 重合 （B ）线段DB 绕点D 顺时针旋转一定能与线段DI 重合 （C ）CAD ∠绕点A 顺时针旋转一定能与DAB ∠重合 （D ）线段ID 绕点I 顺时针旋转一定能与线段IB 重合11．如图，已知△ABC ， △DCE ， △FEG ，△HGI 是4个全等的等腰三角形，底边BC ，CE ，EG ，GI 在同一条直线上，且2AB =，1BC =． 连接AI ，交FG 于点Q ，则QI =（A ）1 （B（C（D ）4312．二次函数)0(4)4(2≠--=a x a y 的图象在2＜x ＜3这一段位于x 轴的下方，在6＜x ＜7这一段位于x 轴的上方，则a 的值为 （A ）1 （B ）－1 （C ）2 （D ）－2第Ⅱ卷注意事项：1．用黑色字迹的签字笔将答案写在“答题卡”上(作图可用2B 铅笔)．2．本卷共13题，共84分．二、填空题（本大题共6小题，每小题3分，共18分）13．不透明袋子中装有7个球，其中有2个红球、2个绿球和3个黑球，这些球除颜色外无其他差别．从袋子中随机取出1个球，则它是绿球的概率是 ． 14．如图，直线y kx =与双曲线)0(2>=x x y 交于点A （1，a ），则k = ．15．已知△ABC ∽△DEF ，若 △ABC 与△DEF 的相似比为34，则△ABC 与△DEF 对 应中线的比为 ．16．如图，AB 是⊙O 的直径，且经过弦CD 的中点H ，过CD 延长线上一点E 作⊙O 的切线，切点为F ，若ACF ∠=65°，则E ∠的大小= （度）．17．在Rt △ABC 内有边长分别为2，x ，3的三个正方形如图摆放，则中间的正方形的边长x 的值为 ．AB C D E F G HIQABCDI.18．如图，在每个小正方形的边长为1的网格中，点A ，B ，C 均在格点上．（Ⅰ）ABC △的面积等于 ；（Ⅱ）若四边形DEFG 是正方形，且点D ，E 在边CA 上，点F 在边AB 上，点G 在边BC 上，请在如图所 示的网格中，用无刻度．．．的直尺，画出点E ，点G ，并 简要说明点E ，点G 的位置是如何找到的（不要求证 明） ．三、解答题（本大题共7小题，共66分．解答应写出文字说明、演算步骤或推理过程） 19．（本小题8分）解方程(3)(2)40x x ---=．20．（本小题8分）求抛物线22y x x =+-与x 轴的交点坐标．21．（本小题10分）已知，△ABC 中，A ∠=68°，以AB 为直径的⊙O 与AC ，BC 的交点分别为D ，E ， （Ⅰ）如图①，求CED ∠的大小；（Ⅱ）如图②，当DE BE =时，求C ∠的大小．22．（本小题10分）如图，水渠边有一棵大木瓜树，树干DO （不计粗细）上有两个木瓜A ，B （不计大小），树干垂直于地面，量得2AB =m ，在水渠的对面与O 处于同一水平面的C 处测得木瓜A 的仰角为45°、木瓜B 的仰角为30°．求C 处到树干DO 的距离CO （结果精确到1m ）1.73≈1.41≈）．23．（本小题10分）一位运动员推铅球，铅球运行时离地面的高度y （米）是关于运行时间x （秒）的二次函数．已知铅球刚出手时离地面的高度为35米；铅球出手后，经过4秒到达离地面3米的高度，经过10秒落到地面．如图建立平面直角坐标系．（Ⅰ）为了求这个二次函数的解析式，需要该二次函数图象上三个点的坐标．根据题意可知，该二次函数图象上三个点的坐标分别是 ；（Ⅱ）求这个二次函数的解析式和自变量x 的取值范围．BCD AO图① 图②ACB.24．（本小题10分）在平面直角坐标系中，O 为坐标原点，点A （0，1），点C （1，0），正方形AOCD 的两条对角线的交点为B ，延长BD 至点G ，使DG BD =．延长BC 至点E ，使CE BC =，以BG ，BE 为邻边做正方形BEFG ．（Ⅰ）如图①，求OD 的长及ABBG的值； （Ⅱ）如图②，正方形AOCD 固定，将正方形BEFG 绕点B 逆时针旋转，得正方形BE F G '''，记旋转角为α（0°＜α＜360°），连接AG '． ①在旋转过程中，当BAG '∠=90°时，求α的大小；②在旋转过程中，求AF '的长取最大值时，点F '的坐标及此时α的大小（直接写出结果即可）．25．（本小题10分）已知抛物线2y ax bx c =++．（Ⅰ）若抛物线的顶点为A （－2，－4），抛物线经过点B （－4，0）． ①求该抛物线的解析式；②连接AB ，把AB 所在直线沿y 轴向上平移，使它经过原点O ，得到直线l ，点P 是直线l 上一动点．设以点A ，B ，O ，P 为顶点的四边形的面积为S ，点P 的横坐标为x，当4+S≤6+x 的取值范围；（Ⅱ）若a ＞0，c ＞1，当x c =时，0y =，当0＜x ＜c 时，y ＞0，试比较ac 与1的大小，并说明理由．图① 图②.和平区2017－2018学年度第二学期九年级结课质量调查 数学学科试卷参考答案一、选择题（本大题共12小题，每小题3分，共36分）1．C 2．A 3．B 4．B 5．A 6．C 7．C 8．B 9．A 10．D 11．D 12．A 二、填空题（本大题共6小题，每小题3分，共18分）13．27 14．2 15．34 16．50° 17．518．（Ⅰ）6；（Ⅱ）如图，取格点K ，J ，连接KJ ，KJ 与AC 交于点E ．取格点H ，I ，连接HI ，HI 与BC 交于点G ．点E ，G 即为所求．三、解答题（本大题共7小题，共66分） 19．（本小题8分）解：方程化为2520x x -+= ……………………………1分1a =，5b =-，2c =．224(5)41217b ac ∆=-=--⨯⨯=＞0．x ===． …………………………6分即1x =，2x =． …………………………8分 20．（本小题8分）解：令0y =，即220x x +-=． ……………………………2分 解得11x =，22x =-． ……………………………6分 ∴该抛物线与x 轴的交点坐标为（－2，0），（1，0）． ……………………………8分 21．（本小题10分）解：（Ⅰ）∵四边形ABED 是圆内接四边形，∴A DEB ∠+∠=180°． ………………………………2分 ∵CED DEB ∠+∠=180°，∴CED A ∠=∠． ………………………………4分 ∵A ∠=68°,∴CED ∠=68°． ………………………………5分 （Ⅱ）连接AE ， ………………………………6分∵DE BE =，∴DE BE =．7分∴1122DAE EAB CAB ∠=∠=∠=⨯68°=34°． ………………………………8分∵AB 为直径，∴AEB ∠=90°． ………………………………9分 ∴AEC ∠=90°．∴C ∠=90°－DAE ∠=90°－34°=56°． ……………………………10分 22．（本小题10分）解：设OC x =， 在Rt △AOC 中， ∵ACO ∠=45°， ∴CAO ∠=45°． ∴ACO CAO ∠=∠．∴OA OC x ==． …………………………3分 在Rt △BOC 中，tan OBBCO OC∠=， ∵BCO ∠=30°， ∴tan OB OC =30°=， …………………………6分 A CBK J H IEG。
人教版2018-2019年第二学期 九年级数学月考试题 含答案
2019年3月份月考九年级数 学 试 题一、选择题（共8小题，每小题3分，共24分）1．反比例函数y ＝－3x(x ＜0)如图所示，则矩形OAPB 的面积是( )A ．3B ．－3 C.32 D ．－32（第3题图)2．如图，将两个形状和大小都相同的杯子叠放在一起，则该实物图的主视图为( )3．如图，在直角坐标系中，有两点A(6，3)，B(6，0)，以原点O 为位似中心，相似比为13，在第一象限内把线段AB 缩小后得到线段CD ，则点C 的坐标为( )A ．(2，1)B ．(2，0)C ．(3，3)D ．(3，1)4．如图，以原点O 为圆心，半径为1的弧交坐标轴于A ，B 两点，P 是AB ︵上一点(不与A ，B 重合)，连接OP ，设∠POB ＝α，则点P 的坐标是( )A ．(sin α，sin α)B ．(cos α，cos α)C ．(cos α，sin α)D ．(sinα，cos α)第4题图)第5题图)第6题图)5．如图，AB 是⊙O 的直径，D ，E 是半圆上任意两点，连接AD ，DE ，AE 与BD 相交于点C ，要使△ADC 与△BDA 相似，可以添加一个条件．下列添加的条件中错误的是( )A ．∠ACD ＝∠DAB B ．AD ＝DEC ．AD ·AB ＝CD ·BD D ．AD 2＝BD ·CD6．如图，一次函数y 1＝k 1x ＋b 的图象和反比例函数y 2＝k 2x 的图象交于A(1，2)，B(－2，－1)两点，若y 1＜y 2，则x 的取值范围是( )A ．x ＜1B ．x ＜－2C ．－2＜x ＜0或x ＞1D ．x ＜－2或0＜x ＜17．如图，有一轮船在A 处测得南偏东30°方向上有一小岛P ，轮船沿正南方向航行至B 处，测得小岛P 在南偏东45°方向上，按原方向再航行10海里至C 处，测得小岛P 在正东方向上，则A ，B 之间的距离是( )A ．103海里B ．(102－10)海里C ．10海里D ．(103－10)海里,（第7题） （第8题第11题第128．如图，正方形ABCD 的对角线AC 与BD 相交于点O ，∠ACB 的角平分线分别交AB ，BD 于M ，N 两点．若AM ＝2，则线段ON 的长为( )A.22 B.32 C ．1 D.62二、填空题（本大题共8个小题，每小题3分，共24分）9．△ABC 中，∠A ，∠B 都是锐角，若sin A ＝32，cos B ＝12，则∠C ＝ ．10．已知点A(－1，y 1)，B(－2，y 2)和C(3，y 3)都在反比例函数y ＝kx(k<0)的图象上，则y 1，y 2，y 3的大小关系为__ ．(用“<”连接)11．如图，P(12，a)在反比例函数y ＝60x 的图象上，PH ⊥x 轴于点H ，则tan ∠POH 的值为____．第13题) 第14题 第15题图)12．如图，▱ABCD 中，点E 是边BC 上一点，AE 交BD 于点F ，若BE ＝2，EC ＝3，△BEF 的面积是1，则▱ABCD 的面积为_ _．13．全球最大的关公塑像矗立在荆州古城东门外，如图，张三同学在东门城墙上C 处测得塑像底部B处的俯角为18°48′，测得塑像顶部A 处的仰角为45°，点D 在观测点C 正下方城墙底的地面上，若CD＝10米，则此塑像的高AB 约为____米．(参考数据：tan78°12′≈4.8)14. 如图是一个几何体的三视图，已知主视图和左视图都是边长为2的等边三角形，则这个几何体的表面积为 .15．如图是由一些大小相同的小正方体搭成的几何体的主视图和俯视图，则搭成该几何体的小正方体最多是____个．16．如图，在△ABC 中，AB ＝AC ＝10，点D 是边BC 上一动点(不与B ，C 重合)，∠ADE ＝∠B ＝α，DE交AC 于点E ，且cos α＝45.下列结论：①△ADE ∽△ACD ；②当BD ＝6时，△ABD 与△DCE 全等；③△DCE为直角三角形时，BD 为8或252；④0＜CE ≤6.4.其中正确的结论是 .(填序号) 第16题图)三、解答题（共8题，共72分） 17．（本题8分）解下列方程： (1). 2sin 60°－4cos 230°＋sin 45°·tan 60°； (2). (－2018)0＋|1－3|－2sin60°＋2tan45°－4cos30°.18．(8分)如图是由两个长方体组合而成的一个立体图形的三视图，根据图中所标尺寸(单位：mm )，求这个立体图形的表面积．19．(9分)如图，△ABC 中，A(－4，4)，B(－4，－2)，C(－2，2)．(1)请画出将△ABC 向右平移8个单位长度后的△A 1B 1C 1； (2)求出∠A 1B 1C 1的余弦值；(3)以O 为位似中心，将△A 1B 1C 1缩小为原来的12，得到△A 2B 2C 2，请在y 轴右侧画出△A 2B 2C 2.20．(8分)如图，在平面直角坐标系x Oy 中，一次函数y ＝kx ＋b 的图象与反比例函数y ＝mx 的图象交于A(2，3)，B(－3，n)两点．(1)求一次函数和反比例函数的解析式；(2)若P 是y 轴上一点，且满足△PAB 的面积是5，直接写出OP 的长．20题21题22题 21．(8分)如图，某塔观光层的最外沿点E 为蹦极项目的起跳点．已知点E 离塔的中轴线AB 的距离OE 为10米，塔高AB 为123米(A B 垂直地面BC)，在地面C 处测得点E 的仰角α＝45°，从点C 沿CB方向前行40米到达D 点，在D 处测得塔尖A 的仰角β＝60°，求点E 离地面的高度EF.(结果精确到1米，参考数据2≈1.4，3≈1.7)22．(9分)如图，在△ABC 中，∠ABC ＝90°，BC ＝3，D 为AC 延长线上一点，AC ＝3CD ，过点D 作DH ∥AB ，交BC 的延长线于点H.(1)求BD ·cos ∠HBD 的值； (2)若∠CBD ＝∠A ，求AB 的长．23．(10分)如图，以点O 为圆心，AB 长为直径作圆，在⊙O 上取一点C ，延长AB 至点D ，连接DC ，过点A 作⊙O 的切线交DC 的延长线于点E ，且∠DCB ＝∠DAC.(1)求证：CD 是⊙O 的切线；(2)若AD ＝6，tan ∠DCB ＝23，求AE 的长．（23题）（24题）24．(12分) (12分)如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝8，B C ＝6，CD ⊥AB 于点D.点P从点D 出发，沿线段DC 向点C 运动，点Q 从点C 出发，沿线段CA 向点A 运动，两点同时出发，速度都为每秒1个单位长度，当点P 运动到C 时，两点都停止．设运动时间为t 秒．(1)求线段CD 的长；(2)设△CPQ 的面积为S ，求S 与t 之间的函数关系式，并确定在运动过程中是否存在某一时刻t ，使得S △CPQ ∶S △ABC ＝9∶100？若存在，求出t 的值；若不存在，说明理由；(3)当t 为何值时，△CPQ 为等腰三角形？九年级数学参考答案一、选择题（共8小题，每小题3分，共24分）题号 1 2 3 4 5 6 7 8 答案ABACCDDC二、填空题（共8小题，每小题3分，共24分） 9．60° 10．y 3＜y 2＜y 1_ 11．51212. 13，5814．_3π15． 716．①②③④三、解答题（共8题，共72分） 17．解：(1) 解：原式＝2×32－4×(32)2＋22×3＝6－3. (2) 解：原式＝1＋3－1－2×32＋2×1－4×32＝2－2 3. 18．解：根据三视图可得：上面的长方体长4 mm ，高4 mm ，宽2 mm ，下面的长方体长6 mm ，宽8 mm ，高 2 mm ，∴立体图形的表面积是4×4×2＋4×2×2＋4×2＋6×2×2＋8×2×2＋6×8×2－4×2＝200(mm 2)19．解： (1)△A 1B 1C 1如图所示．(2)B 1C 1＝22＋42＝2 5，cos ∠A 1B 1C 1＝42 5＝2 55.(3)△A 2B 2C 2如图所示．20．解：(1)y ＝6x，y ＝x ＋1 (2)对于一次函数y ＝x ＋1，令x ＝0求出y ＝1，即该函数与y 轴的交点为C (0，1)，∴OC ＝1，根据题意得S △ABP ＝12PC ×2＋12PC ×3＝5，解得PC ＝2，则OP ＝OC ＋PC ＝1＋2＝3或OP ＝PC －OC ＝2－1＝12１．解：在直角△ABD 中，BD ＝AB tan β＝123tan60°＝413(米)，则DF ＝BD －OE ＝413－10(米)，CF ＝DF ＋CD ＝413－10＋40＝413＋30(米)，则在直角△CEF 中，EF ＝CF ·tan α＝413＋30≈41×1.7＋30＝99.7≈100(米)，则点E 离地面的高度EF 是100米．22．解： (1)∵DH ∥AB ，∴∠BHD ＝∠ABC ＝90°，∴△ABC ∽△DHC ，∴AC CD ＝BCCH＝3, ∴CH ＝1，BH ＝BC ＋CH ＝4，在Rt △BHD 中，cos ∠HBD ＝BHBD，∴BD ·cos ∠HBD ＝BH ＝4(2)∵∠CBD ＝∠A ，∠ABC ＝∠BHD ，∴△ABC ∽△BHD ，∴BC HD ＝AB BH ，∵△ABC ∽△DHC ，∴AB DH ＝ACCD ＝3，∴AB ＝3DH ，∴3DH ＝3DH4，解得DH ＝2，∴AB ＝3DH ＝3×2＝6，即AB 的长是623．解： (1)连接OC ，OE ，∵AB 为直径，∴∠ACB ＝90°，即∠BCO ＋∠ACO ＝90°，又∵∠DCB ＝∠CAD ，∠CAD ＝∠ACO ，∴∠ACO ＝∠DCB ，∴∠DCB ＋∠BCO ＝90°，即∠DCO ＝90°，∴CD 是⊙O 的切线(2)∵EA 为⊙O 的切线，∴EC ＝EA ，EA ⊥AD ，OE ⊥AC ，∴∠BAC ＋∠CAE ＝90°，∠CAE ＋∠OEA ＝90°，∴∠BAC ＝∠OEA ，∴∠DCB ＝∠OEA.∵tan ∠DCB ＝23，∴tan ∠OEA ＝OA AE ＝23，易证Rt △DCO ∽Rt △DAE ，∴CDDA ＝OC AE ＝OD DE ＝23，∴CD ＝23×6＝4，在Rt △DAE 中，设AE ＝x ，∴(x ＋4)2＝x 2＋62，解得x ＝52，即AE 的长为5224．解：(1)线段CD 的长为4.8(2)过点P 作PH ⊥AC ，垂足为H ，由题意可知DP ＝t ，CQ ＝t ，则CP ＝4.8－t.由△CHP ∽△BCA 得PH AC ＝PC AB ，∴PH 8＝4.8－t 10，∴PH ＝9625－45t ，∴S △CPQ ＝12CQ ·PH ＝12t (9625－45t )＝－25t 2＋4825t.设存在某一时刻t ，使得S △CPQ ∶S △ABC ＝9∶100.∵S △ABC ＝12×6×8＝24，且S △CPQ ∶S △ABC ＝9∶100，∴(－25t 2＋4825t )∶24＝9∶100，整理得5t 2－24t ＋27＝0，即(5t －9)(t －3)＝0，解得t ＝95或t ＝3，∵0≤t ≤4.8，∴当t ＝95或t＝3时，S △CPQ ∶S △ABC ＝9∶100(3)①若CQ ＝CP ，则t ＝4.8－t.解得t ＝2.4；②若PQ ＝PC ，作PH ⊥QC 于点H ，∴QH ＝CH ＝12QC ＝t 2，∵△CHP ∽△BCA ，∴CH BC ＝CPAB ，∴t 26＝4.8－t 10，解得t ＝14455； ③若QC ＝QP ，过点Q 作QE ⊥CP ，垂足为E ，同理可得t ＝2411.综上所述：当t 为2.4或14455或2411时，△CPQ 为等腰三角形。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
密封线学校：班级：姓名：考号：2018-2019学年度第二学期学业水平模拟考试九年级数学试卷（满分：120分考试时间：120分钟）真情提示：亲爱的同学，欢迎你参加本次考试，祝你答题成功！本试题分第Ⅰ卷和第Ⅱ卷两部分，共有24道题．第Ⅰ卷1—8题为选择题，共24分；第Ⅱ卷9—14题为填空题，15题为作图题，16—24题为解答题，共96分．要求所有题目均在答题卡上作答，在本卷上作答无效．第Ⅰ卷一、选择题（本题满分24分，共有8道小题，每小题3分）下列每小题都给出标号为A、B、C、D的四个结论，其中只有一个是正确的．每小题选对得分；不选、选错或选出的标号超过一个的不得分．1.如图，数轴上有A，B，C，D这4个点，其中表示互为相反数的点是( ).A.点A与点DB.点A与点CC.点B与点DD.点B与点C2.下列图形中，既是轴对称图形又是中心对称图形的是( ).A B C D3.青岛“最美地铁线”、连接崂山和即墨的地铁11号线全长约58 km，数据58 km用科学记数法可表示为( )m．A.0.58×105B.58×104C.5.8×104D.5.8×1054.计算（2a3b2）2÷ab2的结果为( ).A.2a2B.2a5b2C.4a5b2D.4a4b25.如图，△ABC的顶点坐标分别为A(4，6)，B(5，2)，C(2，1)，如果将△ABC绕点C按逆时针方向旋转90°，得到△A′B′C，那么点A，B的对应点A′，B′的坐标分别是( ).A.（﹣3，3），（﹣2，4）B.（﹣3，3），（1，4）C.（3，﹣3），（﹣2，4）D.（3，﹣3），（1，4）6.如图，若AB是⊙O的直径，CD是⊙O的弦，∠ABD=50º，则∠BCD的度数为( ).A.40ºB.45ºC.55ºD.75º7.已知反比例函数kyx=的图象如图所示，则二次函数2224y kx x k=-+的图象大致为( ).8.我们知道,一元二次方程x2= -1没有实数根,即不存在一个实数的平方等于-1.若我们规定一个新数i,使其满足i2= -1(即x2= -1方程有一个根为i),并且进一步规定：一切实数可以与新数进行四则运算,且原有的运算法则仍然成立，于是有i1=i，i2= -1，i3=i2·i=(-1)·i=-i，i4=(i2)2=(-1)2=1，从而对任意正整数n，我们可得到i4n+1=i4n·i=(i4)n·i，同理可得i4n+2=-1，i4n+3=-i，i4n=1，那么i+i2+i3+i4+…+i2018+i2019的值为().A.0B.-1C.iD.1座号密封线 第Ⅱ卷二、填空题（本题满分18分，共有6道小题，每小题3分） 9.化简：()282--= .10.甲、乙两位同学参加学校运动会铅球项目选拔赛，各投掷6次，记录成绩，计算平均数和方差的结果为10.5x =甲，10.5x =乙，20.61s =甲，20.50s =乙，则成绩较稳定的是 （填“甲”或“乙”）.11.已知一元二次方程01582=+-x x 的两个解恰好分别是等腰△ABC 的底边长和腰长，则△ABC 的周长为 .12.某内陆城市为了落实国家“一带一路”战略，促进经济发展，增强对外贸易的竞争力，把距离港口420 km 的普通公路升级成了同等长度的高速公路，结果汽车行驶的平均速度比原来提高了50%，行驶时间缩短了 2 h ．求汽车原来的平均速度.设汽车原来的平均速度为x km/h ，则可列方程为____________________.13.如图，C 为半圆内一点，O 为圆心，直径AB 的长为2 cm ，∠BOC ＝60°，∠BCO ＝90°，将△BOC 绕圆心O 逆时针旋转至△B ′OC ′位置，点C ′在OA 上，则边BC 扫过区域（图中阴影部分）的面积为 cm 2．B'C'COAEPBACD第13题图 第14题图14.如图，在Rt △ABC 中，∠ACB =90°，AC =2，BC =4，点D 在边AB 上，以CD 为折痕将△CBD 折叠，得到△CPD ，CP 与边AB 交于点E .若△DEP 为直角三角形，则BD 的长是 .三、作图题（本题满分4分，用圆规、直尺作图，不写作法，但要保留作图痕迹） 15.已知：如图，四边形ABCD ．求作：点P ，使PC ∥AB ，且点P 到点A 和点B 的距离相等．BCD结论：四、解答题（本题满分74分，共有9道小题） 16.（本小题满分8分，每题4分）（1）化简：221122121a a a a a a --⎛⎫+÷- ⎪-+⎝⎭. （2）解不等式组：17.（本小题满分6分）在学校开展的数学活动课上,小明和小刚制作了一个正三棱锥(质量均匀，四个面完全相同),并在各个面上分别标记数字1，2，3，4，游戏规则如下：每人投掷三棱锥一次,并记录底面的数字,如果底面数字的和为奇数，那么小明赢；如果底面数字的和为偶数,那么小刚赢. （1）请用列表或画树状图的方法表示上述游戏中的所有可能结果.（2）请分别求出小明和小刚能赢的概率,并判断此游戏对双方是否公平.18.（本小题满分6分）为了丰富校园文化，某校决定举行学生趣味运动会，将比赛项目确定为袋鼠跳、夹球跑、跳大绳、绑腿跑和拔河赛5项，为了解学生对这5项运动的喜欢情况，随机调查了该校部分学生最喜欢的一种项目（每名学生必选且只能选择5项中的一种），并将调查结果绘制成如图所示的不完整的统计图表：()21,321 4.x x x x <+⎧⎪⎨--≤⎪⎩密封线 学校： 班级： 姓名： 考号：根据图表中提供的信息解答下列问题：（1）求a ，b 的值.（2）请将条形统计图补充完整.（3）根据调查结果，请你估计该校2500名学生中有多少名学生最喜欢绑腿跑．19.（本小题满分6分）共享单车为人们的生活带来了极大的便利.如图，一辆单车放在水平的地面上，车把头下方A 处与坐垫下方B 处在平行于地面的水平线上，A ，B 之间的距离为49 cm ，现测得AC ，BC 与AB 的夹角分别为45°，68°.若点C 到地面的距离CD 为28 cm ，坐垫中轴E 处与点B 的距离BE 为5 cm ，求点E 到地面的距离.（结果保留一位小数，参考数据：sin68°≈0.93，cos68°≈0.37，tan68°≈2.50.）20.（本小题满分8分）如图，在平面直角坐标系xOy 中，一次函数y 1=ax ＋b （a ，b 为常数，且a ≠0）与反比例函数2my x=（m 为常数，且m ≠0）的图象交于点A (－4，2)，B (2，n )．（1）求反比例函数和一次函数的解析式. （2）连接OA ，OB ，求△AOB 的面积.（3）直接写出当0＜y 1＜y 2时，自变量x 的取值范围．21.（本小题满分8分）如图，在△ABC 中，AD 是BC 边上的中线，E 是AD 的中点，过点A 作BC 的平行线，交BE 的延长线于点F ，连接CF ．（1）求证：AF=DC ．（2）△ABC 满足什么条件时，四边形ADCF 是矩形？证明你的结论． EDCBF22.（本小题满分10分）某文具厂商设计了一款成本为18元的文具盒，投放市场进行试销，经过调查，得到每月销售量 y (万件)与销售单价x (元)之间的部分数据如下：销售单价x (元) … 20 25 30 35 … 每月销售量y (万件)…60504030…（1）求每月销售量y (万件)与销售单价x (元)之间的函数关系式． （2）求每月的利润z (万元)与销售单价x (元)之间的函数关系式．（3）根据相关部门规定，这种文具盒的销售利润率不能高于50%，而且该文具厂制造这种文具盒每月的制造成本不能超过900万元．那么，当销售单价定为多少元时，厂商每月能获得最大利润？最大利润是多少？（利润=售价-制造成本）密封线23.（本小题满分10分）【问题提出】|a-1|+|a-2|+|a-3|+…+|a-2019|的最小值是多少？【阅读理解】为了解决这个问题，我们先从最简单的情况入手.|a|的几何意义是a这个数在数轴上对应的点到原点的距离，那么|a-1|可以看作a这个数在数轴上对应的点到1的距离；|a-1|+|a-2|就可以看作a这个数在数轴上对应的点到1和2两个点的距离之和.下面我们结合数轴研究|a-1|+|a-2|的最小值.我们先看a表示的点可能的3种情况，如图所示：图①图②图③（1）如图①，a在1的左边，从图中很明显可以看出a到1和2的距离之和大于1.（2）如图②，a在1，2之间(包括在1，2上)，可以看出a到1和2的距离之和等于1.（3）如图③，a在2的右边，从图中很明显可以看出a到1和2的距离之和大于1.因此，我们可以得出结论：当a在1，2之间(包括在1，2上)时，|a-1|+|a-2|有最小值1.【问题解决】（1）|a-2|+|a-5|的几何意义是 .请你结合数轴探究：|a-2|+|a-5|的最小值是 .（2）|a-1|+|a-2|+|a-3|的几何意义是 .请你结合数轴探究：|a-1|+|a-2|+|a-3|的最小值是，并在图④的数轴上描出得到最小值时a所在的位置，由此可以得出a为 .图④（3）求出|a-1|+|a-2|+|a-3|+|a-4|+|a-5|的最小值.（4）求出|a-1|+|a-2|+|a-3|+…+|a-2019|的最小值.【拓展应用】请在图⑤的数轴上表示出a，使它到2，5的距离之和小于4，并直接写出a的范围.图⑤24.（本小题满分12分）如图，四边形ABCD为矩形，AB=4 cm，AD=3 cm，动点M，N分别从点D，B同时出发，都以1 cm/s的速度运动，点M沿DA向终点A运动，点N沿BC向终点C运动.过点N作NP⊥BC，交AC于点P，连接MP.已知动点运动了t s (0<t<3) .（1）当t为多少时，PM∥AB？（2）若四边形CDMP的面积为S，试求S与t的函数关系式.（3）在运动过程中，是否存在某一时刻t使四边形CDMP的面积与四边形ABCD的面积比为3:8？若存在，请求出t的值；若不存在，请说明理由.（4）在点M，N运动过程中，△MPA能否成为一个等腰三角形？若能，求出所有可能的t值；若不能，试说明理由．PNCAM。